[a]Biplab Dey, on behalf of the LHCb collaboration
Angular analyses of rare decays at the LHC
Abstract
Loop-suppressed penguin transitions are sensitive to heavy New Physics particles propagating inside the loops. Thanks to the large sample sizes from the LHC, we are able to perform multidimensional angular analyses that are sensitive to interferences between the Standard Model and New Physics terms. This article surveys the latest results, primarily from LHCb, on electroweak and radiative penguins.
1 Introduction and theory

In the Standard Model (SM), the flavor-changing neutral current process is forbidden at the tree-level and proceeds only via loop-suppressed diagrams as shown in Fig. 1. These provide excellent avenues to probe New Physics (NP) contributions that can enter either in loop- or tree-level processes such as via Leptoquarks (LQ) or heavy boson, as shown in Fig. 1. This article focuses on the electroweak (EWP) and radiative (Rad) penguin diagrams, but gluonic penguins can also be an important NP source. A convenient theoretical formalism to study such decays is to regard the SM as a low energy effective field theory containing dimension local operators from renormalizability requirements. Higher dimensional operators can be added with an appropriate cutoff scale , as
| (1) |
whereby the NP amplitudes have behavior in the energy, : divergent at high energies, but suppressed at . Most relevant for rare decays are operators that yield . The basis comprises 10 operators [1]: (4-quark tree), (4-quark penguins) and (gluonic penguin) that are suppressed for the EWP/Rad modes. The dominant left-handed contributions are from the electromagnetic dipole and weak vector (axialvector) operators
| (2) |
The corresponding right-handed (quark side) operators are suppressed in the SM, but can be enhanced in NP scenarios. The dimensionless couplings (Wilson coefficients) associated with the operators in Eq. 2 encode the short distance physics. They are calculated at the scale by integrating out the heavy degrees of freedom from the full theory and evolving to the scale using renormalization group equations. The total amplitudes also contains the long-distance physics (QCD/hadronization) which mostly comes from local form-factors (FFs) that are computed from lattice QCD and other theory tools, but can get important non-local contributions (rescattering, charm loops) that are hard to estimate theoretically.
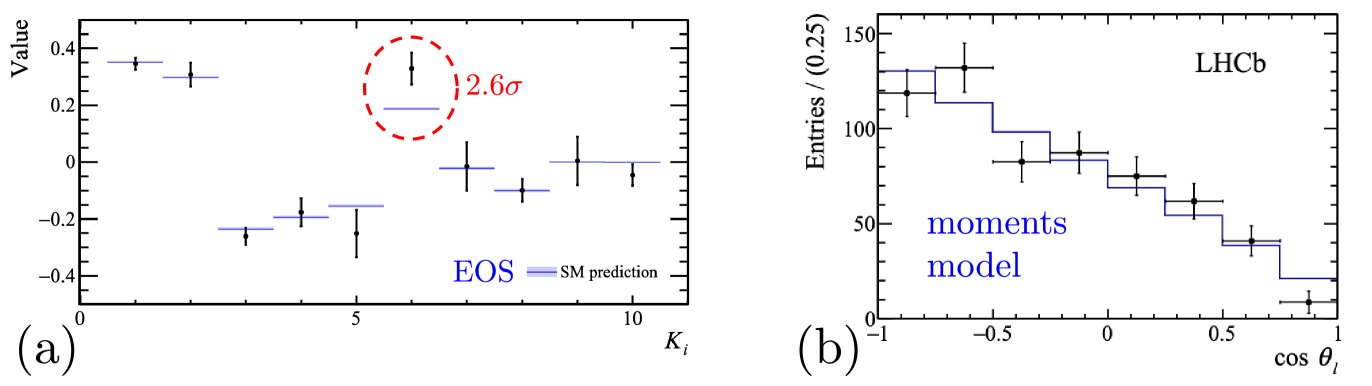
Thanks to the large samples available at the LHC, a comprehensive effort on multidimensional angular analyses in and is ongoing. These offer a rich set of angular observables sensitive to . The thrust has been to identify and probe “theoretically clean observables” with reduced dependence on the QCD contributions that often form the largest theory uncertainties. The angles for a typical 4-body final state decay is shown in Fig. 2 for ; the two other kinematic variables being and . For an unpolarized parent (or spin-0 mesons), is set to 0 and is the single azimuthal angle between the dilepton and dihadron decay planes. Equivalent variables apply for and .

2 Electroweak penguins
2.1 The golden channel:
has been a gold-plated channel [1] since the -factory era due to the relatively narrow resonance. Especially in the low regime, where the recoiling has a large -factor in the parent frame, QCD sum rules on the light-cone (LCSR) affords control over the FF calculations. However, with the BaBar/Belle statistics, only 1-dimensional angular analyses in either the lepton or hadron helicity angles ( or ) were possible [3]. Full 3-dimensional analysis in in bins was possible only with the advent of LHCb. For instance, while the full BaBar dataset had events, the existing Run1+2 LHCb dataset already includes clean signal events for this muonic mode. On the other hand, -factories, including Belle II, have complementary advantages, with better reconstruction for the isospin modes as well the dielectron channels.
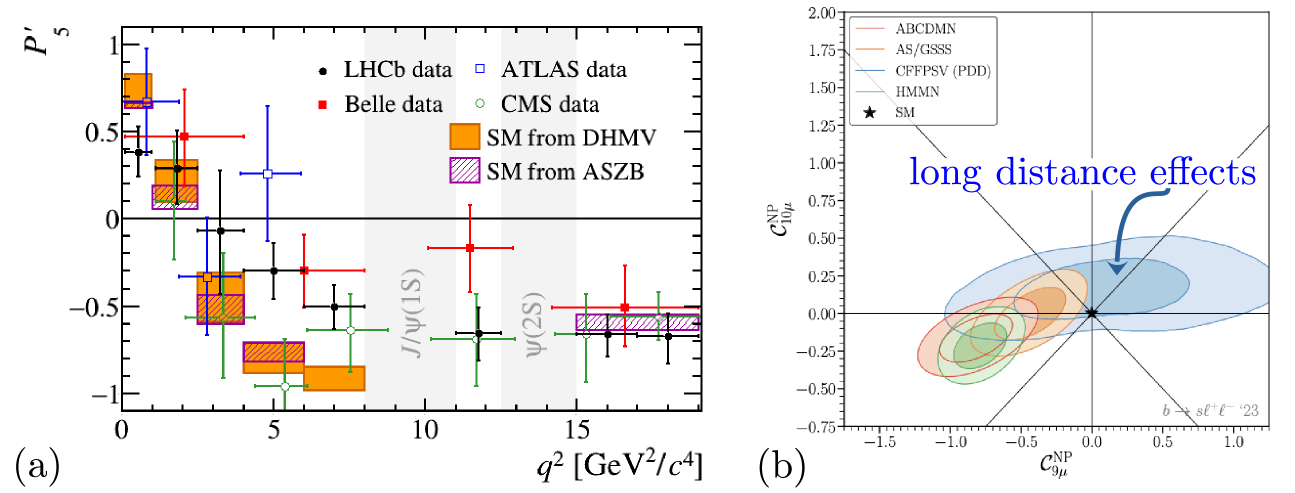
An important result from the muonic analyses at LHCb is tension with SM predictions in the angular observable [4] (see Fig. 3a). Similar tensions have also been seen in [5] and [6]. A related tension is observed in the overall branching fractions in several modes which tend to consistently lie lower than the SM predictions [7, 8, 9]. Competitive results have also come from ATLAS/CMS [10, 11, 12] where the advantage is higher overall luminosity, but the disadvantage is the limited -physics trigger bandwidth and lack of a RICH detector for separation. Numerous global fits with different data subsets, statistical methods and theory priors have been performed [2] pointing to a preferred negative . The major point of contention, however, has been the effect of non-factorizable long-distance contributions due to soft+hard gluons from charm-loops that can mimic NP effects (see Fig. 3b). To constrain the non-factorizable part in a data-driven fashion, LHCb has performed an unbinned angular analysis [13, 14] using the same dataset as in Ref. [5]. The underlying transversity amplitudes are
| (3) |
where are the usual local FFs (taken from LCSR and lattice QCD) and are the new non-factorizable part which are extracted from a -dependent parameterization. The values of are taken from theory, while allowing for to be floated. The results of the fit are shown in Fig. 4. Good consistency is found in the extracted binned observables compared to Ref. [5]. The overall tension with the SM is reduced to in , and in global fits. The full Run 1+2 analysis and more precise theory FFs will improve upon these results.
2.2 Access to tensor states in
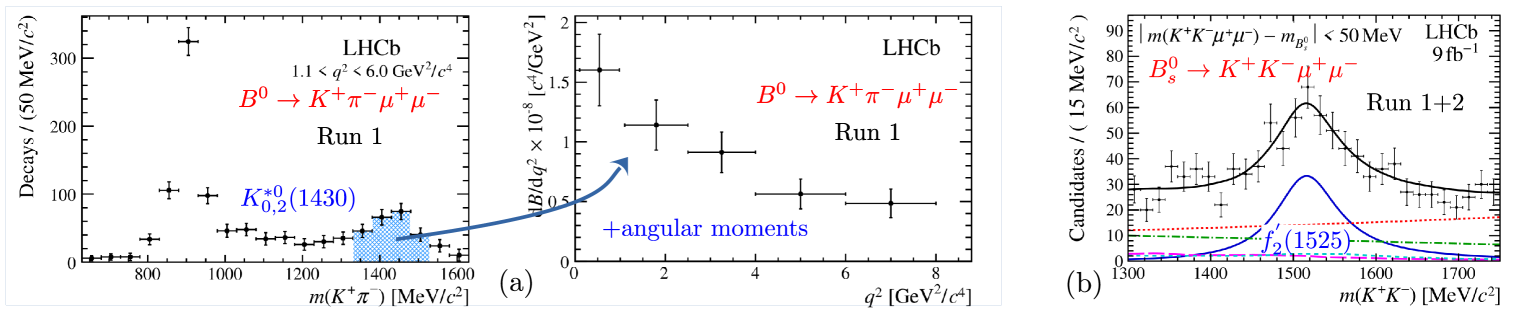
While most of the theory and experimental investigations have focused on the ground state vector states and in -meson decays, LHCb has also probed the excited [15] and [7], including an angular moments analysis [16] for the former, to separate the -, - and -wave states. The results are shown in Fig. 5. The theory interpretation however will require reliable FFs for decays to these excited states.
2.3 Angular analysis of
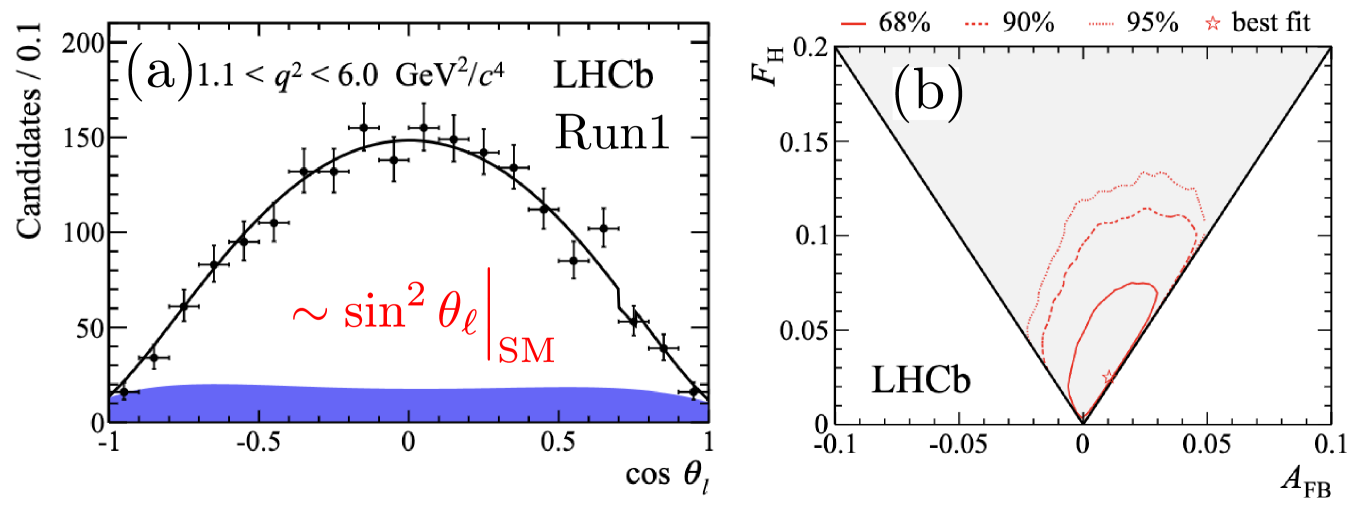
For the 3-body final state , only the lepton helicity angle, , can be defined and the SM predicts an almost pure distribution save for small effects due to the muon mass. The angular distribution is be sensitive to new scalar and tensor operators via the new terms and :
| (4) |
Figure 6 shows the results of the fit to Run 1 data for both [17], subject to the constraints , , such that the rate in Eq. 4 is positive. The extracted and in different bins are also consistent with SM.
2.4 moments analysis
LHCb is unique among the -factories to have access to all -hadron species, including large samples of baryons. Therefore it is possible to probe penguin decays in the baryonic sector as well. For transition, the narrow state allows lattice QCD calculations [18] for the FFs. For a given value of , the decay rate for polarized and depends on five angles, (see Fig. 2) and is expanded in an orthonormal angular basis as
| (5) |
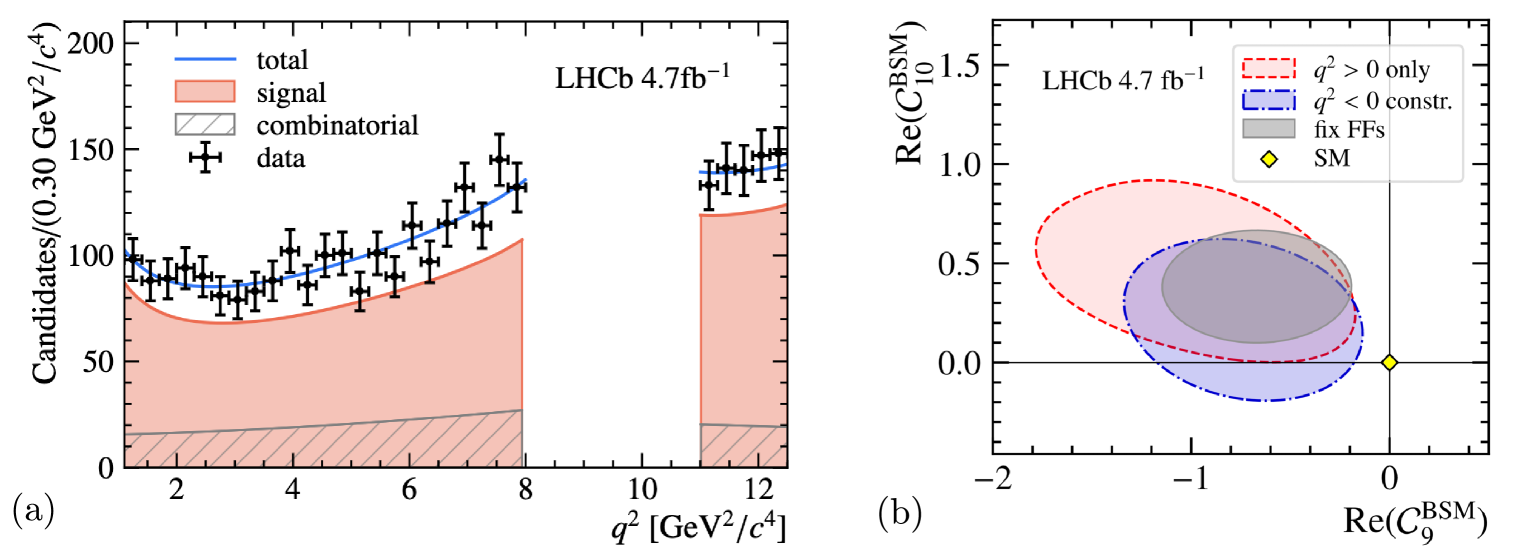
The moments can be related to more familiar observables such as forward-backward asymmetries in the angles: , , . If the is unpolarized, only the first 10 moments are non-zero [19]. Due to the long-lived nature of the , its reconstruction in LHCb is somewhat non-trivial. At low , the Run 1 analysis [8] found very few events. Therefore the analysis using Run 1 + partial Run 2 (collected between 2011-16) [20] focused on the high- region, GeV2. The results are shown in Fig. 7. The SM predictions are taken from the EOS [19] software package and show a slight tension with the data in the observable.
2.5 Differential cross-sections for
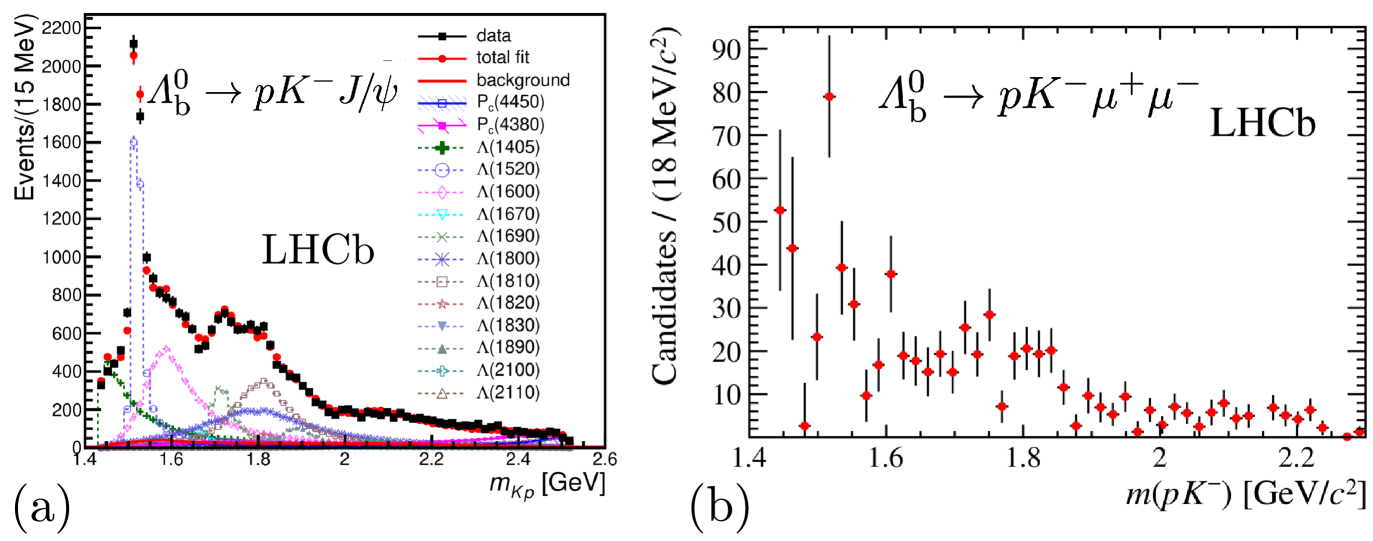
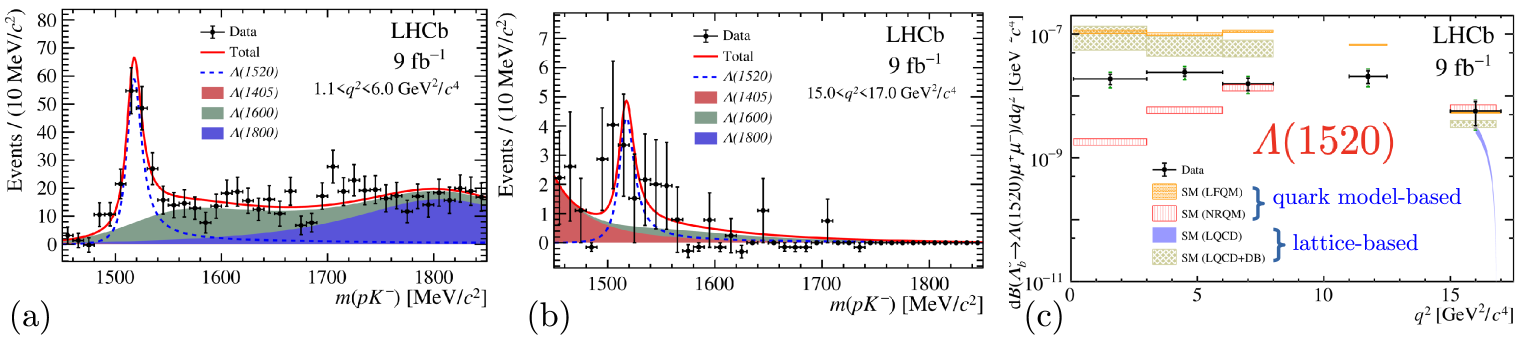
The first observation of decay using LHCb Run 1 data [22] demonstrated a rich spectrum. The comparison between the resonant and non-resonant spectra is shown in Fig. 8. Employing the full Run 1+2 datasets, LHCb has examined the region around the narrow resonance. Integrating over the angles and including the resonances , , and , 1-dimensional fits are performed in . Differential cross-sections for the decay are also provided [23] that show large discrepancies with theory calculations in the low region (see Fig. 9).
3 Radiative penguins
In the SM, due to the left-handed nature of the weak interaction, the photon from a is almost purely left-handed; the right-handed component is suppressed () and is a sensitive NP probe. However, one needs angular analyses to extract the interferences. LHCb probes this in several ways: very low angular analysis of [24] and ; angular analysis of [25],; time-dependent CP violation of [26] and ; angular analyses of [27].
3.1 Angular analysis of
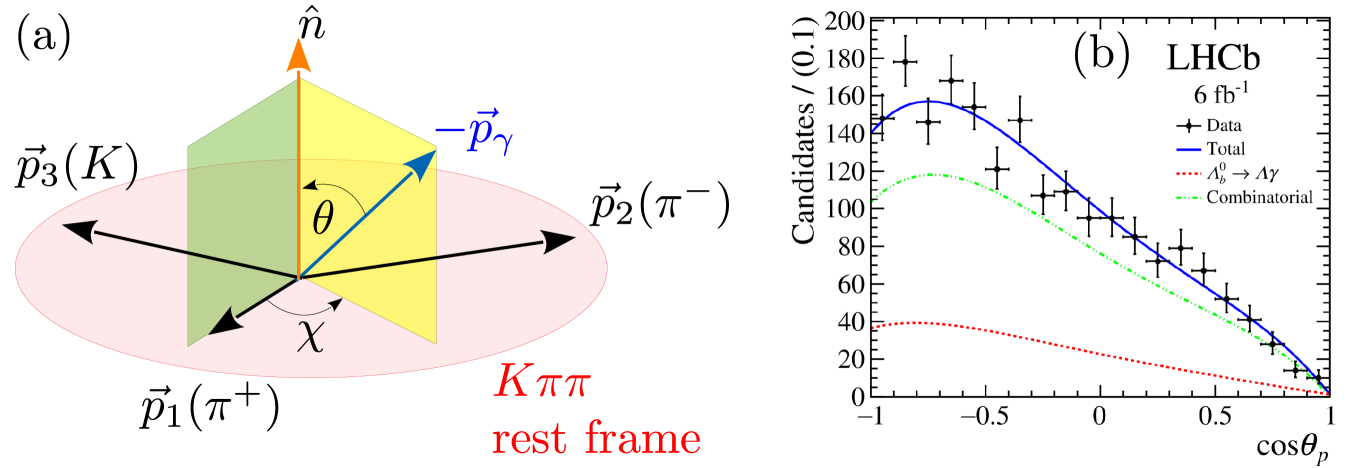
To measure the photon polarization in , the hadronic system must undergo a 3-body decay, so that the normal to the plane defines a preferred direction and the up-down asymmetry is proportional to the photon polarization, . For example, this has been utilized in [25] as shown in Fig 10a. In such cases, due to poor knowledge of the resonant structures in the system and thereby the hadronic current , the proportionality factor remains unknown and can still not be extracted out. An exception is the 2-body decay of , where the self-analyzing nature of the polarization provides the preferred direction. Moreover, the differential rate is where the decay asymmetry parameter is known quite precisely [28] and thereby can be extracted from a fit to the slope, as shown in Fig 10b. Experimentally, is challenging due to lack of a reconstructible secondary vertex for the decay. Employing dedicated reconstruction to reject the high background, the first observation with Run 2 2016 data was reported in Ref. [29] and the polarization measurement with full Run 2 was reported in Ref. [27]. The measured value of is compatible with the SM expectation of 1 and from global fits, reducing a 4-fold ambiguity in the phase to a 2-fold ambiguity.
3.2 Angular analysis of
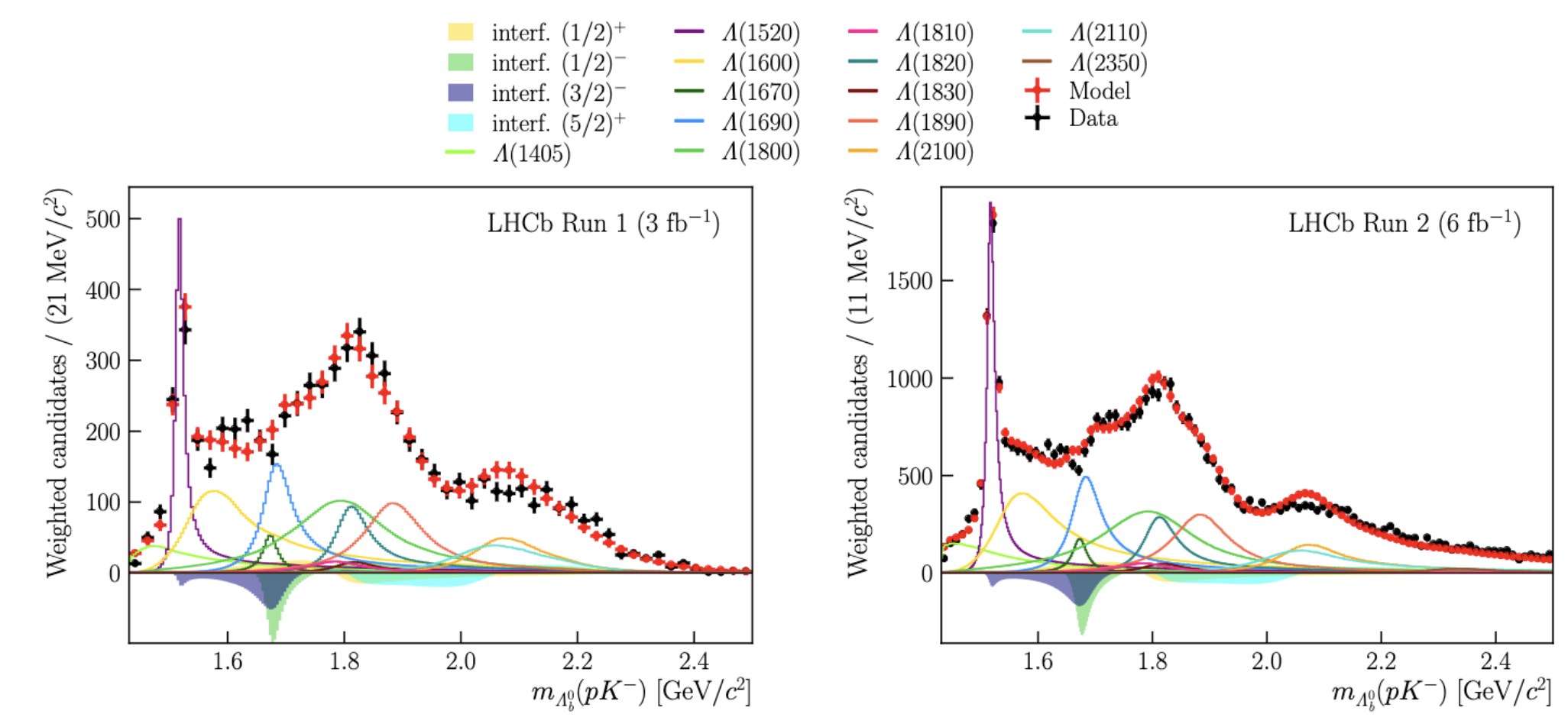
As for the electroweak penguin case in Sec. 2.5, for the radiative decay, the system is dominated by a large number of overlapping resonances. Employing the full Run1+2 data, LHCb has performed a 2-dimensional angular analysis of this mode in . All well-established states [28] are included in an isobar model with Breit-Wigner lineshapes incorporating mass-dependent widths. The only exception is the resonance where a two-pole Flatte-form is used. To reduce the large set of parameters, the maximum orbital angular momentum of the decay is taken to be . The result from such a reduced model is shown in Fig. 11. The fit fractions and interference fit fractions are reported from the amplitude analysis.
4 Summary and outlook
The large existing Run 1+2 data samples at the LHC has already allowed the hitherto (pre-LHC) “rare” decays to be probed in an unprecedented fashion. This will continue into the LHCb upgrade era, with Run 3 having already commenced. Multi-dimensional angular analyses in both the electroweak and radiative penguin sectors have given rise to surprising tensions. A large and mature angular analysis effort exists at LHCb which will continue to be evolve. The thrust will be to include time-dependent CP violation [30] in more rare decay angular analyses, as well as to probe the further Cabibbo-suppressed transitions [31, 32].
References
- [1] W. Altmannshofer, P. Ball, A. Bharucha, A.J. Buras, D.M. Straub and M. Wick, Symmetries and Asymmetries of Decays in the Standard Model and Beyond, JHEP 01 (2009) 019 [0811.1214].
- [2] B. Capdevila, A. Crivellin and J. Matias, Review of Semileptonic Anomalies, Eur. Phys. J. ST 1 (2023) 20 [2309.01311].
- [3] BaBar collaboration, Measurement of Branching Fractions and Rate Asymmetries in the Rare Decays , Phys. Rev. D 86 (2012) 032012 [1204.3933].
- [4] LHCb collaboration, Measurement of -Averaged Observables in the Decay, Phys. Rev. Lett. 125 (2020) 011802 [2003.04831].
- [5] LHCb collaboration, Angular Analysis of the Decay, Phys. Rev. Lett. 126 (2021) 161802 [2012.13241].
- [6] LHCb collaboration, Angular analysis of the rare decay , JHEP 11 (2021) 043 [2107.13428].
- [7] LHCb collaboration, Branching Fraction Measurements of the Rare and - Decays, Phys. Rev. Lett. 127 (2021) 151801 [2105.14007].
- [8] LHCb collaboration, Differential branching fraction and angular analysis of decays, JHEP 06 (2015) 115 [1503.07138].
- [9] LHCb collaboration, Differential branching fractions and isospin asymmetries of decays, JHEP 06 (2014) 133 [1403.8044].
- [10] ATLAS collaboration, Angular analysis of decays in collisions at TeV with the ATLAS detector, JHEP 10 (2018) 047 [1805.04000].
- [11] CMS collaboration, Measurement of angular parameters from the decay in proton-proton collisions at 8 TeV, Phys. Lett. B 781 (2018) 517 [1710.02846].
- [12] CMS collaboration, Angular analysis of the decay B+ K∗(892) in proton-proton collisions at 8 TeV, JHEP 04 (2021) 124 [2010.13968].
- [13] LHCb collaboration, Amplitude analysis of the decay, 2312.09115.
- [14] LHCb collaboration, Determination of short- and long-distance contributions in decays, 2312.09102.
- [15] LHCb collaboration, Differential branching fraction and angular moments analysis of the decay in the region, JHEP 12 (2016) 065 [1609.04736].
- [16] B. Dey, Angular analyses of exclusive with complex helicity amplitudes, Phys. Rev. D 92 (2015) 033013 [1505.02873].
- [17] LHCb collaboration, Angular analysis of charged and neutral decays, JHEP 05 (2014) 082 [1403.8045].
- [18] W. Detmold and S. Meinel, form factors, differential branching fraction, and angular observables from lattice QCD with relativistic quarks, Phys. Rev. D 93 (2016) 074501 [1602.01399].
- [19] D. van Dyk et al., Eos – a hep program for flavor observables, 2016. 10.5281/zenodo.886055.
- [20] LHCb collaboration, Angular moments of the decay at low hadronic recoil, JHEP 09 (2018) 146 [1808.00264].
- [21] LHCb collaboration, Observation of Resonances Consistent with Pentaquark States in Decays, Phys. Rev. Lett. 115 (2015) 072001 [1507.03414].
- [22] LHCb collaboration, Observation of the decay and a search for violation, JHEP 06 (2017) 108 [1703.00256].
- [23] LHCb collaboration, Measurement of the differential branching fraction, Phys. Rev. Lett. 131 (2023) 151801 [2302.08262].
- [24] LHCb collaboration, Strong constraints on the photon polarisation from decays, JHEP 12 (2020) 081 [2010.06011].
- [25] LHCb collaboration, Observation of Photon Polarization in the b→s Transition, Phys. Rev. Lett. 112 (2014) 161801 [1402.6852].
- [26] LHCb collaboration, First experimental study of photon polarization in radiative decays, Phys. Rev. Lett. 118 (2017) 021801 [1609.02032].
- [27] LHCb collaboration, Measurement of the photon polarization in decays, Phys. Rev. D 105 (2022) L051104 [2111.10194].
- [28] Particle Data Group collaboration, Review of Particle Physics, PTEP 2022 (2022) 083C01.
- [29] LHCb collaboration, First Observation of the Radiative Decay , Phys. Rev. Lett. 123 (2019) 031801 [1904.06697].
- [30] LHCb collaboration, Measurement of -violating and mixing-induced observables in decays, Phys. Rev. Lett. 123 (2019) 081802 [1905.06284].
- [31] LHCb collaboration, Observation of the suppressed decay , JHEP 04 (2017) 029 [1701.08705].
- [32] LHCb collaboration, First measurement of the differential branching fraction and asymmetry of the decay, JHEP 10 (2015) 034 [1509.00414].