Antagonistic Phenomena in Network Dynamics
Abstract
Recent research on the network modeling of complex systems has led to a convenient representation of numerous natural, social, and engineered systems that are now recognized as networks of interacting parts. Such systems can exhibit a wealth of phenomena that not only cannot be anticipated from merely examining their parts, as per the textbook definition of complexity, but also challenge intuition even when considered in the context of what is now known in network science. Here we review the recent literature on two major classes of such phenomena that have far-reaching implications: (i) antagonistic responses to changes of states or parameters and (ii) coexistence of seemingly incongruous behaviors or properties—both deriving from the collective and inherently decentralized nature of the dynamics. They include effects as diverse as negative compressibility in engineered materials, rescue interactions in biological networks, negative resistance in fluid networks, and the Braess paradox occurring across transport and supply networks. They also include remote synchronization, chimera states and the converse of symmetry breaking in brain, power-grid and oscillator networks as well as remote control in biological and bio-inspired systems. By offering a unified view of these various scenarios, we suggest that they are representative of a yet broader class of unprecedented network phenomena that ought to be revealed and explained by future research.
Annu. Rev. Condens. Matter Phys. 9, 463 (2018)
I 1. INTRODUCTION
Many systems in nature and society can be conceptualized as a collection of parts coupled through a web of interactions and suitably modeled as a network. A network can be represented as a collection of nodes—e.g., particles, genes, or individuals—connected by links reflecting the interactions between them. Two main lines of research have contributed to the study of such systems: reductionist studies, focused on separating the parts to determine their individual properties; and complex systems research, focused on the whole-system behavior. The emerging field of network science owes its success to the recognition that collective behavior is largely determined by the network of interactions between the parts. Substantial attention in this field has been dedicated to the study of network structure alone and to efforts to attribute as much as possible of the observed collective behavior to the properties of this structure. Attempts to infer the collective behavior solely from the properties of the parts are prone to failure, and this has long been appreciated in condensed matter physics and other fields, which nevertheless does not make those properties unimportant. Here we consider phenomena that depend on both the network structure and the properties of the parts, and are thus determined by the interplay between the network structure and dynamics.
The first part of this article is focused on scenarios in which the removal of resources from a network—e.g., through the removal of nodes and/or links—can in fact improve network function or performance. The notion that “less can be more” has been long appreciated in connection with minimalism in architecture and arts, the paradox of choice in psychology, diminishing returns in economics, calls to stop the seemingly endless gadget feature explosion, and even the rise of microblogs such as Twitter. What is not widely appreciated (albeit common, as we argue) is that a similar notion could govern complex networks, which in many cases have evolved to have more (not less) nodes and links.
The key network property underlying such phenomena is that the equilibrium state spontaneously reached by a decentralized network is not necessarily the global optimum of the system. Thus, even though the removal of resources constrains the solution space, which cannot improve (and generally worsens) the optimum of the objective function, it can counterintuitively do so while bringing the equilibrium state closer to the optimum. In the economics literature this mechanism has been known for at least a century pigou1932economics , and it now forms the basis of the Pigou-Knight-Downs paradox, which describes scenarios in which investment in roads does not improve door-to-door equilibrium speed because it incentivizes people to shift from public transportation to driving (see Figure 1a). The mechanism was rediscovered in different contexts over the years (likely independently), and by the 1950’s variants of it had been reported in the mainstream transportation literature wardrop1952road ; beckmann1956studies . In transportation, the best-known formulation comes from the work of Braess, who in 1968 described what is now known as the Braess paradox Braess1969 ; braess2005paradox . The paradox arises when the addition of an intermediate road to a traffic network—which effectively increases its capacity—has the consequence of increasing rather than decreasing the average travel time between origin and destination even if the total number of cars remains the same (see Figure 1b). Related concepts have been explored in computer science and operations research, where the difference between the equilibrium and the optimum of the objective function (i.e., the travel time in the example just given) is often called the price of anarchy roughgarden2005selfish .
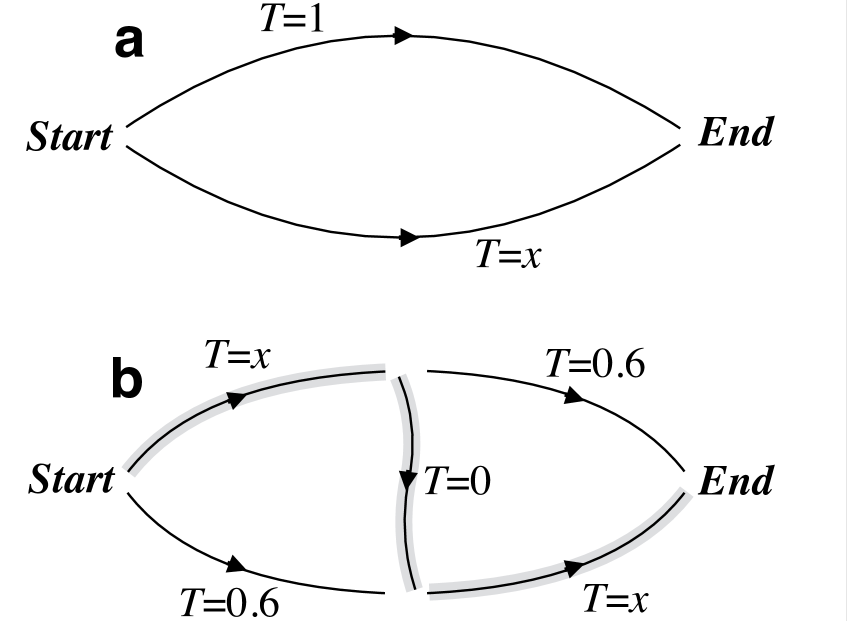
This class of problems also admits a natural formulation in game theory, where they can be formally related to social dilemmas, namely situations in which an agent profits from being selfish unless everyone chooses to be selfish, in which case everyone loses. Indeed, in the example of Figure 1b, it is the selfish routing roughgarden2005selfish of the drivers, who seek to optimize their own travel time with no regard to the travel time of the others, that causes the shift of the system to a less desirable equilibrium characterized by a longer travel time. Once the shift has occurred, no faster route is available to a driver no matter what individual choices the driver may make. In the literature of non-cooperative games nash1950equilibrium , this scenario is known as a Nash equilibrium and is described as a stable state in which no agent can gain from a unilateral change of strategy. In this language, the Braess paradox emerges from the fact that the Nash equilibrium is not necessarily optimal and thus a capacity increase can further lower its fitness. As discussed below, the recent network literature shows that analogous behaviors may be generic in many physical and biological networks, where they give rise to a wealth of seemingly disparate phenomena.
The second part of the article is centered on network phenomena that invoke coexistence of seemingly incompatible properties or behaviors. One may figuratively argue that things that occur and stay together must ultimately fit together. In networks, however, the verification of this principle is far from obvious. For example, the time evolution of two isolated chaotic systems diverges even if they are identical—owing to their inherent sensitive dependence on initial conditions—but when weakly coupled, they can synchronize stably to the exact same trajectory, which may even be a solution of their isolated dynamics pecora1990synchronization . Using synchronization as a model process of behavioral uniformity that can emerge from interactions, below we discuss a selection of phenomena that seem implausible in the absence of detailed analysis.
Before proceeding we note that although it is almost impossible to talk about collective behavior without thinking of the notion popularized by Anderson that “more is different” anderson1972more , the ideas covered here are closer in content to Watts’ notion that the common sense to which our intuition has been trained is not a valid scientific tool in the study of network systems watts2011everything . He argues for the need of a form of “uncommon sense,” which a rigorous wholistic network-based description that integrates structure and dynamics would conceivably help provide. A key difference from Watt’s description is that his examples are mostly in the context of social sciences, where a failure of intuition can be partly attributed to unknowns, while the phenomena we describe here manifest themselves in a form that is counterintuitive even when the mathematical description is assumed to be known, exact, complete, and deterministic.
II 2. ANTAGONISTIC DYNAMICS
Consider a weight supported by a system of two identical springs connected by a linking string, and assume the setup includes two identical slack support strings, as shown in Figure 2. If the linking string is cut, the support strings become taut and, contrary to the common-sense expectation, the weight can rise. This occurs because the removal of the linking string causes the springs to go from a series configuration to a parallel configuration, prompting them to contract. Indeed, initially each spring holds the entire weight , leading to an equilibrium height , where is the spring constant, is the length of the individual unstretched springs, is the length of the linking string, is the length of the individual support strings, and is the amount of slack the support strings have. After the removal of the linking string, each spring holds only half of the weight , which leads to an equilibrium height . It follows that the weight rises by when the linking string is removed, which is positive if is chosen to be smaller than .
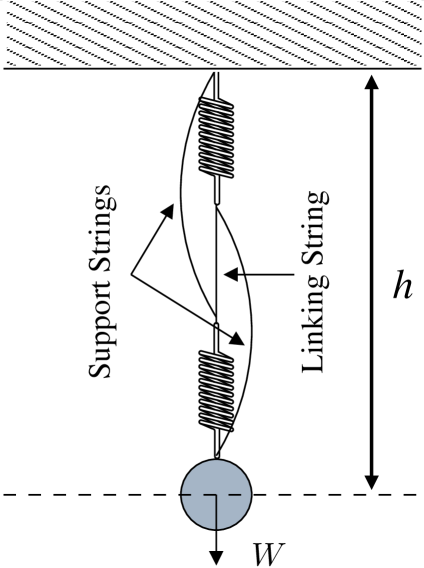
This behavior has long been known and was popularized in Reference cohen1991paradoxical . It can be regarded as a mechanical network effect that is formally equivalent to the Braess paradox discussed above. This mechanical analog illustrates both that the conditions underlying the paradox can occur in disparate network systems and that the resulting effect can lead to a rich variety of otherwise unrelated network phenomena. We now turn to network problems of significant current interest that expand on these points.
II.1 2.1. Synthetic Rescues in Biological Networks
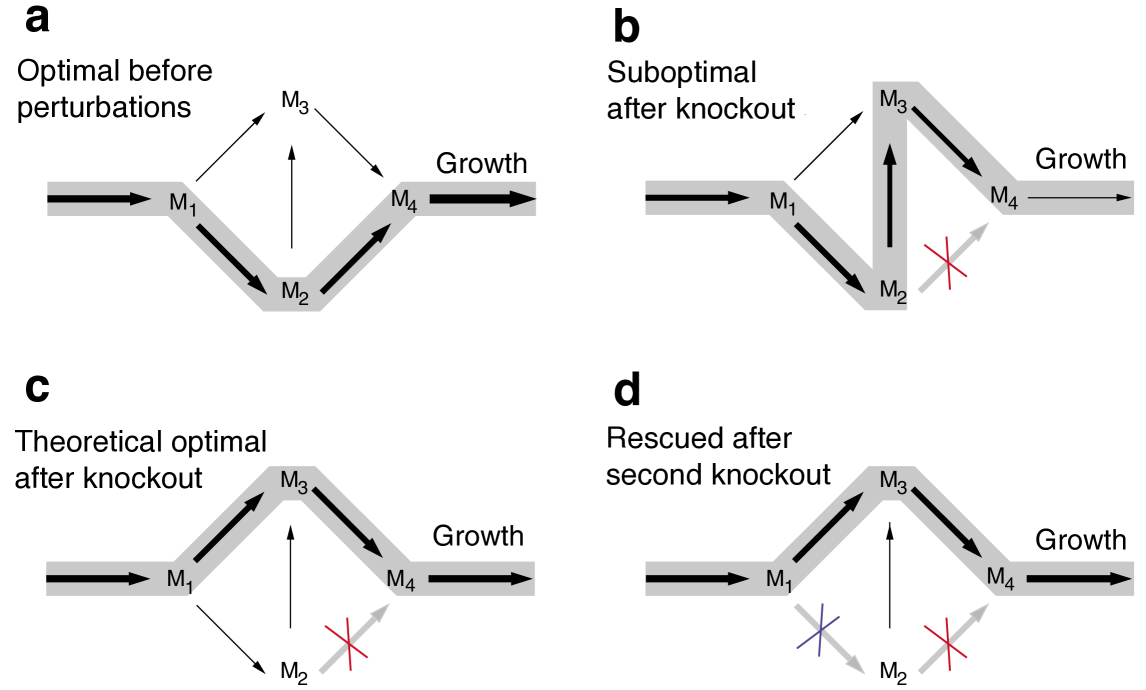
In living cells, the loss of biological function caused by the inactivation of a gene can sometimes be compensated by the inactivation of additional genes. This phenomenon, which has been confirmed experimentally, was first predicted in Reference motter2008predicting in the context of metabolic networks and can be seen as a biological analog of the Braess paradox. For concreteness, consider a single-cell organism for which the biological function of interest is growth (i.e., reproduction) rate, and assume that the cells are fully adapted to their environment, meaning that they maximize growth rate under the given conditions. The knockout of otherwise active metabolic genes leads to the inactivation of the associated metabolic reactions to which the proteins coded by those genes serve as catalyzers. Following such a perturbation, the cells are generally no longer in an optimal growth state. An optimal state may nevertheless be approached when certain additional genes (hence metabolic reactions) are knocked out, which gives rise to the predicted synthetic rescue, as illustrated in Figure 3.
As a minimal description of the phenomenon, we can use flux balance analysis edwards2000escherichia to model the optimal growth state of the cell as a linear programming problem. In this problem, one seeks to maximize the rate of a putative reaction that models the overall biomass production (and hence growth rate) under the constraints imposed by the stoichiometry of the metabolic network, nutrient availability, thermodynamics, and any imposed reaction inactivation:
| (1) |
where are the entries of the stoichiometric matrix and are the reaction fluxes. The suboptimal response to the knockout of a gene can be modeled in its simplest form using the “minimization of metabolic adjustment” hypothesis segre2002analysis , which can be implemented as a quadratic programming problem. The model identifies the available state in the space of metabolic fluxes that, under the additional constraint imposed by the gene inactivation, is closest to the pre-knockout state : subject to constraints in the form of those in Equation 1. Thus, this model effectively predicts that metabolic fluxes are rerouted mostly locally, whereas the new optimal state could require a more global flux rearrangement. The rescue state can then be predicted by applying the same quadratic optimization to the combined perturbation of the primary and rescue gene knockouts. From a biological standpoint, the second knockout effectively precipitates adaptation of the perturbed network that could in principle be eventually achieved by long-term adaptive evolution cornelius2011dispensability .
An interesting potential application of this phenomenon is to the development of pairs of antibiotic drugs that can select against resistant cells. Each gene knockout of a synthetic rescue pair has the potential to inhibit growth when implemented in isolation, but one of them suppresses the impact of the other when applied concurrently. Thus, they serve as targets for antibiotic drugs that would interact antagonistically motter2010improved , and previous research has shown that the combination of two antagonistically interacting antibiotics will select against cells that have developed resistance to the suppressor chait2007antibiotic .
II.2 2.2. Metamaterials with Negative Compressibility
While ordinary materials expand when tensioned, it has been shown that a material can be designed to undergo a negative compressibility transition (i.e., a transition to a contracted phase) in response to increasing tension nicolaou2012mechanical . As in the case of other metamaterials, such a material is engineered to gain its unusual property from its structure rather than composition. In other words, this is a property of the underlying mechanical network, which can in fact be seen as a nontrivial generalization of the spring-string system discussed above. To understand this generalization, we can imagine the constituents of the material as consisting of four particles that interact with each other through attractive forces, which are nevertheless nonlinear, allowing the system to be bistable. When two stable states coexist, one generally corresponds to an expanded configuration while the other corresponds to a contracted one. Ignoring dissipation for simplicity, each such constituent is characterized by a potential of the form
| (2) |
where is the total length and is the applied tensional force (see Figure 4a). As is increased, the stable state corresponding to larger first becomes marginally stable and then disappears. If the system was initially in this extended state, it will then transition to the other stable state, which corresponds to a smaller .
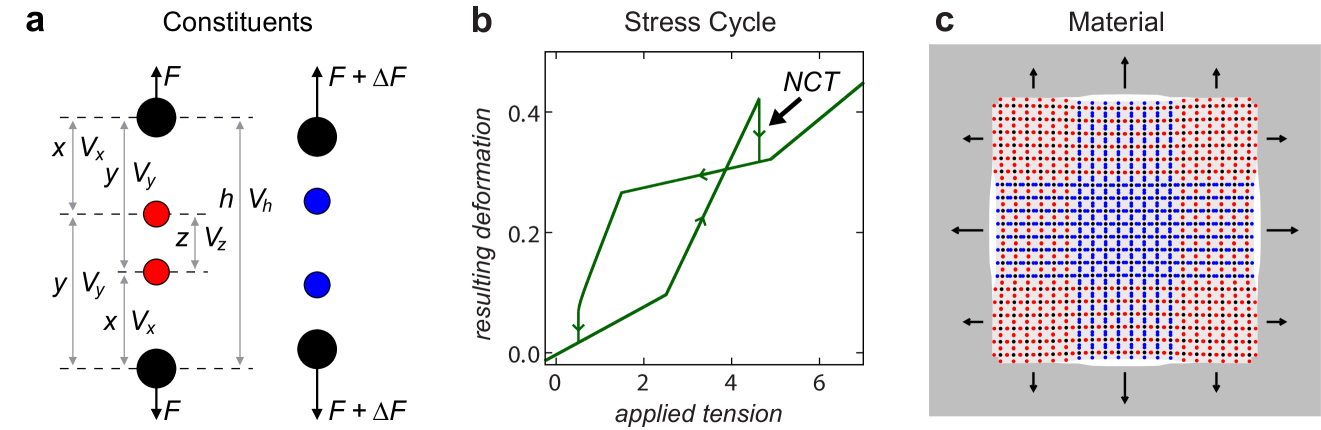
Mathematically, this transition is determined by a bifurcation analogous to one observed for the potential , where is the tunable parameter. This potential has a stable equilibrium point at and an unstable one at for , has a single (degenerate) equilibrium point at for , and has no equilibrium point for . Thus, as is varied from positive to negative, the stable equilibrium point vanishes and the system responds discontinuously. Physically, the disappearance of the occupied stable state is analogous to the cutting of the linking string in Figure 2: it causes the inner particles in Figure 4a to move closer to (and hence attract more strongly) the external particles, which is similar to the transition from a parallel to a series configuration in the spring-string system. A key difference here is that the process can be cycled by varying the tensional force, as shown in the hysteresis diagram of Figure 4b.
The material itself can be formed by aggregating such constituents, as shown in Figure 4c for a square lattice network. In the thermodynamic limit, the bifurcations undergone by the constituents give rise to a transition between the corresponding extended and contracted phases, which can be rigorously characterized at finite temperature using tools from statistical physics nicolaou2013longitudinal . Such materials can find applications in the design of micro-mechanical controls and protective mechanical devices, but they also suggest a more general principle to design metamaterials with inverted responses that can in theory be applied not only to stress-and-strain but also to any pair of thermodynamically conjugated variables.
II.3 2.3. Synchronization Improvement by Interaction Pruning
In the synchronization of coupled oscillators, a parallel with the Braess paradox has been established in which the addition or strengthening of connections between oscillators has the adverse effect of removing a previously existing synchronous state. This possibility has attracted special attention in connection with power-grid networks, where the addition of new line capacity for power transmission could eliminate a phase-locked operating state among power generators and motors in an AC network witthaut2012braess ; coletta2016linear . A minimal model to illustrate this effect is
| (3) |
where both generator nodes () and motor nodes () are represented as damped second-order phase oscillators and represents the network structure as well as the capacity of the transmission lines filatrella2008analysis ; rohden2012self . Of special interest are the frequency-synchronized states satisfying at all times and thus for all and .
This synchronization condition leads to equations of the form , where is to be determined for given and . When such a solution for exists, the resulting power flows through the lines are and they automatically respect the line capacities. A new solution for may exist if line capacities are increased (or, in particular, if new lines are added), but therein lies the rub: for the actual state to exist, not only a solution for each has to exist but also each phase angle has to be uniquely defined, and the latter is not guaranteed when line capacities are increased even if the solution continues to exist. That is, the set of equations (which must be simultaneously satisfied for every pair of nodes and connected by a transmission line with non-zero capacity ) is no longer guaranteed to have a solution. Indeed, as demonstrated in References witthaut2012braess ; witthaut2013nonlocal , a capacity increase will frequently induce conflicts between the phases in this set of equations, which are reminiscent of the phenomenon of geometric frustration as the conflicts necessarily occur along loops in the network. (In the familiar case of geometric frustration in spin systems, not all pairwise interaction energies can be minimized simultaneously precisely due to geometric constraints similar to the ones considered here.) This effect is illustrated in Figure 5 for a simple network of four identical generators (), four identical motors (), and lines with identical capacity ( for any line with nonzero capacity).
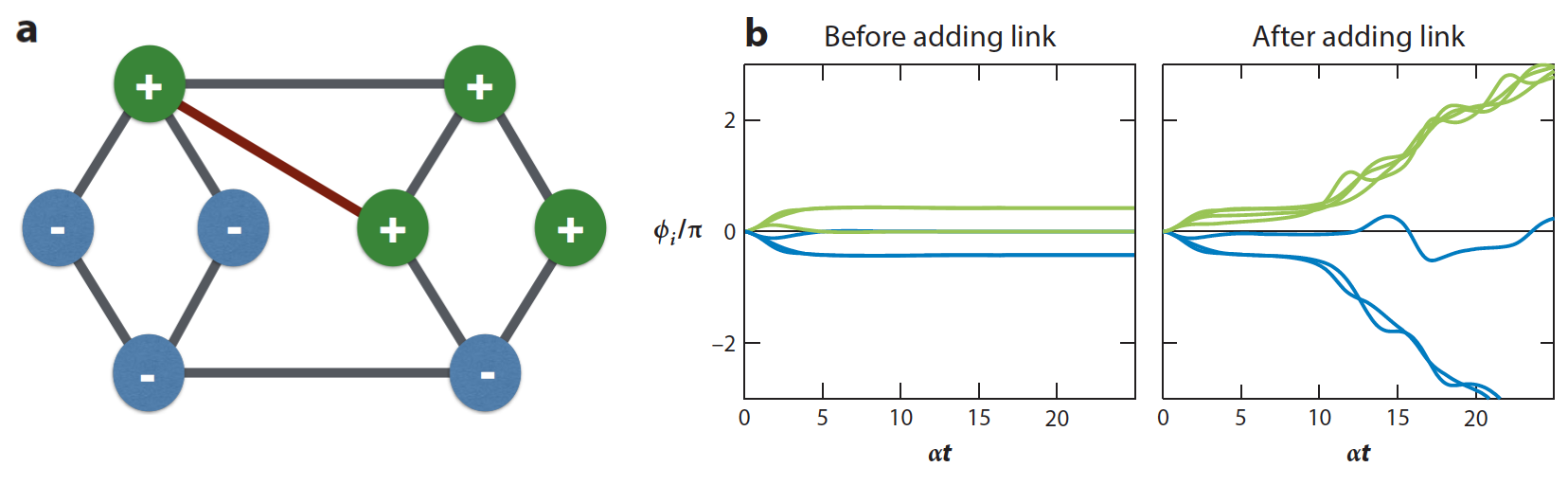
In networks of diffusively coupled oscillators, which describe the dynamics of power generators in the vicinity of their synchronization manifold motter2013spontaneous , an analogous effect can be observed even in the absence of any loops nishikawa2006synchronization . The simplest such model reads , where is the Laplacian matrix representing the (possibly directed) network of interactions, and the stability of a synchronous solution is determined by a master stability function that often has a bounded stability region pecora1998master ; nishikawa2006maximum . Accordingly, the system is synchronizable for a wider range of the coupling strength when the nonidentically-null eigenvalues of the Laplacian matrix are less scattered; the optimally synchronizable networks are those for which these eigenvalues satisfy . As shown in References nishikawa2006synchronization ; nishikawa2006maximum , every network that can be spanned from one of its nodes (a necessary condition for stable synchronization to be possible) can also be converted into an optimally synchronizable network by removing edges or reducing edge strengths. In particular, any unweighted oriented tree spanning the entire network is an optimally synchronizable network. Therefore, starting from an arbitrary network that is not synchronizable, one can always turn it into a synchronizable network by pruning the interactions between oscillators nishikawa2006maximum .
Because such systems can have a bounded stability region, they exhibit a number of other counterintuitive effects as a result of the nontrivial dependence of the eigenvalue spread on the interaction network. For example, it has been shown that otherwise unstable synchronous states can be stabilized by transiently uncoupling the oscillators schroder2015transient ; Schroeder2016 (see also stilwell2006sufficient ; Chen2009onoffcoupling ; jeter2015synchronization ). In different work, it was shown that an otherwise nonsynchronizable network can become synchronizable not only by removing nodes but also by adding nodes despite the resulting increase in the number of eigenvalues that need to fit inside the stability region nishikawa2010network .
II.4 2.4. Control by Antagonistic Interventions
A problem of fundamental interest in network dynamics is the one of preventing the loss of resources by means of interventions that are themselves limited to only further removing resources. As a concrete example, consider a food-web network in which a primary extinction triggers a cascade of secondary extinctions. The question of interest is to design a control intervention that if applied after the first extinction (but before the propagation of the cascade) would prevent the other extinctions. An elementary model to conceptualize the problem is the -species Lotka-Volterra predator-prey model cohen1990stochastic :
| (4) |
where is the population of species and parameter is the growth rate for basal species (those that do not feed on others) and the mortality rate for non-basal ones. Upon removal of one species, this system generically has one fixed point at which all other species populations are nonzero when the matrix is invertible (for simplicity let us ignore the possible presence of a nonfixed-point attractor in which all other species survive).
The primary extinction will cause subsequent extinctions if 1) this fixed point is unstable and/or outside the positive ()-dimensional orthant or 2) the fixed point is stable and in the positive orthant but the initial extinction laid the network state outside its basin of attraction. Within this simplified picture, control to prevent secondary extinctions should be geared towards manipulating the position and stability of this fixed point and/or directing the state to its basin of attraction. Recognizing that realistic interventions over the relevant time scale cannot directly increase species populations, recent research sahasrabudhe2011rescuing has considered interventions that either temporarily suppress certain species’ populations —to bring the state to the desired basin of attraction—or permanently reduce (increase) their growth (mortality) rates —to manipulate the fixed point and/or basins of attraction. Figure 6 shows for both types of interventions examples in which they would prevent all secondary extinctions for the model in Equation 4.
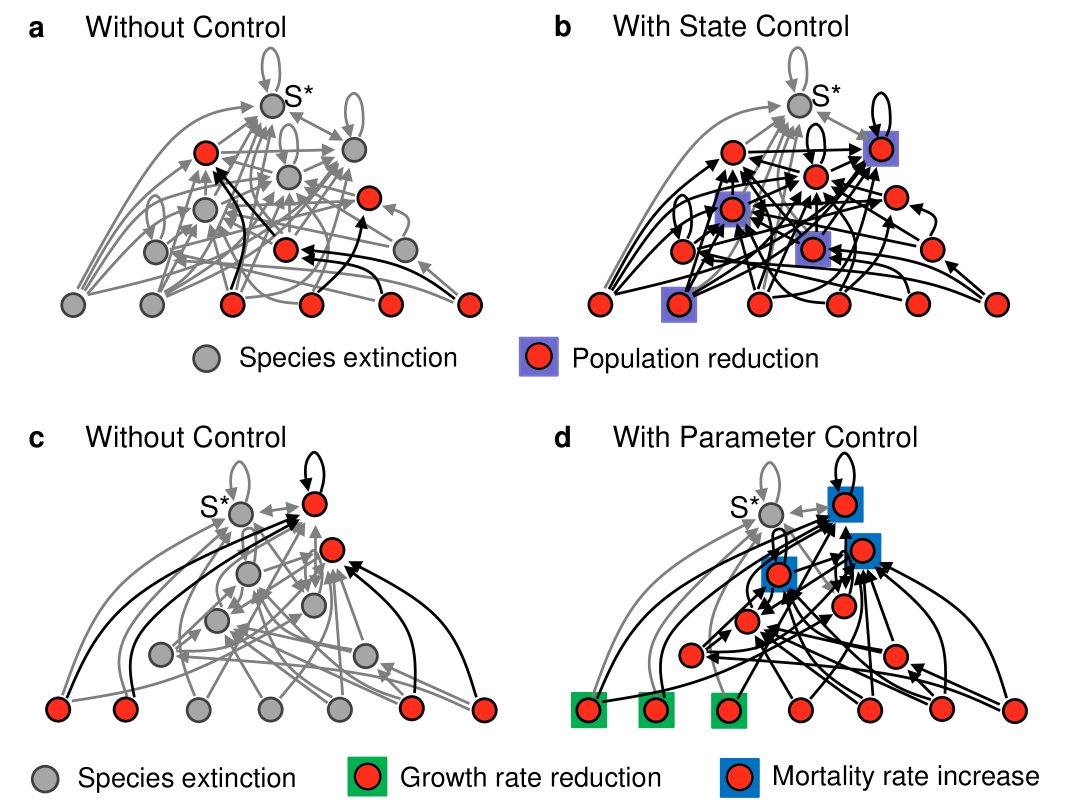
The scenario just described is ecologically plausible in view of other antagonistic effects that take place in food-web networks, such as the paradox of enrichment rosenzweig1971paradox , in which increasing food availability to a prey may eventually lead to the extinction of its predator. More important, the concept generalizes to other network processes, including the control of cascading failures in power-grid networks and the reprogramming of intracellular networks, where, owing to scenarios similar to the one above, the most effective beneficial interventions often appear to be deleterious cornelius2013realistic .
II.5 2.5. Other More-for-Less Paradoxes in Networks
The “inefficiency” of the Nash equilibrium dubey1986inefficiency —that follows from the equilibrium not being globally optimal—has been shown to lead to numerous other “more-for-less” paradoxes in networks. To be specific, we focus on variants and implications of the Braess paradox and note that related effects can be recognized across diverse network systems.
For example, in traffic networks exhibiting the Braess paradox, as originally formulated in Reference Braess1969 , the paradox has been shown to actually disappears for sufficiently high traffic demand nagurney2010negation . This means that new routes that inadvertently give rise to the paradox may slow traffic when demand is low and not even be used when demand is high. Other work has shown that, in networks with multiple origin and destination nodes, a decrease in demand can in fact lead to an increase in average travel time fisk1979more ; fujishige2017matroids . An even stronger effect has been established in which an increase in travel time along a route can result in a new equilibrium characterized by the abandonment of a different route connecting the same origin and destination nodes while the original route may continue to be used steinberg1988prevalence . In addition, there are also numerous essentially equivalent restatements of the same underlying phenomena, such as in the conclusion that an increase in the local travel time can lead to a reduction in the global travel time smith1978road , or that the overall transport capacity of a network can be reduced upon addition of capacity to individual links yang1998capacity .
Such paradoxes have also been considered in numerous concrete settings, both in the context of complex networks youn2008price ; skinner2015price ; sole2016congestion and in specific application domains, including computer networks korilis1999avoiding ; kameda2000braess , chemical reaction networks cornelius2011dispensability ; lepore2011computational , and electric networks cohen1991paradoxical ; skinner2015price ; blumsack2007quantitative ; nagurney2016physical . In electric networks, in particular, it has been shown that for graph topologies similar to the one in Figure 1b, the addition of the intermediate (current-carrying) link can create overloads in other links for certain AC circuits blumsack2007quantitative and lead to an increase in voltage drop for a fixed current source in certain two-terminal DC circuits cohen1991paradoxical ; nagurney2016physical .
Among physical systems, a major class of applications concerns the study of fluid networks. Using simplified models of the fluid dynamics, it has been shown that increase in the conductivity of individual pipes in a fluid network can lead to increase in power loss, which can be regarded as a fluid analog of resistance. While generally not observed for two-terminal networks calvert1991braess , this behavior has been predicted for single-source multiple-destination delivery networks of both water calvert1991braess ; keady1995colebrook and natural gas andre2010optimization ; ayala2013braess . This behavior can also be characterized as a need for pressure difference increases to maintain the same outputs following the capacity increase of specific pipes ayala2013braess , thus bearing direct analogy with previous results on simple electric circuits cohen1991paradoxical . Finally, it is interesting to note that similar transport inefficiency has recently been observed also in the quantum regime in mesoscopic material networks pala2012transport ; sousa2013braess , where the addition of a transport path induces a decrease in the overall conductance.
III 3. INCONGRUOUS COEXISTENCE
Consider a network of identical oscillators. It appears intuitive to assume that synchronization into a common state for all oscillators would be facilitated when the interactions between the oscillators are attractive. This assumption is false, however, as it can be shown that in many cases an otherwise unstable synchronous state can be stabilized by turning part of the network interactions repulsive nishikawa2010network (this is common, for example, for networks of diffusively-coupled chaotic oscillators with a bounded stability region). But why would our intuition suggest the opposite in the first place? One explanation is that we tend to reason in terms of individual interactions—the interaction between an isolated pair of oscillators must indeed be attractive for them to synchronize. Such a local view fails to capture the effect that comes from the other interactions in the network, suggesting a situation that may be common in the study of network dynamics. In this section, we discuss a selection of phenomena of significant current interest involving similar (albeit more intricate) apparent oxymora. To keep the discussion focused, we continue to use synchronization dynamics as a main model process, although we anticipate that many conclusions extend naturally to other forms of collective dynamics, including pattern formation, self-organization, herd behavior, and consensus processes.
III.1 3.1. Converse of Symmetry Breaking
Consider a network of phase oscillators of the form
| (5) |
where and . Each individual oscillator is identified by its natural frequency , while the other terms represent interactions between oscillators. What natural frequencies should the oscillators have in order to facilitate complete synchronization of the form ? This question can be answered using a small angle approximation in the vicinity of the synchronous state to obtain , where is the indegree of node . The synchronization condition implies for some constant , which leads to for and . The synchronous state is stable if and only if all except the identically null eigenvalue of the Laplacian matrix have positive real parts, which is guaranteed to be the case in any network that can be spanned from a node (as generally assumed in the study of synchronization). On closer examination, the actual condition for synchronization stability is thus that , meaning that the natural frequencies of the individual oscillators have to be nonidentical unless the network has identical indegrees for all nodes. This is intuitive because, in order to achieve an identical state, the oscillators need to be nonidentical to compensate for their nonidentical couplings. A generalization of this argument can be used to optimize synchronization in complex networks in general skardal2014optimal , and analogous results are expected if a different characteristic of the system (e.g., delays, noise level, or coupling strength) is nonuniform across components. For a long time, cases involving such compensatory nonuniformities were the only ones in which differences between the oscillators were found to help minimize differences between their states.
However, it was recently shown that stable identical synchronization can require the oscillators to be nonidentical even when they are identically coupled and indeed equal with respect to all other aspects. A simple scenario in which this was first demonstrated nishikawa2016symmetric was for phase-amplitude oscillators characterized by a phase variable and an amplitude variable such that the system always has one synchronous solution corresponding to and . The question is whether this solution is stable or not. The uncoupled dynamics of the amplitude variable takes the form , where is the only parameter allowed to vary from node to node. All other parameters and the network structural properties are identical for all oscillators. As illustrated in Figure 7 for a rotationally invariant network of three such oscillators, there are scenarios for which the synchronous state is not stable for any choice of , but it becomes stable for specific choices of nonidentical . This is remarkable because the synchronous state is the state that would reflect the rotational symmetry of the system and, nevertheless, this symmetric state is stable only when the symmetry of the system is broken by making the oscillators nonidentical.
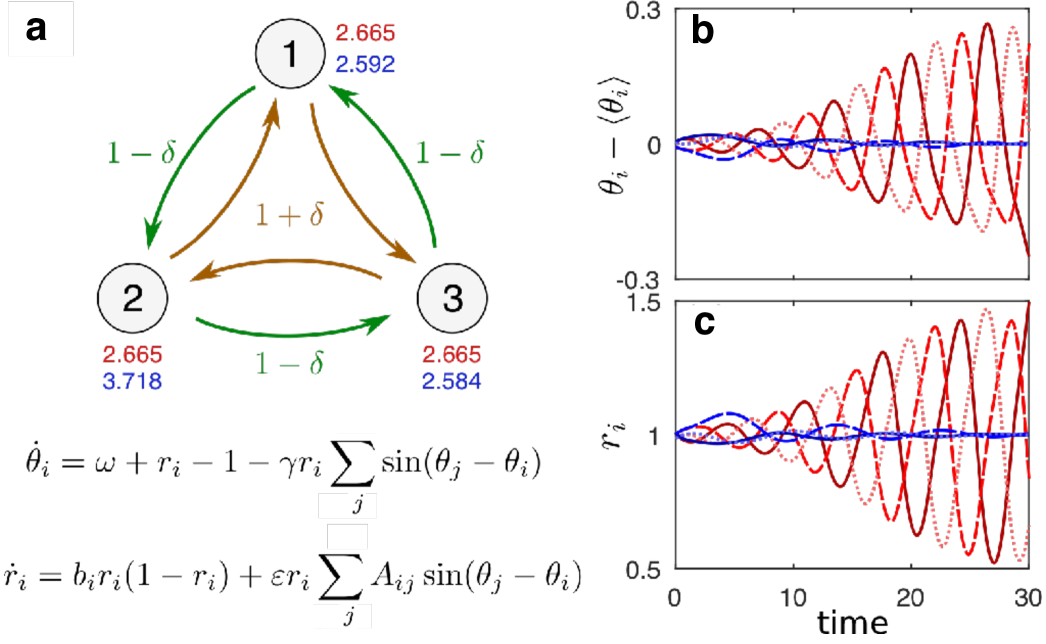
It is instructive to contrast this effect with the well-studied phenomenon of symmetry breaking. The fact that the symmetric system does not exhibit a stable synchronous (hence symmetric) solution can be seen as an ordinary manifestation of spontaneous symmetry breaking. On the other hand, the fact that the symmetry of the stable solution is preserved when (and only when) the symmetry of the system is broken can be seen as the converse of symmetry breaking. More generally, in the same way the former shows that an asymmetric reality may be described by a symmetric theory, the latter shows that a symmetric reality may require an asymmetric theory.
The specific observation that synchronization can be stabilized or enhanced by tuning the oscillators to be nonidentical has potential implications for power-grid networks, whose operation requires frequency synchronization among power generators. As shown in Reference nishikawa2015stability , the stability of the synchronous state of interest can be significantly enhanced when an effective parameter that depends on the damping, inertia and droop coefficients of the power generators is set to be suitably different for different generators.
III.2 3.2. Chimera States
In networks of coupled oscillators, symmetry breaking itself can lead to rather surprising spatiotemporal patterns formed by two or more domains of qualitatively different dynamics, some in which the oscillators are mutually synchronized and others in which they evolve incoherently. First identified by Kuramoto kuramoto2003reduction and later termed chimeras abrams2004chimera , such states may provide insights into unihemispheric sleep in some animal species rattenborg2000behavioral and fibrillation in the cardiac muscle of ventricles davidenko1992stationary .
The first model in which chimera states were systematically described was a ring network of nonlocally coupled phase oscillators kuramoto2002coexistence ,
| (6) |
where the kernel is a decreasing function that determines the distance-dependent strength of the coupling. This equation, which can be derived via phase reduction from a nonlocally coupled complex Ginzburg-Landau equation, describes identically-coupled identical oscillators in the limit of a large number of oscillators. The complete synchronous state is always a solution and can in fact be stable. But its basin of attraction is not global and the system also exhibits persistent chimera states that are approached for other initial conditions. Inspection of the phases of the oscillators along the ring, as in the snapshot in Figure 8, shows a clear separation into a domain of incoherence (center) and a domain of coherence (extremes). Dynamical variants of such patterns, including spiral chimeras in two-dimensional arrays of oscillators, have been known to exist from the very first studies kuramoto2003rotating , and experimental demonstrations of chimeras states have been successful on various systems, including networks of coupled electro-optic hagerstrom2012experimental , chemical tinsley2012chimera , and mechanical martens2013chimera oscillators.
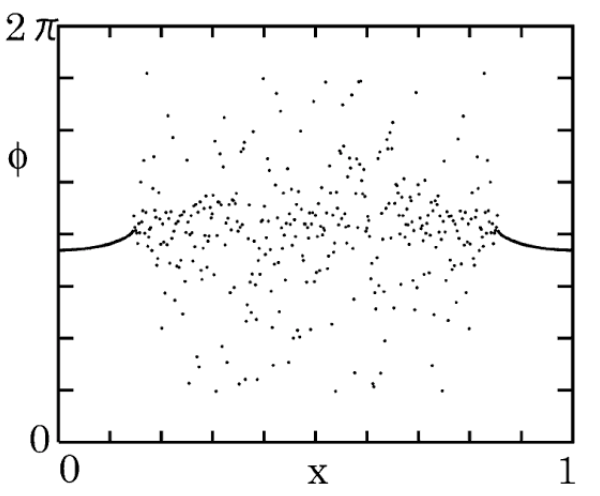
In part because the original theory to describe chimera states was based on a self-consistent mean-field solution, it was initially believed that such states would not emerge in systems with local or global coupling abrams2004chimera and, moreover, that they would be long lived but not permanently stable in finite-size networks wolfrum2011chimera . Subsequent research demonstrated that chimeras can emerge across a surprising range of models and conditions, which include examples of locally and globally coupled systems panaggio2015chimera . Moreover, while the question of stability remains open for many systems, stable chimera states have now been rigorously identified in finite-size networks of chaotic oscillators cho2017stable (see also suda2015persistent ; hart2016experimental ; bick2016chaotic ). Yet, previous work focused exclusively on discrete systems or systems in which the coupling was not strictly local schmidt2014coexistence , leaving open the question of whether locally coupled continuous systems could exhibit chimera states (not to be confused with the continuous representation of discrete systems, such as in Equation (6), whose variables are not spatially continuous, as illustrated in Figure 8). The latter was addressed by recent research, which demonstrated the existence of symmetry-breaking chimera states whose coherent and incoherent phases are analogous to laminar and turbulent phases of a fluid system nicolaou2017continuous , thereby revealing an important connection with the classical field of pattern formation.
III.3 3.3. Remote Synchronization
Distant oscillators in a network can synchronize stably even when they are connected exclusively through oscillators that are asynchronous. This remote form of cluster synchronization has potential implications for information processing in the brain nicosia2013remote and for secure communication zhang2017incoherence , and has been recognized in many systems. For example, in an initially synchronized undirected star network of diffusively coupled chaotic oscillators, an increase in coupling strength can lead to a short wavelength bifurcation that drives the center node off pace but keeps all the other nodes synchronized; this long-known behavior is observed when the stability region is limited, and has been referred to as a drum-head-mode bifurcation pecora1998master (see also winful1990synchronized ).
More recently it has been noticed that variants of this behavior extend to complex networks in general, largely owing to cluster synchronous states that derive from network symmetry. For example, Reference nicosia2013remote considered the system in Equation 5 for identical to show that suitable choices of the phase parameter lead to a frustrated state in which directly connected oscillators do not synchronize whereas certain oscillators that are distant from each other do. The oscillators that synchronize are those symmetrically coupled to the network (i.e., in the same symmetry cluster). This is so because the equation of motion remains invariant under the action of the symmetry group of the network, meaning that the system admits a synchronous solution among those nodes, which in this case is stable even when they are not directly connected.
Several variants of remote synchronization are particularly intriguing. For example, in the study of so-called relay synchronization, it has been shown that two delay-coupled oscillators can synchronize identically (thus without delay) when connected through a third oscillator that lags behind fischer2006zero . In a different study, two chaotic oscillators have been shown to synchronize stably while connected through an intermediate cluster of oscillators that are incoherent both with the outer nodes and with themselves; termed incoherence-mediated remote synchronization zhang2017incoherence , this scenario blends together the properties of remote synchronization with those of chimera states (see Figure 9). It has the advantage of being robust to perturbation of the intermediate oscillators and can in principle be useful for encryption key distribution.
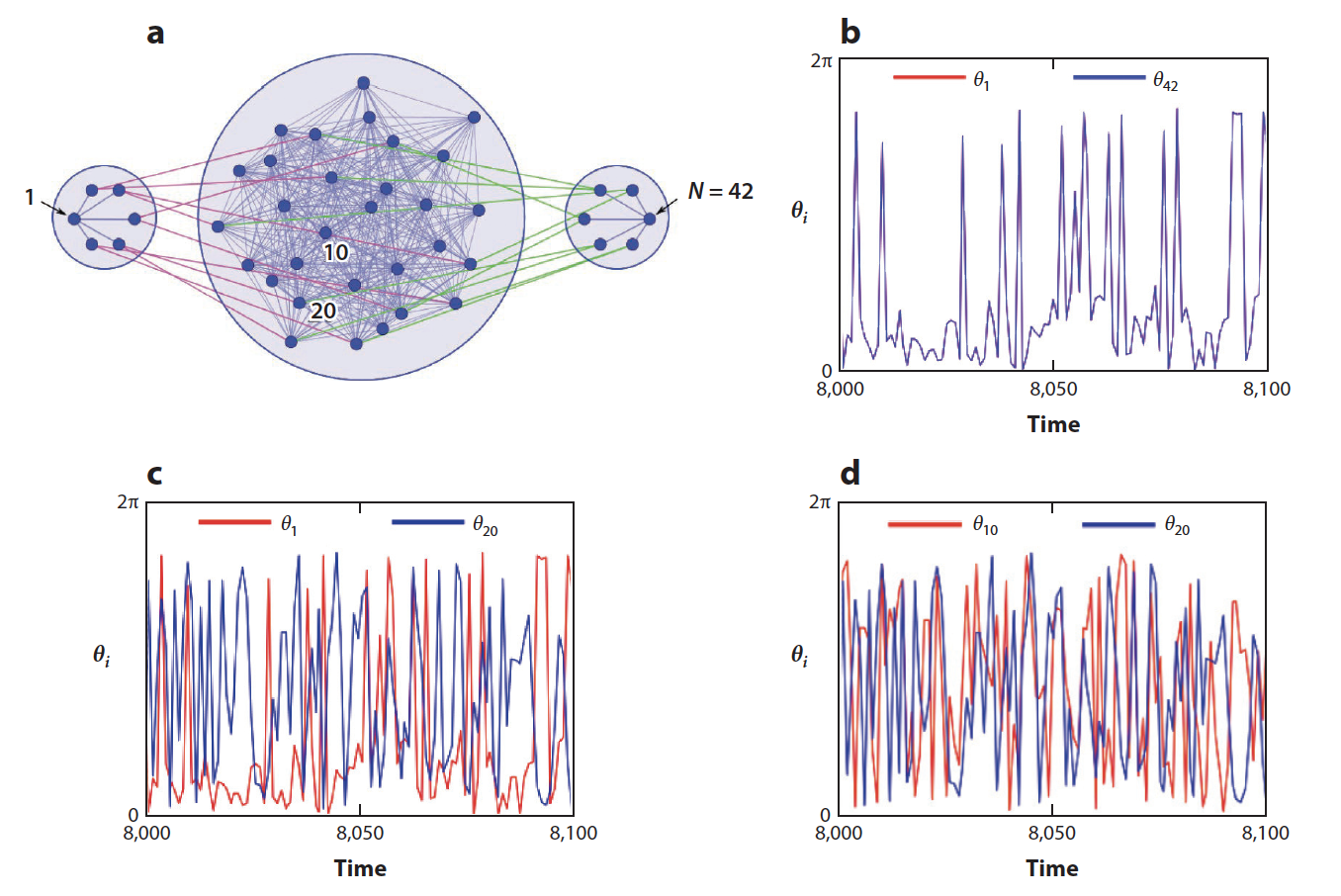
A common theme underlying all forms of remote synchronization just mentioned is indeed symmetry in the network. To appreciate how general symmetry-based remote synchronization can be, it is important to notice that even random networks can exhibit a large number of nontrivial symmetry clusters, and that the nodes in such clusters are often not directly connected macarthur2008symmetry . Recently developed techniques pecora2013symmetries to study the stability of cluster synchronous states while exploring their relation with symmetries promise to be useful in future studies of this phenomenon.
III.4 3.4. Remote Control of Information Routing
In network systems, the hallmarks of emergent distributed phenomena are found not only in overt manifestations of collective dynamics but also in the associated information transmission and processing. These characteristics are common across numerous systems in biology, physics, and engineering, ranging from neural and biochemical circuits to self-organized communication networks Hopfield1982 ; Cardelli2017 ; Klinglmayr2012applied ; Klinglmayr2012theory . In biological systems, in particular, information handling is often referred to as distributed, but how information may be specifically communicated and dynamically routed in such systems is not yet well understood. Recent work Kirst2012 offers concrete hints on what distributed information routing actually means and what it might condense to, qualitatively and quantitatively.
A theoretical framework for networks of oscillatory units Kirst2016 predicts the patterns of information routing in networks and their dependence on the interaction network and other factors. The framework is established using model systems of the form
| (7) |
where represents the intrinsic time evolution rules and interaction structure of the network and represents an external (stochastic) input. The theory determines how routing patterns depend on the dynamical reference state (taken to be a periodic or fixed-point solution of ) in the presence of small external inputs. Because and are system-wide variables, local modifications of individual unit properties, network interactions, and external inputs provide mechanisms to flexibly change information routing throughout the entire network.
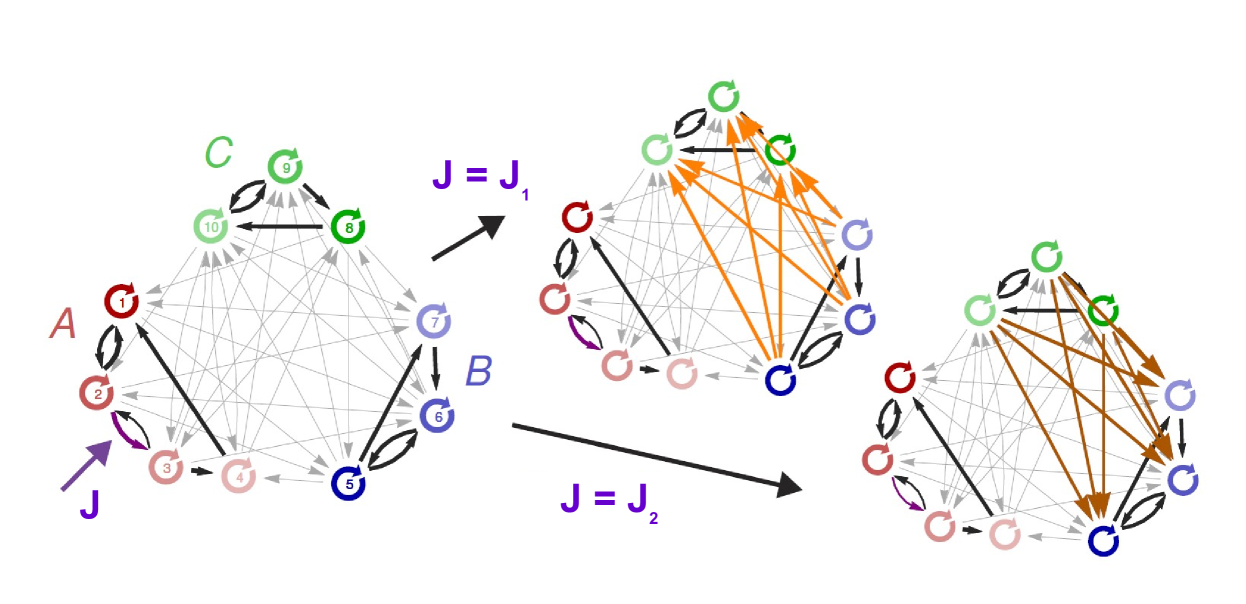
As a particularly intriguing property, we mention that local modifications in one part of the network may remotely influence and even reverse the direction of information routing between two other parts (see Figure 10). This points to a potentially general mechanism of remote control that is possible because information routing is ultimately determined by the network dynamics, which are collective and distributed.
III.5 3.5. Other Unconventional Phenomena in Networks
Limiting ourselves to synchronization dynamics for concreteness, we note that delays, noise, and correlations between node parameters and network structure have been found to lead to other unanticipated phenomena. For example, scenarios have been described in which time delay in node-to-node communication can facilitate rather than inhibit in-phase (zero-lag) synchronization atay2004delays . This has been observed, for instance, for pulse-coupled oscillators with inhibitory coupling ernst1995synchronization and for relay-coupled oscillators fischer2006zero . For excitatory coupling, on the other hand, networks of pulse-coupled oscillators can be shown to often exhibit attracting periodic orbits with points that are isolated from their basins of attraction, and thus have the peculiar property of being both attractive and unstable timme2002prevalence .
Another notable class of behaviors comes from considering coupled oscillators in the presence of noise, where it has been shown that, due to coupling, modular networks can synchronize in response to noise even when the noise applied to different modules is uncorrelated meng2016independent . In networks of globally coupled oscillators, different work has demonstrated that independent noise at individual nodes can also stabilize otherwise unstable states of partial synchronization clusella2017noise . Moreover, in systems of directionally coupled non-identical oscillators, it has been shown that the phase diffusion in an oscillator can depend non-monotonically on the noise intensity in a coupled oscillator, and thus become more coherent as noise is further strengthened amro2015phase .
Finally, following the discovery of explosive percolation achlioptas2009explosive —characterized by abrupt transitions da2010explosive ; riordan2011explosive ; grassberger2011explosive ; nagler2011impact —analogous transitions (in fact strictly discontinuous ones vlasov2015explosive ) have been identified also in synchronization processes, giving rise to so-called explosive synchronization gomez2011explosive . Explosive synchronization occurs when, as the coupling strength is increased, an otherwise second-order phase transition to synchronization becomes first order. This behavior has been demonstrated for both phase oscillators gomez2011explosive and chaotic oscillators leyva2012explosive in scale-free networks, where the oscillator frequency is positively correlated with the node degree. Such transitions exhibit hysteresis, in which the transformation from coherence to incoherence occurs at a smaller critical coupling than that from incoherence to coherence. The dynamical origin of the hysteretic behavior has been explicitly related to a change in the basin of attraction of the synchronization state zou2014basin .
IV 4. OUTLOOK
What do we learn from these examples of collective dynamics? We have illustrated various types of network phenomena, highlighted conditions for their occurrence, and identified some common mechanisms underlying them. Can we expect to achieve a more unified view of collective network dynamics in the near future?
The question of “unification” is indeed a recurrent one in the study of complex systems horgan1995complexity . Many argue that the similarities observed in certain phenomena across disparate systems are suggestive of common governing principles. Others further contend that an overarching goal of 21st century physics is to construct a unified theory of complex systems, which is a pursuit that implicitly assumes that such a unified account of everything would be both simple and useful. The question of whether all observed phenomena can be the result of simple rules determined by common theories is non-controversial—if we abstract from the fact that we probably do not know all fundamental laws of physics, they would all follow from a handful of fundamental interactions. But such a description, however simple, is of limited practical use at the scale relevant to most complex systems phenomena. Conversely, computer experiments are useful as broadly applicable approaches to simulate the intricate behavior of complex systems but may be no simpler to interpret than the empirical data. This limitation is all-important precisely because complex systems tend to defy our ability to understand them. Thus, whether a unified description satisfying the basic requirements of simplicity and usefulness can be constructed (even in principle) remains an open question.
On the other hand, networks definitely offer a unified way of thinking about a broad range of complex systems. While not all complex systems lend themselves to being described as a network, the existence of an underlying network of interactions is indeed a defining property of complex systems and many complex systems can be usefully represented as a network. The network description may not result in a theory of everything, but it constitutes a unifying principle in and of itself and offers a common framework for the development of broadly applicable mathematical, computational, and experimental tools, which are conducive to new discoveries. Such a description is sufficiently general to apply to many systems yet sufficiently flexible to account for system-specific features as needed. In particular, complex systems generally require different portrayals at different scales anderson1972more , and networks do offer a versatile representation across scales.
It appears to be the natural progress of network research that—as more is learned—new principles will be discovered, new tools will be developed, and new relations between different systems and phenomena will be established. The end product of such a research program, no matter how successful, may not be a unified theory. After all, it may be argued that there are principles that govern all, principles that govern some, and principles that govern specific systems. This does not reduce the importance of identifying common mechanisms in disparate complex systems. This article represents an effort to help bring such mechanisms to light and offer a unified view of a broad class of network phenomena, even though the systems hosting these phenomena can be very different and with their own idiosyncratic properties in each case.
Looking forward, it is legitimate to posit that further methodological advances would permit development of better understanding and possibly allow us to predict the limits of, for instance, antagonistic responses or remote actions in networks. In condensed matter physics, for example, several innovative forms of representing and analyzing collective behavior of many-particle systems have become standard and now facilitate synergy between subfields. If similar overarching techniques are developed for collective dynamics in network systems, they would likely be drastically different from current methods in dynamical systems theory, where the focus has traditionally been on low-dimensional systems. As illustrated in various examples of network phenomena considered here, the joint presence of high dimensionality, complex coupling structure, and nonlinearity leads to new phenomena but also pose new challenges. These examples may thus provide some common starting ground to not only explore new collective phenomena in their own right but also to develop new tools applicable to a broader range of systems and settings. Again, developing such tools will likely require a shift in theoretical perspective, possibly comparable in significance to the shift required to go from individual particle dynamics to statistical mechanics. This shift might, nevertheless, already be underway as a co-product of the wider adoption of network representations of complex systems.
Finally, we note that the phenomena reported here raise numerous immediate questions for future research. For instance, it is instructive to reflect on the more-for-less paradoxes as they relate to the formation and evolution of networks in real systems. Conceptually, forming a network is often seen as a mode to establish connections, which is a bottom up view that tacitly assumes that the system is built from isolated (or less connected) parts. But a network is also a way to set constraints, which is a top down view that conceptualizes the notion that the system realizes only a subset of all potential interactions. The latter is relevant in our discussion of network phenomena resulting from the equilibrium state not being the optimal state, since they all are examples in which the state realized by the system can be brought closer to the optimum by constraining the structure (or dynamics) of the network.
Still, in real systems, this alone does not explain why network resources whose removal increases performance have not been trimmed over time. This question is particularly relevant in the case of growing networks, such as many biological and infrastructure ones, which exhibit a net gain rather than loss of links and nodes as they evolve. One contributing explanation for this apparent oxymoron is the pressure imposed by the need to perform under multiple conditions: while the presence of certain network components may lower performance under the considered condition, they may be needed for improved performance under different conditions. For instance, a living cell activates different parts of its metabolic network depending on the nutrients available in the surrounding medium. A complementary explanation is that systems often operate under the competing pressures of two or more objectives. For example, in a power grid the addition of a link to increase power transmission capacity may inadvertently cause desynchronization witthaut2012braess , which illustrates scenarios in which the addition of resources required to improve one function can be strictly deleterious for a different function. The need to understand such scenarios is yet another motivation for future research.
A common theme in the network phenomena we described is that, in general, one cannot disentangle the network structure from the network dynamics or attribute the behavior solely to structural properties. This is rooted in the collective and decentralized nature of the dynamics, in which the observed behavior emerges from interactions. For example, the relevance of chimera states lies in them being emergent rather than in the mere coexistence of ordered and disordered phases, which could be realized by collections of certain bistable oscillators in the absence of any coupling. Much is left for future work, however. In particular, it is important to recognize that, as much as networks of simple nodes and links have been powerful in representing a broad range of complex systems, in real systems links and nodes are often complex dynamical systems on their own.
In the broader context of the phenomena illustrated in this review, it is where they run most strongly against our intuition that we can learn the most and possibly make the most progress into novel conceptual directions. We argue for this perspective of research to make advances into unanticipated network phenomena currently unexplained, or still unknown.
ACKNOWLEDGMENTS
The authors acknowledge interactions with Daniel Case, Zachary Nicolaou, Thomas Wytock, Christoph Kirst, Jan Nagler, and Takashi Nishikawa, as well as financial support from the National Institutes of Health under grant No. NIGMS-1R01GM113238 (AEM), the Army Research Office under award No. W911NF-15-1-0272 (AEM), the Max Planck Society (MT), the Federal Ministry for Education and Research (BMBF) under grant Nos. 03SF0472E and 03SF0472F (MT), and the German Science Foundation (DFG) through a grant towards the Cluster of Excellence “Center for Advancing Electronics Dresden” (MT).
References
- (1) A. C. Pigou, The Economics of Welfare. Macmillan, London, UK, 1920.
- (2) J. G. Wardrop, Some theoretical aspects of road traffic research, Proc. Institute of Cioil Engineers (Part II), vol. 1, no. 3, pp. 325–362, 1952.
- (3) M. Beckmann, C. McGuire, and C. B. Winsten, Studies in the Economics of Transportation. Yale University Press, New Haven, CT, 1956.
- (4) D. Braess, Über ein Paradoxon aus der Verkehrsplanung, Unternehmensforschung, vol. 12, pp. 258–268, 1968.
- (5) D. Braess, A. Nagurney, and T. Wakolbinger, On a paradox of traffic planning, Transportation Science, vol. 39, no. 4, pp. 446–450, 2005.
- (6) T. Roughgarden, Selfish Routing and the Price of Anarchy. MIT Press, Cambridge, MA, 2005.
- (7) J. F. Nash, Equilibrium points in n-person games, Proceedings of the National Academy of Sciences USA, vol. 36, no. 1, pp. 48–49, 1950.
- (8) L. M. Pecora and T. L. Carroll, Synchronization in chaotic systems, Physical Review Letters, vol. 64, no. 8, pp. 821–824, 1990.
- (9) P. W. Anderson, More is different, Science, vol. 177, no. 4047, pp. 393–396, 1972.
- (10) D. J. Watts, Everything is Obvious Once You Know the Answer: How Common Sense Fails Us. Crown Business, New York, NY, 2011.
- (11) J. E. Cohen and P. Horowitz, Paradoxical behaviour of mechanical and electrical networks, Nature, vol. 352, no. 6337, pp. 699–701, 1991.
- (12) A. E. Motter, N. Gulbahce, E. Almaas, and A.-L. Barabási, Predicting synthetic rescues in metabolic networks, Molecular Systems Biology, vol. 4, no. 1, 168, 2008.
- (13) J. Edwards and B. Palsson, The Escherichia coli MG1655 in silico metabolic genotype: Its definition, characteristics, and capabilities, Proceedings of the National Academy of Sciences USA, vol. 97, no. 10, pp. 5528–5533, 2000.
- (14) D. Segrè, D. Vitkup, and G. M. Church, Analysis of optimality in natural and perturbed metabolic networks, Proceedings of the National Academy of Sciences USA, vol. 99, no. 23, pp. 15112–15117, 2002.
- (15) S. P. Cornelius, J. S. Lee, and A. E. Motter, Dispensability of Escherichia coli’s latent pathways, Proceedings of the National Academy of Sciences USA, vol. 108, no. 8, pp. 3124–3129, 2011.
- (16) A. E. Motter, Improved network performance via antagonism: From synthetic rescues to multi-drug combinations, BioEssays, vol. 32, no. 3, pp. 236–245, 2010.
- (17) R. Chait, A. Craney, and R. Kishony, Antibiotic interactions that select against resistance, Nature, vol. 446, no. 7136, pp. 668–671, 2007.
- (18) Z. G. Nicolaou and A. E. Motter, Mechanical metamaterials with negative compressibility transitions, Nature Materials, vol. 11, no. 7, pp. 608–613, 2012.
- (19) Z. G. Nicolaou and A. E. Motter, Longitudinal inverted compressibility in super-strained metamaterials, Journal of Statistical Physics, vol. 151, no. 6, pp. 1162–1174, 2013.
- (20) D. Witthaut and M. Timme, Braess’s paradox in oscillator networks, desynchronization and power outage, New Journal of Physics, vol. 14, no. 8, 083036, 2012.
- (21) T. Coletta and P. Jacquod, Linear stability and the Braess paradox in coupled-oscillator networks and electric power grids, Physical Review E, vol. 93, no. 3, 032222, 2016.
- (22) G. Filatrella, A. H. Nielsen, and N. F. Pedersen, Analysis of a power grid using a Kuramoto-like model, The European Physical Journal B, vol. 61, no. 4, pp. 485–491, 2008.
- (23) M. Rohden, A. Sorge, M. Timme, and D. Witthaut, Self-organized synchronization in decentralized power grids, Physical Review Letters, vol. 109, no. 6, 064101, 2012.
- (24) D. Witthaut and M. Timme, Nonlocal failures in complex supply networks by single link additions, The European Physical Journal B, vol. 86, no. 9, pp. 1–12, 2013.
- (25) A. E. Motter, S. A. Myers, M. Anghel, and T. Nishikawa, Spontaneous synchrony in power-grid networks, Nature Physics, vol. 9, no. 3, pp. 191–197, 2013.
- (26) T. Nishikawa and A. E. Motter, Synchronization is optimal in nondiagonalizable networks, Physical Review E, vol. 73, no. 6, 065106, 2006.
- (27) L. M. Pecora and T. L. Carroll, Master stability functions for synchronized coupled systems, Physical Review Letters, vol. 80, no. 10, pp. 2109–2112, 1998.
- (28) T. Nishikawa and A. E. Motter, Maximum performance at minimum cost in network synchronization, Physica D, vol. 224, no. 1, pp. 77–89, 2006.
- (29) M. Schröder, M. Mannattil, D. Dutta, S. Chakraborty, and M. Timme, Transient uncoupling induces synchronization, Physical Review Letters, vol. 115, no. 5, 054101, 2015.
- (30) M. Schröder, S. Chakraborty, D. Witthaut, J. Nagler, and M. Timme, Interaction control to synchronize non-synchronizable networks, Scientific Reports, vol. 6, 37142, 2016.
- (31) D. J. Stilwell, E. M. Bollt, and D. G. Roberson, Sufficient conditions for fast switching synchronization in time-varying network topologies, SIAM Journal on Applied Dynamical Systems, vol. 5, no. 1, pp. 140–156, 2006.
- (32) L. Chen, C. Qiu, and H. B. Huang, Synchronization with on-off coupling: Role of time scales in network dynamics, Physical Review E, vol. 79, 045101, 2009.
- (33) R. Jeter and I. Belykh, Synchronization in on-off stochastic networks: Windows of opportunity, IEEE Transactions on Circuits and Systems I, vol. 62, no. 5, pp. 1260–1269, 2015.
- (34) T. Nishikawa and A. E. Motter, Network synchronization landscape reveals compensatory structures, quantization, and the positive effect of negative interactions, Proceedings of the National Academy of Sciences USA, vol. 107, no. 23, pp. 10342–10347, 2010.
- (35) J. Cohen, T. Luczak, C. Newman, and Z.-M. Zhou, Stochastic structure and nonlinear dynamics of food webs: Qualitative stability in a Lotka-Volterra cascade model, Proceedings of the Royal Society of London B, vol. 240, no. 1299, pp. 607–627, 1990.
- (36) S. Sahasrabudhe and A. E. Motter, Rescuing ecosystems from extinction cascades through compensatory perturbations, Nature Communications, vol. 2, 170, 2011.
- (37) M. L. Rosenzweig, Paradox of enrichment: Destabilization of exploitation ecosystems in ecological time, Science, vol. 171, no. 3969, pp. 385–387, 1971.
- (38) S. P. Cornelius, W. L. Kath, and A. E. Motter, Realistic control of network dynamics, Nature Communications, vol. 4, 1942, 2013.
- (39) P. Dubey, Inefficiency of Nash equilibria, Mathematics of Operations Research, vol. 11, no. 1, pp. 1–8, 1986.
- (40) A. Nagurney, The negation of the Braess paradox as demand increases: The wisdom of crowds in transportation networks, Europhysics Letters, vol. 91, no. 4, 48002, 2010.
- (41) C. Fisk, More paradoxes in the equilibrium assignment problem, Transportation Research Part B: Methodological, vol. 13, no. 4, pp. 305–309, 1979.
- (42) S. Fujishige, M. X. Goemans, T. Harks, B. Peis, and R. Zenklusen, Matroids are immune to Braess’ paradox, Mathematics of Operations Research, vol. 42, no. 3, pp. 745–761, 2017.
- (43) R. Steinberg and R. E. Stone, The prevalence of paradoxes in transportation equilibrium problems, Transportation Science, vol. 22, no. 4, pp. 231–241, 1988.
- (44) M. Smith, In a road network, increasing delay locally can reduce delay globally, Transportation Research, vol. 12, no. 6, pp. 419–422, 1978.
- (45) H. Yang and M. G. Bell, A capacity paradox in network design and how to avoid it, Transportation Research Part A: Policy and Practice, vol. 32, no. 7, pp. 539–545, 1998.
- (46) H. Youn, M. T. Gastner, and H. Jeong, Price of anarchy in transportation networks: Efficiency and optimality control, Physical Review Letters, vol. 101, no. 12, 128701, 2008.
- (47) B. Skinner, Price of anarchy is maximized at the percolation threshold, Physical Review E, vol. 91, no. 5, 052126, 2015.
- (48) A. Solé-Ribalta, S. Gómez, and A. Arenas, Congestion induced by the structure of multiplex networks, Physical Review Letters, vol. 116, no. 10, 108701, 2016.
- (49) Y. A. Korilis, A. A. Lazar, and A. Orda, Avoiding the Braess paradox in non-cooperative networks, Journal of Applied Probability, vol. 36, no. 1, pp. 211–222, 1999.
- (50) H. Kameda, E. Altman, T. Kozawa, and Y. Hosokawa, Braess-like paradoxes in distributed computer systems, IEEE Transactions on Automatic Control, vol. 45, no. 9, pp. 1687–1691, 2000.
- (51) D. M. Lepore, C. Barratt, and P. M. Schwartz, Computational models of chemical systems inspired by Braess’ paradox, Journal of Mathematical Chemistry, vol. 49, no. 2, pp. 356–370, 2011.
- (52) S. Blumsack, L. B. Lave, and M. Ilić, A quantitative analysis of the relationship between congestion and reliability in electric power networks, The Energy Journal, pp. 73–100, 2007.
- (53) L. S. Nagurney and A. Nagurney, Physical proof of the occurrence of the Braess paradox in electrical circuits, Europhysics Letters, vol. 115, no. 2, 28004, 2016.
- (54) B. Calvert, G. Keady, and B. Calvert, Braess’s paradox and power-law nonlinearities in networks, Journal of the Australian Mathematical Society, Series B, vol. 35, p. 1–22, 1993.
- (55) G. Keady, The Colebrook-White Formula for Pipe Networks. Electronic Report, Department of Mathematics, University of Western, Nedlands, Australia, 1995.
- (56) J. André, Optimization of Investments in Gas Networks. PhD Thesis, Université du Littoral Côte d’Opale, Lille, France, 2010.
- (57) L. Ayala and S. Blumsack, The Braess paradox and its impact on natural-gas-network performance, Oil and Gas Facilities, vol. 2, no. 03, pp. 52–64, 2013.
- (58) M. Pala, S. Baltazar, P. Liu, H. Sellier, B. Hackens, F. Martins, V. Bayot, X. Wallart, L. Desplanque, and S. Huant, Transport inefficiency in branched-out mesoscopic networks: An analog of the Braess paradox, Physical Review Letters, vol. 108, no. 7, 076802, 2012.
- (59) A. Sousa, A. Chaves, G. Farias, and F. Peeters, Braess paradox at the mesoscopic scale, Physical Review B, vol. 88, no. 24, 245417, 2013.
- (60) P. S. Skardal, D. Taylor, and J. Sun, Optimal synchronization of complex networks, Physical Review Letters, vol. 113, no. 14, 144101, 2014.
- (61) T. Nishikawa and A. E. Motter, Symmetric states requiring system asymmetry, Physical Review Letters, vol. 117, no. 11, 114101, 2016.
- (62) T. Nishikawa, F. Molnar, and A. E. Motter, Stability landscape of power-grid synchronization, IFAC-PapersOnLine, vol. 48, no. 18, pp. 1–6, 2015.
- (63) Y. Kuramoto, Reduction methods applied to non-locally coupled oscillator systems. In Nonlinear Dynamics And Chaos: Where Do We Go From Here. CRC Press, Boca Raton, FL, 2002.
- (64) D. M. Abrams and S. H. Strogatz, Chimera states for coupled oscillators, Physical Review Letters, vol. 93, no. 17, 174102, 2004.
- (65) N. C. Rattenborg, C. J. Amlaner, and S. L. Lima, Behavioral, neurophysiological and evolutionary perspectives on unihemispheric sleep, Neuroscience & Biobehavioral Reviews, vol. 24, no. 8, pp. 817–842, 2000.
- (66) J. M. Davidenko, A. V. Pertsov, R. Salomonsz, W. Baxter, and J. Jalife, Stationary and drifting spiral waves of excitation in isolated cardiac muscle, Nature, vol. 355, no. 6358, pp. 349–351, 1992.
- (67) Y. Kuramoto and D. Battogtokh, Coexistence of coherence and incoherence in nonlocally coupled phase oscillators, Nonlinear Phenomena in Complex Systems, vol. 5, no. 4, pp. 380–385, 2002.
- (68) Y. Kuramoto and S.-i. Shima, Rotating spirals without phase singularity in reaction-diffusion systems, Progress of Theoretical Physics Supplement, vol. 150, pp. 115–125, 2003.
- (69) A. M. Hagerstrom, T. E. Murphy, R. Roy, P. Hövel, I. Omelchenko, and E. Schöll, Experimental observation of chimeras in coupled-map lattices, Nature Physics, vol. 8, no. 9, pp. 658–661, 2012.
- (70) M. R. Tinsley, S. Nkomo, and K. Showalter, Chimera and phase-cluster states in populations of coupled chemical oscillators, Nature Physics, vol. 8, no. 9, pp. 662–665, 2012.
- (71) E. A. Martens, S. Thutupalli, A. Fourrière, and O. Hallatschek, Chimera states in mechanical oscillator networks, Proceedings of the National Academy of Sciences USA, vol. 110, no. 26, pp. 10563–10567, 2013.
- (72) M. Wolfrum and E. Omel’chenko, Chimera states are chaotic transients, Physical Review E, vol. 84, no. 1, 015201, 2011.
- (73) M. J. Panaggio and D. M. Abrams, Chimera states: Coexistence of coherence and incoherence in networks of coupled oscillators, Nonlinearity, vol. 28, no. 3, pp. R67–R87, 2015.
- (74) Y. S. Cho, T. Nishikawa, and A. E. Motter, Stable chimeras and independently synchronizable clusters, Physical Review Letters, vol. 119, no. 8, 084101, 2017.
- (75) Y. Suda and K. Okuda, Persistent chimera states in nonlocally coupled phase oscillators, Physical Review E, vol. 92, no. 6, 060901, 2015.
- (76) J. D. Hart, K. Bansal, T. E. Murphy, and R. Roy, Experimental observation of chimera and cluster states in a minimal globally coupled network, Chaos, vol. 26, no. 9, 094801, 2016.
- (77) C. Bick and P. Ashwin, Chaotic weak chimeras and their persistence in coupled populations of phase oscillators, Nonlinearity, vol. 29, no. 5, pp. 1468–1486, 2016.
- (78) L. Schmidt, K. Schönleber, K. Krischer, and V. García-Morales, Coexistence of synchrony and incoherence in oscillatory media under nonlinear global coupling, Chaos, vol. 24, no. 1, 013102, 2014.
- (79) Z. G. Nicolaou, H. Riecke, and A. E. Motter, Chimera states in continuous media: Existence and distinctness, Physical Review Letters, vol. 119, no. 24, 244101, 2017.
- (80) V. Nicosia, M. Valencia, M. Chavez, A. Díaz-Guilera, and V. Latora, Remote synchronization reveals network symmetries and functional modules, Physical Review Letters, vol. 110, no. 17, 174102, 2013.
- (81) L. Zhang, A. E. Motter, and T. Nishikawa, Incoherence-mediated remote synchronization, Physical Review Letters, vol. 118, no. 17, 174102, 2017.
- (82) H. G. Winful and L. Rahman, Synchronized chaos and spatiotemporal chaos in arrays of coupled lasers, Physical Review Letters, vol. 65, no. 13, pp. 1575–1578, 1990.
- (83) I. Fischer, R. Vicente, J. M. Buldú, M. Peil, C. R. Mirasso, M. Torrent, and J. García-Ojalvo, Zero-lag long-range synchronization via dynamical relaying, Physical Review Letters, vol. 97, no. 12, 123902, 2006.
- (84) B. D. MacArthur, R. J. Sánchez-García, and J. W. Anderson, Symmetry in complex networks, Discrete Applied Mathematics, vol. 156, no. 18, pp. 3525–3531, 2008.
- (85) L. M. Pecora, F. Sorrentino, A. M. Hagerstrom, T. E. Murphy, and R. Roy, Symmetries, cluster synchronization, and isolated desynchronization in complex networks, Nature Communications, vol. 5, 4079, 2014.
- (86) J. J. Hopfield, Neural networks and physical systems with emergent collective computational abilities, Proceedings of the National Academy of Sciences USA, vol. 79, no. 8, pp. 2554–2558, 1982.
- (87) L. Cardelli, R. Hernansaiz-Ballesteros, N. Dalchau, and C.-N. A, Efficient switches in biology and computer science, PLoS Computational Biology, vol. 13, no. 1, e1005100, 2017.
- (88) J. Klinglmayr and C. Bettstetter, Self-organizing synchronization with inhibitory-coupled oscillators: Convergence and robustness, ACM Transactions on Autonomous and Adaptive Systems, vol. 7, no. 3, pp. 30:1–30:23, 2012.
- (89) J. Klinglmayr, C. Kirst, C. Bettstetter, and M. Timme, Guaranteeing global synchronization in networks with stochastic interactions, New Journal of Physics, vol. 14, no. 7, 073031, 2012.
- (90) C. Kirst, Synchronization, Neuronal Excitability, and Information Flow in Networks of Neuronal Oscillators. PhD Thesis, University of Göttingen, Göttingen, Germany, 2012.
- (91) C. Kirst, M. Timme, and D. Battaglia, Dynamic information routing in complex networks, Nature Communications, vol. 7, 11061, 2016.
- (92) F. M. Atay, J. Jost, and A. Wende, Delays, connection topology, and synchronization of coupled chaotic maps, Physical Review Letters, vol. 92, no. 14, 144101, 2004.
- (93) U. Ernst, K. Pawelzik, and T. Geisel, Synchronization induced by temporal delays in pulse-coupled oscillators, Physical Review Letters, vol. 74, no. 9, pp. 1570–1573, 1995.
- (94) M. Timme, F. Wolf, and T. Geisel, Prevalence of unstable attractors in networks of pulse-coupled oscillators, Physical Review Letters, vol. 89, no. 15, 154105, 2002.
- (95) J. H. Meng and H. Riecke, Synchronization by uncorrelated noise: Interacting rhythms in interconnected oscillator networks, Scientific Reports, vol. 8, no. 1, 6949, 2018.
- (96) P. Clusella and A. Politi, Noise-induced stabilization of collective dynamics, Physical Review E, vol. 95, no. 6, 062221, 2017.
- (97) R. M. Amro, B. Lindner, and A. B. Neiman, Phase diffusion in unequally noisy coupled oscillators, Physical Review Letters, vol. 115, no. 3, 034101, 2015.
- (98) D. Achlioptas, R. M. D’souza, and J. Spencer, Explosive percolation in random networks, Science, vol. 323, no. 5920, pp. 1453–1455, 2009.
- (99) R. A. da Costa, S. N. Dorogovtsev, A. V. Goltsev, and J. F. F. Mendes, Explosive percolation transition is actually continuous, Physical Review Letters, vol. 105, no. 25, 255701, 2010.
- (100) O. Riordan and L. Warnke, Explosive percolation is continuous, Science, vol. 333, no. 6040, pp. 322–324, 2011.
- (101) P. Grassberger, C. Christensen, G. Bizhani, S.-W. Son, and M. Paczuski, Explosive percolation is continuous, but with unusual finite size behavior, Physical Review Letters, vol. 106, no. 22, 225701, 2011.
- (102) J. Nagler, A. Levina, and M. Timme, Impact of single links in competitive percolation, Nature Physics, vol. 7, no. 3, pp. 265–270, 2011.
- (103) V. Vlasov, Y. Zou, and T. Pereira, Explosive synchronization is discontinuous, Physical Review E, vol. 92, no. 1, 012904, 2015.
- (104) J. Gómez-Gardeñes, S. Gómez, A. Arenas, and Y. Moreno, Explosive synchronization transitions in scale-free networks, Physical Review Letters, vol. 106, no. 12, 128701, 2011.
- (105) I. Leyva, R. Sevilla-Escoboza, J. Buldú, I. Sendina-Nadal, J. Gómez-Gardeñes, A. Arenas, Y. Moreno, S. Gómez, R. Jaimes-Reátegui, and S. Boccaletti, Explosive first-order transition to synchrony in networked chaotic oscillators, Physical Review Letters, vol. 108, no. 16, 168702, 2012.
- (106) Y. Zou, T. Pereira, M. Small, Z. Liu, and J. Kurths, Basin of attraction determines hysteresis in explosive synchronization, Physical Review Letters, vol. 112, no. 11, 114102, 2014.
- (107) J. Horgan, From complexity to perplexity, Scientific American, vol. 272, no. 6, pp. 104–109, 1995.