Antiferromagnetic Ground State, Charge Density Waves and Oxygen Vacancies Induced Metal-Insulator Transition in Pressurized La3Ni2O7
Abstract
La3Ni2O7 has garnered widespread interest recently due to its high-temperature superconductivity under pressure, accompanied by charge density wave (CDW) ordering and metal-insulator (MI) transitions in the phase diagram. Here, we reveal with comprehensive calculations that La3Ni2O7 possesses an antiferromagnetic ground state under both low and high pressures, with the strong Fermi surface nesting contributed by the flat band that leads to phonon softening and electronic instabilities. Several stable CDW orders with oxygen octahedral distortions are identified, which can trigger the MI transitions. The estimated CDW transition temperature (120 K) at ambient pressure agrees nicely with experimental results. In the presence of apical oxygen vacancies, we identify two different phases, say, half distortion and full distortion phases, respectively, and their competition can lead to a pressure-induced MI transition, in good agreement with experimental observations. In addition, we find that the electron-phonon coupling is too small to contribute to superconductivity. These results appear to indicate an unconventional superconducting pairing mechanism mediated by antiferromagnetic fluctuations. A phase diagram that is consistent with the experimental results is given. The present results not only explain the origins of experimentally observed CDW and MI transitions, but also provide insight for deeply understanding the properties like superconductivity, CDW and the role of oxygen vacancies in pressurized La3Ni2O7.
Introduction.—Over the past decades, exploring and understanding superconductors with high superconducting transition temperatures () have been the pivotal focuses in condensed matter physics [1, 2]. Recently, the Ruddlesden–Popper nickelate La3Ni2O7 was found to exhibit a of nearly 80 K under pressure [3]. Subsequent experiments consistently confirmed this observation, as evidenced by both zero resistance [4, 5, 6, 7, 8] and diamagnetic susceptibility [8]. The electronic configuration with Ni2.5+ in La3Ni2O7 deviates from the 3 configuration of transition metal ions in infinite-layer nickelates and cuprates [3, 9, 10]. Despite diverse views in extensive theoretical studies, broad consensuses have emerged regarding the crucial roles played by interlayer antiferromagnetic coupling, hybridization of orbitals, Hubbard interaction, Hund coupling, etc., for the onset of superconductivity [11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48].
Apart from superconductivity, the system undergoes a potential charge density wave (CDW) transition around 110-140 K under low pressures, as evidenced by nuclear magnetic resonance and anomalous kinks of resistivity, magnetization, specific heat and optical conductivity [49, 50, 51, 52, 53, 5, 54, 4, 7]. On the other hand, despite some La3Ni2O7 samples being identified as metals under ambient pressure, they undergo an unexpected metal-insulator (MI) transition under 2-4 GPa [3]. In contrast, the calculations based on the non-magnetic (NM) state reveal a robust metallic character under both low and high pressures [3, 55, 34, 56]. Therefore, an integrated and reasonable explanation for these experimental results remains elusive so far.
In this Letter, we perform comprehensive calculations based on the density functional theory (DFT) to examine structural, electronic, and phonon properties of La3Ni2O7 under pressures. We find that La3Ni2O7 possesses an antiferromagnetic ground state under both low and high pressures, with the strong Fermi surface (FS) nesting of electronic flat band that gives rise to the phonon softening at high symmetric points and electronic instabilities. We elucidate that CDW orders are originated from Peierls instability and trigger MI transitions. It is also found that the competition between the half distortion and full distortion phases with apical oxygen vacancies induces an MI transition under pressures. These calculated results are in good agreement with recent experimental findings. In addition, the electron-phonon coupling (EPC) is uncovered insufficient to be responsible for superconductivity, suggesting that the Cooper pairing mechanism is unconventional in pressurized La3Ni2O7, and is probably from antiferromagnetic fluctuations.
Superconductivity not from BCS.—The crystal structure of La3Ni2O7 changes from the Cmcm to the Fmmm space group at about 15 GPa [FiG. 1(a)] [3], coinciding with the onset of superconductivity. Based on Bardeen-Cooper-Schrieffer (BCS) scenario, we calculate the superconducting properties of La3Ni2O7 as listed in Table 1. Despite a considerable electronic density of states at the Fermi level N(), we find that the EPC constant remains below 0.25 for both Cmcm and Fmmm phases, and both N() and decrease with increasing pressure. By calculations we reveal that the low results in zero under 0-50 GPa, indicating that the EPC alone cannot account for experimental [3]. This shows that the superconducting pairing mechanism in pressurized La3Ni2O7 is unconventional.
| Pressure (GPa) | Space group | N() (eV-1f.u.-1) | (K) | (K) | ||
|---|---|---|---|---|---|---|
| 0 | Cmcm | 0.245 | 43.50 | 129.17 | 0.01 | 0 |
| 10 | Cmcm | 0.166 | 37.96 | 178.63 | 0.00 | 0 |
| 20 | Fmmm | 0.155 | 37.93 | 304.89 | 0.00 | 82 |
| 30 | Fmmm | 0.145 | 36.25 | 306.15 | 0.00 | 75 |
| 40 | Fmmm | 0.140 | 35.39 | 312.92 | 0.00 | 72 |
| 50 | Fmmm | 0.137 | 34.68 | 324.51 | 0.00 | - |
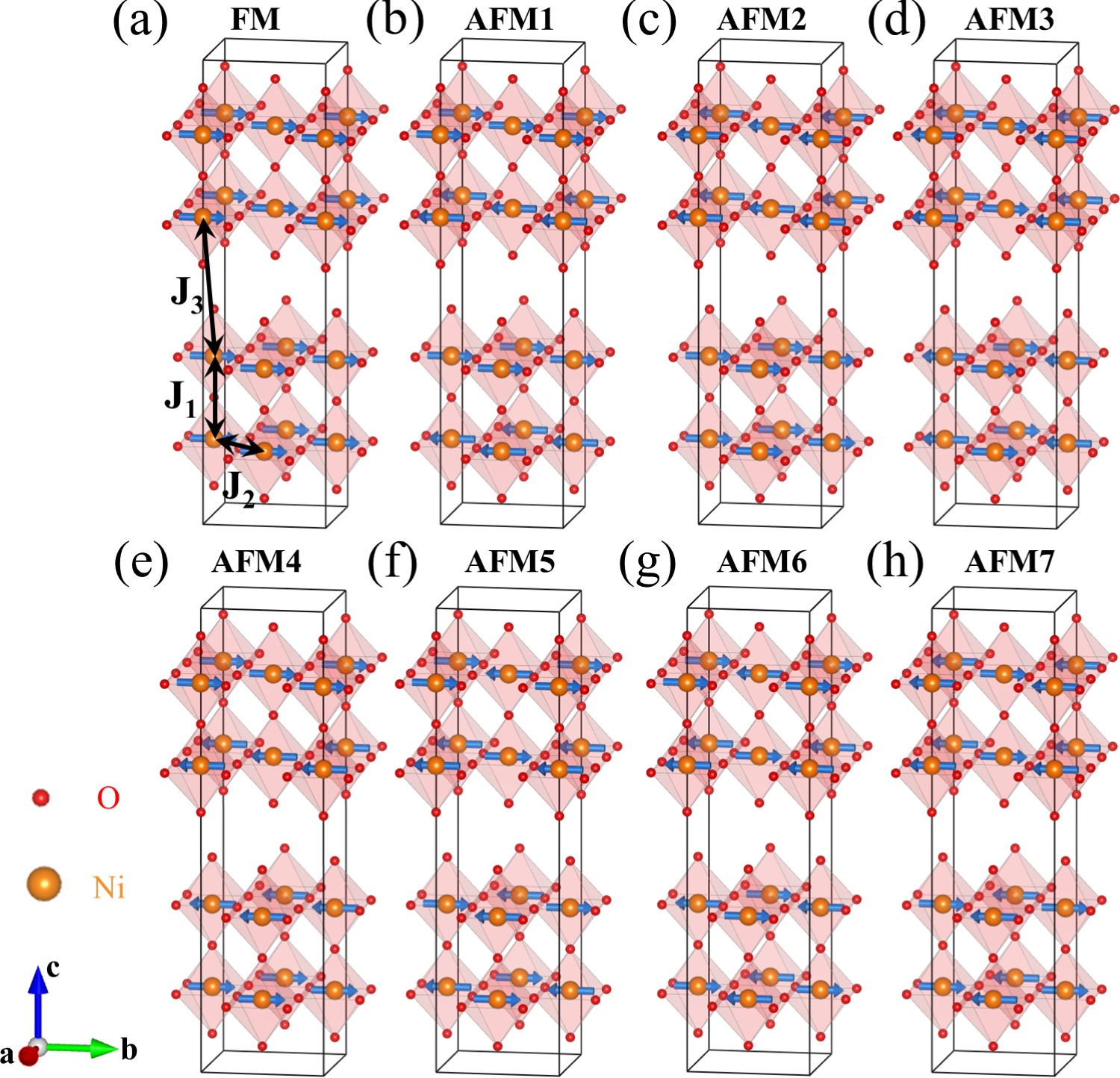
Antiferromagnetic ground state.—We consider the interlayer nearest-neighbor (NN) coupling (), intralayer NN coupling (), and interlayer next NN coupling () among Ni atoms [FiG. 1(a)]. Combining all positive and negative values of , and , we calculate ferromagnetic (FM) and seven antiferromagnetic (AFM1-7) configurations, as depicted in FIG. S1 of supplemental materials (SM) [57]. As seen in FIG. 1(b), the energies of eight magnetic configurations form degenerate pairs, originating from 0. Energies of all magnetic states are lower than that of NM state, suggesting magnetic tendencies favor the stability of system. The magnetic ground state is AFM1 (AFM4), which shows intralayer ferromagnetism and interlayer antiferromagnetism [FiG. 1(a)]. Notably, experimental results including muon spin relaxation (SR), resonant inelastic X-ray scattering and magnetic susceptibility also support the AFM ground state [58, 59, 60, 52]. The AFM ground state suggests that the Cooper pairing in this nickelate may be mediated by AFM fluctuations.
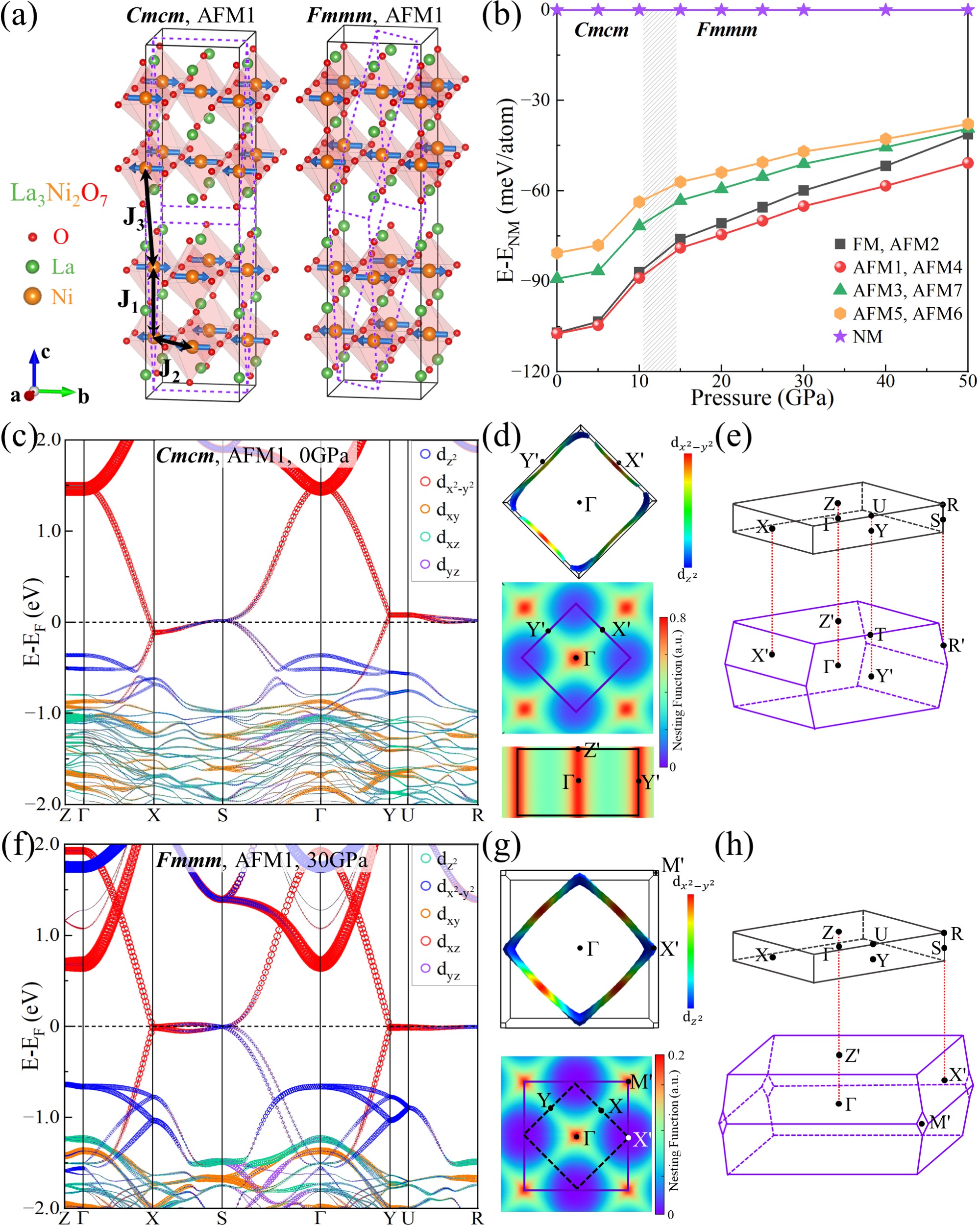
Fermi surface nesting.—Under the AFM1 configuration, the band structures of the Cmcm phase at 0 GPa and the Fmmm phase at 30 GPa are depicted in FIG. 1(c) and (f), respectively. Similar to the NM scenario, their electronic states near are predominantly contributed by the and orbitals. However, a remarkably flat band emerges near , with its flatness significantly increasing as pressure rises to 30 GPa, suggesting an enhanced correlated electron effect. More intriguingly, the FS formed by this flat band exhibits a perfect two-dimensional (2D) square-cylinder characteristic in FIG. 1(d) and (g). The band characteristics near in La3Ni2O7 resemble the results of the Hubbard model on a 2D square lattice [61]. The strong nesting features of this square FS evoke potential electronic instabilities. The calculated FS nesting function in FIG. 1(d) [62, 57], shows strong peaks along -Z′, which aligns with the nesting vector of the FS. Results at 30 GPa in FIG. 1(g) is similar, albeit with a different BZ and high symmetry points.
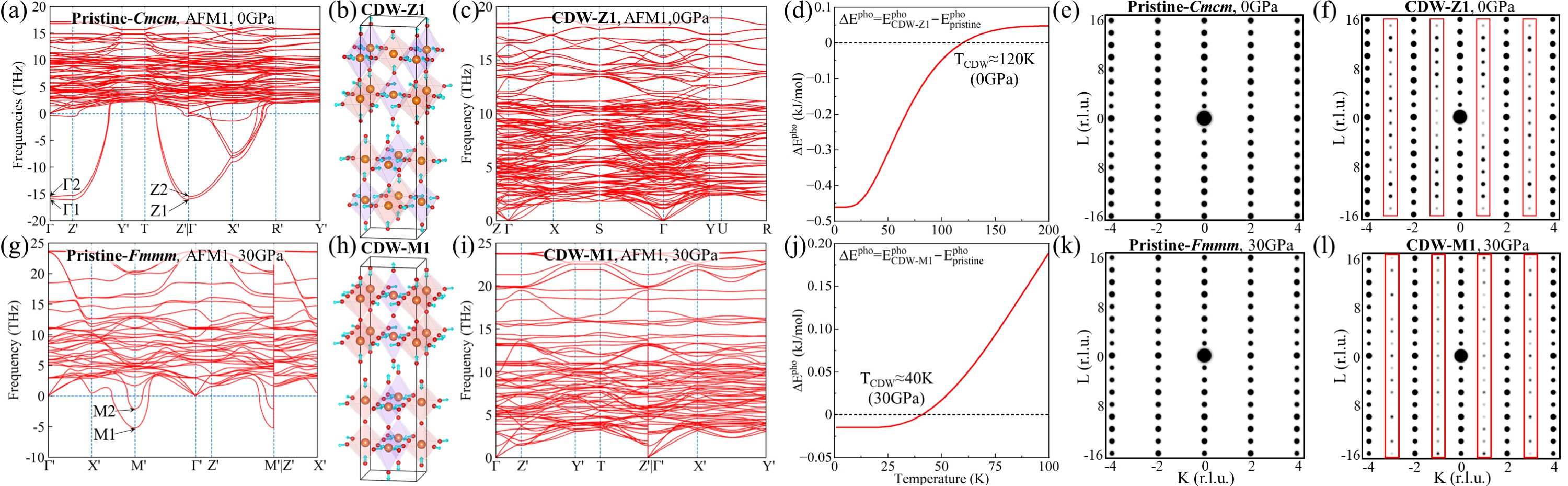
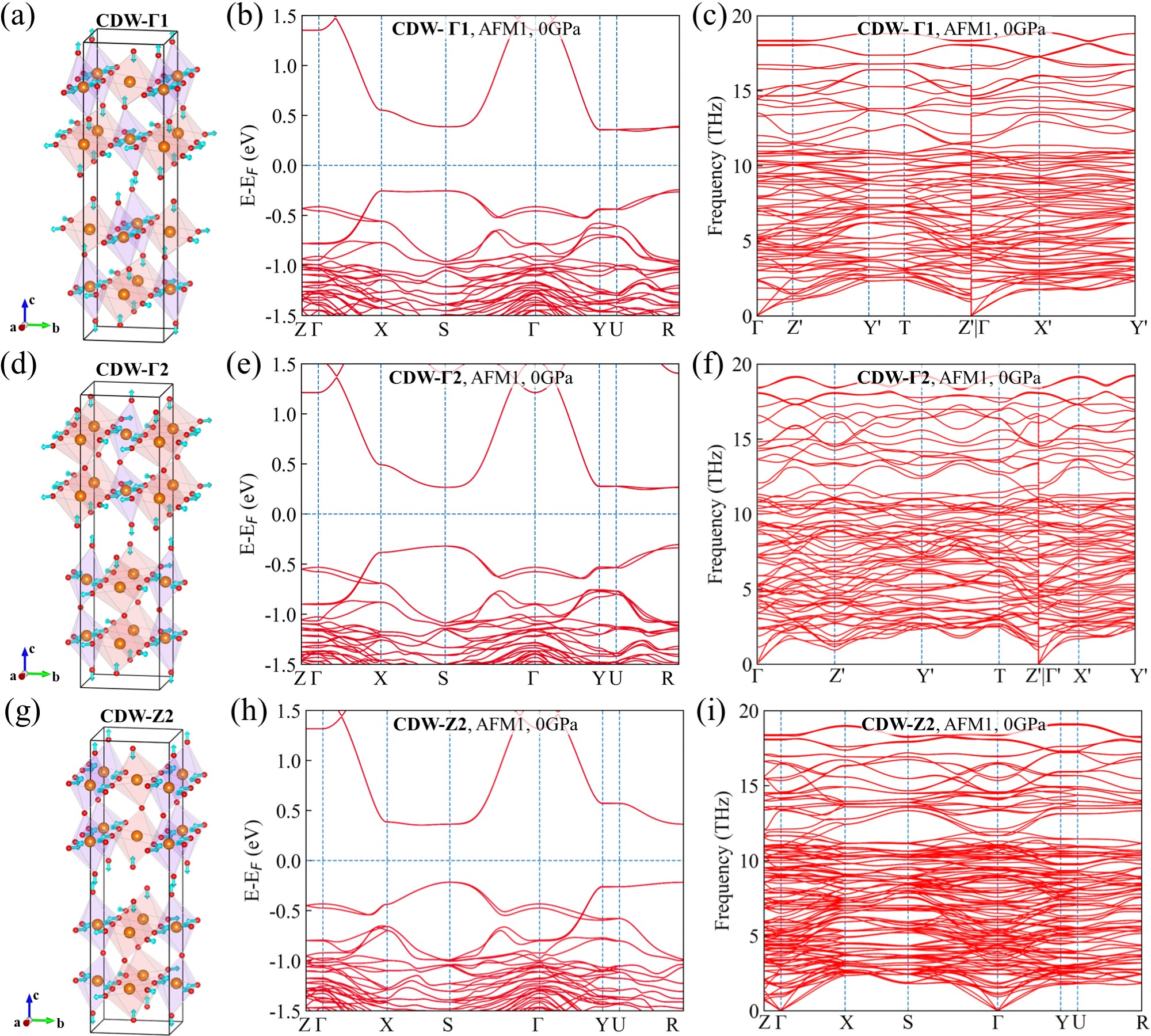
Stable CDW phases.—To explore its structural stability, the phonon spectra at 0 and 30 GPa are calculated in FIG. 2(a) and (g). For the Cmcm phase, two phonon branches exhibit imaginary frequencies along the -Z′ path, with four imaginary modes at and Z′ points denoted as , , Z1, and Z2, respectively, each leading to distinct structural distortions. Following careful structural relaxation, stable phases are obtained named as CDW- (space group: ), CDW- (Amm2), CDW-Z1 (Pnma) and CDW-Z2 (Pmmn), respectively. Detailed lattice information for these phases can be found in Table S3. These phases share a similarity in the in-plane expansion (fat) and contraction (skim) of oxygen octahedra alternating in each layer, with difference lying in the arrangement and orientation of the octahedra [FIG. 2(b) and S5]. For the CDW-Z1 phase corresponding to the lowest imaginary mode Z1 as an example, the phonon spectrum in FIG. 2(c) confirms its stability. By comparing the harmonic phonon energy of the NM state of pristine phase with the AFM1 state of the CDW-Z1 phase, we estimate the transition temperature of CDW phase () to be 120 K [FIG. 2(d)], consistent with experimental results [49, 51, 52, 53, 5, 54, 4, 7, 50].
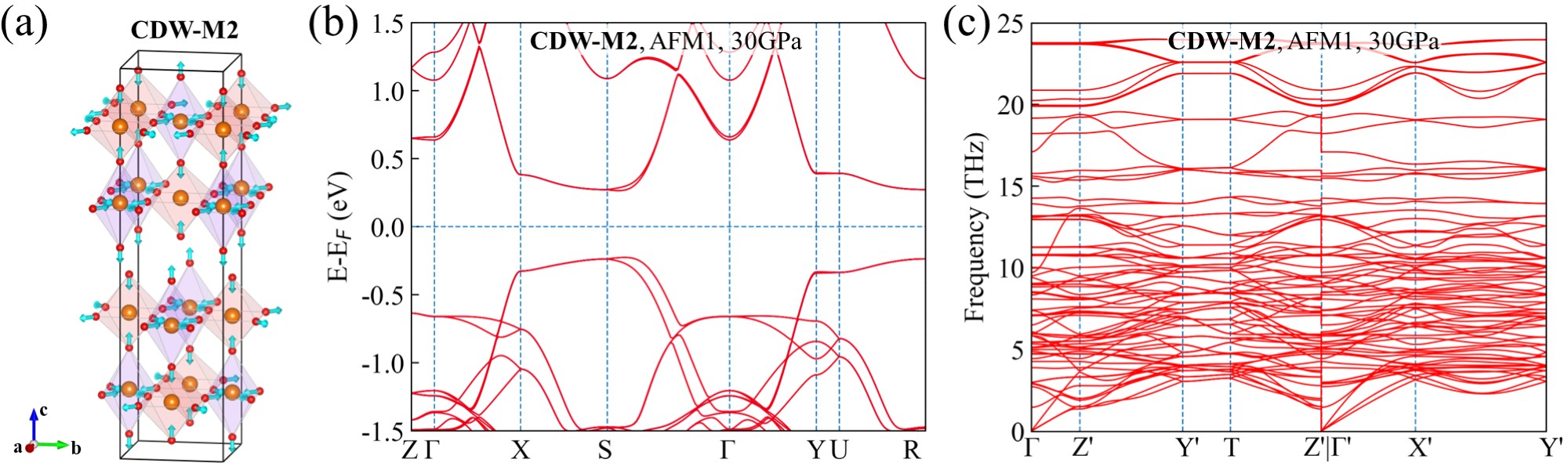
For the Fmmm phase, only phonon branches near the M′ point show imaginary frequencies, with a softer effect compared to the Cmcm phase at 0 GPa [FiG. 2(g)]. Two imaginary modes at the M′ point are labeled as M1 and M2, corresponding to stable distorted structures named CDW-M1 (Cmmm) and CDW-M2 (Cmcm), respectively. CDW-M1 exhibits similar octahedral distortions to CDW-Z1 but includes an additional horizontal mirror symmetry of the Ni-O bilayer [FiG. 2(h)]. The estimated of CDW-M1 at 30 GPa is around 40 K, much lower than that at 0 GPa. Other CDW phases at various pressures also exhibit stable phonon spectra, as shown in FIG. S5 and S6.
Notably, the momenta with imaginary phonons in FIG. 2(a) and (g) correspond to those exhibiting strong peaks of in FIG. 1(d) and (g), confirming that CDW originates from Peierls instability related to FS nesting. The imaginary phonons in the AFM1 state contrasts with the stable phonons in the NM state [55], implying the instabilities are related to antiferromagnetism.
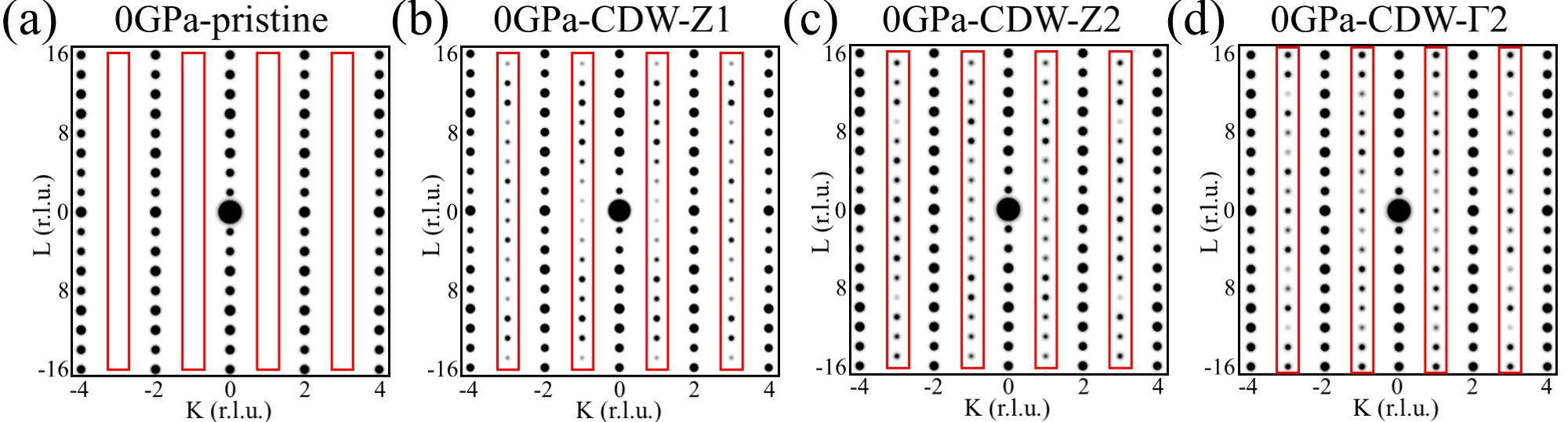
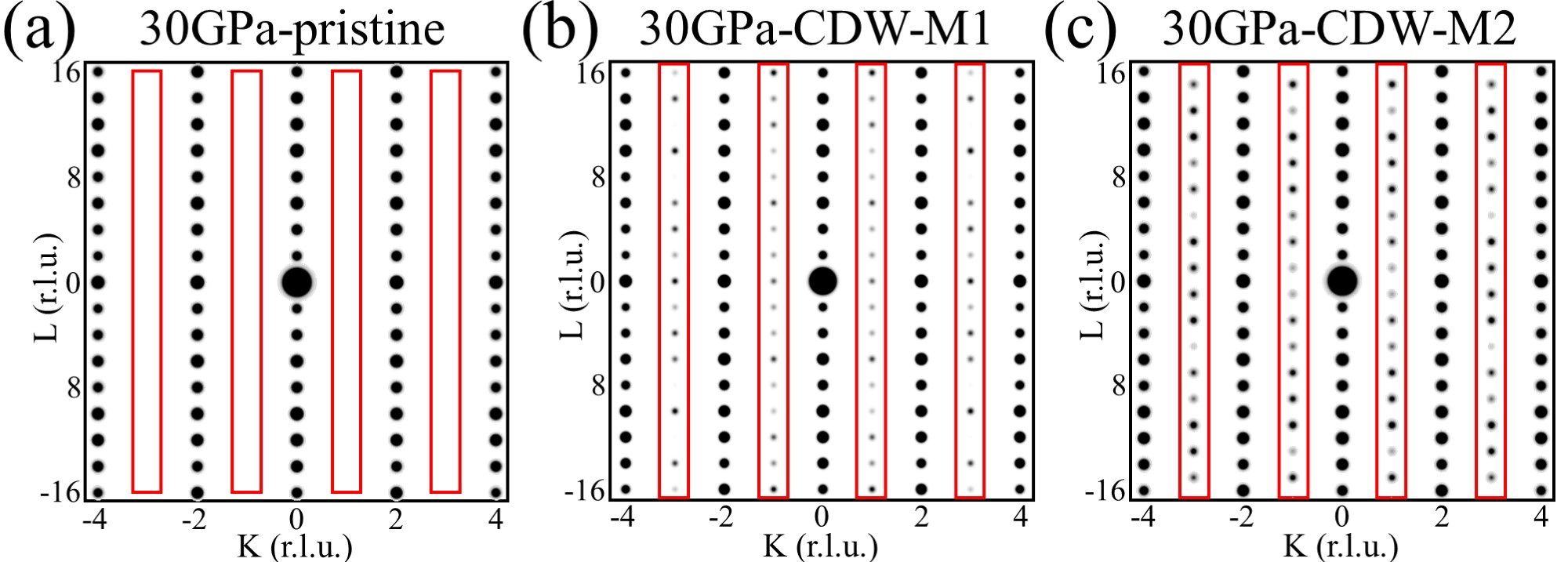
The distortion of Ni-O bond length is less than 0.1 Å, posing challenges in probing predicted CDW structures in experiments. Simulated XRD spectra show that most CDW phases exhibit nearly identical peak positions and intensities to pristine phases at both 0 and 30 GPa, except for CDW-1 with a distinct Bravais lattice [FiG. S9 and S10]. To aid in identifying CDW phases in experiments, we simulate diffraction patterns that can be measured using techniques such as XRD and transmission electron microscopy. Diffraction patterns of the CDW-Z1 phase show emergent spots with odd Miller indices K compared with pristine-Cmcm phases in FIG. 2(e) and (f). Similar patterns are observed in the CDW-M1 phase at 30 GPa in FIG. 2(l) and other CDW phases in FIG. S11 and S12.
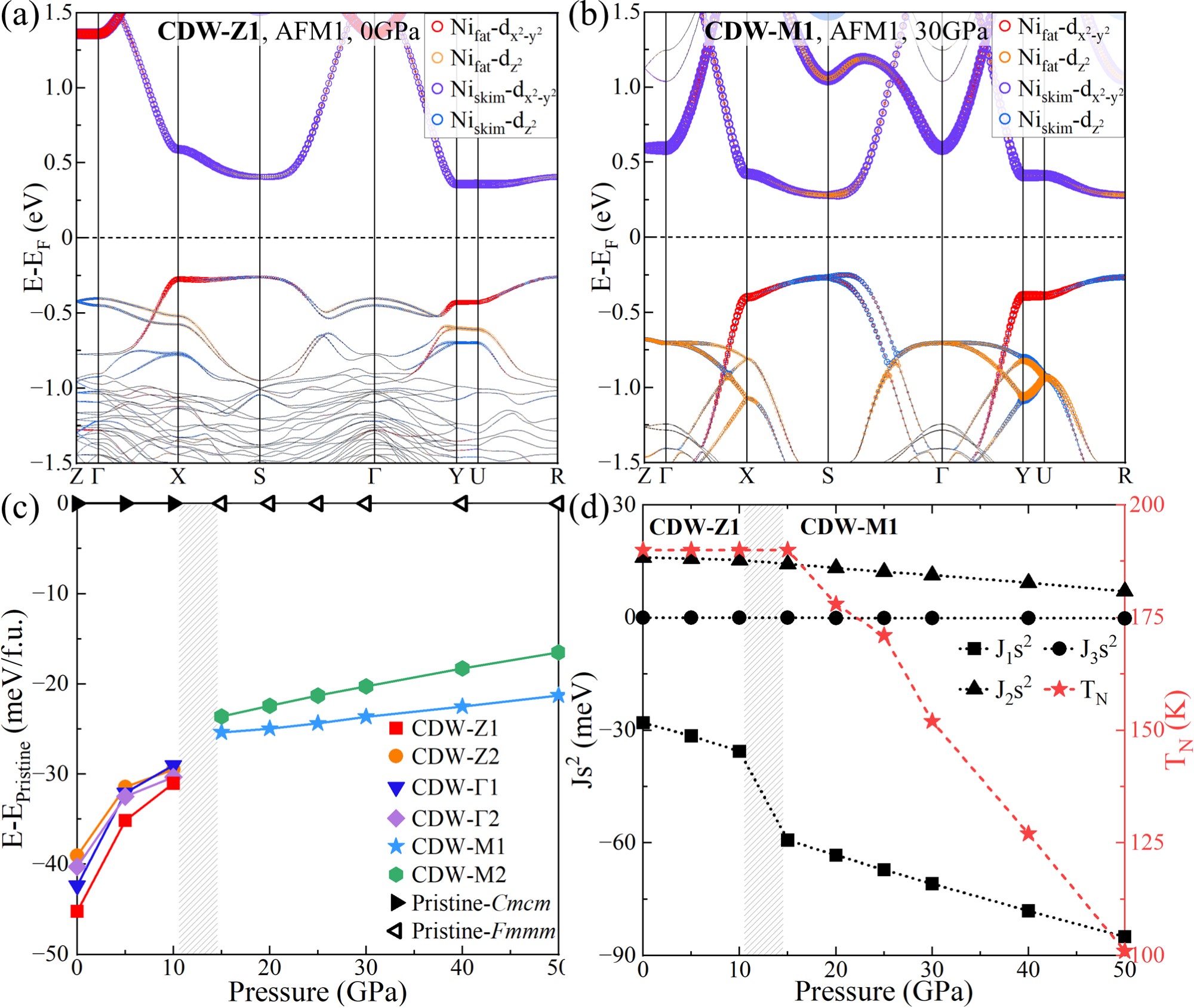
We further analyze the magnetic properties of CDW phases. By comparing the energy of different magnetic states under pressure [FiG. S1], we find a gradual increase in the AFM , alongside a decrease in the FM with increasing pressure, except for 0 as seen in Fig. 3(d). Furthermore, consistently exceeds , indicating strong interlayer AFM coupling. Employing Monte Carlo simulation based on the Heisenberg-type Hamiltonian: , where is the energy independent of the spin configurations, we determine that the Neel temperature remains above 100 K under 0-50 GPa, surpassing the calculated in FIG. 2(g) and (j), suggesting that the presence of robust magnetic coupling is capable of inducing the CDW transition.
Unlike pristine phases with metallic behavior in FIG. 1(c) and (f), both CDW-Z1 and CDW-M1 phases exhibit band gaps of about 0.5 eV in FIG. 3(a) and (b). Similar gaps are observed in other CDW phases [FIG. S5 and S6]. The orbitals of Ni atoms in the expanded and contracted oxygen octahedra (named as Nifat and Niskim) are split, with the orbital shifted downward and upward, respectively. It means that the distinct octahedra caused by CDW transitions leads to this MI transition.
All CDW phases have lower enthalpies compared to pristine phases under pressure in FIG. 3(c), indicating their energetic stability. Specifically, CDW-Z1 and CDW-M1 originating from the lowest imaginary phonon modes have the lowest energy under low and high pressure, respectively.
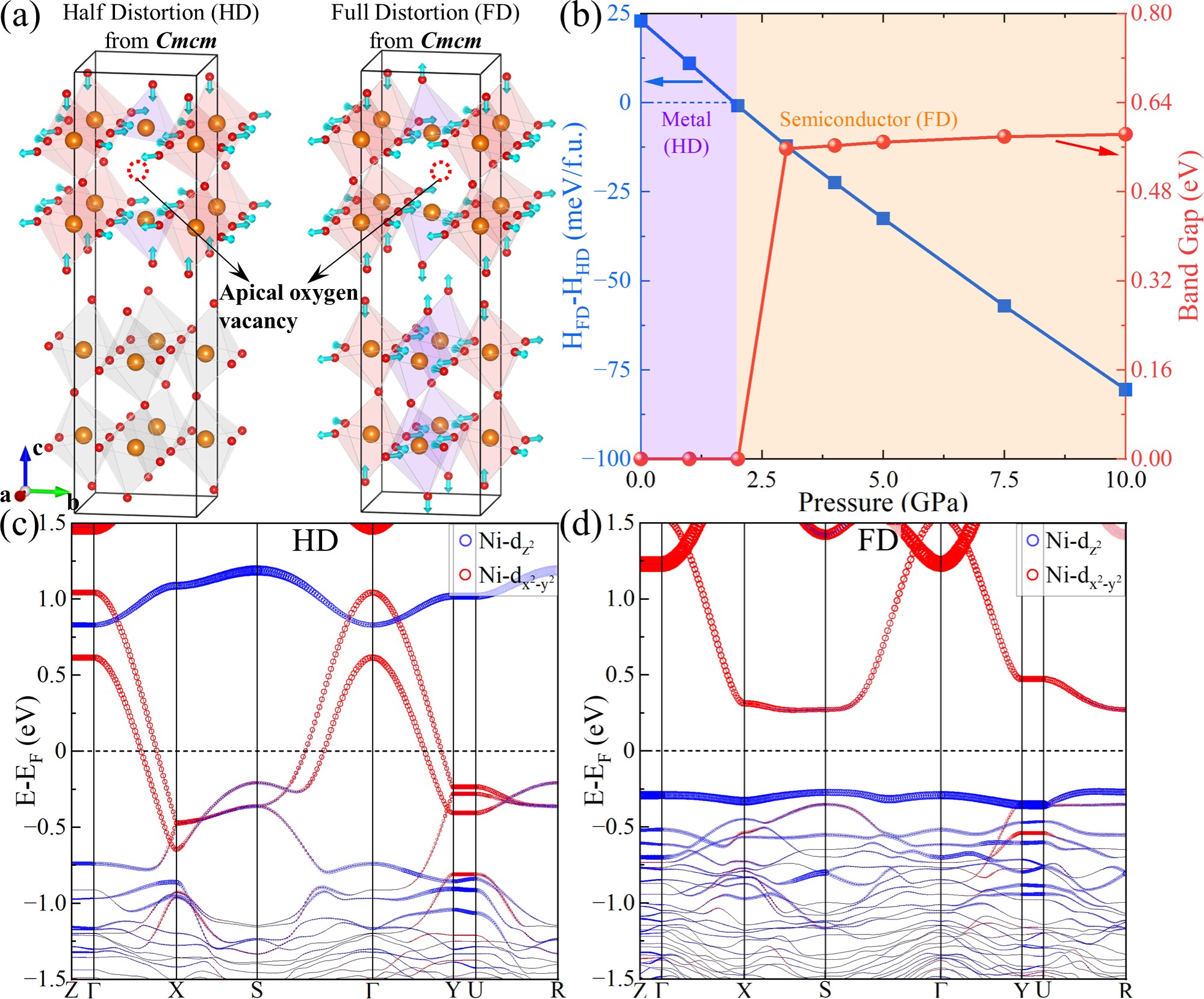
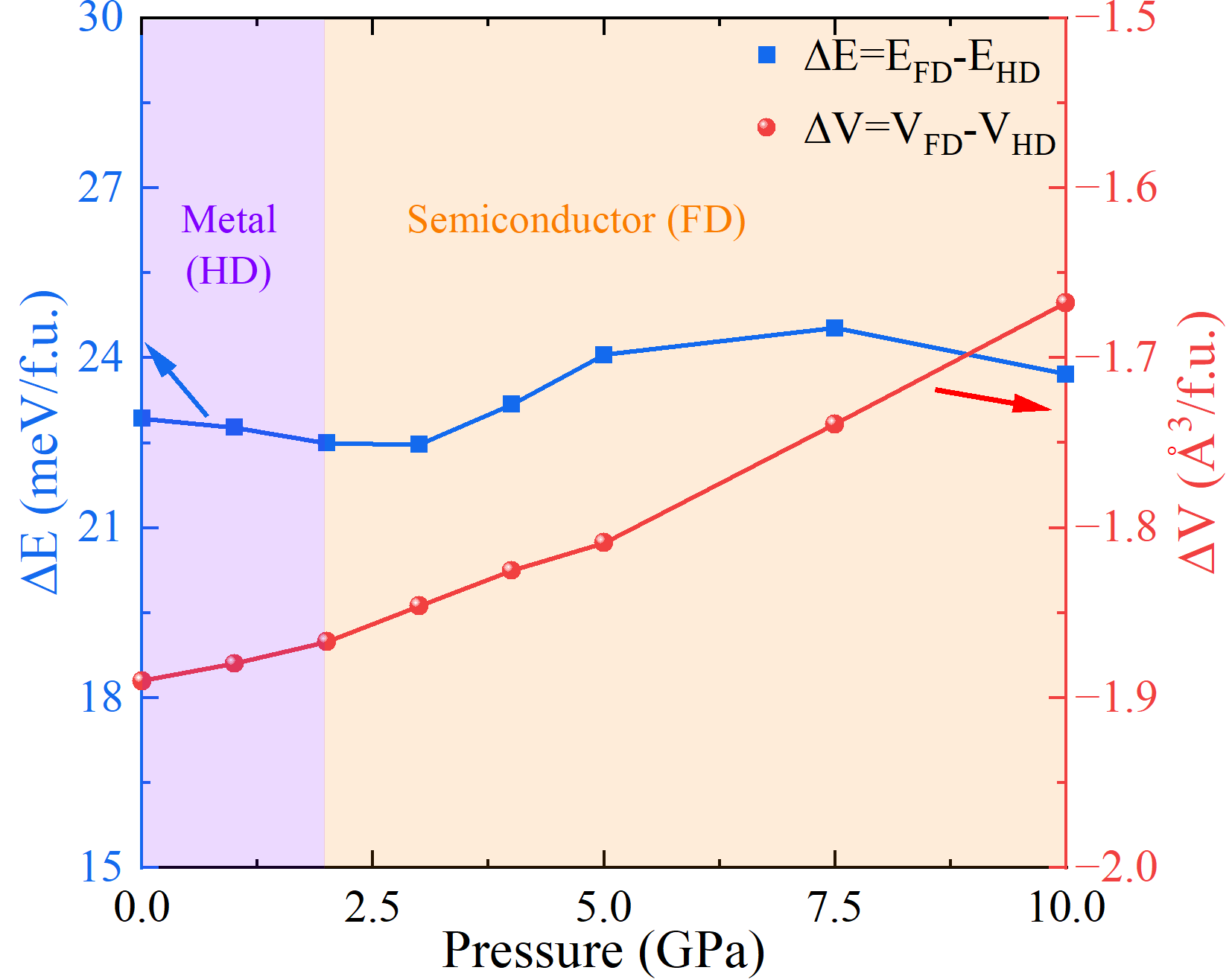
Role of Apical Oxygen Vacancies.—Experimental evidence suggests the existence of oxygen vacancies with a nonstoichiometry of La3Ni2O7-δ as high as 0.34 [63]. Our calculations reveal that the apical oxygen vacancy has the lowest energy compared with vacancies at other sites, consistent with previous reports [63, 64]. After careful structural optimization for La3Ni2O6.75 with apical oxygen vacancies, two unexpectedly stable structures emerge as shown in FIG. 4(a). One structure exhibits structural distortion only near the defect, while the other shows distortion in all NiO bilayers, labeled as half distortion (HD) and full distortion (FD) phases, respectively. Comparing their enthalpies (H) in FIG. 4(b), we observe a phase transition from the HD to the FD phase at 2 GPa. The H can be divided into two terms, H=E+PV, where E, P, and V represent energy, pressure, and volume, respectively. As seen in FIG. S13, although the HD phase consistently displays lower at 0-10 GPa, the smaller V of the FD phase makes it thermodynamically more stable under high pressure.
Further band calculations reveal the HD phase is a metal similar to electron doped La3Ni2O7 in FIG. 1(c). Conversely, the FD phase exhibits a gap of about 0.5 eV and a flat valence band. This indicates an MI transition accompanying the phase transition of the two vacancy structures, which is absent in the pure crystal phase. The FD phase of La3Ni2O6.75 in FIG. 4(a) exhibits expansion and contraction for all oxygen octahedra, similar to the CDW phase in FIG. 2(h). This unexpected similarity is intriguing. The lower H of the FD phase above 2 GPa indicates harmony between oxygen vacancies and CDW under high pressure. On the contrary, the HD phase becomes more stable below 2 GPa, suggesting oxygen vacancies suppress structural distortions of CDW at this stage.
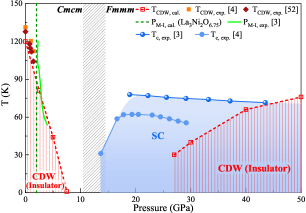
Phase Diagram and Discussions.— We summarize the main findings and related experimental data in a phase diagram shown in FIG. 5. It can be seen that the calculated of the CDW-Z1 phase gradually decreases with increasing pressure, reaching zero at 7.5 GPa, nicely aligning with experimental results [4, 52, 7]. Our calculations clearly reveal that the temperature-induced MI transition stems from the structural distortion of CDW [5, 6, 52, 65]. Beyond 27 GPa, the CDW-M1 phase emerges with 30 K. Recent experiments demonstrate a pronounced insulating behavior under high pressure below 50 K compressed in the diamond anvil cell and above compressed in the cubic anvil cell [5]. These findings may be related to our calculated CDW phases under high pressure, suggesting a potential coexistence or competition between CDW and superconductivity.
We found that the nonstoichiometric La3Ni2O6.75 undergoes an MI transition at 2 GPa, in good consistent with the pressure of MI transition in experiments () as seen in FIG. 5 [3]. The HD and FD phases identified in this work gain the insights for further theoretical and experimental analyses of the role of oxygen vacancies.
The SR experiments reveal a bulk AFM transition near 150 K for La3Ni2O7-δ [58, 59]. Additionally, a continuous increase in magnetic susceptibility suggests a potential AFM order below 350 K for La3Ni2O7.05 [52]. Our calculated for the CDW-Z1, pristine-Cmcm and HD phases are 190, 393 and 95 K at 0 GPa, respectively [Table S2], showing that such variation in among different phases may explain the inconsistency in reported experimental .
Summary.—In this work, we report by performing comprehensive DFT calculations that the La3Ni2O7 possesses an antiferromagnetic ground state, with the strong FS nesting of the electronic flat band, which can drive the CDW transitions and trigger the MI transitions. In addition, we reveal that the competition between two different phases with apical oxygen vacancies can lead to a pressure-induced MI transition. These results are in good agreement with the experimental observations. The EPC in La3Ni2O7 is found insufficient to be responsible for superconductivity, suggesting that the Cooper pairing mechanism is unconventional, and may be from the AFM fluctuations. A complex phase diagram consistent with experiments are given. Our calculations explain well the physical origins behind a few experimental results, and give intensive comprehension for the physical properties such as superconductivity, CDW orders and roles of apical oxygen vacancies in La3Ni2O7, in which some results remain to be examined experimentally.
Acknowledgements.
Acknowledgments.— The authors are indebted to Qing-Bo Yan, Wei Li, Jie Zhang, Xing-Zhou Qu, Dai-Wei Qu and Jia-Lin Chen for useful discussions. This work is supported in part by the National Key RD Program of China (Grant No. 2018YFA0305800), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grants No. XDB28000000), the National Natural Science Foundation of China (Grant No.11834014), and the Innovation Program for Quantum Science and Technology (No. 2021ZD0301800). B.G. is supported in part by the National Natural Science Foundation of China (Grant No. 12074378), the Chinese Academy of Sciences (Grants No. YSBR-030, No. JZHKYPT-2021-08, No. XDB33000000), Beijing Municipal Science and Technology Commission (Grant No. Z191100007219013).References
- Keimer et al. [2015] B. Keimer, S. A. Kivelson, M. R. Norman, S. Uchida, and J. Zaanen, From quantum matter to high-temperature superconductivity in copper oxides, Nature 518, 179 (2015).
- Paglione and Greene [2010] J. Paglione and R. L. Greene, High-temperature superconductivity in iron-based materials, Nat. Phys. 6, 645 (2010).
- Sun et al. [2023] H. Sun, M. Huo, X. Hu, J. Li, Z. Liu, Y. Han, L. Tang, Z. Mao, P. Yang, B. Wang, J. Cheng, D. X. Yao, G. M. Zhang, and M. Wang, Signatures of superconductivity near 80 K in a nickelate under high pressure, Nature 621, 493 (2023).
- Zhang et al. [2023a] Y. Zhang, D. Su, Y. Huang, H. Sun, M. Huo, Z. Shan, K. Ye, Z. Yang, R. Li, M. Smidman, M. Wang, L. Jiao, and H. Yuan, High-temperature superconductivity with zero-resistance and strange metal behavior in La3Ni2O7 (2023a), arXiv:2307.14819 .
- Hou et al. [2023] J. Hou, P.-T. Yang, Z.-Y. Liu, J.-Y. Li, P.-F. Shan, L. Ma, G. Wang, N.-N. Wang, H.-Z. Guo, J.-P. Sun, Y. Uwatoko, M. Wang, G.-M. Zhang, B.-S. Wang, and J.-G. Cheng, Emergence of high-temperature superconducting phase in pressurized La3Ni2O7 crystals, Chin. Phys. Lett. 40, 117302 (2023).
- Zhang et al. [2024a] M. Zhang, C. Pei, Q. Wang, Y. Zhao, C. Li, W. Cao, S. Zhu, J. Wu, and Y. Qi, Effects of pressure and doping on Ruddlesden-Popper phases Lan+1NinO3n+1, J. Mater. Sci. Technol. 185, 147 (2024a).
- Wang et al. [2024] G. Wang, N. N. Wang, X. L. Shen, J. Hou, L. Ma, L. F. Shi, Z. A. Ren, Y. D. Gu, H. M. Ma, P. T. Yang, Z. Y. Liu, H. Z. Guo, J. P. Sun, G. M. Zhang, S. Calder, J. Q. Yan, B. S. Wang, Y. Uwatoko, and J. G. Cheng, Pressure-induced superconductivity in polycrystalline La3Ni2O7-δ, Phys. Rev. X 14, 011040 (2024).
- Zhou et al. [2023] Y. Zhou, J. Guo, S. Cai, H. Sun, P. Wang, J. Zhao, J. Han, X. Chen, Q. Wu, Y. Ding, M. Wang, T. Xiang, H. kwang Mao, and L. Sun, Evidence of filamentary superconductivity in pressurized La3Ni2O7 single crystals (2023), arXiv:2311.12361 .
- Luo et al. [2023a] Z. Luo, X. Hu, M. Wang, W. Wu, and D. X. Yao, Bilayer two-orbital model of La3Ni2O7 under pressure, Phys. Rev. Lett. 131, 126001 (2023a).
- Zhang et al. [2023b] Y. Zhang, L.-F. Lin, A. Moreo, and E. Dagotto, Electronic structure, dimer physics, orbital-selective behavior, and magnetic tendencies in the bilayer nickelate superconductor La3Ni2O7 under pressure, Phys. Rev. B 108, L180510 (2023b).
- Yang et al. [2023a] Q.-G. Yang, D. Wang, and Q.-H. Wang, Possible -wave superconductivity in La3Ni2O7, Phys. Rev. B 108, L140505 (2023a).
- Qin and Yang [2023] Q. Qin and Y.-F. Yang, High-Tc superconductivity by mobilizing local spin singlets and possible route to higher Tc in pressurized La3Ni2O7, Phys. Rev. B 108, L140504 (2023).
- Shen et al. [2023] Y. Shen, M. Qin, and G.-M. Zhang, Effective bi-layer model hamiltonian and density-matrix renormalization group study for the high-Tc superconductivity in La3Ni2O7 under high pressure, Chin. Phys. Lett. 40, 127401 (2023).
- Lechermann et al. [2023] F. Lechermann, J. Gondolf, S. Bötzel, and I. M. Eremin, Electronic correlations and superconducting instability in La3Ni2O7 under high pressure, Phys. Rev. B 108, L201121 (2023).
- Sakakibara et al. [2023] H. Sakakibara, N. Kitamine, M. Ochi, and K. Kuroki, Possible high Tc superconductivity in La3Ni2O7 under high pressure through manifestation of a nearly-half-filled bilayer Hubbard model (2023), arXiv:2306.06039 .
- Gu et al. [2023] Y. Gu, C. Le, Z. Yang, X. Wu, and J. Hu, Effective model and pairing tendency in bilayer Ni-based superconductor La3Ni2O7 (2023), arXiv:2306.07275 .
- Christiansson et al. [2023] V. Christiansson, F. Petocchi, and P. Werner, Correlated electronic structure of La3Ni2O7 under pressure, Phys. Rev. Lett. 131, 206501 (2023).
- Shilenko and Leonov [2023] D. A. Shilenko and I. V. Leonov, Correlated electronic structure, orbital-selective behavior, and magnetic correlations in double-layer La3Ni2O7 under pressure, Phys. Rev. B 108, 125105 (2023).
- Sakakibara et al. [2024] H. Sakakibara, N. Kitamine, M. Ochi, and K. Kuroki, Possible high Tc superconductivity in La3Ni2O7 under high pressure through manifestation of a nearly-half-filled bilayer Hubbard model, Phys. Rev. Lett. 132, 106002 (2024).
- Cao and Yang [2024] Y. Cao and Y.-F. Yang, Flat bands promoted by Hund’s rule coupling in the candidate double-layer high-temperature superconductor La3Ni2O7 under high pressure, Phys. Rev. B 109, L081105 (2024).
- Liu et al. [2023a] Y. B. Liu, J. W. Mei, F. Ye, W. Q. Chen, and F. Yang, -wave pairing and the destructive role of apical-oxygen deficiencies in La3Ni2O7 under pressure, Phys. Rev. Lett. 131, 236002 (2023a).
- Lu et al. [2023a] C. Lu, Z. Pan, F. Yang, and C. Wu, Interlayer coupling driven high-temperature superconductivity in La3Ni2O7 under pressure (2023a), arXiv:2307.14965 .
- Oh and Zhang [2023] H. Oh and Y.-H. Zhang, Type-II t-J model and shared superexchange coupling from Hund’s rule in superconducting La3Ni2O7, Phys. Rev. B 108, 174511 (2023).
- Liao et al. [2023] Z. Liao, L. Chen, G. Duan, Y. Wang, C. Liu, R. Yu, and Q. Si, Electron correlations and superconductivity in La3Ni2O7 under pressure tuning (2023), arXiv:2307.16697 .
- Qu et al. [2024] X.-Z. Qu, D.-W. Qu, J. Chen, C. Wu, F. Yang, W. Li, and G. Su, Bilayer t-J-J⟂ model and magnetically mediated pairing in the pressurized nickelate La3Ni2O7, Phys. Rev. Lett. 132, 036502 (2024).
- Jiang et al. [2024] K. Jiang, Z. Q. Wang, and F. C. Zhang, High temperature superconductivity in La3Ni2O7, Chin. Phys. Lett. 41, 017402 (2024).
- Huang et al. [2023] J. Huang, Z. D. Wang, and T. Zhou, Impurity and vortex states in the bilayer high-temperature superconductor La3Ni2O7, Phys. Rev. B 108, 174501 (2023).
- Tian et al. [2023] Y.-H. Tian, Y. Chen, J.-M. Wang, R.-Q. He, and Z.-Y. Lu, Correlation effects and concomitant two-orbital -wave superconductivity in La3Ni2O7 under high pressure (2023), arXiv:2308.09698 .
- Jiang et al. [2023] R. Jiang, J. Hou, Z. Fan, Z.-J. Lang, and W. Ku, Pressure driven screening of Ni spin results in cuprate-like high-Tc superconductivity in La3Ni2O7 (2023), arXiv:2308.11614 .
- Lu et al. [2023b] D.-C. Lu, M. Li, Z.-Y. Zeng, W. Hou, J. Wang, F. Yang, and Y.-Z. You, Superconductivity from doping symmetric mass generation insulators: Application to La3Ni2O7 under pressure (2023b), arXiv:2308.11195 .
- Luo et al. [2023b] Z. Luo, B. Lv, M. Wang, W. Wú, and D.-X. Yao, High-Tc superconductivity in La3Ni2O7 based on the bilayer two-orbital t-J model (2023b), arXiv:2308.16564 .
- Zhang et al. [2023c] J.-X. Zhang, H.-K. Zhang, Y.-Z. You, and Z.-Y. Weng, Strong pairing originated from an emergent berry phase in La3Ni2O7 (2023c), arXiv:2309.05726 .
- Yang et al. [2023b] H. Yang, H. Oh, and Y.-H. Zhang, Strong pairing from small Fermi surface beyond weak coupling: Application to La3Ni2O7 (2023b), arXiv:2309.15095 .
- LaBollita et al. [2023] H. LaBollita, V. Pardo, M. R. Norman, and A. S. Botana, Electronic structure and magnetic properties of La3Ni2O7 under pressure (2023), arXiv:2309.17279 .
- Lu et al. [2023c] C. Lu, Z. Pan, F. Yang, and C. Wu, Interplay of two orbitals in superconducting La3Ni2O7 under pressure (2023c), arXiv:2310.02915 .
- Zhang et al. [2024b] Y. Zhang, L.-F. Lin, A. Moreo, T. A. Maier, and E. Dagotto, Electronic structure, magnetic correlations, and superconducting pairing in the reduced Ruddlesden-Popper bilayer La3Ni2O6 under pressure: Different role of orbital compared with La3Ni2O7, Phys. Rev. B 109, 045151 (2024b).
- Ryee et al. [2023] S. Ryee, Niklas Witt, and T. O. Wehling, Critical role of interlayer dimer correlations in the superconductivity of La3Ni2O7 (2023), arXiv:2310.17465 .
- Schlömer et al. [2023] H. Schlömer, U. Schollwöck, F. Grusdt, and A. Bohrdt, Superconductivity in the pressurized nickelate La3Ni2O7 in the vicinity of a BEC-BCS crossover (2023), arXiv:2311.03349 .
- Chen et al. [2023a] J. Chen, F. Yang, and W. Li, Orbital-selective superconductivity in the pressurized bilayer nickelate La3Ni2O7: An infinite projected entangled-pair state study (2023a), arXiv:2311.05491 .
- Liu et al. [2023b] H. Liu, C. Xia, S. Zhou, and H. Chen, Role of crystal-field-splitting and longe-range-hoppings on superconducting pairing symmetry of La3Ni2O7 (2023b), arXiv:2311.07316 .
- Chang et al. [2023] W.-X. Chang, S. Guo, Y.-Z. You, and Z.-X. Li, Fermi surface symmetric mass generation: a quantum monte-carlo study (2023), arXiv:2311.09970 .
- Ouyang et al. [2023] Z. Ouyang, J.-M. Wang, J.-X. Wang, R.-Q. He, L. Huang, and Z.-Y. Lu, Hund electronic correlation in La3Ni2O7 under high pressure (2023), arXiv:2311.10066 .
- Qu et al. [2023] X.-Z. Qu, D.-W. Qu, W. Li, and G. Su, Roles of Hund’s rule and hybridization in the two-orbital model for high-Tc superconductivity in the bilayer nickelate (2023), arXiv:2311.12769 .
- Zheng and Wú [2023] Y.-Y. Zheng and W. Wú, Superconductivity in the bilayer two-orbital Hubbard model (2023), arXiv:2312.03605 .
- Kakoi et al. [2023a] M. Kakoi, T. Kaneko, H. Sakakibara, M. Ochi, and K. Kuroki, Pair correlations of the hybridized orbitals in a ladder model for the bilayer nickelate La3Ni2O7 (2023a), arXiv:2312.04304 .
- Heier et al. [2023] G. Heier, K. Park, and S. Y. Savrasov, Competing dxy and s± pairing symmetries in superconducting La3Ni2O7 emerge from LDA+FLEX calculations (2023), arXiv:2312.04401 .
- Fan et al. [2023] Z. Fan, J.-F. Zhang, B. Zhan, D. Lv, X.-Y. Jiang, B. Normand, and T. Xiang, Superconductivity in nickelate and cuprate superconductors with strong bilayer coupling (2023), arXiv:2312.17064 .
- Lange et al. [2024] H. Lange, L. Homeier, E. Demler, U. Schollwöck, F. Grusdt, and A. Bohrdt, Feshbach resonance in a strongly repulsive ladder of mixed dimensionality: A possible scenario for bilayer nickelate superconductors, Phys. Rev. B 109, 045127 (2024).
- Fukamachi et al. [2001] T. Fukamachi, Y. Kobayashi, T. Miyashita, and M. Sato, 139La NMR studies of layered perovskite systems La3Ni2O7-δ and La4Ni3O10, J. Phys. Chem. Solids 62, 195 (2001).
- Kakoi et al. [2023b] M. Kakoi, T. Oi, Y. Ohshita, M. Yashima, K. Kuroki, Y. Adachi, N. Hatada, T. Uda, and H. Mukuda, Multiband metallic ground state in multilayered nickelates La3Ni2O7 and La4Ni3O10 revealed by 139La-NMR at ambient pressure (2023b), arXiv:2312.11844 .
- Liu et al. [2022] Z. Liu, H. Sun, M. Huo, X. Ma, Y. Ji, E. Yi, L. Li, H. Liu, J. Yu, Z. Zhang, Z. Chen, F. Liang, H. Dong, H. Guo, D. Zhong, B. Shen, S. Li, and M. Wang, Evidence for charge and spin density waves in single crystals of La3Ni2O7 and La3Ni2O6, Sci. China Phys. mech. 66, 217411 (2022).
- Wu et al. [2001] G. Wu, J. J. Neumeier, and M. F. Hundley, Magnetic susceptibility, heat capacity, and pressure dependence of the electrical resistivity of La3Ni2O7 and La4Ni3O10, Phys. Rev. B 63, 245120 (2001).
- Zhang et al. [1994] Z. Zhang, M. Greenblatt, and J. B. Goodenough, Synthesis, structure, and properties of the layered perovskite La3Ni2O7-δ, J. Solid State Chem. 108, 402 (1994).
- Liu et al. [2023c] Z. Liu, M. Huo, J. Li, Q. Li, Y. Liu, Y. Dai, X. Zhou, J. Hao, Y. Lu, M. Wang, and H.-H. Wen, Electronic correlations and energy gap in the bilayer nickelate La3Ni2O7 (2023c), arXiv:2307.02950 .
- Zhang et al. [2023d] Y. Zhang, L.-F. Lin, A. Moreo, T. A. Maier, and E. Dagotto, Structural phase transition, -wave pairing and magnetic stripe order in the bilayered nickelate superconductor La3Ni2O7 under pressure (2023d), arXiv:2307.15276 .
- Yang et al. [2023c] J. Yang, H. Sun, X. Hu, Y. Xie, T. Miao, H. Luo, H. Chen, B. Liang, W. Zhu, G. Qu, C.-Q. Chen, M. Huo, Y. Huang, S. Zhang, F. Zhang, F. Yang, Z. Wang, Q. Peng, H. Mao, G. Liu, Z. Xu, T. Qian, D.-X. Yao, M. Wang, L. Zhao, and X. J. Zhou, Orbital-dependent electron correlation in double-layer nickelate La3Ni2O7 (2023c), arXiv:2309.01148 .
- [57] See Supplemental Materials at http://? for more details (see, also, references [62, 66, 67, 3, 68, 69, 70, 10, 3, 71, 17, 55, 72, 56] therein).
- Chen et al. [2023b] K. Chen, X. Liu, J. Jiao, M. Zou, Y. Luo, Q. Wu, Ningyuan Zhang, Y. Guo, and L. Shu, Evidence of spin density waves in La3Ni2O7-δ (2023b), arXiv:2311.15717 .
- Khasanov et al. [2024] R. Khasanov, T. J. Hicken, D. J. Gawryluk, L. P. Sorel, S. Bötzel, F. Lechermann, I. M. Eremin, H. Luetkens, and Z. Guguchia, Pressure-induced split of the density wave transitions in La3Ni2O7-δ (2024), arXiv:2402.10485 .
- Chen et al. [2024] X. Chen, J. Choi, Z. Jiang, J. Mei, K. Jiang, J. Li, S. Agrestini, M. Garcia-Fernandez, X. Huang, H. Sun, D. Shen, M. Wang, J. Hu, Y. Lu, K.-J. Zhou, and D. Feng, Electronic and magnetic excitations in La3Ni2O7 (2024), arXiv:2401.12657 .
- Hirsch [1985] J. E. Hirsch, Two-dimensional Hubbard model: Numerical simulation study, Phys. Rev. B 31, 4403 (1985).
- Johannes and Mazin [2008] M. D. Johannes and I. I. Mazin, Fermi surface nesting and the origin of charge density waves in metals, Phys. Rev. B 77, 165135 (2008).
- Dong et al. [2023] Z. Dong, M. Huo, J. Li, J. Li, P. Li, H. Sun, Y. Lu, M. Wang, Y. Wang, and Z. Chen, Visualization of oxygen vacancies and self-doped ligand holes in La3Ni2O7-δ (2023), arXiv:2312.15727 .
- Sui et al. [2023] X. Sui, X. Han, X. Chen, L. Qiao, X. Shao, and B. Huang, Electronic properties of nickelate superconductor R3Ni2O7 with oxygen vacancies (2023), arXiv:2312.01271 .
- Hosoya et al. [2008] T. Hosoya, K. Igawa, Y. Takeuchi, K. Yoshida, T. Uryu, H. Hirabayashi, and H. Takahashi, Pressure studies on the electrical properties in R2-xSrxNi1-yCuyO4+δ (R=La, Nd) and La3Ni2O7+δ, J. Phys. Conf. Ser. 121, 052013 (2008).
- Kresse and Furthmuller [1996] G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys Rev B Condens. Matter. 54, 11169 (1996).
- Giannozzi et al. [2009] P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari, and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys. Condens. Matter. 21, 395502 (2009).
- McMillan [1968] W. L. McMillan, Transition temperature of strong-coupled superconductors, Phys. Rev. 167, 331 (1968).
- Dynes [1972] R. C. Dynes, McMillan’s equation and the tc of superconductors, Solid State Commun. 10, 615 (1972).
- Togo and Tanaka [2015] A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scripta Mater. 108, 1 (2015).
- Zhang et al. [2023e] Y. Zhang, L.-F. Lin, A. Moreo, T. A. Maier, and E. Dagotto, Trends in electronic structures and -wave pairing for the rare-earth series in bilayer nickelate superconductor R3Ni2O7, Phys. Rev. B 108, 165141 (2023e).
- Chen et al. [2023c] X. Chen, P. Jiang, J. Li, Z. Zhong, and Y. Lu, Critical charge and spin instabilities in superconducting La3Ni2O7 (2023c), arXiv:2307.07154 .
Supplementary Materials for
Antiferromagnetic Ground State, Charge Density Waves and Oxygen Vacancies Induced Metal-Insulator Transition in Pressurized La3Ni2O7
Yi et al.
S1. Methods
Density functional theory (DFT) calculations were performed using two software packages: the Vienna ab initio simulation package (VASP) and QUANTUM ESPRESSO (QE) [66, 67]. In VASP, the atomic force convergence criterion was set to 1 meV/Å, with a plane-wave cutoff energy of 520 eV and a total energy convergence threshold of 10-7 eV/atom. A -centered Monkhorst-Pack k-mesh of 12×12×12 was utilized for self-consistent calculations of primative cell. In QE, the atomic force convergence criterion was set to 10-7 Ry/a.u., with kinetic energy cutoffs for wavefunctions and charge density set to 100 Ry and 1200 Ry, respectively. The convergence threshold of total energy for wavefunction and ionic minimization was set at 10-9 Ry. A -centered Monkhorst-Pack k-mesh of 6×6×6 was used for self-consistent calculations, while a q-point grid of 3×3×3 was employed for electron-phonon coupling (EPC) calculations of the primative cell. The calculated lattice parameters and Wyckoff positions are listed in Table S1, consistent with previous experimental results [3].
The critical temperature () was determined using the McMillan semi-empirical formula [68, 69]:
| (S1) |
Here, is an empirical parameter describing Coulomb repulsion, and is set to = 0.10 for all calculations. and were calculated by:
| (S2) |
| (S3) |
where denotes the Eliashberg electron-phonon spectral function.
The Fermi surface (FS) nesting function is calculated by [62]
| (S4) |
where is the delta function, is the eigenvalue of band and is the nesting vector.
Phonon calculations and analysis of vibration modes are based on VASP and phonopy softwares [66, 70].
Harmonic phonon energy of different structures were calculated by implementing phonopy software [70] with following equation:
| (S5) |
where is the band index and denotes the q-point.
To calculate antiferromagnetic transition temperature , we conducted Monte Carlo (MC) simulations on a 50501 two-dimensional (2D) bilayer square lattice with periodic boundary conditions, with each temperature calculation containing MC steps. We also performed MC simulations on the 303030 three-dimensional (3D) square lattice. Our results indicate that due to the negligible , as seen in FIG. 1(a), the 3D and 2D double-layer square lattices yield the same .
| Pressure (GPa) | Space group | a | b | c | Wyckoff sites |
|---|---|---|---|---|---|
| 0 | Cmcm | 5.4057 | 5.5303 | 20.5526 | La: 8g(-0.250, 0.763, 0.319) La: 4c(0.250, 0.248, 0.500) Ni: 8g(0.250, 0.746, 0.404) O: 8g(0.250, 0.802, 0.295) O: 4c(0.250, 0.679, 0.500) O: 8e(0.500, 0.000, 0.414) O: 8e(0.000, 0.500, 0.389) |
| 30 | Fmmm | 5.1794 | 5.1797 | 19.5734 | La: 4b(0.000, 0.000, 0.500) La: 8i(0.000, 0.000, 0.321) Ni: 8i(0.000, 0.000, 0.098) O: 4a(0.000, 0.000, 0.000) O: 8i(0.000, 0.000, 0.204) O: 16j(0.250, 0.250, 0.096) |
S2. Magnetic calculations
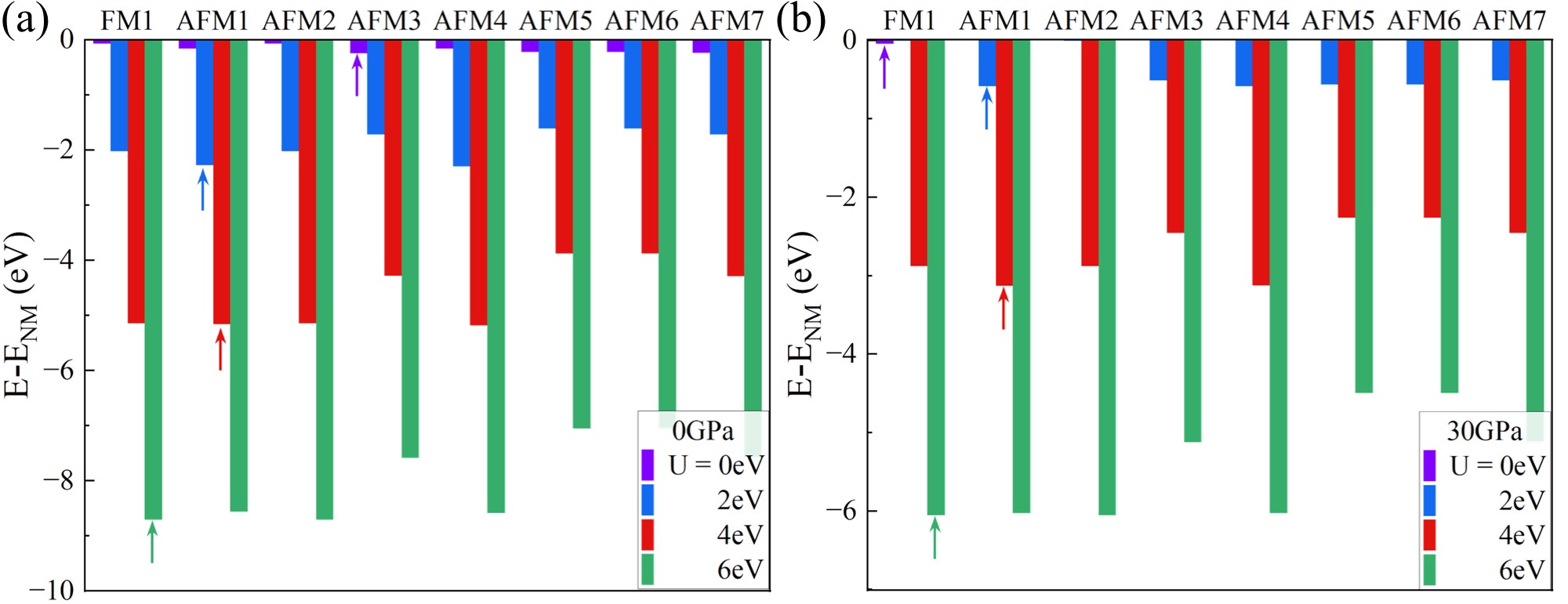
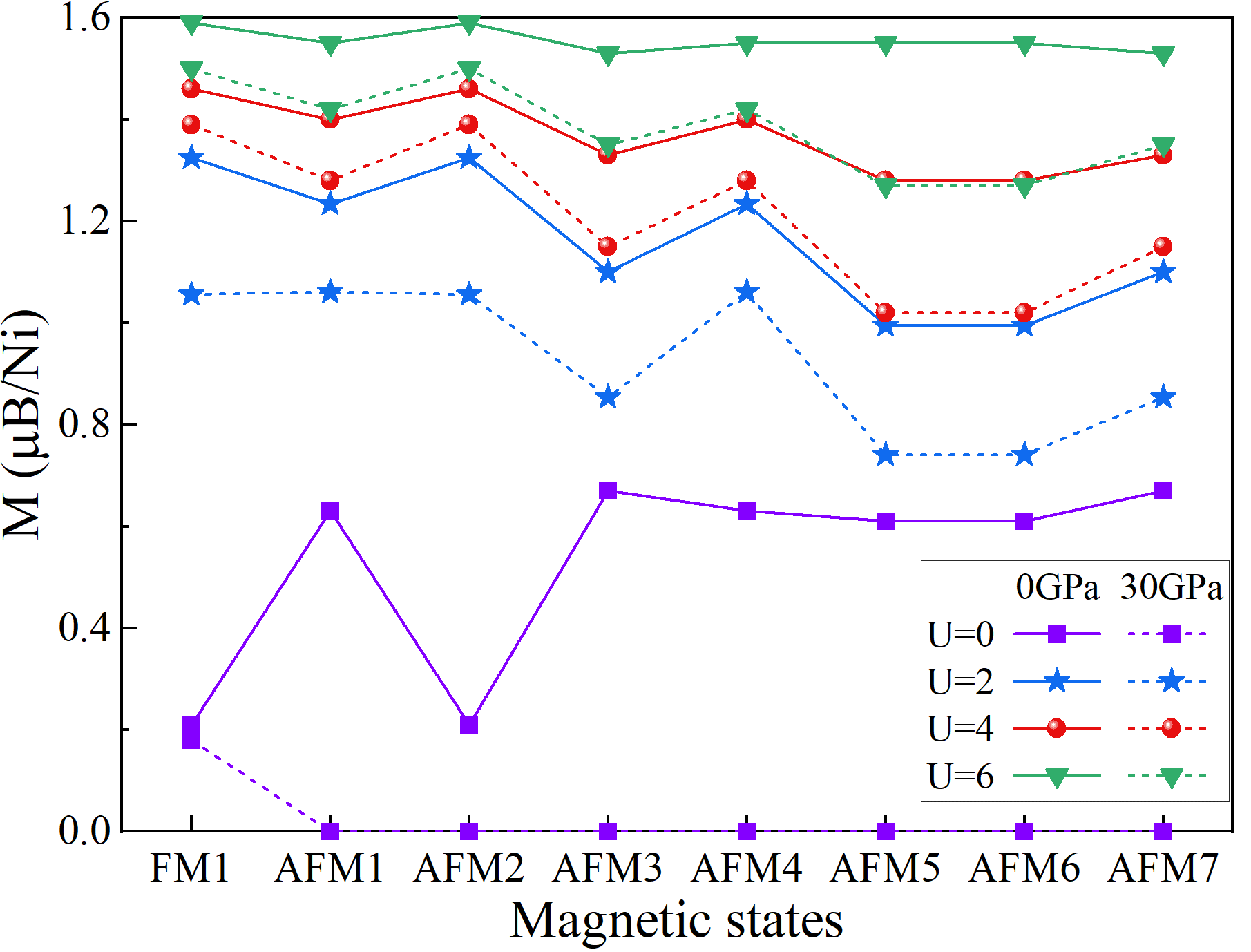
All magnetic configurations, including one ferromagnetic and seven antiferromagnetic configurations, were initially tested with onsite Coulomb interactions U=0, 2, 4, and 6 eV for Ni-3d electrons as illustrated in FIG. S1. For U=0, all configurations exhibit similar energy to the nonmagnetic state, and the magnetic moments become zero under high pressure (see FIG. S2). Results for U=2 and 4 are almost the same, indicating that AFM1 is the magnetic ground state. As U increases to 6, the ground state transitions to FM configuration, possibly due to a double exchange mechanism as explained in a recent work [10].
With increasing pressure, we found that the magnetic moments decrease by 0.1-0.6 B for all magnetic states in FIG. S3. Additionally, the relative energies of eight magnetic configurations with respect to the non-magnetic (NM) state decrease as seen in FIG. 1(b), indicating the pressure-induced suppression of magnetism.
Recent DFT calculations in related studies have considered a reasonable value for Hubbard U in the range of 3-4 eV [3, 71, 17, 55, 72, 56]. So we select U = 4 eV for analysis in our calculations.
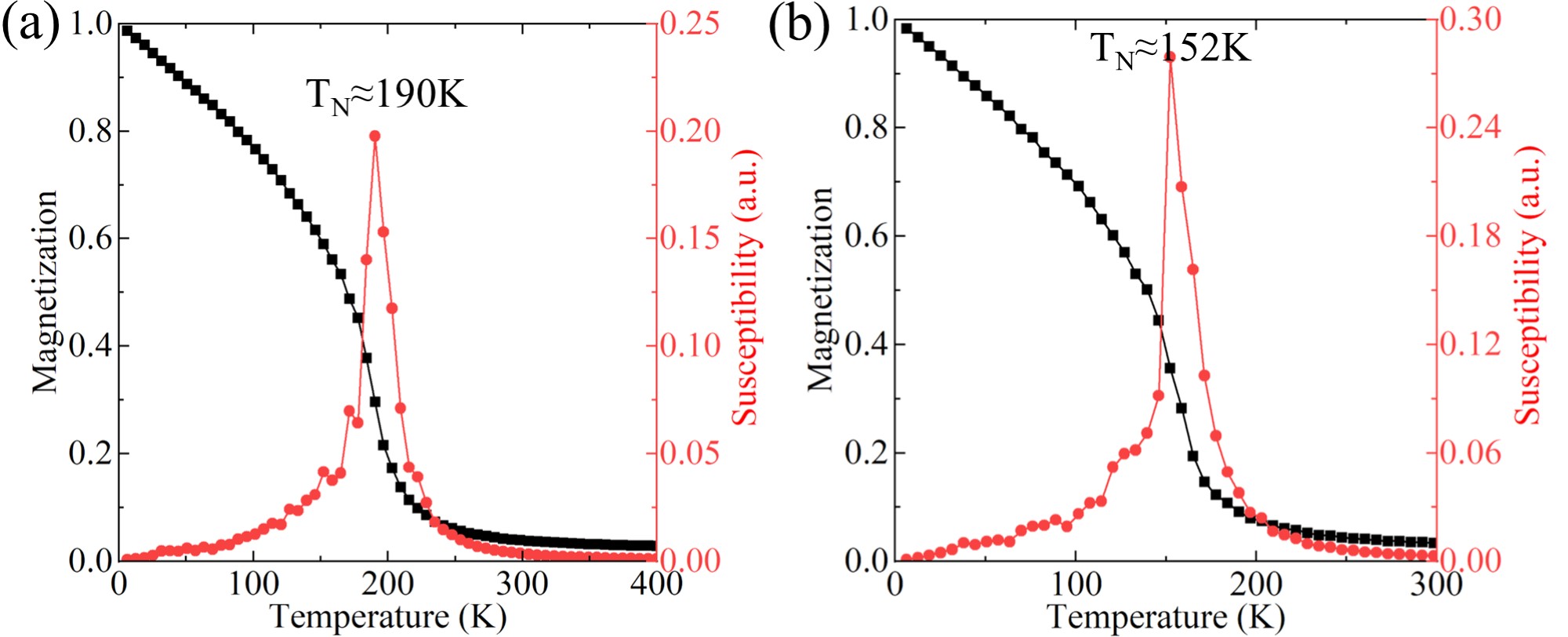
The calculated and , , and for different phases are listed in Table S2. are determined at the temperature corresponding to the discontinuity in susceptibility as illustrated in FIG. S4, where the magnetization is defined as the normalized average magnetic moment per magnetic site. It can be observed that the pristine phase exhibits a higher compared to the charge density wave (CDW) phase, while the HD phase with oxygen vacancies decreases . The significant variation in among different phases may explain the experimental discrepancy of .
| Phase | Pressure (GPa) | J1s2 (meV) | J2s2 (meV) | J3s2 (meV) | T (K) |
|---|---|---|---|---|---|
| Pristine- | 0 | -9.01 | 41.8 | 0 | 393 |
| CDW-Z1 | 0 | -28.0 | 16.0 | 0 | 190 |
| La3Ni2O6.75 (HD) | 0 | -19.7 | 7.6 | 0 | 95 |
| Pristine- | 30 | -42.2 | 25.7 | 0 | 304 |
| CDW-M1 | 30 | -70.9 | 11.3 | 0 | 152 |
S3. Stable CDW phases
For the Cmcm phase at low pressure, we uncovered that four imaginary modes lead to four stable CDW phases named CDW-, CDW-, CDW-Z1 and CDW-Z2, respectively. Their lattice parameters can be found in Table S3. Apart from the CDW-Z1 phase shown in FIG. 2 in the main text, the remaining three phases and their band structures and phonon spectra are shown in FIG. S5.
For the Fmmm phase at high pressure, there are two imaginary modes that lead to two stable CDW phases named CDW-M1 and CDW-M2, respectively. Their lattice information can be found in Table S4. Except for CDW-M1 phase as shown in FIG. 2, the CDW-M2 phase and its band structure and phonon spectrum are presented in FIG. S6.
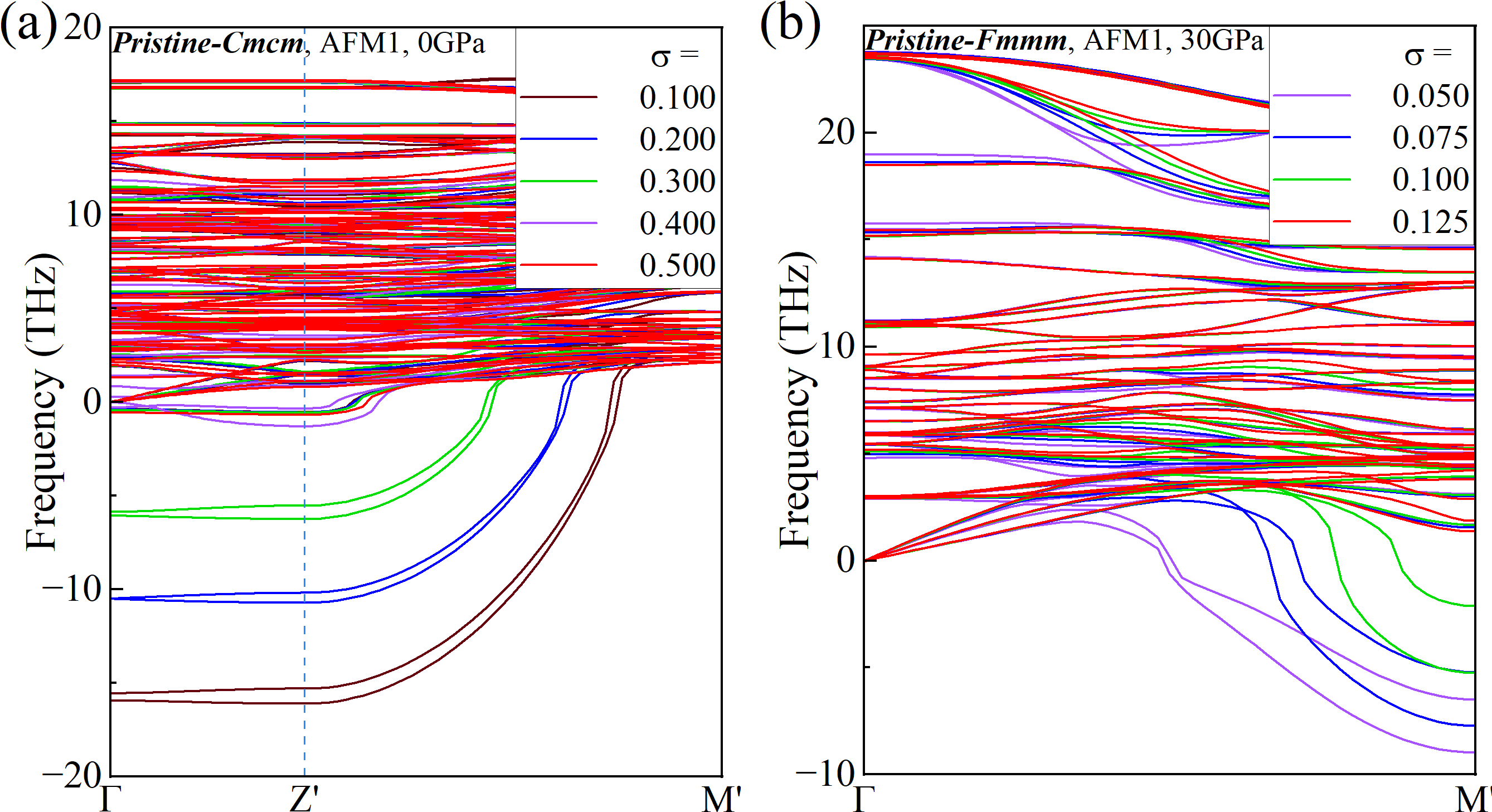
The width of the smearing () for partial occupancies set for each electronic orbital in our DFT calculation qualitatively represents the electronic temperature. Phonon dispersions at 0 and 30 GPa for different values are depicted in FIG. S7, where the phonon soft modes near and Z’ at 0 GPa, as well as those near M’ at 30 GPa, gradually harden until disappearing with increasing . This indicates that temperature can suppress phonon softening, further confirming that the imaginary phonons at both low and high pressure originate from the CDW.
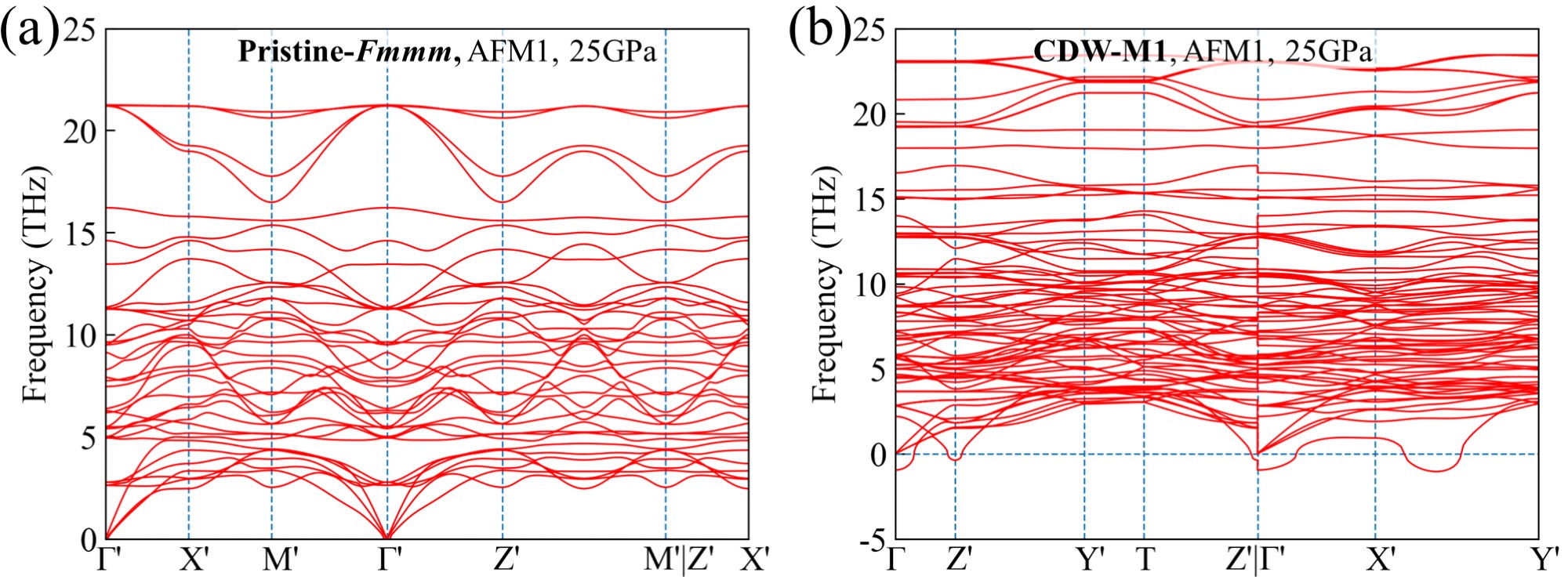
It is noteworthy that the CDW-Z1 phase consistently exhibits a stable phonon spectrum below 10 GPa. By comparing the harmonic phonon energies between the CDW-Z1 phase and the pristine Cmcm phase, the estimated gradually decreases with increasing pressure, dropping to 0 K at about 7.5 GPa as shown in FIG. 5. On the other hand, the CDW-M1 phase only exhibits stable phonon spectra above 25 GPa. For instance, at 25 GPa, the phonon spectrum of CDW-M1 displays imaginary frequencies while the pristine Fmmm phase is stable, as shown in FIG. S8. above 25 GPa increases with increasing pressure.
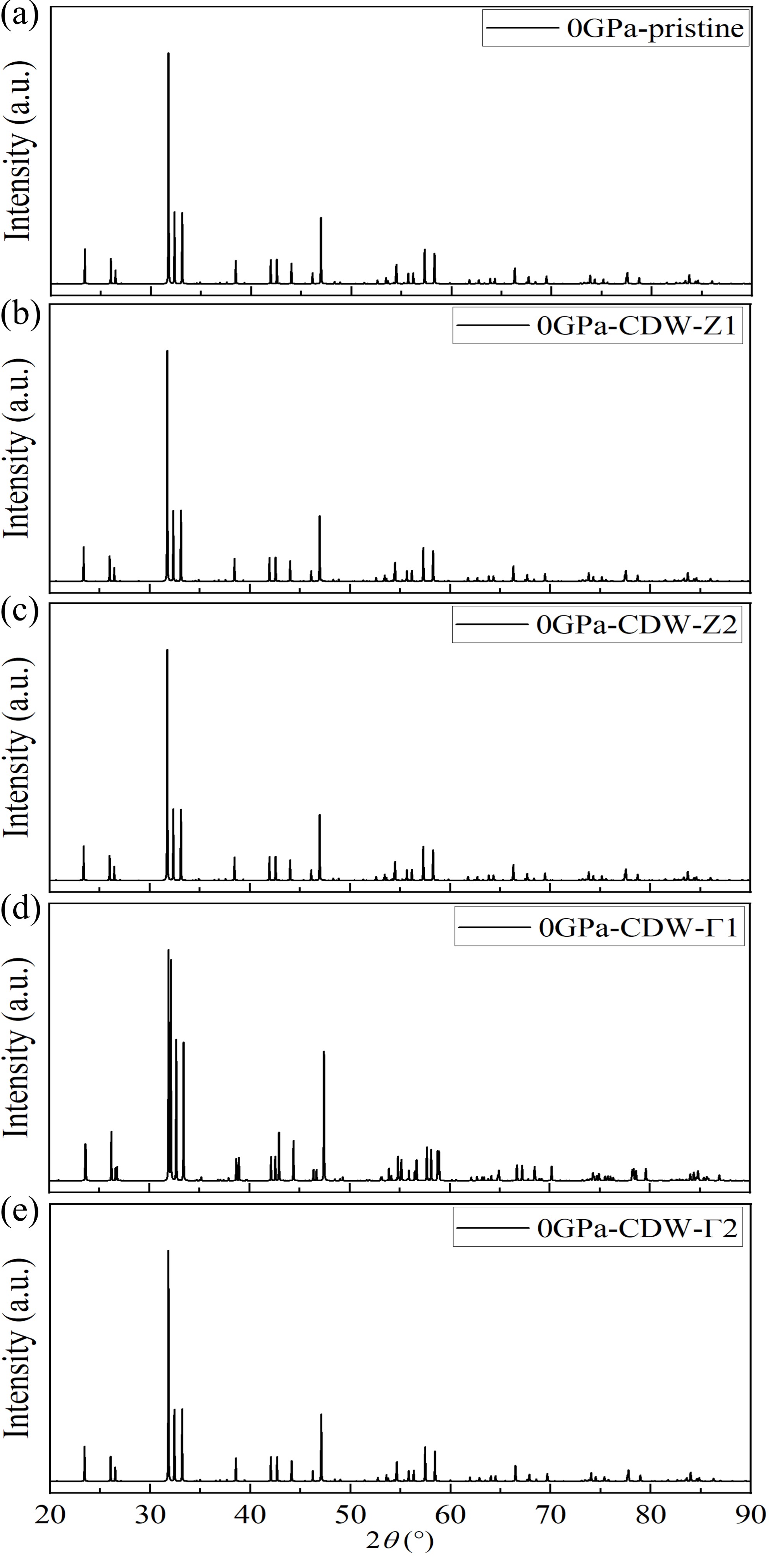
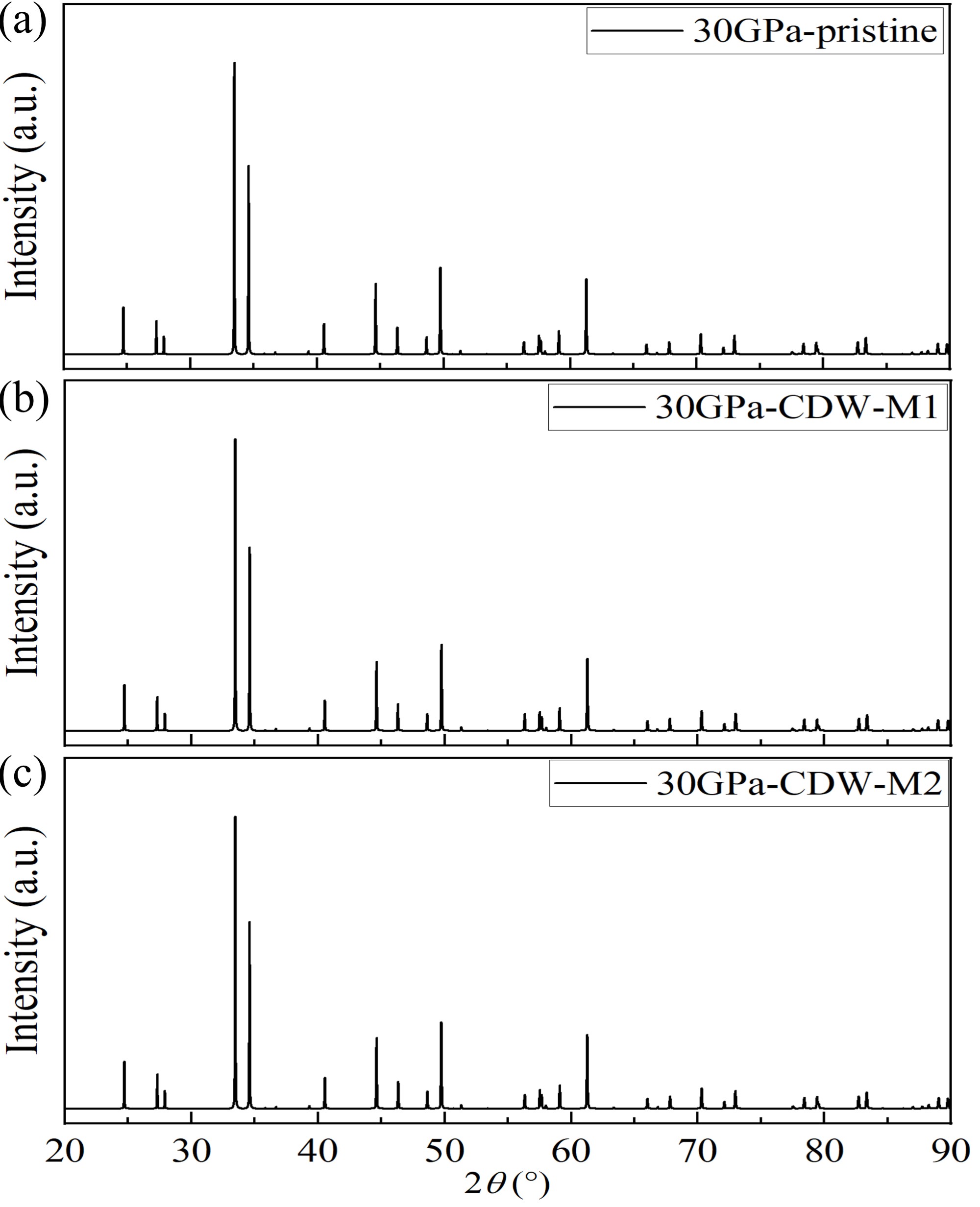
As seen in FIG. S9 and S10, most CDW phases exhibit almost the same peak positions and intensities comparing to the pristine phase at both 0 and 30 GPa in XRD spectra, except CDW-1 with a distinctive Bravais lattice. Diffraction patterns of CDW phases show emergent spots with odd Miller indices K with pristine phases in FIG. S11 and S12.
| Pressure (GPa) | Phase | Space group | a | b | c | Wyckoff sites |
|---|---|---|---|---|---|---|
| 0 | CDW-1 | 10.6243 | 5.4031 | 5.5305 | La: 2e(0.999, 0.750, 0.247) La: 2e(0.361, 0.250, 0.945) La: 2e(0.638, 0.250, 0.581) Ni: 2e(0.191, 0.750, 0.844) Ni: 2e(0.807, 0.750, 0.646) O: 4f(0.171, 0.505, 0.081) O: 4f(0.222, 0.995, 0.620) O: 2e(0.414, 0.750, 0.016) O: 2e(0.593, 0.750, 0.594) O: 2e(0.997, 0.750, 0.677) | |
| 0 | CDW-2 | Amm2 | 5.3971 | 20.5989 | 5.5288 | La: 4e(-0.500, 0.681, -0.734) La: 4d(0.000, 0.320, -0.260) La: 2b(-0.500, 0.500, -0.754) La: 2a(0.000, 0.500, -0.259) Ni: 4e(-0.500, 0.404, -0.246) Ni: 4d(0.000, 0.596, -0.755) O: 8f(-0.754, 0.914, -0.009) O: 8f(-0.246, 0.389, -0.992) O: 4e(-0.500, 0.297, -0.297) O: 4d(0.000, 0.207, 0.190) O: 2b(-0.500, 0.500, -0.186) O: 2a(0.000, 0.500, -0.828) |
| 0 | CDW-Z1 | Pnma | 5.5368 | 5.3987 | 20.5764 | La: 4c(0.252, 0.250, 0.499) La: 4c(0.725, 0.750, 0.681) La: 4c(0.248, 0.750, 0.180) Ni: 4c(0.746, 0.250, 0.596) Ni: 4c(0.263, 0.250, 0.097) O: 8d(0.999, 0.504, 0.086) O: 8d(0.982, 0.003, 0.611) O: 4c(0.212, 0.250, 0.203) O: 4c(0.681, 0.250, 0.707) O: 4c(0.822, 0.250, 0.498) |
| 0 | CDW-Z2 | Pmmn | 5.4006 | 20.6027 | 5.5241 | La: 2b(0.000, 0.500, -0.488) La: 2a(0.000, 0.000, -0.006) La: 4e(0.500, 0.320, -0.011) La: 4e(0.500, 0.819, -0.515) Ni: 4e(0.000, 0.404, -0.991) Ni: 4e(0.000, 0.904, -0.500) O: 8g(0.255, 0.914, -0.762) O: 8g(0.755, 0.389, -0.057) O: 2b(0.000, 0.500, -0.919) O: 4e(0.000, 0.797, -0.549) O: 4e(0.000, 0.293, -0.057) O: 2a(0.000, 0.000, -0.439) |
| Pressure (GPa) | Phase | Space group | a | b | c | Wyckoff sites |
|---|---|---|---|---|---|---|
| 30 | CDW-M1 | Cmmm | 5.179 | 19.585 | 5.178 | La: 4j(0.000, 0.179, -0.500) La: 4i(0.500, 0.180, 0.000) La: 2d(0.000, 0.000, -0.500) La: 2b(0.500, 0.000, 0.000) Ni: 4j(0.000, 0.598, -0.500) Ni: 4i(0.000, 0.098, 0.000) O: 16r(0.754, 0.404, -0.253) O: 2a(0.000, 0.000, 0.000) O: 2c(0.500, 0.000, -0.500) O: 4j(0.000, 0.295, -0.500) O: 4i(0.500, 0.297, 0.000) |
| 30 | CDW-M2 | Cmcm | 5.1794 | 19.5770 | 5.1808 | La: 4c(0.500, 0.929, -0.250) La: 4c(0.500, 0.750, -0.250) La: 4c(0.000, 0.930, -0.750) Ni: 4c(0.500, 0.652, -0.750) Ni: 4c(0.000, 0.652, -0.250) O: 16h(0.753, 0.654, -0.496) O: 4c(0.500, 0.749, -0.750) O: 4c(0.500, 0.547, -0.750) O: 4c(0.000, 0.545, -0.250) |
S4. Role of Oxygen vacancies
As concluded in the main text, with apical oxygen vacancies, there appear two different phases at low and high pressures owing to pressure dependent enthalpy (). The half distortion (HD) phase has a lower than the full distortion (FD) phase below 2 GPa, while the FD phase has a lower above 2 GPa. The can be divided into two components, , where , , and represent energy, pressure, and volume, respectively. By comparing and between the HD and FD phases under pressure in FIG. S13, although the HD phase consistently exhibits lower at 0-10GPa, the smaller of the FD phase makes it thermodynamically more stable under high pressure.