Aperiodic sets of three types of convex polygons

Teruhisa SUGIMOTO^1),2)

Abstract

Sets of three types of convex pentagons that are aperiodic with no matching conditions on the edges are created from a chiral aperiodic monotile Tile $(1,1)$ . This method divides the interior of Tile $(1,1)$ into five convex polygons with five or more edges, and we have so far identified four methods.

¹⁾ The Interdisciplinary Institute of Science, Technology and Art

²⁾ Japan Tessellation Design Association

E-mail: ismsugi@gmail.com

Keywords: Tiling, aperiodic, non-periodic, polygon, tile

1 Introduction

A tiling (or tessellation) of the plane is a collection of sets, called tiles, that covers the plane without gaps or overlaps, except for the boundaries of the tiles. The term “tile” refers to a topological disk, whose boundary is a simple closed curve.

A tiling exhibits periodicity if its translation by a non-zero vector coincides with itself; a tiling is considered periodic if it coincides with its translation by two linearly independent vectors. However, in this study, a tiling with periodicity is referred to as periodic, and a tiling without periodicity is referred to as non-periodic.

In general, when considering tilings, there are only a finite number of tile shapes that can be used. These finite-shape diagrams are called prototiles, and a set of prototiles admits tilings of the plane. The tiling generated by a set of prototiles can cover the plane infinitely. A set of prototiles is said to be aperiodic if copies of the prototiles can be assembled into tilings of the plane such that all tilings with the prototiles are non-periodic [2, 4, 22].

The most well-known problem regarding a set of prototiles (set of tiles, , tile set) that are aperiodic, that is, “aperiodic set of prototiles (aperiodic set of tiles)” (hereafter abbreviated as “ASP”), is “Is there a single aperiodic prototile (with or without a matching condition¹¹1 Matching conditions specify how tiles must connect to form a valid tiling, which can sometimes be represented by assigning colors or orientations to specific edges of the prototiles. ), that is, one that admits only non-periodic tilings by congruent copies?” [2]. Smith et al. presented solutions to this problem for concave diagram tiles without matching conditions [12, 13]. In [2], another major problem concerning ASP was presented as follows:

Problem.

There is a set of three convex polygons that are aperiodic with no matching condition on the edges, but are two or even one such convex prototiles possible?

In this study, our discussion focuses on the above problem. Therefore, we consider a set of tiles (prototiles) that are polygons and have no matching conditions on the edges.

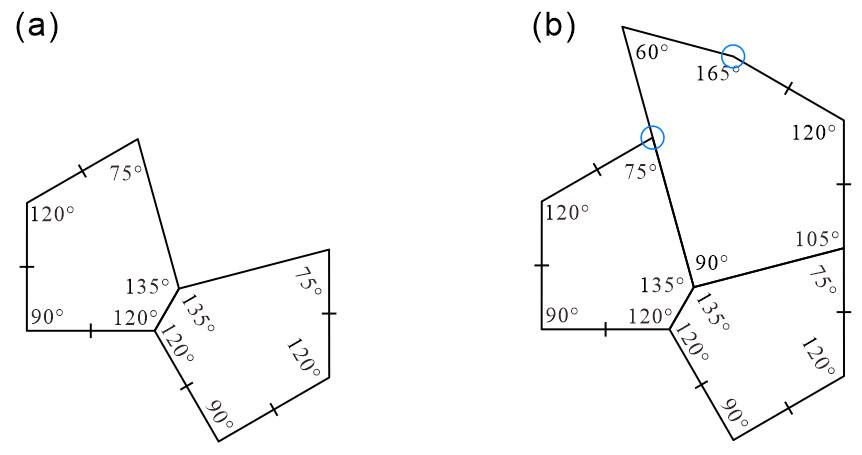
Refer to caption — Figure 1: Tiling (d) generated by an aperiodic set of prototiles created by Ammann, which used three convex polygons with no matching condition on the edges. As shown in (c), this is a recomposition by Penrose tiles (rhombuses) and is obtained by markings of using the points $J$ , $K$ , and $L$ as shown in (a) and (b). These markings are completely determined by the choice of the point $J$ , as we must have GL = DJ, FL = CJ =EK, and HK = BJ. For aperiodicity, the point $J$ must be chosen so that DJ, CJ, BJ, and KL are of different lengths [4, 16].

The “ASP comprising three convex polygons (= the set of three convex polygons that are aperiodic with no matching condition on the edges)” in the above problem is known for the two convex pentagons and one convex hexagon created by Ammann, as shown in Figure 1, based on the Penrose tiles²²2 The Penrose tiles are considered to be an ASP comprising two convex polygons (rhombuses) with matching condition on the edges [2, 4, 16]. [4, 16]. In the tiling of the two convex pentagons and one convex hexagon shown in Figure 1, the reflected (flipped) convex pentagons and hexagon were not used. The tiling is edge-to-edge³³3 A tiling by convex polygons is edge-to-edge if any two convex polygons in a tiling are either disjoint or share one vertex or an entire edge in common. Then other case is non-edge-to-edge [4, 15, 16]..

In tiling problems, it is important to note how the reflected tiles (posterior side tiles) are handled. For example, if all the tiles in a tiling are of the same size and shape, then the tiling is monohedral, which allows the use of reflected tiles in monohedral tilings [4]. In other words, in monohedral tilings, we treat the anterior and posterior side tiles as the same type (the concept is that there is only one type of tile). In this study, a tile that admits monohedral tiling is referred to as a monotile. Note that there are monotiles that require the use of reflected tiles during the tiling generation process (see Appendix A). In some tiling problems, congruent diagrams, including reflection images, are treated as tiles of the same type as in monohedral tiling.

According to Smith et al. [12], Tile $(a,b)$ , which can generate only non-periodic tiling, is an “aperiodic monotile,” in which all tiles are of the same size and shape; however, the tiling generation process requires the use of reflected tiles, and both anterior and posterior side tiles must be treated as the same type. However, according to Smith et al. [13], the tiles “Spectres,” which can generate only non-periodic tiling, do not require the use of reflected tiles during the tiling generation process⁴⁴4 Spectres can generate only non-periodic tiling using only one side, either anterior or posterior, even if it allows the use of reflected tiles during the tiling generation process.. The tiles are referred to as “chiral aperiodic monotiles.”

Let us consider “ASP comprising $n$ types of polygons ( $n$ is an integer greater than or equal to one)” by focusing on “a set of three convex polygons that are aperiodic” in the above-mentioned problem. For the polygons (tiles) contained in the ASP and the set of original problems, if the polygons are congruent, they are treated as the same type; however, from the text (or symbols) alone, it is not clear whether the anterior or posterior side polygons are treated as the same type. Further, similar to the problem of monohedral tiling, it is possible that polygons in those cases may sometimes be treated as the same type of tiles in the reflected image.

Therefore, in this study, we proceed by treating the anterior and posterior side tiles as different types, even if they are congruent diagrams. In other words, we assume that the reflected tiles cannot be used (the tiles in the tile set cannot be reflected) during all tiling generation process with the tiles in a tile set. However, when we use the terms “viewpoint that does not distinguish between anterior and posterior sides” or “monotile,” we treat the anterior and posterior side tiles as the same type.

Following this policy, the case in [12] is “ASP comprising two types of concave polygons,” and the case in [13] is “ASP comprising one type of concave diagram⁵⁵5 Tile $(1,1)$ corresponding to $a=b=1$ of Tile $(a,b)$ shown in [12] is a concave polygon and a concave diagram, and Spectres in [13] are concave diagrams. From a viewpoint that does not distinguish between anterior and posterior sides, both cases of [12] and [13] are considered “ASP comprising one type of concave diagram.” Note that Tile $(1,1)$ with 13-edges is considered an equilateral 14-edges polygon.”. Moreover, the case shown by Ammann in Figure 1 is “ASP comprising three types of convex polygons (two types of convex pentagons and one type of convex hexagon).”

This study presents examples of an “ASP comprising three types of convex polygons,” similar to the case shown in Figure 1.

Note that if we extract the convex polygons of $n-1$ or fewer types contained in the set, we assume that they cannot admit a tiling. It is because it is natural that the convex polygons of $n-1$ or fewer types extracted from the set cannot generate periodic tiling where $n\geq 2$ ; however, if they can generate non-periodic tiling, it is replaced by the result that there exists an ASP comprising fewer types of convex polygons.

The two types of convex pentagons and one type of convex hexagon shown in Figure 1 can be identified as not belonging to known Type families of convex pentagonal monotiles (see Appendix A) or convex hexagonal monotiles (see Appendix B), respectively⁶⁶6 If Rao’s claim in [9] is formally established as correct, there will be no ASP for convex polygonal monotiles (i.e., there does not exist ASP comprising one type of convex polygon with no matching condition on the edges), and furthermore, it can be said that “a convex pentagon does not belong to known Type families” and “a convex pentagon cannot admit tiling” are equivalent. At the stage where these are not truly established [24], it is necessary to confirm whether tiling is truly impossible for a convex pentagon, including whether it is possible to generate only non-periodic tilings. In this study, we assume that Rao’s claim is correct and proceed with the discussion. However, in Section 2 (and Appendix D) of this study, to check whether or not a convex polygon is a monotile, we do not judge based on only the tile conditions of known Types, and are checking whether tiling is actually possible. Note that if convex polygons are convex polygonal monotiles that can generate edge-to-edge tilings, it has been proved that they can always generate periodic tilings [15, 16]. . Because the set of these polygons is the ASP comprising three types of convex polygons, if two types of polygons are extracted from three types of convex polygons, those two types of polygons cannot admit tilings (but the author has not confirmed this).

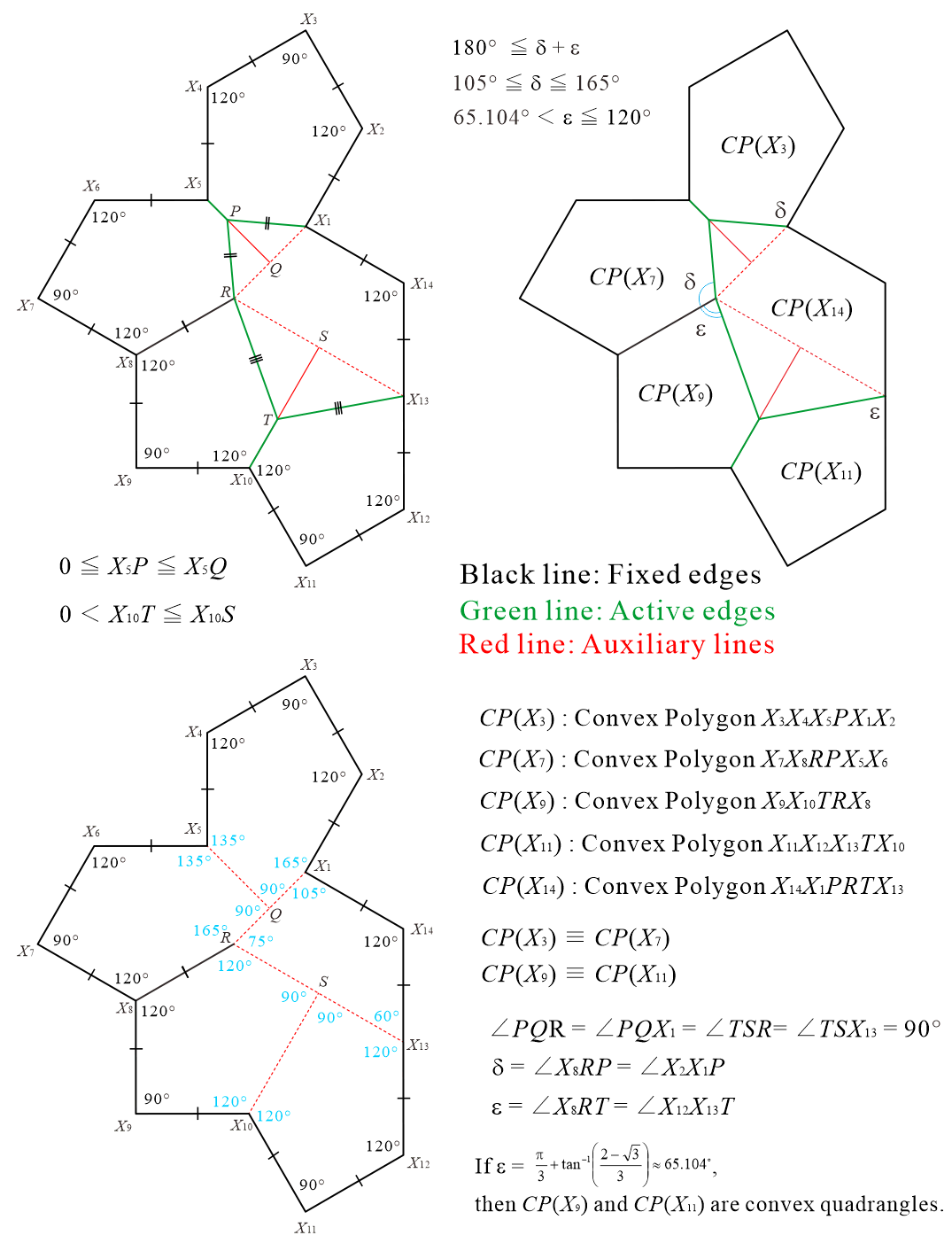
2 Dividing Tile $(1,1)$ into ASP comprising convex polygons

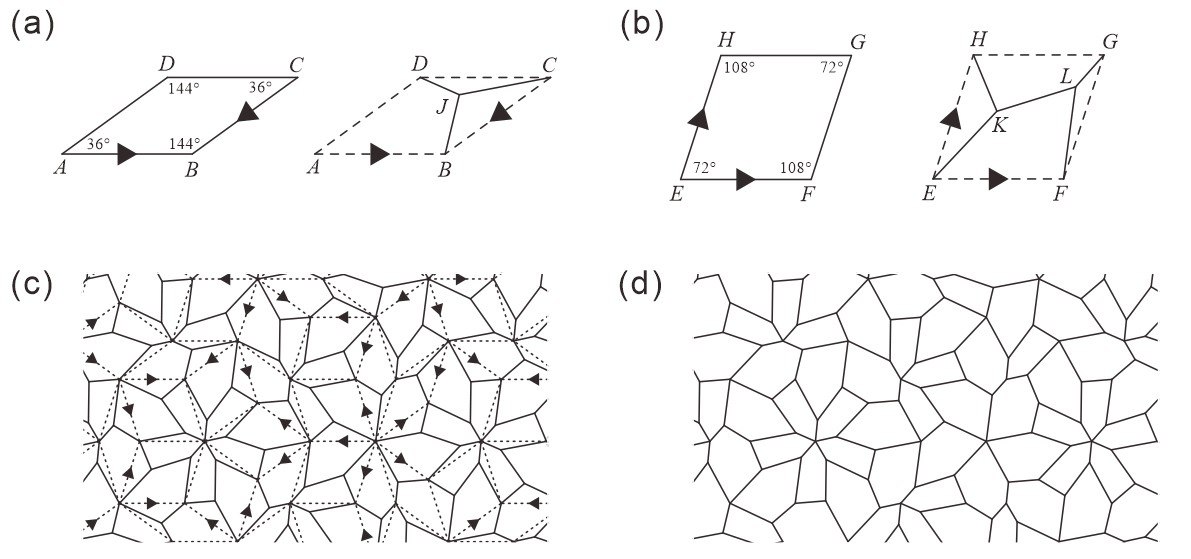
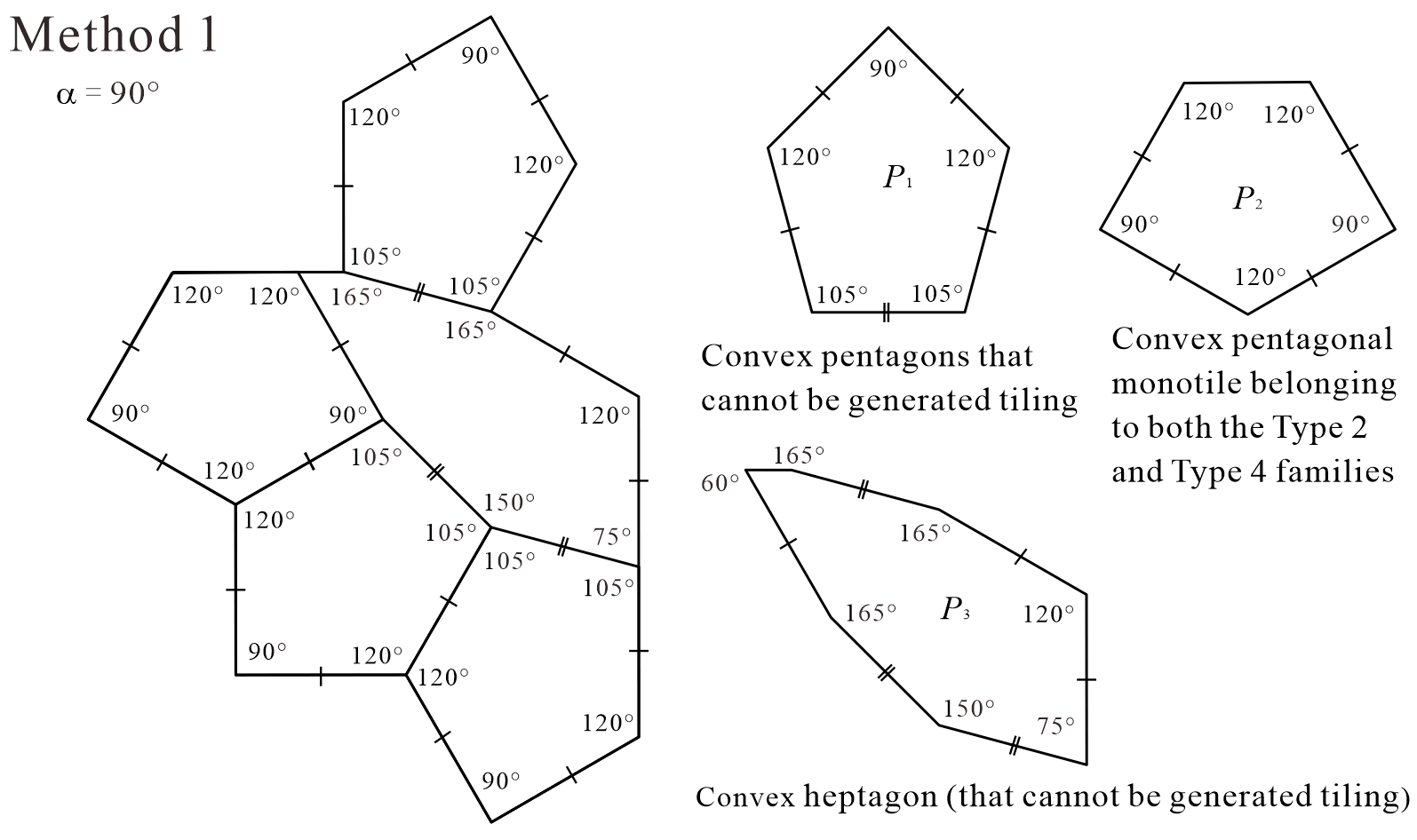
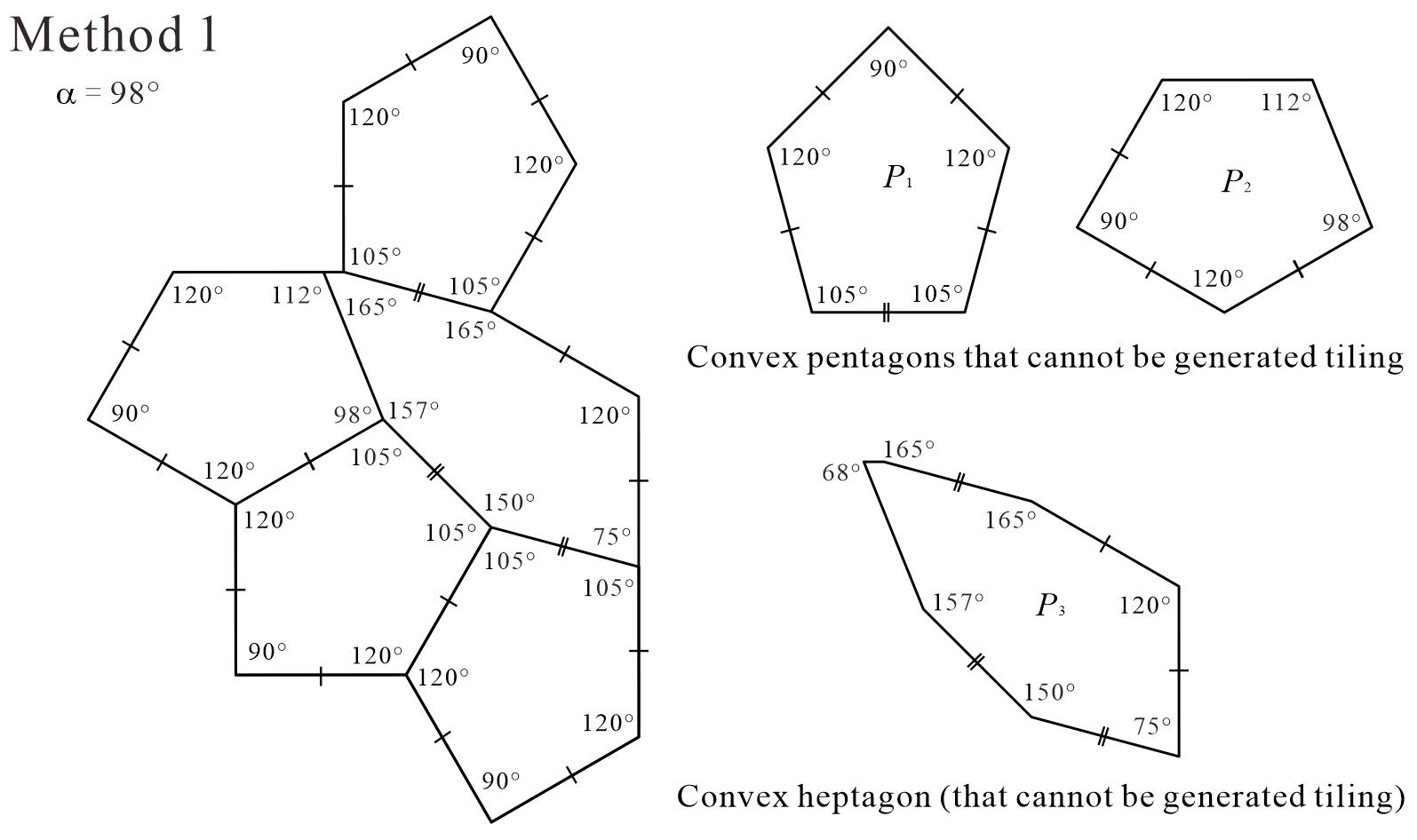
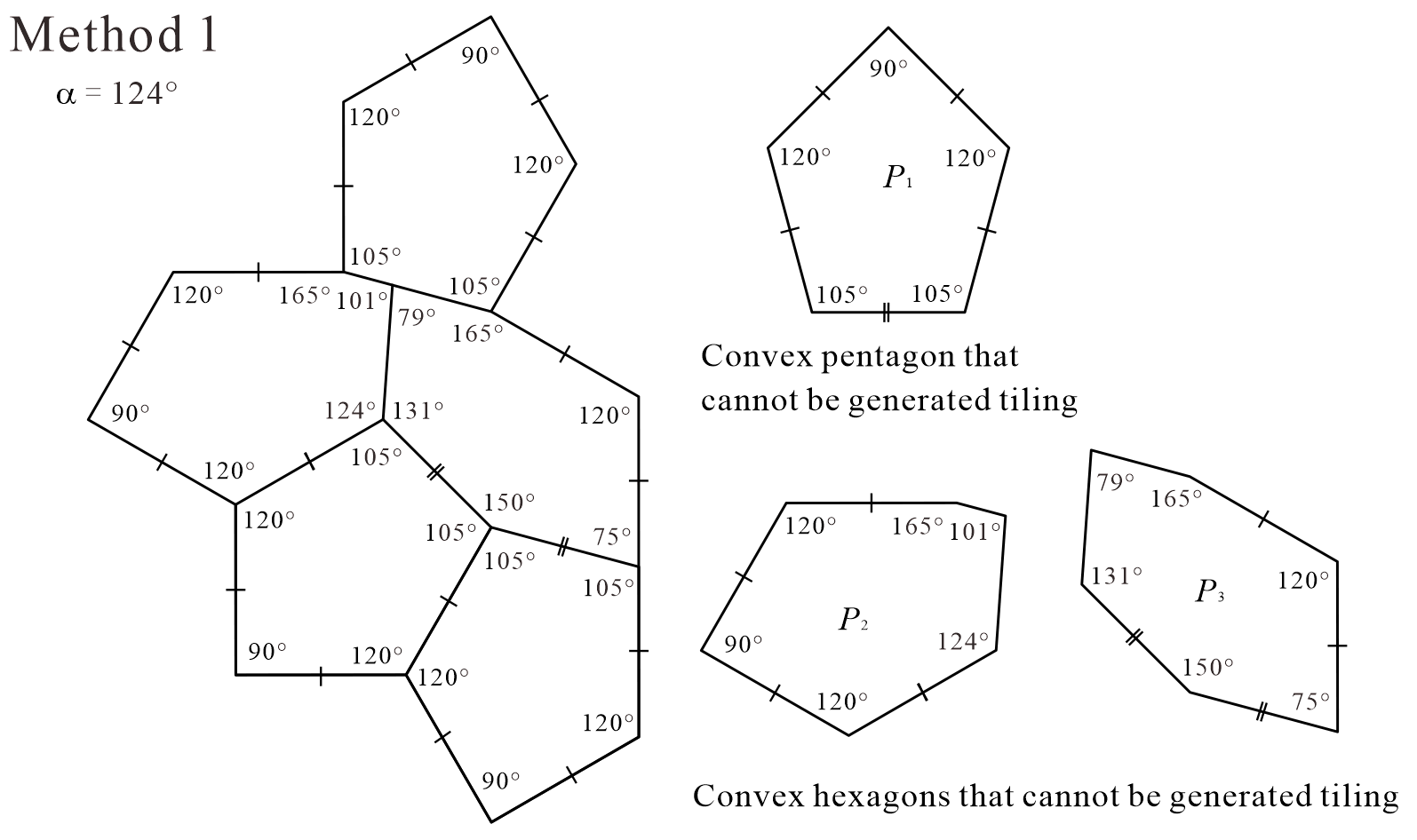
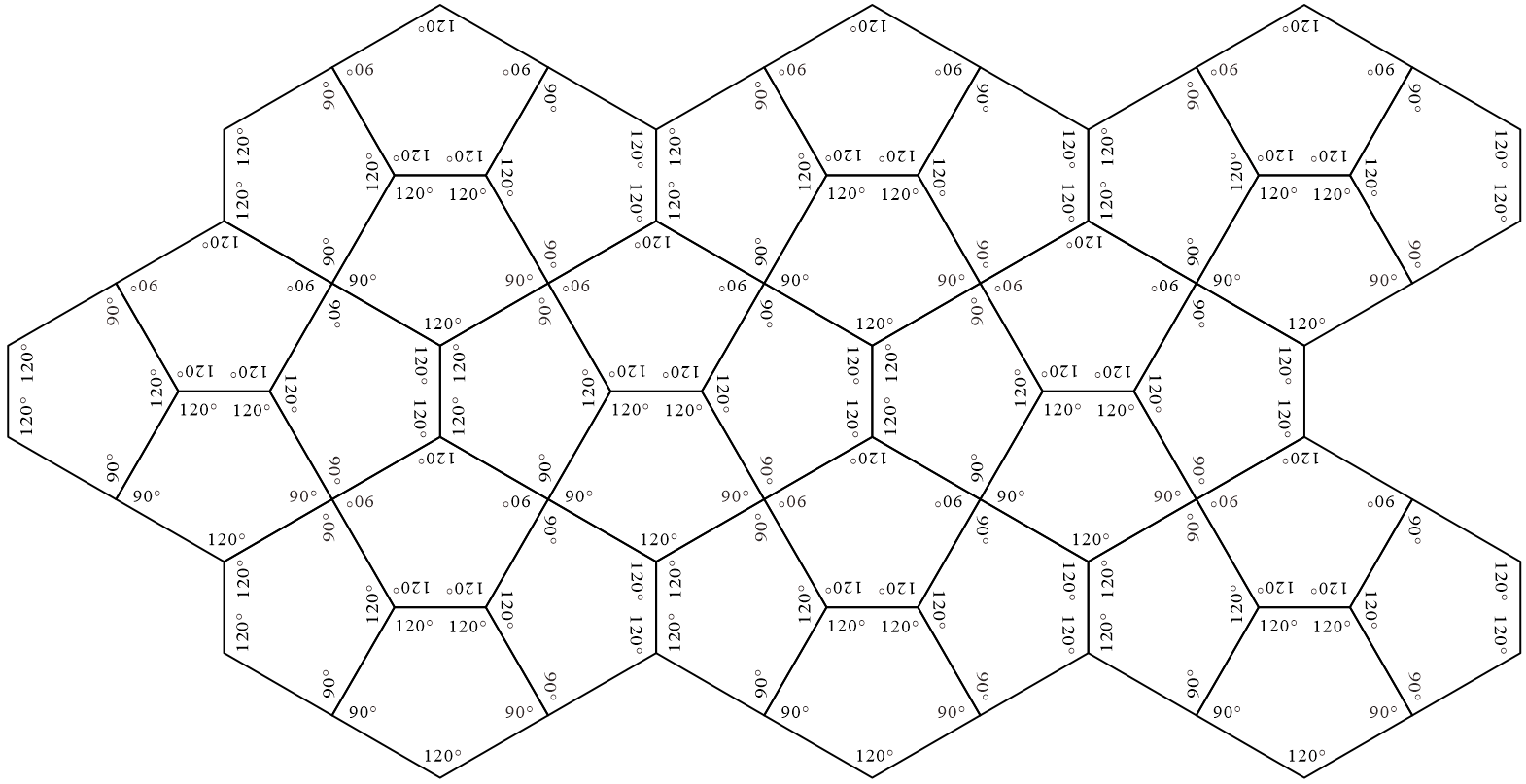
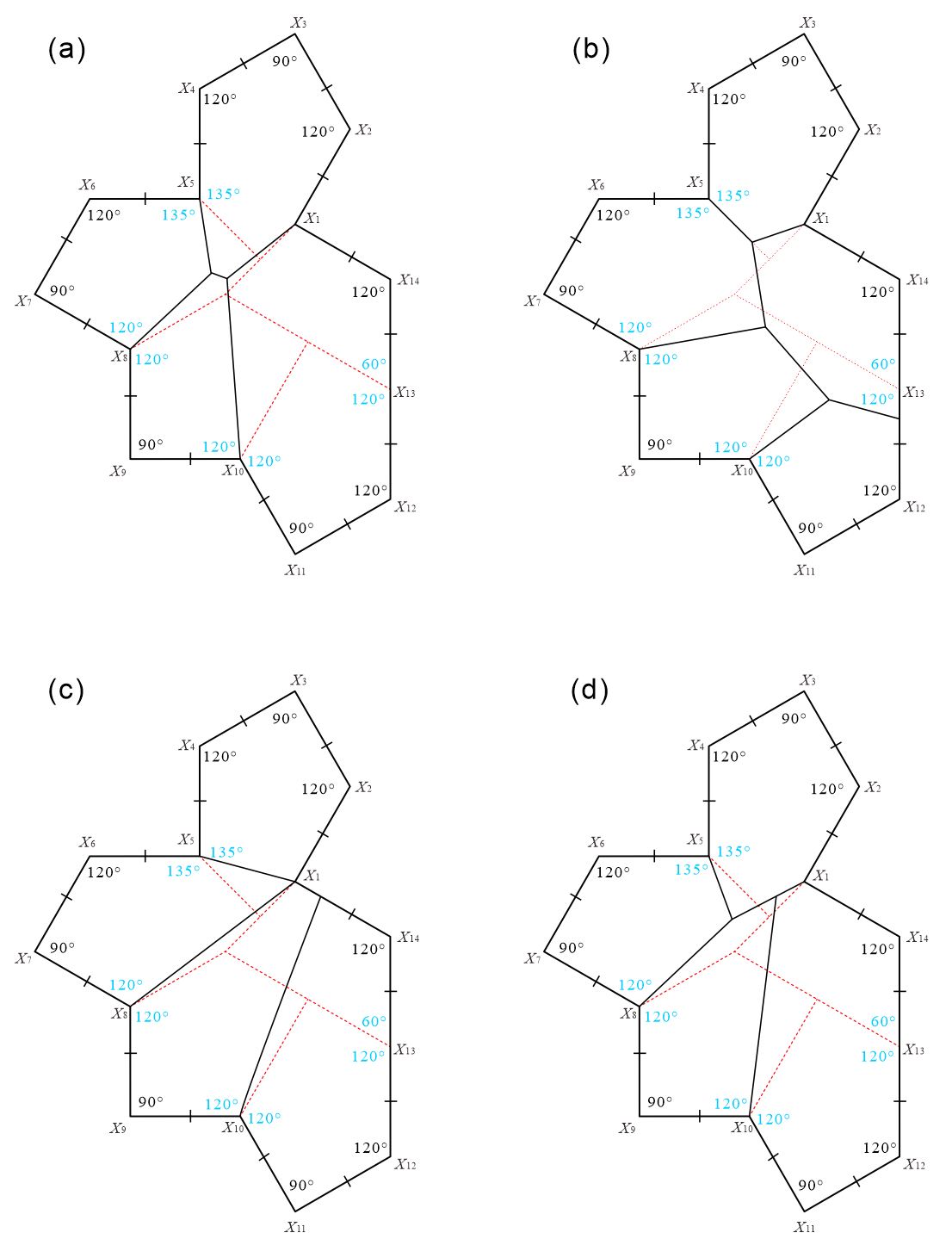
Tile $(1,1)$ , corresponding to $a=b=1$ in Tile $(a,b)$ shown in [12], can generate a periodic tiling if the use of reflected tiles is allowed during the tiling generation process (see Figure 2). However, as shown in [13], Tile $(1,1)$ can only generate non-periodic tiling if and only if it does not allow the use of reflected tiles (see Figure 3). Using this property, ASP comprising three types of convex polygons can be obtained from Tile $(1,1)$ . This method divides the interior of Tile $(1,1)$ into five convex polygons with five or more edges⁷⁷7 Because all triangles and quadrilaterals are monotiles (which do not require the use of reflected tiles to form periodic tilings) the number of edges of convex polygons contained in ASP is at least five. Then, there are no convex polygonal monotiles with seven or more edges [3, 4, 7, 5, 10, 25]. , and we have so far identified four methods (Methods 1–4). The tile sets created by the division of the four methods all contain the convex pentagon $P_{1}$ , which cannot generate a tiling (that is, no monotile) in the upper-left corner of Figure 4 ( $P_{1}$ is convex pentagons with line symmetry and cannot distinguish between the anterior and posterior sides). Methods 1 (Figure 4), 2 (Figure 5), and 4 (Figure 18) divide Tile $(1,1)$ to create five convex polygons containing three $P_{1}$ . In Method 3 (Figure 15), one $P_{1}$ (= $CP_{1}(X_{3})$ ) is contained in the five convex polygons formed by dividing Tile $(1,1)$ . We note that the tilings generated by the ASP, comprising three types of convex polygons created by Methods 1–4, are non-edge-to-edge.

Here again, it is emphasized that each convex polygon in the tile set created by dividing Tile $(1,1)$ satisfies the condition that the reflected tiles cannot be used during all tiling generation processes. As described above, Tile $(1,1)$ can generate periodic tilings if the reflected tiles can be used during the tiling generation process; therefore, it is obvious that the three convex polygons in the tile set can generate periodic tilings if they can be reflected during the tiling generation process. “All tiling generation processes” means that even if we try to generate tiling using only one or two types of convex polygons in a tile set, we cannot use the reflected convex polygons (tiles) during the tiling generation process.

As described in Section 1, some monotiles require the use of reflected tiles during tiling generation process. It is important to note that this property means that some tiling patterns cannot be formed without using reflected tiles, but the tiles forming the patterns do not necessarily have to use reflected tiles to generate tiling (see Appendix A for details) [4, 15, 16].

Note that in this study, we assumed that the reflected tiles cannot be used during the tiling generation process; therefore, even if the convex polygon of a tile set created by dividing Tile $(1,1)$ is a monotile, we do not consider that the tile set is not aperiodic. This is because if the tile set contains convex polygonal monotiles that require the use of reflected tiles during the tiling generation processes and does not contain the reflected convex polygons of the monotiles; then, the possibility that the tile set is aperiodic cannot be ruled out.

2.1 Method 1 and Method 2

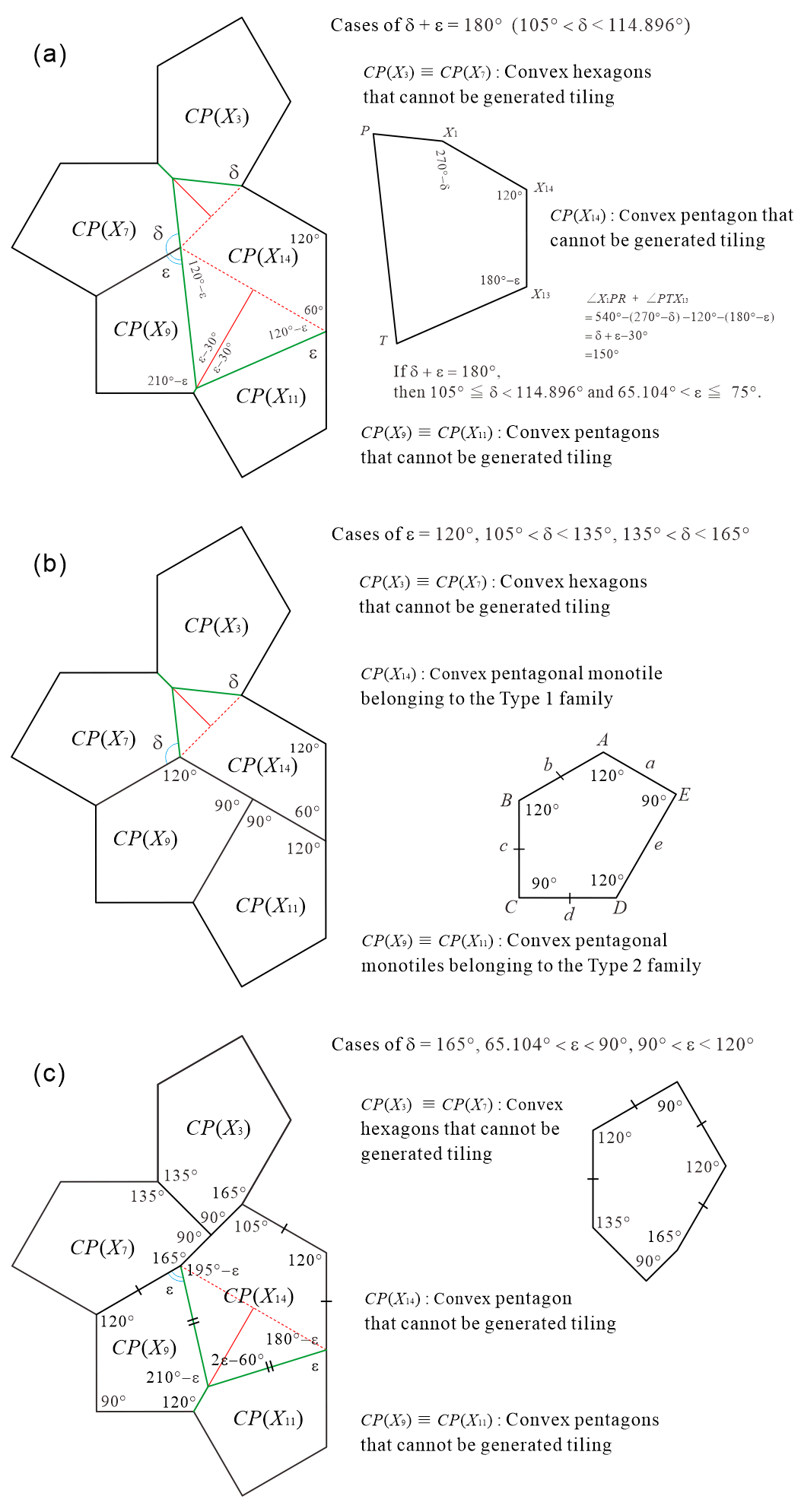
Method 1 in Figure 4 and Method 2 in Figure 5 are based on the division of Tile $(1,1)$ into five convex polygons containing three $P_{1}$ . The division in Method 1 depends on the value of the parameter $\alpha$ shown in Figure 4, and in Method 2, it depends on the value of the parameter $\beta$ shown in Figure 5. In the Methods, there are clear cases in which the tile set is not an ASP. For example, there are the following cases.

•

In the case of $\alpha=75^{\circ}$ in Method 1 (see Figure 4(d)), there is the convex hexagonal monotile $P_{3}$ belonging to the Type 1 family that can form periodic tiling without using reflected tiles (see Appendix B); therefore, the set of three types of convex polygons by this division is not ASP.

•

In the case of $\beta=90^{\circ}$ in Method 2 (see Figure 5(d)), there is the convex pentagonal monotile $P_{2}$ belonging to both the Type 2 and Type 4 families with the property of line symmetry that cannot distinguish between the anterior and posterior sides (see Appendix A); therefore, the set of three types of convex polygons by this division is not an ASP.

•

In the cases of $\alpha=105^{\circ}$ in Method 1 (see Figure 4(e)) and $\beta=105^{\circ}$ in Method 2 (see Figure 5(e)), the convex polygons created by division are identical. The set of two types of convex polygons created by this division is not an ASP, because the convex hexagon $P_{3}$ created by this division is a convex hexagonal monotile belonging to the Type 1 family, which can form periodic tiling without using reflected tiles (see Appendix B).

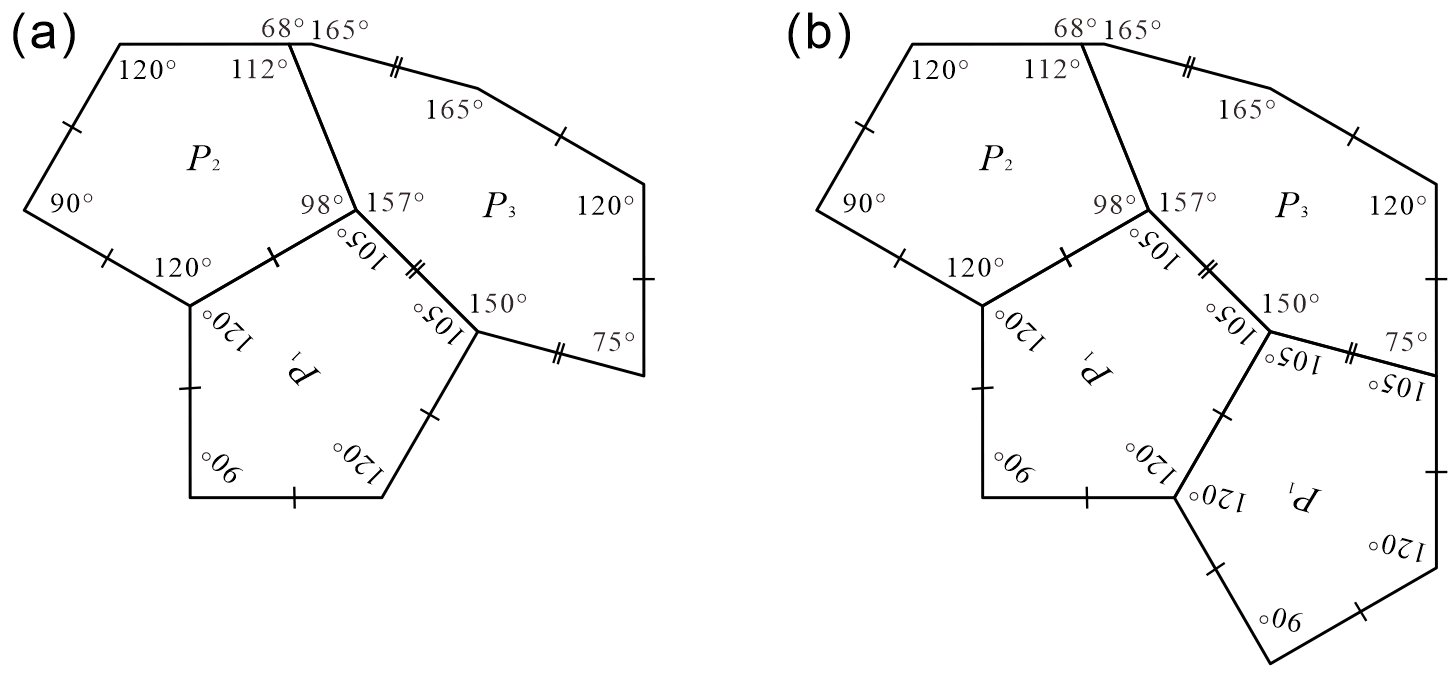
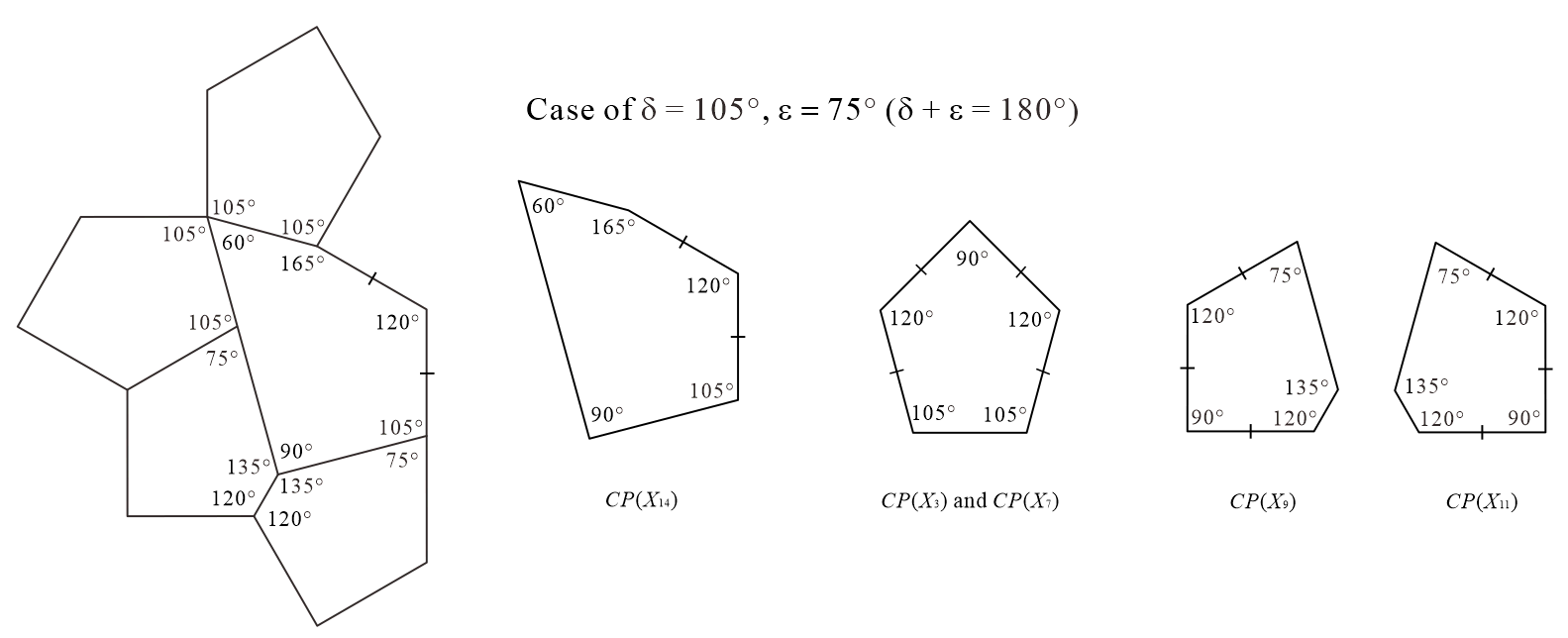
In addition, in the cases of $\alpha=165^{\circ}$ in Method 1 (see Figure 4(f)) and $\beta=165^{\circ}$ in Method 2 (see Figure 5(f)), the three convex polygons created by division are identical. We confirmed that each convex polygon in these cases cannot generate a tiling even if the use of reflected tiles is allowed during the tiling generation process. In other words, $P_{1}$ , $P_{2}$ , and $P_{3}$ in this case are not monotiles. However, the convex pentagon $P_{1}$ and convex hexagon $P_{2}$ can form periodic tilings as shown in Figure 6. Therefore, the set of three convex polygons in the case of $\alpha=165^{\circ}$ in Method 1 ( $\beta=165^{\circ}$ in Method 2) is not an ASP.

In the case of $\alpha=180^{\circ}$ in Method 1 (see Figure 4(g)), we confirmed that each convex polygon created by the division cannot generate a tiling, even if the use of reflected tiles is allowed during the tiling generation process. In other words, $P_{1}$ , $P_{2}$ , and $P_{3}$ in this case are not monotiles. However, the convex pentagons $P_{1}$ and $P_{3}$ can form periodic tilings, as shown in Figure 7. Therefore, the set of three convex polygons in the case of $\alpha=180^{\circ}$ in Method 1 is not an ASP. However, outside the conditions, if convex pentagon $P_{1}$ , convex hexagon $P_{2}$ , and reflected $P_{2}$ are used, a periodic tiling can be formed (see Appendix C). Because such cases are possible, the condition of this study that “reflected tiles cannot be used during all tiling generation processes” is important.

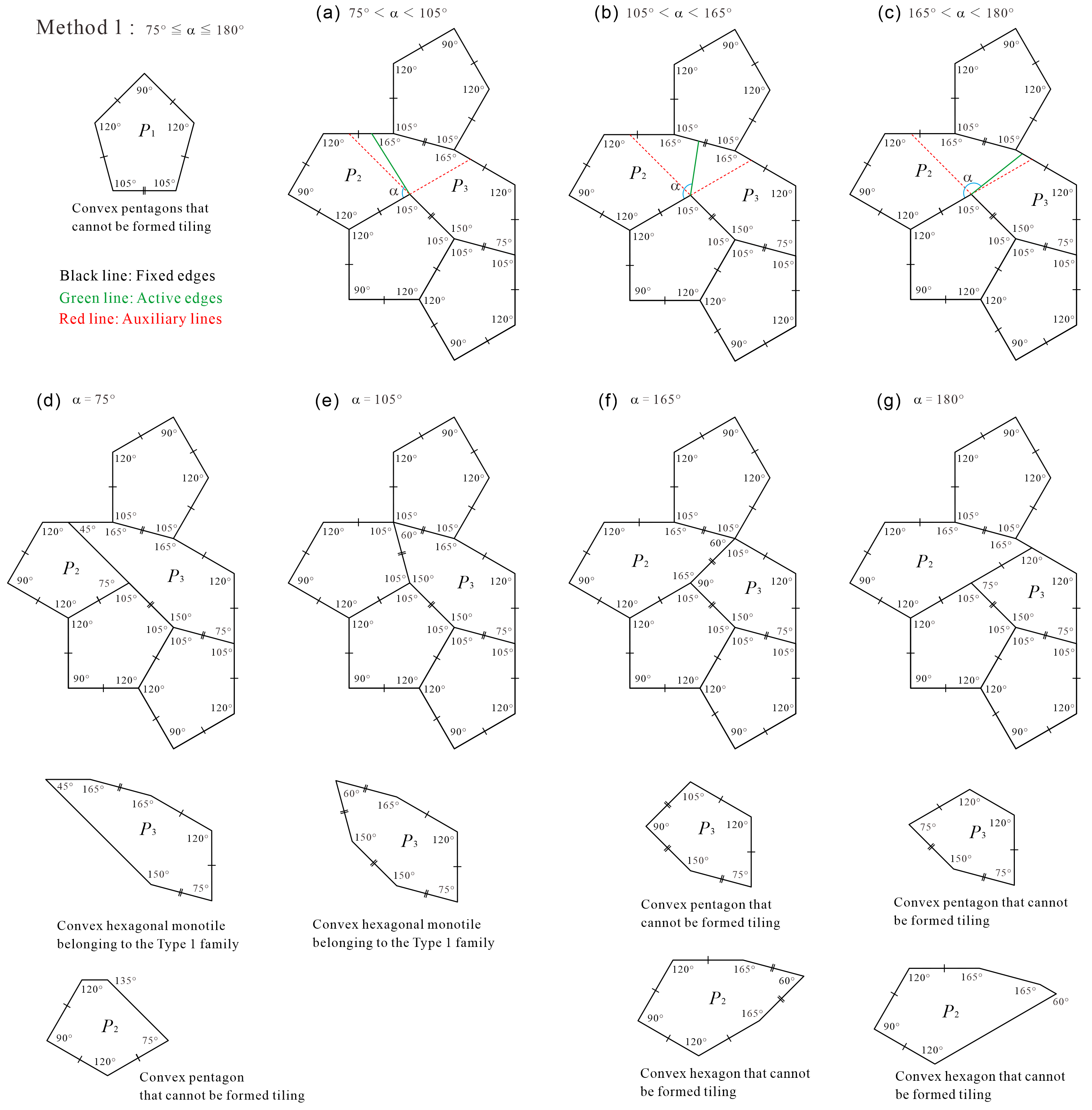
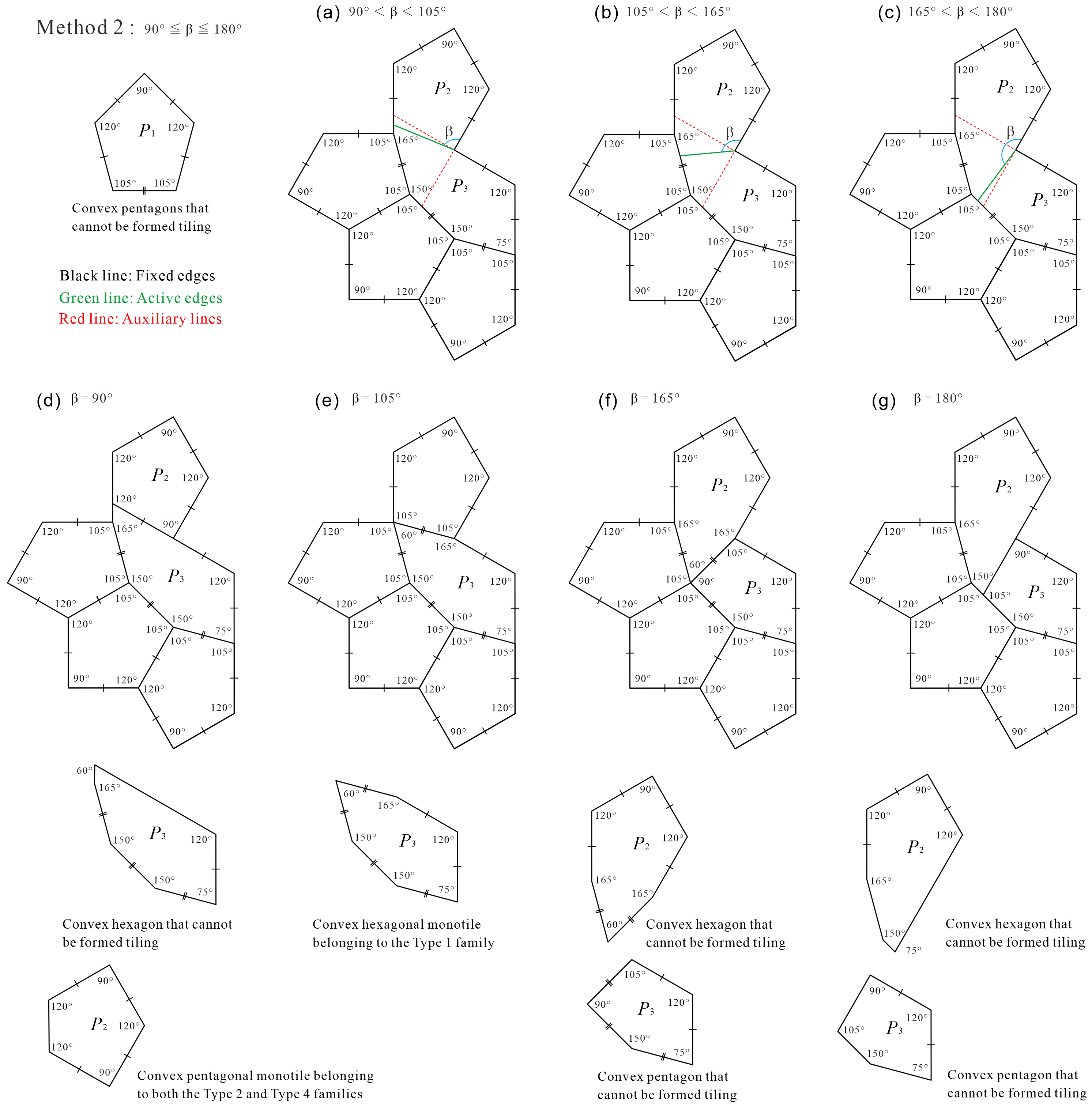
From the cases “(a) $75^{\circ}<\alpha<105^{\circ}$ , (b) $105^{\circ}<\alpha<165^{\circ}$ , (c) $165^{\circ}<\alpha<180^{\circ}$ ” of Method 1 shown in Figure 4 and “(a) $90^{\circ}<\beta<105^{\circ}$ , (b) $105^{\circ}<\beta<165^{\circ}$ , (c) $165^{\circ}<\beta<180^{\circ}$ ” of Method 2 shown in Figure 5, candidates of ASP comprising three types of convex polygons can be created. We refer to it as “candidate” because if we generate tilings with convex polygons contained in the tile set, we have to make sure that there exist only non-periodic tilings using the shape of Tile $(1,1)$ , if and only if all types of convex polygons contained in the tile set are used. For example, the division of $\alpha=90^{\circ}$ in “(a) $75^{\circ}<\alpha<105^{\circ}$ ” of Method 1 creates a convex pentagonal monotile $P_{2}$ belonging to both the Type 2 and Type 4 families with line symmetry, as shown in Figure 8, which can form periodic tiling (see Appendix A). Thus, the set of three types of convex polygons created by the division of $\alpha=90^{\circ}$ in Method 1 is not an ASP.

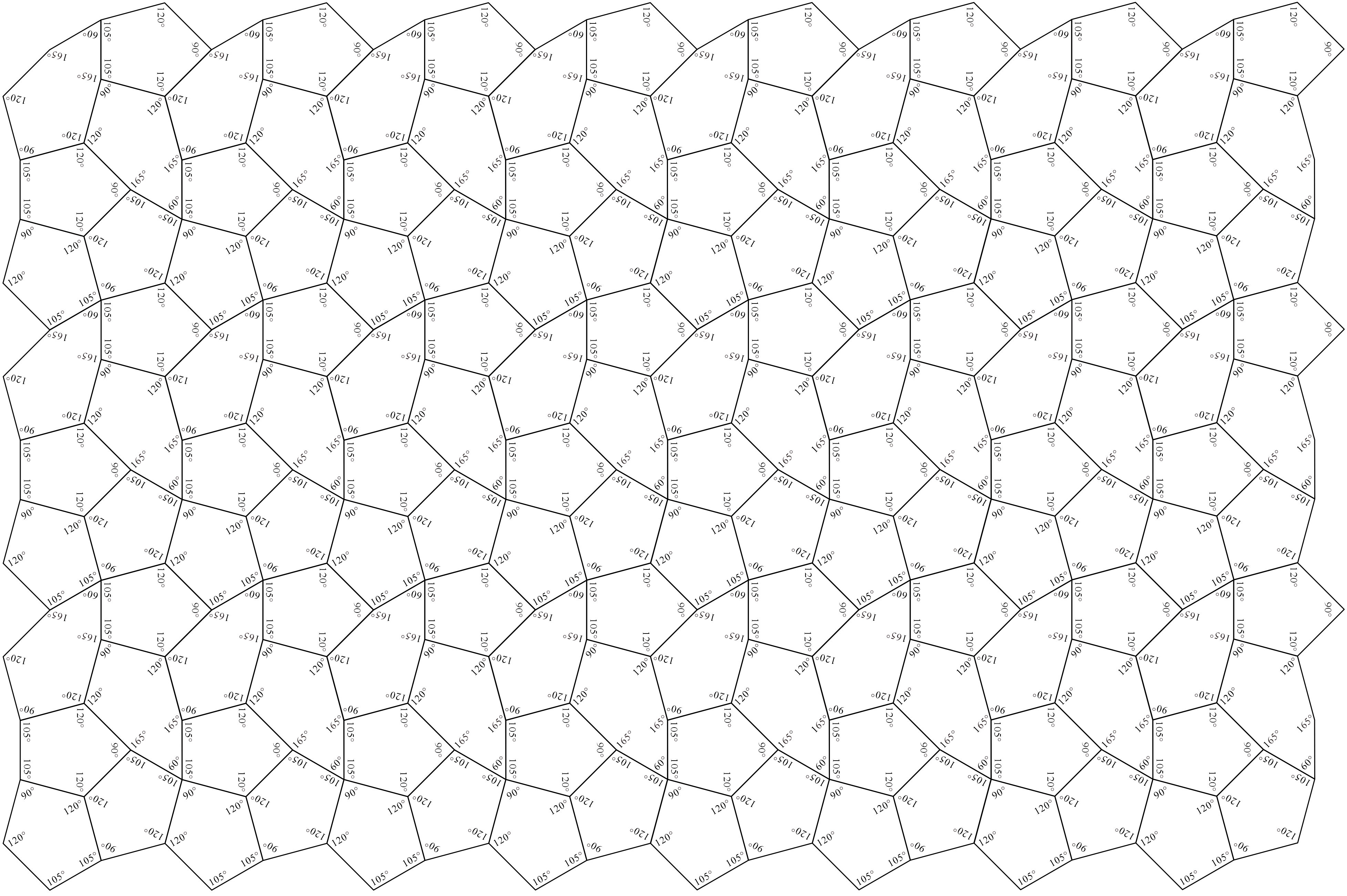
As concrete examples of the “candidate” cases, we investigated the sets of three types of convex polygons in the case of $\alpha=98^{\circ}$ in Method 1 shown in Figure 9 and in the case of $\alpha=124^{\circ}$ in Method 1 shown in Figure 10. We confirmed that these tile sets are ASPs comprising three types of convex polygons. Figures 11 and 12 show the non-periodic tilings generated by the ASP comprising three types of convex polygons in the cases of $\alpha=98^{\circ}$ and $\alpha=124^{\circ}$ in Method 1.

Using the case of the three convex polygons created by the division of $\alpha=98^{\circ}$ in Method 1, as shown in Figure 9, some of the key points of the investigation (identification) method are briefly described. To form tilings, two or more tile vertices must be concentrated at one point and the sum of the interior angles of the vertices at the concentration point must be $180^{\circ}$ or $360^{\circ}$ . Therefore, as there were no convex pentagons with interior angles of $65^{\circ}$ or less, $120^{\circ}$ , $150^{\circ}$ , $157^{\circ}$ , and $165^{\circ}$ cannot be used in a concentration with a sum of $180^{\circ}$ . From the balance with other interior angles, we observed that an even number of vertices with interior angles of $68^{\circ}$ , $98^{\circ}$ , $112^{\circ}$ , and $157^{\circ}$ must always be concentrated at one point, because the place value of one should be zero or five to make $180^{\circ}$ or $360^{\circ}$ . Based on these considerations, it was concluded that the concentration of vertices with an interior angle of $157^{\circ}$ of $P_{3}$ was impossible, except for the arrangements using $P_{1}$ and $P_{2}$ , as shown in Figure 13(a). Subsequently, note the point in Figure 13(a) where $P_{3}$ has an internal angle of $150^{\circ}$ . If a tiling is formed, the only method to obtain a sum of $360^{\circ}$ is to place the vertex of the tile with an interior angle of $105^{\circ}$ at the concentrating point. Figure 13(b) shows the only combination that can form a structure in which the tiling does not collapse. Then, for the positions with vertices having internal angles of $165^{\circ}$ of $P_{3}$ in Figure 13(b), the only combination that can construct a structure in which the tiling does not collapse using $P_{1}$ , $P_{2}$ , and $P_{3}$ in Figure 9 is that of dividing Tile $(1,1)$ (using the shape of Tile $(1,1)$ ), as shown in Figure 9.

If an ASP comprising three types of convex polygons can be constructed from the cases “(a) $75^{\circ}<\alpha<105^{\circ}$ , (b) $105^{\circ}<\alpha<165^{\circ}$ , (c) $165^{\circ}<\alpha<180^{\circ}$ ” of Method 1 in Figure 4 or “(a) $90^{\circ}<\beta<105^{\circ}$ , (b) $105^{\circ}<\beta<165^{\circ}$ , (c) $165^{\circ}<\beta<180^{\circ}$ ” of Method 2 in Figure 5, the combination of three types of convex polygons in the set is as follows.

•

The tile set comprising two types of convex pentagons and one type of convex heptagon.
- $\circ$
  
  Method 1: $75^{\circ}<\alpha<105^{\circ}$ and $165^{\circ}<\alpha<180^{\circ}$
- $\circ$
  
  Method 2: $90^{\circ}<\beta<105^{\circ}$ and $165^{\circ}<\beta<180^{\circ}$

•

The tile set comprising one type of convex pentagon and two types of convex hexagons.
- $\circ$
  
  Method 1: $105^{\circ}<\alpha<165^{\circ}$
- $\circ$
  
  Method 2: $105^{\circ}<\beta<165^{\circ}$

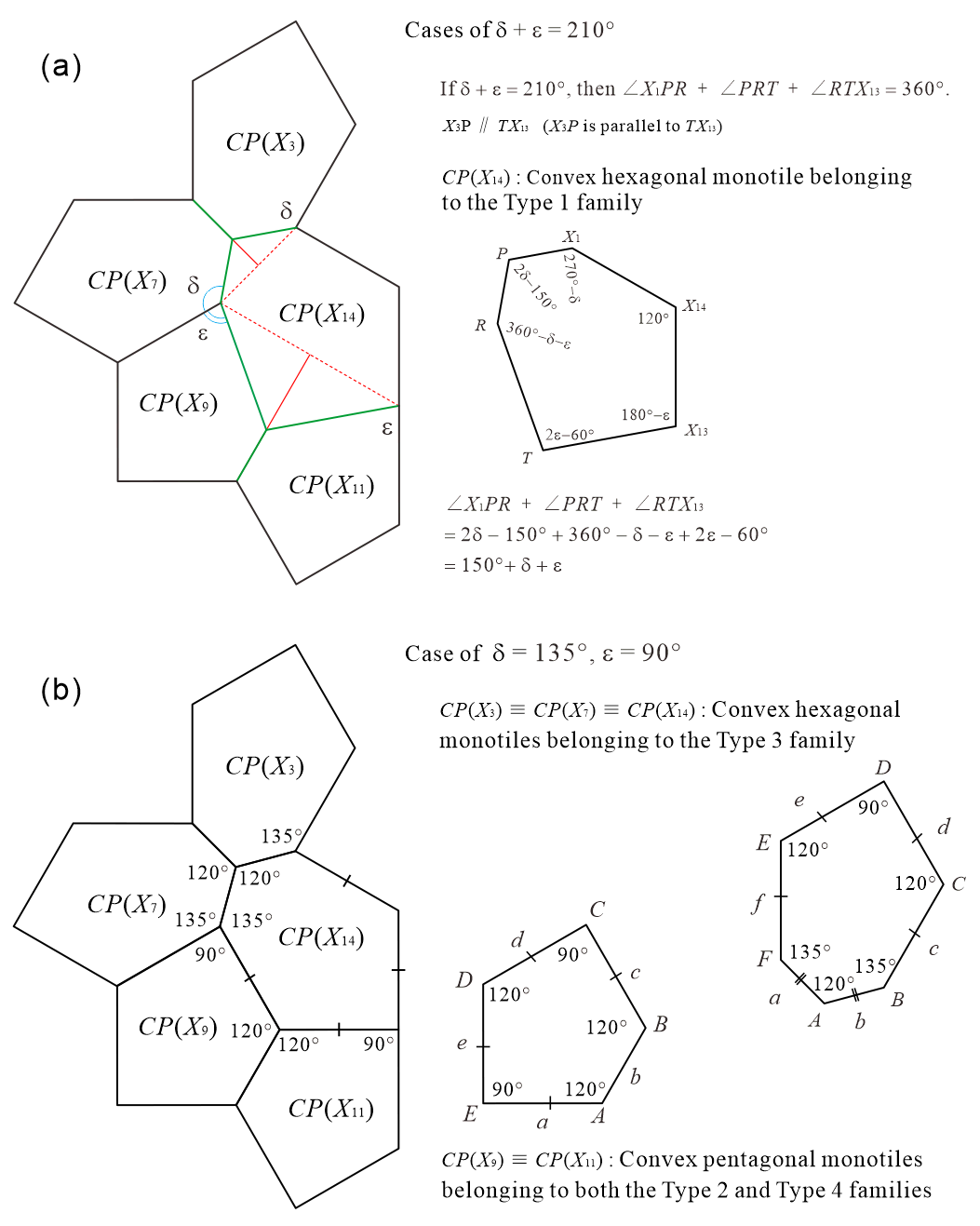
However, in the case of $\beta=180^{\circ}$ in Method 2 (see Figure 5(g)), two types of convex pentagons ( $P_{1}$ and $P_{3})$ and one type of convex hexagon ( $P_{2})$ were created, and we confirmed that this tile set is an ASP comprising three types of convex polygons. Figure 14 shows the non-periodic tiling generated by the ASP comprising three types of convex polygons (two types of convex pentagons and one type of convex hexagon) in the case of $\beta=180^{\circ}$ in Method 2.

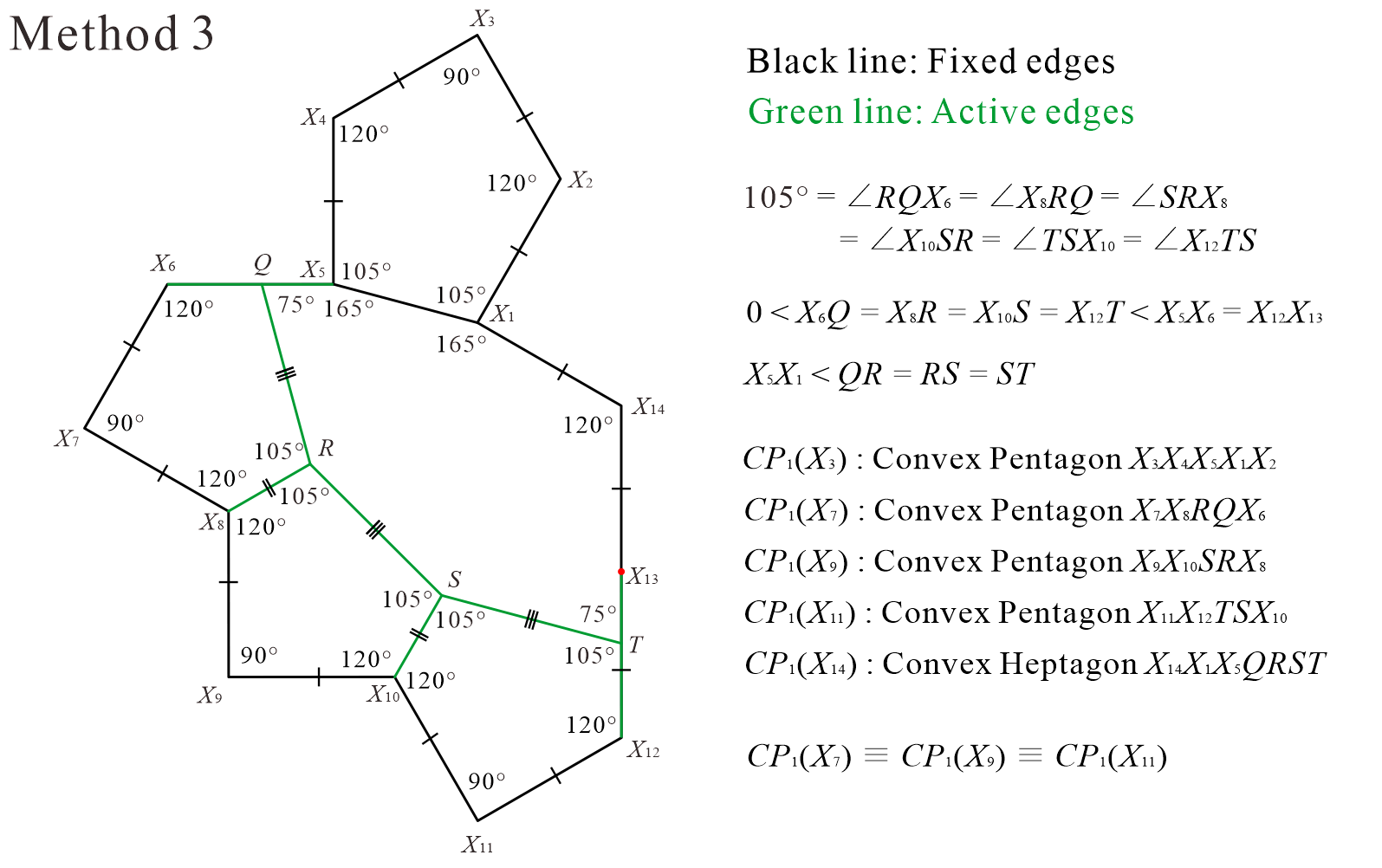
2.2 Method 3

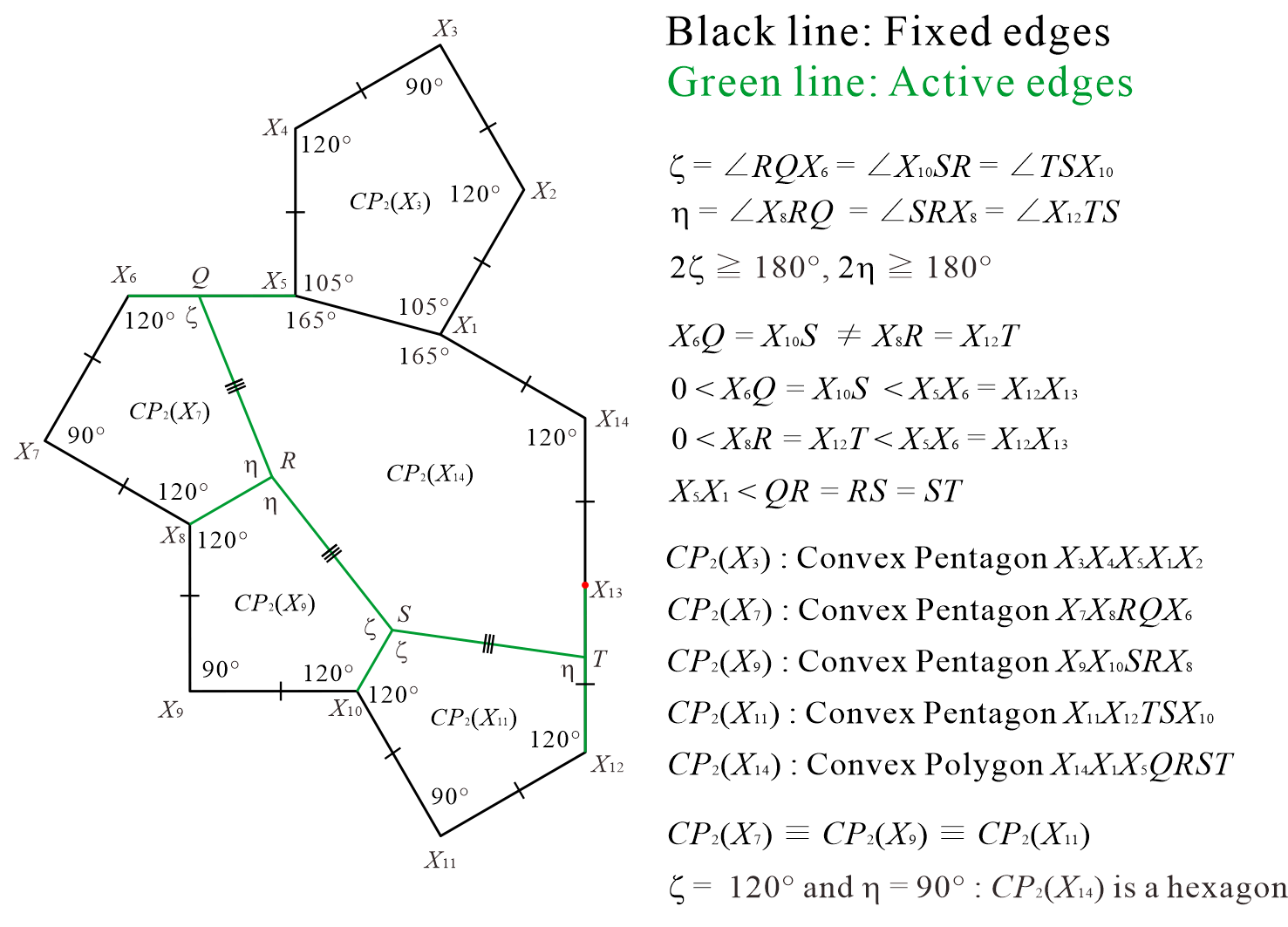
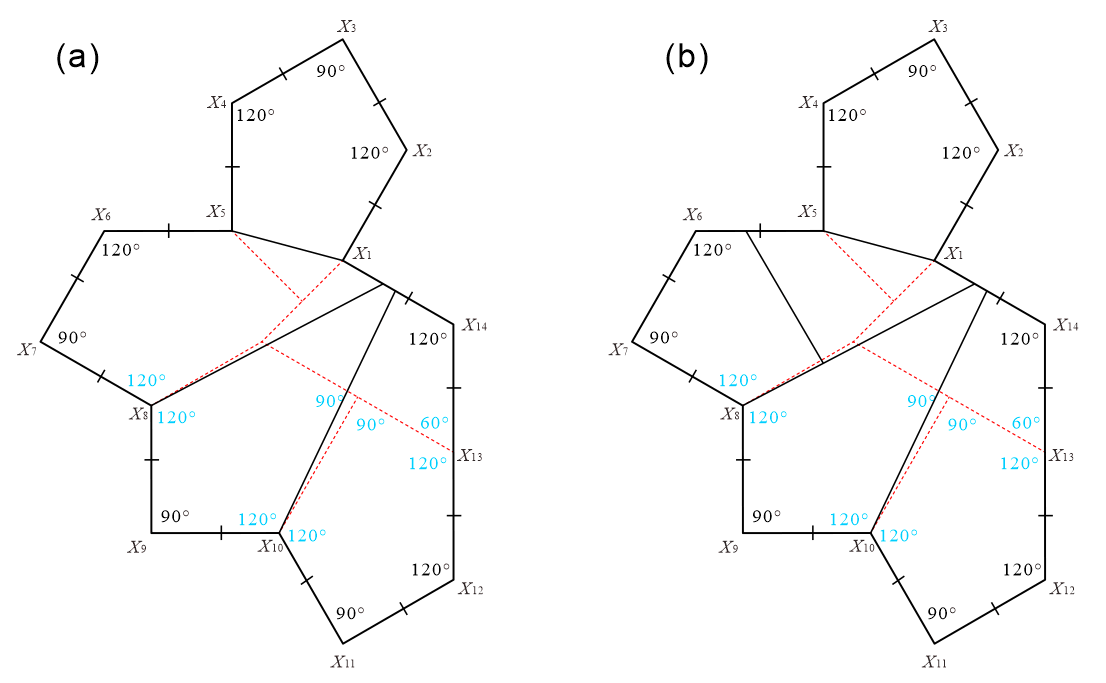
The third division method is Method 3, as shown in Figure 15. This can be regarded as a modified version of the division shown in Figure 4(e). The convex pentagon $P_{1}$ in Figure 4(e), which corresponds to the vertices $X_{7}$ , $X_{9}$ , and $X_{11}$ in Figure 15, can be considered as transformed, maintaining the same values of the interior angles.

In Figure 15, the point $Q$ moves on the edge $X_{5}X_{6}$ and the point $T$ moves on the edge $X_{12}X_{13}$ of Tile $(1,1)$ in the range “ $0<X_{6}Q=X_{10}T<X_{5}X_{6}$ .” In Figure 15, the convex pentagon $CP_{1}(X_{3})$ with the points “ $X_{3}$ , $X_{4}$ , $X_{5}$ , $X_{1}$ , $X_{2}$ ” as vertices is fixed shape, which is the same as the convex pentagon $P_{1}$ in Figure 4. Additionally, the convex pentagon $CP_{1}(X_{7})$ with the points “ $X_{7}$ , $X_{8}$ , $R$ , $Q$ , $X_{6}$ ” as vertices, the convex pentagon $CP_{1}(X_{9})$ with the points “ $X_{9}$ , $X_{10}$ , $S$ , $R$ , $X_{8}$ ” as vertices, and the convex pentagon $CP_{1}(X_{11})$ with the points “ $X_{11}$ , $X_{12}$ , $T$ , $S$ , $X_{10}$ ” as vertices are congruent convex pentagons with interior angles always at “ $90^{\circ},120^{\circ},105^{\circ},105^{\circ},120^{\circ}$ ” and with line symmetry. The convex polygon $CP_{1}(X_{14})$ with the points “ $X_{14}$ , $X_{1}$ , $X_{5}$ , $Q$ , $R$ , $S$ , $T$ ” as vertices is always a convex heptagon.

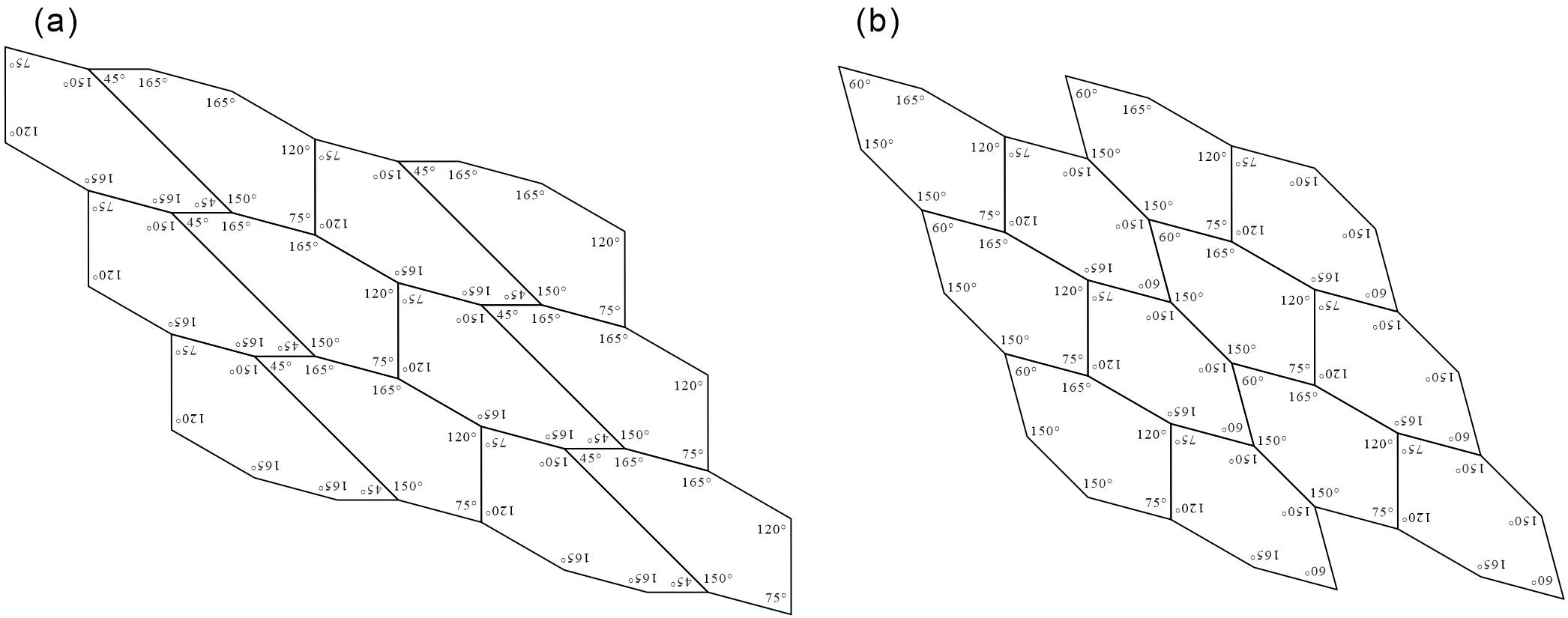
As a concrete example, we investigated using the case where the ratio of the edges is “ $X_{6}Q:X_{5}Q=3:2$ ” as shown in Figure 16. As a result, we confirmed that this tile set is an ASP comprising three types of convex polygons (two types of convex pentagons and one type of convex heptagon). Figure 17 shows the non-periodic tiling generated by the ASP comprising two types of convex pentagons and one type of convex heptagon in Figure 16.

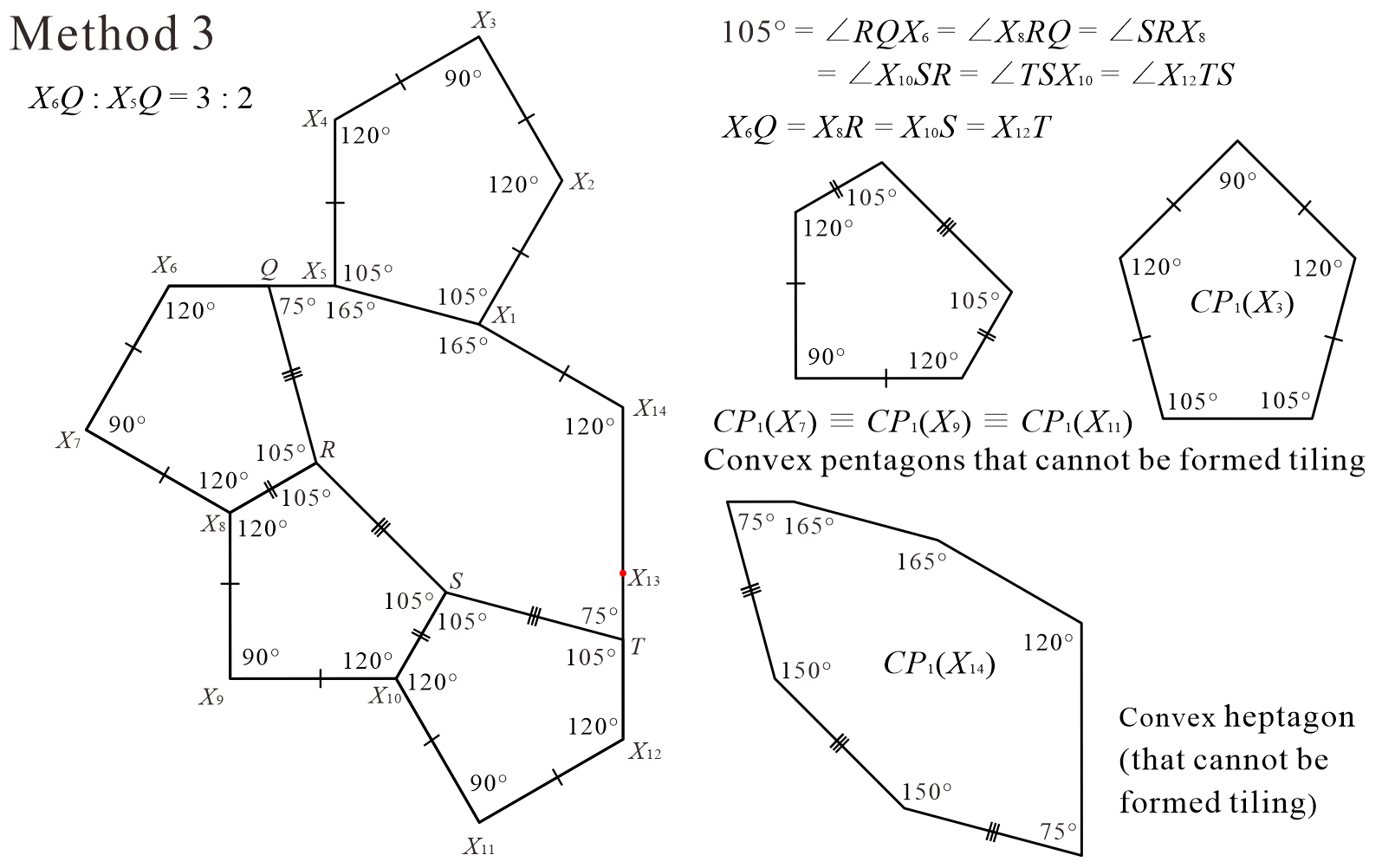
From the process of investigation (identifying) for the case shown in Figure 16, we conjecture that in the case of $X_{6}X_{7}\neq QR$ , the tile set of three convex polygons in Figure 15 is an ASP, comprising two types of convex pentagons and one type of convex heptagon. When the conjecture of $X_{6}X_{7}\neq QR$ was not directly applicable, we individually confirmed that the tile set in the case of $X_{6}X_{7}=QR$ was an ASP comprising two types of convex pentagons and one type of convex heptagon.

2.3 Method 4

The fourth division method is Method 4, as shown in Figure 18. The results of the tile sets (five convex polygons containing three $P_{1}$ ) created by the division of Method 4 differ depending on the value of the parameter $\gamma$ shown in Figure 18.

First, from the cases “(a) $75^{\circ}<\gamma<93.43^{\circ}$ , (b) $93.43^{\circ}<\alpha<180^{\circ}$ ”⁸⁸8 When $\gamma=(3\pi/4)+\tan^{-1}\left({{\left({5-2\sqrt{3}}\right)}\mathord{\left/{\vphantom{{\left({5-2\sqrt{3}}\right)}3}}\right.\kern-1.2pt}\sqrt{3}}\right)\approx 93.43^{\circ}$ in Figure 18(d), $P_{2}$ and $P_{3}$ are both convex pentagons. of Method 4 shown in Figure 18, candidates of ASP comprising three types of convex polygons can be created. We refer to it as “candidate” because if we generate tilings with convex polygons contained in the tile set, we have to make sure that there exist only non-periodic tilings using the shape of Tile $(1,1)$ , if and only if all types of convex polygons contained in the tile set are used. If an ASP comprising three types of convex polygons can be constructed from the cases “(a) $75^{\circ}<\gamma<93.43^{\circ}$ , (b) $93.43^{\circ}<\alpha<180^{\circ}$ ” of Method 4, it is the tile set comprising two types of convex pentagons and one type of convex hexagon.

The cases “(e) $\gamma=150^{\circ}$ , (f) $\gamma=165^{\circ}$ ” of Method 4 shown in Figure 18 are not ASPs. The reasons are shown below.

•

In the case of $\gamma=150^{\circ}$ in Method 4 (see Figure 18(e)), there is the convex hexagonal monotile $P_{3}$ belonging to the Type 1 family that can form periodic tiling without using reflected tiles (see Appendix B); therefore, the set of two types of convex polygons by this division is not ASP. Note that this division is the same as for $\alpha=105^{\circ}$ in Method 1 (see Figure 4(e)).

•

In the case of $\gamma=165^{\circ}$ in Method 4 (see Figure 18(f)), there is the convex pentagonal monotile $P_{2}$ belonging to both the Type 2 and Type 4 families with the property of line symmetry that cannot distinguish between the anterior and posterior sides (see Appendix A); therefore, the set of three types of convex polygons by this division is not an ASP.

By contrast, for the cases “(c) $\gamma=75^{\circ}$ , (d) $\gamma=(3\pi/4)+\tan^{-1}\left({{\left({5-2\sqrt{3}}\right)}\mathord{\left/{\vphantom{{\left({5-2\sqrt{3}}\right)}3}}\right.\kern-1.2pt}\sqrt{3}}\right)\approx 93.43^{\circ}$ , (g) $\gamma=180^{\circ}$ ” of Method 4 shown in Figure 18, under the condition that the tiles in the tile set cannot be reflected (the use of reflected tiles is not allowed) during the tiling generation process, we confirmed that these tile sets are ASPs comprising three types of convex pentagons.

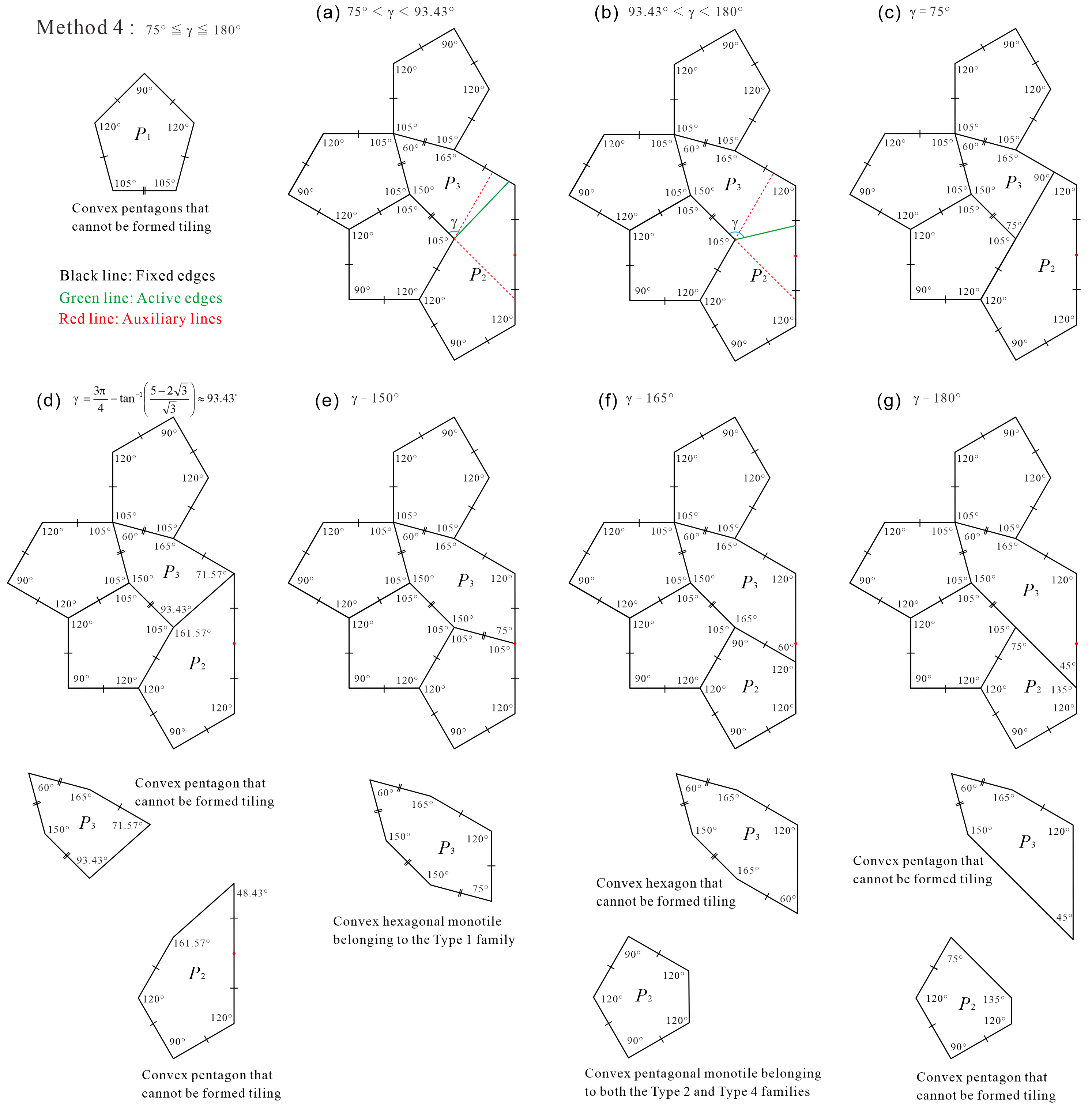
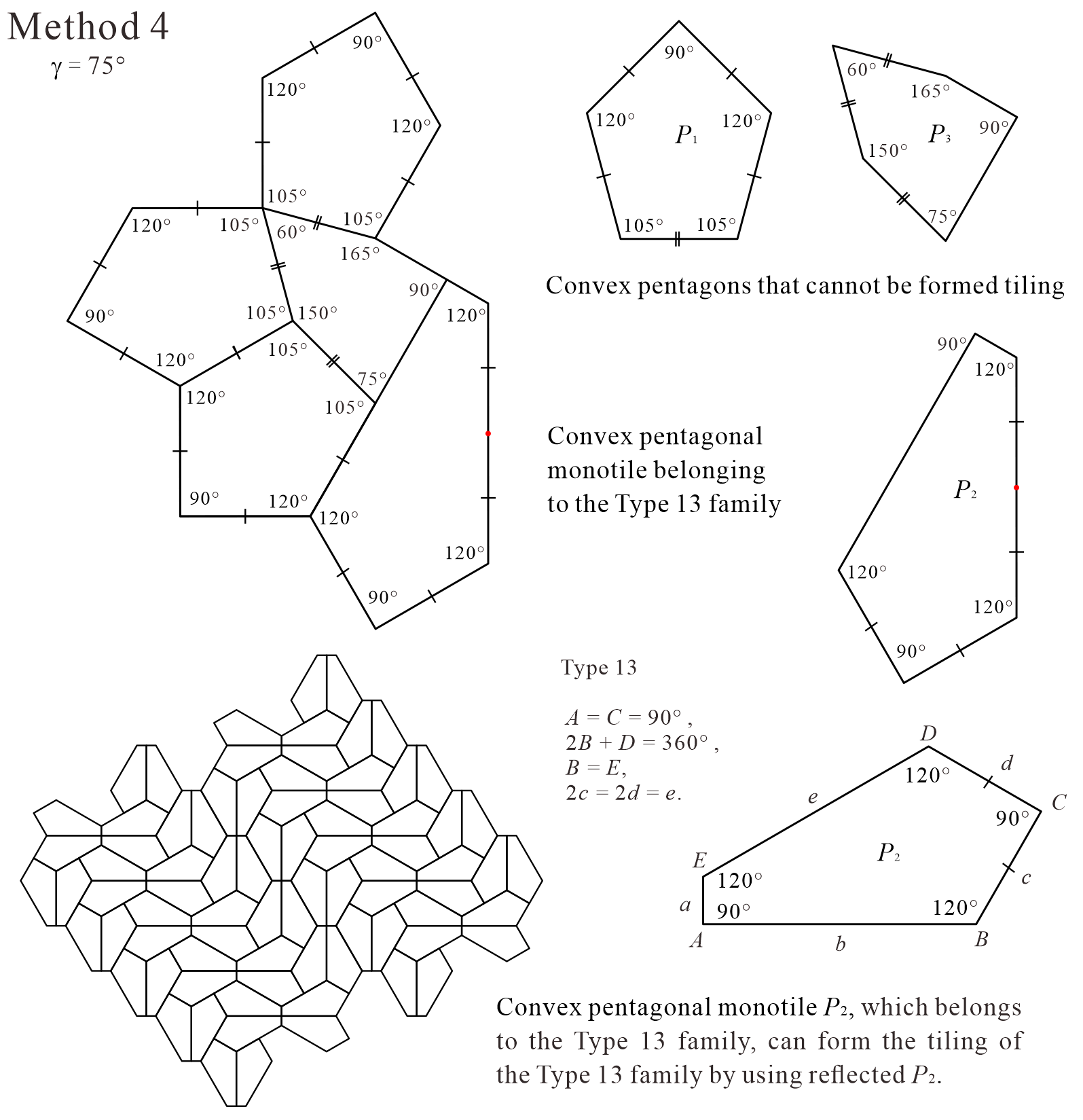
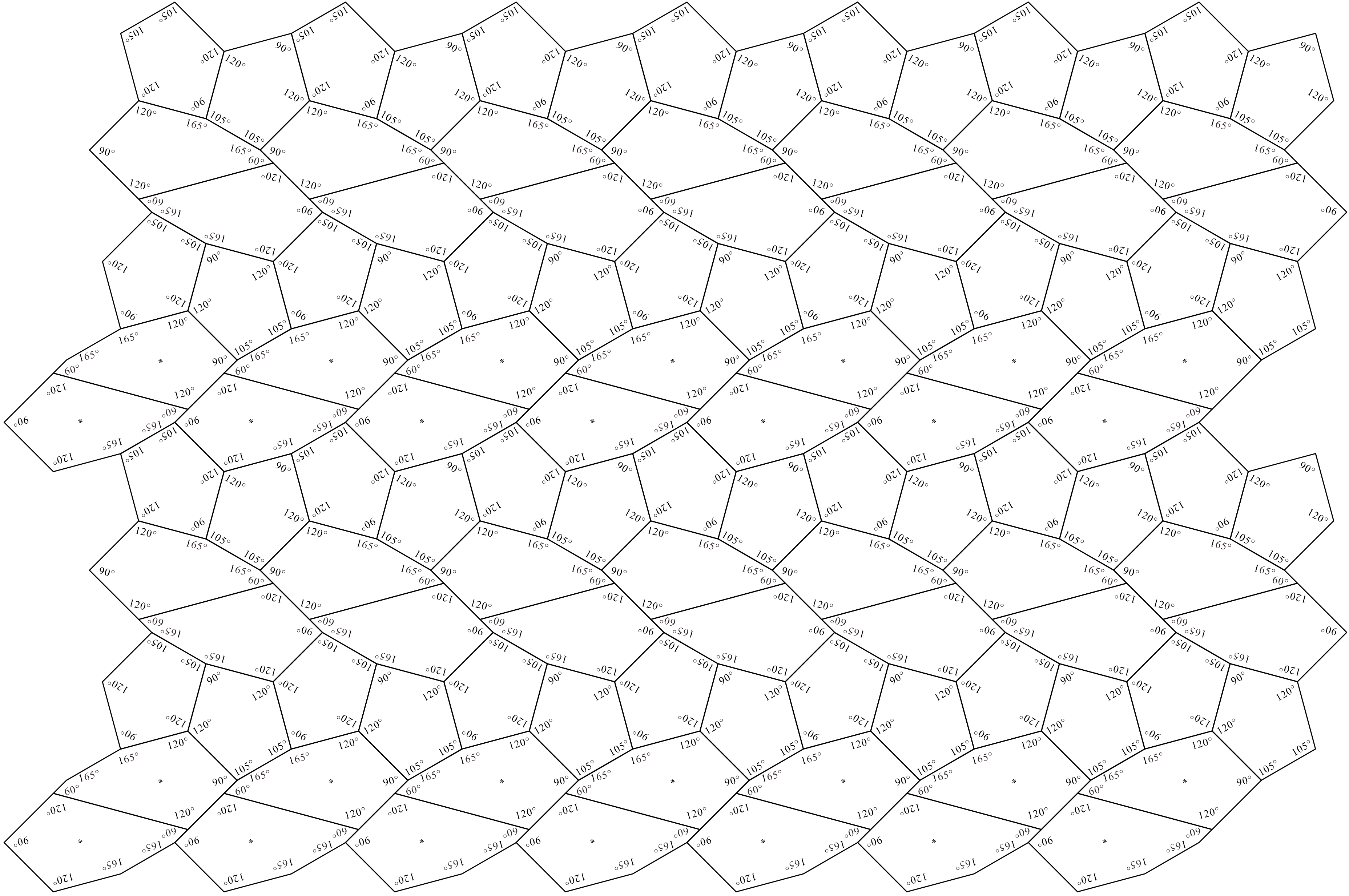
It can be considered that the tile set of $P_{1}$ , $P_{2}$ , and $P_{3}$ in the case of $\gamma=75^{\circ}$ in Method 4 (see Figure 19) is not an ASP, because the set contains the convex pentagonal monotile $P_{2}$ belonging to the Type 13 family. However, in this study, we assumed that the reflected tiles cannot be used during all tiling generation processes. $P_{2}$ , which belongs to the Type 13 family, can form the (representative) tiling of the Type 13 family shown in Figure 19 by using reflected $P_{2}$ . However, the tile set of the three types of convex pentagons created by this division does not contain the reflected $P_{2}$ . We actually confirmed that tiling cannot be generated with only this $P_{2}$ under the condition that “reflected tiles cannot be used during all tiling generation processes”⁹⁹9 If a convex pentagonal monotile belongs to at least one of the Type 1 or 3–6 families, it can generate tilings without the use of reflected tiles (see Appendix A). The convex pentagonal monotiles belonging to the Type 13 families and those belonging to the Type 1 or 3–6 families are disjoint [4, 15, 16, 17, 20, 24]. . We examined whether tiling is possible using $P_{1}$ , $P_{2}$ , and $P_{3}$ , as shown in Figure 19, and confirmed that the only combination that can construct a structure in which the tiling does not collapse using $P_{1}$ , $P_{2}$ , and $P_{3}$ is that of dividing Tile $(1,1)$ (using the shape of Tile $(1,1)$ ), as shown in Figure 19. Therefore, under the condition that the tiles in the tile set cannot be reflected during the tiling generation process, the tile set of the three types of convex pentagons that can be created using the case of $\gamma=75^{\circ}$ in Method 4 is an ASP.

Figures 20, 21, and 22 show the non-periodic tilings generated by the ASP comprising three types of convex pentagons in the cases of $\gamma=75^{\circ}$ , $\gamma=(3\pi/4)+\tan^{-1}\left({{\left({5-2\sqrt{3}}\right)}\mathord{\left/{\vphantom{{\left({5-2\sqrt{3}}\right)}3}}\right.\kern-1.2pt}\sqrt{3}}\right)\approx 93.43^{\circ}$ , and $\gamma=180^{\circ}$ in Method 4.

3 Conclusion

In this study, we presented the ASPs comprising three types of convex polygons other than the “the set of three convex polygons that are aperiodic with no matching condition on the edges” shown in Figure 1. Note that, in this study, we treated the anterior and posterior side tiles as different types, even if they are congruent diagrams, and assumed that the reflected tiles cannot be used during all tiling generation process with the tiles in a tile set.

There appears to be no known ASP comprising two types of convex polygons with no matching conditions on the edges (there also seems to be no proof that there is no such ASP) [22, 23].

Because the ASPs comprising three types of convex polygons shown in this study are based on Tile $(1,1)$ shown in [12] and assumes that Tile $(1,1)$ is the chiral aperiodic monotile shown in [13], it is not confirmed that these sets are actually ASPs.

If the types and number of tiles in a tile set can be freely increased under the condition that the tiles in the tile set cannot be reflected during the tiling generation process, several ASPs comprising multiple types of convex polygons can be created. There will be various methods for dividing Tile $(1,1)$ into four, five, or more types of convex polygons that are likely to be ASP (see Appendix D). This is because the convex pentagon can be divided into six types. Thus, by such a division, it would be easy to create convex pentagons that are not monotiles, or a convex pentagon containing only one side of a convex pentagonal monotile that requires the use of reflected tiles during the tiling generation process, as in the case of $\gamma=75^{\circ}$ in Method 4. However, even if the tile sets that increase the number of tiles in this manner are aperiodic, they are not considered interesting. Therefore, we did not discuss the effects of increasing the type or number of such tiles in this study.

Acknowledgments. The authors would like to express my deep gratitude to Professor Emeritus Yoshio Agaoka, Hiroshima University, for his helpful comments and advice during the preparation of this manuscript. The authors also received constructive comments from Professor Shigeki Akiyama, University of Tsukuba, and Yoshiaki Araki.

References

[1] Bollobás, B. (1963). Filling the plane with congruent convex hexagons without overlapping. Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 6, 117–123.
[2] Croft, H. T., Falconer, K. J., and Guy, R. G. (1991). Unsolved Problems in Geometry. Springer-Verlag, New York, pp.79–80 and pp.101–103 (C18).
[3] Gardner, M. (1975). On tessellating the plane with convex polygon tiles. Scientific American, Vol.233, No.1 (July 1975), 112–119. https://www.jstor.org/stable/24949848
[4] Grünbaum, B. and Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company, New York, pp.15–56 (Chapter 1), pp.471–518 (Chapter 9), pp.520–582 (Chapter 10).
[5] Niven, I. (1978). Convex polygons that cannot tile the plane. The American Mathematical Monthly, 85(10), 785–792. doi:10.1080/00029890.1978.11994704
[6] Kershner, R. B. (1968). On paving the plane. American Mathematical Monthly, 75, 839–844. doi:10.1080/00029890.1968.11971075
[7] Klamkin, M. S. and Liu, A. (1980). Note on a result of Niven on impossible tessellations. American Mathematical Monthly, 87(8), 651–653.
[8] Mann, C., McLoud-Mann, J., and Von Derau, D. (2018). Convex pentagons that admit i-block transitive tilings. Geometriae Dedicata, 194(1), 141–167. doi:10.1007/s10711-017-0270-9
[9] Rao, M. (2017). Exhaustive search of convex pentagons which tile the plane. arXiv:1708.00274 (accessed on 22 December 2024).
[10] Reinhardt, K. (1918). Über die Zerlegung der Ebene in Polygone. Inaugural-Dissertation, Univ. Frankfurt a.M., R. Noske, Boran and Leipzig. https://gdz.sub.uni-goettingen.de/id/PPN316479497
[11] Schattschneider, D. (1978). Tiling the plane with congruent pentagons. Mathematics Magazine, 51, 29–44. doi:10.1080/0025570X.1978.11976672
[12] Smith, D., Myers, J. S., Kaplan, C. S., and Goodman-Strauss, C. (2024). An aperiodic monotile. Combinatorial Theory, 4(1), 1–91. doi:10.5070/C64163843
[13] Smith, D., Myers, J. S., Kaplan, C. S., and Goodman-Strauss, C. (2024). A chiral aperiodic monotile. Combinatorial Theory, 4(2), 1–25. doi:10.5070/C64264241
[14] Stein, R. (1985) A new pentagon tiler. Mathematics Magazine, 58(5), 308. https://www.jstor.org/stable/2690183
[15] Sugimoto, T. (2016). Convex pentagons for edge-to-edge tiling, III. Graphs and Combinatorics, 32, 785–799. doi:10.1007/s00373-015-1599-1
[16] Sugimoto, T. (2017). Convex polygons for aperiodic Tiling. Research and Communications in Mathematics and Mathematical Sciences, 8(1), 69–79. https://www.jyotiacademicpress.net/convex_polygons_for.pdf
[17] Sugimoto, T. (2018). Properties of convex pentagonal tiles for periodic tiling. arXiv:1811.02075 (accessed on 18 November 2024).
[18] Sugimoto, T. (2020). Pentagons and rhombuses that can form rotationally symmetric tilings. arXiv:2005.127098 (accessed on 7 February 2024).
[19] Sugimoto, T. (2020). Rotationally symmetric tilings with convex pentagons belonging to both the Type 1 and Type 7 families. arXiv:2005.13980 (accessed on 7 February 2024).
[20] Sugimoto, T. (2025). Convex pentagonal monotiles in the 15 Type families. arXiv:2501.07090 (accessed on 14 January 2025).
[21] Sugimoto, T. and Araki, Y. (2017). Convex pentagon tilings and heptiamonds, I. arXiv:1704.03997 (accessed on 7 February 2024).
[22] Wikipedia contributors. Aperiodic set of prototiles. Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Aperiodic_set_of_prototiles (accessed on 22 December 2024).
[23] Wikipedia contributors. List of aperiodic set of tiles. Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/List_of_aperiodic_sets_of_tiles (accessed on 22 December 2024).
[24] Wikipedia contributors. Pentagonal tiling. Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/wiki/Pentagonal_tiling (accessed on 22 December 2024).
[25] Zong, C. (2020). Can you pave the plane nicely with identical tiles. Notices of the American Mathematical Society, 67(5), 635–646. doi:10.1090/noti2075
[26]

Appendix Appendix A Convex pentagonal monotiles

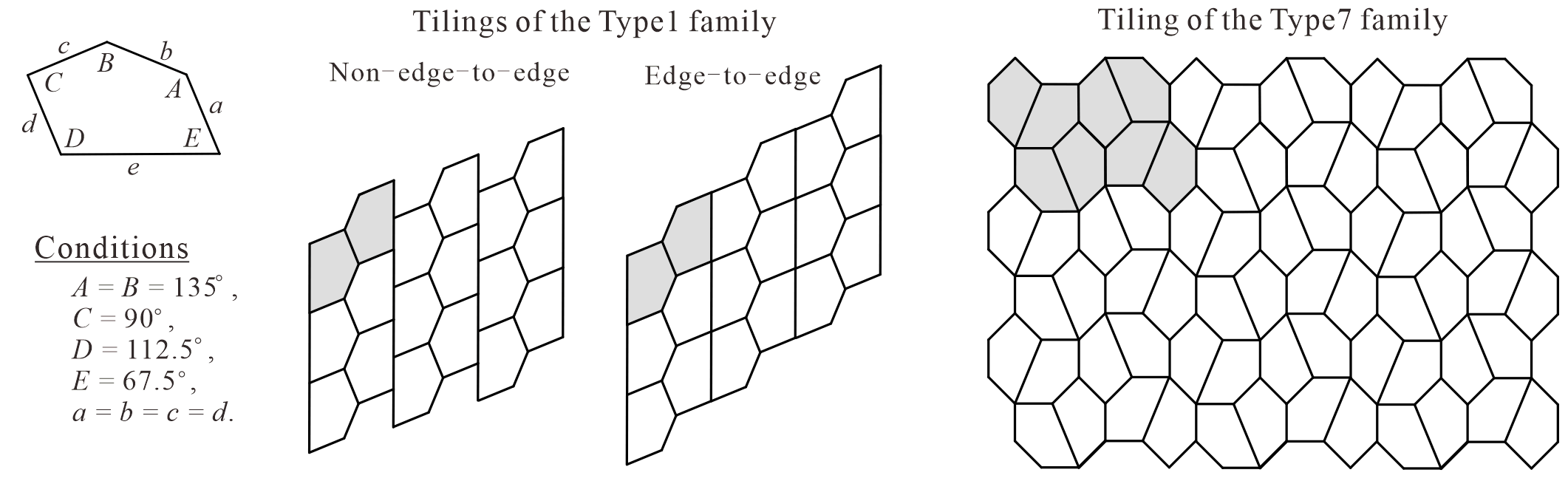
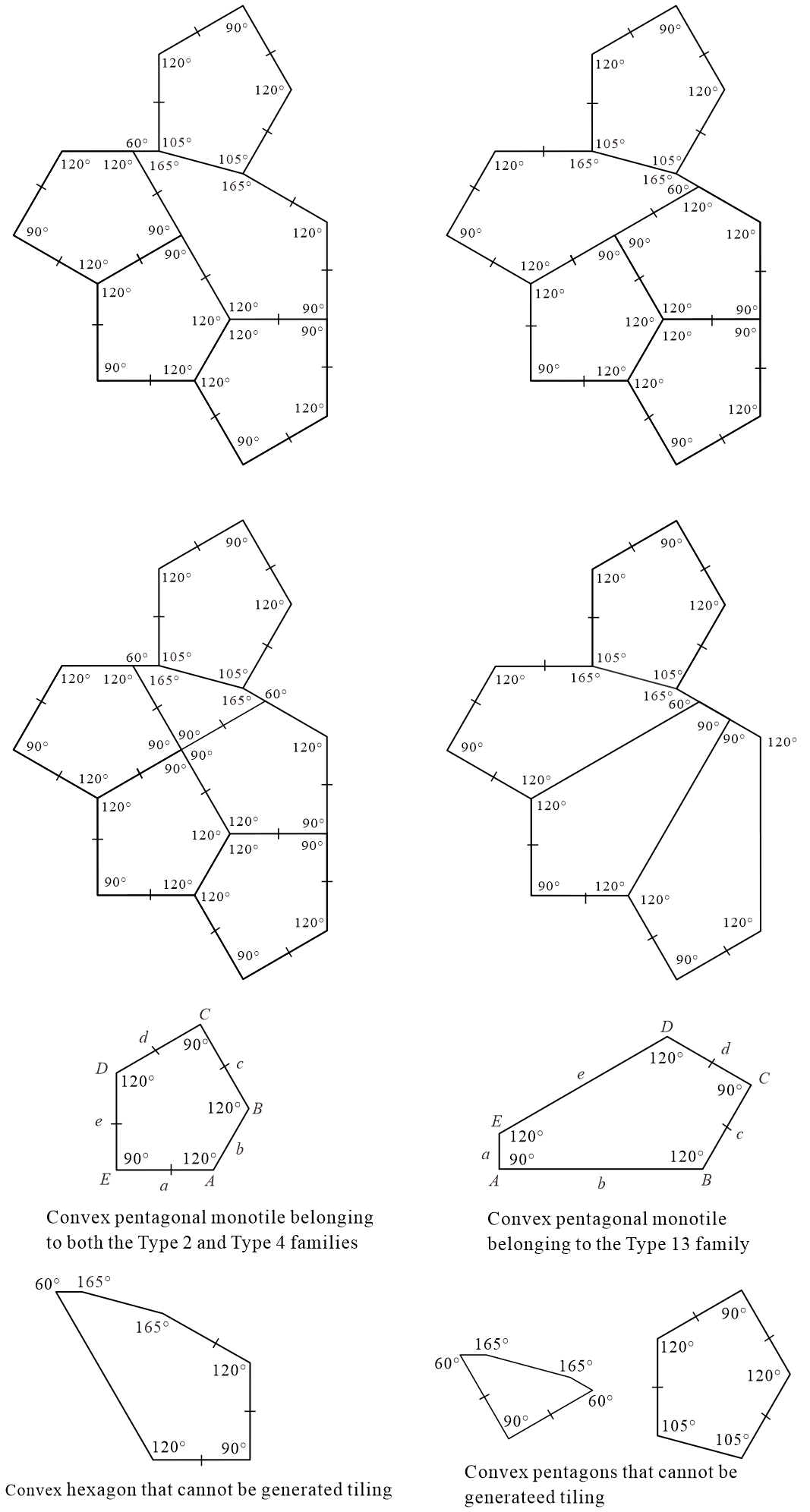
Currently, there are 15 known families of convex pentagonal monotiles, each labeled as a “Type,” as shown in Figure 23 [3, 4, 6, 8, 9, 11, 14, 15, 16, 17, 20, 24, 25]. The tilings depicted with each convex pentagon in Figure 23 are representative of each Type family. A representative tiling can be formed using only the relationships that can be derived from the tile conditions of each Type. As shown in Figure 23, the representative tilings of the Types 2 and 7–15 families use reflected tiles (convex pentagons). By contrast, as shown in Figure 23, the representative tilings of the Types 1 and 3–6 families do not use reflected tiles. Thus, if a convex pentagonal monotile belongs to at least one of the Type 1 or 3–6 families, it can generate tilings without the use of reflected tiles [20].

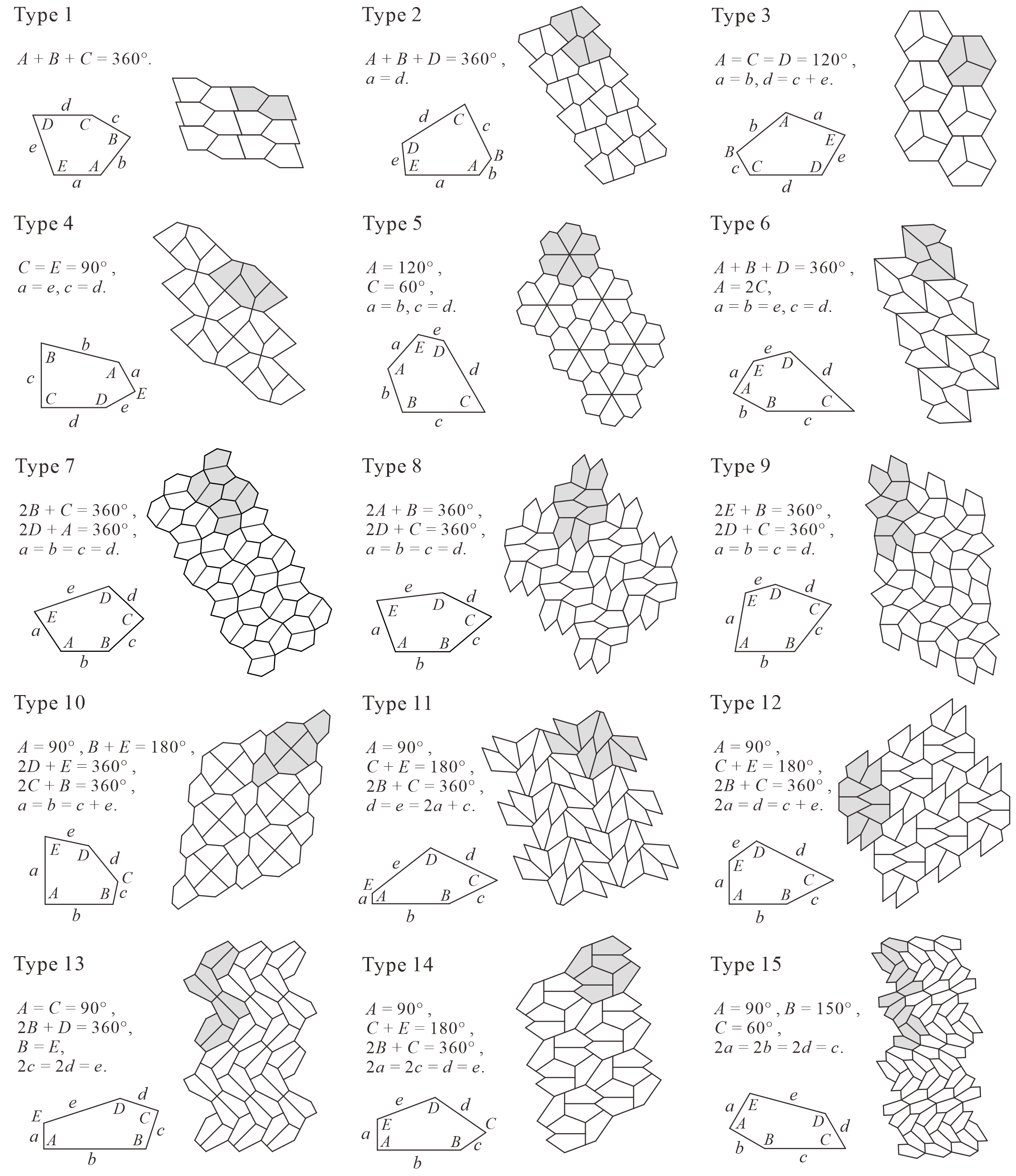
The Type families of convex pentagonal monotiles are not necessarily “disjoint.” That is, there are some convex pentagonal monotiles that belong to more than one Type family [15, 18, 19, 20, 21]. For example, the convex pentagonal monotile in Figure 24 belongs to both the Type 1 and Type 7 families [18, 19]. If $A=86^{\circ}$ for the tile conditions of Type 7 in Figure 23, the convex pentagonal monotile with $A=86^{\circ}$ belongs only to the Type 7 family and can only form the (representative) tiling of the Type 7 family, as depicted in Figure 23. By contrast, the convex pentagonal monotiles in Figure 24, which belong to both the Type 1 and Type 7 families, can form the tiling of the Type 7 family, but they can also form the tiling of the Type 1 family without using reflected tiles. In other words, the convex pentagonal monotiles belonging to both the Type 1 and Type 7 families in Figure 24 can generate tiling without using reflected tiles. It should be noted that some convex pentagonal monotiles can form tilings other than the representative tilings of each Type [18, 19, 20, 21].

Some tiling patterns cannot be formed without using reflected tiles. However, the tile forming the pattern does not necessarily have to be reflected to generate the tilings. There are also monotiles that cannot generate tilings if the use of reflected tiles is not allowed during the tiling generation process.

Figure 25 shows the periodic tiling formed by convex pentagonal monotiles belonging to both the Type 2 and Type 4 families with line symmetry in the cases of $\beta=90^{\circ}$ in Method 2 (Figure 5(d)), $\alpha=90^{\circ}$ in Method 1 (Figure 8), and $\gamma=165^{\circ}$ in Method 4 (Figure 18(f)).

Appendix Appendix B Convex hexagonal monotiles

Three families of convex hexagonal monotiles are known, called “Type,” as shown in Figure 26 [1, 3, 4, 6, 10, 16, 25]. The tilings depicted with each convex hexagon in Figure 26 are representative tilings of each Type family. Representative tiling can be formed using only those relations that can be derived from the tile conditions of each Type. As shown in Figure 26, the representative tiling of the Type 2 family uses reflected tiles (convex hexagons). If convex hexagonal monotiles do not belong to the Type 1 or Type 3 families, then the convex hexagonal monotiles cannot generate tilings without using reflected tiles. The Type families of convex hexagonal monotiles are not “disjoint.” For example, a regular hexagon belongs to all Type families.

Figures 27(a) and 27(b) show the periodic tilings formed by convex hexagonal monotiles belonging to the Type 1 family in the cases of $\alpha=75^{\circ}$ (Figure 4 (d)) and $\alpha=105^{\circ}$ (Figure 4(e)) in Method 1, respectively.

Appendix Appendix C Periodic tiling with $P_{1}$ , $P_{2}$ , and reflected $P_{2}$

As introduced in Section 2, if $P_{1}$ , $P_{2}$ , and reflected $P_{2}$ in the case of $\alpha=180^{\circ}$ in Method 1 (see Figure 4(g)) are used, it is possible to form a periodic tiling, as shown in Figure 28. In this case, the merged diagram of $P_{2}$ and reflected $P_{2}$ can be regarded as forming a convex octagon. In other words, Figure 28 can be regarded as periodic tiling using anterior and posterior convex octagons and convex pentagons without any distinction between the anterior and posterior sides (two types of convex pentagons and octagons that are not monotiles from a viewpoint that does not distinguish between the anterior and posterior sides).

Appendix Appendix D ASPs comprising four or five types of convex polygons¹⁰¹⁰10 The contents (the results of study) in this appendix were obtained prior to the main results of this manuscript.

Appendix D.1 Preparation

In this appendix (i.e., Appendix D), we present examples of “ASP comprising four types of convex polygons” and “(candidates of) ASP comprising five types of convex polygons.” Let $ASPcvx(n)$ denote an ASP comprising $n$ types of convex polygons. However, we limit ourselves to $ASPcvx(4)$ and $ASPcvx(5)$ that satisfy the “restriction on the number of types of congruent diagrams” below and show examples of them.

Restriction on The Number of Types of Congruent Diagrams .

For a viewpoint that does not distinguish between the anterior and posterior sides (a viewpoint that treats congruent diagrams, including reflected images, as tiles of the same type), the number of prototile types in a set must be less than or equal to three.

In this study, the “prototiles” mentioned in the above restriction corresponds to convex polygons; let $ASPcvx(n,m)$ be ASP comprising $n$ types of convex polygons such that there are $m$ types of convex polygons from a viewpoint that does not distinguish between anterior and posterior sides ( $m$ is an integer greater than or equal to one). Thus, it is always $n\geq m.$ Let $ASPcvx(n,m\leq 3)$ denote $ASPcvx(n)$ satisfying the restriction on the number of types of congruent diagrams. Because these “ASP comprising four types of convex polygons” and “candidate of ASP comprising five types of convex polygons” satisfy the restriction on the number of types of congruent diagrams, they can be regarded as “ASP comprising three types of convex polygons” from the viewpoint that does not distinguish between anterior and posterior sides.

The restriction on the number of types of congruent diagrams is imposed because the method of creating the ASP introduced in the study of this appendix would create a variety of $ASPcvx(n)$ with $n\geq 4$ ( $ASPcvx(n\geq 4,m\geq 4)$ ) that do not satisfy this restriction. In addition, considering that only a small number of types of prototype tiles contained in an ASP has been explored so far, we thought that it would be meaningful to consider cases that satisfy this restriction.

Appendix D.2 Dividing Tile $(1,1)$ into convex pentagons and convex hexagons

This method divides the interior of Tile $(1,1)$ into convex polygons with at least five edges. However, the purpose of the study of this appendix was to conduct $ASPcvx(4,m\leq 3)$ and $ASPcvx(5,m\leq 3)$ . The method for dividing Tile $(1,1)$ such that the restriction on the number of types of congruent diagrams is satisfied is to divide the interior into five convex polygons, as shown in Figure 29. (Refer to the Appendix D.5 and Appendix D.6 for other methods of dividing Tile $(1,1)$ that satisfy the restriction on the number of types of congruent diagrams that we are currently identifying.) It is inferred that there are various methods to divide Tile $(1,1)$ that are likely to result in ASP that do not satisfy the restriction on the number of types of congruent diagrams (see Appendix D.5).

Figure 29 shows how to divide the interior into five convex polygons so that the parts with vertices “ $X_{3},X_{7},X_{9},X_{11}$ ” at $90^{\circ}$ in Tile $(1,1)$ are convex pentagons or convex hexagons. Therefore, a line segment $X_{8}R$ is added to bisect interior angle $X_{8}$ of Tile $(1,1)$ , and its length is the same as that of its edge when Tile $(1,1)$ is considered an equilateral 14-edges polygon. Subsequently, to satisfy the restriction on the number of types of congruent diagrams, the convex polygon $CP(X_{3})$ with the points “ $X_{3}$ , $X_{4}$ , $X_{5}$ , $P$ , $X_{1}$ , $X_{2}$ ” as vertices and the convex polygon $CP(X_{7})$ with the points “ $X_{7}$ , $X_{8}$ , $R$ , $P$ , $X_{5}$ , $X_{6}$ ” as vertices are congruent convex polygons with reflection relation. In addition, the convex polygon $CP(X_{9})$ with the points “ $X_{9}$ , $X_{10}$ , $T$ , $R$ , $X_{8}$ ” as vertices and the convex polygon $CP(X_{11})$ with the points “ $X_{11}$ , $X_{12}$ , $X_{13}$ , $T$ , $X_{10}$ ” are congruent convex pentagons with reflection relation.

As shown in Figure 29, by changing the parameters $\delta$ and $\epsilon$ , the shape of the five convex polygons inside Tile $(1,1)$ changes as point $P$ moves on the bisector $X_{5}Q$ of the interior angle $X_{5}$ and point $T$ moves on the bisector $X_{10}S$ of the interior angle $X_{10}$ (the edge corresponding to the green line in Figure 29 has its length changed by changing $\delta$ and $\epsilon$ ). Based on the change, the following cases appear inside Tile $(1,1)$ from a viewpoint that does not distinguish between anterior and posterior sides: “one type of convex pentagon and two types of convex hexagons,” “two types of convex pentagons and one type of convex hexagon,” and “three types of convex pentagons.”

The convex polygon $CP(X_{14})$ with the points “ $X_{14}$ , $X_{1}$ , $P$ , $R$ , $T$ , $X_{13}$ ” as vertices in Figure 29 must be $105^{\circ}\leq\delta\leq 165^{\circ}$ , $65.104^{\circ}<\epsilon\leq 120^{\circ}$ , and $\delta+\epsilon\geq 180^{\circ}$ to be convex¹²¹²12 When $\epsilon=(\pi/3)+\tan^{-1}\left({{\left({2-\sqrt{3}}\right)}\mathord{\left/{\vphantom{{\left({2-\sqrt{3}}\right)}3}}\right.\kern-1.2pt}3}\right)\approx 65.104^{\circ}$ (i.e., $T=X_{10})$ in Figure 29, $CP(X_{9})$ and $CP(X_{11})$ are convex quadrilaterals, therefore $65.104^{\circ}<\epsilon\leq 120^{\circ}$ .. Moreover, $CP(X_{14})$ is a convex pentagon in the following three cases: “ $\delta+\epsilon=180^{\circ}$ (Figure 30(a)),” “ $\epsilon=120^{\circ}$ ( $T=S)$ and $105^{\circ}\leq\delta<165^{\circ}$ (Figure 30(b)),” and “ $\delta=165^{\circ}$ and $105^{\circ}\leq\epsilon<120^{\circ}$ (Figure 30(c)).” If $\delta=105^{\circ}$ , $P=X_{5}$ holds, $CP(X_{3})$ and $CP(X_{7})$ are convex pentagons (otherwise, convex hexagons). Note that during $\delta=165^{\circ}$ and $\epsilon=120^{\circ}$ , $CP(X_{14})$ is a convex quadrangle; therefore, it is beyond the scope of the study of this appendix.

Let $S_{t}(\delta,\epsilon)$ be the tile set of { $CP(X_{14})$ , $CP(X_{3})$ , $CP(X_{7})$ , $CP(X_{9})$ , $CP(X_{11})$ } for parameters $\delta$ and $\epsilon$ . The convex polygons contained in $S_{t}(\delta,\epsilon)$ become convex pentagonal or hexagonal monotiles if $\delta$ and $\epsilon$ satisfy certain conditions, as listed in Table 1 [4, 15, 16, 24]. All cases in in Table 1 contain the convex pentagonal or hexagonal monotiles that can form periodic tilings without using reflected tiles (see Appendix A and Appendix B)¹³¹³13 The case of $\epsilon=120^{\circ}$ and $105^{\circ}\leq\delta<165^{\circ}$ also contains the convex pentagonal monotiles belonging only to the Type 2 family which require the use of reflected tiles during the tiling generation process. However, the tile set in the case contains the anterior and posterior sides of convex pentagonal monotiles belonging to the Type 2 family. Thus, they can form the representative tiling of the Type 2 family. .

Table 1: Cases where

CP(X_{14})

CP(X_{3})

CP(X_{7})

CP(X_{9})

, and

CP(X_{11})

are monotiles.

	$CP(X_{14})$	$CP(X_{3})$ and $CP(X_{7})$	$CP(X_{9})$ and $CP(X_{11})$	Examples
$\delta+\epsilon=210^{\circ}$	Convex hexagonal monotile belonging to the Type 1 family			Figure 31(a)
$\delta=135^{\circ}$		Convex hexagonal monotiles belonging to the Type 3 family		Figure 31(b)
$\epsilon=90^{\circ}$			Convex pentagonal monotiles belonging to both the Type 2 and Type 4 families	Figure 31(b)
$\delta=135^{\circ}$ and $\epsilon=90^{\circ}$	Convex hexagonal monotile belonging to the Type 3 family	Convex hexagonal monotiles belonging to the Type 3 family	Convex pentagonal monotiles belonging to both the Type 2 and Type 4 families	Figure 31(b)
$\epsilon=120^{\circ}$ and $105^{\circ}\leq\delta<165^{\circ}$	Convex pentagonal monotile belonging to the Type 1 family		Convex pentagonal monotiles belonging to the Type 2 family	Figure 30(b)

Appendix D.3 ASPs satisfying the restriction on the number of types of congruent diagrams created from Tile $(1,1)$

If the convex polygons contained in $S_{t}(\delta,\epsilon)$ are not convex pentagonal or hexagonal monotiles, we can create candidates of $ASPcvx(4,3)$ and $ASPcvx(5,3)$ from Tile $(1,1)$ . We refer to it as “candidate” because if we generate tilings with convex polygons contained in $S_{t}(\delta,\epsilon)$ , we have to make sure that there exist only non-periodic tilings using the shape of Tile $(1,1)$ , if and only if all types of convex polygons contained in $S_{t}(\delta,\epsilon)$ are used. Therefore, we will confirm it with the following steps:

•

Step 1. Check that the convex polygons contained in $S_{t}(\delta,\epsilon)$ are not monotile.
•

Step 2. If it uses more than one type (but not all) of the convex polygons contained in $S_{t}(\delta,\epsilon)$ , it cannot admit tilings.
•

Step 3. Check that with all the convex polygons contained in $S_{t}(\delta,\epsilon)$ , they cannot admit tilings in any combination other than the shape of Tile $(1,1)$ , as shown in Figure 29.

For example, we confirmed that $S_{t}(\delta=105^{\circ},\epsilon=75^{\circ})$ , which contains five convex pentagons created by dividing Tile $(1,1)$ shown in Figure 32, satisfies Steps 1–3. As shown in Figure 32, when $\delta=105^{\circ}$ and $\epsilon=75^{\circ}$ are used, $CP(X_{3})$ and $CP(X_{7})$ are convex pentagons with line symmetry and cannot distinguish between the anterior and posterior sides. Therefore, $S_{t}(\delta=105^{\circ},\epsilon=75^{\circ})$ is $ASPcvx(4,3)$ . In $S_{t}(\delta,\epsilon)$ , we conjecture that Figure 32 is the only case where the ASP comprises of four types of convex pentagons, and the ASP comprises of three types of convex pentagons from a viewpoint that does not distinguish between the anterior and posterior sides.

In Steps 1–3, we briefly describe some of the key points for identifying cases where the convex polygons in Figure 32 cannot form tilings. We focused on the interior angles of the convex polygons at $75^{\circ}$ , $105^{\circ}$ , $135^{\circ}$ , and $165^{\circ}$ . To form tilings, two or more tile vertices must be concentrated at one point, and the sum of the interior angles of the vertices at the concentration point must be $180^{\circ}$ or $360^{\circ}$ . Therefore, as there are no convex pentagons with interior angles of $60^{\circ}$ or less, $135^{\circ}$ and $165^{\circ}$ cannot be used in a concentration with a sum of $180^{\circ}$ . We also observe that an even number of vertices with interior angles of $75^{\circ}$ , $105^{\circ}$ , $135^{\circ}$ , and $165^{\circ}$ must always be concentrated at one point because the place value of one is “five.” Based on these considerations, it was concluded that the concentration of vertices with an interior angle of $135^{\circ}$ was impossible, except for the arrangements using $CP(X_{9})$ and $CP(X_{11})$ , as shown in Figure 33(a). Subsequently, note the point in Figure 33(a) where the two vertices have an internal angle of $135^{\circ}$ . If a tiling is formed, the only method to obtain a sum of $360^{\circ}$ is to place the vertex of the tile with an interior angle of $90^{\circ}$ at the concentrating point. Figure 33(b) shows the only combination that can form a structure in which the tiling does not collapse. Then, for the positions with vertices having internal angles of $75^{\circ}$ and $165^{\circ}$ circled in blue in the cluster in Figure 33(b), the only combination that can construct a structure in which the tiling does not collapse using $S_{t}(\delta=105^{\circ},\epsilon=75^{\circ})$ is that of dividing Tile $(1,1)$ (using the shape of Tile $(1,1)$ ), as shown in Figure 32.

Figure 34 shows non-periodic tiling generated by an ASP comprising the four types of convex pentagons shown in Figure 32. The tiling is non-edge-to-edge.

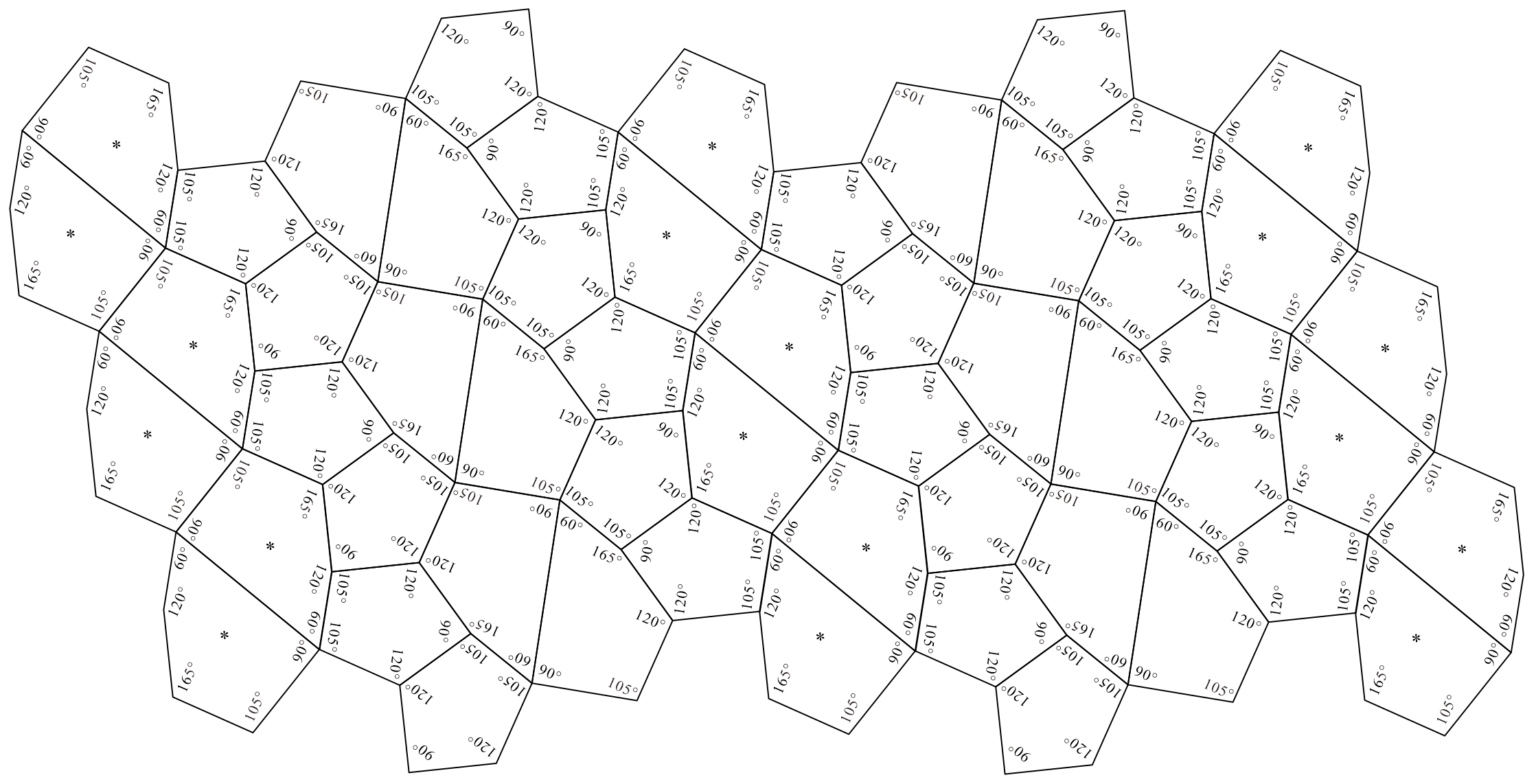
Other candidates for $ASPcvx(4,3)$ and $ASPcvx(5,3)$ related to $S_{t}(\delta,\epsilon)$ are as follows:

•
Candidates for $ASPcvx(4,3)$
- $\circ$
  
  Case 1. When $\delta=105^{\circ}$ , $75^{\circ}<\epsilon<120^{\circ}$ , $\epsilon\neq 90^{\circ}$ , and $\delta+\epsilon\neq 210^{\circ}$ (Figures 29 and 32), there is a “set of three types of convex pentagons ( $CP(X_{3})$ , $CP(X_{7})$ , $CP(X_{9})$ , $CP(X_{11})$ ) and one type of convex hexagon ( $CP(X_{14})$ ),” and, from the viewpoint that does not distinguish between anterior and posterior sides, it is a “set of two types of convex pentagons and one type of convex hexagon.”

•
Candidates for $ASPcvx(5,3)$
- $\circ$
  
  Case 2. When $\delta+\epsilon=180^{\circ}$ and $\delta\neq 105^{\circ}$ (Figure 30(a)), there is a “set of three types of convex pentagons ( $CP(X_{14})$ , $CP(X_{9})$ , $CP(X_{11})$ ) and two types of convex hexagons ( $CP(X_{3})$ , $CP(X_{7})$ ),” and, from the viewpoint that does not distinguish between anterior and posterior sides, it is a “set of two types of convex pentagons and one type of convex hexagon.”
- $\circ$
  
  Case 3. When $\delta=165^{\circ}$ , $65.104^{\circ}<\epsilon<120^{\circ}$ , and $\epsilon\neq 90^{\circ}$ (Figure 30(c)), there is a “set of three types of convex pentagons ( $CP(X_{14})$ , $CP(X_{9})$ , $CP(X_{11})$ ) and two types of convex hexagons ( $CP(X_{3})$ , $CP(X_{7})$ ),” and, from the viewpoint that does not distinguish between anterior and posterior sides, it is “set of two types of convex pentagons and one type of convex hexagon.”
- $\circ$
  
  Case 4. When $105^{\circ}<\delta<165^{\circ}$ , $\delta\neq 135^{\circ}$ , $65.104^{\circ}<\epsilon<120^{\circ}$ , $\epsilon\neq 90^{\circ}$ , $\delta+\epsilon>180^{\circ}$ , and $\delta+\epsilon\neq 210^{\circ}$ (Figure 29), there is a “set of two types of convex pentagons ( $CP(X_{9})$ , $CP(X_{11})$ ) and three types of convex hexagons ( $CP(X_{14})$ , $CP(X_{3})$ , $CP(X_{7})$ ),” and, from the viewpoint that does not distinguish between anterior and posterior sides, it is a “set of one type of convex pentagon and two types of convex hexagon.”

As can be observed from the parameters $\delta$ and $\epsilon$ , in contrast to the case shown in Figure 32, the shapes of the convex polygons in the tile sets in Cases 1–4 are not uniquely determined. Tilings using the shape of Tile $(1,1)$ in the tile sets of Cases 1 and 4 were edge-to-edge tilings with convex polygons. Tilings using the shape of Tile $(1,1)$ in the tile sets of Cases 2 and 3 were non-edge-to-edge tilings with convex polygons.

Note that, because the ASPs comprising several types of convex polygons shown in the study of this appendix are based on Tile $(1,1)$ shown in [12] and assumes that Tile $(1,1)$ is the chiral aperiodic monotile shown in [13], it is not confirmed that these sets are actually ASPs. Thus, because [13] is still a preview version, it does not hold if Tile $(1,1)$ is not a chiral aperiodic monotile.

Appendix D.4 Conditions for treating anterior and posterior sides as the same type

The ASP created by $S_{t}(\delta,\epsilon)$ that satisfies the restriction on the number of types of congruent diagrams can be regarded as “an ASP comprising three types of convex polygons” from the viewpoint that does not distinguish between anterior and posterior sides.

If $S_{t}(\delta,\epsilon)$ is subject to the same rules as the monohedral tiling, that is, “the use of reflected tiles is allowed in the tiling,” then $S_{t}(\delta,\epsilon)$ is not ASP. Tile $(1,1)$ can generate a periodic tiling if the use of reflected tiles is allowed during the tiling generation process [12]. In other words, if the reflected $CP(X_{14})$ is allowed in tiling, the set comprises of six types of convex polygons that can generate periodic tiling.

On the contrary, $S_{t}(\delta,\epsilon)$ considered the following “tile combination specification condition” as a method to be able to argue that “ASP comprises of three types of convex polygons” from the viewpoint that does not distinguish between anterior and posterior sides.

Tile Combination Specification Condition.

A set of convex polygons must contain two or more convex polygons that cannot be reflected during the tiling generation process. Convex polygons that cannot be reflected during the tiling generation process do not exhibit line symmetry (i.e., they can be distinguished between the anterior and posterior sides).

If “must contain two or more convex polygons that cannot be reflected during the tiling generation process” of the above condition is satisfied and the set contains one type of convex polygon, then it is a convex polygonal monotile, which does not require the use of reflected tiles for tiling, belongs to the known Type families, and can generate periodic tiling. Therefore, we added “contains two or more convex polygons” to the condition.

Moreover, “convex polygons that cannot be reflected during the tiling generation process are assumed not to have the property of line symmetry” is important. As mentioned previously, the set of six convex polygons with $S_{t}(\delta,\epsilon)$ and reflected $CP(X_{14})$ can form periodic tiling; however, it may also be possible to form periodic tiling in other cases. For example, for the case of $S_{t}(\delta=105^{\circ},\epsilon=75^{\circ})$ in Figure 32, if $CP(X_{14})$ , $CP(X_{3})$ , and reflected $CP(X_{14})$ are used, periodic tiling is possible, as shown in Figure 35. In this case, the merged diagram of $CP(X_{14})$ and reflected $CP(X_{14})$ can be regarded as forming a convex octagon. In other words, Figure 35 can be regarded as periodic tiling using anterior and posterior convex octagons and convex pentagons without any distinction between the anterior and posterior sides (two types of convex pentagons and octagons that are not monotiles from a viewpoint that does not distinguish between the anterior and posterior sides).

Appendix D.5 Supplement 1

In addition to Figure 29, there is another method for dividing Tile $(1,1)$ such that the number of convex polygonal types is less than or equal to three from a viewpoint that does not distinguish between the anterior and posterior sides, as shown in Figure 36. However, the sets of convex polygons created by the divisions in Figure 36 always contain convex pentagonal monotiles. The convex pentagonal monotile belonging to both the Type 2 and Type 4 families with line symmetry can form periodic tiling (see Appendix A). For the division that makes the convex pentagonal monotiles belonging to the Type 13 family in Figure 36, the tile set of the four types of convex polygons contains the anterior and posterior sides of convex pentagonal monotiles belonging to the Type 13 family. (For the convex pentagonal monotiles belonging to the Type 13 family in Figure 36, the tile set of the convex polygons created by the division contains the reflected tile. Thus, the convex pentagons can form the representative tiling of the Type 13 family.) Therefore, the tile sets of convex polygons shown in Figure 36 are not ASP.

Using the division method that makes the convex pentagonal monotiles belong to the Type 13 family in Figure 36, we created a set with three types of convex pentagons and one type of convex hexagon, as shown in Figure 37(a). If the set in Figure 37(a) is an ASP, it is an $ASPcvx(4,4)$ and does not satisfy the restriction on the number of types of congruent diagrams.

If the restriction on the number of types of congruent diagrams does not have to be satisfied, there are various methods for dividing Tile $(1,1)$ into four, five, or more types of convex polygons that are likely to be ASP. Examples of these divisions are shown in Figure 38. There is no guarantee that the sets of convex polygons in these divides are ASP. However, it can be inferred that there are various methods for dividing a Tile $(1,1)$ into four or more convex polygons, such that it is an ASP.

A convex polygon with six or more edges can be successfully divided into two or more convex polygons with five or more edges. Figure 37(b) shows an example of dividing the convex hexagon in Figure 37(a) into two convex pentagons. Another example is the division of the interior of a convex pentagon into six convex pentagons. Using this division, it is possible to increase the number of convex polygon types in the ASP. Conversely, merging several convex polygons into a single convex polygon may be possible. However, changing the type of convex polygon in a set by dividing or merging is not essential for the search and discussion of ASP. Therefore, in this study, we only discuss whether it is possible to construct an ASP comprising fewer types of convex polygons.

Appendix D.6 Supplement 2

As shown in Figure 39, we found that there is another method for dividing Tile $(1,1)$ such that the number of convex polygonal types is less than or equal to three from a viewpoint that does not distinguish between the anterior and posterior sides. In Figure 39, the point $Q$ moves on the edge $X_{5}X_{6}$ and the point $T$ moves on the edge $X_{12}X_{13}$ of Tile $(1,1)$ . In Figure 39, the convex pentagon $CP_{2}(X_{3})$ with the points “ $X_{3}$ , $X_{4}$ , $X_{5}$ , $X_{1}$ , $X_{2}$ ” as vertices is fixed shape. Additionally, the convex pentagon $CP_{2}(X_{7})$ with the points “ $X_{7}$ , $X_{8}$ , $R$ , $Q$ , $X_{6}$ ” as vertices, the convex pentagon $CP_{2}(X_{9})$ with the points “ $X_{9}$ , $X_{10}$ , $S$ , $R$ , $X_{8}$ ” as vertices, and the convex pentagon $CP_{2}(X_{11})$ with the points “ $X_{11}$ , $X_{12}$ , $T$ , $S$ , $X_{10}$ ” as vertices are congruent convex pentagons. However, $CP_{2}(X_{7})$ and $CP_{2}(X_{11})$ have a reflection relation with $CP_{2}(X_{9})$ . The convex polygon $CP_{2}(X_{14})$ with the points “ $X_{14}$ , $X_{1}$ , $X_{5}$ , $Q$ , $R$ , $S$ , $T$ ” as vertices is a heptagon, but it is a hexagon if $\zeta=120^{\circ}$ and $\eta=90^{\circ}$ .

If the five convex polygons in Figure 39 are not convex pentagonal or hexagonal monotiles, we consider that a set of four types of convex polygons is a candidate of $ASPcvx(4,3)$ .

•
Candidates for $ASPcvx(4,3)$
- $\circ$
  
  Case 5. When $\zeta=120^{\circ}$ and $\eta=90^{\circ}$ in Figures 39, there is a “set of three types of convex pentagons ( $CP_{2}(X_{3})$ , $CP_{2}(X_{7})$ , $CP_{2}(X_{9})$ , $CP_{2}(X_{11})$ ) and one type of convex hexagon ( $CP_{2}(X_{14})$ ),” and, from the viewpoint that does not distinguish between anterior and posterior sides, it is a “set of two types of convex pentagons and one type of convex hexagon.”
- $\circ$
  
  Case 6. When $\zeta\neq 120^{\circ}$ and $\eta\neq 90^{\circ}$ in Figures 39, there is a “set of three types of convex pentagons ( $CP_{2}(X_{3})$ , $CP_{2}(X_{7})$ , $CP_{2}(X_{9})$ , $CP_{2}(X_{11})$ ) and one type of convex heptagon ( $CP_{2}(X_{14})$ ),” and, from the viewpoint that does not distinguish between anterior and posterior sides, it is a “set of two types of convex pentagons and one type of convex heptagon.”