Arch-LLM: Taming LLMs for Neural Architecture Generation via Unsupervised Discrete Representation Learning

Deshani Geethika Poddenige¹, Sachith Seneviratne¹, Damith Senanayake ¹,
Mahesan Niranjan², PN Suganthan³, Saman Halgamuge¹
¹School of Electrical, Mechanical and Infrastructure Engineering, University of Melbourne, Australia
²School of Electronics and Computer Science, University of Southampton, Southampton, UK
³KINDI Computing Research Center, College of Engineering, Qatar University, Doha, Qatar
dpoddenige@student.unimelb.edu.au, {sachith.seneviratne, damith.senanayake}@unimelb.edu.au,
mn@ecs.soton.ac.uk, p.n.suganthan@qu.edu.qa, saman@unimelb.edu.au

Abstract

Unsupervised representation learning has been widely explored across various modalities, including neural architectures, where it plays a key role in downstream applications like Neural Architecture Search (NAS). These methods typically learn an unsupervised representation space before generating/ sampling architectures for the downstream search. A common approach involves the use of Variational Autoencoders (VAEs) to map discrete architectures onto a continuous representation space, however, sampling from these spaces often leads to a high percentage of invalid or duplicate neural architectures. This could be due to the unnatural mapping of inherently discrete architectural space onto a continuous space, which emphasizes the need for a robust discrete representation of these architectures. To address this, we introduce a Vector Quantized Variational Autoencoder (VQ-VAE) to learn a discrete latent space more naturally aligned with the discrete neural architectures. In contrast to VAEs, VQ-VAEs (i) map each architecture into a discrete code sequence and (ii) allow the prior to be learned by any generative model rather than assuming a normal distribution. We then represent these architecture latent codes as numerical sequences and train a text-to-text model leveraging a Large Language Model to learn and generate sequences representing architectures. We experiment our method with Inception/ ResNet-like cell-based search spaces, namely NAS-Bench-101 and NAS-Bench-201. Compared to VAE-based methods, our approach improves the generation of valid and unique architectures by over 80% on NASBench-101 and over 8% on NASBench-201. Finally, we demonstrate the applicability of our method in NAS employing a sequence-modeling-based NAS algorithm.

1 Introduction

Refer to caption — Figure 1: Illustration of the proposed Arch-LLM Framework. (1) Step 1 - we train a VQ-VAE to build a discrete latent space of neural architectures. We input neural architectures in an adjacency matrix and one-hot encoding format to the Encoder E, and it produces an encoded vector $Z_{e}$ . The VQ component leverages a learnable look-up table, Codebook e to find the nearest neighbour indices Z, and the corresponding vector $Z_{q}$ for $Z_{e}$ . Then Decoder D reconstructs $Z_{q}$ back to the neural architecture in its original format. (2) Step 2 - the numerical sequence Z is converted to a ”sentence” and the LLM is finetuned on text-to-text generation task. (3) Step 3 - we use the finetuned LLM to generate architecture sequences by providing prompts ”generate” and ”fill:”.

Unsupervised representation learning has been widely adopted across various modalities, including images [1, 2], natural language [3, 4, 5], and neural architectures [6, 7]. In the context of neural architectures, learning an unsupervised representation space is particularly useful for downstream tasks such as neural architecture search (NAS). Early NAS methods operated directly in the original encoding space of neural architectures [8, 9, 10, 11], where the most commonly used encoding represents a searchable cell via an adjacency matrix along with a list of operations. However, as these encodings lack structural organization based on architectural attributes, recent approaches employ dedicated networks, such as Variational Autoencoders (VAE) [6, 7, 12, 13], to learn a latent space that captures meaningful features of neural architectures. VAEs learn a continuous latent space of neural architectures by regularizing it to follow a Gaussian distribution, then sampling latent points from this continuous distribution to generate architectures for NAS. However, sampling from a continuous latent space often results in a high percentage of invalid [7] or duplicate samples [12, 13, 6]. This issue arises because the continuous latent prior is unnatural for the distributions of neural architectures, which are inherently discrete. Consequently, larger sample sizes are required when searching for architectures, increasing the overall computational cost. Therefore, it is important to develop a method for learning a meaningful discrete latent space of neural architectures, while maintaining robust generative capabilities.

The task of learning a discrete representation space has been crucial in other discrete modalities such as image, audio, video, etc. In response, Vector-Quantized Variational Autoencoder (VQ-VAE) [14] has shown promising results in the aforementioned modalities [14, 15, 16, 17]. However, to the best of our knowledge, the potential of VQ-VAE in the neural architecture domain remains unexplored. VQ-VAE offers several key advantages over VAEs including the construction of a discrete latent space by mapping each input into a set of discrete latent vectors. Additionally, unlike the normally distributed prior in VAE, the prior in the VQ-VAE is learnt, enabling flexibility to pair with sophisticated generative models for generation. Hence, we utilize a VQ-VAE to obtain a discretized latent space for neural architectures, where each architecture is represented by a sequence of latent vectors selected from a learnt embedding table (aka codebook). Consequently, we can represent each neural architecture as a sequence of codebook indices corresponding to their latent vectors.

In other VQ-VAE applications, such as image generation, the prior is learned by training an autoregressive model like a transformer [15]. Similarly, we require a sequential model that captures the motifs in the codebook vector sequences for diverse architectures. However, training a high-bias, low-variance model (e.g., a Bayesian/ ARIMA like autoregressor) is insufficient as they do not capture under-represented architectures. Conversely, training a high-variance, low-bias model (e.g., a transformer) is infeasible due to the difficulty of curating a sufficiently large dataset—one would need a vast number of both valid and invalid architectures to build a robust latent representation for an autoregressive/sequential prior. For instance, NASBench-101[18] includes around 420k architectures, while NASBench-201[19] only has about 15k. To circumvent these challenges, we adopt a domain transplant approach. This process involves adapting a model trained on one domain to perform effectively on a different domain, transferring learned knowledge across domains. Specifically, we leverage Large Language Models (LLMs), pretrained on data-abundant domains (e.g., natural language), and apply fine-tuning to adapt them to our target domain of discrete neural architecture codes. In doing so, we fine-tune an LLM for modeling sequences of neural architectures, which is done for the first time, to the best of our knowledge. We introduce our method Arch-LLM, and demonstrate its improvements in generating valid and unique architectures.

We test Arch-LLM on Inception/ ResNet-like cell-based architecture benchmarks; NASBench-101 [18] and NASBench-201 [19]. Our method achieves the best performance in generating valid and unique architectures, (which we call absolute uniqueness) with over 80% and 8% improvement on the NASBench-101 and NASBench-201 datasets respectively. Moreover, we demonstrate the trade-off between generating valid and unique architectures (absolute uniqueness) vs valid and novel architectures (absolute novelty). Our method achieves a 68% improvement for absolute novelty on NASBench-201 and ranks second-best for absolute novelty on NASBench-101. Finally, we demonstrate the applicability of our method to NAS by introducing a sequence modeling based NAS algorithm for conditional generation.

Our contributions are summarized as follows:

•

We propose a novel vector-quantized variational autoencoder (VQ-VAE) approach, that builds a discrete latent space of neural architectures.
•

We propose a novel approach to employing LLMs for neural architecture generation through the discrete representation of neural architectures.
•

We demonstrate the applicability of our method on NAS by proposing an algorithm using a conditional generation approach.

2 Related Work

Neural Architecture Search (NAS)

Early NAS methods typically represent architectures in their original encoding format and use various search strategies such as random search [20], RL [8] [21], evolutionary search [22], [23], or BO [24] [25]. To address the challenges of the original unstructured space, recent NAS methods use unsupervised pertaining to learn a continuous representation space of neural architectures commonly using Variational Autoencoders (VAEs). Examples include, D-VAE [6], Arch2vec [7], SVGe [12] and DGMG [26].

Vector-Quantized Variational AutoEncoder (VQ-VAE)

VQ-VAE [14] introduces the concept of learning a discrete latent space, in contrast to the continuous latent space typically learned in VAEs. VQ-VAE has been successfully applied to various discrete data modalities, including image, [14], [15], audio [16], and video [17]. Although VQ-VAE has found success in many areas, the use of VQ-VAE in NAS is not explored in the literature.

Large Language Models (LLMs) in neural architecture domain and NAS

Due to LLM’s growing capabilities, recent approaches employ LLMs in the NAS domain. Evoprompting [27] and LLMatic [28], focus on code-level architecture search, by converting neural architectures into Python code and using evolutionary algorithms to search for the best architecture. GENIUS [29], and GPT4GNAS [30] use GPT-4 by translating NAS problems into text prompts, and guiding GPT-4 with iterative feedback. LeMo-NADe [31] conduct architecture search based on user-specific metrics, by iteratively guiding the LLM using an intermediate model. In contrast to the existing methods in the NAS domain, our method, Arch-LLM employs LLMs differently, as we finetune LLMs using learnt sequences of neural architectures, leveraging the intrinsic language modelling capabilities of LLMs.

3 Arch-LLM

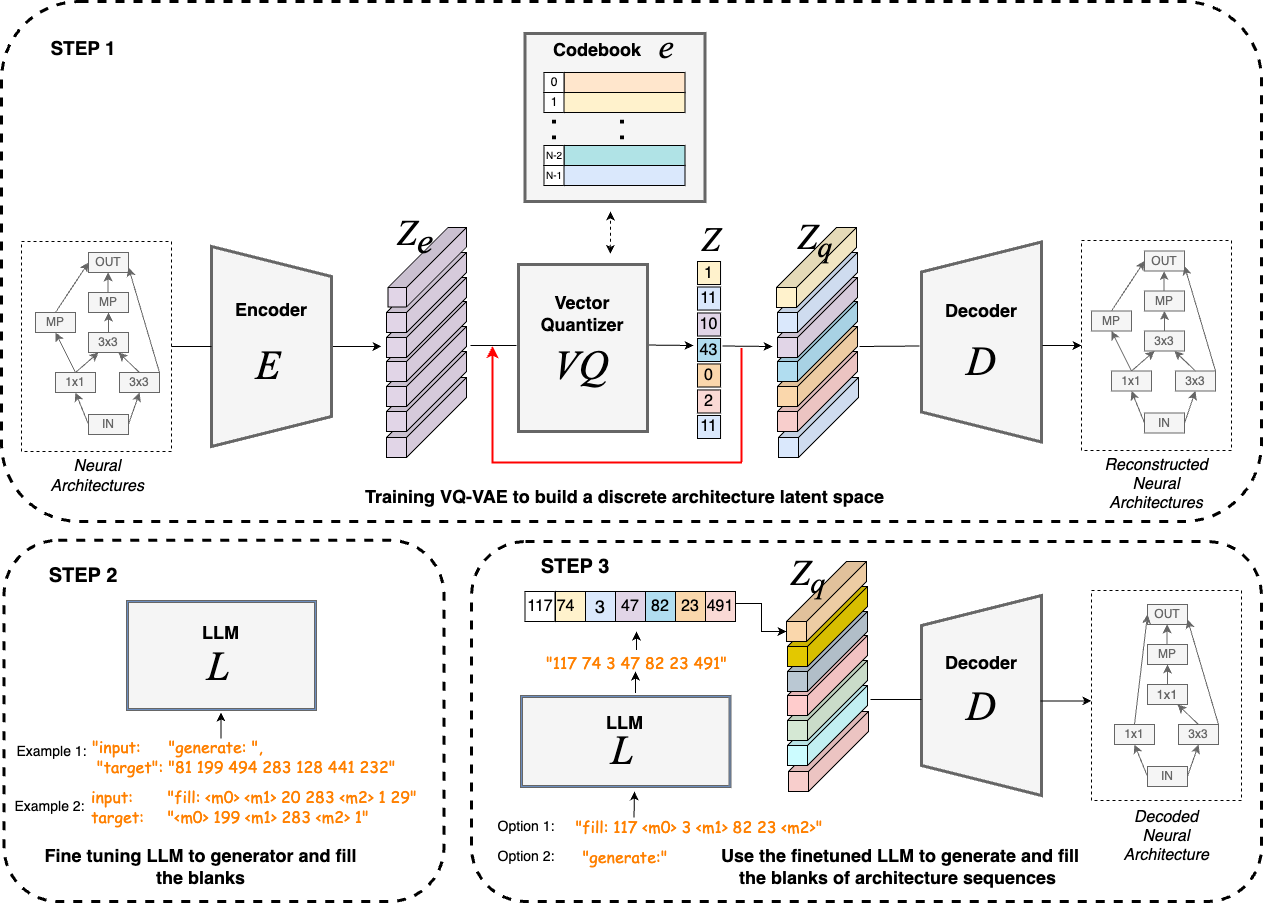
This section outlines our method; Arch-LLM (See Figure 1). First, we build a discrete latent space of neural architectures using a VQ-VAE. We adopt the Variational Graph Isomorphism Autoencoder from arch2vec [7], with slight modifications to the encoder while keeping the original decoder intact. We then integrate a Vector Quantizer component [14] to effectively discretize the latent space. Second, we finetune an LLM for sequence modelling using our discrete neural architecture sequences. Finally, we conduct NAS through guided generation using the fine-tuned LLM.

3.1 Vector-quantized variational autoencoder

Preliminaries

We confine our search space to cell-based architectures similar to NAS-Bench-101 [18]. Each cell is a directed acyclic graph (DAG) $G=(V,E)$ , where V represents a set of N nodes and E denotes the corresponding set of edges. Each node is associated with an operation type from K pre-defined operations. The structure of a cell is represented by its node connectivity using an adjacency matrix $\mathbf{A}\in\mathbb{R}^{N\times N}$ , and its node types are represented by a one-hot operation matrix $\mathbf{X}\in\mathbb{R}^{N\times K}$ .

3.1.1 Encoder

The encoder consists of Graph Isomorphism Network (GIN)[32] layers to produce an encoded vector $\mathbf{Z_{e}}(\mathbf{\tilde{A}},\mathbf{X})$ of an architecture ( $\mathbf{A},\mathbf{X}$ ). Similar to arch2vec, first we allow bi-directional information flow by converting the original directed graphs to undirected graphs, augmenting the adjacency matrix A to $\mathbf{\tilde{A}=A+A^{T}}$ . L-layer GIN is used to get the node embedding matrix $\mathbf{H}$ :

$\mathbf{H}^{(k)}=\mathbf{MLP}^{(k)}\left((1+\epsilon^{(k)})\cdot\mathbf{H}^{(k-1)}+\mathbf{\tilde{A}}\mathbf{H}^{(k-1)}\right),k=1,2,...,L$

(1)

where the initial value of $\mathbf{H}$ , $\mathbf{H}^{(0)}=\mathbf{X}$ , $\epsilon$ is a trainable bias, and $\mathbf{MLP}$ is a multi-layer perception where each layer consists of a linear-batchnorm-ReLU triplet. The encoder output $\mathbf{Z}_{e}(\mathbf{\tilde{A}},\mathbf{X})$ is obtained by feeding the final node embedding matrix $\mathbf{H}^{(L)}$ to a fully connected layer. Unlike in arch2vec, we don’t obtain the mean and the variance of a posterior approximation, as our posterior is categorical and defined by the vector-quantizer component.

3.1.2 Vector-quantizer

We incorporate a vector-quantizer [14] as a discretization bottleneck to our framework. It employs a learnable codebook, which acts as a lookup table defining the discrete latent embedding space $e\in\mathbb{R}^{K\times D}$ . Here $K$ is the number of vectors in the discrete latent space (i.e. $K$ -way categorical), and $D$ is the dimensionality of each embedding vector $e_{j}\in\mathbb{R}^{D},j=1,2,...,K$ . The discrete latent variable $\mathbf{Z}$ corresponding to $\mathbf{Z}_{e}(\mathbf{\tilde{A}},\mathbf{X})$ is calculated by nearest neighbourhood lookup using the codebook vectors $e$ as described in equation (2). The input to the decoder is the corresponding embedding vector $e_{k}$ as shown in equation (3). The posterior categorical distribution $q(\mathbf{Z}|\mathbf{\tilde{A}},\mathbf{X})$ probabilities, can be described as one-hot encoding as follows:

q(\mathbf{Z}=k|\mathbf{\tilde{A}},{\mathbf{X}})=\begin{cases}1&k=\text{argmin}_{j}||\mathbf{Z}_{e}(\mathbf{\tilde{A}},\mathbf{X})-\mathbf{e}_{j}||_{2},\\ 0&\text{otherwise}\end{cases}

(2)

Equation (2) outputs a set of nearest indices $\mathbf{Z}$ of the $\mathbf{Z}_{e}$ . Then these indices are mapped into the corresponding embedding vectors $\mathbf{Z}_{q}$ as given in the following equation:

\mathbf{Z}_{q}(\mathbf{\tilde{A}},{\mathbf{X}})=\mathbf{e}_{k},\text{ where }k=\text{argmin}_{j}||\mathbf{Z}_{e}(\mathbf{\tilde{A}},\mathbf{X})-\mathbf{e}_{j}||_{2}

(3)

In our experiments, we used $K$ =512 following [14], and $D$ =16 following [7].

3.1.3 Decoder

The decoder uses the input $\mathbf{Z}_{q}$ from the latent space and reconstructs the adjacency matrix $\mathbf{\hat{A}}$ and operations $\mathbf{\hat{X}}$ similar to the original inputs of $\mathbf{\tilde{{A}}}$ and $\mathbf{X}$ respectively.

$p(\mathbf{\hat{A}}|\mathbf{Z}_{q})={\displaystyle\prod_{i=1}^{N}}{\displaystyle\prod_{j=1}^{N}}P(\hat{A}_{ij}|\mathbf{z}_{i},\mathbf{z}_{j}),\text{ with }P(\hat{A}_{ij}=1|\mathbf{z}_{i},\mathbf{z}_{j})=\sigma{(\mathbf{z}_{i}^{T},\mathbf{z}_{j})}$

(4)

$p(\mathbf{\hat{X}}=[k_{1},...,k_{N}]^{T}|\mathbf{Z}_{q})={\displaystyle\prod_{j=1}^{N}}P(\mathbf{\hat{X}}_{i}=k_{i}|\mathbf{z}_{i})={\displaystyle\prod_{i=1}^{N}\text{softmax}(\mathbf{W}_{o}\mathbf{Z}_{q}+\mathbf{b}_{o})_{i,k_{i}}}$

(5)

where $\sigma(\cdot)$ is the sigmoid activation function, and softmax(·) is the softmax activation function applied row-wise. $k_{n}\in{1,2,...,K}$ denotes the operation chosen from the predefined set of $K$ operations at the $\text{n}^{th}$ node. $\mathbf{W}_{o}$ and $\mathbf{b}_{o}$ are learnable weights and biases of the decoder.

3.1.4 Training objective of VQ-VAE

Since the quantization process is non-differentiable, we utilize a straight-through estimator to approximate gradient computation [14] by copying gradients from the decoder’s input $\mathbf{Z}_{q}(\mathbf{X},\mathbf{\tilde{A}})$ to the encoder output $\mathbf{Z}_{e}(\mathbf{X},\mathbf{\tilde{A}})$ . The loss function of the VQ-VAE training comprises three components as defined in equation (6). The first term, the reconstruction loss assesses the similarity between the input and output reconstructed by the decoder. The second term of the loss function, the quantization loss, aims to move the embedding vectors $e_{i}$ towards the encoder outputs $\mathbf{Z}_{e}(\mathbf{X},\mathbf{\tilde{A}})$ . The final term, the commitment loss, prevents the encoder from deviating arbitrarily from the embeddings.

The training objective is formulated as below.

$L=\text{log}p(\mathbf{\hat{X}},\mathbf{\hat{A}}|\mathbf{Z}_{q})+\parallel sg[\mathbf{Z}_{e}(\mathbf{X},\mathbf{\tilde{A}})]-\mathbf{e}\parallel+\beta\parallel\mathbf{Z}_{e}(\mathbf{X},\mathbf{\tilde{A}}))-sg[\mathbf{e}]\parallel^{2}_{2}$

(6)

Here sg stands for stop gradient operator, which allows its operand to be used in forward computations without affecting the backward pass, treating it as a constant during gradient calculations. The decoder is optimized using the first loss term, the encoder is optimized using both the first and the last loss terms, and the embedding space is optimized using the middle term. Our VQ-VAE converged after 25 epochs for NASBench-101 and 26 epochs for NASBench-201.

3.2 Finetuning large language models

Once the latent space is discretised using VQ-VAE, we can represent each neural architecture in terms of the codebook indices of their encodings. More specifically, the quantized encoding of an architecture $(\mathbf{X},\mathbf{\tilde{A}})$ is given by $\mathbf{Z}_{q}\in\mathbb{R}^{K\times D}$ and is obtained by mapping a sequence of closest codebook indices $s\in\{0,1,2,...|Z|-1\}$ to their respective vectors.

s_{i}=k\text{ such that }{(\mathbf{z}_{q})}_{i}=z_{k}

(7)

We represent each architecture as a numerical sequence $s$ and then convert $s$ into a sentence-like format. We use this dataset to fine-tune an LLM with teacher forcing, converting it to a text-to-text NLP problem, in which the model learns to generate sequences and fill in the blanks. We choose Text-to-Text Transfer Transformer (T5) [33] and fine-tune it for NASBench-101 and NASBench-201 datasets; all hyperparameters are detailed in the appendix. We finetune our model to either generate a sequence or predict the tokens of a masked sequence. When masking the sequences, we randomly pick the number of items to mask, and the positions of masks. We use 2 types of input/target pairs for “generate” and “fill” as below:

(i) input - “generate: ”/ target - “81 19 44 283 8 4 232”

(ii) input - “fill: 81 36 71 [tok-0] 70 [tok-1] 150 / target - “[tok-0] 36 [tok-1] 465”

3.3 Conducting architecture search

We prompt our fine-tuned LLM with “generate” and “fill” commands to produce architecture sequences, which are then used for architecture search. We introduce an algorithm for NAS and call it “Sequence Modeling-based NAS algorithm” as discussed in Algorithm 1.

Algorithm 1 Sequence Modeling-based NAS Algorithm

Input: Number of iterations T
Randomly generate $n$ architecture sequences using “generate:” prompt and train them.

for t = 1, …, T do

Pick

m

number of best-performing architectures based on validation accuracy.

Remove the remaining

(n-m)

architectures.

Mask

m

architectures randomly using “fill” prompt to create

2m

architectures.

Generate

(n-3m)

architectures again using the “generate:” prompt.

Train the newly added architectures.

end for

Output: Architecture with the highest validation accuracy

4 Experimental Results

4.1 Datasets

We evaluate Arch-LLM on two commonly used cell-based search spaces from the NAS literature.

NAS-Bench-101

NAS-Bench-101 [18] is a cell-based tabular benchmark which contains 423k unique architectures evaluated on the CIFAR-10 image classiﬁcation task. The cell structure has a few constraints, such as the number of nodes $|V|\leq$ 7 (including the input and output node) and edges $|E|\leq 9$ . Each intermediate node represents an operation from the set of operations $O=\{1\times 1\text{ convolution},3\times 3\text{ convolution},3\times 3\text{ max pooling}\}$ . We used 90% for the training split and 10% for the validation split.

NAS-Bench-201

NAS-Bench-201 [19] is also a cell-based tabular benchmark, with 15,625 unique architectures trained and evaluated on CIFAR-10, CIFAR-100 and ImageNet-16-120 for image classiﬁcation. The cell representation of NAS-Bench-201 differs from NAS-Bench-101, as the nodes represent the feature maps and the edges represent an operation from $O=\{1\times 1\text{ convolution},3\times 3\text{ convolution},3\times 3\text{ avg pooling, skip, zero}\}$ . Each cell is generated by 4 nodes and 5 associated operations. We used 90% for the training split and 10% for the validation split.

Method	Reconstruct Accuracy	Validity	Uniqueness	Absolute Uniqueness	Novelty	Absolute Novelty
D-VAE* [6]	25.89	82.55	19.84	16.38	16.52	13.64
DGMG* [26]	99.99	89.7	29.24	26.23	16.72	15
SVGe* [12]	99.57	79.16	32.1	25.41	16.37	12.96
Arch2Vec [7]	98.13	46.96	99.10	46.54	79.83	37.49
Arch-LLM t=0.7	98.18	88.58	96.07	85.10	12.02	10.65
Arch-LLM t=1.8	98.18	46.47	99.78	46.37	63.59	29.55

Table 1: Comparison between VAE-based methods and ours for NAS-Bench-101. * indicates results from [12]. The top 4 rows are VAE-based approaches. Arch-LLM t=0.7, and Arch-LLM t=1.8 both have the same VQ-VAE and LLM model, and in the generation stage, different temperature values are introduced for randomness. Arch-LLM t=0.7, with temperature=0.7, is optimized for better Absolute Uniqueness with more than 80% improvement compared to Arch2Vec, the best VAE model while Arch-LLM t=1.8, with temperature=1.8, is optimized for better Absolute Novelty. Results are represented in percentages.

4.2 Evaluation metrics

We evaluate the quality of the latent space using four metrics; Reconstruction Accuracy, Validity, Uniqueness, and Novelty, as suggested in previous work [6, 7, 12]. To ensure a comprehensive and fair comparison, we also introduce combined metrics: Absolute Uniqueness, and Absolute Novelty. Following are the definitions of the metrics: (i) Reconstruction Accuracy: the percentage of architectures in the validation set correctly reconstructed by the decoder. (ii) Validity: the percentage of valid architectures among those generated from the latent space. (iii) Uniqueness: the percentage of unique architectures among the valid ones generated. (iv) Novelty: the percentage of architectures among the valid ones that were not seen during training. Since both Uniqueness and Novelty are conditional upon valid generations, comparing these metrics directly may not imply the overall quality of the method. For instance, a method might generate a smaller number of valid samples but still maintain 100% Uniqueness. To address this issue, we propose the metric Absolute Uniqueness to indicate the percentage of unique and valid architectures generated out of all generated architectures. We define Absolute Uniqueness = (Validity $\times$ Uniqueness)/100. We argue the same for Novelty and propose Absolute Novelty = (Validity $\times$ Novelty)/100 as a new metric.

4.3 Generative capabilities

Table 1 summarizes the results for these metrics in comparison to existing VAE-based methods for NAS-Bench-101, and Table 2 summarizes the results for the NAS-Bench-201 dataset. All the listed VAE-based methods generate neural architectures by sampling the continuous latent space which is a normal distribution, while in Arch-LLM, the LLM is used to generate architectures. Therefore, in Arch-LLM, the Reconstruction Accuracy is a performance metric for VQ-VAE, while all the other metrics capture the generative capabilities of the fine-tuned LLMs.

Both Arch2Vec and Arch-LLM utilize a deterministic decoder, meaning a given latent vector is always decoded in the same manner. In contrast, other VAE-based methods employ stochastic decoders, which can decode a given latent vector stochastically. The results shown in the tables are based on generating 10,000 neural architectures from the latent space. For Arch2Vec and Arch-LLM, 10,000 latent points were generated directly. The other methods, as reported in [12], sampled 1,000 architectures and decoded each 10 times to produce a total of 10,000 samples.

NAS-Bench-101 results

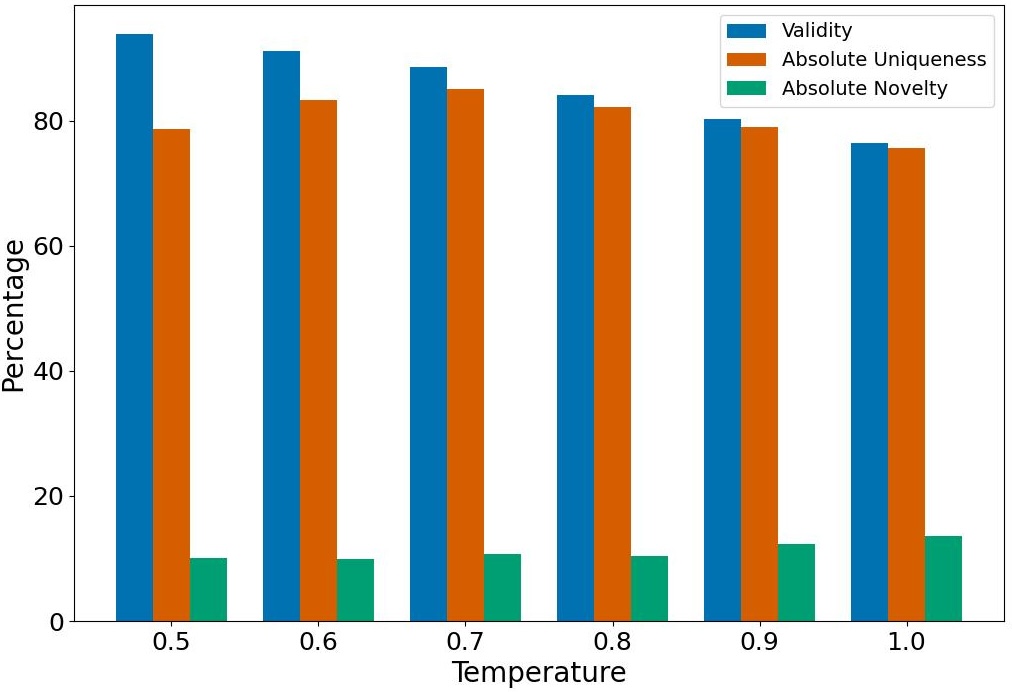
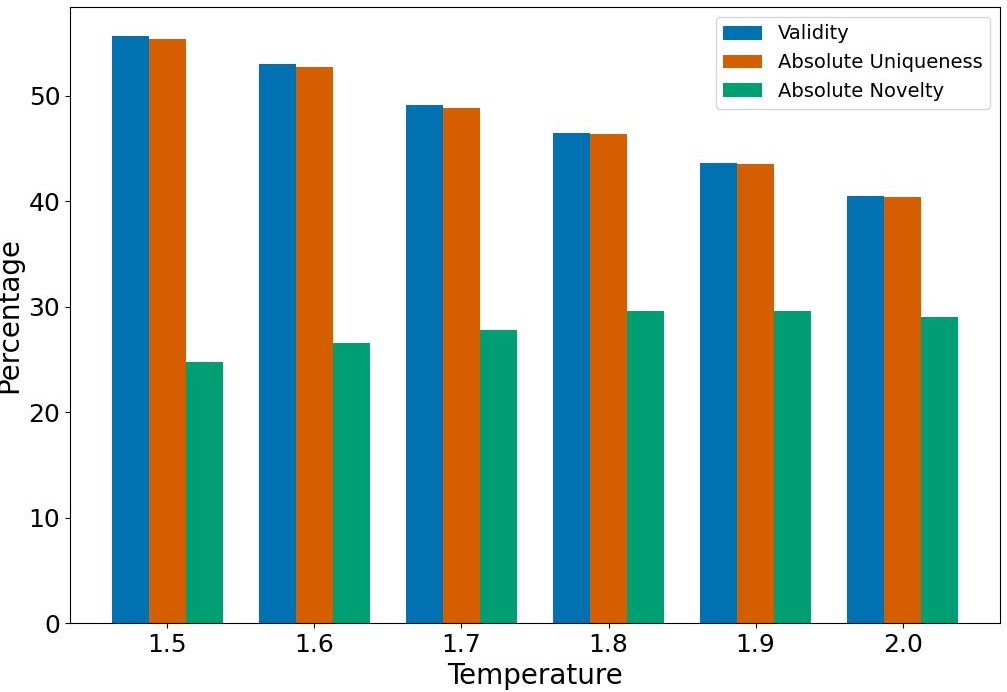
Table 1, details two variations of our method. Arch-LLM t=0.7 corresponds to generations optimized for Absolute Uniqueness, while Arch-LLM t=1.8 corresponds to generations optimized for Absolute Novelty. Both variations share the same VQ-VAE model and the same LLM model, with the temperature of the LLM (t) being varied during the generation stage to optimize for Absolute Uniqueness and for Absolute Novelty. Temperature is a hyperparameter in language models that influences the randomness and creativity of the generated outputs. High temperature values lead to more random generations while lower temperature values produce more predictable generations. Arch-LLM t=0.7 demonstrates comparable Reconstruction Accuracy and Validity, while significantly outperforming other methods in Absolute Uniqueness, showcasing its capability to generate valid and unique architectures. Figure 2 (a) illustrates the impact of different temperature values on Validity, Absolute Uniqueness, and Absolute Novelty, with the highest Absolute Uniqueness achieved at a temperature of 0.7. Conversely, Arch-LLM t=1.8 introduces more randomness into the generation process, yielding the second-best Absolute Novelty. Figure 2 (b) shows the effect of higher temperature values on the metrics, with t=1.8 identified as the optimal point for Absolute Novelty.

NAS-Bench-201 results

Similarly, we present our results for NAS-Bench-201 in Table 2, with two variations, Arch-LLM t=1.8 optimized for Absolute Uniqueness and Arch-LLM t=2.0 optimized for Absolute Novelty. Our method has a comparable Reconstruction Accuracy, while Arch-LLM t=1.8 has a comparable Validity and outperforms Absolute Uniqueness by 8% current-best arch2vec. Arch-LLM t=2.0 on the other hand, outperforms Uniqueness, Novelty, and most importantly outperforms Absolute Novelty by 68%.

Method	Reconstruct Accuracy	Validity	Uniqueness	Absolute Uniqueness	Novelty	Absolute Novelty
DGMG* [26]	99.97	100	5.35	5.35	12.62	13.26
SVGe* [12]	99.99	100	8.28	8.28	10.24	12.62
Arch2Vec [7]	99.99	96.57	72.87	70.36	12.89	12.45
Arch-LLM t=1.8	99.60	89.03	85.58	76.19	39.14	34.85
Arch-LLM t=2.0	99.60	84.10	90.30	75.94	50.83	42.75

Table 2: Comparison between VAE-based methods and ours for NAS-Bench-201. * indicates the results taken from [12]. The top 3 rows are VAE-based approaches. Arch-LLM t=1.8, and Arch-LLM t=2.0 both have the same VQ-VAE and LLM model and in the generation stage, different temperature values are introduced for randomness. Arch-LLM t=1.8, with temperature=1.8, is optimized for better Absolute Uniqueness, while Arch-LLM t=2.0, with temperature=2.0, is optimized for better Absolute Novelty. Results are represented in percentages.

4.4 Analysis of the latent space

Autoregressive property of the sequences

We generated 1,000 latent code sequences from NAS-Bench-101, permuted each sequence in 100 random ways, and evaluated the model’s ability to regenerate the original architectures. Only 47 of 1,000 architectures had duplicates after permutation, which shows that the decoder relies on sequence patterns over 95% of the time, confirming the autoregressive nature of our sequences.

LLM’s novel architecture generation

In this experiment, we compare the distribution of originally trained architecture sequences with the novel architectures generated by the LLM. We use the Arch-LLM t=1.8 model, fine-tuned on the NASBench101 dataset, which gives us the maximum number of novel generations. Figure 3 shows the distribution comparison for positions 1 and 2 in the sequence. Details of all the positions from 0 to 6 can be found in the appendix. This analysis demonstrates that the distribution of novel-generated sequences closely follows the original distribution, indicating that the LLM has effectively learned the distribution of the dataset.

4.5 Neural Architecture Search Results

We evaluate the applicability of our architecture generator in the neural architecture search (NAS). Table 3 summarizes the results obtained on NASBench-101 for CIFAR-10 dataset, while Table 4 presents the results obtained on NASBench-201 for CIFAR-10, CIFAR-100 and ImageNet datasets. We report the mean over 10 trials for the search of the architecture with the highest validation accuracy [34]. Our method demonstrates NAS performance comparable to other approaches. However, supervised methods like AG-Net often yield the best results in this benchmark. In supervised approaches, the architecture representation space and the downstream search are jointly optimized, relying on architecture-accuracy data during training. While this leads to superior performance, it assumes access to a large number of architecture-accuracy pairs, which is an impractical requirement in real-world scenarios due to the significant cost and effort needed to curate such datasets. In contrast, the unsupervised representation space built by our method does not rely on accuracies.

NAS Method	Val. Acc (%)	Test Acc (%)	Encoding	Search Method	Queries
Optimum	95.06	94.32
NAO*[35]	94.66	93.49	Supervised Continuous Learnt	Gradient Decent	192
BANANAS* [24]	94.73	94.09	Discrete Unlearnt	Bayesian Optimization	192
BO* [36]	94.57	93.96	Discrete Unlearnt	Bayesian Optimization	192
Local Search* [37]	94.57	93.96	Discrete Unlearnt	Local Search	192
Random Search* [20]	94.31	93.61	Discrete Unlearnt	Random	192
Regularized Evolution* [18]	94.47	93.89	Discrete Unlearnt	Evolution	192
AG-Net* [34]	94.90	94.18	Supervised Continuous Learnt	Generative LSO	192
Arch2vec-RL* [7]	-	94.10	Unsupervised Continuous Learnt	REINFORCE	400
Arch2vec-BO* [7]	-	94.05	Unsupervised Continuous Learnt	Bayesian Optimization	400
Arch-LLM (ours)	94.67	93.98	Unsupervised Discrete Learnt	Sequence Modelling	400

Table 3: NAS results of NAS-Bench101. *results are taken from [34]. We report the mean over 10 trials for the search of the architecture with the highest validation accuracy.

NAS Methods	CIFAR-10		CIFAR-100		ImageNet-16-120		Queries	Search Method
NAS Methods	Val. Acc (%)	Test Acc (%)	Val. Acc (%)	Test Acc (%)	Val. Acc (%)	Test Acc (%)	Queries	Search Method
Optimum	91.61	94.37	73.49	73.51	46.77	47.31
SGNAS* [22]	90.18	93.53	70.28	70.31	46.77	47.31	-	Supernet
Arch2vec + BO* [7]	91.41	94.18	73.35	73.37	46.34	46.27	100	Bayesian Optimization
BANANAS* [24]	91.56	94.3	73.49	73.50	46.65	46.51	192	Bayesian Optimization
BO* [36]	91.54	94.22	73.26	73.22	46.43	46.40	192	Bayesian Optimization
RS* [38]	91.12	93.89	72.08	72.07	45.87	45.98	192	Random
AG-Net* [39]	91.61	94.37	73.49	73.51	46.73	46.42	400	Generative LSO
Diffusion-NAG** [40]	-	94.37	-	73.51	-	-	-	Diffusion
Arch-LLM (ours)	91.32	94.08	72.94	72.96	45.71	45.48	400	Sequence Modelling

Table 4: NAS results of NAS-Bench201 on CIFAR-10, CIFAR-100, and ImageNet-16-120 for validation and test sets. * indicates the results are taken from [39], and **results are taken from their original papers. We report the mean over 10 trials for the search of the architecture with the highest validation accuracy.

5 Conclusion

We introduce Arch-LLM, a novel method for neural architecture generation that combines a Vector-Quantized Variational Autoencoder (VQ-VAE) with a Large Language Model (LLM). The VQ-VAE learns an unsupervised discrete representation space of neural architectures, while the LLM generates discrete latent code sequences corresponding to neural architectures. This approach provides a natural mapping of discrete architectures onto a discrete latent space, achieving a high percentage of valid and unique architecture generations (absolute uniqueness). Compared to existing VAE-based methods that map discrete architectures onto continuous representation space, Arch-LLM demonstrates state-of-the-art (SOTA) performance on two benchmark datasets. Additionally, we explore the trade-off between absolute uniqueness and absolute novelty, achieving SOTA or competitive results for absolute novelty on the benchmark datasets.

We apply our method to Neural Architecture Search (NAS) using a sequence modeling algorithm. Notably, Arch-LLM operates in an unsupervised manner, eliminating the need for large-scale architecture-accuracy datasets that many supervised NAS methods rely on. By avoiding the computationally intensive process of curating such datasets, our approach offers a more practical alternative and provides more usability. Our primary goal is not to surpass NAS benchmarks but to learn an unsupervised representation space for neural architectures and leverage an LLM for architecture generation. Therefore, when training Arch-LLM, we did not update Arch-LLM parameters based on the accuracies of generated architectures. However, reinforcement learning-based fine-tuning could be applied to further optimize Arch-LLM for NAS.

By integrating advancements from Natural Language Processing (NLP) into neural architecture domain, our approach fosters cross-disciplinary innovation. We believe our novel method of taming LLMs for neural architecture generation will open up new avenues in integrating neural architecture domain with LLMs. However, one limitation of our method is that fine-tuning LLMs for numerical sequences can increase randomness, sometimes leading to invalid samples, such as random strings or sequences of incorrect lengths. Addressing this requires additional post-processing steps to filter out such data.

References

[1] Aaron van den Oord, Nal Kalchbrenner, Oriol Vinyals, Lasse Espeholt, Alex Graves, and Koray Kavukcuoglu. Conditional Image Generation with PixelCNN Decoders. 6 2016.
[2] Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick. Momentum Contrast for Unsupervised Visual Representation Learning. 11 2019.
[3] Tomas Mikolov, Kai Chen, Greg Corrado, and Jeffrey Dean. Distributed Representations of Words and Phrases and their Compositionality. Technical report.
[4] Jacob Devlin, Ming-Wei Chang, Kenton Lee, Kristina Toutanova Google, and A I Language. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. Technical report.
[5] Alec Radford Openai, Karthik Narasimhan Openai, Tim Salimans Openai, and Ilya Sutskever Openai. Improving Language Understanding by Generative Pre-Training. Technical report.
[6] Muhan Zhang, Shali Jiang, Zhicheng Cui, Roman Garnett, and Yixin Chen. D-VAE: A Variational Autoencoder for Directed Acyclic Graphs. 4 2019.
[7] Shen Yan, Yu Zheng, Wei Ao, Xiao Zeng, and Mi Zhang. Does Unsupervised Architecture Representation Learning Help Neural Architecture Search? Technical report, 2020.
[8] Barret Zoph and Quoc V. Le. Neural Architecture Search with Reinforcement Learning. 11 2016.
[9] Jiechao Yang, Yong Liu, and Hongteng Xu. HOTNAS: Hierarchical Optimal Transport for Neural Architecture Search. Technical report.
[10] Esteban Real, Sherry Moore, Andrew Selle, Saurabh Saxena, Yutaka Leon Suematsu, Jie Tan, Quoc V Le, and Alexey Kurakin. Large-Scale Evolution of Image Classifiers. Technical report, 2017.
[11] Esteban Real, Alok Aggarwal, Yanping Huang, and Quoc V Le. Regularized Evolution for Image Classifier Architecture Search. 2 2018.
[12] Jovita Lukasik, David Friede, Arber Zela, Frank Hutter, and Margret Keuper. Smooth Variational Graph Embeddings for Efficient Neural Architecture Search. 10 2020.
[13] Yujia Li, Oriol Vinyals, Chris Dyer, Razvan Pascanu, and Peter Battaglia. Learning Deep Generative Models of Graphs. 3 2018.
[14] Aaron van den Oord DeepMind, Oriol Vinyals DeepMind, and Koray Kavukcuoglu DeepMind. Neural Discrete Representation Learning. Technical report.
[15] Patrick Esser, Robin Rombach, and Björn Ommer. Taming Transformers for High-Resolution Image Synthesis. Technical report.
[16] Andros Tjandra, Berrak Sisman, Mingyang Zhang, Sakriani Sakti, Haizhou Li, and Satoshi Nakamura. VQVAE Unsupervised Unit Discovery and Multi-scale Code2Spec Inverter for Zerospeech Challenge 2019. 5 2019.
[17] Wilson Yan, Yunzhi Zhang, Pieter Abbeel, and Aravind Srinivas. VideoGPT: Video Generation using VQ-VAE and Transformers. 4 2021.
[18] Chris Ying, Aaron Klein, Esteban Real, Eric Christiansen, Kevin Murphy, and Frank Hutter. NAS-Bench-101: Towards Reproducible Neural Architecture Search. Technical report.
[19] Xuanyi Dong and Yi Yang. NAS-Bench-201: Extending the Scope of Reproducible Neural Architecture Search. 1 2020.
[20] Liam Li and Ameet Talwalkar. Random Search and Reproducibility for Neural Architecture Search. 2 2019.
[21] Bowen Baker, Otkrist Gupta, Nikhil Naik, and Ramesh Raskar. Designing Neural Network Architectures using Reinforcement Learning. 11 2016.
[22] Esteban Real, Alok Aggarwal, Yanping Huang, and Quoc V Le. Regularized Evolution for Image Classifier Architecture Search. Technical report.
[23] Hanxiao Liu, Karen Simonyan, Oriol Vinyals, Chrisantha Fernando, and Koray Kavukcuoglu. Hierarchical Representations for Efficient Architecture Search. 11 2017.
[24] Colin White, Willie Neiswanger, and Yash Savani. BANANAS: Bayesian Optimization with Neural Architectures for Neural Architecture Search. Technical report, 2021.
[25] Kirthevasan Kandasamy, Willie Neiswanger, Jeff Schneider, Barnabas Poczos, and Eric Xing. Neural Architecture Search with Bayesian Optimisation and Optimal Transport. 2 2018.
[26] Yonatan Geifman and Ran El-Yaniv. Deep Active Learning with a Neural Architecture Search. Technical report.
[27] Angelica Chen, David M Dohan, David R So, and Jane Street. EvoPrompting: Language Models for Code-Level Neural Architecture Search. Technical report.
[28] Muhammad U. Nasir, Sam Earle, Christopher Cleghorn, Steven James, and Julian Togelius. LLMatic: Neural Architecture Search via Large Language Models and Quality Diversity Optimization. 6 2023.
[29] Xuefei Ning, Changcheng Tang, Wenshuo Li, Zixuan Zhou, Shuang Liang, Huazhong Yang, and Yu Wang. Evaluating Efficient Performance Estimators of Neural Architectures. Technical report.
[30] Haishuai Wang, Yang Gao, Xin Zheng, Peng Zhang, Hongyang Chen, Jiajun Bu, and Philip S. Yu. Graph Neural Architecture Search with GPT-4. 9 2023.
[31] Md Hafizur Rahman and Prabuddha Chakraborty. LeMo-NADe: Multi-Parameter Neural Architecture Discovery with LLMs. 2 2024.
[32] Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. HOW POWERFUL ARE GRAPH NEURAL NETWORKS? Technical report.
[33] Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J. Liu. Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer. 10 2019.
[34] Jovita Lukasik, Steffen Jung, and Margret Keuper. Learning Where To Look – Generative NAS is Surprisingly Efficient. 3 2022.
[35] Renqian Luo, Fei Tian, Tao Qin, Enhong Chen, and Tie-Yan Liu. Neural Architecture Optimization. 8 2018.
[36] Jasper Snoek, Oren Rippel, Kevin Swersky, Ryan Kiros, Nadathur Satish, Narayanan Sundaram, Md Mostofa, Ali Patwary, and Ryan P Adams. Scalable Bayesian Optimization Using Deep Neural Networks Prabhat PRABHAT@LBL.GOV. Technical report.
[37] Colin White, Sam Nolen, and Yash Savani. Exploring the Loss Landscape in Neural Architecture Search. 5 2020.
[38] Chaojian Li, Zhongzhi Yu, Yonggan Fu, Yongan Zhang, Yang Zhao, Haoran You, Qixuan Yu, Yue Wang, and Yingyan Lin. HW-NAS-BENCH: HARDWARE-AWARE NEURAL AR-CHITECTURE SEARCH BENCHMARK. Technical report.
[39] Jovita Lukasik, Steffen Jung, and Margret Keuper. Learning Where To Look-Generative NAS is Surprisingly Efficient. Technical report, 2022.
[40] Sohyun An, Hayeon Lee, Jaehyeong Jo, Seanie Lee, and Sung Ju Hwang. DiffusionNAG: Predictor-guided Neural Architecture Generation with Diffusion Models. 5 2023.