Arithmetic representations of mapping class groups
Abstract.
Let be a closed oriented surface and a finite group of orientation preserving automorphisms of whose orbit space has genus at least . There is a natural group homomorphism from the -centralizer in to the -centralizer in . We give a sufficient condition for its image to be a subgroup of finite index.
Key words and phrases:
Mapping class group, Arithmetic group2020 Mathematics Subject Classification:
Primary: 57K20, 57M12; Secondary: 11E391. Introduction and statement of the main result
Let be a closed connected oriented surface of genus . The group of orientation preserving diffeomorphisms of acts on via its connected component group , known as the mapping class group of , and it is a classical fact that the image of this representation is the full symplectic group of integral linear transformations which preserve the intersection form on . This paper concerns an equivariant version, where it is assumed that we are given a finite subgroup . The centralizer of in lands under the above symplectic representation in and the question we address here is how much smaller the image is. Besides its intrinsic interest, the answer has consequences for understanding the mapping class group of the -orbit space of . We shall regard the latter as an orbifold surface and denote it by ; the regular orbits then define an open subset with finite complement. This punctured surface has negative Euler characteristic. The image of in the mapping class group of the punctured surface is of finite index and thus makes a ‘virtual representation’ of that mapping class group.
The work of Putman-Wieland [6] relates our question to the Ivanov conjecture as follows. Let us say that the -action on has the Putman-Wieland property if has no finite orbit in . These authors prove that if that property holds for a given genus of (no matter what and are), then every finite index subgroup of a mapping class group of a connected oriented surface of finite type of genus has zero first Betti number. The first part of our main result is about that property.
Theorem 1.1.
Let be a -cover as above.
-
(i)
If this cover is trivial over a compact genus one subsurface of with connected boundary, then the action of on has no nonzero finite orbits.
-
(ii)
If this cover is trivial over a compact genus two subsurface of with connected boundary, then the image of in is of finite index.
We will also obtain an arithmeticity property in the setting of (i). See the discussion and the end of this introduction as well as Remark 5.6.
Remark 1.2.
Note that in either case the cover over the complement of such a subsurface of must be connected (for the subsurface has a connected boundary and is connected). Since this complement has a boundary component over which the covering is trivial, we may contract that component (and each of the components lying over it) to obtain a -covering , where the genus of is now 1 resp. 2 less than that of . As this covering represents all the topological input, we may paraphrase our main theorem as saying that the Putman-Wieland property resp. the arithmeticity property holds after a ‘stabilization’ by taking a connected sum of the base orbifold with a closed surface of genus 1 resp. 2.
We will prove this theorem under the apparently weaker assumption that there exists a closed one-dimensional submanifold nonempty , so a disjoint union of say embedded circles (with in case (i) and in case (ii)) such that is trivial over and connected over . This looks as if this is a more general result, because it is easy to find in the respective cases such an inside the postulated subsurface with the property that its complement is connected. But we will see that this generalization is only apparent.
There is also a useful geometric interpretation for this last formulation: given such an , then we can obtain the -covering as above as follows: regard as a punctured surface (so with two punctures for each component of ) and let be the closed orbifold obtained by filling in these punctures as non-orbifold points. Our assumptions say that is a closed connected surface (the genus drop is the number of connected components of ) and that the given -covering arises from a -covering with for each component of an identification of the fibers of this covering over the two associated points (as principal -sets). If we give a complex structure and thus turn it into a smooth complex-projective curve with an orbifold structure, then an algebraic geometer might be tempted to regard this orbifold curve as being in its moduli space near the Deligne-Mumford stratum where the orbifold acquires nodes, but for which the -covering stays irreducible and does not ramify over the nodes. The covering then appears as the normalization of such a degeneration. No algebraic geometry is used in the proof, though, for the topological part of this paper uses methods that directly generalize those of [3].
Let us compare the above theorem with the work of Grünewald-Larsen-Lubotzky-Malestein [1],
whose main motivation was to construct, via the virtual isomorphism mentioned above, new arithmetic quotients of the mapping class
group of . They assume that acts freely so that and impose another, more technical condition, which in our set-up translates into that we are in the context of (i) and demand that the covering is of ‘handlebody type’, in the sense that it extends to a handlebody that has as boundary.
They prove that the image of in each simple factor of is arithmetic.
Our approach differs from theirs in several aspects, but mostly in our direct and relatively simple way of constructing -equivariant mapping classes.
When speaking of arithmetic subgroups of , it is of course tacitly understood that the latter can be regarded as the group of rational points of an algebraic group defined over . Let us make this explicit.
Denote by the set of irreducible characters of and choose for every a representing irreducible (left) -module . We also fix on every a -invariant inner product (which can be obtained as the -average of an arbitrary inner product). This exhibits as a self-dual -module. Then is a skew field which is of finite -dimension. We denote its opposite by (meaning that the underling -vector space is , but that composition is taken in opposite order) so that is now a right -module. Adopting as a convention that used as superscript (resp. subscript) indicates that we are dealing with right (resp. left) -module endomorphisms, then the natural map
is an isomorphism of -algebras. This is in fact the Wedderburn decomposition of , as each factor is a minimal -sided ideal.
The group algebra comes with an anti-involution which takes each basis element () to the basis element . This identifies with its opposite. Since is self-dual, the involution leaves in the above decomposition each factor invariant and induces one in the skew-field : the involution on is given by taking the -adjoint: . Since we have acting on on the right, this means that . (We note in passing that any other -invariant inner product on is of the form for some nonzero with ; the associated anti-involution of is then a conjugate of .) The center of , which we denote by , is a number field and the fixed point set of in is a subfield with .
For a finitely generated -module , we denote by the associated -isogeny space . The right -module structure on determines a left -module structure on and the isotypical decomposition of is the assertion that the natural map
is an isomorphism of -modules. So the -isotypical subspace of , ie, the image of in , has the structure of a -vector space.
Assume now that comes equipped with a nondegenerate -invariant symplectic form . Then the isotypical decomposition of is symplectic, so that we also have a decomposition . Every factor can be understood with the help of the skew-hermitian form
which is characterized by the property that for all ,
(skew-hermitian means that the form is -linear in the first variable and ). Indeed, for fixed and , the map is a bilinear form on . Since is nondegenerate, there exists a unique -linear endomorphism of such that . The -invariance of both bilinear forms implies that is -equivariant, ie, is an element of . We prefer to regard it as an element of its opposite , so that . This is evidently -linear in both and and that is why we denote it . It is then a little exercise to check that is skew-hermitian. This form is nondegenerate in an obvious sense. The group of automorphisms that preserve this form is a generalized unitary group and therefore denoted .
Any element of acts via the isomorphism as an element of the form with and this identifies with . The group is the group of -points of a reductive algebraic group defined over , whereas is the group of -points of an algebraic group defined over . Indeed, the latter is obtained from the former by the restriction of scalars .
Theorem 1.1 then amounts to the assertion that the image of in the product of unitary groups
is arithmetic. We use this decomposition to prove the theorem, since we first prove arithmeticity for a single factor. This leads to a somewhat stronger result, for we show that in setting of (i) of our main theorem (so when is trivial over a genus 1 subsurface) the image of in is almost always arithmetic (see Remark 5.6).
Here is a brief description of the structure of the paper. Of the four sections, only the last one is topological, but in order to put the constructions given there to work, we need a considerable amount of algebra and that explains the nature of the preceding sections.
Section 2 collects useful (and essentially known) algebraic proprieties of constructs that we encounter in the symplectic representation theory of a finite group over .
So there is little or no claim of originality here, although it was (for us) a bit of an effort to extract this material from the literature.
In Section 3 we introduce and study what we might regard as the basic symplectic module
associated to an irreducible -module, where is a finite group. The main result is Proposition 3.1 which states an arithmeticity property and also lists the (few) cases for which this arithmetic group has real rank . This prepares us for stating and proving the arithmeticity criterion Theorem 4.2 in Section 4, which furnishes the main algebraic input for Section 5. As mentioned, this last section is essentially topological: we there construct sufficiently many -equivariant mapping classes to ensure that we can apply the said theorem to obtain our main Theorem 1.1.
At various stages of this work I benefited from correspondence with colleagues on this material. These include many enlightening exchanges with Marco Boggi, who in 2019 provided me with a number of helpful comments on earlier drafts of the present paper. Tyakal Venkataramana explained to me in 2018 some of the implications of [9] and [7]. Justin Malestein helped me to better understand parts of [1]. I thank all of them. I am also very grateful to a number of referees for their sometimes extensive comments on an earlier version. The paper greatly improved as a result.
2. Brief review of special unitary groups
The Albert classification
In this subsection is a skew field of finite dimension over endowed with an anti-involution . We assume that the involution is positive in the sense that is a positive definite form. We remark that this is so for the cases that matter here, for the given anti-involution on is evidently positive: for , the -trace of is times the coefficient of in and hence is positive definite. The same is then true for its Wedderburn factors and their associated skew fields .
We denote the center of by (so that is a number field) and by resp. the -invariant part of resp. . Albert’s classification of such pairs (see for example [5], Ch. IV, Thm. 2) then tells us that is totally real, so that , where runs over the distinct field embeddings , and that there are essentially four cases:
-
(I)
so that for each ,
-
(II)
and for each there exists an isomorphism which sends to taking the transpose (so ),
-
(III)
and for each there exists an isomorphism , where denotes the Hamilton quaternions, which sends to quaternion conjugation (so ),
-
(IV)
is a purely imaginary extension of (in other words, is a CM field) and for each there exists an isomorphism , which takes to (so ) and sends to taking the conjugate transpose.
Let be a left -module of finite rank. We write for endowed with the structure of a right -module via the rule (, ). So if is another left -module, then is defined. It is a -vector space with the property that for all , and . In particular, we have in a -linear involution defined by . We denote its fixed point set . As a -subspace of it is spanned by the symmetric tensors .
Isotropic transvections and Eichler transformations
Suppose given a skew-hermitian form on . We denote its radical by so that the form descends to a nondegenerate one on . We define the associated unitary group as the group of -linear automorphisms of that preserve the form and act as the identity on . It is the group of -points of an algebraic group defined over . If the form is nondegenerate (), then is what is called in [2] (§5.2B) a classical unitary group.
If is isotropic (meaning that ), then we have the associated isotropic transvection defined by (so is here understood as an element of ). It ‘generates’ an abelian unipotent subgroup of defined by
Isotropic transvections are particular cases of Eichler transformations. These are defined as follows. Let be isotropic, perpendicular to and such that (equivalently, ). Then the associated Eichler transformation is
It is a -linear transformation which preserves the form. When , we shall write instead. Since , isotropic transvections are Eichler transformations as asserted.
One checks that each Eichler transformation lies in as defined above. In fact, is a closed one-parameter subgroup of whose infinitesimal generator is represented by (or rather by its image in , for if both and lie in , then we get the identity). By a general property of algebraic groups ([8], Cor. 2.2.7) such subgroups then generate a closed algebraic -subgroup of . Following [2] we denote that group by .
We note the commutator identity
| (1) |
It follows that if we fix , but let and vary (subject to the conditions above, so with ), then the generate a unipotent group that appears as an extension of the vector group by the abelian subgroup of defined by the .
The group is already generated by the isotropic transvections: When is nontrivial this follows from (6.3.1) of [2]. The remaining case is the one we labelled (I): this is when and is a symplectic group over , but then there is no issue for then every is isotropic, and then .
Unipotent radical and Levi quotient
If the form is nondegenerate (ie, ), then is a -form of a classical semisimple algebraic group and hence has finite center. To be precise, it is a group of symplectic type in the cases (I) and (II), of orthogonal type in case (III) and of special linear type in case (IV).
If is possibly nonzero, then per convention the elements of act trivially on . The natural map is evidently onto. Its kernel consists of the transformations that act trivially on both and and is therefore the unipotent radical of (recall that is reductive): we have an exact sequence
The elements of are the Eichler transformations with and arbitrary. In this case only depends on the image of in , so that the resulting map
is an isomorphism. So is a vector group over (ie, a -vector space regarded as the group of -points of a -algebraic group of additive type). Since is a normal semisimple subgroup of , it has the same unipotent radical: .
The relation between and
Since in what follows the notion of real rank of an algebraic group shows up, let us begin with reviewing this concept briefly.
Let be a reductive algebraic group. Suppose first that is defined over . Then the real rank of is by definition the dimension of a Cartan subgroup of defined over . For example, if is the orthogonal group of a nondegenerate quadratic form over , then its real rank is the Witt index of this form: the dimension of a maximal isotropic subspace defined over . If is defined over a number field , then we restrict scalars à la Weil so that is a group defined over . We then regard (by base change) as a group over and define the real rank of to be the real rank of the latter. Concretely, if are the real embeddings of in and are the remaining distinct (complex) embeddings (they come in complex conjugate pairs), then the definition comes down to
(this is also the sum over all the archimedean valuations of , taking as general term the real rank of the corresponding completion of ). The Dirichlet unit theorem often gives lower bounds for the rank. For example, if the skew field is as in the Albert classification, the group of units is a reductive group defined over and its group of real points and its real rank are then as follows: putting , then
-
(I)
is open in ; the real rank of is ,
-
(II)
is open in ; the real rank of is ,
-
(III)
is open in ; the real rank of is ,
-
(IV)
is open in ; the real rank of is .
So has real rank , unless equals (I) or is
a definite quaternion algebra with center (III) or is an imaginary quadratic extension of .
It is clear that is a normal subgroup of . We already noticed that it is closed in and hence the quotient is also an algebraic group. Note however that if has no nonzero isotropic vectors, then is trivial. We mention for future reference a consequence of a theorem of G.E. Wall [10]:
Lemma 2.1.
Suppose that is nondegenerate and contains a nonzero isotropic vector. Then is anisotropic (all its real forms are compact). So and have the same real rank and any arithmetic subgroup of will have finite image in .
Proof.
Thm. 1 of [10] identifies as a quotient of by a normal subgroup which contains . It is easy to check that in all four cases (I)-(IV) in the Albert classification such a quotient must be anisotropic. ∎
Wall’s result is more specific and tells us that is often an anisotropic torus. But this need not be so when .
Lemma 2.2.
If is nondegenerate isotropic, then the -algebraic group is almost simple (by which we mean that is perfect and every proper normal subgroup is contained in its center) unless and is endowed with a nondegenerate symmetric form which admits an isotropic plane defined over .
Proof.
This follows from [2], Thm. 6.3.16 combined with Thm. 6.3.15. ∎
The excepted case is genuine, for in that case as modules endowed with -forms, where is a 2-dimensional -vector space endowed with a nondegenerate symplectic form. The resulting map has image and its kernel has as its unique nonidentity element.
Remark 2.3.
The reduced norm is the homomorphism characterized by the following property: if , then for some (or equivalently, every) real embedding , the -linear induces a linear transformation of the -vector space whose determinant is . The kernel of , usually denoted , contains and is often equal to it. But in our context this group does not show up in a natural manner.
3. The hyperbolic module attached to a finite group
A hermitian extension
Our discussion of symplectic -modules also applies to orthogonal -modules. One such module is itself (regarded as a left module): it comes indeed with -invariant pairing , the trace form, which assigns to the pair the trace of considered as an endomorphism of as a -vector space (this is simply times the coefficient of ). This pairing is symmetric and nondegenerate.
The Wedderburn decomposition is also the isotypical decomposition, for the -linear map
which assigns to the endomorphism is well-defined and is an isomorphism of left -modules (and also as right -modules). This also shows that as a right -module.
We claim that as left -modules. This is based on a hermitian extension of to : if we follow the same recipe as in the introduction for a symplectic representation, then we find that there is a hermitian form characterized by the property that for all and ,
This formula implies that is -invariant (we let act on the right of ). By taking , we also see that , so that is a hermitian extension of . For every , the expression yields an element of and defines the stated isomorphism.
Isotropic transvections
Here and in the rest of this paper, we write for the integral group ring . Let be a finitely generated (left) -module, free over and let be a nondegenerate (but not necessarily unimodular) -equivariant symplectic form. We extend this in the standard manner to a form
This form is skew-hermitian: it is -linear in the first variable and . A -linear automorphism of is -equivariant and preserves the symplectic form if and only if it is an -module automorphism which preserves this skew-hermitian form. We denote the group of such automorphisms by .
Let stand for the fixed point set of in ; this is an additive subgroup of . If is -isotropic in the sense that , then for every the isotropic transvection
| (2) |
lies in and is a homomorphism from (the additively written) to (the multiplicatively written) . Since only depends on , we also denote this transformation by .
The basic hyperbolic module
Let be a (not necessarily commutative) unital ring with unit endowed with an anti-involution . The basic hyperbolic -module is the free left -module of rank (whose generators we denote and ) endowed with the skew-hermitian form defined by and . It can be regarded as the -form of the standard symplectic module . In vector notation:
| (3) |
It is unimodular in the sense that is an antilinear isomorphism. We will write resp. for resp. . The latter contains in an obvious manner. Let be the set of -invariant elements. One verifies that and the similarly defined have the matrix form
where stands for right multiplication with .
The group
We take . The elements of the form with , make up a subgroup of such that is a finite dimensional -vector space. Let resp. denote the subgroup of generated by resp. and let stand for the subgroup generated by and . Since is a -conjugate of , the group contains . The right (inverse) action of on defines an embedding of in . One checks that
and so normalizes . We put .
Arithmetic nature of
The notion of a basic hyperbolic module generalizes in a straightforward manner to , the skew-hermitian form being given by
| (4) |
So we have defined ; it is the group of -points of a reductive algebraic group defined over . If we write an element of in block form , with in , then the subgroup defined by is a parabolic subgroup. Its unipotent radical is given by requiring that in addition and are the identity. The corresponding subgroup is then the vector group for which is hermitian relative to . In other words, identifies with an element of (that is, a symmetric element of ) and hence defines an isotropic transvection. In particular, this is also the unipotent radical of the corresponding subgroup of . An opposite parabolic subgroup is defined by and has a similar description of its unipotent radical. Let us denote these unipotent radicals resp. .
We run into this when we consider the isotypical decomposition of . The isogeny space is then a left -module that is naturally identified with . This gives rise to a decomposition
The image of in clearly lands in . Since is a Wedderburn factor of , it follows that the image of in is an order (a lattice that is also a unital algebra). This is compatible with the anti-involutions and hence the image of in is a lattice in the subspace of hermitian matrices. So the image of in is a lattice in .
It is clear that maps to .
Proposition 3.1.
The image of in is an arithmetic subgroup. The real rank of is unless . In that last case, where we can assume that with acting on the right and mapping to its group of units, one of the following holds:
-
(i)
and maps to ,
-
(iia)
is the Gaussian field and maps onto , or
-
(iib)
is the Eisenstein field and maps onto or , or
-
(iiia)
and maps onto its group of units (a binary tetrahedral group of order ) or onto the quaternion group of order , or
-
(iiib)
and maps onto the binary dihedral group of order .
In all cases, acts -irreducibly in .
Remark 3.2.
It is well-known that the quaternion group appearing in 3.1-(iiia) is realized as the Galois group of a torus ramified at four points (the covering surface has genus 3). This example is like a Swiss army knife for illustrating (and refuting) statements in complex dynamics, which is why that community refers to it as the eierlegende Wollmilchsau. We do not know whether its appearance here is just a coincidence.
For the proof we need:
Theorem 3.3 (Raghunathan [7], Venkataramana [9]).
Let be an almost simple, simply connected -algebraic group of real rank . Let and be -subgroups that contain the unipotent radicals of opposite -parabolic subgroups of . Then for any pair of lattices , , the subgroup of generated by their union is a congruence subgroup of .
Proof.
We first prove the arithmeticity property of in . Let us first observe that the group is almost-simple by Lemma 2.2. Indeed, this can only fail if and the form is symmetric (with ) and this is clearly not the case.
If the real rank of is , then the theorem of Raghunathan-Venkataramana applies and we conclude that is an arithmetic subgroup of . It is then also easy to see that acts -irreducibly in .
Since the real rank of is , it remains to treat the case when . In other words, we can assume that . The real rank of is then still most of the time. As we saw above, the exceptions are the cases for which and is either , a definite quaternion algebra over with center or an imaginary quadratic extension of . Since is also an irreducible -module, we have a homomorphism whose image contains a -basis of . In particular, is generated over by its units. So if is an imaginary quadratic extension of , then is either , the Gaussian field or the Eisenstein field. In the definite quaternion case, is the group of unit quaternions and hence is one of the subgroups classified by Klein: this group must be binary tetrahedral, binary octahedral, binary icosahedral of binary dihedral group (of order ). In these cases equals resp. , , , . Since we want this intersection to be , only the two groups listed have that property.
Note that in each of these exceptional cases, . The isotropic subspaces in are defined over and hence . The group is then a copy of . So is arithmetic in . In view of Lemma 2.1 this also implies the arithmeticity of in . The actions of (on the right) and (on the left) on commute and make an exterior tensor product of irreducible -representations: it is the right -module tensored with the tautological representation of on (which is absolutely irreducible). Hence is irreducible as a representation of . This implies that is irreducible as a -module. ∎
4. An arithmeticity criterion
In this section we fix a rational character . We therefore suppress the subscript and write for and for .
Proposition 3.1 tells us that is an arithmetic subgroup which acts -irreducibly on and that with a few exceptions, the group is of real rank .
Eichler transformations revisited
Let be (left) -module of finite rank endowed with a nondegenerate skew-hermitian form . Given a -submodule , we denote by the subgroup of the group of transformations that act trivially on . This group preserves and acts trivially on its radical . Hence ‘restriction to ’ defines homomorphism . This homomorphism is easily shown to be onto. Its kernel consists of the unitary transformations that act trivially on and one checks that this is the image of under . We saw that the homomorphism is also onto and we identified its kernel with the vector group . So the Levi quotient of is and its unipotent radical is an extension of vector groups:
As is clear from the Equation (1), this extension is usually nontrivial. In case is spanned by a single element , then we can write this sequence as
| (5) |
Any element of is an Eichler transformation whose image in is (where is the image of ). We will often use the following lemma.
Lemma 4.1.
Let be a discrete subgroup whose image in is arithmetic and which acts -irreducibly in . If contains an Eichler transformation with , then is arithmetic in .
Proof.
We are given that in the exact sequence of algebraic groups
the image of in is arithmetic. Hence for to be arithmetic, it suffices that be a lattice. For this we turn to the exact sequence (5). The Eichler transformation has image in and this image is nonzero by assumption. The image of the -conjugacy class of in is equal to . Since our assumptions also imply that acts -irreducibly in , it follows that the image of in is a lattice in .
Next observe that if and lie in , then so does their commutator, which by the identity (1) is with . Since the generate a lattice in , it follows that the generate a lattice in . In other words, the preimage of in is also a lattice. Hence is a lattice. ∎
Hyperbolic submodules
If is an embedding of hermitian -modules, then is the orthogonal direct sum of the image of and its perp (for is nondegenerate), so that gives rise to an injective homomorphism of groups . Let us refer to such an embedding as a -hyperbolic summand in .
The following criterion for arithmeticity will be central to our argument.
Theorem 4.2.
Let be a nondegenerate skew-hermitian -module of finite rank and
a collection of -linear embeddings (with finite, nonempty) whose images span over and are such that for each the pair defines a hyperbolic summand of . In case and , assume in addition that there exist for which and are perpendicular.
Then the subgroup of generated by is an arithmetic subgroup of which acts -irreducibly in .
The proof will be by induction on . As may be inferred from the statement of the theorem, the case when is a bit more delicate. Indeed, the first induction step then requires special care and so we do that case first. Once we have dealt with it, we indicate how to modify the arguments in order to obtain a proof of the unrestricted version of Theorem 4.2.
Let us say that a -subspace is -arithmetic if is arithmetic in and acts -irreducibly in (the last property is a consequence of the first if the real rank of is ).
The case
We then identify with and and each with the image of under these embeddings so that for all . Note that consists of isotropic elements and generates over . We write for the image of under , so that is generated by . As any lies , it follows that .
By Proposition 3.1, is -arithmetic for every . We therefore assume that is not of the form . So there exist with such that .
Lemma 4.3.
Put . Then is -arithmetic.
Proof.
We verify that the assumptions of the Lemma 4.1 are satisfied by . It is clear that the radical of is spanned by so that is the isomorphic image of . We know that is -arithmetic and so has arithmetic image in . Since and lie in , so does . We check that
So the image of in contains . Now apply Lemma 4.1. ∎
From this point onward the argument will be inductive. The union of Lemmas 4.4 and 4.5 will establish the theorem in case .
Lemma 4.4.
Let be a -subspace which contains and whose the radical is of -dimension one. If is -arithmetic, then there exists a such that is nondegenerate and -arithmetic, and the real rank of is .
Proof.
Let span the radical of . Since is nondegenerate and -spanned by , there must exist a such that is not in the radical of . Then it is easily seen that is nondegenerate so that . In case (where we can take ) one checks that is the perpendicular sum of two copies of . Otherwise, contains such a sum. This implies that has real rank .
The -stabilizer of is equal to and hence contains as an arithmetic subgroup. Observe that is another isotropic element with and so . The two -stabilizers of and are opposite parabolic subgroups of whose unipotent radicals are contained in resp. . Since is a -conjugate of , it follows that is an arithmetic subgroup of . We have thus satisfied the hypotheses of Theorem 3.3 and we conclude that is arithmetic in . The fact that acts -irreducibly in follows from the fact that has this property in , for the -translates of span over , but do not decompose . ∎
Lemma 4.5.
Let be a proper nondegenerate -subspace of dimension and contain . If is -arithmetic, then so is for every .
Proof in case is degenerate.
We verify that the assumptions of the Lemma 4.1 are satisfied by . The radical of is necessary spanned by an element of the form where is characterized by the property that for all . So maps then isomorphically onto . In particular, the natural map is an isomorphism and hence maps onto an arithmetic subgroup of .
Let be a positive integer such that . Then
So and this element has image in . It then follows from Lemma 4.1 that is -arithmetic. ∎
Proof in case is nondegenerate.
Then is degenerate with radical spanned by . We first prove that is -arithmetic by verifying the assumptions of the Lemma 4.1. The subspace supplements in . It is therefore nondegenerate and maps isomorphically onto . This enables us to regard as a subgroup of that acts trivially on both and its orthogonal projection in .
Since is arithmetic in , its subgroup is arithmetic in and has arithmetic image in . We show that for some . Then Lemma 4.1 will imply that is -arithmetic.
For this we recall that is perpendicular to and has nonzero image in . Let take to . Since is perpendicular to , is perpendicular to (so lies in ) and has nonzero image in . Since is a -conjugate of , it lies in .
Now is and so is arithmetic in . As , the same is true for . Since and span a copy of , their -stabilizers contain the unipotent radicals of opposite parabolic subgroups of . The real rank of is , so that Theorem 3.3 applies and tells us that is -arithmetic. ∎
The case when
The same scheme for the proof works when . The difference is that we deal with larger hyperbolic packets, to wit, the images of hyperbolic embeddings . The essential difference is that we start off in a better position, since we begin with a -hyperbolic embedding and we already know that its image is -arithmetic and that has real rank .
5. Finding liftable mapping classes
In this section the -covering is as in the introduction and is a nonempty closed -submanifold
such that the covering is trivial over and is connected over . We also choose a connected component of , so that might be empty.
We orient and regard it as the oriented image of an embedding of the circle in . We will see that this gives rise to enough copies of in the representation
of the -equivariant mapping classes as to satisfy the hypotheses of our arithmeticity criterion Theorem 4.2.
We denote by the singular surface obtained from by contracting to a point (that we will denote by ). Its topological normalization is a closed connected surface, denoted , whose genus is one less than that of . The surface comes with two points over and the orientation of enables us to tell them apart: we let be ‘to the left’ of and is ‘to the right’ of . If we regard also as a submanifold of , then the surjection defines a map from the set of path homotopy classes in from to to the fundamental group . This map is injective. We do the same (in a -equivariant manner) for the preimage of in and thus get -covers , and -orbits , , so that we end up with the diagram below (in which the vertical maps are -coverings):
This construction comes with -equivariant bijections . Our assumption on the covering amounts to the following two properties: (i) is connected and stays so if we remove the preimage of and (ii) the three -orbits , are regular. So the choice of a point in (which is equivalent to the choice of a lift of ) identifies these -sets with (on which acts by left translation). In particular, we thus identify with (where acts on by right translation over ).
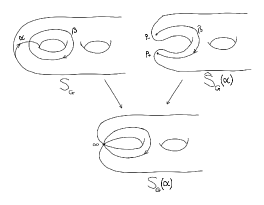
For any path in from to , the covering is trivial over it, so that we have an associated -bijection . Since the -covering over is connected, the resulting map
is onto by standard covering theory. We will say that an element of is -trivial if its image in under the above map is the identity. Such elements make up a coset for the kernel of the natural homomorphism .
Lemma 5.1.
Every element of is representable by some arc ( embedded unit interval) in from to . We can arrange that this arc lifts to an embedding of the circle in which meets in a single point with intersection number . In particular, every element of is realized by the monodromy along an embedded circle which does not meet and meets in one point only and does so transversally with intersection number .
Proof.
We first represent the homotopy class by an immersion of the unit interval with only transversal self-intersections. That number of self-intersections is finite and if this number is positive, we lower it by moving the last point of self-intersection towards and then slide the path over . By iterating this procedure we obtain a representative which is an embedding. It is clear that we can make this arc lift to an embedded circle. The second assertion then follows. ∎
We choose a lift of and write for its homology class. Since is an an isotropic sublattice of , we have that . We let be the homology supported by the preimage of : this is a free -submodule (where as before, ) with a generator for every connected component of . It is clear that is isotropic. We saw that the lift identifies with the group with acting on itself by right translations. Lemma 5.1 above shows that all such elements are obtained from a loop of the type described there. From that lemma we also derive:
Corollary 5.2.
Let be such that and for . Then some can be represented by a lift of an embedded circle in which meets transversally at a unique point (and for which necessarily ). In particular, is -isotropic and the -linear map defined by
is an embedding of skew-hermitian -modules whose orthogonal complement supplements its image: we obtain a basic hyperbolic summand of the -module .
Proof.
It is not difficult to see that the homology class is representable by a map from the circle to which meets the preimage of exactly once (hence in a point of ) and does not meet the preimage of . We apply Lemma 5.1 to its image in or rather to the resulting arc in which connects with : this then produces an embedding of the circle in which meets only once and with intersection number over which the -covering is trivial. The lift of which meets defines a homology class which differs from by by a class supported by the preimage of , that is, an element of .
The proof of the last paragraph is straightforward. ∎
Let us call an ordered pair in -hyperbolic if and . Such a pair defines a
basic hyperbolic summand and gives rise to an embedding of in . We shall denote the latter’s image by and the image of by .
We write for the set of for which the pair is -hyperbolic and resp. for the subgroup of generated by its subgroups resp. with .
Fix a base point on and write for its preimage in .
Let and regard as an element of . Let be as in Lemma 5.1, which we may (and will) assume to meet in such that the lift of (as an arc) which begins in ends in . Let be a closed regular neighborhood of in . This is a compact genus one surface whose boundary is connected. The homotopy class of this boundary (with its natural orientation) is in the free homotopy class of the commutator (we write path composition functorially, so the order of travel is read from right to left). This commutator has trivial image in (since has), and so the -covering is trivial over . The preimage of in is the boundary of the preimage of and the Dehn twist along lifts in a -equivariant manner to a multi-Dehn twist along that boundary. The following lemma generalizes one of the constructions given in [3] for the case when is cyclic (in that paper they are depicted as Figs. 2 and 3).
Lemma 5.3.
The multi-Dehn twist acts on as (where we use formula (2), noting that ).
Proof.
The lift of the commutator that passes through first traverses the embedded circle , then traverses , then traverses the circle in the opposite direction and then returns via the inverse of to . So the homology class of this lift of the commutator (and hence of the corresponding lift of ) is . If we replace by with , then this replaces by and by , so that the corresponding class is . By a standard formula, the resulting action on is given by
Proposition 5.4.
Let be such that is an -hyperbolic pair. Then the image of contains .
Proof.
We first show this for . Let be as in Corollary 5.2 (and thus represent an element of ). The diffeomorphisms of with support in the interior of have as their image in the mapping class group of a centrally extended copy of with the central subgroup generated by the Dehn twist along the boundary of . This Dehn twist acts trivially on . These diffeomorphisms lift to diffeomorphisms of with support in with the central subgroup acting trivially on . We thus obtain in the image of a copy of .
The multi-Dehn twist associated to acts on as . By lemma 5.3 the image of also contains the transvections for all . Hence that image contains all of . This proves that the image of contains .
So it remains to show that the image of in is realized by . For this we use mapping classes of push type. Consider the smooth surface that is obtained as a quotient of by contracting to a point (that we shall call ). If we do the same for the connected components of in we get a -cover fitting in the commutative diagram
The covering on the right does not branch over and so its preimage in is a regular -orbit. For every , there is a closed loop of based at which avoids branch points and induces in right multiplication by . The corresponding point-pushing map on (chosen to fix branch points) lifts to a -equivariant diffeomorphism of that extends this permutation.

Such a point-pushing map is isotopic to the identity on and hence the same is true for its lift . In particular, acts trivially on . It is not difficult to see that the point pushing map and its lift can be ‘lifted’ to and by ‘small circle pushing’. Since is an isomorphism, the action on will be trivial. Clearly the components of will be permuted according to the right action of and thus realizes in the image of . ∎
Part (ii) of the corollary below establishes the Putman-Wieland property of Theorem 1.1.
Corollary 5.5 (Hyperbolic generation).
The following properties hold:
-
(i)
the subset of spans the latter over ,
-
(ii)
the subgroup of generated by the subgroups with (and hence ) has no nonzero finite orbit in .
Proof.
Let be perpendicular to . We prove that is then perpendicular to every ; since the intersection form is nondegenerate, this will imply that and hence that the -submodule of generated is of finite index. To this end, let . Then has the property that . By Corollary 5.2 is is a hyperbolic pair for some , so that .
For (ii) it suffices to show that for every finite index subgroup , the fixed part is trivial. Note that is the perp of in with respect to the intersection pairing. The -invariant part of is not changed if we replace by the finite index subgroup and hence is perpendicular to . As this is true for all and generates as an -module, it follows that must be trivial. ∎
We can now finish the proof of our main theorem.
Proof of the main theorem 1.1.
Let us denote the image of in by and the image of the latter in the factor of by . By combining Corollary 5.5 with Theorem 4.2, we see that under the assumptions of (ii), is an arithmetic subgroup of .
Note that is a normal subgroup of . It remains to see that is of finite index in . Since is almost simple and of real rank , it follows from a general result of Margulis ([4], Assertion (A), Ch. VIII) that this is the case unless meets in the center. But Proposition 5.4 shows that contains a subgroup isomorphic to and so this last possibility does not occur. ∎
Remark 5.6.
This argument shows that if we are in the setting of (i) (triviality of the cover over a genus one subsurface of ), then is an arithmetic subgroup of , unless and the image of in is of the type given in Proposition 3.1. Denote that image by and let stand for the kernel of . Since already arises on the -cover in the sense that , we may for the arithmeticity question just as well focus on this intermediate cover.
In the cases (i) and (ii) of 3.1, so when equals , the Gaussian field or the Eisenstein field, then is a group of roots of unity and hence cyclic. When the genus of is at least , we can always find a closed subsurface of genus 2 over which the covering is trivial and so is then arithmetic. In the remaining cases, is a particular kind of Kleinian group. It might well be that a -cover is then also trivial over the complement of a genus two subsurface of the quotient surface when the genus of the latter is . If true, then it would follow that would always be arithmetic if the genus of is at least and the covering is trivial over a genus one subsurface of .
References
- [1] F. Grünewald, M. Larsen, A. Lubotzky, J. Malestein: Arithmetic quotients of the mapping class group. Geom. Funct. Anal. 25 (2015) 1493–1542, https://arxiv.org/pdf/1307.2593v2
- [2] A. J. Hahn, O. T. O’Meara: The classical groups and K-theory. Grundlehren Math. Wiss. 291, Springer-Verlag (1989).
- [3] E. Looijenga: Prym Representations of Mapping Class Groups. Geom. Dedicata 64 (1997), 69–83.
- [4] G. A. Margulis: Discrete subgroups of semisimple Lie groups. Ergeb. Math. Grenzgeb. 17, Springer-Verlag, Berlin.
- [5] D. Mumford: Abelian varieties. TIFR Studies in Math. 5, Oxford University Press, London (1970).
- [6] A. Putman, B. Wieland: Abelian quotients of subgroups of the mappings class group and higher Prym representations, J. Lond. Math. Soc. 88 (2013), 79–96.
- [7] M. S. Raghunathan: A note on generators for arithmetic subgroups of algebraic groups. Pacific J. Math. 152 (1992), 365–373.
- [8] T. A. Springer: Linear algebraic groups. Birkhäuser Boston, Inc., Boston, MA (2009).
- [9] T. N. Venkataramana: On systems of generators of arithmetic subgroups of higher rank groups. Pacific J. Math. 166 (1994), 193–212.
- [10] G. E. Wall: The structure of a unitary factor group. Inst. Hautes Études Sci. Publ. Math. 1 (1959).