Arrested phase separation in double-exchange models:
machine-learning enabled large-scale simulation
Abstract
We present large-scale dynamical simulations of electronic phase separation in the single-band double-exchange model based on deep-learning neural-network potentials trained from small-size exact diagonalization solutions. We uncover an intriguing correlation-induced freezing behavior as doped holes are segregated from half-filled insulating background during equilibration. While the aggregation of holes is stabilized by the formation of ferromagnetic clusters through Hund’s coupling between charge carriers and local magnetic moments, this stabilization also creates confining potentials for holes when antiferromagnetic spin-spin correlation is well developed in the background. The dramatically reduced mobility of the self-trapped holes prematurely disrupts further growth of the ferromagnetic clusters, leading to an arrested phase separation. Implications of our findings for phase separation dynamics in materials that exhibit colossal magnetoresistance effect are discussed.
The subject of phase separation dynamics is of significant importance in many branches of physics, materials science, and biology gunton83 ; puri09 ; cross12 ; onuki02 ; bray94 . Dynamically, phase separation occurs when a homogeneous system is placed in an out-of-equilibrium state due to a rapid change in thermodynamic variables such as temperature. The system then evolves toward an inhomogeneous state of coexisting phases. This intrinsically non-equilibrium and nonlinear process involves the formation, growth, and coarsening of domains of ordered phases. Substantial progress has been made in understanding the phase-separation kinetics over the past few decades. In particular, it has been shown that phase separation at late times exhibits a dynamical scaling and is controlled by a characteristic length scale which follows a power-law , where the growth-exponent depends mainly on dimensionality and conservation of the order-parameter.
Phase separation also plays a crucial role in the functionality of strongly correlated electron systems schulz89 ; emery90 ; white00 ; tranquada95 ; yee15 ; kivelson03 ; dagotto_book ; dagotto05 ; moreo99 ; dagotto01 ; mathur03 ; nagaev02 . A case in point is the complex inhomogeneous states observed in manganites and magnetic semiconductors that exhibit the colossal magnetoresistance (CMR) effect dagotto_book ; dagotto05 ; moreo99 ; dagotto01 ; mathur03 ; nagaev02 . These nanoscale textures arise from the segregation of hole-rich ferromagnetic clusters from the half-filled antiferromagnetic domains fath99 ; renner02 ; salamon01 . An intriguing scenario for CMR is the field-induced percolating transition of metallic nano-clusters in such a phase-separated state uehara99 ; zhang02 . Since the number of doped carriers is conserved, the segregation process of such conserved field was first studied in the classic works of Lifshitz, Slyozov lifshitz61 , and Wagner wagner61 (LSW), who predicted a growth exponent of .
Despite extensive works on properties of mixed-phase states in CMR materials, the kinetics of phase separation driven by electron-correlation has yet to be investigated. Important questions, such as whether the phase separation exhibits dynamical scaling and does the late-stage domain growth indeed follow the LSW power law, remain unanswered. On the theoretical side, the lack of progress is partially due to the difficulty in performing large-scale dynamical simulations of electronic phase separation. While several numerical techniques, such as molecular dynamics and phase-field method collins86 ; valls90 ; steinbach13 , have been developed to simulate pattern formation in material systems such as binary alloys or polymers, conventional approaches often rely on empirical energy models and cannot describe the intricate electron correlation effects. A comprehensive modeling of correlation-induced phase separation requires properly incorporating microscopic electronic processes into mesoscopic spatial-temporal pattern dynamics. Yet, such multi-scale approaches are limited to small systems due to the expensive repeated electronic structure calculations.
In this paper, we overcome the difficulties of multi-scale modeling by applying machine learning (ML) methods to enable large-scale simulations of phase separation phenomena in the double-exchange (DE) model zener51 ; anderson55 ; degennes60 , which plays a center role in the modeling of CMR materials. The central idea of our approach is to develop deep-learning neural networks (NN) that emulate the time-consuming exact diagonalization required for computing the exchange forces on spins. In this respect, the NN can be viewed as a complex empirical potential model, which offers the accuracy of quantum calculations. We consider the single-band DE model on a square lattice,
| (1) |
where are creation/annihilation operators of electron with spin at site , repeated indices implies spin summation, indicates the nearest neighbors (NN), is the NN electron hopping constant, is the local Hund’s rule coupling between electron spin and local magnetic moment , which are assumed to be classical spins of length . The square-lattice DE model has been extensively studied theoretically varma96 ; yunoki98 ; dagotto98 ; chattopadhyay01 ; pekker05 . In particular, when the system is slightly hole-doped from half-filling, a mixed-phase state consisting of hole-rich ferromagnetic puddles embedded in the half-filled antiferromagnetic insulator emerges as a stable thermodynamic phase at strong Hund’s coupling yunoki98 ; dagotto98 ; chattopadhyay01 .
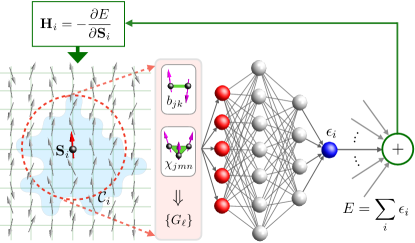
The evolution of the DE system in the adiabatic limit, similar to the Born-Oppenheimer approximation in quantum molecular dynamics marx09 , is governed by the stochastic Landau-Lifshitz-Gilbert (LLG) equation landau35 ; brown63 ; garanin97
| (2) |
where is a Gaussian stochastic field of zero mean, is a damping coefficient, is the local exchange force acting on the -th spin. The effective energy is given by , where is the instantaneous density matrix of the electron liquid. Repeated calculation of , which is required at every time-step, based on exact diagonalization (ED), can be overwhelmingly time consuming note_KPM ; furukawa04 ; alvarez05 ; weisse06 ; barros13 ; wang18 .
To overcome this computational bottleneck, we develop a neural network (NN) model for the potential energy surface of spins. We first express the effective energy as a sum of local contributions
| (3) |
where the energy is associated with the -th lattice site and is assumed to depend only on spin configuration in its neighborhood. The partitioning of into local energies is based on the locality principle kohn96 ; prodan05 , which also underlies the ML interatomic potentials that allow for large-scale molecular dynamics simulations with the accuracy of density function theory behler07 ; bartok10 ; li15 ; behler16 ; smith17 ; zhang18 ; deringer19 ; mueller20 or other many-body techniques mcgibbon17 ; chmiela17 ; suwa19 .
As shown in Fig. 1, the dependence of energy function on the local spin-environment is encoded in a feed-forward neural network. To ensure that symmetries of the DE Hamiltonian, which are described by the SO(3) spin-rotation and D4 point groups, are preserved in the energy function, we have developed a descriptor that translates local spin configuration into effective coordinates that are invariant under both symmetry operations. First, the SO(3) rotation symmetry can be manifestly maintained by using only bond variables and scalar chirality as building blocks; they are defined as
| (4) |
The collection of these variables around the -th spin form the basis of a high-dimensional representation of the D4 group, which is then decomposed into the fundamental irreducible representations (irrep). The basis of each irreps , , , , where enumerates the multiplicity, are proper linear combinations of the bond and scalar chirality variables. Finally, generalized coordinates that are invariant under lattice symmetry operations are obtained from the amplitudes and relative phases of these irrep basis ma19 ; suppl1 . These generalized coordinates are then fed into a NN, which produces the local energy at its output. Exchange forces acting on spins are obtained by applying automatic differentiation to the total energy; see Fig. 1.
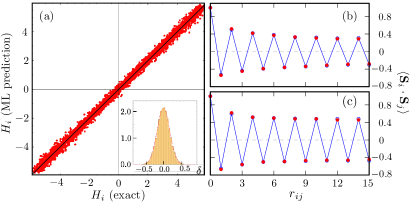
A six-layer NN model is constructed and trained using PyTorch paszke19 . The training dataset consists of 3500 snapshots of spins and local exchange forces, obtained from exact LLG simulations of a lattice suppl2 . Fig. 2(a) shows components of local exchange forces predicted by our trained NN model versus the exact results on a test dataset consisting of 500 snapshots of spins during the relaxation process. The difference between the ML prediction and exact calculation is well described by a Gaussian distribution with a rather small MSE of , as shown in the inset. Interestingly, the normal distribution of the deviation implies that the statistical error of the ML model can be interpreted as an effective temperature in the Langevin-type dynamics. This interesting observation has also been verified in our simulations. As shown in Fig. 2(b) and (c), the spin-spin correlations obtained from ML-LLG simulations agree very well with those from ED-based LLG at the temperature .
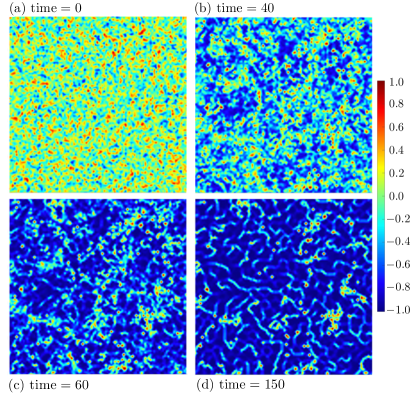
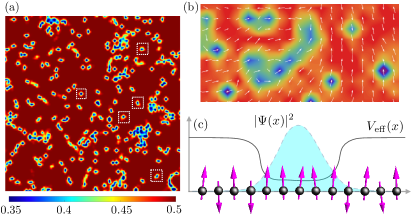
Having successfully benchmarked the NN model, we used it to perform large-scale quench simulations in which a system, initially in a random configuration, is suddenly quenched to a low-temperature phase. Fig. 3 shows density plots of local spin-correlation obtained by averaging over 4 nearest-neighbor bonds of a given site, , at different times after quench. Positive corresponds to regions with predominately ferromagnetic (FM) alignment of spins, while negative indicates antiferromagnetic (AFM) domains. Our ML-LLG simulations clearly showed a relaxation process that leads to an inhomogeneous state with large AFM domains interspersed with small FM clusters. We have trained another NN-model which successfully predicts the on-site electron density based on the neighborhood spins . Applying this NN to spin configurations obtained form the ML-LLG quench simulations, we verified that the doped holes are indeed confined to puddles with FM spins, as shown in Fig. 4(a) and (b). Interestingly, compared with the electron density, the spins exhibit more complex structures. In particular, in addition to FM clusters, a web of string-like features can be seen in the AFM background of the phase-separated states; see e.g. Fig. 3(d).
Next we turn to the kinetics of FM-domain growth. Fig. 5(a) shows the distribution of nearest-neighbor bond-variable at different times after quench. The initially flat distribution function , corresponding to random spins, starts to develop a peak at representing AFM spin correlation at earlier times (e.g. at ). This then turns into a bimodal distribution at late times, clearly indicating the evolution of the system toward phase separation, although the peak at the FM-bond is rather weaker. Since doped holes in the phase-separated states are mostly confined in FM-clusters, the smaller value of is consistent with the small doping of our system.
We define a FM cluster in such a way that all nearest-neighbor bonds within it are greater than a threshold . The time dependence of the characteristic length of such FM clusters is shown in Fig. 5(b). Qualitatively similar behaviors were obtained using larger threshold . In the initial state with random spins, a fraction of bonds are above the threshold. Although this fraction is still below the bond-percolation threshold on square lattice, relatively large FM clusters can still be found in the random spins, which explains the initially large average size of such FM clusters. As the system relaxes toward equilibrium, the average cluster size quickly decreases as shown in the inset of Fig. 5(b). After reaching a minimum, the hole-rich FM-clusters start to grow again.
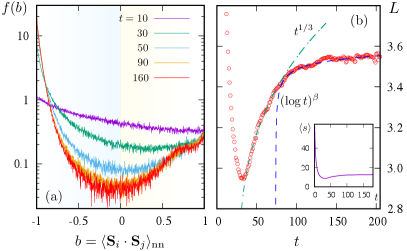
Since the number of doped holes is conserved, phenomenologically the growth of such conserved fields is described by the Cahn-Hilliard equation cahn58 , also called the model-B dynamics hohenberg77 , and a power-law growth is expected. Moreover, since the density of doped holes is very small in the mixed-phase states of DE model, the phase-separation dynamics in such off-critical or asymmetric quenches is supposed to be well described by the original LSW theory lifshitz61 ; wagner61 , which convincingly predicts the same growth. However, as shown in Fig. 5(b), only a short initial period of the domain growth can be described by the power law. At late times, the length scale increases with a significantly slower rate than that predicted by the LSW theory, and is better described by a sublogarithmic growth law.
The LSW theory describes the diffusive interactions between domains of conserved minority phase. Clusters of the minority phase compete for growth through an evaporation-condensation mechanism, whereby larger clusters grow at the expense of smaller ones. According to this scenario, growth of the hole-rich FM clusters requires the diffusion of doped holes migrating from smaller cluster to larger ones in the mixed-phase state. The initial aggregation of the charge carriers into proto-FM domains can probably be described by the LSW mechanism, as evidenced by the early-stage power-law growth in our simulations. However, the phase-separation process is dramatically slowed down when the AFM correlation is established in the background of the half-filled majority phase. At this point, the doped holes induce a cloud of surrounding parallel spins through the double-exchange mechanism, which in turn provide a confining potential. Fig. 4(b) shows examples of hole-rich FM clusters embedded in a AFM background, and the self-confinement of holes in such domains is schematically shown in Fig. 4(c). Importantly, as a result of such self-trapping, evaporation of doped holes from FM clusters is strongly suppressed, leading to the breakdown of the LSW mechanism.
Moreover, even if some charge carriers manage to escape confinement of the emerging FM-clusters described above, they are soon transformed to relatively immobile quasi-particles called magnetic polarons degennes60 ; kasuya68 ; nagaev74 ; mauger83 ; daghofer04 ; pereira08 ; jing21 , some of which are highlighted in Fig. 4(b). Magnetic polaron of the single-band DE model consists of as few as five parallel spins that trap exactly one fundamental electric charge jing21 . In fact, magnetic polarons to some extent can be viewed simply as the smallest FM cluster dagotto_book .
Another mechanism for domain-growth, proposed by Binder and Stauffer (BS) binder74 ; binder77 , is based on the Brownian motion and collision of the minority-phase droplets. For the single-band DE Hamiltonian studied in this work, the FM clusters, including magnetic polarons, are pretty much immobile up to temperatures close to the magnetic phase transition daghofer04 ; pereira08 ; jing21 . This indicates the BS scenario cannot produce a sustained domain growth in our case. On the other hand, taking into account the quantum nature of localized spins, it has been argued that diffusive motion of small magnetic polarons can be achieved through quantum-tunneling kemeny75 ; liu79 ; ioselevich93 or large paramagnetic fluctuations calderon00 ; wegener02 . For most CMR materials, however, such quantum tunneling is suppressed due to the large magnitude of local spins. At any rate, even with diffusive magnetic-polarons, a consistent treatment of tunneling-induced evaporation of holes is required in order to see whether the LSW scaling might be restored.
In CMR materials and magnetic semiconductors, the formation of FM clusters and magnetic polarons are accompanied by local lattice distortion and orbital ordering dagotto_book , both of which are expected to further stabilize the composite structure, thus reducing the mobility of charge-carriers. Consequently, similar freezing effect is likely to take place in the phase separation process of real materials. The presence of quenched disorder most likely enhances the glassy behaviors discussed above. For example, it has been shown that charge carriers can be trapped by impurities, forming bound magnetic polarons dietl83 ; mohan88 ; kaminski03 . Other factors that affect the carrier mobility include hole concentration, external electric and magnetic fields. In particular, higher doping percentage could increase the overlap of the carrier wave function, thus enhancing the tunneling mobility.
The functionality of correlated electron materials, such as CMR manganites, depends intimately on the structure of the mixed-phase states, which in turn are determined by the phase-separation process. Some of reported anomalous or glassy dynamics in CMR manganites yan11 ; ward11 ; kundhikanjana15 might be related to the freezing behavior studied in this work. With powerful ML methods, generalizations to more realistic models which include, e.g. multi-orbital or Jahn-Teller effect, are straightforward. ML-enabled large-scale simulations offer the capability to systematically investigate and characterize phase-separation dynamics, paving the way toward engineering electronic mixed-phase states with desired properties.
Acknowledgements.
The authors thank Sheng Zhang for useful discussions. The work was supported by the US Department of Energy Basic Energy Sciences under Contract No. DE-SC0020330. The authors also acknowledge the support of Advanced Research Computing Services at the University of Virginia.References
- (1) J. D. Gunton, M. San Miguel, and P. S. Saint, The dynamics of first order phase transitions, in “Phase Transitions and Critical Phenomena”, edited by C. Domb and J. L. Lebowitz, vol. 8, pp.269-466 (Academic, New York, 1983).
- (2) A. J. Bray, Theory of phase-ordering kinetics, Adv. Phys. 43, 357 (1994).
- (3) S. Puri and V. Wadhawan, Ed. Kinetics of Phase Transitions (CRC Press, Taylor & Francis Group, London, 2009).
- (4) A. Onuki, Phase Transition Dynamics (Cambridge University Press, Cambridge, UK, 2002).
- (5) M. Cross and H. Greenside, Pattern formation and dynamics in nonequilibrium systems (Cambridge University Press, 2012).
- (6) H. J. Schulz, Domain walls in a doped antiferromagnet, J. Phys. France 50, 2833 (1989).
- (7) V. J. Emery, S. A. Kivelson, and H. Q. Lin, Phase separation in the t-J model, Phys. Rev. Lett. 64, 475 (1990).
- (8) S. White and D. Scalapino, Phase separation and stripe formation in the two-dimensional t-J model: A comparison of numerical results, Phys. Rev. B 61, 6320 (2000).
- (9) J. M. Tranquada, B. J. Sternlleb, J. D. Axe, Y. Nakamura, and S. Uchida, Evidence for stripe correlations of spins and holes in copper oxide superconductors, Nature 375, 561 (1995).
- (10) S. A. Kivelson, I. P. Bindloss, E. Fradkin, V. Oganesyan, J. M. Tranquada, A. Kapitulnik, and C. Howald, How to detect fluctuating stripes in the high-temperature superconductors, Rev. Mod. Phys. 75, 1201 (2003).
- (11) C.-H. Yee and L. Balents, Phase separation in doped Mott insulators, Phys. Rev. X 5, 021007 (2015).
- (12) E. Dagotto, Nanoscale phase separation and colossal magnetoresistance (Berlin, Springer 2002).
- (13) E. Dagotto, Complexity in strongly correlated electronic systems, Science 309, 257 (2005).
- (14) A. Moreo, S. Yunoki, and E. Dagotto, Phase separation scenario for manganese oxides and related materials, Science 283, 2034 (1999).
- (15) E. Dagotto, T. Hotta, A. Moreo, Colossal magnetoresistant materials: The key role of phase separation, Phys. Rep. 344, 1 (2001).
- (16) N. Mathur and P. Littlewood, Mesoscopic texture in manganites, Phys. Today 1, 25 (2003).
- (17) E. L. Nagaev, Colossal Magnetoresistance and Phase Separation in Magnetic Semiconductors (Imperial College Press, London, 2002).
- (18) M. Fäth, S. Freisem, A. A. Menovsky, Y. Tomioka, J. Aarts, and J. A. Mydosh, Spatially inhomogeneous metal-insulator transition in doped manganites, Science 285, 1540 (1999).
- (19) M. B. Salamon and M. Jaime, The physics of manganites: Structure and transport, Rev. Mod. Phys. 73, 583 (2001).
- (20) Ch. Renner, G. Aeppli, B.-G. Kim, Y.-A. Soh, and S.-W. Cheong, Atomic-scale images of charge ordering in mixed-valance manganite, Nature 416, 518 (2002).
- (21) M. Uehara, S. Mori, C. H. Chen, and S.-W. Cheong, Percolative phase separation underlies colossal magnetoresistance in mixed-valent manganites, Nature 399, 560 (1999).
- (22) L. Zhang, C. Israel, A. Biswas, R. L. Greene, A. de Lozanne, Direct observation of percolation in a maganite thin film, Science 298, 805 (2002).
- (23) I. M. Lifshitz and V. V. Slyozov, The kinetics of precipitation from supersaturated solid solutions, J. Phys. Chem. Solids 19, 35 (1961).
- (24) C. Wagner, Theorie der Alterung von Niederschlagen durch Umlosen, Z. Elektrochem 65, 581 (1961).
- (25) J. B. Collins and H. Levine, Diffuse interface model of diffusion-limited crystal growth, Phys. Rev. B 31, 6119(R) (1986).
- (26) O. T. Valls and G. F. Mazenko, Nucleation in a time- dependent Ginzburg-Landau model: A numerical study, Phys. Rev. B 42, 6614 (1990).
- (27) I. Steinbach, Phase-Field Model for Microstructure Evolution at the Mesoscopic Scale, Annu. Rev. Mater. Res. 43, 89 (2013).
- (28) C. Zener, Interaction between the -Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure, Phys. Rev. 82, 403 (1951).
- (29) P. W. Anderson and H. Hasegawa, Considerations on Double Exchange, Phys. Rev. 100, 675 (1955).
- (30) P. -G. de Gennes, Effects of Double Exchange in Magnetic Crystals, Phys. Rev. 118, 141 (1960).
- (31) C. M. Varma, Electronic and magnetic states in the giant magnetoresistive compounds, Phys. Rev. B 54, 7328 (1996).
- (32) S. Yunoki, J. Hu, A. L. Malvezzi, A. Moreo, N. Furukawa, and E. Dagotto, Phase Seperation in Electronic Models for Manganites, Phys. Rev. Lett. 80, 845 (1998).
- (33) E. Dagotto, S. Yunoki, A. L. Malvezzi, A. Moreo, J. Hu, S. Capponi, D. Poilblanc, and N. Furukawa, Ferromagnetic Kondo model for manganites: Phase diagram, charge segregation, and influence of quantum localized spins, Phys. Rev. B 58, 6414 (1998).
- (34) A. Chattopadhyay, A. J. Millis, and S. Das Sarma, phase diagram of the double-exchange model, Phys. Rev. B 64, 012416 (2001).
- (35) D. Pekker, S. Mukhopadhyay, N. Trivedi, and P. M. Goldbart, Double-exchange model for noninteracting electron spins coupled to a lattice of classical spins: Phase diagram at zero temperature, Phys. Rev. B 72, 075118 (2005).
- (36) D. Marx and J. Hutter, Ab initio molecular dynamics: basic theory and advanced methods (Cambridge University Press, Cambridge, 2009).
- (37) L. D. Landau and E. M. Lifshitz, On the theory of the dispersion of magnetic permeability in ferromagnetic bodies, Z. Phys. Sowjet. 8, 153 (1935).
- (38) W. F. Brown, Jr., Thermal Fluctuations of a Single-Domain Particle, Phys. Rev. 130, 1677 (1963)
- (39) D. A. Garanin, Fokker-Planck and Landau-Lifshitz-Bloch equations for classical ferromagnetsm, Phys. Rev. B 55, 3050 (1997).
- (40) Linear-scaling approaches, such as the kernel polynomial method, have also been developed for the simulating DE systems; see Refs. furukawa04 ; alvarez05 ; barros13 ; weisse06 ; wang18 for examples. The ML-approaches proposed in this work offers more flexibility and can be generalized to include effects such as multi-orbitals, Jahn-Teller coupling, without much overhead.
- (41) N. Furukawa and Y. Motome, Order Monte Carlo Algorithm for Fermion Systems Coupled with Fluctuating Adiabatical Fields, J. Phys. Soc. Jpn. 73, 1482 (2004).
- (42) G. Alvarez, C. Sen, N. Furukawa, Y. Motome, and E. Dagotto, The truncated polynomial expansion Monte Carlo method for fermion systems coupled to classical fields: a model independent implementation, Comput. Phys. Commun. 168, 32 (2005).
- (43) A. Weisse, G. Wellein, A. Alvermann, and H. Fehske, The kernel polynomial method, Rev. Mod. Phys. 78, 275 (2006).
- (44) K. Barros and Y. Kato, Efficient Langevin simulation of coupled classical fields and fermions, Phys. Rev. B 88, 235101 (2013).
- (45) Z. Wang, G.-W. Chern, C. D. Batista, and K. Barros, Gradient-based stochastic estimation of the density matrix, J. Chem. Phys. 148, 094107 (2018).
- (46) K. Walter, Density functional and density matrix method scaling linearly with the number of atoms, Phys. Rev. Lett. 76(17), 3168.
- (47) E. Prodan, and K. Walter, Nearsightedness of electronic matter, Proc. Natl. Acad. Sci. U.S.A. 102.33 (2005): 11635-11638.
- (48) J. Behler and M. Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, Phys. Rev. Lett. 98, 146401 (2007).
- (49) A. P. Bartók, M. C. Payne, R. Kondor, G. Csányi, Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons, Phys. Rev. Lett. 104, 136403 (2010).
- (50) Z. Li, J. R. Kermode, and A. De Vita, Molecular Dynamics with On-the-Fly Machine Learning of Quantum-Mechanical Forces, Phys. Rev. Lett. 114, 096405 (2015).
- (51) J. S. Smith, O. Isayev, and A. E. Roitberg, ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost, Chem. Sci. 8, 3192 (2017).
- (52) L. Zhang, J. Han, H. Wang, R. Car, and Weinan E, Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics, Phys. Rev. Lett. 120, 143001 (2018).
- (53) J. Behler, Perspective: Machine learning potentials for atomistic simulations, J. Chem. Phys. 145, 170901 (2016).
- (54) V. L. Deringer, M. A. Caro, and G. Csányi, Machine learning interatomic potentials as emerging tools for materials science, Adv. Mater. 31, 1902765 (2019).
- (55) T. Mueller, A. Hernandez, and C. Wang, Machine learning for interatomic potential models, J. Chem. Phys. 152, 050902 (2020).
- (56) R. T. McGibbon, A. G. Taube, A. G. Donchev, K. Siva, F. Hernández, C. Hargus, K.-H. Law, J. L. Klepeis, and D. E. Shaw, Improving the accuracy of Moller-Plesset perturbation theory with neural networks, J. Chem. Phys. 147, 161725 (2017).
- (57) S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt, and K.-R. Müller, Machine learning of accurate energy-conserving molecular force fields, Sci. Adv. 3, e1603015 (2017).
- (58) H. Suwa, J. S. Smith, N. Lubbers, C.D. Batista, G.-W. Chern, and K. Barros, Machine learning for molecular dynamics with strongly correlated electrons, Phys. Rev. B 99, 161107 (2019).
- (59) J. Ma, P. Zhang, Y. Tan, A. W. Ghosh, and G.-W. Chern, Machine learning electron correlation in a disordered medium, Phys. Rev. B 99, 085118 (2019).
- (60) See supplemental material for more details about the descriptor, in particular the group-theoretical methods for constructing invariants of the point group.
- (61) A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, and A. Desmaison, PyTorch: An imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems 2019 (pp. 8024-8035).
- (62) See supplemental material for training details including dataset selection, and loss function.
- (63) J. W. Cahn and J. E. Hilliard, Free Energy of a Nonuniform System. I. Interfacial Free Energy, J. Chem. Phys. 28, 258 (1958).
- (64) P. C. Hohenberg and B. I. Halperin, Theory of dynamic critical phenomena, Rev. Mod. Phys. 49, 435 (1977).
- (65) T. Kasuya and A. Yanase, Anomalous transport phenomena in Eu-Chalcogenide alloys, Rev. Mod. Phys. 40, 684 (1968).
- (66) E. L. Nagaev, Spin Polaron Theory for Magnetic Semiconductors with Narrow Bands, Phys. Status Solidi B 65, 11 (1974).
- (67) A. Mauger, Magnetic polaron: Theory and experiment, Phys. Rev. B 27, 2308 (1983).
- (68) M. Daghofer, W. Koller, H. G. Evertz, and W. von der Linden, Polaronic aspects of the two-dimensional ferromagnetic Kondo model, J. Phys.: Condens. Matter 16, 5469 (2004).
- (69) V. M. Pereira, J. Lopes dos Santos, A. H. Castro Neto, Double Exchange Model at Low Densities: Magnetic Polarons and Coulomb Suppressed Phase Separation, arXiv:0804.3094 (2008).
- (70) J. Luo, and G.-W Chern, Dynamics of electronically phase-separated states in the double exchange model, Phys. Rev. B 103, 115137 (2021).
- (71) K. Binder and D. Stauffer, Theory for the Slowing Down of the Relaxation and Spinodal Decomposition of Binary Mixtures, Phys. Rev. Lett. 33, 1006 (1974).
- (72) K. Binder, Theory for the dynamics of “clusters.” II. Critical diffusion in binary systems and the kinetics of phase separation, Phys. Rev. B 15, 4425 (1977).
- (73) G. Kemeny and S. D. Mahanti, Theory of Rate Processes and the Compensation Rule, Proc. Natl. Acad. Sci. U.S.A. 72, 999 (1975).
- (74) N. L. Huang Liu and D. Emin, Double Exchange and Small-Polaron Hopping in Magnetic Semiconductors, Phys. Rev. Lett. 42, 71 (1979).
- (75) A. S. Ioselevich, Spin Polarons and Variable Range Hopping in Magnetically Disordered Systems, Phys. Rev. Lett. 71, 1067 (1993).
- (76) M. J. Calderon, L. Brey, and P. B. Littlewood, Stability and dynamics of free magnetic polarons, Phys. Rev. B 62, 3368 (2000).
- (77) L. G. L. Wegener and P. B. Littlewood, Fluctuation-induced hopping and spin-polaron transport, Phys. Rev. B 66, 224402 (2002).
- (78) T. Dietl and J. Spalek, Effect of thermodynamic fluctuations of magnetization on the bound magnetic polaron in dilute magnetic semiconductors, Phys. Rev. B 28, 1548 (1983).
- (79) L. R. Ram-Mohan and P. A. Wolff, Energetics of acceptor-bound magnetic polarons in diluted magnetic semiconductors, Phys. Rev. B 38, 1330 (1988).
- (80) A. Kaminski and S. Das Sarma, Magnetic and transport percolation in diluted magnetic semiconductors, Phys. Rev. B 68, 235210 (2003).
- (81) Z. B. Yan and J.-M. Liu, Anomalous phase separation in La0.225Pr0.4Ca0.375MnO3: consequence of temperature and magnetic-field cycles, Appl. Phys. A 104, 471 (2011).
- (82) T. Z. Ward, Z. Gai, H. W. Guo, L. F. Yin, and J. Shen, Dynamics of a first-order electronic phase transition in manganites, Phys. Rev. B 83, 125125 (2011).
- (83) W. Kundhikanjana, Z. Sheng, Y. Yang, K. Lai, E. Y. Ma, Y.-T. Cui, M. A. Kelly, M. Nakamura, M. Kawasaki, Y. Tokura, Q. Tang, K. Zhang, X. Li, and Z.-X. Shen, Phys. Rev. Lett. 115, 265701 (2015).