Arrow Relations in Lattices of Integer Partitions
Abstract
We give a complete characterisation of the single and double arrow relations of the standard context of the lattice of partitions of any positive integer under the dominance order, thereby addressing an open question of Ganter, 2022.
keywords:
Integer partition, Lattice, Dominance order, Arrow relation , Subdirect representationMSC:
[2020] 05A17, 11P81, 06B23, 06A07, 06B05, 06B15[TTU]organization=Department of Mathematics, Tafila Technical University, addressline=PO Box 179, postcode=66110, city=Tafila, country=Jordan \affiliation[TUWien]organization=Institute of Discrete Mathematics and Geometry, TU Wien, addressline=Wiedner Hauptstr. 8–10, postcode=1040, city=Vienna, country=Austria \affiliation[ITAM]organization=Department of Mathematics, ITAM, addressline=Río Hondo 1, city=Ciudad de México, postcode=CP 01080, country=Mexico
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/c45e8120-fb67-4543-ade3-d5b4fa10419a/x1.png)
For there are exactly one-generated arrow-closed -subcontexts of .
1 Introduction
Integer partitions have captivated mathematicians for centuries, starting as early as 1674 with Leibniz investigating the number of ways in which a natural number can be partitioned, that is, expressed as a sum of a non-increasing sequence of positive integer summands, see [14, p. 37]. Recursive presentations of , for example, following from Euler’s pentagonal number theorem, are well known, and the search for more explicit formulæ or approximations for culminated with the celebrated asymptotic expressions given by Hardy and Ramanujan [11] and with Rademacher’s representations by convergent series [16, 17].
The partitions of a given integer can be ordered by dominance, that is, by pointwise comparing their sequences of partial sums; the resulting ordered set carries the structure of a finite (hence complete) lattice , see [5]. The cardinalities of these lattices , that is, the numbers of (unrestricted) partitions of , grow fast as is increasing, the asymptotics shown in [11] to be for . Their size alone suggests an increasing complexity of the lattices for larger values of , wherefore splitting them up into smaller parts would be an important step towards enhancing our understanding of their structure. Fortunately, formal concept analysis and lattice theory offer techniques for this task in the form of subdirect representations of complete lattices, see, e.g., [10, Chapter 4]. These are embeddings of the given lattice into a direct product of smaller lattices, the subdirect factors, such that for each coordinate the corresponding projection is surjective. Of course, the subdirect factors may themselves be again subdirectly representable by even smaller factors, leading eventually to the concept of subdirect irreducibility: a lattice is subdirectly irreducible if in each subdirect representation at least one of the coordinate projections is not only surjective, but bijective, that is, an isomorphism onto the corresponding subdirect factor. The most efficient decompositions are hence given by representations using subdirectly irreducible factors. Such decompositions exist for any doubly founded (in particular any finite) complete lattice, such as , see [10, Theorem 18].
Formal concept analysis [10] offers a powerful framework to study complete lattices (up to isomorphism) as lattices of Galois closed sets of a suitable Galois connection between completely join-dense and completely meet-dense subsets of the lattice. This is part of the basic (or fundamental) theorem of formal concept analysis, see [10, Theorem 3]. The Galois connection is, up to isomorphism, induced by the order relation of the lattice between the elements of the two dense subsets, and this inducing binary relation is usually represented in a tabular form, called formal context. A canonically derived complete lattice, the concept lattice, is isomorphic (anti-isomorphic) to the lattice of Galois closed sets and serves to represent the given complete lattice . For finite lattices there is, up to isomorphism, a unique way of representation, namely through the so-called standard context, which is given by the order relation between all completely join-irreducible and complete meet-irreducible elements of , see [10, Proposition 12]. Formal concept analysis further defines binary relations and as certain subsets of the complement of the relation represented by a formal context, cf. [10, Definition 25]. These arrow relations appear in the ‘empty cells’ of the context table, and from them one may determine so-called one-generated arrow-closed subcontexts. This is done by adding attributes (resp. objects) pointed to by arrows ensuing from objects (resp. attributes) already appearing in the subcontext until the configuration stabilises. According to [10, Proposition 62] the one-generated arrow-closed subcontexts of the standard context of a finite lattice give subdirectly irreducible concept lattices, and taking sufficiently many of them, one may construct a subdirect decomposition of , see [10, Proposition 61]. A thorough understanding of the arrow relations in the standard context is hence a crucial step towards systematically obtaining subdirect decompositions of .
For the lattice of partitions of an integer , the sets of completely join-irreducible and completely meet-irreducible elements were described by Brylawski [5]; moreover, a very intuitive understanding of the covering relation in (and thus of the irreducibles) was later given in [13]. Recursive and non-recursive constructions of the standard contexts for increasing values of were studied in [3] and [9]. In [3], supported by [4], also the non-embeddability of into was argued, the proof of which was later refined in [8] for the symmetric case, extending previous work in [9, 2].
We have computationally determined the standard contexts of for parameters and our results show some curious patterns regarding the appearing one-generated arrow-closed subcontexts and the corresponding subdirectly irreducible factors, cf. [15] for a limited prospect. In order to be able, at a later stage, to substantiate these experimental results with rigid proofs, we aim in this paper at a complete characterisation of the arrow relations in for every , a question that was raised in [9, p. 40]. Our work has partially evolved in parallel with [7], which also mentions some of the more basic results of this article and has, for example, inspired the graphical presentation of including all arrows in Fig. 6. We first describe all double arrows of in Theorems 4.10, 4.17 and 4.23. After that we provide characterisations of all down-arrows that fail to be up-arrows in Theorems 5.2, 5.4 and 5.6, with a summary in Corollary 5.7; then we use partition conjugation to obtain the dual results, i.e., up-arrows without down-arrows, in Corollaries 5.5 and 5.8. Our knowledge regarding arrows is schematically summarised in Tables 1 and 2, and illustrated within the lattice in Fig. 6. As a proof of concept we finally show in Section 6 how our characterisations can be used to determine and count, for each , all one-generated arrow-closed one-by-one subcontexts of , which correspond to two-element subdirectly irreducible lattice factors of .
2 Preliminaries
2.1 Lattices and ordered sets
Throughout the text we write for the set of natural numbers, and we set . An ordered set is a pair where is a set and is a reflexive, antisymmetric and transitive binary relation on it. For we have if and only if , and we write for and as usual. Moreover, we say that is covered by in (or covers in ), symbolically , if and implies for each . The dual of is the ordered set . An order-isomorphism is given by a map such that for all the inequality in is equivalent to in . The ordered sets and are then said to be (order-)isomorphic. An order-antiisomorphism or dual isomorphism is an order isomorphism between and the dual of , and and are then called antiisomorphic or dually isomorphic; is self-dual (or autodual) if it is dually isomorphic to itself. Furthermore, we define as the principal down-set of , and as the principal up-set of .
A complete lattice is an ordered set where any subset has a greatest common lower bound (called infimum of ) and a least common upper bound (called supremum of ). It is customary to write for and for for finitely many elements . A subset is called (completely) join-dense in if for every there is a subset with ; is (completely) meet-dense in if for each there is some with . We say that is completely join-irreducible, denoted by -irreducible, if for all such that we necessarily have that . Dually, is completely meet-irreducible, or -irreducible, if for all such that we must have . For a finite non-empty lattice, it is sufficient to check this condition for the empty and all two-element subsets of . That is, for finite , an element is completely join-irreducible, if is not the minimum element of and for all the condition implies that or . This happens exactly if covers exactly one element below it, cf. [10, Proposition 2]. Dually, for a finite lattice, is completely meet-irreducible if it is not the top element of and for all with it follows that or . This condition is met precisely if has exactly one upper cover. For a complete lattice , we denote by and by the sets of all completely join-irreducible elements, and of all completely meet-irreducible elements of , respectively. Elements of are called doubly completely irreducible. In the lattice diagrams shown in Fig. 3 and 6, the completely irreducible elements have been highlighted using half or completely filled nodes.
A (complete) lattice is supremum-founded if, for any two from , the set contains a -minimal element; the dual property that for any in the set includes a -maximal element is called infimum-founded. The lattice is doubly founded if it is both supremum-founded and infimum-founded, see [10, p. 33]. Every chain-finite and hence every finite lattice is doubly founded, cf. [10, p. 33 et seqq., Fig. 1.11, p. 35].
2.2 Notions of formal concept analysis
Formal concept analysis (FCA) is a theoretical framework that harnesses the powers of general abstract Galois theory and the structure theory of complete lattices for data analysis and many other applications. At its core lies the notion of a Galois connection between (the power sets of) sets and , induced by a binary relation . This data is collected in a formal context , and the elements of and are given the interpretative names objects and attributes, respectively. The set is called the incidence relation, and is usually written as and read as ‘object has attribute ’. When and are finite, the context is often given as a cross table, where the objects form the rows, the attributes label the columns, and the crosses represent the characteristic function of on . Formal concept analysis extends the ‘prime notation’ for the Galois derivatives, which is common in classical Galois theory [12, Chapter V, Theorem 2.3 et seqq.], to general formal contexts . For every set of objects, assigns to it the set of attributes commonly shared by all objects of . Dually, for , the set contains exactly those objects possessing all the attributes in . A formal concept is a pair where the extent and the intent are sets that are mutually Galois closed: and . Intents of the form with are called object intents and are written as , for short; dually extents with are referred to as attribute extents. The equivalent conditions and define an order on the set of all formal concepts. becomes a complete lattice under this order, the concept lattice of . The fundamental theorem of formal concept analysis [10, Theorem 3] states that, in fact, every complete lattice is a concept lattice, up to isomorphism. Namely, if is a complete lattice, then . For finite lattices, which are always complete, this construction can be improved: , where is the standard context of [10, Proposition 12]. This applies to partition lattices in particular.
A central notion for this paper will be the arrow relations of a formal context, which fill up some of the empty cells in the cross table.
Definition 2.1 ([10, Definition 25]).
If is a context, an object, and an attribute, we write
Thus, if and only if is maximal among all object intents which do not contain ; dually we have if and only if is maximal among all attribute extents which do not contain .
We will now derive a useful characterisation of the arrow relations in standard contexts of doubly founded lattices.
Remark 2.2.
Consider the (standard) context of any complete lattice . Note that for and we have
This allows us to reformulate the definition of the arrow relations of in terms of the up-sets and down-sets of . Consider again and . Then we have
The following sufficient condition will lead to our main tool to establish arrow relations in standard contexts, in particular in .
Lemma 2.3.
Let be any complete lattice. Consider any with unique lower cover and with unique upper cover such that . Then in the context the following implications regarding arrow relations hold.
-
1.
If and there is a set such that , then .
-
2.
If and there is a set such that , then .
-
3.
If and (thus doubly completely irreducible), then .
-
4.
If and (thus doubly completely irreducible), then .
Proof.
We only prove statement (1), for (2) is completely dual; (3) follows by setting in (1), and (4) by setting in (2). By assumption we have . To show , according to Remark 2.2, we take any and assume . From the hypothesis of (1) we have with , thus we infer . Therefore, is a common lower bound of the elements of , hence . Since , we have , and, as , we infer , as it is required for . ∎
We shall need the following statement for infimum/supremum founded complete lattices, which can be read from [10, Fig. 1.11, p. 35]. For completeness, we provide a proof of this fundamental fact.
Lemma 2.4.
Let be a complete lattice with completely join-irreducibles and meet-irreducibles .
-
1.
If is infimum-founded, then is completely meet-dense.
-
2.
If is supremum-founded, then is completely join-dense.
Proof.
Part (2) follows from (1) by duality, thus we only show the latter. Consider any and define the subset . By its construction, satisfies . Let us assume for a contradiction that . By infimum-foundedness, there is hence a maximal element with the properties but . If , then and thus , being a contradiction. Therefore, we consider now . This means there must exist a subset with . It follows for each that , and, in fact, since . From the maximality of we infer now that fails, i.e., . Since this holds for all , we conclude , which is again a contradiction. Both contradictions show . ∎
For our purposes the following characterisation of the arrow relations is the most appropriate one since the lattice is finite, thus all its chains have only a finite number of elements, and it hence is doubly founded.
Proposition 2.5.
Let be a doubly founded complete lattice, e.g., a finite lattice. In the formal context the arrow relations can be characterised as follows (cf. Fig. 1). Consider any with unique lower cover and with unique upper cover . Then we have
-
1.
;
-
2.
.
Proof.
We shall only prove (1) since (2) is completely dual. To show ‘’ we use infimum-foundedness, which implies that the set is infimum-dense, see Lemma 2.4(1). This means that every can be written as for some set , namely, we may take . This is true, in particular, for all , hence , and Lemma 2.3(1) imply .
For the converse implication, let us assume that holds. This implies by Remark 2.2. By infimum-foundedness, there is that is maximal with respect to the property but . Let . For every we have , thus, in order to not violate the maximality of , the element must fail the property , that is, must hold. Therefore, is a common lower bound for the elements of , and hence we have . As , we know that , thus in fact, since all are above . Consequently, if for some subset , then , for otherwise and thus . This shows that . Since is supremum-founded, the set is supremum-dense, see Lemma 2.4(2). Thus we can write for some set . For every we have , wherefore . As and , we have , but certainly since . Thus, , i.e., . Now and Remark 2.2 imply . As was arbitrary, we conclude that . ∎

In Section 1 we explained that so-called arrow-closed subcontexts (of the standard context) are a key ingredient in order to obtain subdirect decompositions of finite lattices. We now provide concrete definitions as far as they are needed in this paper. A subcontext of a context is a context where , and . For a clarified context , that is, implies , and implies for all and , such a subcontext is arrow-closed if for all , , and the condition implies , and implies , see [10, Definition 46]. Note that the standard context of a finite lattice is always clarified and reduced [10, Proposition 12]. For a finite clarified context and and there is always a smallest arrow-closed subcontext of with and . It can be obtained by constructing the directed graph and considering the (not necessarily strongly) connected directed components of each . One then forms , which can be written in a unique way as with and . In particular, starting from and with (or dually from and with ), we get the one-generated arrow-closed subcontexts of , cf. [10, Section 4.1]. Note that if the context is reduced, we may always concentrate on using either only objects or attributes for constructing all its one-generated arrow-closed subcontexts.
2.3 Integer partitions
Our aim is to study the arrow relations of the standard context of the lattice of positive integer partitions, which is formed by the sets and . First, we define formally, what a partition and the dominance order is.
Definition 2.6.
An (ordered) partition of a number is an -tuple of natural numbers such that
If there is such that and for all , we also allow for the partition to be written in the form , where we have deleted the zeros at the end.
For example, is a partition of because and . By removing the trailing zeros we can represent it more compactly as . Graphically, we can illustrate a partition using a diagram drawn with small squares or ‘bricks’ arranged in a downward ladder shape (cf. Fig. 2), which is known as Ferrers diagram (usually Ferrers diagrams are drawn rotated clockwise by a degrees angle, but the chosen presentation is more useful to us, cf. Definition 2.9). Given a partition of , one obtains the conjugated or dual partition in the sense of [5] and [9] as where for all . The Ferrers diagram of can be seen from the diagram of by reading it by rows, from bottom to top. For instance, the partition of has the Ferrers diagram shown in Fig. 2, and its conjugate consists of bricks from the first row, bricks from the second to fourth, and brick from the fifth row. We thereby obtain the partition ; its Ferrers diagram is also depicted in Fig. 2.

We denote the set of all partitions of an integer by . From the construction of the conjugate via the Ferrers diagram, it is easy to see that holds for every . Therefore, partition conjugation is an involutive permutation of . One may order the set in different ways, for example, lexicographically, or pointwise. In this paper we are interested in the dominance order established by Brylawski [5].
Definition 2.7 ([5]).
Let and be two partitions of . We define the dominance order between and by setting if and only if holds for all .
Brylawski showed in [5, Proposition 2.2] that the set forms a lattice under the dominance order; further arguments for this were given in [6, Chapter 3] and [9, Section 2]. We denote by the lattice of all partitions of with the dominance order. It follows from [5, Proposition 2.8] that for partitions we have if and only if , that is, partition conjugation is an order-antiautomorphism of , making is self-dual.
Brylawski in [5, Proposition 2.3] characterised precisely two possibilities for downward movement along the covering relation of . These were later given a more intuitive geometric interpretation as transition rules by Latapy and Phan [13, Fig. 2, p. 1358], which we are going to follow in this article. The subsequent definitions are required for this.
Definition 2.8 (cf. [13, p. 1358]).
Let and . The partition has
-
1.
a cliff at if ;
-
2.
a slippery step at if there is such that and .
For example, the left Ferrers diagram in Fig. 2 has a cliff in the second position () and its dual has a cliff at and a slippery step (with ) at .
Definition 2.9 (Transition rules, cf. [5, 13]).
Let and .
-
1.
If for some with has a slippery step, then the brick at the slippery step may slip across the step to give . The subsequent illustration shows the application of such a transition to a slippery step at position (with ).
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/c45e8120-fb67-4543-ade3-d5b4fa10419a/x4.png)
-
2.
If for some with has a cliff, then the brick may fall from the cliff to give . Again, this is illustrated with a cliff of height at position .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/c45e8120-fb67-4543-ade3-d5b4fa10419a/x5.png)
Since the completely join-irreducible elements of have exactly one lower cover, according to Lemma 2.10, the partitions in are precisely those to which exactly one of the transition rules (1) or (2) applies. Therefore, the -irreducible partitions of can be characterised as those that have exactly one cliff (and no slippery step) or exactly one slippery step (and no cliff). Based on this Brylawski [5] split the set into four categories, extending this by conjugation to . To be able to express our results more compactly, in the following statement we have slightly modified the borders between the different types of irreducibles compared to [5], making them in particular disjoint.
Lemma 2.11 (cf. [5, Corollary 2.5]).
For the completely join-irreducible partitions of can be categorised into four types where , :
-
1.
for .
-
2.
for , .
-
3.
for .
-
4.
for , .
Also the -irreducible elements can be split into four groups where :
-
1.
for , , i.e., appears at least twice.
-
2.
for .
-
3.
for , , i.e., there are at least two s.
-
4.
for , , i.e., appears at least twice.
Observe that for each we have that if has type , then has type , and if has type , then has type . Therefore, the pairs of categories of completely irreducible elements of are completely dual to each other.
We mentioned that is a self-dual lattice under partition conjugation as involutive antiautomorphism, see [5, Proposition 2.8]. Using this fact we obtain the following simple but useful results to switch down and up-arrows.
Lemma 2.12.
Let and with duals and , respectively. Then it holds that
Proof.
The proof is a routine calculation exploiting the involutive antiautomorphism and the duality of the involved concepts. ∎
Similarly, one can prove the following lemma.
Lemma 2.13.
Let and with duals and , respectively. Then it holds that
Corollary 2.14.
Let and with duals and . Then it holds that
To obtain some familiarity with the completely irreducible elements of and the characterisations concerning the arrow relations given in Subsection 2.2, we consider the lattice shown in Fig. 3.
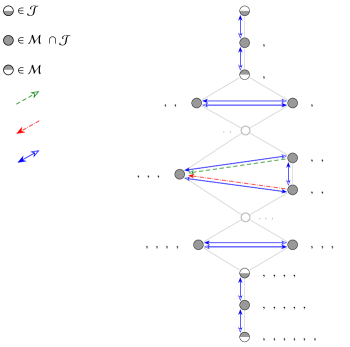
Example 2.15.
For we have from Lemma 2.11, cf. also [9, Proposition 2], that
The standard context is presented in Fig. 4. In both Fig. 4 and Fig. 3 we have indicated the arrow relations. Note that is the first case where single arrows appear. In fact there is exactly one single up-arrow and one single down-arrow in (where the respective opposite arrow is not present). We shall investigate this in the case of the down-arrow , shown in red in Fig. 3. The green up-arrow can then be explained by self-duality of using Lemma 2.13.
The partition is completely join-irreducible of type 3, while is completely meet-irreducible of type 4. To explain the down-arrow we shall use Proposition 2.5(1). Clearly, since the condition on the partial sums already fails with in the first position. The partition has a single cliff in the first position, from which a brick may fall to obtain the unique lower cover , cf. transition rule (2) and Fig. 3. Indeed, the lattice diagram confirms that , which can also be checked with Definition 2.7. Thus, by Proposition 2.5(1) we conclude . Moreover, that this arrow is not a double arrow, can also be explained with the help of Proposition 2.5. Namely, the unique upper cover of is since we may let the brick fall from the cliff in the second position of to get , cf. transition rule (2). Since , we have by Proposition 2.5(2).
The fact that there is a unique up-arrow (and a unique down-arrow) in that fails to be a double arrow, and why non-double arrows appear for for the first time, cannot be explained yet. This requires the characterisations in Sections 4 and 5.
| 1111111 | 211111 | 31111 | 2221 | 4111 | 322 | 331 | 511 | 43 | 52 | 61 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | |||||||||||
| 61 | |||||||||||
| 511 | |||||||||||
| 43 | |||||||||||
| 4111 | |||||||||||
| 331 | |||||||||||
| 322 | |||||||||||
| 31111 | |||||||||||
| 2221 | |||||||||||
| 22111 | |||||||||||
| 211111 |
3 General facts concerning the dominance order of integer partitions
We start with a lemma giving a simple sufficient condition for the dominance order among partitions.
Lemma 3.1.
Let be such that and let . If and for each with , while for each with , then .
Proof.
Let . If , then we have since for . Let now . If , we have since for . Otherwise, , and then we have as . ∎
As an easy corollary we have the situation where is not longer than and lies pointwise above .
Corollary 3.2.
Let and let . If for all , then .
Proof.
This follows from Lemma 3.1 for and . ∎
We may also have the somewhat opposite situation.
Corollary 3.3.
Let and let . If for all , then .
Proof.
For we have ; for we have . Hence holds for all . Thus we can apply Lemma 3.1 with and to get . ∎
We now introduce two natural geometric parameters of partitions.
Definition 3.4.
Let and .
-
1.
The height of is the value of its first entry, that is, .
-
2.
For we define to be the set of partitions of height at most .
-
3.
The length, synonymously width, of is the value of the first index such that , that is to say, .
-
4.
For we define to be the set of partitions of length (width) at most .
Lemma 3.5.
For the length of is the value of the largest index where , that is, .
Proof.
For we have , thus the maximum exists. We have , but, by maximality, . By antitonicity of we have for , thus is the first index where . Hence . ∎
Lemma 3.6.
For we have .
Proof.
Let and . If , then the minimality in the definition of length implies , thus . Conversely, if , then by the antitonicity of . ∎
For parameter values at least the concept of bounded height or width trivialises.
Lemma 3.7.
For such that , we have .
Proof.
For every we have , thus . If , then for every we would have , thus , which is a contradiction. Therefore, and by Lemma 3.6. ∎
In a similar fashion, for , we have since implies and thus . Therefore, for we may safely restrict our attention to parameter values to bound the height or width of a partition, which is, of course, clear from the geometric intuition via the Ferrers diagrams.
It is useful to observe that height and width are dual concepts with respect to partition conjugation.
Lemma 3.8.
For and we have and . Moreover, for we have exactly if .
Proof.
Let such that with for . From the definition of the conjugate we infer that the first entry of is , hence . The second equality follows from since . Finally, for we have if and only if , i.e., if and only if . ∎
We may also observe a basic necessary condition following from the dominance order: the dominated partition is always at least as long as the dominating one.
Lemma 3.9.
Let and . If , then .
Proof.
Assume . Then and . Since we have , whence . Thus , demonstrating . ∎
The following lemma describes the largest partition of a given least length .
Lemma 3.10.
Let with , let and set . If , then ; if , then .
Proof.
There is also a second largest partition of a given least length .
Corollary 3.11.
Let with . Then is of type 3 and has as its unique lower cover (the part appearing as of ); moreover any with satisfies .
Proof.
We can also identify a largest partition with a given height bound.
Lemma 3.12.
Let with and factorise where , . Then and every satisfies .
Proof.
Since , we have . If , then ; thus and therefore , i.e., . By antitonicity, for each we have , hence by Corollary 3.2. ∎
By duality we have a least partition of a given bounded width.
Lemma 3.13.
Let , and factorise where , . Then and every satisfies .
Proof.
Corollary 3.14.
4 Description of the double arrow relation in the standard context .
It is our aim to describe the arrow relations of the standard context . To do this, we start by giving a complete characterisation of all arrow relations of . To this end we present the following lemmata, which are true for in general. The first lemma is quite elementary, but useful, as it describes the top part of .
Lemma 4.1.
Let such that .
-
1.
Then and is its unique lower cover.
-
2.
If , then .
-
3.
If , then is the unique lower cover of . Hence the top part of has the shape depicted in Fig. 5.
Proof.
The top partition is completely join-irreducible, since ensures that it is of type 1. Letting a brick fall from the cliff, we obtain via transition rule (2) its unique lower cover . The latter partition is completely meet-irreducible, for it is of type 1 when and of type 2 if . This shows part (1).
Lemma 4.2.
For , we have , , and in .
Proof.
Lemma 4.3.
For we have , , and in .
Proof.
Applying Corollary 2.14 to Lemmata 4.2 and 4.3, respectively, we obtain two additional double arrows in .
Lemma 4.4.
In the standard context of the following facts hold:
-
1.
For we have , , and .
-
2.
For we have , , and .
Proof.
To prove the first statement, let and . Then and . From Lemma 4.2, we infer that , and . Applying Corollary 2.14 to the latter expression, we obtain , as required; moreover, using partition conjugation, it follows that and . Similarly, combining Corollary 2.14 with Lemma 4.3, one can prove the second statement. ∎
Proof.
If , then is of type 1 and has got a unique cliff at position , from which a brick may fall and produce , see transition rule (2). If , then has got no cliffs but a unique slippery step at position . Therefore its unique lower cover is obtained by applying transition rule (1) to , that is, by letting a brick slip across the step at position to obtain . ∎
Lemma 4.6.
Let with ; set . Then we have of type 3, having as its unique upper cover, where the part only appears for , that is, , or and .
Proof.
As , we have of type 3. Since partition conjugation is an order-antiautomorphism of , the unique upper cover of can be obtained by conjugating the unique lower cover of . Since , the join-irreducible has got a unique cliff in its first position and no slippery step. Applying transition rule (2), we obtain its lower cover , which we can conjugate to obtain , the unique upper cover of . Knowing that there is a unique upper cover of from , the fact that looks as given before can also be verified by checking that is a lower cover of . Indeed, by simply applying transition rule (1) to the slippery step in the second position of when , or by applying transition rule (2) to the cliff in the second position of when and , we see that we get . ∎
Lemma 4.7.
Let , , and set . Then, for and we have ; moreover, .
Proof.
Clearly, the statement about and will follow from the one about and by Corollary 2.14. We therefore let with , and consider and . We have that because the partial sums up to index exhibit the relation . From Lemma 4.5 we know that has the unique lower cover ; from Lemma 4.6 we infer that has the unique upper cover .
First we prove that . We shall verify that by comparing the sequences of partial sums. For the sum up to the index we have by hypothesis. The sequence of partial sums of continues after with the terms . If , then the partial sum of up to index yields since . For indices both partial sums coincide with the value , until they reach the common maximum . Hence , and thus we may rely on Proposition 2.5(2) to show that .
Our next goal is to demonstrate that . For this we first show that by comparing the sequences of partial sums. For we obtain the sequence , while for it begins with and then continues with . For we have , and for indices both sequences coincide. Thus we have established , and hence Proposition 2.5(1) yields . ∎
Corollary 4.8.
Let , and set . Under these assumptions we have the two double arrow relations and .
Proof.
Fig. 4 shows the arrow relations of . Using Lemmata 4.2, 4.3 and 4.4, one can verify some of those:
| by Lemma 4.2 | by Lemma 4.3 | ||||||
| by Lemma 4.4 | by Lemma 4.4 |
All remaining double arrows of will be collected in the following remark, whose proof will illustrate several similar cases. In subsequent sections we introduce parameters to prove general statements and avoid such repetitions.
Remark 4.9.
Proof.
First, we verify a). Using the definition or inspecting Fig. 4, we get . Clearly, we have of type 3 and of type 2. Applying transition rule (2), the unique lower cover of is , which lies below . Hence Proposition 2.5(1) entails . To prove the relation , we note that the unique upper cover of is , which is the conjugate of the unique lower cover of , as explained in the proof of Lemma 4.6. Using the definition or inspecting Fig. 3, we observe . Then, as , Proposition 2.5(2) entails . We conclude that . Furthermore, since and , Corollary 2.14 gives the second double arrow in a), namely .
Next, we verify b). We repeat the arguments of a) and get with of type 3 and of type 2. Applying the same transition rules yields the unique lower cover and the unique upper cover . Also, the definition or inspecting Fig. 3 gives and . Therefore, since , Proposition 2.5 confirms . Furthermore, since and , Corollary 2.14 gives the second double arrow in b), namely .
4.1 Double arrows involving completely join-irreducibles of type 1 or 2
The subsequent theorem exhibits the following one-to-one relation: For every of type 1 or 2 there is exactly one such that . This unique has the form and for each of this shape there is exactly one of type 1 or 2 such that , namely .
Theorem 4.10.
Proof.
First, we consider the cases and individually. If , then we get , , hence (since ), and thus is of type 1 and . Hence the case was proved in Lemma 4.2. Moreover, if , then , i.e., , and is of type 2, wherefore this case was proved in Corollary 4.8.
Accordingly, it remains to show the statement for and . Then, as , we have because it is completely join-irreducible of type 1 (for ) and of type 2 (for ). Moreover, is of type 3 as due to and . Since is ‘shorter’ than , Lemma 3.9 asserts .
The unique lower cover of is , where the middle part only appears for . The partition is obtained by letting a brick fall from the cliff in the last position of (transition rule (2)). The unique upper cover of is , where, to obtain , we can let a brick fall from the cliff in the second position if , or let a brick slip across the slippery step if and the part is present. We shall prove that and ; then Proposition 2.5 will entail . By Lemma 3.10, is the largest partition of length ; hence . By Corollary 3.11, is the second largest partition of length , while, according to Lemma 3.10, is the largest. Since we have ; hence .
Lemma 4.11.
Let , be such that and set . If satisfies , then and the final entry of is .
Proof.
Under the given conditions, is completely join-irreducible of type 1 or 2, see Corollary 3.14. Let us assume that with . If , then , and thus Corollary 3.14 shows that , in contradiction to . Therefore, . The unique lower cover of satisfies . By Proposition 2.5(1), our assumption entails , wherefore is impossible by Lemma 3.9. Consequently, we conclude and hence , which also yields . Moreover, we have due to and ; thus , and therefore . ∎
Lemma 4.12.
Proof.
We assume that the given and satisfy . From Lemma 4.11 we know that and that . If is of type 1, 3, or 2 with , then is of the form with . Since its total sum amounts to , we have and is exactly of the form described in Theorem 4.10.
Finally, let us consider the case that is of type 2 with and has the form where and . Thus, if , then by Corollary 3.2, which contradicts . Therefore, we know that . Hence the unique lower cover of is obtained by letting a brick fall from the cliff in position , and thus with its first entry satisfying . Now and Proposition 2.5(1) entail , hence . Using this, we can finally estimate , which implies the contradiction . Therefore, the third case, where is of type 2 with , is impossible and the lemma has been shown. ∎
Proof.
First, we prove that of type 2, of type 2 and is impossible. Note that any arrow relation for of type 2 requires , because otherwise Corollary 3.14 yields and , which by Proposition 2.5 prevents any arrow. Therefore, we have and thus . The proof of Lemma 4.12 confirms that a relation with of type 2 with is impossible.
The following simple observation will be used more than once.
Lemma 4.14.
Let be such that and and set . In we have the covering relation . Furthermore, is the unique upper cover of .
Proof.
If , we apply transition rule (2) to the cliff in the second position of , yielding . If , we apply rule (1) to the slippery step in the second position of . In both cases the result is , and thus Lemma 2.10 yields . Moreover, is completely meet-irreducible of type 3 (if ) and 4 (if ), wherefore is the unique upper cover. ∎
Lemma 4.15.
Let , be such that and set . If is of type 4 and satisfies , then fails.
Proof.
We assume that of type 4 satisfies . Then Lemma 4.11 implies that and that the last non-zero entry of equals . Hence if , then , which is forbidden for of type 4; we therefore know and actually by Lemma 4.11. We thus have with and . By Lemma 4.14, the unique upper cover of is , where the part appears as of . Since , we have by Lemma 3.9. According to Proposition 2.5(2), this renders impossible. ∎
The following result shows that Theorem 4.10 indeed describes all double arrows involving partitions of type 1 or 2.
Corollary 4.16.
Let , be such that and set . Every in relation is of the form described in Theorem 4.10.
4.2 Double arrows involving completely join-irreducibles of type 3
The following result exhibits further one-to-one double arrows , originating from any of type 3, and covering two exceptional cases. These are and , which are also discussed in Theorem 4.10.
Theorem 4.17.
Let be such that and where . We have , , and .
Moreover, if is of type 3, and holds, then must be of the shape as described before.
Proof.
Lemma 4.18.
Let be such that and set . If satisfies or , then .
Proof.
Corollary 4.19.
Proof.
Let be of type 3, that is with . Suppose that is of type 3, with or . Then with , and Lemma 4.18 implies and . Then the unique upper cover of is by Lemma 4.14. Hence , and Proposition 2.5(2) proves . Therefore . Now, the unique lower cover of is since . Then, we get , and thus Lemma 3.9 yields , contradicting by Proposition 2.5(1). ∎
Proof.
By Lemma 4.20, with of type 3 is impossible. Therefore, aiming for a contradiction, we assume that with of type 4. Then , and, by Lemma 4.18, we must have , i.e., where , and . Now, by Lemma 4.14, the upper cover of is , implying that . Therefore, , and consequently Proposition 2.5(2) excludes , in contradiction to . ∎
We can now finally observe that for of type 3 all double arrows were characterised in the first part of Theorem 4.17.
Corollary 4.22.
Let be such that and set . If satisfies , then is of the form as described in Theorem 4.17.
4.3 Double arrows involving completely join-irreducibles of type 4
Theorem 4.23.
Let , with and set . Now, choose , set and decompose with and . Then we have and of type 4 and .
Moreover, if is of type 4, and holds, then must be of the shape as described before.
Note that if is of type 4, then its dual partition is of type 4. Since Theorem 4.23 exhibits double arrow relationships between -irreducibles of type 4 and -irreducibles of type 4, the dual result of Theorem 4.23 under partition conjugation is contained within the original statement.
Moreover, Theorem 4.23 represents a one-to-many double arrow relationship, as can be observed from the example and where in both cases.
Proof.
First, we check that is of type 4 by verifying the inequalities and . We have since and , hence . For the other inequality we see that
where we have used that and . Thus, due to , we have , i.e., or . Hence is completely meet-irreducible of type 4. We also observe that is completely join-irreducible of type 4 since , and .
We have that because summing up the first entries of gives , which is larger than the corresponding value of , namely .
The unique lower cover of is , in which the part only appears for and only appears for . We obtain from by letting the brick in position fall from the cliff (transition rule (2)). Since , Lemma 3.1 with position and common sum directly implies . Therefore, Proposition 2.5(1) yields .
The following lemma in particular applies to completely join-irreducible elements of any type.
Lemma 4.24.
Let , and set . For and we have that implies .
Proof.
As , we have . There are with such that decomposes modulo as . As , we have , hence , i.e., . If , then and so ; otherwise . In both cases lies pointwise below . Now we have , and since with and , Lemma 3.13 implies . Hence we obtain for each with . If , then for each we have , and thus for any . Therefore, we conclude . ∎
Also the following lemma applies to any possible completely join-irreducible partition .
Lemma 4.25.
Let , with and set . If and , we additionally assume . Define and let be such that . Then .
Proof.
Let and assume . By Lemma 4.24, we must have because would entail , in contradiction to , see Proposition 2.5(1). On the other hand, we know from Proposition 2.5(1), that holds for the unique lower cover of , wherefore, we have . It only remains to observe that the latter sum indeed amounts to . We do this by considering three different cases: if , then , and . Next, if and , then , , and , and . The last case is and . Now is of the general form given in the statement and its unique lover cover is where the part only appears for and only for . Again, we get as . Therefore, we conclude that in all cases mentioned in the lemma the inequalities , i.e., , hold. ∎
Lemma 4.26.
Let , be such that , and set . Consider and any . If , then there are such that , , , , and . In particular, is of type 4. Moreover, if is such that , then , and fails.
Proof.
Suppose that ; then Proposition 2.5(1) entails for the unique lower cover of . Since , we thus have . If were of type 1 or 2, then for some , and thus would be the largest member of (see Lemma 3.12). Since , we would have , hence , contradicting by Proposition 2.5(1).
Therefore, is neither of type 1 nor 2, thus is must be of type 3 or 4. Hence it has the form where and . The total sum of being , we note that . If , then and hence by Corollary 3.2. By Proposition 2.5(1), this is in contradiction to , wherefore . As , Lemma 4.25 shows that the partial sum of up to position is . Since , we must have , hence and . Since , Proposition 2.5(1) yields for the unique lower cover of . Thus, , i.e., . Since , we have . With the intent to derive a contradiction, we assume that , hence . We know that , thus and Lemma 3.9 imply ; hence our assumption and Lemma 3.10 yield , contradicting by Proposition 2.5(1). Therefore, , and has type 4. Moreover, from we infer
From we infer that and hence . If we now additionally assume that , then , and we may cancel this common summand from both sides of the equation, leading to , or , i.e., . Consequently, we have , being of type 4 with , and thus the unique upper cover of is , see Lemma 4.14. Therefore, we obtain and hence . By Proposition 2.5(2) fails. ∎
The following corollary shows that all double arrows involving of type 4 were described in Theorem 4.23. In particular, dualising the statements of Theorem 4.23 yields double arrow relations that are already described as a part of that theorem.
Corollary 4.27.
Proof.
We summarise our understanding of the double arrow relation in Table 1.
5 Results regarding single arrows
Since results for up-arrows can be deduced from down-arrows by partition conjugation and Lemma 2.13, we focus here on the complete description of the relation where and . As, by definition, implies , the results from Section 4 yield part of the description of the down-arrows. Subsequently, we need to concentrate on finding the remaining ‘single’ down-arrows, where but not . Our strategy will be to derive necessary conditions that follow from , to isolate the cases that were already covered in Section 4, and then to prove in the remaining cases from a subset of the necessary conditions that actually holds. We organise our investigations according to the different types may have.
For of type 1 or 2, Lemma 4.12 confirms that all down-arrows involving of types 1, 2 and 3 are contained in Theorem 4.10 and hence are double arrows. Therefore, we here only discuss down-arrows between of type 1 or 2 and of type 4. In this respect, Lemma 5.1 gives necessary conditions for the down-arrows; these necessary conditions will be shown to be sufficient in Theorem 5.2.
Lemma 5.1.
Proof.
Lemma 4.11 yields and that with and must end with . If , then this implies the contradiction , hence and thus by Lemma 4.11. Therefore, with , and since two values must appear, we obtain . Finally, we prove in two steps. First, we cannot have because under this assumption the partial sum of exceeds as . Thus, we have , i.e., , wherefore has a cliff in position , and by transition rule (2) the unique lower cover of is . Our assumption and Proposition 2.5(1) imply , hence we get , i.e., . Therefore, , finishing the proof. ∎
We now show that the conditions in Lemma 5.1 are sufficient for a down-arrow between of type 1 or 2 and of type 4, and that this arrow is not a double arrow.
Theorem 5.2.
Proof.
As we have that is of type 1 (if ) or 2 (if ). In Lemma 5.1 we saw that the unique lower cover of is . Since is shorter than , Lemma 3.9 yields . Next, we verify that is of type 4. First, given , we get that appears times. Next, we have since . Furthermore, from , and , we get , hence and is of type 4.
We are now starting to deal with for partitions of type 3. Theorem 4.17 and Corollary 4.19 cover the case when is of type 1 or 2. Here the down-arrow automatically is a double arrow. We therefore focus in the subsequent two results on of types 3 or 4. As done earlier we first derive necessary conditions from , which we then prove to be sufficient for a down-arrow that is not a double arrow.
Lemma 5.3.
Proof.
Theorem 5.4.
Observe that satisfies and . Hence Theorem 5.4 represents a one-to-many relationship. The number of distinct such that with a fixed grows with , e.g., if and , then for .
Proof.
First, we check that . By the definition of and , we have . Moreover, since , and , we obtain , which yields , i.e., . Thus, is completely meet-irreducible of type 4. We have as the first entries are . Since and , we observe that is completely join-irreducible of type 3 and that its unique lower cover is , which is obtained from by letting the brick in position fall from the cliff (transition rule (2)). Since and for , we obtain from Corollary 3.2. Thus, Proposition 2.5(1) confirms .
Corollary 4.19, Lemma 5.3 and Theorem 5.4 characterise all in relation with of type 3. Dualising Theorem 5.4 with the help of Lemmata 2.12 and 2.13 yields the following result.
Corollary 5.5.
It remains to discuss of type 4 where , , , and . Then we may deduce via Lemma 4.26 from for some that is of type 4 with , , , and . In this situation there are two cases: the first is that , in which Theorem 4.23 entails that is not only present, but that it is actually a double arrow. The second case is that , in which Lemma 4.26 implies , and that is impossible. Under these necessary conditions, the following result shows that is actually present (and clearly is not a double arrow).
Theorem 5.6.
Proof.
Since and , we have and . Moreover, we observe
whence . We check that as and . Hence, as and , we conclude that is of type 4. Since , and , it is also clear that of type 4. Furthermore, we have because the partial sums up to position satisfy . Applying transition rule (2) to the cliff in position of , we obtain its unique lower cover as , with appearing for . Note that the partial sums of both and reach at position . Therefore, as for , Lemma 3.1 with yields , and hence Proposition 2.5(1) implies .
Finally, since , , , and , Lemma 4.26 implies that is impossible. ∎
Corollary 5.7.
Let , with and ; set . Furthermore, choose with and set . Then we have , of type 4 with , and and satisfy but not .
Observe that satisfies and . Hence Corollary 5.7 represents a one-to-many relationship. Similarly to Theorem 5.4 the number of distinct such that with a fixed grows with , e.g., if and , then for .
Proof.
For the hypotheses and partitions and simplify to those of Theorem 5.2, since is equivalent to . Therefore, Theorem 5.2 proves but not .
For the hypotheses restate those of Theorem 5.6. Hence but not . ∎
Corollary 5.8.
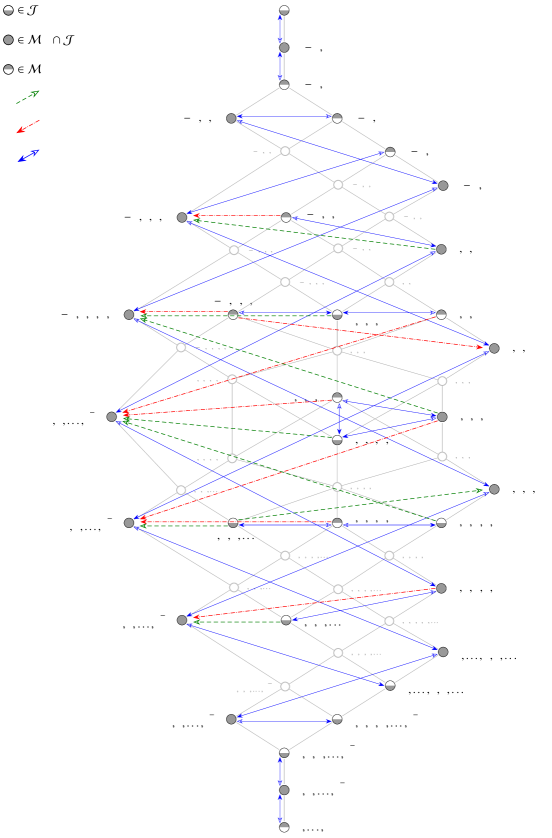
We finally collect our knowledge about single arrows in Table 2. Moreover, with Fig. 6 depicting we aim to illustrate for the concrete case the various up, down and double arrow relations appearing in Tables 1 and 2.
| Result | Arrow | ||
|---|---|---|---|
| Theorem 5.4: | , , | ||
| Corollary 5.5: | , | ||
| Corollary 5.7: | , , | ||
| Corollary 5.8: |
We are now ready to discuss once more the single arrows in Example 2.15. The first where a single arrow appears in is . This is justified by our Theorem 5.4 since its assumptions require and , which gives . Moreover, Corollary 5.7 can only be applied for as it requires and , wherefore as . The dual results Corollary 5.5 and Corollary 5.8 are also valid for and , respectively.
Finally, for , if , then the restriction of Theorem 5.4 shows that , wherefore the partition satisfies with a unique . Hence, considering the dual arrow (justified by Corollary 5.5) there exist exactly two single-directional arrows in . These two arrows are the ones exhibited in Example 2.15 and illustrated in Fig. 3.
6 One-generated arrow-closed one-by-one subcontexts
We have implemented a brute-force algorithm (based on Definition 2.1) and an algorithm that uses the information given in Tables 1 and 2 to discover one-generated arrow-closed subcontexts of . Both implementations suggest that as of there exist exactly arrow-closed -subcontexts. To demonstrate the applicability of our general characterisations of the arrow relations in to the original problem of describing one-generated arrow-closed subcontexts (with the ultimate intent to obtain subdirect decompositions), we prove in this section that is the correct number of one-generated arrow-closed subcontexts of format .
Lemma 6.1.
Let be such that . Then generates the following arrow-closed -subcontext of with .
Proof.
Under the given conditions, is of type 1 or 2, see Corollary 3.14. We apply the procedure to arrow-close the context. The summarising Tables 1 and 2 show that by Theorem 4.10 (in fact ) and that this is the only one in relation . It remains to justify that no other partition satisfies for the given . Considering the summarising Tables 1 and 2 and the shape of , we realise that Theorem 4.10 describes all such that (the cases and can be handled by Theorem 4.17, as well, and yield the same as Theorem 4.10). Therefore, the partitions satisfying are exclusively of type 1 or 2 and have length . Then the uniqueness of the decomposition modulo where entails that coincides with the given . ∎
We now dualise Lemma 6.1 and thereby cover in particular all arrow-closed subcontexts of generated by any of type 3.
Lemma 6.2.
Let , with , set and decompose with such that . Then the partition generates the following arrow-closed -subcontext of with .
Proof.
This result is the exact dual of Lemma 6.1. An explicit proof can be obtained by dualising the argument of Lemma 6.1 where applications of Theorem 4.10 need to be replaced by Theorem 4.17 and types 1 and 2 become types 1 and 2. The lemma can also be proved directly using the arrow-closing procedure and the tables. In fact, if is of type 1 or 2, then Tables 1 and 2 confirm that Theorem 4.17 describes all such that (there are (only) two cases, and , which are handled by Theorem 4.10 and 4.17 simultaneously). ∎
Proposition 6.3.
For , there are exactly one-generated arrow-closed -subcontexts in .
Proof.
Considering Lemmata 6.1 and 6.2 we may count the arrow-closed -subcontexts. First, Lemma 6.2 allows to choose the parameter . Hence, choices are available, and each leads to a distinct and thus a distinct -subcontext. Moreover, Lemma 6.1 is exactly the dual of Lemma 6.2, wherefore we have once more choices, and thus distinct subcontexts, available. The only that are captured by Lemma 6.1 and 6.2 at the same time are either , or have length at least two and thus, according to Lemma 6.2, end with , have height at least and satisfy . Now, according to the shapes of considered in Lemma 6.1, the height must be equal to since ends in , and so . We therefore have to reduce the sum by and thus have at least distinct arrow-closed -subcontexts generated by of types 1, 2 or 3.
Finally, if is of type 4 with and , then Theorem 4.23 exhibits some of type 4 with , and Corollary 5.5 yields some of type 3 with . Since the type classes are disjoint, we therefore have two distinct such that , and hence arrow-closed subcontexts generated by of type 4 cannot be of format . Consequently, the subcontexts shown in Lemmata 6.1 and 6.2 are the only ones of this shape. ∎
7 Conclusion
| Arrow vs. type | For | First example | Result | ||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | Theorem 4.10 | |||||
| 2 | 1 | Theorem 4.10 | |||||
| 1 | 2 | Theorem 4.10 | |||||
| 1 | 3 | Theorem 4.10 | |||||
| 2 | 3 | Theorem 4.10 | |||||
| 3 | 1 | Theorem 4.17 | |||||
| 3 | 2 | Theorem 4.17 | |||||
| 4 | 4 | Theorem 4.23 | |||||
| 3 | 4 | Theorem 5.4 | |||||
| 1 | 4 | Corollary 5.7 | |||||
| 2 | 4 | Corollary 5.7 | |||||
| 4 | 4 | Corollary 5.7 | |||||
| 4 | 3 | Corollary 5.5 | |||||
| 4 | 1 | Corollary 5.8 | |||||
| 4 | 2 | Corollary 5.8 | |||||
| 4 | 4 | Corollary 5.8 | |||||
In this paper, for every , we characterised all arrow relations appearing in the standard context of the lattice of partitions of under the dominance order. When looking at Tables 1 and 2, collecting our results, some curious patterns with respect to the three arrow shapes and the partition types connected by arrows of a specific form arise. These will be summarised subsequently; more detailed information for which values of these patterns appear and which result justifies them, can seen from Table 3. Inspecting Table 3, we note that all of these connections can be observed in as soon as . The following patterns caught our eye:
-
1.
If is of type 1, 2 or 3 and satisfies , then is not of type 4 and is unique. Conversely, if is of types 1, 2 or 3 and with , then is not of type 4 and it is also unique. Therefore, the double arrows establish a one-to-one relationship between elements of the union of the type classes 1–3 and the union of the classes 1–3.
More specifically, if is of type 1 or 2 such that , and , then Theorem 4.10 implies that is of type 3, and the whole class of type 3 partitions is exhausted by those . The two exceptional double arrow relations are with of type 1 and of type 2 (or 1 for ), and with of type 2 and of type 1. In particular, of type 1 is never -connected to of type 1 (or 4) when , and of type 2 is never -connected to of type 2 (or 4). In fact, of type 2 is never connected via any kind of arrow to of type 2, as shown in Corollary 4.13. Having observed the bijective correspondence given by the double arrow relation, this leaves that the of type 3 correspond in a one-to-one way to the of types 1 or 2. This can also be verified directly using Theorem 4.17 for parameters . Note also that of type 3 is not even or -related to of type 3, as shown in Lemma 4.20.
-
2.
If , and , then is of type 4 if and only if is of type 4, see Table 1. However, this correspondence is not unique because for sufficiently large values of , and , Theorem 4.23 allows for several choices of the parameter determining distinct shapes of of type 4. Dually, a given of type 4 may only be double arrow related to of type 4, and these may not be unique.
-
3.
Every up-arrow originating in of type 1, 2 or 3 is actually a double arrow described in Table 1. This is so because Table 2 does not contain any up-arrows of such type. Conversely, every down-arrow connecting with some of type 1, 2 or 3 is necessarily a double arrow. This implies that of types 1, 2 or 3 receive down-arrows from that are not double-arrows only if is of type 4. Dually, are in relation and with of types 1, 2 or 3 only if is of type 4.
On the other hand, of type 4 exhibit up-arrows to of all four types that fail to be double arrows; likewise of type 4 satisfy but with of all four types. All of these single directional arrow relationships are in general not one-to-one as Theorem 5.4 and Corollary 5.7 exhibit a flexible parameter range for with fixed and sufficiently large and . This happens as of for Theorem 5.4 and as of for Corollary 5.7.
As a side-product of Proposition 6.3, we discovered that the number of ways a natural number can be decomposed yielding partitions of type 1 or 2 is exactly , for this is the same as the number of partitions of of the shape with . This is an example of a bijective proof as they are typical for counting the number of restricted partitions in the combinatorial theory of integer partitions, see, e.g., [1, Section 2.2].
Finally, in order to demonstrate the applicability of our general descriptions, we started by characterising all one-generated arrow-closed subcontexts of of format . We determined that their number is exactly , see Proposition 6.3. Working on this we observed that also the characterisation of other arrow-closed subcontexts of small shape seems to be within reach of our results. We leave the complete description of the one-generated arrow-closed subcontexts of as a task for future investigation.
References
- [1] G. E. Andrews, K. Eriksson, Integer partitions, Cambridge University Press, Cambridge, 2004. doi:10.1017/CBO9781139167239.
- [2] M. Behrisch, Symmetric embeddings between standard contexts of lattices of integer partitions [dataset], Zenodo (Dec. 2021). doi:10.5281/zenodo.5810903.
- [3] M. Behrisch, A. Chavarri Villarello, E. Vargas-García, Representing partition lattices through FCA, in: A. Braud, A. Buzmakov, T. Hanika, F. Le Ber (Eds.), Formal Concept Analysis – 16th International Conference, ICFCA 2021, Strasbourg, France, June 29 – July 2, 2021, Proceedings, Vol. 12733 of Lecture Notes in Artificial Intelligence, Springer, Cham, 2021, pp. 3–19. doi:10.1007/978-3-030-77867-5_1.
- [4] M. Behrisch, E. Vargas-García, Non-embeddability of standard contexts of lattices of integer partitions [dataset], Zenodo (Dec. 2021). doi:10.5281/zenodo.5805981.
- [5] T. Brylawski, The lattice of integer partitions, Discrete Math. 6 (3) (1973) 201–219. doi:10.1016/0012-365X(73)90094-0.
- [6] A. Chavarri Villarello, El retículo de particiones de enteros positivos y su contexto estándar, Undergraduate honors thesis, ITAM, Río Hondo 1, Ciudad de México (Jul. 2020).
- [7] S. A. Díaz Miranda, Retículos de números naturales y sus relaciones de flechas, Undergraduate honors thesis, ITAM, Río Hondo 1, Ciudad de México (Mar. 2024).
- [8] L. A. Franco Solorio, Encajes entre contextos estándar de los retículos de particiones de números enteros, Undergraduate honors thesis, ITAM, Río Hondo 1, Ciudad de México (Mar. 2022).
- [9] B. Ganter, Notes on integer partitions, International Journal of Approximate Reasoning 142 (2022) 31–40. doi:10.1016/j.ijar.2021.11.004.
- [10] B. Ganter, R. Wille, Formal concept analysis. Mathematical foundations, Springer, Berlin, 1999, translated from the 1996 German original by Cornelia Franzke. doi:10.1007/978-3-642-59830-2.
- [11] G. H. Hardy, S. Ramanujan, Asymptotic formulæ in combinatory analysis, Proc. London Math. Soc. (2) 17 (1) (1918) 75–115. doi:10.1112/plms/s2-17.1.75.
- [12] T. W. Hungerford, Algebra, Vol. 73 of Graduate Texts in Mathematics, Springer, New York, NY, 2011, reprint of the 1974 original. doi:10.1007/978-1-4612-6101-8.
- [13] M. Latapy, T. H. D. Phan, The lattice of integer partitions and its infinite extension, Discrete Math. 309 (6) (2009) 1357–1367. doi:10.1016/j.disc.2008.02.002.
-
[14]
D. Mahnke, Leibniz auf der
Suche nach einer allgemeinen Primzahlgleichung, Bibl.
Math. (3) XIII (1912–1913) 29–61.
URL https://www.ophen.org/pub-102519 - [15] A. Páramo Pitol, Factores subdirectamente irreducibles de pequeños retículos de particiones, Undergraduate honors thesis, ITAM, Río Hondo 1, Ciudad de México (Jul. 2022).
- [16] H. Rademacher, On the partition function , Proc. London Math. Soc. (2) 43 (4) (1937) 241–254. doi:10.1112/plms/s2-43.4.241.
- [17] H. Rademacher, On the expansion of the partition function in a series, Ann. of Math. (2) 44 (3) (1943) 416–422. doi:10.2307/1968973.