Artificial spin-orbit coupling in ultra-cold Fermi superfluids
Abstract
The control and understanding of interactions in many particle systems has been a major challenge in contemporary science, from atomic to condensed matter and astrophysics. One of the most intriguing types of interactions is the so-called spin-orbit coupling - the coupling between the spin (rotation) of a particle and its momentum (orbital motion), which is omnipresent both in the macroscopic and microscopic world. In astrophysics, the spin-orbit coupling is responsible for the synchronization of the rotation (spinning) of the Moon and its orbit around Earth, such that we can only see one face of our natural satellite. In atomic physics, the spin-orbit coupling of electrons orbiting around the nucleus gives rise to the atom’s fine structure (small shifts in its energy levels). In condensed matter physics, spin-orbit effects are responsible for exotic electronic phenomena in semiconductors (topological insulators) and in superconductors without inversion symmetry. Although spin-orbit coupling is ubiquitous in nature, it was not possible to control it in any area of physics, until it was demonstrated in a breakthrough experiment spielman-2011 that the spin of an atom could be coupled to its center-of-mass motion by dressing two atomic spin states with a pair of laser beams. This unprecedented engineered spin-orbit coupling was produced in ultra-cold bosonic atoms, but can also be created for ultra-cold fermionic atoms spielman-2011 ; sinova-2009 ; chapman-sademelo-2011 . In anticipation of experiments, we develop a theory for interacting fermions in the presence of spin-orbit coupling and Zeeman fields, and show that many new superfluids phases, which are topological in nature, emerge. Depending on values of spin-orbit coupling, Zeeman fields, and interactions, initially gapped -wave superfluids acquire -wave, -wave, -wave and higher angular momentum components, which produce zeros in the excitation spectrum, rendering the superfluid gapless. Several multi-critical points, which separate topological superfluid phases from normal or non-uniform, are accessible depending on spin-orbit coupling, Zeeman fields or interactions, setting the stage for the study of tunable topological superfluids.
pacs:
03.75.Ss, 67.85.Lm, 67.85.-dThe effects of spin-orbit coupling in few body systems like the Earth-Moon complex in astrophysics or the electron spin and its orbital motion around the nucleus in isolated atoms of atomic physics are reasonably well understood due to the simplificity of these systems. However, in the setting of many identical particles, spin-orbit effects have revealed quite interesting surprises recently running from topological insulators in semiconductors kane-2005 to exotic superconductivity gorkov-2001 and non-equillibrium effects galitski-2007 depending on the precise form of the spin-orbit coupling. In atomic physics the coupling arises from the interaction of the magnetic moment of the electron and a magnetic field, present in the frame of electron, due to the electric field of the nucleus. Similarly in condensed matter physics, the coupling arises from the magnetic moment of electrons, which move in the background of ions. In the electron’s reference frame, these ions are responsible for a magnetic field , which depends on the electron’s momentum and couple to electron’s spin. The resulting spin-orbit coupling has the form where represents the Pauli matrices and describes the -th component of the effective magnetic field vector . For some materials can take the Dresselhaus dresselhaus-1955 form the Rashba rashba-1984 form or more generally a linear combination of the two In all these situations the type of spin-orbit coupling can not be changed arbitrarily and the magnitude can not be tuned from weak to strong, making the experimental control of spin-orbit effects very difficult.
Recently, however, it has been demonstrated experimentally that spin-orbit coupling can be engineered in a ultra-cold gas of bosonic atoms in their Bose-Einstein condensate phase spielman-2011 , when a pair of Raman lasers creates a coupling between two internal spin states of the atoms and its center-of-mass motion (momentum). Thus far, the type of spin-orbit field that has been created in the laboratory spielman-2011 has the equal-Rashba-Dresselhaus (ERD) form , where . Other forms of spin-orbit fields require additional lasers and create further experimental difficulties dalibard-2010 . In ultra-cold bosons the momentum-dependent ERD coupling has been created in conjunction with uniform Zeeman terms, which are independent of momentum, along the z axis (controlled by the Raman coupling ), and along the y-axis (controled by the detuning ). The simultaneous presence of , and leads to the Zeeman-spin-orbit (ZSO) Hamiltonian
for an atom with center-of-mass momentum and spin basis , . The fields , and can be controlled independently, and thus can be used as tunable parameters to explore the available phase space and to investigate phase transitions, as achieved in the experiment involving a bosonic isotope of Rubidium (87Rb). Although current experiments have focused on Bose atoms, there is no fundamental reason that impeeds the realization of a similar set up for Fermi atoms spielman-2011 ; sinova-2009 ; chapman-sademelo-2011 designed to study fermionic superfluidity chapman-sademelo-2011 . Considering possible experiments with fermionic atoms such as 6Li, 40K, we discuss in this letter phase diagrams, topological phase transitions, spectroscopic and thermodynamic properties at zero and finite temperatures during the evolution from BCS to BEC superfluidity in the presence of controllable Zeeman and spin-orbit fields in three dimensions.
To investigate artificial spin-orbit and Zeeman fields in ultra-cold Fermi superfluids, we start from the Hamiltonian density
| (1) |
where the single-particle term is simply
| (2) |
Here, is the kinetic energy in reference to the chemical potential , is the combined effective field including Zeeman and spin-orbit components along the -direction , and are creation operators for fermions with spin at position . Notice that we allow the chemical potential to be different from , such that the number of fermions with spin may be different from the number of fermions with spin . The interaction term is
| (3) |
where represents a contact interaction that can be expressed in terms of the scattering length via the Lippman-Schwinger relation The introduction of the average pairing field and its spatio-temporal fluctuation produce a complete theory for superfluidity in this system.
From now on, we focus on the experimental case where a) the Raman detuning is zero indicating that there is no component of the Zeeman field along the direction; b) the Raman coupling is non-zero meaning that a Zeeman component along the direction exists, that is, ; and c) the spin-orbit field has components and along the and directions. To start our discussion, we neglect fluctuations, and transform into momentum space as . Using the basis where is the vacuum state, the Fourier-transformed Hamiltonian becomes the matrix
Such matrix can be diagonalized in the helicity basis where the spins and are aligned or antialigned with respect to the effective magnetic field Here, is a measure of the average kinetic energy in relation to the average chemical potential While is the spin-orbit field and is the effective Zeeman field, with where is the internal Zeeman field due to initial population imbalance, and is the external Zeeman field. When there is no population imbalance the internal Zeeman field is , and we have only . In general, the eigenvalues of the Hamiltonian matrix are and where is the magnitude of the effective magnetic field, with the transverse component being expressed in terms of the complex function In the limit where the internal and external Zeeman fields vanish and the spin-orbit field is null , the energies of the helicity bands are identical producing no effect in the original energy dispersions shenoy-2011 .
When interactions are added to the problem, pairing can occur within the same helicity band (intra-helicity pairing) or between two different helicity bands (inter-helicity pairing). This leads to a tensor order parameter for superfluidity that has four components corresponding to the helicity projection ; and corresponding to helicity projection ; and corresponding to helicity projection . The phase is defined from the amplitude-phase representation of the complex spin-orbit field while the amplitude for helicities are directly proportional to the scalar order parameter and to the relative magnitude of the spin-orbit field with respect to the magnitude of the effective magnetic field . Additionally, has the simple physical interpretation of being the triplet component of the order parameter in the helicity basis, which is induced by the presence of non-zero spin-orbit field , but vanishes when . Analogously the amplitude for helicity are directly proportional to the scalar order parameter and to the relative magnitude of the total Zeeman field with respect to the magnitude of the effective magnetic field . Additionally, has the simple physical interpretation of being the singlet component of the order parameter in the helicity basis. It is interesting to note the relation which, for fixed , shows that as increases, decreases and vice-versa. Such relation indicates that the singlet and triplet channels are not separable in the presence of spin-orbit coupling. Furthermore, the order parameter in the triplet sector and contains not only -wave, but also -wave and even higher odd angular momentum contributions, as long as the total Zeeman field is non-zero. Similarly, the order parameter in the singlet sector and contains not only only -wave, but also -wave and even higher even angular momentum contributions, as long as the total Zeeman field is non-zero. Higher angular momentum pairing in the helicity basis, occurs because the original local (zero-ranged) interaction in the original spin basis is transformed into a finite-ranged interaction in the helicity basis . In the limiting case of zero total Zeeman field , the singlet component vanishes , while the triplet component becomes independent of momentum , leading to order parameter , and which contains only -wave contributions chuanwei-2008 , since the components of depend linearly on momentum .
The eigenvalues of the Hamiltonian including the order parameter contribution emerge from the diagonalization of a matrix (see supplementary material). The two eigenvalues for quasiparticles are
| (4) |
corresponding to the highest-energy quasiparticle band, and
| (5) |
corresponding to the lowest-energy quasiparticle band, while the eigenvalues for quasiholes are for highest-energy quasihole band and for the lowest-energy quasihole band. The energy is momentum-dependent, corresponds to the average energy difference between the helicity bands and can be written as while the energy is also momentum dependent, corresponds to the averaged energy sum of the helicity bands and can be written as
There are a few important points to notice about the excitation spectrum of this system. First, notice that . Second, that the eigenergies are symmetric about zero, such that we can regard quasiholes (negative energy solutions) as anti-quasiparticles. Third, that only can have zeros (nodal regions) corresponding to the locus in momentum space satisfying the following conditions: a) which corresponds physically to the equality between the effective magnetic field energy and the excitation energy for the singlet component and b) corresponding to zeros of the triplet component of the order parameter in momentum space.
Since , and only can have zeros, the low energy physics is dominated by this eingenvalue. In the case of equal Rashba-Dresselhaus (ERD) where , zeros of can occur when , leading to the following cases: (a) two possible lines (rings) of nodes at for the outer ring, and for the inner ring, when ; (b) doubly-degenerate line of nodes for , doubly-degenerate point nodes for , or no-line of nodes for , when ; (c) no line of nodes when . In addition, case (a) can be refined into cases (a2), (a1) and (a0). In case (a2), two rings indeed exist provided that . However, the inner ring disappears when . In case (a1), there is only one ring when In case (a0), the outer ring disappears at , and for no rings exist.
We choose our momentum, energy and velocity scales through the Fermi momentum defined from the total density of fermions This choice leads to the Fermi energy and to the Fermi velocity , as energy and velocity scales respectively. In Fig. 1, we show the phase diagram of Zeeman field versus chemical potential describing possible superfluid phases according to their quasiparticle excitation spectrum. We label the uniform superfluid phases with zero, one or two rings of nodes as US-0, US-1, and US-2, respectively. Non-uniform (NU) phases also emerge in regions where uniform phases are thermodynamically unstable. The US-2/US-1 phase boundary is determined by the condition , when ; the US-0/US-2 boundary is determined by the Clogston-like condition when , where the gapped US-0 phase disappears leading to the gapless US-2 phase; and the US-0/US-1 phase boundary is determined by , when . Furthermore, with the US-0 boundaries, a crossover line between an indirectly gapped and a directly gapped US-0 phase occurs at . Lastly, some important multi-critical points arise at the intersections of phase boundaries. First the point and corresponds to a tri-critical point for phases US-0, US-1, and US-2. Second, the point and corresponds to a tri-critical point for phases N, US-1 and US-2. In the limit where both and vanish no phase transitions take place and the problem is reduced to a crossover zhai-2011 ; hu-2011 ; han-2011 .
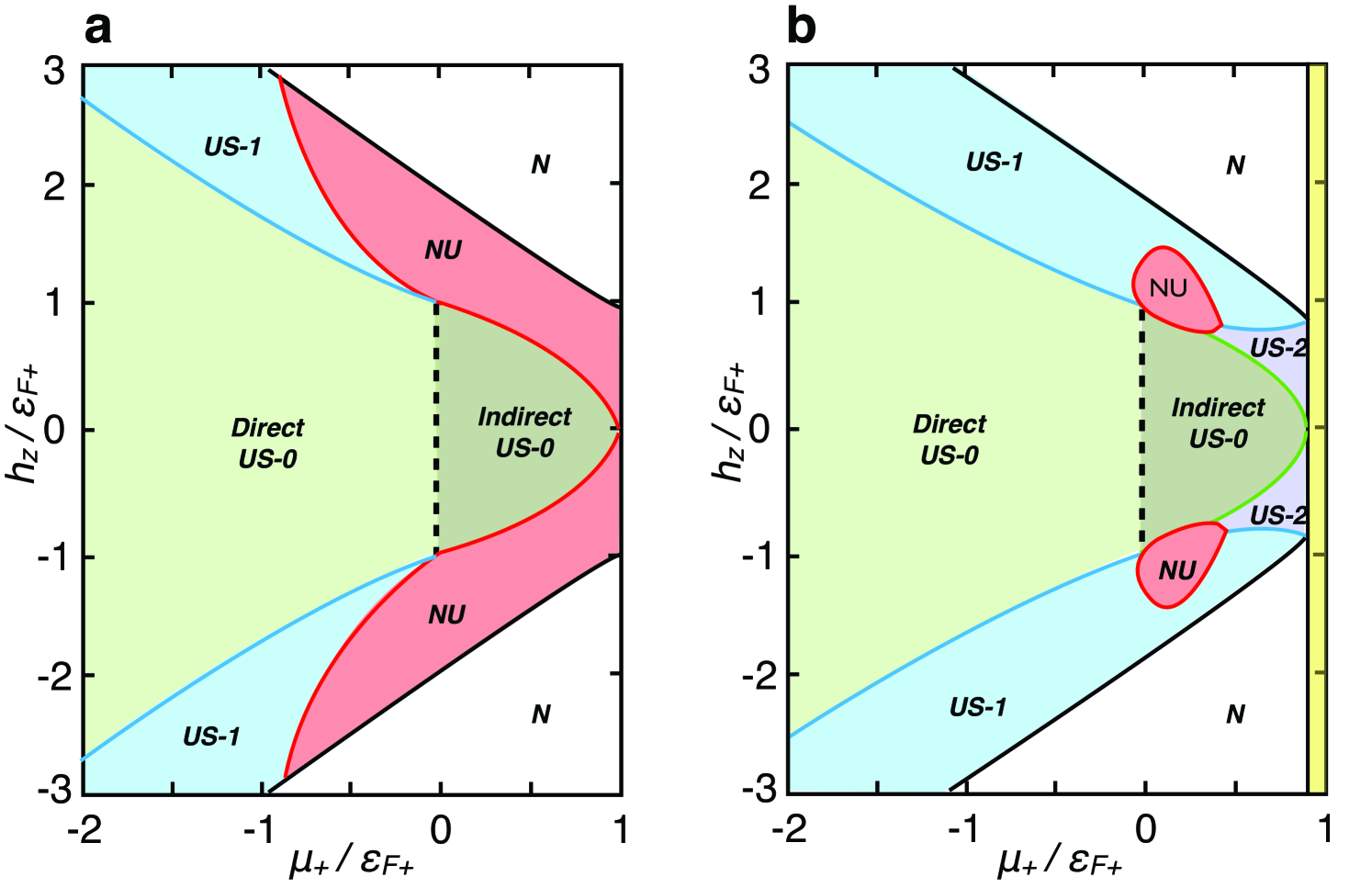
In the US-1 and US-2 phases near the zeros of , quasiparticles have linear dispersion and behave as Dirac fermions. Such change in nodal structures is associated with bulk topological phase transitions of the Lifshitz class as noted for -wave volovik-1992 and -wave duncan-2000 ; botelho-2005 superfluids. Such Lifshitz topological phase transitions are possible here because the spin-orbit coupling field induces the triplet component of the order parameter . The loss of nodal regions correspond to annihilation of Dirac quasiparticles with opposite momenta, which lead to the disappearance of rings. The transition from phase US-2 to indirect gapped US-0 occurs through the merger of the two-rings at the phase boundary followed by the immediate opening of the indirect gap at finite momentum. However, the transition from phase US-2 to US-1 corresponds to the disappearance of the inner ring through the origin of momenta, similarly the transition from US-1 to the directly gappped US-0 corresponds to the disappearance of the last ring also through the origin of momenta. In the case of Rashba-only coupling rings of nodes are absent and it is possible to have at most nodal points chuanwei-2011 ; iskin-2011 . The last two phase transitions are special because the zero-momentum quasiparticles at these phase boundaries correspond to true Majorana zero energy modes if the phase of the spin-orbit field and the phase of the order parameter have opposite phases at zero momentum: . This can be seen from an analysis of the quasiparticle eigenfunction
corresponding to the eigenvalue . The emergence of zero-energy Majorana fermions requires the quasiparticle to be its own anti-quasiparticle: . This can only happen at zero momentum , where the amplitudes and . Such requirement leads to the conditions , and , showing that Majorana fermions can exist only at the US-0/US-1 and US-2/US-1 phase boundaries. It is important to emphasize that the Majorana fermions found here exist in the bulk, and thus their emergence or disappeareance affect bulk thermodynamic properties, unlike Majorana fermions found at the edge (surfaces) of topological insulators and some topological superfluids. The common ground between bulk and surface Majorana fermions is that both exist at boundaries: the bulk Majorana zero-energy modes may exist at the phase boundaries between two topologically distinct superfluid phases, while surface Majorana zero-energy modes may exist at the spatial boundaries of a topologically non-trivial superfluid.
It is evident that the transition between different superfluid phases occurs without a change in symmetry in the order parameter , and thus violates the symmetry-based Landau classification of phase transitions. In the present case, the simultaneous existence of spin-orbit and Zeeman fields (internal or external) couple the singlet and triplet channels and all the superfluid phases US-0, US-1 and US-2 just have different weights from each order parameter component. However a finer classification based on topological charges can be made via the construction of topological invariants. Since the superfluid phases US-0, US-1, US-2 are characterized by different excitation spectra corresponding to the eigenvalues of the Hamiltonian matrix including interactions , we can use the resolvent matrix and the methods of algebraic topology nakahara-1990 to construct the topological invariant
where The topological invariant is in the gapped US-0 phase, is in the gapless US-1 phase and in the gapless US-2 phase, showing that, for ERD spin-orbit coupling, counts the number of rings of zero-energy excitations in each superfluid phase. The integral above has a hyper-surface measure and a domain that encloses the region of zeros of . Here run from 0 to 3, and has components , , , and . The topological invariant measures the flux of the four-dimensional vector through a hypercube including the singular region of the resolvent matrix , much in the same way that the flux of the electric field in Gauss’ law of classical electromagnetism measures the electric charge enclosed by a Gaussian surface: . Thus, the topological invariant defined above defines the topological charge of fermionic excitations, in the same sense as Gauss’ law for the electric flux defines the electric charge.
A full phase diagram can be constructed only upon verification of thermodynamic stability of all the proposed phases. For this purpose it becomes imperative to investigate the maximum entropy condition (see supplementary material). Independent of any microscopic approximations, the necessary and sufficient conditions for thermodynamic stability of a given phase are: positive isovolumetric heat capacity positive chemical susceptibility matrix i.e, eigenvalues of the matrix are both positive; and positive bulk modulus or isothermal compressibility Using these conditions, we construct the full phase diagram described in Fig. 1 for equal Rasha-Dresselhaus (ERD) spin-orbit coupling. The regions, where the uniform superfluid phases are unstable are labeled by the abbreviation NU to indicate that non-uniform phases such as phase separation or modulated superfluid (supersolid) may emerge. In Fig. 2, we show the phase diagram of Zeeman field versus interaction parameter , for population balanced fermions, where the number of spin-up fermions is equal to the number of spin-down fermions .
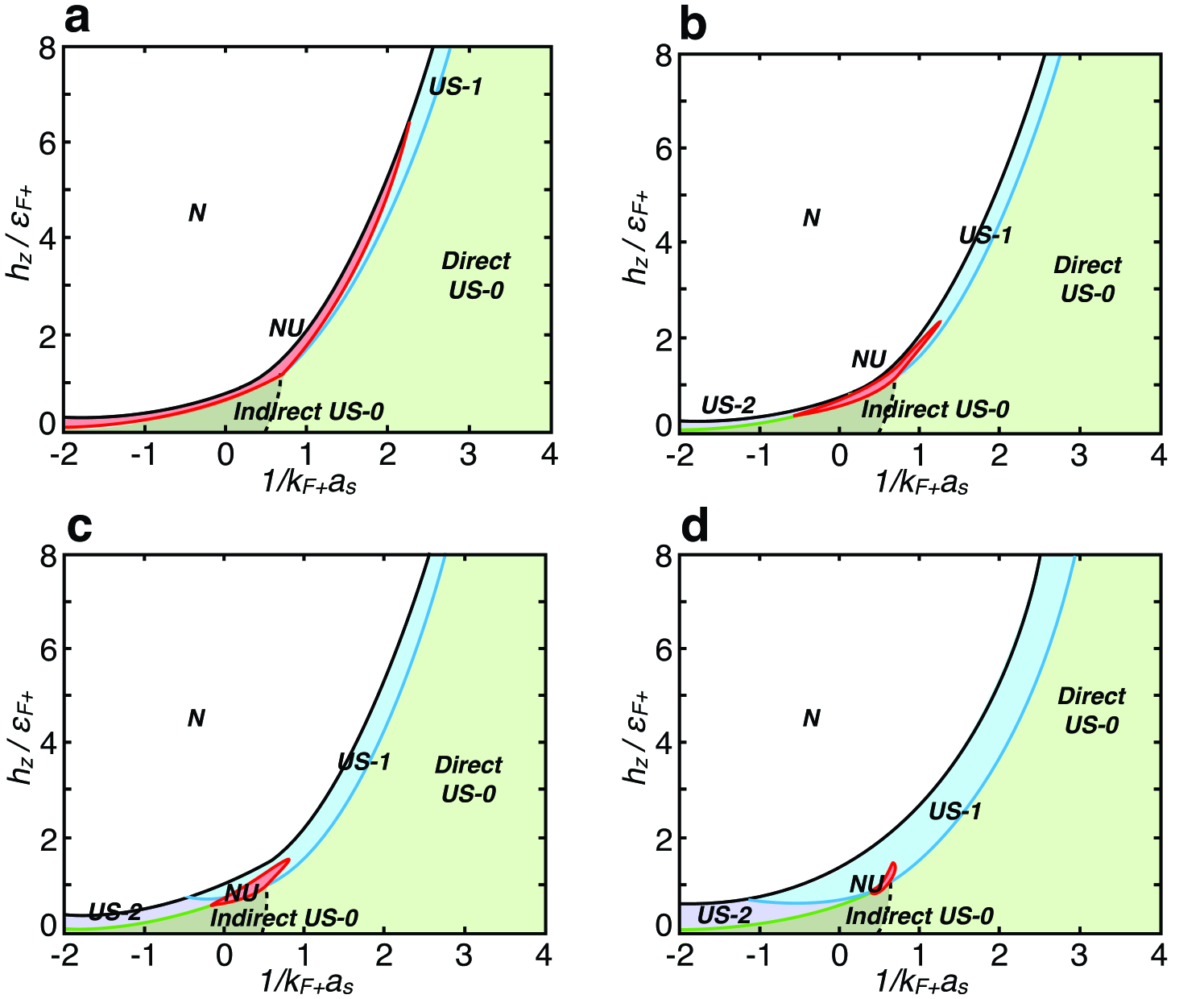
Since these superfluid phases exhibit major changes in momentum-frequency space as evidenced by their single particle excitation spectrum, it is important to explore additional spectroscopic quantitities to characterize further the nature of these phases and the phase transitions between them. An important quantity is the resolvent matrix
| (6) |
from where the spectral density for spin can be extracted. The spectral function in the plane of momenta - with and frequency reveals the existence of rings of zero-energy excitations in the US-1 and US-2 phases. The density of states for spin as a function of frequency is also an important spectroscopic quantity which is shown in Fig. 3 along with excitation spectra for phases US-1 and US-2 at fixed ERD spin-orbit coupling . The parameters used for phase US-1 are and , while for phase US-2 they are and . Notice that, even though the excitation spectrum is symmetric, the coherence factors appearing in the matrix are not, such that the density of states is not an even function of , and thus it is not particle-hole symmetric. The main feature of at low frequencies is the linear behavior due to the existence of Dirac quasiparticles and quasiholes in the US-1 and US-2 phases, which are absent in the direct-gap and the indirect-gap US-0 phases. The peaks and structures in mostly emerge due to the maxima and minima of . Notice that for finite Zeeman field , the density of states because the induced population imbalance is non-zero. For the US-2 case shown in Fig. 3b, the induced population imbalance since is small, while for the US-1 case shown in Fig. 3e, as the spins are almost fully polarized since is large.
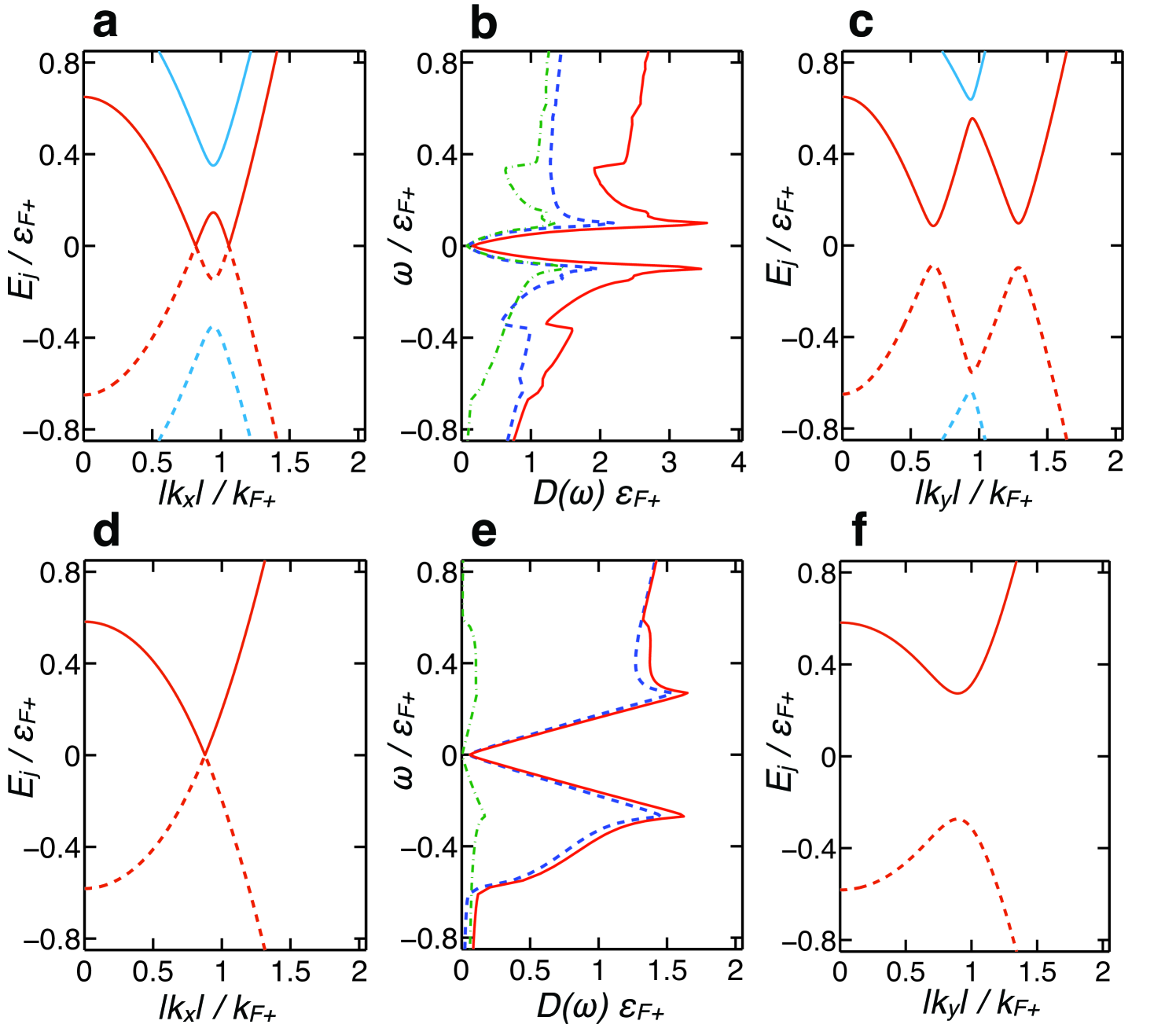
In summary, we have discussed the effects of spin-orbit and Zeeman fields in ultra-cold Fermi superfluids, obtained the phase diagrams of Zeeman field versus interaction parameter or versus chemical potential, and identified several bulk topological phase transitions between gapped and gapless superfluids as well as a variety of multi-critical points. We have shown that the presence of simultaneous Zeeman and spin-orbit fields induces higher angular momentum pairing, as manifested in the emergence of momentum dependence of the singlet and triplet components of order parameter expressed in the helicity basis. Finally, we have characterized topological phases and phase transitions between them through their excitation spectra (existence of Dirac quasiparticles or Majorana zero-energy modes), topological charges, and spectroscopic and thermodynamic properties, such as density of states and isothermal compressibility.
Acknowledgements.
We thank ARO (W911NF-09-1-0220) for support.References
- (1) Y. J. Lin, K. Jimenez-Garcia, and I. B. Spielman, Nature 471, 83-86 (2011).
- (2) X. J. Liu, M. F. Borunda, X. Liu, and J. Sinova, Phys. Rev. Lett. 102, 046402 (2009).
- (3) M. Chapman and C. Sá de Melo, Nature 471, 41-42 (2011).
- (4) C. L. Kane and E. J. Mele, Phys. Rev. Lett. 95, 146802 (2005).
- (5) L. P. Gor’kov and E. I. Rashba, Phys. Rev. Lett. 87, 037004 (2001).
- (6) T. D. Stanescu, C. Zhang, and V. Galitski, Phys. Rev. Lett. 99 110403 (2007).
- (7) G. Dresselhaus, Phys. Rev. 100, 580 (1955).
- (8) Y. A. Bychkov and E. I. Rashba, J. Phys. C 17, 6039 (1984).
- (9) J. Dalibard, F. Gerbier, G. Juzeliunas, and P. Ohberg, arXiv:1008.5378 (2010).
- (10) J. P. Vyasanakere, S. Zhang, and V. B. Shenoy, arXiv:1104.5633 (2011).
- (11) C. Zhang, S. Tewari, R. M. Lutchyn, and S. Das Sarma, Phys. Rev. Lett. 101 160401 (2008).
- (12) Z.-Q. Yu and H. Zhai, arXiv:1105.2250 (2011).
- (13) H. Hu, L. Jiang, X. Jiu, and H. Pu, arXiv:1105.2488 (2011).
- (14) L. Han and C. A. R. Sá de Melo, arXiv:1106.3613 (2011).
- (15) G. E. Volovik, World Scientific, Singapore (1992).
- (16) R. D. Duncan and C. A. R. Sá de Melo, Phys. Rev. B 62, 9675 (2000).
- (17) S. S. Botelho and C. A. R. Sá de Melo, Phys. Rev. B 71, 134507 (2005).
- (18) M. Gong, S. Tewari, and C. Zhang, arXiv:1105.1796 (2011).
- (19) M. Iskin and A. L. Subasi, arXiv:1106.0473 (2011).
- (20) M. Nakahara, Adam Hilger, Bristol (1990).
I Artificial spin-orbit coupling in ultra-cold Fermi superfluids: (Supplementary Material)
The method used to study the spin-orbit and Zeeman effects in ultra-cold Fermi superfluids is the functional integral method and its saddle-point approximation in conjunction with fluctuation effects. To describe the thermodynamic phases and the corresponding phase diagram in terms of the interactions, Zeeman and spin-orbit fields, we calculate partition function at temperature with action
where the Hamiltonian density is given in Eq. (1).
Using the standard Hubbard-Stratanovich transformation that introduces the pairing field and integrating over the fermion variables lead to the effective action
where The matrix is
| (7) |
where corresponds to the transverse component of the spin-orbit field, to the parallel component with respect to the quantization axis , , and .
To make progress, we use the saddle point approximation and write . The matrix is obtained via the saddle point which takes , and the fluctuation matrix depends only on and its Hermitian conjugate. Thus, we write the effective action as . The first term is
in momentum-frequency coordinates , where . Here, are the eigenvalues of
| (8) |
which describes the Hamiltonian of elementary excitations in the four-dimensional basis The fluctuation action is
The spin-orbit field is , where is of Rashba-type and is of Dresselhaus-type, has magnitude For Rashba-only (RO) and for equal Rashba-Dresselhaus (ERD) couplings , the magnitude of the transverse fields are () and (), respectively.
The Hamiltonian in the helicity basis , where is the unitary matrix that diagonalizes the Hamiltonian in the normal state, is
The components of the order parameter in the helicity basis are given by and for the triplet channel and by and for the singlet channel. The eigenvalues of for quasiparticles , are listed in Eqs. (4) and (5), while the eigenvalues for quasiholes are , and .
The thermodynamic potential is , where
with is the saddle point contribution and , with is the fluctuation contribution. The order parameter is determined via the minimization of with respect to , leading to
| (9) |
where is the Fermi function for energy . The contact interaction is expressed in terms of the scattering parameter via the Lippman-Schwinger relation discussed in the main text.
The total number of particles is defined from the thermodynamic relation and can be written as
| (10) |
The saddle point contribution is
and the fluctuation contribution is leading to
with the partial derivative being
Knowledge of the thermodynamic potential , of the order parameter Eq. (9) and number Eq. (10) provides a complete theory for spectroscopic and thermodynamic properties of attractive ultra-cold fermions in the presence of Zeeman and spin-orbit fields. Representative Saddle point solutions for chemical potential and order parameter amplitude as a function of in the equal Rashba-Dresselhaus (ERD) case are shown in Fig. 4 for . These parameters are used to obtain the phase diagrams described in Figs. 1 and 2 in combination with an analysis of the excitation spectrum given in Eqs. (4) and (5) and the thermodynamic stability conditions for all the uniform superfluid phases: directly or indirectly gapped superfluid with zero nodal rings (US-0); gapless superfluid with one ring of nodes (US-1); and gapless superfluid with two rings of nodes (US-2).

A thermodynamic stability analysis of all proposed phases can be performed by investigating the maximum entropy condition. The total change in entropy due to thermodynamic fluctuations, irrespective to any approximations imposed on the microscopic Hamiltonian, can be written as
where the repeated index indicates summation, and the condition guarantees that the entropy is maximum. Considering the entropy to be a function of temperature , number of particles and volume , we can elliminate the fluctuations , , and in favor of fluctuations , and , and show that the fluctuations are statistically independent of and , while fluctuations and are not. The first condition for thermodynamic stability leads to the requirement that the isovolumetric heat capacity Additional conditions are directly related to number and volume fluctuations. They require the chemical susceptibility matrix to be positive definite, i.e, that its eigenvalues are both positive. This is guaranteed by and . The last condition for thermodynamic stability is that the bulk modulus or the isothermal compressibility are positive. Since the number and volume fluctuations are not statistically independent, the bulk modulus is related to the matrix via The positivity of the volumetric specific heat , chemical susceptibility matrix and bulk modulus are the necessary and sufficient conditions for thermodynamic stability, which must be satisfied irrespective of approximations used at the microscopic level.
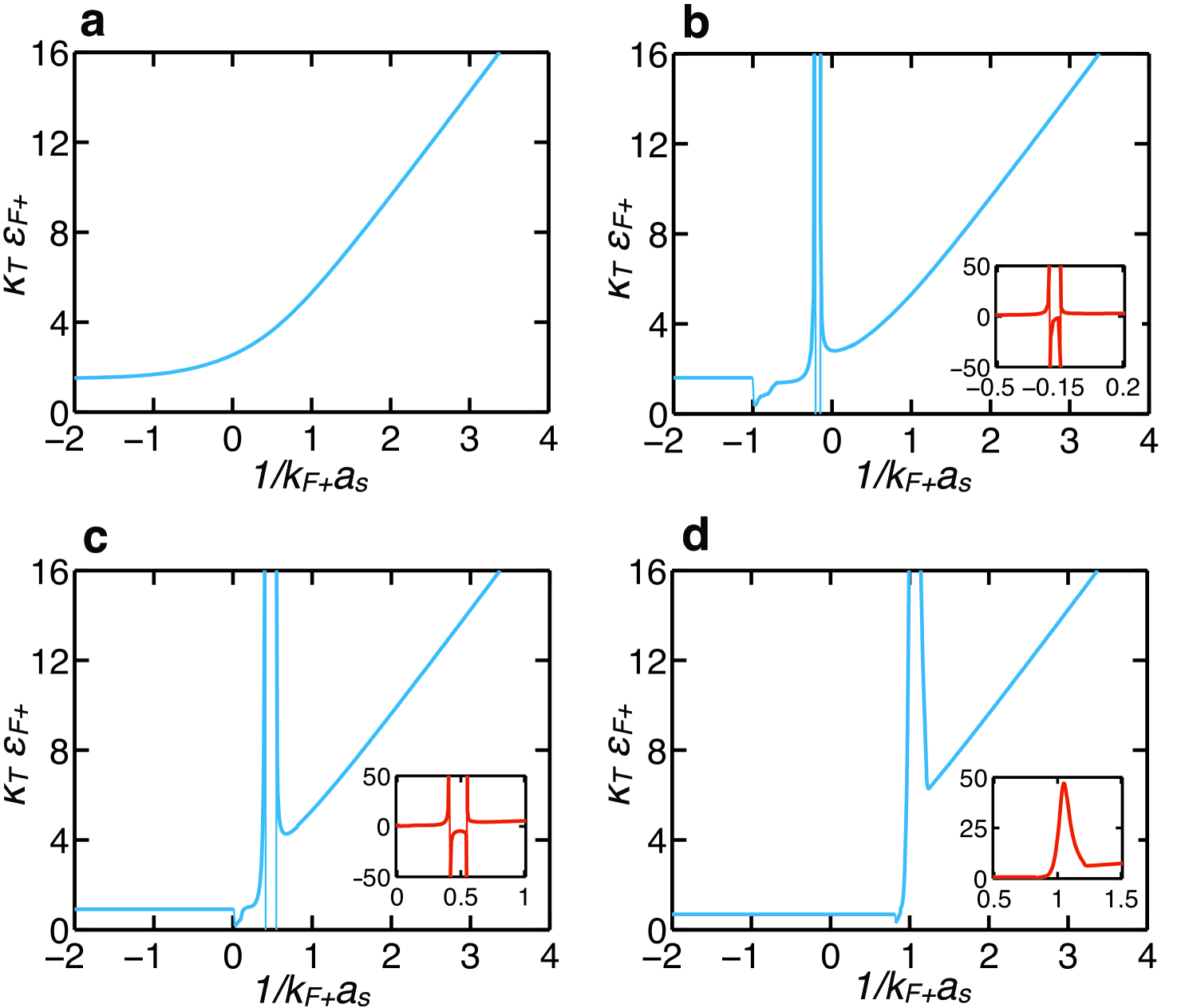
Further characterization of phases US-0, US-1 and US-2 is made via thermodynamic properties such as the isothermal compressibility which is shown in Fig. 5 versus for the values of the Zeeman field and spin-orbit coupling . Notice the negative regions of indicating that the uniform superfluid phases are unstable, and its discontinuities at phase boundaries. The normal state compressibility or can be obtained analytically for arbitrary Zeeman and spin-orbit parameter in the BCS limit where as
| (11) |
where the auxiliary function is
and its derivative is
with , , and . Notice that, as and , and is reduced to the standard result, since . In addition, or can be obtained analytically in the BEC limit where . When and are zero, then
| (12) |
can also be written in terms of bosonic properties
| (13) |
where is the boson mass and in the boson-boson interaction. In the case where and , a similar expression can be derived for but the effective boson mass , and the effective boson-boson interaction are now functions of and . Notice that the ratio in the BEC limit can be directly extracted from the behavior of for large .