Aspects of and
Abstract
In the present work we investigate the , , and hidden-charm decay modes for the four-quark system in the molecular and compact tetraquark scenarios using the quark-exchange model. Our theoretical results indicate that if the newly observed states and are two different states, may be interpreted as the mixture of which the partial decay width is about MeV, while may be explained as the mixture of which the partial decay width is small to zero. Moreover, if the state can be explained as the mixed state indeed, the partial decay width ratio between and is close to unit, which indicates the decay channel may be a ideal channel as well to decode the inner structure of . In addition, the partial decay width for the tensor molecular state decaying into can reach up to a few MeV, which shows this tensor molecular state has a good potential to be observed in this decay channel.
1 Introduction
In the last twenty years there is an explosion in the observation of hidden-charmed multiquark states [1, 2, 3, 4, 5, 6]. For example: dozens of charmonium-like states have been observed since 2003 [7], most of which are good candidates of four-quark states with quark components ( denotes or quark)[1, 2, 3, 4, 5, 6]; The LHCb collaboration reported hidden-charm pentaquark states and in 2015 [8] and updated the data in 2019 [9], which minimally contain four quarks and one antiquark() [10]; Last year, the LHCb collaboration observed a narrow structure around 6.9 Gev in the -pair invariant mass spectrum [11], which may be good candidates of compact tetraquark state [12]. All of the experimental progress in the observation of hadrons with anomalous properties has attracted a great deal of attention from the hadron physics community.
Very recently the BESIII collaboration made a great breakthrough in searching for hidden-charmed multiquark states with strangeness and reported a new structure near the and mass thresholds in the recoil-mass spectrum [13], whose mass and width are respectively
| (1) |
From its decay modes, it is reasonable to assign it as the first candidate of the hidden-charm tetraquark with strangeness(). Thus, Most of theoretically references are under the four-quark scenario to exploring its genuine properties of the excess [14, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 17, 18, 19, 20, 21, 22, 23, 24, 25, 15, 16, 36]. There also exist a few discussions that assign this structure as a threshold effect [37] or a threshold cusp [38]. Furthermore, explaining as a reflection structure of charmed-strange meson is also presented [39].
Later the LHCb collaboration further observed a exotic states with quark content (denoted as ) from an amplitude analysis of the decay [40]. Its mass and width are measured to be
| (2) |
The mass of this state is comparable to that of observed by BESIII [13], while its width is about ten times larger than that of . Thus, whether they are two different states or not, and how to decode their inner structures are now pretty much the agenda for theorists. So far, there are some discussions of their inner structures with various theoretical methods [41, 42, 43, 44, 45, 46, 47, 48, 49, 50]. The most papular interpretation of is explaining them as two different states: molecular states [43, 48] or compacted tetraquark states with different spin-parity [44, 41, 49].
The masses of the and states are comparable and both slightly higher than the mass thresholds of and . In the molecular scenario, we take the and states as two / resonance molecular states. Meanwhile, according to experimental measurement, the state is observed in the decay channel and non-observation of the signal in this decay mode. Thus, to clarify whether and are two different states and further show light on the inner structures of the two states, it is critical to study the decay mode for the and molecular states. In addition, the authors in Ref. [48] predicted the existence of a tensor resonance. As the expansion it is necessary to investigate the decay properties of this tensor resonance. Based on the above considerations, in the present work we conduct a systematically study of the hidden-charm strong decays of the molecular states in the framework of the quark-exchange model. Furthermore, for comparison we also investigate the hidden-charm decay properties of the four-quark system in the compact tetraquark scenario. We hope that our theoretical results can provide some reference for the properties of the and states.
This paper is structured as follows. In Sec.II, we give a brief introduction of the quark-exchange model. In Sec.III, we present our theoretical results and discussions. Finally, we make a short summary in Sec.IV.
2 Model introduction
In this work we calculate the , , and decay modes for the four-quark system in the molecular and compact tetraquark scenarios using the quark-exchange model [51]. This phenomenological model has been used to study the hidden-charm decay properties for the milt-quark states in our previous works [52, 53, 54]. Here we give a brief presentation for this model and more detail information can refer to our previous work [53].
For a two-body decay process(), the decay width in the rest frame of the initial particle reads
| (3) |
Here, represents the three-momentum of the final meson ; is the mass of the initial state ; denotes the transition amplitude, which is related to the -matrix via
| (4) |
where and represent the energy of the final mesons and , respectively. The -matrix has the form
| (5) | |||||
Here, the initial state is a four-quark state, which concludes constituent clusters and . In molecular scenario, the constituents are mesons, while in tetraquark scenario the constituents are the diquark and antidiquark . Thus, is the normalized relative spatial wave function between the constituent clusters and . denotes the relative spatial wave function between the final mesons and . represents the effective potential, which is a function of the initial and final relative momentum and .
Considering the four-quark state may be a superposition of terms with different orbital angular momenta, the relative spatial wave function in the momentum space reads
| (6) |
Then, the Eq. (4) can be written as
| (7) | |||||
where
| (8) |
In this equation, represents the cosine of the angle between the momenta and ; is Legendre function.
Finally, the decay width of two-body decay progress with the relativistic phase space has the form
| (9) |
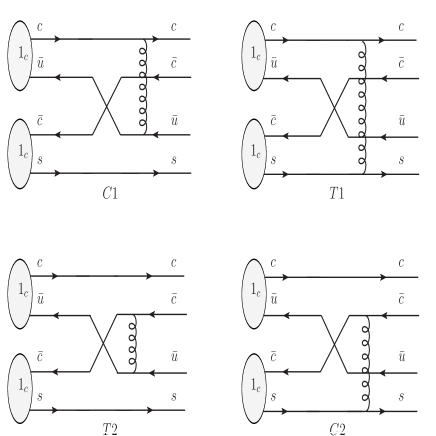
In the molecular scenario, we treat the four-quark system as the loosely bound -wave molecular states. At Born order, the effective potential is related to the reacting amplitude of the meson-meson scattering process, which is estimated by the sum of the interactions between the inner quarks as illustrated in Fig. 1 within the quark-exchange model. Moreover, the short-range interactions are dominant and can be approximated by the one-gluon-exchange (OGE) potential at quark level,
| (10) |
where is the quark (antiquark) generator; represents the transferred momentum; corresponds to the string tension; and are the interacting constituent quark mass and spin operator; denotes the range parameter in the hyperfine spin-spin interaction; represents the running coupling constant,
| (11) |
Here, denotes the square of the invariant masses of the interacting quarks.
In the quark model, the wave function for a meson is
| (12) |
where , , and represent the wave functions in the color, flavor, spin and momentum space, respectively. Thus, the effective potential can be given as the product of the factors,
| (13) |
In this equation, with the subscripts color, flavor and spin-space represent the overlaps of the initial and final wave functions in the corresponding space.
In addition, to calculate the decay widths by Eq. (9), expecting the obtained effective potential , we also need the relative spatial wave function between mesons and . In this work, we adopt an -wave harmonic oscillator function to estimate the relative spatial wave function in Eq. (6), which is
| (14) |
The value of the harmonic oscillator strength is related to the root mean square radius , which varies in the range of (1.0-3.0) fm in the present work.
Similar to the molecular case, the in the tetraquark scenario can be approximated by the interaction between the inner quarks(shown in Fig. 2), and be obtained with Eq. (13) as well. However there is a difference between the two scenarios for the color factor : in the molecular scenario the color configuration is -, while in the tetraquark scenario it is -. The difference in color configurations may result in quite different decay properties.
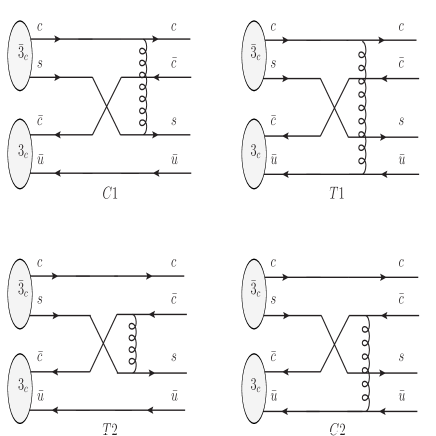
The spatial wave function of the initial tetraquark states are estimated by the -wave harmonic oscillating wave function,
| (15) |
where represent the momentum between the and quarks in the diquark (antidiquark), and denotes the one between the diquark and antidiquark . The with the subscripts is the oscillating parameter along the corresponding Jacobi coordinates, which value is given via imitating the wave function of in Ref. [55] and listed in Table 1.
| States | tetraquark | |||
|---|---|---|---|---|
| [55] | 0.90 | 0.90 | 0.48 | |
| 0.90 | 0.90 | 0.48 | ||
| 0.90 | 0.90 | 0.48 |
3 Results and discussion
The narrow state reported by BESIII collaboration [13] is observed in the and final channels, while the wide state reported by LHCb collaboration [40] is observed in the decay mode. The mass thresholds of ( MeV) and ( MeV) are slightly lower than the masses of and . Hence it is vital to investigate the decay properties of the molecular states and . Meanwhile, the mass degeneracy between the molecular states and indicates that the states may well be mixed. Namely the physical states probably are the mixed states between and . It is necessary to introduce a parameter to describe the mixability for a better understanding the decay properties. In addition, we also investigate the decay properties of the molecular state and hope to give some useful theoretical reference for the future experimental exploring. Moreover, we give a brief discussion of the strong decay properties of the four-quark system in the compact tetraquark scenario. Our theoretical results are presented as follows.
3.1 the molecular mixture of and
Considering the mass degeneracy between the molecular states and , we treat the physical states as the mixed states between and , i.e.,
| (16) |
The mixing angle can vary in the range of . Thus, taking the mixing angle we obtain that
| (17) |
We notice that for the systems with heavy flavour quarks, proper consideration of the heavy quark spin symmetry is necessary. Thus, the and systems are factorizable in the product of two parts: pure heavy and light flavour quark systems. That reads
| (18) |
Here, the number 1 and 0 in equations with the subscripts H or L denote the spin of the regrouped daughter heavy or light flavour quark systems.
Combining with Eq. (3.1), we further obtain that
| (19) |
It should be pointed out that each direct product decomposition corresponds to a possible decay mode. The corresponding relations are listed as follows:
| (20) |
The above correspondences indicate that based on heavy quark spin symmetry the mixed molecular state can decay into the and hidden-charm final channels, while its partner state can’t decay via these two decay modes. Meanwhile, the partial width ratio between and for is
| (21) |
According to the experimental data, the masses of the newly observed states and are comparable. Moreover, the state is observed in the decay channel while non-observation of the signal in this decay mode. Thus, if the two newly observed states are two different states, our theoretical results under the heavy quark spin symmetry imply that the molecular state may be the candidate of the state and its partner state may correspond to the state. In addition, if the mixed state is the newly observed state indeed, except for the decay mode the future experiments may find this state in the final channel as well.
Based on heavy quark spin symmetry we analyse the decay properties of the molecular mixtures and . Our results imply that the newly observed states and may be explained as and , respectively. Considering the heavy quark spin symmetry is only an approximation, more reliable calculations are desperately needed. Hence we further explore the decay properties of the molecular mixtures in the framework of the quark-exchange model.
| state | mass(MeV) | observed state | |||
|---|---|---|---|---|---|
| 4003 | 2.89 | 3.19 | 0.01 | ||
| 3982 | 0.01 | 0.04 | - |
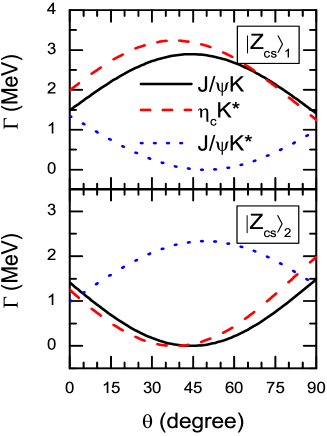
According to the mixing scheme defined in Eq. (16), in Fig. 3 we plot the hidden-charm decay widths of the mixed states and as a function of the mixing angle in the region of () by fixing the masses of the two states at MeV and root mean square radius at fm. From the figure, we get that the variation curves like a bowel structure when the mixing angle varies from to , and the changing trends of the decay modes and are opposite to that of the decay mode . Meanwhile, we notice that with the mixing angle increasing to , the partial decay widths of the and modes for the mixed state can reach a maximum about MeV, while that for the mixed state decrease into the minimum about MeV. The above decay properties of the mixed states and obtained here are consistent with those gotten under heavy quark spin symmetry.
Fixing the mixing angle at (see Table 2 ), we obtain
| (22) |
which are large enough to be observed in experiments. Observation of the state in the decay mode indicates may be a candidate of the mixed state . Meanwhile, the partial decay widths ratio between and is
| (23) |
which is close to unit. Namely if the observed state can be explained as the mixed state , the mode may be a ideal channel as well to further decode its inner structure.
Then, we investigate the decay properties of its partner state and collect in Table 2 as well. From the table, it is obvious that for the state , the partial decay width of is small to zero which agrees with the decay properties of the newly observed state : non-observation in the mode. Thus, we take the mixed state as the state , and fix the mass on MeV. We obtain that the decay width of the mode is small to zero as well. Meanwhile, the mode is forbidden for the mass below the threshold of .
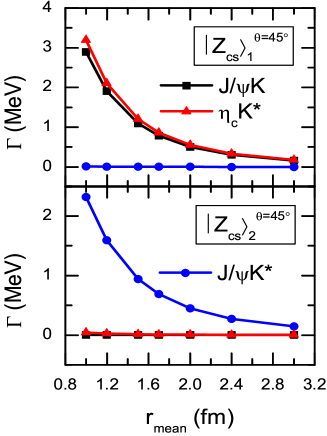
It should be mentioned that all of the above theoretical predictions are obtained with the root mean square radius fm. However, the root mean square radius is not determined absolutely, which bares a large uncertainty. Thus fixing the masses of the mixed states and at MeV, we further explore the decay properties as a function of the root mean square radius . The results are shown in Fig. 4. One notes that the bigger value leads to a narrower decay width. A loose understanding is that with the increasing the two mesons( and ) in the four-quark state farther separate from each other, thus, the charm and anti-charm quarks are more difficult to form a charmonium.
In addition, we notice that as the consequence of and being most pure and states, respectively, the branching ratio for or . This result is consistent with the experimental analysis for the state [13].
The big difference of their decay widths leads to intensive discussions on whether and are two different states and possible implications if they are different states in literature [48]. In the present work, we adopted the quark-exchange model, which is a suitable framework for the hidden-charm decay modes. Unfortunately, the quark-exchange model is not suitable for the so-called ”fall-apart” open-charm decay modes. For the states, the open-charm decay modes are the dominant decay modes according to BESIII and BELLEII measurement. Therefore, we do not discuss the total widths of the states in this work.
3.1.1 The molecular state
As mentioned in the previous section, the authors in Ref. [48] suggested a tensor resonance, and its mass and decay width were predicted to be MeV and MeV, respectively. The sizable predicted decay width and advanced experimental methods indicate that this tensor resonance has a good potential to be observed in future experiments by BESIII or LHCb collaborations. In this work we investigate the hidden-charm decay properties of the molecular states with different spin-parity, and hope to provide reference for future experimental explorations.
For the molecular state , the spin-parity() has three different values: , and . Here we label them as , and , respectively. Similarly, the system can be factorized into pure heavy and light flavour quark parts under heavy quark spin symmetry, i.e.,
| (24) |
Here the direct product decomposition corresponds to the possible decay mode .
From Eq. (3.1.1), we can see that the molecular state can decay into the and final channels, and the partial decay width ratio between the two channels is
| (25) |
For the molecular state , the decay channel is forbidden and the partial decay width ratio between and is
| (26) |
As to the molecular state , it can decay into only in all hidden-charm strong decay modes.
Of course, the above results are obtained based on heavy quark spin symmetry, which is rather rough for the quark having a limited mass. While the main predictions should hold and be helpful for future experiments.
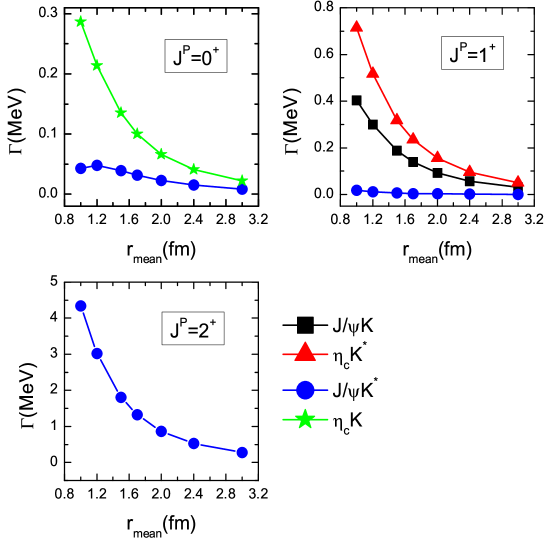
Furthermore, we analyze the hidden-charm decay properties of the molecular state using the quark-exchange model. Fixing the masses at MeV, we plot the variations of the decay widths as functions of the root mean square radius in Fig. 5. From the figure, we find that with the increasing in the range of (1.0-3.0) fm, the partial decay widths for decaying into the hidden-charm channels decrease. Moreover, the partial decay widths for and decaying into the hidden-charm channels are less than MeV with the root mean square radius varied in the whole range we considered in the present work, while the decay width of the molecular state can reach up to a few MeV.
| state | ||||
|---|---|---|---|---|
| 0.14 | - | - | 0.04 | |
| - | 0.19 | 0.32 | 0.01 | |
| - | - | - | 1.81 |
Fixing the root mean square radius at fm, we collect the predicted decay properties in Table 3. As show in table, we can see that the decay width of the molecular state is small to zero, which is consistent with the prediction within heavy quark spin symmetry. The decay width of the molecular state is small as well, which is much smaller than that of the molecular state . The ratio is
| (27) |
Thus, the decay channel can be used to distinguish those three molecular states from each other. Moreover, the sizable decay width for decaying into indicates that this tensor molecular state has a good potential to be observed in the channel.
3.2 The tetraquark scenario
For comparison, we further explore the strong decay properties of the four-quark system as a compact tetraquark state. We consider the mixing between and ,i.e.,
| (28) |
Similarly we investigate the decay properties of the mixed tetraquark states and as a function of the mixing angle with the masses fixed at MeV. Our calculations indicate that all the partial decay widths for the two mixed tetraquark states decaying into , and are less than 0.1 MeV with the mixing angle in the range of .
| state | mass | |||
|---|---|---|---|---|
| 4003 | 0.07 | 0.08 | 0.01 | |
| 3982 | 0.00 | 0.02 | - |
In the same way, we fix the mixing angle at and collected the decay properties in Table 4. From the table, it is seen that the decay properties of the mixed states and are inconsistent with that of the newly observed state. Thus, the possibility of the mixed tetraquark states as the candidates of the newly observed states may be excluded.
In addition, we also systematically study the hidden-charm decay properties of the compact tetraquark states . Fixing the masses at MeV, we collect their decay properties in Table 5.
| state | ||||
|---|---|---|---|---|
| 0.13 | - | - | 0.77 | |
| - | 0.11 | 0.18 | 0.01 | |
| - | - | - | 0.02 |
According to the table, it is found that in the compact tetraquark scenario the partial decay widths are rather small( MeV) except for decaying into , which is about MeV. Moreover,
| (29) |
Thus, the compact tetraquark state may be found in the channel in future experiments.
4 Summary
In the present work we explore the partial decay widths of the , , and modes for the four-quark system in the molecular and compact tetraquark scenrios using the quark-exchange model. Our main theoretical results are listed as follows.
In the molecular scenario, we systematically investigate the decay properties of the molecular states . For the mixed molecular states between and , we get that the decay width of the mixture () is about MeV, while that of the mixture () is small to zero. Considering observed in the and non-observation of the signal in this decay mode, if those two newly observed states are two different states, may be interpreted as the mixture , while may correspond to the mixture . In addition, if the state can be explained as the mixed state , the partial decay width ratio between and is close to unit, which indicates the decay channel may be a ideal channel as well to decode the inner structure of .
For the molecular state , our results imply that the partial decay width for decaying into can reach up to MeV, which is large enough to be observed in experiments.
In the tetraquark scenario, we consider the mixing between and as well. Our calculations indicate that all the partial hidden-charm decay widths are less than MeV with the mixing angle in the range of (). Thus, the possibility of the mixed compact tetraquark states as the candidates of the newly observed states may be excluded.
For the compact tetraquark states , Except the partial decay width for decaying into being sizable( MeV), the rest of the partial decay widths are small( MeV).
Acknowledgements
We would like to thank Shi-Lin Zhu and Guang-Juan Wang for very helpful discussions. This work is supported by the National Natural Science Foundation of China under Grants No.12005013, No.11947048.
References
- [1] A. Esposito, A. Pilloni and A. D. Polosa, Multiquark Resonances, Phys. Rept. 668, 1 (2017).
- [2] N. Brambilla, S. Eidelman, C. Hanhart, A. Nefediev, C. P. Shen, C. E. Thomas, A. Vairo and C. Z. Yuan, The states: experimental and theoretical status and perspectives, Phys. Rept. 873, 1 (2020).
- [3] Y. R. Liu, H. X. Chen, W. Chen, X. Liu and S. L. Zhu, Pentaquark and Tetraquark states, Prog. Part. Nucl. Phys. 107, 237 (2019).
- [4] S. L. Olsen, T. Skwarnicki and D. Zieminska, Nonstandard heavy mesons and baryons: Experimental evidence, Rev. Mod. Phys. 90, 015003 (2018).
- [5] F. K. Guo, C. Hanhart, U. G. Meiner, Q. Wang, Q. Zhao and B. S. Zou, Hadronic molecules, Rev. Mod. Phys. 90, 015004 (2018).
- [6] H. X. Chen, W. Chen, X. Liu and S. L. Zhu, The hidden-charm pentaquark and tetraquark states, Phys. Rept. 639, 1 (2016).
- [7] M. Tanabashi et al. [Particle Data Group], Review of Particle Physics, Phys. Rev. D 98, 030001 (2018).
- [8] R. Aaij et al. [LHCb Collaboration], Observation of Resonances Consistent with Pentaquark States in Decays, Phys. Rev. Lett. 115, 072001 (2015).
- [9] R. Aaij et al. [LHCb Collaboration], Observation of a narrow pentaquark state, , and of two-peak structure of the , Phys. Rev. Lett. 122, 222001 (2019).
- [10] L. Zhang, T. Skwarnicki and Y. Gao, The pentaquarks observed by the LHCb experiment, Sci. Bull. 64, 1119 (2019).
- [11] R. Aaij et al. [LHCb Collaboration], Observation of structure in the -pair mass spectrum, Sci. Bull. 65, 1983 (2020).
- [12] K. T. Chao and S. L. Zhu, The possible tetraquark states observed by the LHCb experiment, Sci. Bull. 65, 1952 (2020).
- [13] M. Ablikim et al. [BESIII Collaboration], Observation of a Near-Threshold Structure in the Recoil-Mass Spectra in ), Phys. Rev. Lett. 126, 102001 (2021).
- [14] L. Meng, B. Wang and S. L. Zhu, as the -spin partner of and implication of other states in the symmetry and heavy quark symmetry, Phys. Rev. D 102, 111502 (2020).
- [15] Z. Yang, X. Cao, F. K. Guo, J. Nieves and M. P. Valderrama, Strange molecular partners of the (3900) and (4020), Phys. Rev. D 103,074029 (2021).
- [16] M. Z. Liu, J. X. Lu, T. W. Wu, J. J. Xie and L. S. Geng, Can be a molecular state of and ?, arXiv:2011.08720 [hep-ph].
- [17] B. D. Wan and C. F. Qiao, About the exotic structure of , Nucl. Phys. B 968, 115450 (2021).
- [18] M. C. Du, Q. Wang and Q. Zhao, The nature of charged charmonium-like states and its strange partner , arXiv:2011.09225 [hep-ph].
- [19] R. Chen and Q. Huang, : A strange hidden-charm tetraquark resonance or not?, Phys. Rev. D 103, 034008 (2021).
- [20] Z. F. Sun and C. W. Xiao, Explanation of the newly obseaved as a molecular state, arXiv:2011.09404 [hep-ph].
- [21] Q. N. Wang, W. Chen and H. X. Chen, Exotic molecular states and tetraquark states with , arXiv:2011.10495 [hep-ph].
- [22] X. Cao, J. P. Dai and Z. Yang, Photoproduction of strange hidden-charm and hidden-bottom states, Eur. Phys. J. C 81, 184 (2021).
- [23] K. Azizi and N. Er, The newly observed state: in vacuum and a dense medium, Eur. Phys. J. C 81, 61 (2021).
- [24] Z. G. Wang, Analysis of the as the axialvector tetraquark state, Chin. Phys. C 45, 073107 (2021).
- [25] X. Jin, X. Liu, Y. Xue, H. Huang and J. Ping, Strange hidden-charm tetraquarks in constituent quark models, arXiv:2011.12230 [hep-ph].
- [26] B. Wang, L. Meng and S. L. Zhu, Decoding the nature of and establishing the spectrum of charged heavy quarkoniumlike states in chiral effective field theory,” Phys. Rev. D 103, L021501 (2021).
- [27] Y. A. Simonov, Recoupling Mechanism for exotic mesons and baryons, JHEP 2104, 051 (2021).
- [28] Y. J. Xu, Y. L. Liu, C. Y. Cui and M. Q. Huang, molecular state with : the mass and magnetic moment, arXiv:2011.14313 [hep-ph].
- [29] J. Y. Süngü, A. Türkan, H. Sundu and E. V. Veliev, Impact of a thermal medium on newly observed resonance and its -partner, arXiv:2011.13013 [hep-ph].
- [30] Z. H. Guo and J. A. Oller, Unified description of the hidden-charm tetraquark states , and , Phys. Rev. D 103, 054021 (2021).
- [31] Z. G. Wang, Analysis of the hidden-charm tetraquark molecule mass spectrum with the QCD sum rules, Int. J. Mod. Phys. A 35, 2150107 (2021).
- [32] X. K. Dong, F. K. Guo and B. S. Zou, A survey of heavy-antiheavy hadronic mlecules, Progr. Phys. 41, 65 (2021).
- [33] U. Ozdem and K. Azizi, Magnetic dipole moment of the state: diquark-antidiquark and molecular pictures, arXiv:2102.09231 [hep-ph].
- [34] M. J. Yan, F. Z. Peng, M. Sánchez Sánchez and M. Pavon Valderrama, Axial meson exchange and the and resonances as heavy hadron molecules, arXiv:2102.13058 [hep-ph].
- [35] K. Zhu, Triangle relations for XY Z states, Int. J. Mod. Phys. A 36, 2150126 (2021).
- [36] R. M. Albuquerque, S. Narison and D. Rabetiarivony, -like spectra from QCD Laplace sum rules at NLO, Phys. Rev. D 103, 074015 (2021).
- [37] N. Ikeno, R. Molina and E. Oset, The as a threshold effect from the interaction, Phys. Lett. B 814, 136120 (2021).
- [38] X. K. Dong, F. K. Guo and B. S. Zou, Explaining the Many Threshold Structures in the Heavy-Quark Hadron Spectrum, Phys. Rev. Lett. 126, 152001 (2021).
- [39] J. Z. Wang, Q. S. Zhou, X. Liu and T. Matsuki, Toward charged structure under a reflection mechanism, Eur. Phys. J. C 81, 51 (2021).
- [40] R. Aaij et al. [LHCb Collaboration], Observation of new resonances decaying to and , arXiv:2103.01803 [hep-ex].
- [41] P. P. Shi, F. Huang and W. L. Wang, Hidden charm tetraquark states in a diquark model, Phys. Rev. D 103, 094038 (2021).
- [42] P. G. Ortega, D. R. Entem and F. Fernandez, The strange partner of the structures in a coupled-channels model, Phys. Lett. B 818, 136382 (2021).
- [43] H. X. Chen, Hadronic molecules in B decays, arXiv:2103.08586 [hep-ph].
- [44] L. Maiani, A. D. Polosa and V. Riquer, The new resonances (3985) and (4003) (almost) fill two tetraquark nonets of broken SU(3)f, arXiv:2103.08331 [hep-ph].
- [45] Y. H. Ge, X. H. Liu and H. W. Ke, Threshold effects as the origin of , and observed in , arXiv:2103.05282 [hep-ph].
- [46] J. F. Giron, R. F. Lebed and S. R. Martinez, Spectrum of Hidden-Charm, Open-Strange Exotics in the Dynamical Diquark Model, arXiv:2106.05883 [hep-ph].
- [47] U. Ozdem and A. K. Yildirim, Magnetic dipole moments of the , , and states in light-cone QCD, arXiv:2104.13074 [hep-ph].
- [48] L. Meng, B. Wang, G. J. Wang and S. L. Zhu, Implications of the and as two different states, arXiv:2104.08469 [hep-ph].
- [49] G. Yang, J. Ping and J. Segovia, Hidden-charm tetraquarks with strangeness in the chiral quark model, Phys. Rev. D 104, 094035 (2021).
- [50] M. Karliner and J. L. Rosner, Configuration mixing in strange tetraquarks , Phys. Rev. D 104, 034033 (2021).
- [51] T. Barnes, N. Black and E. S. Swanson, Meson meson scattering in the quark model: Spin dependence and exotic channels, Phys. Rev. C 63, 025204 (2001).
- [52] G. J. Wang, L. Y. Xiao, R. Chen, X. H. Liu, X. Liu and S. L. Zhu, Probing hidden-charm decay properties of states in a molecular scenario, Phys. Rev. D 102, 036012 (2020).
- [53] L. Y. Xiao, G. J. Wang and S. L. Zhu, Hidden-charm strong decays of the states, Phys. Rev. D 101, 054001 (2020).
- [54] G. J. Wang, L. Meng, L. Y. Xiao, M. Oka and S. L. Zhu, Mass spectrum and strong decays of tetraquark states, Eur. Phys. J. C 81, 188 (2021).
- [55] C. Deng, J. Ping, H. Huang and F. Wang, Systematic study of Z family from a multiquark color flux-tube model, Phys. Rev. D 92, 034027 (2015).