Assemblies of Neurons Learn to Classify Well-Separated Distributions

The brain has been a productive source of inspiration for AI, from the perceptron and the neocognitron to deep neural nets. Machine learning has since advanced to dizzying heights of analytical understanding and practical success, but the study of the brain has lagged behind in one important dimension: After half a century of intensive effort by neuroscientists (both computational and experimental), and despite great advances in our understanding of the brain at the level of neurons, synapses, and neural circuits, we still have no plausible mechanism for explaining intelligence, that is, the brain’s performance in planning, decision-making, language, etc. As Nobel laureate Richard Axel put it, “we have no logic for translating neural activity into thought and action” (Axel, 2018).

Recently, a high-level computational framework was developed with the explicit goal to fill this gap: the Assembly Calculus (AC) (Papadimitriou et al., 2020), a computational model whose basic data type is the assembly of neurons. Assemblies, called “the alphabet of the brain” (Buzsáki, 2019), are large sets of neurons whose simultaneous excitation is tantamount to the subject’s thinking of an object, idea, episode, or word (see Piantadosi et al. (2016)). Dating back to the birth of neuroscience, the “million-fold democracy” by which groups of neurons act collectively without central control was first proposed by Sherrington (1906) and was the empirical phenomenon that Hebb attempted to explain with his theory of plasticity (Hebb, 1949). Assemblies are initially created to record memories of external stimuli (Quiroga, 2016), and are believed to be subsequently recalled, copied, altered, and manipulated in the non-sensory brain (Piantadosi et al., 2012; Buzsáki, 2010). The Assembly Calculus provides a repertoire of operations for such manipulation, namely project, reciprocal-project, associate, pattern-complete, and merge encompassing a complete computational system. Since the Assembly Calculus is, to our knowledge, the only extant computational system whose purpose is to bridge the gap identified by Axel in the above quote (Axel, 2018), it is of great interest to establish that complex cognitive functions can be plausibly expressed in it. Indeed, significance progress has been made over the past year, see for example Mitropolsky et al. (2021) for a parser of English and d’Amore et al. (2021) for a program mediating planning in the blocks world, both written in the AC programming system. Yet despite these recent advances, one fundamental question is left unanswered: If the Assembly Calculus is a meaningful abstraction of cognition and intelligence, why does it not have a learn command? How can the brain learn through assembly representations?

This is the question addressed and answered in this paper. As assembly operations are a new learning framework and device, one has to start from the most basic questions: Can this model classify assembly-encoded stimuli that are separated through clustering, or by half spaces? Recall that learning linear thresholds is a theoretical cornerstone of supervised learning, leading to a legion of fundamental algorithms: Perceptron, Winnow, multiplicative weights, isotron, kernels and SVMs, and many variants of gradient descent.

Following Papadimitriou et al. (2020), we model the brain as a directed graph of excitatory neurons with dynamic edge weights (due to plasticity). The brain is subdivided into areas, for simplicity each containing $n$ neurons connected through a $G_{n,p}$ random directed graph (Erdős and Rényi, 1960). Certain ordered pairs of areas are also connected, through random bipartite graphs. We assume that neurons fire in discrete time steps. At each time step, each neuron in a brain area will fire if its synaptic input from the firings of the previous step is among the top $k$ highest out of the $n$ neurons in its brain area. This selection process is called $k$-cap, and is an abstraction of the process of inhibition in the brain, in which a separate population of inhibitory neurons is induced to fire by the firing of excitatory neurons in the area, and through negatively-weighted connections prevents all but the most stimulated excitatory neurons from firing. Synaptic weights are altered via Hebbian plasticity and homeostasis (see Section 2 for a full description). In this stylized mathematical model, reasonably consistent with what is known about the brain, it has been shown that the operations of the Assembly Calculus converge and work as specified (with high probability relative to the underlying random graphs). These results have also been replicated by simulations in the model above, and also in more biologically realistic networks of spiking neurons (see Legenstein et al. (2018); Papadimitriou et al. (2020)). In this paper we develop, in the same model, mechanisms for learning to classify well-separated classes of stimuli, including clustered distributions and linear threshold functions with margin. Moreover, considering that the ability to learn from few examples, and with mild supervision, are crucial characteristics of any brain-like learning algorithm, we show that learning with assemblies does both quite naturally.

Here we outline the basics of the model in Papadimitriou et al. (2020). There are a finite number $a$ of brain areas, denoted $X,Y,\ldots$ (but in this paper, we will only need one brain area where learning happens, plus another area where the stimuli are presented). Each area is a random directed graph with $n$ nodes called neurons with each directed edge present independently with probability $p$ (for simplicity, we take $n$ and $p$ to be the same across areas). Some ordered pairs of brain areas are also connected by random bipartite graphs, with the same connection probability $p$. Importantly, each area may be inhibited, which means that its neurons cannot fire; the status of the areas is determined by explicit inhibit/disinhibit commands of the AC. ¹¹1The brain’s neuromodulatory systems (Jones, 2003; Harris and Thiele, 2011) are plausible candidates to implement these mechanisms. This defines a large random graph $G=(N,E)$ with $|N|=an$ nodes and a number $|E|$ of directed edges which is in expectation $(a+b)pn^{2}-apn$, where $b$ is the number of pairs of areas that are connected. Each edge $(i,j)\in E$ in this graph, called a synapse, has a dynamic non-negative weight $w_{ij}(t)$, initially $1$.

This framework gives rise to a discrete-time dynamical system, as follows: The state of the system at any time step $t$ consists of (a) a bit for each area $X$, inh$(X,t)$, initially $0$, denoting whether the area is inhibited; (b) a bit for each neuron $i$, fires$(i,t)$, denoting whether $i$ spikes at time $t$ (zero if the area $X$ of $i$ has inh$(X,t)=1$); and (c) the weights of all synapses $w_{ij}(t)$, initially one.

The state transition of the dynamical system is as follows: For each neuron $i$ in area $A$ with inh$(X,t+1)=0$ (see the next paragraph for how inh$(X,t+1)$ is determined), define its synaptic input at time $t+1$,

For each $i$ in area $X$ with inh$(X,t+1)=0$, we set fires$(i,t)=1$ iff $i$ is among the $k$ neurons in its area that have highest SI$(i,t+1)$ (breaking ties arbitrarily). This is the $k$-cap operation, a basic ingredient of the AC framework, modeling the inhibitory/excitatory balance of a brain area.²²2Binas et al. (2014) showed rigorously how a $k$-cap dynamic could be emerge in a network of excitatory and inhibitory neurons. As for the synaptic weights,

That is, if $j$ fires at time $t$ and $i$ fires at time $t+1$, Hebbian plasticity dictates that $w_{ji}$ be increased by a factor of $1+\beta$ at time $t+1$. So that the weights do not grow unlimited, a homeostasis process renormalizes, at a slower time scale, the sum of weights along the incoming synapses of each neuron (see Davis (2006) and Turrigiano (2011) for reviews of this mechanism in the brain).

Finally, the AC is a computational system driving the dynamical system by executing commands at each time step $t$ (like a programming language driving the physical system that is the computer’s hardware). The AC commands (dis)inhibit$(X)$ change the inhibition status of an area at time $t$; and the command fire$(x)$, where $x$ is the name of an assembly (defined next) in a disinhibited area, overrides the selection by $k$-cap, and causes the $k$ neurons of assembly $x$ to fire at time $t$.

An assembly is a highly interconnected (in terms of both number of synapses and their weights) set of $k$ neurons in an area encoding a real world entity. Initially, assembly-like representations exist only in a special sensory area, as representations of perceived real-world entities such as a heard (or read) word. Assemblies in the remaining, non-sensory areas are an emergent behavior of the system, copied and re-copied, merged, associated, etc., through further commands of the AC. This is how the model is able to simulate arbitrary $\frac{n}{k}$ space bounded computations (Papadimitriou et al., 2020). The most basic such command is project$(x,Y,y)$, which, starting from an assembly $x$ in area $X$, creates in area $Y$ (where there is connectivity from $X$ to $Y$) a new assembly $y$, which has strong synaptic connectivity from $x$ and which will henceforth fire every time $x$ fires in the previous step, and $Y$ is not inhibited. This command entails disinhibiting the areas $X,Y$, and then firing (the neurons in) assembly $x$ for the next $T$ time steps. It was shown by Papadimitriou and Vempala (2019) that, with high probability, after a small number of steps, a stable assembly $y$ in $Y$ will emerge, which is densely intraconnected and has high connectivity from $x$. The mechanism achieving this convergence involves synaptic input from $x$, which creates an initial set $y^{1}$ of firing neurons in $Y$, which then evolves to $y^{t},t=2,\ldots$ through sustained synaptic input from $x$ and recurrent input from $y^{t-1}$, while these two effects are further enhanced by plasticity.

Incidentally, this convergence proof (see Legenstein (2018); Papadimitriou and Vempala (2019); Papadimitriou et al. (2020) for a sequence of sharpened versions of this proof over the past years) is the most mathematically sophisticated contribution of this theory to date. The theorems of the present paper can be seen as substantial generalizations of that result: Whereas in previous work an assembly is formed as a copy of one stimulus firing repeatedly (memorization), so that this new assembly will henceforth fire whenever the same stimulus us presented again, in this paper we show rigorously that an assembly will be formed in response to the sequential firing of many stimuli, all drown from the same distribution (generalization), and the formed assembly will fire reliably every time another stimulus from the same distribution is presented.

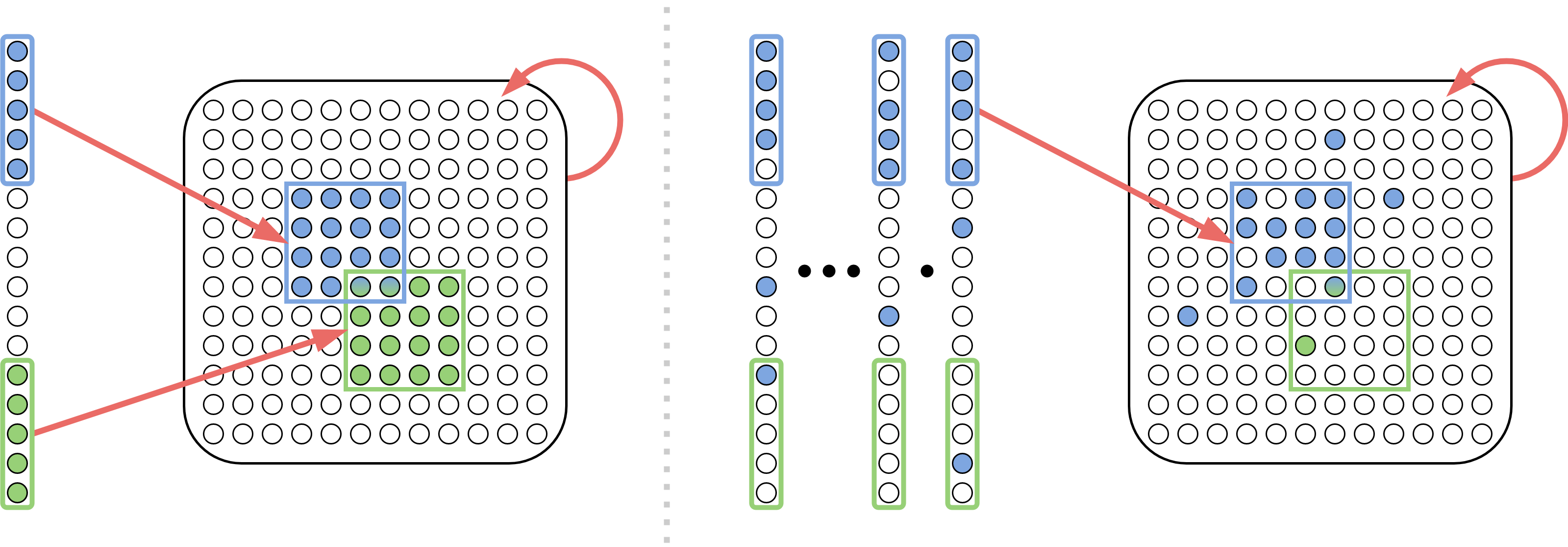
The key parameters of our model are $n,k,p$, and $\beta$. Intended values for the brain are $n=10^{7},k=10^{4},p=10^{-3},\beta=0.1$, but in our simulations we have also had success on a much smaller scale, with $n=10^{3},k=10^{2},p=10^{-1},\beta=0.1$. $\beta$ is an important parameter, in that adequately large values of $\beta$ guarantee the convergence of the AC operations. For a publicly available simulator of the Assembly Calculus (in which the Learning System below can be readily implemented) see \urlhttp://brain.cc.gatech.edu.

Very few stimuli sampled from an input distribution are activated sequentially at the sensory area. The only form of supervision required is that all training samples from a given class are presented consecutively. Plasticity and inhibition alone ensure that, in response to this activation, an assembly will be formed for each class, and that this same assembly will be recalled at testing upon presentation of other samples from the same distribution. In other words, learning happens. And in fact, despite all these limitations, we show that the device is an efficient learner of interesting concept classes.

Our first theorem is about the creation of an assembly in response to inputs from a stimulus class. This is a generalization of a theorem from Papadimitriou and Vempala (2019), where the input stimulus was held constant; here the input is a stream of random samples from the same stimulus class. Like all our results, it is a statement holding with high probability (WHP), where the underlying random event is the random graph and the random samples. When sampled stimuli fire, the assembly in the brain area changes. The neurons participating in the current assembly (those whose synaptic input from the previous step is among the $k$ highest) are called the current winners. A first-time winner is a current winner that participated in no previous assembly (for the current stimulus class).

This time the proof relies on the fact that the average weight of incoming connections to a neuron in ${A}^{*}$ is upper-bounded by

Finally, we consider the setting where the labeling function is a linear threshold function, parameterized by an arbitrary nonnegative vector $v$ and margin $\Delta$. We will create a single assembly to represent examples on one side of the threshold, i.e. those for which $v\cdot X\geq\|v\|_{1}k/n$. We define $\mathcal{D}_{+}$ denote the distribution of these examples, where each coordinate is an independent Bernoulli variable with mean $\mathbb{E}(X_{i})=k/n+\Delta v_{i}$, and define $\mathcal{D}_{-}$ to be the distribution of negative examples, where each coordinate is again an independent Bernoulli variable yet now all identically distributed with mean $k/n$. (Note that the support of the positive and negative distributions is the same; there is a small probability of drawing a positive example from the negative distribution, or vice versa.) To serve as a classifier, a fraction $1-\epsilon_{+}$ of neurons in the assembly must be guaranteed to fire for a positive example, and a fraction $\epsilon_{-}<1-\epsilon_{+}$ guaranteed not to fire for a negative one. A test example is then classified as positive if at least a $1-\epsilon$ fraction of neurons in the assembly fire (for $\epsilon\in[\epsilon_{-},1-\epsilon_{+}]$), and negative otherwise. The last theorem shows that this can in fact be done with high probability, as long as the normal vector $v$ of the linear threshold is neither too dense nor too sparse. Additionally, we assume synapses are subject to homeostasis in between training and evaluation; that is, all of the incoming weights to a neuron are normalized to sum to 1.

Since our focus in this paper is on highlighting the brain-like aspects of this learning mechanism, we emphasize stimulus classes as a case of particular interest, as they are a probabilistic generalization of the single stimuli considered in Papadimitriou and Vempala (2019). Linear threshold functions are an equally natural way to generalize a single $k$-sparse stimulus, say $v$; all the 0/1 points on the positive side of the threshold $v^{\top}x\geq\alpha k$ have at least an $\alpha$ fraction of the $k$ neurons of the stimulus active.

Finally, reading the output of the device by the Assembly Calculus is simple: Add a readout area to the two areas so far (stimulus and learning), and project to this area one of the assemblies formed in the learning area for each stimulus class. The assembly in the learning area that fires in response to a test sample will cause the assembly in the readout area corresponding to the class to fire, and this can be sensed through the readout operation of the AC.

The learning algorithm has been run on both synthetic and real-world datasets, as illustrated in the figures below. Code for experiments is available at \urlhttps://github.com/mdabagia/learning-with-assemblies.

Beyond the basic method of presenting a few examples from the same class and allowing plasticity to alter synaptic weights, the training procedure is slightly different for each of the concept classes (stimulus classes, linearly-separated, and MNIST digits). In each case, we renormalize the incoming weights of each neuron to sum to one after concluding the presentation of each class, and classification is performed on top of the learned assemblies by predicting the class corresponding to the assembly with the most neurons on.

• •

  For stimulus classes, we estimate the assembly for each class as composed of the neurons which fired in response to the last training example, which in practice are the same as those most likely to fire for a random test example.

• •

  For a linear threshold, we only present positive examples, and thus only form an assembly for one class. As with stimulus classes, the neurons in the assembly can be estimated by the last training cap or by averaging over test examples. We classify by comparing against a fixed threshold, generally half the cap size.

Additionally, it is important to set the plasticity parameter ($\beta$) large enough that assemblies are reliably formed. We had success with $\beta=0.1$ for stimulus classes and $\beta=1.0$ for linear thresholds.

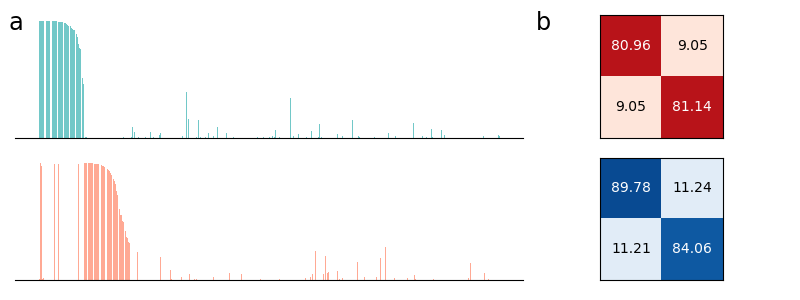
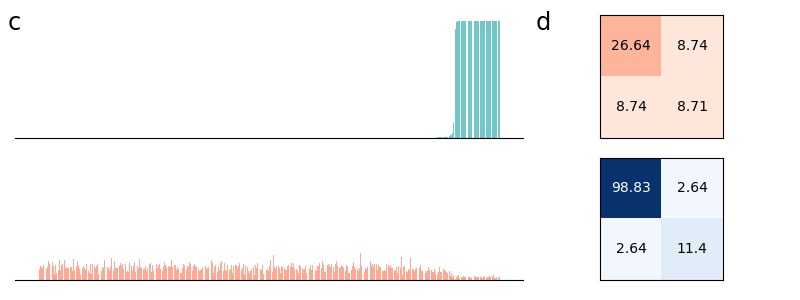
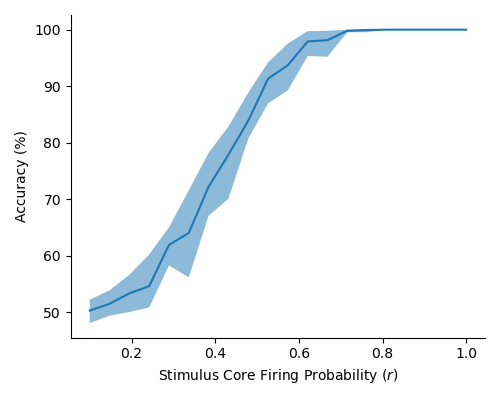
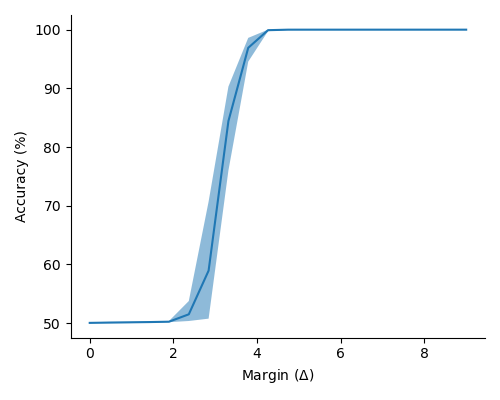
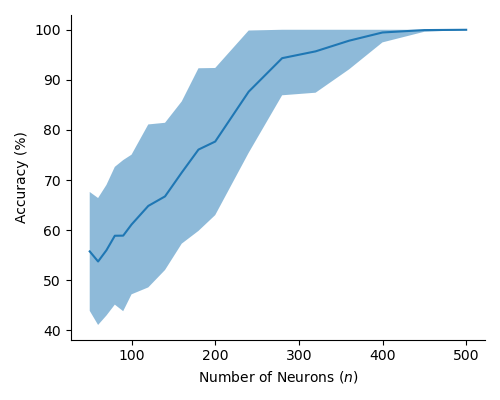
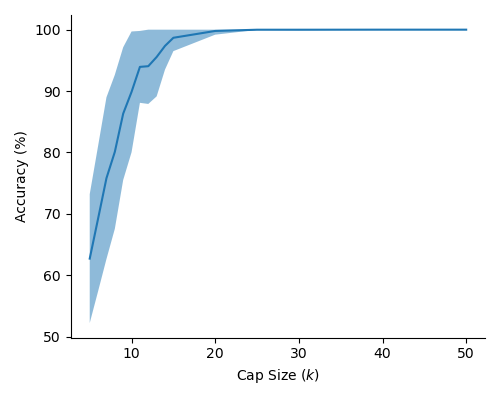
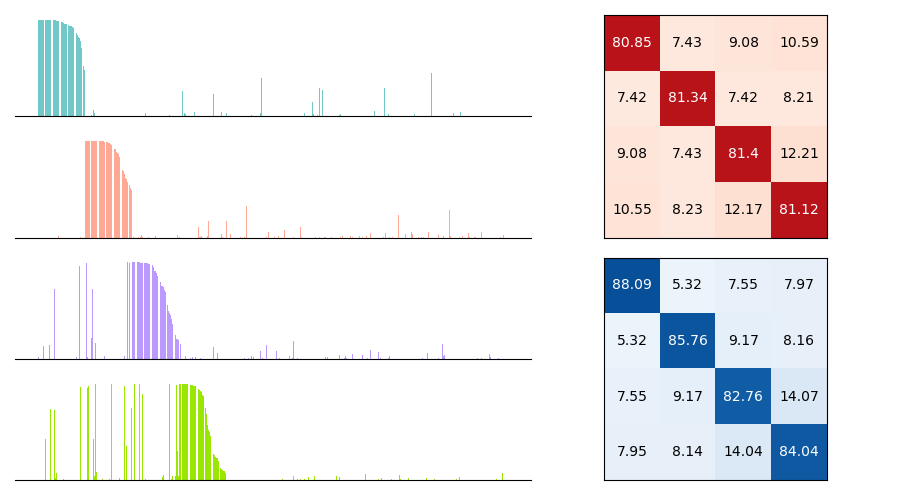
In Figure 2 (a) & (b), we demonstrate learning of two stimulus classes, while in Figure 2 (c) & (d), we demonstrate the result of learning a well-separated linear threshold function with assemblies. Both had perfect accuracy. Additionally, assemblies readily generalize to a larger number of classes (see Figure 6 in the appendix). We also recorded sharp threshold transitions in classification performance as the key parameters of the model are varied (see Figures 3 & 4).

There are a number of possible extensions to the simplest strategy, where within a single brain region we learn an assembly for each concept class and classify based on which assembly is most activated in response to an example. We compared the performance of various classification models on MNIST as the number of features increases. The high-level model is to extract a certain number of features using one of the five different methods, and then find the best linear classifier (of the training data) on these features to measure performance (on the test data). The five different feature extractors are:

• •

  Linear features. Each feature’s weights are sampled i.i.d. from a Gaussian with standard deviation $0.1$.

• •

  Nonlinear features. Each feature is a binary neuron: it has $784$ i.i.d. Bernoulli$(0.2)$ weights, and ‘fires’ (has output $1$, otherwise $0$) if its total input exceeds the expected input ($70\times 0.2$).

• •

  Large area assembly features. In a single brain area of size $m$ with cap size $m/10$, we attempt to form an assembly for each class. The area sees a sequence of $5$ examples from each class, with homeostasis applied after each class. Weights are updated according to Hebbian plasticity with $\beta=1.0$. Additionally, we apply a negative bias: A neuron which has fired for a given class is heavily penalized against firing for subsequent classes.

• •

  ’Random’ assembly features. For a total of $m$ features, we create $m/100$ different areas of $100$ neurons each, with cap size $10$. We then repeat the large area training procedure above in each area, with the order of the presentation of classes randomized for each area.

• •

  ’Split’ assembly features: For a total of $m$ features, we create $10$ different areas of $m/10$ neurons each, with cap size $m/100$. Area $i$ sees a sequence of $5$ examples from class $i$. Weights are updated according to Hebbian plasticity, and homeostasis is applied after training.

After extracting features, we train the linear classification layer to minimize cross-entropy loss on the standard MNIST training set ($60000$ images) and finally test on the full test set ($10000$ images).

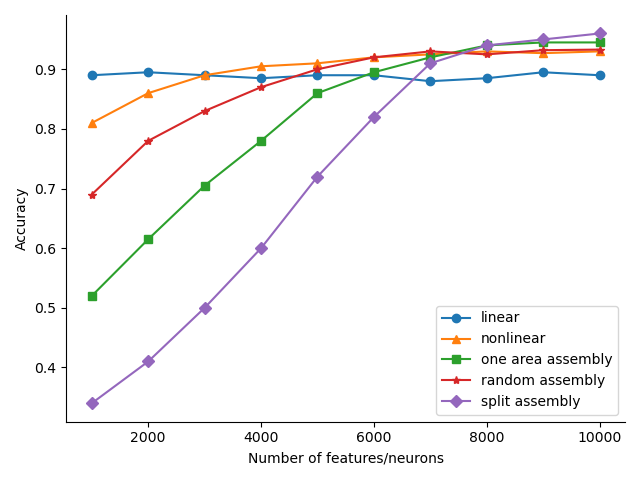
The results as the total number of features ranges from $1000$ to $10000$ is shown in Fig. 5. ’Split’ assembly features are ultimately the best of the five, with ’split’ features achieving $96\%$ accuracy with $10000$ features. However, nonlinear features outperform ’split’ and large-area features and match ’random’ assembly features when the number of features is less than $8000$. For reference, the linear classifier gets to $89\%$, while a two-layer neural network with width $800$ trained end-to-end gets to $98.4\%$.

Going further, one could even create a hierarchy of brain areas, so that the areas in the first “layer” all project to a higher-level area, in hopes of forming assemblies for each digit in the higher-level area which are more robust. In this paper, our goal was to highlight the potential to form useful representations of a classification dataset using assemblies, and so we concentrated on a single layer of brain areas with a very simple classification layer on top. It will be interesting to explore what is possible with more complex architectures.

Assemblies are widely believed to be involved in cognitive phenomena, and the AC provides evidence of their computational aptitude. Here we have made the first steps towards understanding how learning can happen in assemblies. Normally, an assembly is associated with a stimulus, such as Grandma. We have shown that this can be extended to a distribution over stimuli. Furthermore, for a wide range of model parameters, distinct assemblies can be formed for multiple stimulus classes in a single brain area, so long as the classes are reasonably differentiated.

A model of the brain at this level of abstraction should allow for the kind of classification that the brain does effortlessly — e.g., the mechanism that enables us to understand that individual frames in a video of an object depict the same object. With this in mind, the learning algorithm we present is remarkably parsimonious: it generalizes from a handful of examples which are seen only once, and requires no outside control or supervision other than ensuring multiple samples from the same concept class are presented in succession (and this latter requirement could be relaxed in a more complex architecture which channels stimuli from different classes). Finally, even though our results are framed within the Assembly Calculus and the underlying brain model, we note that they have implications far beyond this realm. In particular, they suggest that any recurrent neural network, equipped with the mechanisms of plasticity and inhibition, will naturally form an assembly-like group of neurons to represent similar patterns of stimuli.

But of course, many questions remain. In this first step we considered a single brain area — whereas it is known that assemblies draw their computational power from the interaction, through the AC, among many areas. We believe that a more general architecture encompassing a hierarchy of interconnected brain areas, where the assemblies in one area act like stimulus classes for others, can succeed in learning more complex tasks — and even within a single brain area improvements can result from optimizing the various parameters, something that we have not tried yet.

In another direction, here we only considered Hebbian plasticity, the simplest and most well-understood mechanism for synaptic changes. Evidence is mounting in experimental neuroscience that the range of plasticity mechanisms is far more diverse (Magee and Grienberger, 2020), and in fact it has been demonstrated recently (Payeur et al., 2021) that more complex rules are sufficient to learn harder tasks. Which plasticity rules make learning by assemblies more powerful?

We showed that assemblies can learn nonnegative linear threshold functions with sufficiently large margins. Experimental results suggest that the requirement of nonnegativity is a limitation of our proof technique, as empirically assemblies readily learn arbitrary linear threshold functions (with margin). What other concept classes can assemblies provably learn? We know from support vector machines that linear threshold functions can be the basis of far more sophisticated learning when their input is pre-processed in specific ways, while the celebrated results of Rahimi and Recht (2007) demonstrated that certain families of random nonlinear features can approximate sophisticated kernels quite well. What would constitute a kernel in the context of assemblies? The sensory areas of the cortex (of which the visual cortex is the best studied example) do pre-process sensory inputs extracting features such as edges, colors, and motions. Presumably learning by the non-sensory brain — which is our focus here — operates on the output of such pre-processing. We believe that studying the implementation of kernels in cortex is a very promising direction for discovering powerful learning mechanisms in the brain based on assemblies.

We thank Shivam Garg, Chris Jung, and Mirabel Reid for helpful discussions. MD is supported by an NSF Graduate Research Fellowship. SV is supported in part by NSF awards CCF-1909756, CCF-2007443 and CCF-2134105. CP is supported by NSF Awards CCF-1763970 and CCF-1910700, and by a research contract with Softbank.