Association of Atoms into Universal Dimers
using an Oscillating Magnetic Field

Introduction. The field of ultracold atoms has extended the frontiers of few-body and many-body physics by providing pristine systems in which the interactions between the constituents are simple and have strengths that can be controlled experimentally. The frontiers of few-body physics include the study of universal molecules, which have properties determined by the large scattering length $a$ of the atoms, and universal reaction rates, whose dependence on $a$ and on kinematic variables is consistent with asymptotic scale invariance or discrete scale invariance Braaten:2004rn . The need for accurate calculations of universal properties has pushed the computational frontiers to the 4-body problem and beyond. In many-body physics, the frontiers include the study of superfluidity and other novel phases of matter IKS:0801 . Accurate measurements of the properties of systems of ultracold atoms present a challenge to many-body calculational methods because of the strong correlations produced by a large scattering length. Particularly challenging is the unitary limit in which $a$ is infinitely large and the interactions between the constituents are the strongest allowed by quantum mechanics.

Few-body physics provides powerful constraints on many-body physics through universal relations pioneered by Tan Tan0505 ; Tan0508 ; Tan0803 . Many of these relations involve the contact, an extensive property of the system that is conjugate to $1/a$ and provides a measure of the probability for pairs of particles to be very close together. The contact controls the thermodynamics of a many-body system and also determines the high-momentum and high-frequency tails of correlation functions Braaten:2010if .

One way to produce universal molecules in a system of ultracold atoms is magneto-association – the modulation of the magnetic field near a Feshbach resonance with frequency near that determined by the binding energy of the molecule. This method was first used by Thompson, Hodby, and Wieman to produce shallow dimers composed of ⁸⁵Rb atoms Wieman0505 . It has since been used to produce dimers with various other atoms as constituents and to measure their binding energies Wieman0607 ; Jin0703 ; Jin0712 ; Inguscio0808 ; Grimm0810 ; Khaykovich1009 ; Hulet1302 . Magneto-association has also been used to associate ⁷Li atoms into Efimov trimers Khaykovich1201 .

In this paper, we derive the magneto-association rate for universal molecules in a many-body system of ultracold atoms. Many-body effects are taken into account through a transition matrix element of the contact operator. We deduce simple expressions for the transition rate for producing universal dimers in a thermal gas of bosons or fermions and in a Bose-Einstein condensate (BEC) as a function of frequency. The dramatic increase in the width of the peak in the transition rate near an atom-dimer resonance provides a signature for new universal tetramers that are Efimov states consisting of two atoms and a dimer.

Transition rate. We consider a system of ultracold atoms in a magnetic field that has a constant value $\bar{B}$ for $t<0$ and oscillates with a small amplitude $b$ for $t>0$: $B(t)=\bar{B}+b\sin(\omega t)$. Near a Feshbach resonance, the scattering length is a function of the magnetic field: $a(B)=a_{\rm bg}[1-\Delta/(B-B_{0})]$, where $a_{\rm bg}$ is the background scattering length, and $B_{0}$ and $B_{0}+\Delta$ are the positions of the pole and the zero of the scattering length, respectively. The inverse scattering length can be expanded in powers of $b$:

where $\bar{a}=a(\bar{B})$. The deviation of $1/a(t)$ from $1/\bar{a}$ can be treated as a periodic time-dependent perturbation. By Tan’s adiabatic relation, a small change in $1/a$ produces a change in the energy that is proportional to the contact $C$ Tan0508 . Thus the perturbing Hamiltonian is proportional to the contact. In the case of identical bosons with mass $m$, it can be expressed as

(In the case of fermions with two spin states, the prefactor should be multiplied by 2.) The leading term of order $b$ in $H_{\rm pert}(t)$ drives transitions to states with energies that are higher or lower by $\hbar\omega$. Higher order terms drive transitions to states whose energies differ by larger integer multiples of $\hbar\omega$. If $\bar{a}$ is large and positive and if $\hbar\omega$ is near the binding energy $\hbar^{2}/m\bar{a}^{2}$ of the shallow dimer, the first-order perturbation can associate pairs of atoms into dimers.

The transition rate $\Gamma(\omega)$ of the initial state $|i\rangle$ into final states $|f\rangle$ at leading order in $b$ is given by Fermi’s Golden Rule:

where $E_{i}$ and $E_{f}$ are the energies of the initial state and the final states, respectively. (In the case of fermions with two spin states, the prefactor should be multiplied by 4.) The Lorentzian factor allows for the possibility that the final state involves the excitation of a resonance with lifetime $1/\Gamma_{f}$. In the limit $\Gamma_{f}\to 0$, this factor reduces to $2\pi\delta(E_{i}\pm\hbar\omega-E_{f})$.

The association of molecules in a time-dependent magnetic field has been considered previously by Hanna, Köhler, and Burnett HKB0609 . They calculated the probability for producing a dimer as a function of time by solving the time-dependent Schroedinger equation for two atoms in a two-channel model with a closed channel. A major disadvantage of this approach is its inability to account for many-body effects, which are taken into account in Eq. (2) through the transition matrix element of $C$.

It is convenient to express the contact operator in Eq. (2) as the integral of the contact density operator: $C=\int d^{3}r\,{\cal C}(\bm{r})$. The field theoretic definition of the contact Braaten:2008uh reveals that the contact density operator can be expressed as ${\cal C}=\phi^{\dagger}\phi$, where the contact field $\phi(\bm{r})$ is a local operator that annihilates two atoms at a point. The transition matrix element can be expressed as

A complete set of states $\sum_{n}|n\rangle\langle n|=1$ can be inserted between $\phi^{\dagger}$ and $\phi$. If only one term in the sum is nonzero, the matrix element factors into a matrix element of $\phi$ that involves the initial state and a matrix element of $\phi^{\dagger}$ that involves the final state.

For a many-body system whose number density $n(\bm{R})$ varies slowly with the position $\bm{R}$, the transition rate can be simplified by using the local density approximation. The matrix element of ${\cal C}$ can be expressed in terms of the matrix element for the homogeneous system whose initial state $|i\rangle$ has constant number density equal to $n(\bm{R})$. By exploiting the translational invariance of the homogeneous system, the modulus squared of the matrix element summed over final states can be reduced to

where $P_{i}$ and $P_{f}$ are the total momenta of the initial and final states of the homogeneous system, respectively.

In a system of ultracold trapped bosonic atoms, a low-momentum dimer produced by magneto-association will eventually suffer an inelastic collision, producing energetic particles that escape from the trapping potential. An inelastic collision with a single atom results in the loss of 3 atoms. An inelastic collision with two atoms results in the loss of 4 atoms. The transition rate can be determined from measurements of the loss of trapped atoms. For fermionic atoms, a different method would be required to measure the transition rate.

Thermal gas. We first consider a dilute thermal gas of atoms, whose momentum distribution can be approximated by a Boltzmann distribution with temperature $T$ and local number density $n$. If the gas consists of a large number $N$ of bosonic atoms, any of the $N^{2}/2$ pairs of atoms can make the transition to the dimer. The transition matrix element reduces to the matrix element of $\phi^{\dagger}\phi$ between the dimer state $\langle{\rm D}|$ and the state $|{\rm AA}\rangle$ for the pair of atoms that makes the transition. Upon inserting the projector $|0\rangle\langle 0|$ onto the vacuum state between $\phi^{\dagger}$ and $\phi$, the square of the matrix element can be expressed as the product of the contact for a dimer, which is equal to $16\pi/\bar{a}$, the contact for a pair of atoms with relative wavenumber $k$, which can be deduced from the contact for a pair of atoms in thermal equilibrium derived in Ref. Braaten:2013eya , and factors of the volume $V$ associated with the normalization of plane-wave states:

The factor of $N^{2}/V^{2}$ can be replaced by $n^{2}(\bm{R})$. The Lorentzian function in Eq. (3) reduces to a delta function. The transition rate is zero if $\hbar\omega<\hbar^{2}/m\bar{a}^{2}$. For larger $\omega$, the transition rate is

where $k(\omega)=(m\omega/\hbar-1/\bar{a}^{2})^{1/2}$ and $\lambda_{T}=(2\pi\hbar^{2}/mkT)^{1/2}$. (The transition rate for fermions is obtained by replacing $n^{2}$ by $2n_{1}n_{2}$, where $n_{i}$ is the number density for spin state $i$.) The first subharmonic transition rate due to the order-$b^{2}$ perturbation in Eq. (2) can be obtained from Eq. (7) by multiplying by $[b/2(\bar{B}-B_{0}-\Delta)]^{2}$ and making the substitution $\omega\to 2\omega$.

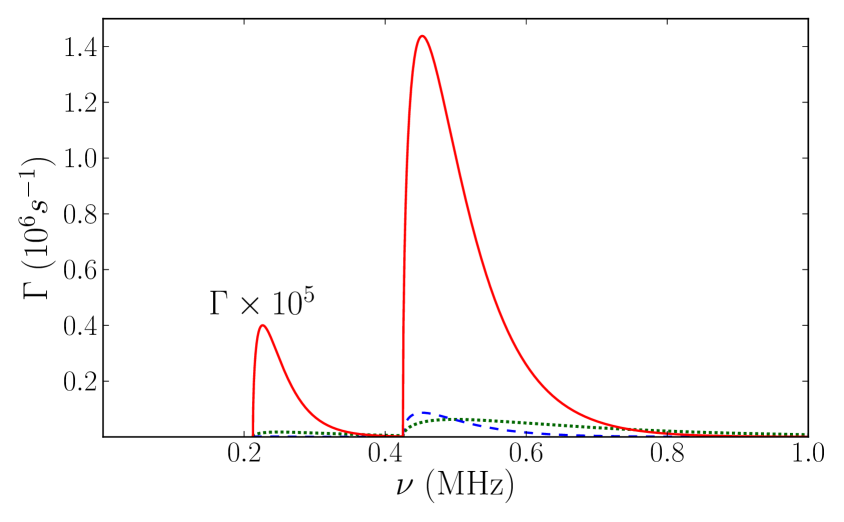
The loss of atoms from magneto-association into dimers has been studied by Dyke et al. using a thermal gas of ⁷Li atoms at a magnetic field $\bar{B}=734.5$ G, where the scattering length is $\bar{a}=1100~a_{0}$ Hulet1302 . They reported the fraction of atoms remaining after an unspecified time as a function of the frequency for three combinations of the modulation amplitude and the temperature. In Fig. 1, the predicted transition rates $\Gamma(\omega)$ for these three conditions, including the first subharmonic, are shown as functions of the frequency $\nu=\omega/2\pi$.

Bose-Einstein condensate. We next consider a dilute BEC of atoms at zero temperature with local number density $n$. The contact field $\phi$ can be expressed as the sum of its expectation value $\bar{\phi}$ and a quantum fluctuation field $\tilde{\phi}$: $\phi(\bm{r})=\bar{\phi}+\tilde{\phi}(\bm{r})$. The field $\tilde{\phi}^{\dagger}$ has a nonzero amplitude to create a dimer in the BEC. The contribution to the matrix element of $\phi^{\dagger}\phi$ between the state $\langle i+{\rm D}|$ in which a dimer has been excited and the BEC $|i\rangle$ comes from the $\tilde{\phi}^{\dagger}\bar{\phi}$ term. The product of $\bar{\phi}$ and its complex conjugate is the contact density of the BEC, which in the dilute limit is $\bar{\phi}^{*}\bar{\phi}=16\pi^{2}\bar{a}^{2}n^{2}$. The square of $\langle i+{\rm D}|\tilde{\phi}^{\dagger}|i\rangle$ is the contact of the dimer, which in the dilute limit is simply $16\pi/\bar{a}$. The most dramatic dependence on the frequency comes from the Lorentzian in Eq. (3). The dimer in the BEC behaves like a resonance whose complex energy $E_{\rm D}-i\hbar\Gamma_{\rm D}/2$ is the sum of the binding energy $-\hbar^{2}/m\bar{a}^{2}$ and the mean field energy from forward scattering of the dimer from 0-momentum atoms in the condensate. The transition rate to dimers in the BEC is

The spatial integral is a density-weighted average of a Lorentzian with a density-dependent width $\Gamma_{\rm D}$.

The complex energy of a dimer in the BEC is given by

The leading mean-field correction to $E_{\rm D}$ comes from the atom-dimer (AD) scattering length $a_{\rm AD}$. By the optical theorem, $\Gamma_{\rm D}$ is determined by the inelastic scattering rate of the dimer. If there are deep dimers, the leading contribution to $\Gamma_{\rm D}$ comes from AD scattering into an atom and a deep dimer, whose rate coefficient is $\beta_{\rm AD}=6\pi\hbar(-{\rm Im}\,a_{\rm AD})/m$. The universal results for $a_{\rm AD}$ and $\beta_{\rm AD}$ are given in Ref. Braaten:2004rn as functions of $a_{*}$ and $\eta_{*}$, where $a_{*}\exp(-i\eta_{*}/s_{0})$ is the complex scattering length where $a_{\rm AD}$ diverges. In the absence of deep dimers, the leading contributions to $\Gamma_{\rm D}$ come from atom-atom-dimer (AAD) recombination into two shallow dimers or into an Efimov trimer and an atom. We define $\alpha_{\rm AAD}$ so that the event rate per volume in a dilute thermal gas with atom and dimer number densities $n$ and $n_{D}$ is $\alpha_{\rm AAD}n^{2}n_{D}$.

Atom-atom-dimer recombination. The universal result for the AAD recombination rate at threshold has been calculated by Deltuva Deltuva:2012xf . The rate constant $\alpha_{\rm AAD}$ can be expressed as $\hbar a^{4}/m$ multiplied by a log-periodic function of $a$ with discrete scaling factor $e^{\pi/s_{0}}\approx 22.7$, where $s_{0}\approx 1.00624$. The log-periodic function has a minimum value of $118$ at $a=5.5~a_{*}$. It increases dramatically as $a$ approaches $a_{*}$ as a consequence of the Efimov effect in the AAD system. The associated Efimov states are universal tetramers whose existence was first pointed out by Braaten and Hammer Braaten:2004rn . Their binding energies and widths in the zero-range limit have been calculated by Deltuva Deltuva:2012ms . The constituents of the AAD system have a mass ratio of 2 and the most resonant interaction is between an atom and a dimer. The associated discrete scaling factor for $a_{\rm AD}$ is $e^{\pi/s_{2}}\approx 2\times 10^{5}$, where $s_{2}\approx 0.257206$. The universal 3-body recombination rates for systems with two identical particles that have resonant interactions with a third particle have been calculated by Helfrich, Hammer, and Petrov for arbitrary mass ratio Helfrich:2010yr . Near an AD resonance $a_{*}$ where $a_{\rm AD}=\pm\infty$, the limiting behavior of $\alpha_{\rm AAD}$ is $(k_{\rm AT}+k_{\rm DD})\hbar a_{\rm AD}^{4}/m$, where $k_{\rm AT}+k_{\rm DD}$ is a log-periodic function of $a_{\rm AD}$ with discrete scaling factor $e^{\pi/s_{2}}$. For $a$ approaching $a_{*}$ from above, the separate contributions from final states consisting of shallow trimer and atom or two dimers are

The atom-trimer contribution has interference minima when $a_{\rm AD}$ is equal to $(e^{\pi/s_{2}})^{n}a_{2+}$, where $n$ is an integer. For $a$ approaching $a_{*}$ from below, the combined contribution from final states consisting of two dimers or deeper trimer and atom are

There are resonance peaks when $a_{\rm AD}$ is equal to $(e^{\pi/s_{2}})^{n}a_{2-}$, where $n$ is an integer, from Efimov states passing through the AAD threshold. The coefficient $k_{2}=36.3367$ and the ratio $|a_{2-}|/a_{2+}=e^{\pi/2s_{2}}\approx 449.053$ are universal constants. Efimov states disappear through the atom-trimer threshold when $a_{\rm AD}$ is equal to $(e^{\pi/s_{2}})^{n}a_{2*}$, where $n$ is an integer. The universal ratio $a_{2*}/|a_{2-}|\approx 0.90$ can be determined by interpolating between numerical results given in Ref. Helfrich:2010yr . The value of $a_{2*}$ was determined by Deltuva in Ref. Deltuva:2012ms : $a_{2*}\approx 1.608~a_{*}$. The value of $\eta_{2*}$ can be determined by fitting Deltuva’s results in Ref. Deltuva:2012xf : $\eta_{2*}\approx 0.01$. If there are deep dimers, they provide additional recombination channels. Their effects can be taken into account by making the substitution $a_{*}\to a_{*}e^{-i\eta_{*}/s_{0}}$ in the amplitudes that give the rate constants in Eqs. (10) and (11).

Dimer width in the BEC. In a dilute BEC of trapped atoms, the transition rate for producing dimers given by Eq. (8) has a peak for $\omega$ near $\hbar/ma^{2}$. For a generic scattering length, the effect of the AD scattering term in Eq. (9a) is to shift the peak by a fractional amount of order $na^{3}$, which is small if the BEC is dilute. Near an AD resonance $a_{*}$, the fractional shift increases to order $na^{2}|a_{\rm AD}|$. However the fractional shift from AAD scattering is of order $n^{2}a^{2}|a_{\rm AD}|^{4}$, which can be larger if $n|a_{\rm AD}|^{3}$ is much larger than 1.

The width $\Gamma_{\rm D}$ of the peak in the transition rate is given by Eq. (9b). For a generic scattering length, the contributions to $\Gamma_{\rm D}$ from inelastic AD scattering and from AAD recombination are suppressed relative to $\hbar^{2}/ma^{2}$ by factors of order $\eta_{*}na^{3}$ and $n^{2}a^{6}$, respectively. Near an AD resonance $a_{*}$, these factors increase to order $\eta_{*}na|a_{\rm AD}|^{2}$ and $n^{2}a^{2}|a_{\rm AD}|^{4}$, respectively. When $na|a_{\rm AD}|^{2}$ is much larger than $\eta_{*}$, the AAD contribution to $\Gamma_{\rm D}$ can be larger than the AD contribution.

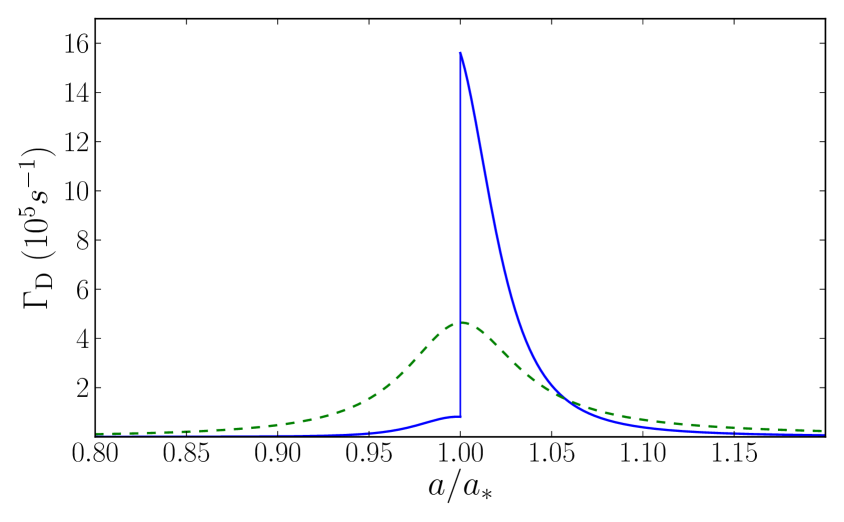
In Ref. Hulet1302 , Dyke et al. also studied the loss of atoms from their magneto-association into dimers in a BEC of about $4\times 10^{5}$ ⁷Li atoms at a magnetic field $\bar{B}=734.5$ G with modulation amplitude $b=0.14$ G. The local number density can be approximated by a Thomas-Fermi density profile with central number density $n=2.85/\mu m^{3}$. In Fig. 1, the dimer width $\Gamma_{\rm D}$ for $a_{*}=317~a_{0}$ and $\eta_{*}=0.038$ is shown as a function of $a$. The AD contribution is a Lorentzian centered at $a_{*}$. The AAD contribution is discontinuous at $a_{*}$, because there is an additional contribution for $a>a_{*}$ from recombination into an atom and the Efimov trimer that disappears through the atom-dimer threshold at $a_{*}$. The AAD contribution is smaller than the AD contribution for $a<a_{*}$, but it is larger in the range $a_{*}<a<1.05~a_{*}$. If $n$ is changed by a factor of $x$, the AD and AAD contributions change by factors of $x$ and $x^{2}$, respectively.

Summary. We have derived a simple expression for the magneto-association rate of universal molecules that takes into account many-body effects through the transition matrix element of the contact. We have applied it to the magneto-association of atoms into dimers in a thermal gas and in a BEC. The width of the dimer peak in a BEC is dramatically enhanced near an atom-dimer resonance. The contribution to the width from atom-atom-dimer recombination provides a signature for universal tetramers that are Efimov states consisting of two atoms and a dimer. There are many other applications of the transition rate in an oscillating magnetic field, including the magneto-association of atoms into Efimov trimers and the magneto-dissociation of paired fermions in a superfluid. Thus the transition rate in an oscillating magnetic field provides a new window into the constraints on many-body physics provided by few-body physics.