Asymmetry in the presence of migration stabilizes multistrain disease outbreaks
Abstract
We study the effect of migration between coupled populations, or patches, on the stability properties of multistrain disease dynamics. The epidemic model used in this work displays a Hopf bifurcation to oscillations in a single well mixed population. It is shown numerically that migration between two non-identical patches stabilizes the endemic steady state, delaying the onset of large amplitude outbreaks and reducing the total number of infections. This result is motivated by analyzing generic Hopf bifurcations with different frequencies and with diffusive coupling between them. Stabilization of the steady state is again seen, indicating that our observation in the full multistrain model is based on qualitative characteristics of the dynamics rather than on details of the disease model.
I Introduction
In this work we study the stability of a multistrain disease model in two coupled populations. Multistrain diseases are diseases with multiple coexisting strains, such as influenza (Andreasen et al.,, 1997), HIV (Hu et al.,, 1996), and dengue (Ferguson et al., 1999b, ). We consider two kinds of strain interactions: cross immunity and antibody-dependent enhancement. When the disease infects an individual, his or her immune system creates serotype-specific antibodies, which will protect the individual against that serotype. However, antibodies may also give some cross-protection to the other serotypes (Halstead,, 2007). This reduced susceptibility to the other serotypes may be temporary. When the temporary cross immunity wanes, heterologous secondary infections are possible. Low level antibodies developed from primary infections may form complexes with the virus so that more cells are affected, and viral load is increased (Vaughn et al.,, 2000). This effect is called antibody-dependent enhancement (ADE), and it has been observed in vitro in diseases such as ebola (Takada et al.,, 2003) and dengue (Halstead and O’Rourke,, 1977). Throughout this work we make the hypothesis that ADE increases the infectiousness of secondary infective cases due to the higher viral load (Cummings et al.,, 2005; Schwartz et al.,, 2005). Alternative views of ADE as an increase in mortality associated with secondary infectives can be considered (Kawaguchi et al.,, 2003). We focus in this paper on the multistrain disease dengue, which is believed to exhibit both temporary cross immunity and antibody-dependent enhancement (Halstead,, 2007). Dengue is a subtropical mosquito-borne disease that exhibits up to four serotypes. It is widespread in tropical regions of southeast Asia, Africa, and the Americas, infecting an estimated 50 to 100 million people every year (World Health Organization Website,, 2006). Primary infections may be asymptomatic, while secondary infections are more severe, with about of secondary infections leading to dengue hemorrhagic fever (DHF) or dengue shock syndrome (DSS), the potentially fatal forms of the disease (World Health Organization Website,, 2006). An effective vaccine against dengue is very difficult to achieve. Because of ADE, infection with an unvaccinated strain following a single strain vaccination may lead to the more severe symptoms associated with secondary infections (Halstead and Deen,, 2002). Therefore, an effective vaccine must protect against all four serotypes simultaneously. A recent theoretical study (Billings et al.,, 2008) has shown that eradication of dengue using only single-strain vaccines is unlikely. Because a tetravalent vaccine is not immediately forthcoming, deepening our understanding of the dynamics of dengue in more realistic models is of great importance.
The dynamics of dengue in a single, well mixed population has been studied in several recent publications, including but not limited to Ferguson et al., 1999a ; Schwartz et al., (2005); Cummings et al., (2005); Wearing and Rohani, (2006); Bianco et al., (2009). ADE and cross immunity have been shown to play a fundamental role in the spreading of dengue, causing instability, desynchronization of serotypes, and chaotic outbreaks (Schwartz et al.,, 2005; Cummings et al.,, 2005; Bianco et al.,, 2009). However, real populations may be spatially heterogeneous. To gain further insight into the wide spectrum of possible dengue dynamics, we relax the assumption of a well mixed population. The division of a population into spatially distinct patches simulates the potentially heterogeneous environment in which the disease spreads. Spatial heterogeneity has been invoked in the past to account for the persistent character of some infectious diseases (Lloyd and May,, 1996; Hagenaars et al.,, 2004) and to explain in-phase and out-of-phase dynamics of diseases (He and Stone,, 2003). A multipatch model with age structure has been used to explain bi- and tri-annual oscillations in the spread of measles (Bolker and Grenfell,, 1995).
Including human mobility patterns has a significant influence on the spreading of infectious disease. We will assume here that the coupling between patches is via migration, movement of individuals from one patch into another (as in Liebovitch and Schwartz, (2004); Ruan et al., (2006); Sattenspiel and Dietz, (1995); Grais et al., (2003)). An alternative coupling strategy is mass action coupling, in which susceptibles in one patch are assumed to interact with infectives in another patch, introducing nonlinear coupling terms (Bolker and Grenfell,, 1995; Lloyd and May,, 1996; Rohani et al.,, 1999). Stochastic coupling has also been modeled (see Keeling and Rohani, (2002) and references therein, and Colizza and Vespignani, (2008)).
The purpose of this work is to analyze the stability of a model for multistrain diseases with interacting strains, using dengue as an example, in a system of two coupled patches. Since chaotic outbreaks are likely to produce a higher number of infected individuals, understanding the stability properties may play an important role in public health. The case of non-identical parameters in the two patches will be of particular interest, as this serves as a model for spatial heterogeneity. The paper is divided as follows. In Section II we introduce the epidemic model. Section III summarizes the bifurcation structure for a single patch. In Section IV we present numerical results for bifurcations in two coupled patches. Section V motivates these results via analysis of a simple, lower dimensional model, and Section VI concludes.
II Model
We use a compartmental model for multistrain disease spread with cross immunity and antibody-dependent enhancement, which was previously studied in a single well-mixed population by Bianco et al., (2009). In this model, individuals may develop a primary infection with any of the serotypes. Immediately after recovering, the individual experiences a period of temporary partial cross immunity to all other serotypes. When the cross immunity wears off, immunity to the primary infecting strain is retained, but the individual may develop a secondary infection with a different serotype. Infectiousness of the secondary infectives is increased due to antibody-dependent enhancement. After the secondary infection, complete immunity to all serotypes is assumed. A flow diagram for the single patch model with two serotypes is shown in Figure 1 for simplicity, but we present results here for all four serotypes. We extend the model to two spatially distinct patches, which are coupled by linear migration terms. For two patches (indexed by ) and strains ( arbitrary), the model is as follows:
| (1) | |||||
| (2) | |||||
| (3) | |||||
| (4) | |||||
| (5) | |||||
where the variables are , the fraction of susceptibles in patch ; , the fraction of primary infectives with strain in patch ; , the fraction of individuals in patch with partial cross immunity to strain ; , the fraction of individuals in patch that are recovered from a primary infection with strain and no longer have cross immunity to the other strains; and , the fraction of individuals in patch that were previously infected with strain and currently infected with strain . The parameters are the number of strains , the contact rate in patch , the recovery rate , the ADE factor , the strength of cross immunity , the rate for cross immunity to wear off, the birth and mortality rate in patch , and the migration rate between patches . A list of parameters appears in Table 1.
For simplicity, the birth and death rates in a patch are set equal to each other so that the total population of each patch is constant. The model of Eqs. 1-5 allows for one reinfection. The parameter determines how susceptible the cross immune compartments are to a secondary infection, where means no cross immunity (the infection rate is identical for compartments and ) and confers complete cross immunity (cross immunes are immune to a secondary infection for an average time ). We allow to take any value between and . The ADE factor is the enhancement in the infectiousness of secondary infectives. means that secondary infectives are as infectious as primary infectives, while means that secondary infectives are twice as infectious as primary, and so forth. In contrast to Aguiar and Stollenwerk, (2007), we will not consider values of smaller than . The migration rate from patch to , and from patch to , is . All individuals migrate with equal probability, independent of their infection status. The migration rate is assumed to be slow compared to the infection spread. For convenience, we put it on the same order as the birth/death rate. We assume that the social parameters, which are the contact rate and birth/death rate , may vary between patches, while the epidemic parameters are the same in all regions. Because the social parameters depend on human factors (and in the case of the contact rate also include mosquito levels, which are weather-dependent), these parameters are the most likely to be different in adjacent regions. We use parameter values compatible with dengue fever, which are summarized in Table 1. Our contact rate corresponds to a reproductive rate of infection of , which is consistent with previous estimates (Ferguson et al., 1999b, ; Nagao and Koelle,, 2008).
| Parameter | Value | Reference |
|---|---|---|
| , birth and death rate, years-1 | Ferguson et al.(1999) | |
| , transmission coefficient, years-1 | Ferguson et al.(1999) | |
| , recovery rate, years-1 | Rigau-Perez et al., (1998) | |
| , rate to leave the cross | Wearing and Rohani (2006) | |
| immune compartment, years-1 | ||
| , ADE factor | Schwartz et al. (2005) | |
| , strength of cross immunity | Bianco et al. (2009) | |
| , migration rate, years-1 | - | |
| , number of strains | 4 | - |
III Single patch bifurcation structure
A similar model to the one of Eqs. 1-5 has recently been used to analyze the dynamics of dengue fever in a single, well mixed, population (Bianco et al.,, 2009). The ADE and cross immunity strength were varied as bifurcation parameters. In the absence of cross immunity (), ADE alone generates instability, desynchronization, and ultimately chaotic outbreaks (Cummings et al.,, 2005; Schwartz et al.,, 2005). A Hopf bifurcation is observed for a critical value of the ADE factor , above which oscillatory solutions are obtained. Weak cross immunity stabilizes the system, while strong cross immunity triggers instability and chaos even in the absence of ADE (Bianco et al.,, 2009). In the latter case, destabilization occurs via a Hopf bifurcation for a critical value of the cross immunity strength . At the bifurcation, three identical complex pairs of eigenvalues of the Jacobian simultaneously become unstable. Although Bianco et al., (2009) discusses the full two parameter bifurcation structure (in and ), we will consider the cross immunity and ADE effects separately in the present work.
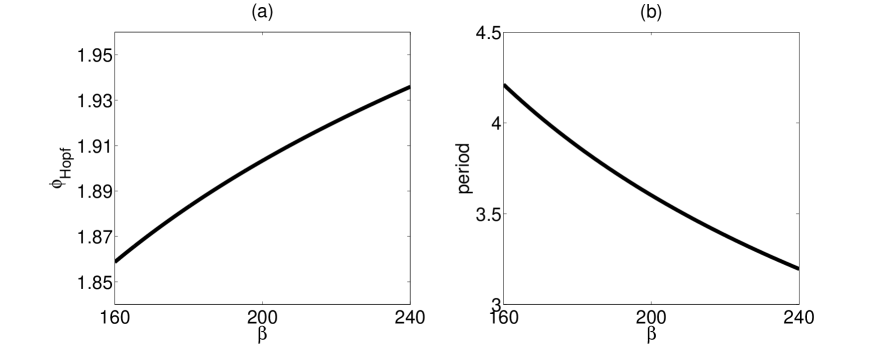
Figure 2a shows the bifurcation behavior of the single patch model with no cross immunity as the contact rate is varied. The bifurcation structure was computed using a continuation routine (Doedel et al.,, 1997). The ADE value at which the bifurcation occurs increases slightly as increases, and the dependence is approximately linear. The period of the periodic orbit, shown in Figure 2b for a fixed ADE value, also varies with . (Note that multistrain models with ADE can display subcritical Hopf bifurcations (Billings et al.,, 2007), so the periodic orbit shown in Figure 2b exists throughout the range of values shown.) Similarly, varying the contact rate in the absence of ADE affects the location of the Hopf bifurcation in cross immunity and its characteristic frequency of oscillation. Likewise, varying the other social parameter, the birth rate , affects the location and frequency of the Hopf bifurcations in and (data not shown).
IV Coupled patches
We next examine the effect of coupling between distinct regions on the dynamics previously observed in the single patch model. In particular, we consider how migration between nonidentical patches affects the stability of the steady state. We investigate the dynamics of the coupled systems by numerically integrating Eqs. 1-5 and by tracking the bifurcations using a continuation routine (Doedel et al.,, 1997). As mentioned in the previous Section, the model has a Hopf bifurcation at critical values of the bifurcation parameters , the ADE factor, and , the cross immunity strength. We study the effect of coupling and asymmetry on the stability by observing their effect on the location of the Hopf bifurcations. We consider cross immunity and ADE separately; that is, we analyze the system either with ADE and no cross immunity or with cross immunity and no ADE. Including both cross immunity and ADE together leads to qualitatively similar behavior to that reported here, at least locally when the asymmetry is not too large.
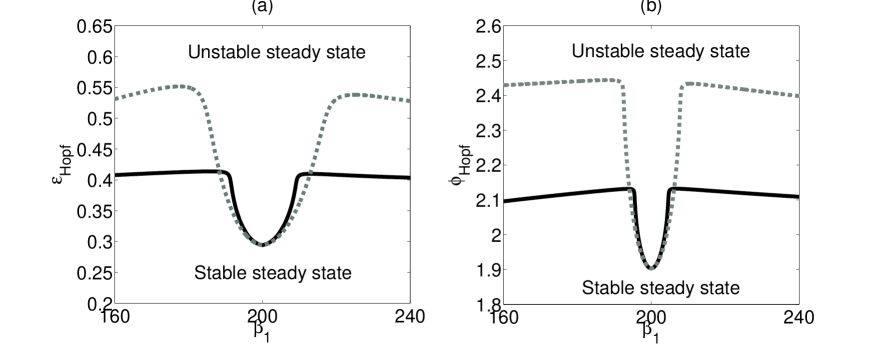
We proceed by fixing the patch-specific parameters in patch 2 and varying a social parameter ( or ) in patch 1 to observe the effect of increasing asymmetry on the dynamics. As previously mentioned, changing the social parameters modifies the natural frequency of the system. For each value of asymmetry, we look for the critical points at which the coupled system loses stability. We also consider several migration rates .
The effect of asymmetry in the contact rate is shown in Figs. 3(a) and 3(b) for two migration rates, namely (black) and (gray). The value of the critical parameter (Fig. 3(a)) or (Fig. 3(b)) at which the Hopf bifurcation occurs is plotted against the varying contact rate. The symmetric case is at the bottom of the curve. We see that two identical patches have the same bifurcation point as a single, well mixed population even when migration is present (cf. Fig. 2a). However, a striking difference in the dynamics appears when we make the two patches weakly asymmetric. The values of and at which the Hopf bifurcation occurs are dramatically different from the symmetric case. The steady state stability persists well into the parameter regime where a single patch would display chaotic oscillations (Billings et al.,, 2007; Bianco et al.,, 2009). The location of the single patch Hopf point does not depend strongly on , and decreasing the contact rate is actually destabilizing (Figure 2a), so the stabilization observed here is clearly a result of the coupling between asymmetric systems. Slightly increasing the migration rate (from to in Figure 3) further increases the stability of the system.
Similar results are obtained if the asymmetry occurs in the other social parameter, the birth rate. Again, for asymmetric patches either stronger cross immunity or stronger ADE is needed to destabilize the steady state through a Hopf bifurcation (figure in Supplementary Material).
V Analytical motivation
We now motivate the results of the preceding Section using a simple lower dimensional model and show that the qualitative features depend only on the bifurcation structure and characteristic frequencies rather than on details of the epidemic model. In this Section we study the general behavior of two coupled systems, each displaying a Hopf bifurcation, but with different characteristic frequencies.
The generic form for a Hopf bifurcation is the following, in polar coordinates (Strogatz,, 2001):
| (6) |
A Hopf bifurcation occurs at , where periodic oscillations with frequency are observed. We now couple two systems of the sort in Eq. 6, each with a potentially different frequency , via linear migration terms with migration rate . To lowest order (not displaying cubic terms), the coupled system in cartesian coordinates is
| (7) |
Stability is determined by evaluating the Jacobian of Eq. 7 at the steady state . At the Hopf bifurcation, the real part of the largest eigenvalue crosses zero, with nonzero imaginary part. We obtain the Hopf point directly by setting the real part of the eigenvalue to zero and solving for the critical value of at the bifurcation. Details may be found in the Supplementary Material. The Hopf bifurcation occurs at
| (8) |
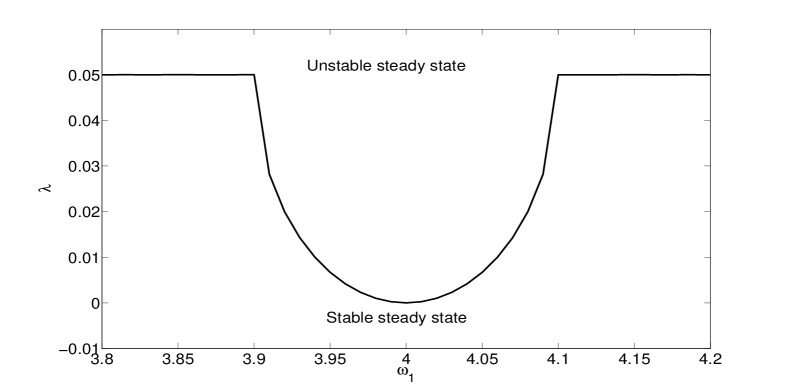
In Fig. 4 we show the location of the Hopf bifurcation given by Eq. 8 as a function of the asymmetry between the two systems for . Comparison with Fig. 3 (and Fig. 1 of the Supplementary Material) shows the qualitative agreement of the theoretical results for the lower dimensional system with the full multistrain system. Increasing the migration rate increases the value of the bifurcation parameter to which the Hopf point saturates (not shown), as in Fig. 3. It is also worth noticing that, in the case of identical frequencies , the Hopf bifurcation occurs at , the location in the absence of coupling. This is consistent with the numerical results for the multistrain system in the case of symmetric patches.
VI Conclusions and discussion
We have studied the endemic steady state stability properties for a multistrain epidemic model on two migration-coupled patches. Interactions between strains in the model were governed by temporary partial cross immunity and antibody-dependent enhancement. In the absence of coupling, the system displayed Hopf bifurcations in two epidemic parameters. Coupling between patches with non-identical parameters, which gave them non-identical characteristic frequencies of oscillation, was shown to shift the Hopf bifurcations, stabilizing the steady state. This behavior was observed for the Hopf bifurcation obtained by sweeping the cross immunity in the absence of ADE and the bifurcation obtained by sweeping the ADE in the absence of cross immunity. It occurred for asymmetry in either of our two social parameters, the birth rate and the contact rate.
To motivate this result, we diffusively coupled two low dimensional Hopf bifurcations with different characteristic frequencies and analyzed the stability of the steady state. We again saw that coupling between asymmetric systems led to stabilization. This indicates that the stabilization in the epidemic model is a result of the underlying dynamics, rather than the details of the model. The stabilization may occur because when the frequencies of oscillation in two coupled systems are different, the oscillations tend to cancel each other because of phase differences. This topic will be studied in more detail in a future work.
Bifurcations from steady state to oscillatory behavior can be associated with an increased number of infection cases, particularly if chaotic oscillations occur, as in previous dengue models (Billings et al.,, 2007; Bianco et al.,, 2009). Our results suggest that if control strategies in one region are able to generate enough asymmetry, this could lead to a stabilization of the outbreaks, which would have a positive effect on adjacent regions. Asymmetry could be generated in the effective contact rate by mosquito control, which could include reducing mosquito breeding sites (Slosek,, 1986), or through new genetic controls which are under development (Barbazan et al.,, 2008). Asymmetry in the birth rate could be generated by lowering the effective birth rate through vaccination of new susceptibles once a vaccine is available. However, because the bifurcation point saturates rather than increasing indefinitely as asymmetry increases, such a strategy would be successful only if the epidemic parameters in the real system are moderately close to the bifurcation. (Extreme asymmetry may even be destabilizing, so this strategy works best locally when the asymmetry is not too strong.) In addition, the role of seasonality in exciting oscillations should not be ignored. Seasonal variations in the contact rate have been included in previous dengue models (Schwartz et al.,, 2005). The interplay of seasonality and coupling is a topic for future study.
The results of the present work may also be useful in lower bound estimation of the parameter values for ADE and cross immunity. ADE especially is difficult to measure in vivo and must be estimated by other means. Since recent publications have suggested that epidemiological data from Thailand show chaotic outbreaks (Schwartz et al.,, 2005), and given the certainty of human migration and asymmetry between adjacent regions of the country, it is possible that the actual parameter values for ADE and cross immunity are higher than the ones estimated by studying a single well mixed population.
Finally, the work discussed here shows a potential effect of human movement between heterogeneous regions. As spatial effects are further studied in epidemic models, it remains to be seen how this phenomenon will extend to more complicated spatial geometries, including more patches and perhaps non-symmetric coupling terms. Because the migration-induced stabilization depends only on the existence of a Hopf bifurcation in the model, it is expected that the stabilization will be observed in other population models that also contain Hopf bifurcations (e.g., Fussmann et al., (2000); Greenhalgh et al., (2004)).
VII Acknowledgements
This work was supported in part by the Jeffress Memorial Trust. The authors wish to thank Ira Schwartz for helpful discussions.
References
- Aguiar and Stollenwerk, (2007) Aguiar, M. and Stollenwerk, N. A new chaotic attractor in a basic multistrain epidemiological model with temporary cross immunity. ArXiv:0704.3174 (2007).
- Andreasen et al., (1997) Andreasen, V., Lin, J., and Levin, S. A. The dynamics of cocirculating influenza strains conferring partial cross-immunity. J. Math. Bio., 35:825–842 (1997).
- Barbazan et al., (2008) Barbazan, P., Tuntaprasart, W., Souris, M., Demoraes, F., Nitatpattana, N., Boonyuan, W., and Gonzalez, J.-P. Assessment of a new strategy, based on Aedes aegypti (L.) pupal productivity, for the surveillance and control of dengue transmission in Thailand. Annals of Tropical Medicine and Parasitology, 102:161–71 (2008). doi:10.1179/136485908X252296.
- Bianco et al., (2009) Bianco, S., Shaw, L. B., and Schwartz, I. B. Epidemics with multistrain interactions: The interplay between cross immunity and antibody-dependent enhancement. Submitted; http://arxiv.org/abs/0812.3840. (2009).
- Billings et al., (2008) Billings, L., Fiorillo, A., and Schwartz, I. B. Vaccinations in disease models with antibody-dependent enhancement. Math. Biosci., 211:265–281 (2008).
- Billings et al., (2007) Billings, L., Schwartz, I. B., Shaw, L. B., Burke, D. S., and Cummings, D. A. T. Instabilities in multiserotype disease models with antibody-dependent enhancement. J. Theo. Biol., 246:18–27 (2007).
- Bolker and Grenfell, (1995) Bolker, B. and Grenfell, B. Space, persistence and dynamics of measles epidemics. Phil. Trans. R. Soc. Lond. B, 348:309–320 (1995).
- Colizza and Vespignani, (2008) Colizza, V. and Vespignani, A. Epidemic modeling in metapopulation systems with heterogenous coupling patter: Theory and simulations. J. Theo. Biol., 251:450–467 (2008).
- Cummings et al., (2005) Cummings, D. A. T., Schwartz, I. B., Billing, L., Shaw, L. B., and Burke, D. S. Dynamic effect of antibody-dependent enhancement on the fitness of viruses. Proc. Natl. Acad. Sci. U.S.A., 102(42):15259 (2005).
- Doedel et al., (1997) Doedel, E. et al. Auto97: Continuation and bifurcation software for ordinary differential equations (1997). Available from ftp://ftp.cs.concordia.ca/pub/doedel/auto/auto.ps.gz.
- (11) Ferguson, N., Anderson, R., and Gupta, S. The effect of antibody-dependent enhancement on the transmission dynamics and persistence of multiple-strain pathogens. Proc. Natl. Acad. Sci. U.S.A., 96:790 (1999a).
- (12) Ferguson, N. M., Donnelly, C. A., and Anderson, R. M. Transmission dynamics and epidemiology of dengue: insights from age-stratified sero-prevalence surveys. Philosophical transactions of the Royal Society of London. Series B, Biological sciences, 354:757–68 (1999b). doi:10.1098/rstb.1999.0428.
- Fussmann et al., (2000) Fussmann, G. F., Ellner, S. P., and Shertzer, K. W. Crossing the Hopf bifurcation in a live predator-prey system. Science, 290:1358–1360 (2000).
- Grais et al., (2003) Grais, R. F., Ellis, J. H., and Glass, G. E. Assessing the impact of airline travel on the geographic spread of pandemic influenza. Eur. J. Epidemiol., 18:1065–1072 (2003).
- Greenhalgh et al., (2004) Greenhalgh, D., Khan, Q., and Lewis, F. Hopf bifurcation in two SIRS density dependent epidemic models. Mathematical and Computer Modelling, 39:1261–1283 (2004). doi:10.1016/j.mcm.2004.06.007.
- Hagenaars et al., (2004) Hagenaars, T. J., Donnelly, C. A., and Ferguson, N. M. Spatial heterogeneity and the persistence of infectious diseases. J. Theo. Biol., 229:349–359 (2004).
- Halstead, (2007) Halstead, S. B. Dengue. The Lancet, 370:1644–1652 (2007). doi:10.1016/S0140-6736(07)61687-0.
- Halstead and Deen, (2002) Halstead, S. B. and Deen, J. The future of dengue vaccines. The Lancet, 360:1243 (2002).
- Halstead and O’Rourke, (1977) Halstead, S. B. and O’Rourke, E. J. Antibody-enhanced dengue virus infection in primate leukocytes. Nature, 265:739 (1977).
- He and Stone, (2003) He, D. and Stone, L. Spatio-temporal synchronization of recurrent epidemics. Proc. R. Soc. Biol. Sci., 270(1523):1519–1526 (2003).
- Hu et al., (1996) Hu, D. J., Dondero, T. J., Rayfield, M. A., George, J. R., Schochetman, G., Jaffe, H. W., Luo, C. C., Kalish, M. L., Weniger, B. G., Pau, C. P., Schable, C. A., and Curran, J. W. The emerging genetic diversity of HIV. the importance of global surveillance for diagnostics, research, and prevention. JAMA : the journal of the American Medical Association, 275:210–6 (1996).
- Kawaguchi et al., (2003) Kawaguchi, I., Sasaki, A., and Boots, M. Why are dengue virus serotypes so distantly related? Enhancement and limiting serotype similarity between dengue virus strains. Proc. R. Soc. Biol. Sci., 270:2241–7 (2003). doi:10.1098/rspb.2003.2440.
- Keeling and Rohani, (2002) Keeling, M. J. and Rohani, P. Estimating spatial coupling in epidemiological systems: a mechanistic approach. Ecol. Lett., 5:20–29 (2002).
- Liebovitch and Schwartz, (2004) Liebovitch, L. S. and Schwartz, I. B. Migration induced epidemics: dynamics of flux-based multipatch models. Phys. Lett. A, 332:256–267 (2004).
- Lloyd and May, (1996) Lloyd, A. L. and May, R. M. Spatial heterogeneity in epidemic models. J. Theor. Biol., 179:1–11 (1996).
- Nagao and Koelle, (2008) Nagao, Y. and Koelle, K. Decreases in dengue transmission may act to increase the incidence of dengue hemorrhagic fever. Proceedings of the National Academy of Sciences of the United States of America, 105:2238–43 (2008). doi:10.1073/pnas.0709029105.
- Rigau-Perez et al., (1998) Rigau-Perez, J., Clark, G., Gubler, D., Reiter, P., Sanders, E., and Vancevorndam, A. Dengue and dengue haemorrhagic fever. The Lancet, 352:971–977 (1998). doi:10.1016/S0140-6736(97)12483-7.
- Rohani et al., (1999) Rohani, P., Earn, D. J. D., and Grenfell, B. T. Opposite patterns of synchrony in sympatric disease metapopulations. Science, 286:968–971 (1999).
- Ruan et al., (2006) Ruan, S., Wang, W., and Levin, S. A. The effect of global travel on the spread of SARS. Math. Biosci. Eng, 3(1):205–218 (2006).
- Sattenspiel and Dietz, (1995) Sattenspiel, L. and Dietz, K. A structured epidemic model incorporating geographic mobility among regions. Math. Biosci., 127:71–91 (1995).
- Schwartz et al., (2005) Schwartz, I. B., Shaw, L. B., Cummings, D. A. T., Billings, L., McCrary, M., and Burke, D. S. Chaotic desynchronization of multistrain diseases. Phys. Rev. E, 72:066201 (2005).
- Slosek, (1986) Slosek, J. Aedes aegypti mosquitoes in the Americas: a review of their interactions with the human population. Social science and medicine (1982), 23:249–57 (1986).
- Strogatz, (2001) Strogatz, S. H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering. Westview Press (2001).
- Takada et al., (2003) Takada, A., Feldmann, H., Ksiazek, T. G., and Kawaoka, Y. Antibody-dependent enhancement of ebola virus infection. J. Virology, 77(13):7539–7544 (2003).
- Vaughn et al., (2000) Vaughn, D. W., Green, S., Kalayanarooj, S., Innis, B. L., Nimmannitya, S., Suntayakorn, S., Endy, T. P., Raengsakulrach, B., Rothman, A. L., Ennis, F. A., and Nisalak, A. Dengue viremia titer, antibody response pattern, and virus serotype correlate with disease severity. J. Infect. Diseases, 181:2–10 (2000).
- Wearing and Rohani, (2006) Wearing, H. J. and Rohani, P. Ecological and immunological determinants of dengue epidemics. Proc. Natl. Acad. Sci. U.S.A., 103(31):11802 (2006).
-
World Health Organization Website, (2006)
World Health Organization Website (2006).
http://www.who.int/mediacentre/factsheets/fs117/en/.
Appendix A Asymmetric birth rates
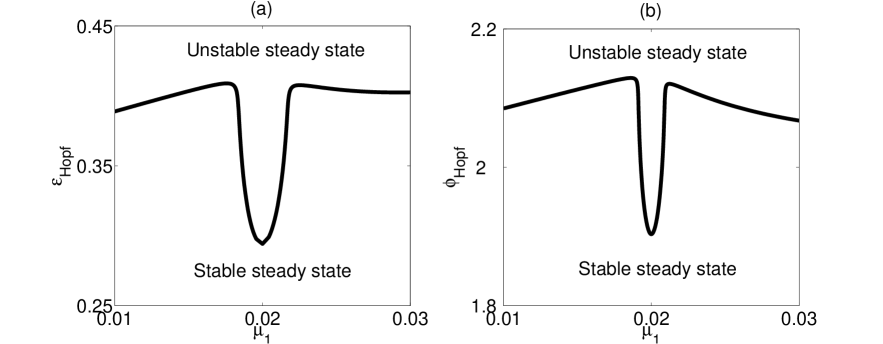
The effect of asymmetric birth rates is shown in Fig. 5 of this supplementary material. The birth rate in patch 2 was held fixed while that in patch 1 was varied. For asymmetric patches either stronger cross immunity or stronger ADE is needed to destabilize the steady state through a Hopf bifurcation, compared to the symmetric patch case.
Appendix B Details of Hopf bifurcation analysis
We evaluate the Jacobian for the ODE system given in Eq. 7 of the paper at the steady state . The roots of the characteristic polynomial of the Jacobian are the eigenvalues . The four eigenvalues are
| (9) | |||||
| (10) |
but it is not easy to see from these expressions where the Hopf bifurcation occurs. Instead, we solve directly for the Hopf point.
At a Hopf bifurcation, a pair of eigenvalues has zero real part. Thus to obtain the Hopf point, we can set , where is real. If is an eigenvalue, we require , so
| (11) |
and
| (12) |
If , Eq. 12 has nonzero roots . When this is substituted into Eq. 11, we obtain four potential roots for at the Hopf point. Two are complex, which is unphysical and can be ignored. The one corresponding to the Hopf bifurcation is . (The fourth root is larger and corresponds to loss of stability of the second pair of eigenvalues.) This is real and thus gives the Hopf point location when . When and , is positive, indicating stabilization due to the asymmetry and coupling.