Asymptotic formula for balanced words

Let ${\mathcal{A}}=\{0,1\}$ and we denote by ${\mathcal{A}}^{*}$ the monoid generated by ${\mathcal{A}}$ by concatenation, where the empty word $\lambda$ is its identity. The length of $x\in{\mathcal{A}}^{*}$ is $|x|$. We denote $|x|_{1}$ the cardinality of $1$ in $x\in{\mathcal{A}}^{*}$. ${\mathcal{A}}^{{\mathbb{N}}}$ (resp. ${\mathcal{A}}^{{\mathbb{Z}}}$) is the set of right infinite (resp. bi-infinite) words. If $y\in{\mathcal{A}}^{*}$ is a factor (a subword) of $x\in{\mathcal{A}}^{*}\cup{\mathcal{A}}^{{\mathbb{N}}}\cup{\mathcal{A}}^{{\mathbb{Z}}}$, we write $y\prec x$. A word in $x\in{\mathcal{A}}^{*}\cup{\mathcal{A}}^{{\mathbb{N}}}\cup{\mathcal{A}}^{{\mathbb{Z}}}$ is balanced if $||u|_{1}-|v|_{1}|\leq 1$ holds for any $u,v\prec x$ with $|u|=|v|$. An infinite word $w\in{\mathcal{A}}^{{\mathbb{N}}}$ is sturmian if $\text{Card}\{u\prec w\ |\ |u|=n\}=n+1$ for all $n\in{\mathbb{N}}$. Morse and Hedlund characterized a sturmian word as an aperiodic balanced word in ${\mathcal{A}}^{{\mathbb{N}}}$. They also characterized sturmian words as a coding of irrational rotation. More precisely a lower mechanical word $(s_{n})\in{\mathcal{A}}^{{\mathbb{N}}}$ is defined by

with a given slope $\alpha\in[0,1]$ and an intercept $\rho\in[0,1)$. An upper mechanical word is similarly defined by replacing $\lfloor\cdot\rfloor$ with $\lceil\cdot\rceil$, which is denoted by $\hat{s}_{n}(\alpha,\rho)$. Then a sturmian word is a (lower or upper) mechanical word of an irrational slope $\alpha$ and vice versa. It is known that every balanced word is a factor of a lower and an upper mechanical word [17]. Indeed, for every balanced word $x=x_{1}\dots x_{n}$ we can find a slope $\alpha$ and an intercept $\rho$ such that $x_{i}=s_{i}(\alpha,\rho)=\hat{s}_{i}(\alpha,\rho)$. Note that the choice of $\alpha$ and $\rho$ is not unique. In fact, a balanced $x$ word corresponds to $(\rho,\alpha)$ in a convex polygon in $[0,1)\times[0,1]$. This geometric idea for enumeration is found in [1, 25, 14, 3]. Let $\phi(n)$ be the Euler totient function. The formula for the number of balanced words of length $n$ is given by

Several different proofs are found in [17, 16, 1, 5, 18].

In this paper we refine the formula (1) and give its asymptotic behavior. Denote by $B(n,t,u)$ the cardinality of the set of balanced words of length $n$ whose slope $\alpha\in[1-t,1]$¹¹1The statement of Theorem 1 is simpler by this choice than taking $[0,t]$ because the lines in the proof do not intersect $(0,1)\times\{0\}$. and its intercept $\rho\in[0,u)$ and let ${\mathcal{B}}(n)$ be the set of balanced words of length $n$. Then we show

Theorem 1 slightly generalizes Yasutomi [25, Proposition 4], shown in a different context. By using Theorem 1, we will derive asymptotic formulas. Hereafter, we use conventional terminology in analytic number theory, i.e., Landau $O$, $o$ symbol and Vinogradov symbol $\ll$. The symbol $\varepsilon$ is reserved as an arbitrary positive constant, and the symbol $c$ in Landau $O$ is a suitably chosen positive constant, which may differ among formulas.

For almost all $t$, the estimate (2) can be sharpened with the help of Fujii [9], see the discussion in the end of §3. Denote by $\chi_{A}(x)$ the indicator function of the set $A$. For a rectangle $(a,b]\times[c,d)$ in the unit square $[0,1)\times[0,1]$, we see

from

Moreover for a Jordan measurable region $W$ in the unit square, we have

Farey series $(f_{m}(i))$ of order $m$ is the finite increasing sequence composed of irreducible fractions in $[0,1)$ whose denominators are not larger than $m$:

with $\Phi(m)=\sum_{k=1}^{m}\phi(k)$. Clearly $A(m,t,1)=\max\left\{j\ |\ f_{m}(j)\leq t\right\}$. It is well-known that Riemann Hypothesis is equivalent to

a strong uniform distribution property of Farey fractions. As pointed out in [8], Franel [7] already noticed that

is also equivalent to Riemann Hypothesis. One can see

similarly to (8) and (10) in §3, but we expect it is much smaller in average. See also [21, 8, 15]. We state another equivalent statement directly related to the number of balanced words:

We elucidate a geometric counting discussion of Yasutomi [25, Proposition 4] in our convenient terminology, which is more straightforward than the one in [1]. Let $m$ be a fixed positive integer and put $X:=[0,1)\times[0,1]$. The map $\psi:(\rho,\alpha)\to(s_{n}(1-\alpha,\rho))_{n=1}^{m}$ gives a natural partition

Then $X$ is cut into convex cells by segments:

We obtain essentially the same partition by using $\hat{s}_{n}$, the difference is seen only on the boundary of $Y$. In this paper, we use $s_{n}$ for the partition. Fixing $\alpha\in[0,1]$, the intersections of the line $y=1-\alpha$ and $x=ny-\ell$ are written as

where $R:(x,1-\alpha)\mapsto(x+\alpha,1-\alpha)$ is the rotation map acting on the unit interval $[0,1)\times\{1-\alpha\}$ which is identified with the torus ${\mathbb{T}}:={\mathbb{R}}/{\mathbb{Z}}$. The partition of $[0,1)\times\{1-\alpha\}$ by $R^{-n}(0)\ (n=1,\dots,m)$ gives cylinder sets of rotation $R$, i.e., the points in the same cylinder share the same coding

They are the $m+1$ different words which correspond to the words of length $m$ appear in the sturmian word of slope $\alpha$ when $\alpha$ is irrational. Slicing $X$ by the line $y=1-\alpha$, we observe the $m$-th level cylinder sets of the rotation $R$ on ${\mathbb{T}}$ of slope $\alpha$ acting on the unit interval $[0,1)\times\{1-\alpha\}$. Considering $\alpha$ as a variable, we reconstruct the partition (4) of $X$ that every convex cell corresponds to an element of ${\mathcal{B}}(m)$, which is consistent with the cylinder partition of $[0,1)\times\{1-\alpha\}$ for each $\alpha\in[0,1]$. In this manner, the partition (4) is seen as a pile of cylinder sets of level $m$ for all (rational/irrational) rotations. The case $m=4$ is depicted in Figure 1.

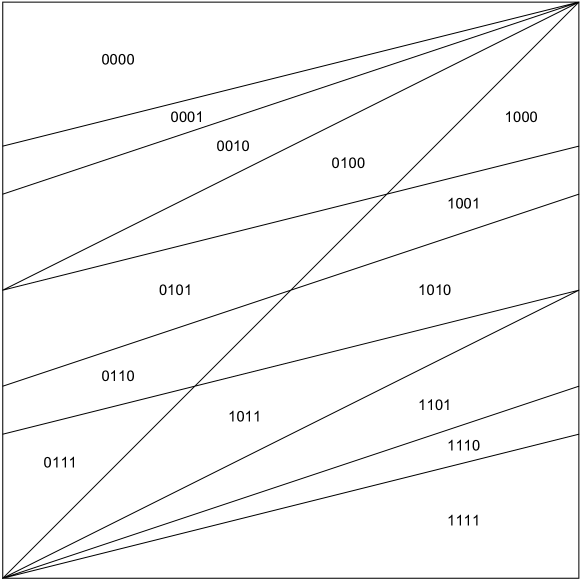
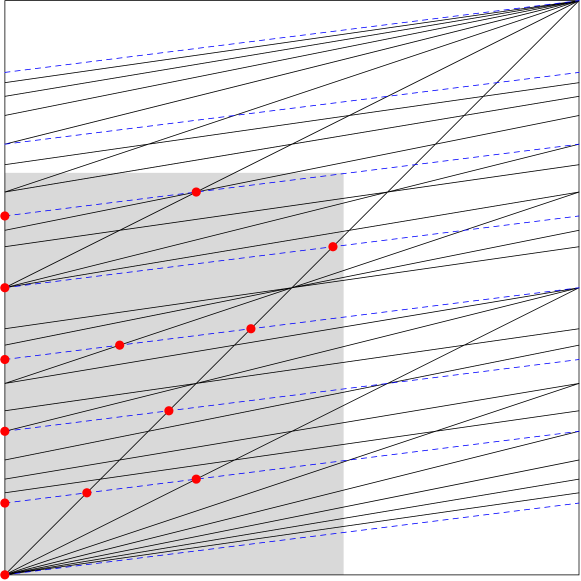
To enumerate $B(n,t,u)$, we compute $B(m,t,u)-B(m-1,t,u)$ for $m\geq 2$, that is, the increase of number of cells as we add a new slope $1/m$. Equivalently, we count the number of intersections in $[0,u)\times[0,t]$ which appear by adding new segments of slope $1/m$, see Figure 2. The intersection points $(x,y)\in[0,u)\times[0,t]$ of $x=my-b$ and $x=\ell y-c\ (\ell<m)$ are in one to one correspondence with the set of their $y$-coordinates:

We claim that $P(m)$ coincides with the set

where $\langle x\rangle=x-\lfloor x\rfloor$ and $\mathrm{den}(y)$ is the denominator of $y\in{\mathbb{Q}}$. In fact $P(m)\subset Q(m)$ is clear. Let $x=p/q\in Q(m)$ with $1\leq q\leq m$, $(p,q)=1$, $p/q\leq t$ and $\langle mx\rangle<u$. Put $\ell=m-q$ and choose $b$ with $b/m\leq p/q<(b+1)/m$ and let $c=b-p$. Since $p/q<(b+1)/m$, we have $p\leq b$ and $c\geq 0$. From the property of Farey fraction, we have $(b-p)/(m-q)<b/m<p/q$, which implies $c=b-p<m-q=\ell$. The inequality $0\leq\frac{\ell b-mc}{m-\ell}<1$ follows from $\frac{b}{m}\leq\frac{b-c}{m-\ell}<\frac{b+1}{m}$. Thus $\langle mx\rangle=\frac{\ell b-mc}{m-\ell}$ and therefore $x\in P(m)$. The claim is proved. Set $A(m,t,u)=\mathrm{Card}(Q(m))$ for $m\geq 1$. From $B(1,t,u)=2$ and $A(1,t,u)=1$, we obtain Theorem 1.∎

We illustrate this proof by an

Hereafter we show an asymptotic formula of $B(n,t,u)$.

We show a

Let $\mathbf{e}(x)=\exp(2\pi\mathfrak{i}x)$. Let $\mathbf{d}$ be the natural metric on the torus ${\mathbb{T}}={\mathbb{R}}/{\mathbb{Z}}$. For a given interval $[\alpha,\beta]\subset[0,1)$ and a positive $J>2/(1-\beta+\alpha)$ there exists a smooth function $V_{J}$ of period $1$ such that

whose Fourier expansion is

with

see [23, Chapter 1,Lemma 12]. We shall use a large sieve inequality [12, Theorem 7.2],[2, Lemma 2.4]:

We prepare two more lemmas.

Our strategy is to treat $B(n,t,u)$ as a function on $t$. Then $B(n,t,u)$ is a non-decreasing step function having a finite number of rational discontinuities. Every gap between the discontinuities of $B(n,s,t)$ as a function on $t$ is greater than $1/n^{2}$. Depending on $n$, we will choose $t_{1}\leq t\leq t_{2}$ that $t_{2}-t_{1}$ is small and $t_{1},t_{2}$ have a suitable property to estimate error terms. If we get the same asymptotic formulas and their implied constants of the Landau and Vinogradov symbols are independent of this choice of $t_{i}$, we obtain the estimate for $t$ by the non-decreasing property, because it is sandwiched by the same formula. Therefore if we could perturb $t$ and get the same error term (up to negligible terms), then we are done. Hereafter we shall be cautious on the above implied constants, whether they can be independent of the choices of $t_{i}$.

At the cost of an additional error term $O(n^{2})$ which takes care of the case $i/j=t$, we may assume that $0<t<1$, $t$ is rational and $B(n,t,u)$ is continuous at $t$, i.e., constant in the neighborhood of $t$. Recall that from the middle of §3, $i$ and $j$ are positive integers and

Taking $V_{J}(x)$ with respect to the interval $[0,u]$, we have

As (14) implies $v_{J}(0)=u+O(1/J)$, the main term is

from (12). The remainder is

with positive integers $a,b$. From (15), our target is to estimate