Asymptotic properties of generalized eigenfunctions for multi-dimensional quantum walks

In this paper, we consider the time-independent scattering theory for the position-dependent $d$-dimensional quantum walk ($d$DQW or simply QW for short) as a finite rank perturbation of the $d$D free QW which is defined as follows. The states of quantum walker on ${\bf Z}^{d}=\{x=(x_{1},\ldots,x_{d})\ ;\ x_{1},\ldots,x_{d}\in{\bf Z}\}$ are represented by $\psi=\{\psi(x)\}_{x\in{\bf Z}^{d}}$ which are ${\bf C}^{2d}$-valued sequences. Letting $*^{\mathsf{T}}$ be the transpose operator for matrices or vectors, we denote by the column vector

for ${\bf C}$-valued sequences $\psi^{\pm}_{j}$ for $j=1,\ldots,d$ on ${\bf Z}^{d}$. Each component $\psi_{j}^{\pm}(x)$ corresponds the “probability amplitude” at $x\in{\bf Z}^{d}$ of the chirality $(j,\pm)$. The $d$D free QW is defined by the operator $U_{0}=S$ where $S$ is the shift operator :

where $e_{1},\ldots,e_{d}$ are the standard basis on ${\bf Z}^{d}$. The position-dependent QW is defined by the operator $U=SC$ where $C$ is the operator of multiplication by a matrix $C(x)=(c_{k,l}(x))_{k,l=1}^{2d}\in\mathrm{U}(2d)$ for every $x\in{\bf Z}^{d}$. Throughout of this paper, we assume that the following statements hold.

• •

  There exists a positive integer $n_{0}$ such that $C(x)$ is the $2d\times 2d$ identity matrix $I_{2d}$ for $x\in{\bf Z}^{d}\setminus D$ where $D=\{x\in{\bf Z}^{d}\ ;\ |x_{1}|\leq n_{0},\ldots,\ |x_{d}|\leq n_{0}\}$.

• •

  For every $x\in D$,

  $$\mathrm{det}(c_{2k-1,2l-1}(x))_{k,l=1}^{d},\quad\mathrm{det}(c_{2k,2l}(x))_{k,l=1}^{d},$$

  do not vanish.

These assumptions will be used in order to prove a unique continuation property for generalized eigenfunctions of $U$ in Lemma 3.7 and Corollary 3.8. The unique continuation property guarantees a radiation condition for non-homogeneous equations and the absence of eigenvalues of $U$. See Corollaries 3.11 and 3.12.

In the following, almost all of our arguments are restricted to the case $d=2$ in order to avoid the complication of notations. Our results can be generalized easily for higher dimensional cases. For the case $d=2$, we use more explicit notations. Components of ${\bf C}^{4}$-valued sequences $\psi$ are written as

The chirality of $\psi$ is represented by $p\in\{\leftarrow,\rightarrow,\downarrow,\uparrow\}$. Typical examples of $C(x)$ for every $x\in D$ such that the second assumption holds are

On the other hand, the 2D Grover coin and the 2D Fourier coin

do not satisfy the second assumption.

Obviously, operators $U_{0}$ and $U$ are unitary on the Hilbert space $\ell^{2}:=\ell^{2}({\bf Z}^{2};{\bf C}^{4})$ equipped with the standard inner product

The discrete time evolutions of these QWs are given by

for an initial state $\psi$. If $\psi\in\ell^{2}$, these time evolutions preserve the $\ell^{2}$-norm of $\psi$ i.e. $\|\Psi(t,\cdot)\|_{\ell^{2}}=\|\Psi^{(0)}(t,\cdot)\|_{\ell^{2}}=\|\psi\|_{\ell^{2}}$ for any $t\in{\bf Z}$.

In view of the quantum scattering theory, the scattering matrix (S-matrix) is an important object. There are several equivalent definitions of the S-matrix. In the time-dependent scattering theory, we can prove that the wave operators

exist and asymptotically complete under our assumption by the similar way of Suzuki [21]. Namely, we have the following fact on the long time behavior of QWs. See also Figure 1.

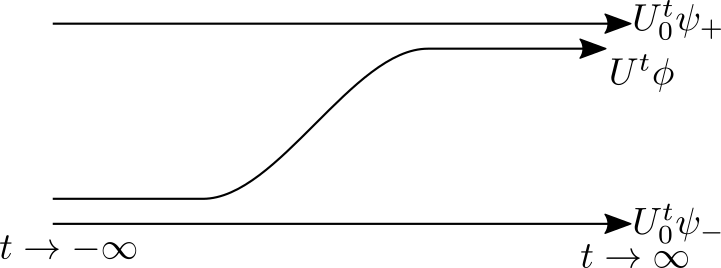
Note that this proposition holds under the short-range condition. Namely, the first assumption for $C(x)$ can be replaced by $\|C(x)-I_{4}\|\leq c(1+|x|)^{-1-\epsilon}$ for some constants $c,\epsilon>0$ for Proposition 1.1.

The scattering operator $\Sigma=W_{+}^{*}W_{-}:\psi_{-}\mapsto\psi_{+}$ is another important object. In view of Proposition 1.1, $\Sigma$ connects the behavior of the quantum walker as $t\to-\infty$ to $t\to\infty$ in terms of the 2D free QW i.e. $\Sigma$ represents a transition from the 2D free quantum walker $\psi_{-}$ to another free quantum walker $\psi_{+}$. The S-matrix $\widehat{\Sigma}(\theta)$ for $\theta\in[0,2\pi)$ is given by the spectral decomposition of $\widehat{\Sigma}$ which is a spectral transform of $\Sigma$ which will be introduced in the formula (4.18) as

For details of the time-dependent scattering theory for QWs, see Suzuki [21] or Morioka [15]. In these previous works, the authors consider 1DQWs. However, their arguments rely on abstract operator theory and spectral theory for unitary operators. Then it can be applied for our case easily.

The wave operators and the scattering operator are considered in the Hilbert space $\ell^{2}$. From the physical point of view, it is reasonable to consider plane waves and corresponding scattered waves in certain classes larger than $\ell^{2}$. Moreover, the S-matrix naturally appears in a spatial asymptotic behavior at infinity of a generalized eigenfunction to the equation

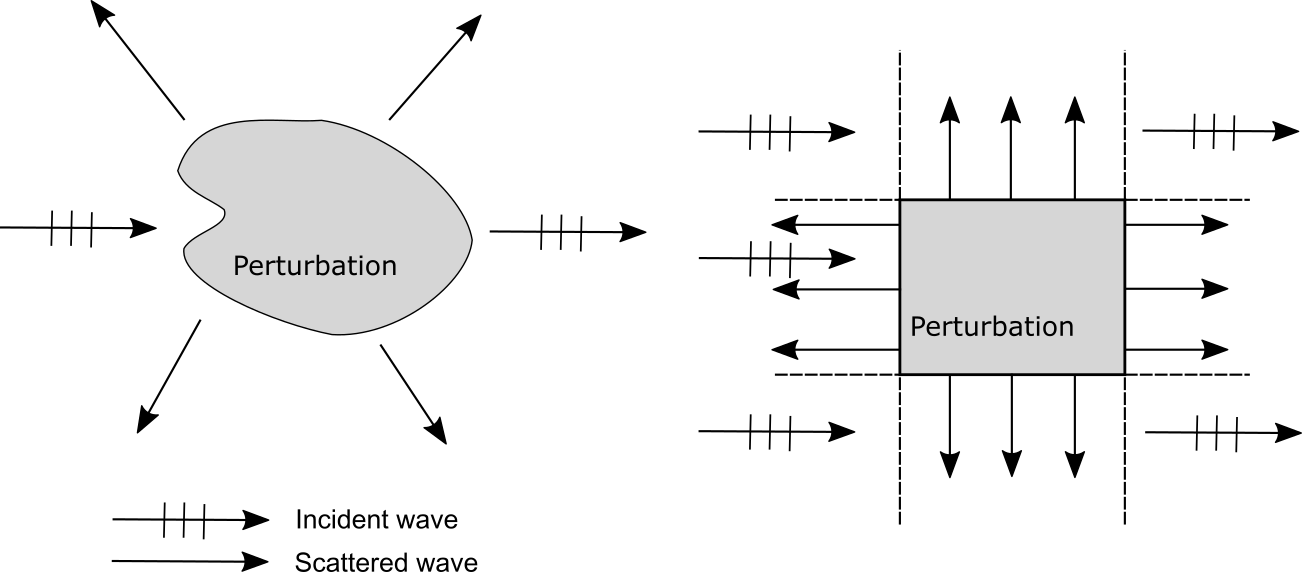
In view of the separation of variables $\Psi(t,x)=e^{it\theta}u(x)$ where $u$ satisfies the above equation, we have a time evolution $\Psi(t,\cdot)=U^{t}u$ for any $t\in{\bf Z}$. Note that generalized eigenfunctions do not belong to $\ell^{2}$ when $e^{i\theta}$ is included in the continuous spectrum of $U$. Generalized eigenfunctions associated with a continuous spectrum consist of an incident plane wave and the corresponding scattered wave. The S-matrix appears in the scattered wave as its amplitude and phase shift. See Figure 2. Thus the spectral theory for $U$ is an important topic in the research area of the scattering theory for QWs.

The main purpose of this paper is to construct and to characterize generalized eigenfunctions in an anisotropic Banach space on ${\bf Z}^{2}$. The spectral theory for the unitary operator $U$ allows us to see the behavior of the outgoing scattered wave. In order to study the distorted Fourier transformation, we often use the Green function which is the kernel of the resolvent operator $R_{0}(\kappa)=(U_{0}-e^{i\kappa})^{-1}$, $\kappa\in{\bf C}\setminus{\bf R}$. If $\kappa\in{\bf R}$, the operator $R_{0}(\kappa)$ does not make sense in $\ell^{2}$. However, we will show that the limit $R_{0}(\theta\pm i0)$ for $\theta\in{\bf R}$ exists in the sense of Agmon-Hörmander’s $\mathcal{B}$-$\mathcal{B}^{*}$ spaces ([1]).

Agmon-Hörmander’s $\mathcal{B}$-$\mathcal{B}^{*}$ spaces are often used in the time-independent scattering theory for Schrödinger equations. Consider the equation

where $V\in C_{0}^{\infty}({\bf R}^{d})$ is a real-valued function. The solution to this equation can be characterized by the Banach space $\mathcal{B}^{*}$ equipped with the norm

The solution $u$ has the asymptotics

as $|x|\to\infty$ where $\omega=x/|x|$. It is well-known that the S-matrix for Schrödinger operators relates $\phi_{+}$ and $\phi_{-}$. For this topic, see Yafaev [25].

For our 2DQW, it is inadequate to adopt the usual separation of variables and to derive the asymptotic expansion with respect to the radius due to anisotropy of $U$ and $U_{0}$. Then we introduce a pair of anisotropic $\mathcal{B}$-$\mathcal{B}^{*}$ spaces. We will derive the asymptotic behaviors of generalized eigenfunctions by evaluating functions for each direction depending on its chirality.

The scattering theory for one dimensional QWs has been studied in some previous works. Feldman-Hillery [5, 6] are pioneering studies of QWs in view of the scattering theory. As has been mentioned above, Suzuki [21] proved the existence and the asymptotic completeness of the wave operators. Richard et al. [18, 19] considered more general cases. Note that the authors adopted commutator method for unitary operators (see [2], [7], [20]). Morioka [15], Morioka-Segawa [16], Maeda et al. [14] and Komatsu et al. [12] considered the time-independent scattering theory and the absence of eigenvalues embedded in the continuous spectrum. Tiedra de Aldecoa [23] studied an abstract theory of time-independent scattering for unitary operators and its applications to QWs. Maeda et al. [13] solved an inverse scattering problem for a nonlinear QW.

Our method adopted in this paper is an analogue of the time-independent scattering theory for self-adjoint Hamiltonians. Over the past few years, the time-independent scattering theory for discrete Schrödinger operators has been studied. The following works are deeply related with our arguments: Isozaki-Korotyaev [9], Isozaki-Morioka [10, 11], Ando et al. [3, 4]. Nakamura [17] constructed the S-matrix as a pseudo-differential operator for discrete Schrödinger operators (as one of examples of applications) by using the microlocal analysis. Tadano [22] studied the scattering theory for discrete Schrödinger operators with long-range perturbations.

In Section 2, we introduce some functional spaces. The anisotropic $\mathcal{B}$-$\mathcal{B}^{*}$ spaces are defined here. Some properties of these functional spaces will be proven.

In Section 3, we study some properties of the Green function associated with the 2D free QW. By using the Green function of the 1D free QW, we can derive an explicit formula of the Green function of the 2D free QW. Then we can see the asymptotic behavior of the solution in $\mathcal{B}^{*}$ to the equation $(U_{0}-e^{i\theta})u=f$ for $f\in\mathcal{B}$. In view of this asymptotics, we can define the radiation condition which guarantees the uniqueness of the solution to the equation $(U_{0}-e^{i\theta})u=f$. Here we apply a multi-dimensional generalization of the unique continuation property for QWs (Corollary 3.8). As a consequence of the argument in Section 3, we have the absence of eigenvalues of $U$ (Corollary 3.12).

In Section 4, we consider the generalized eigenfunction for $U$. We introduce a combinatorial construction of generalized eigenfunctions in $\mathcal{B}^{*}$. This construction is a multi-dimensional version of the result in [12]. This approach is based on the long time limit of the dynamics of QWs. After that, we discuss the spectral theory for $U$ in order to characterize rigorously the set of generalized eigenfunctions in $\mathcal{B}^{*}$. The existence of the limits $R(\theta\pm i0)$ in $\mathcal{B}$-$\mathcal{B}^{*}$ spaces for $R(\kappa)=(U-e^{i\kappa})^{-1}$ is proved here. The spectral representation of $U$ is introduced as a distorted Fourier transformation associated with $U$. Due to the closed range theorem, we prove a characterization of generalized eigenfunctions in $\mathcal{B}^{*}$ (Theorem 4.15). Finally, we show that the S-matrix $\widehat{\Sigma}(\theta)$ naturally appears in the asymptotic behavior of generalized eigenfunctions. We observe that the scattered wave does not spread radially but passes along some corridors (Theorem 4.20).

The notation used throughout of this paper is as follows. ${\bf T}^{2}:={\bf R}^{2}/(2\pi{\bf Z}^{2})$ denotes the flat torus. For $u,v\in{\bf C}^{n}$, $\langle u,v\rangle$ denotes the inner product of ${\bf C}^{n}$, and we put $|u|=\sqrt{\langle u,u\rangle}$. For a matrix $A$, $A^{*}$ denotes the Hermitian conjugate $\overline{A^{\mathsf{T}}}$. $\mathrm{diag}[a_{1},\ldots,a_{n}]$ denotes the $n\times n$ diagonal matrix.

For a ${\bf C}^{4}$-valued sequence $f=\{f(x)\}_{x\in{\bf Z}^{2}}$, the mapping $\mathcal{U}$ is the Fourier transformation

The Fourier coefficients of a distribution $\widehat{g}$ on ${\bf T}^{2}$ is given by

For Banach spaces $X$ and $Y$, ${\bf B}(X;Y)$ denotes the set of bounded linear operators from $X$ to $Y$. For an operator $L\in{\bf B}(\ell^{2};\ell^{2})$, $L^{*}$ is the adjoint operator of $L$ with respect to the inner product of $\ell^{2}$. As usual, for an operator $L\in{\bf B}(X;Y)$ for Banach spaces $X$ and $Y$, $L^{*}$ is its adjoint operator in ${\bf B}(Y^{*};X^{*})$. However, for $U=SC$ and $U_{0}=S$, we often adopt the abuse of notations $U^{*}=C^{*}S^{-1}$ and $U_{0}^{*}=S^{-1}$ on some Banach spaces.

The Banach spaces $\mathcal{B}$ and $\mathcal{B}^{*}$ which are defined here are used for the proof of boundedness of $R_{0}(\kappa)=(U_{0}-e^{i\kappa})^{-1}$ and $R(\kappa)=(U-e^{i\kappa})^{-1}$ with $\kappa\in{\bf C}\setminus{\bf R}$. Let $r_{-1}=0$, $r_{j}=2^{j}$ for $j\geq 0$, and $I_{j}=\{y\in{\bf Z}\ ;\ r_{j-1}\leq|y|<r_{j}\}$. For a ${\bf C}^{4}$-valued sequence $f=\{f(x)\}_{x\in{\bf Z}^{2}}$, we put

The Banach space $\mathcal{B}$ is defined by

Proof. We take $f^{(k)}\in\mathcal{B}$ such that $\mathrm{supp}f_{\leftarrow}^{(k)},\,\mathrm{supp}f_{\rightarrow}^{(k)}\subset\{x\in{\bf Z}^{2}\ ;\ r_{k-1}\leq|x_{1}|<r_{k}\}$ and $\mathrm{supp}f_{\downarrow}^{(k)},\,\mathrm{supp}f_{\uparrow}^{(k)}\subset\{x\in{\bf Z}^{2}\ ;\ r_{k-1}\leq|x_{2}|<r_{k}\}$. For $T\in\mathcal{B}^{*}$, we consider the restriction $T^{(k)}$ on the subspace $\mathcal{H}_{k}:=\mathcal{V}_{k}\oplus\mathcal{W}_{k}$ where

Note that $\mathcal{H}_{k}$ for every $k$ is a Hilbert space. We have

Applying the Riesz representation theorem on $\mathcal{H}_{k}$, we see that there exists $u^{(k)}\in\mathcal{H}_{k}$ such that

and

Taking a sequence $u$ such that $u=u^{(k)}$ on every subspace $\mathcal{H}_{k}$, we have

which implies $\|u\|_{\mathcal{B}^{*}}\leq\|T\|$.

For any $f\in\mathcal{B}$, we can write $f=\sum_{k=0}^{\infty}f^{(k)}$ for $f^{(k)}\in\mathcal{H}_{k}$. In fact, we see

where $\chi_{\mathcal{V}_{k}}$ and $\chi_{\mathcal{W}_{k}}$ are characteristic functions of $I_{k}\times{\bf Z}$ and ${\bf Z}\times I_{k}$, respectively. In view of the definition of $\|\cdot\|_{\mathcal{B}}$, we have

We have

It follows from (2.1) that

This inequality implies

Therefore, we obtain $\|T\|=\|u\|_{\mathcal{B}^{*}}$. Since $T\in\mathcal{B}^{*}$ is arbitrary, we have proven the lemma. ∎

The following equivalent norm of $\mathcal{B}^{*}$ is easier to handle :

Proof. For any $\epsilon>0$, there exists a nonnegative integer $k$ such that

Letting $\rho=r_{k}$, we have

On the other hand, for any $\epsilon>0$, there exists $\rho_{0}>1$ such that

Taking a positive integer $k$ such that $r_{k-1}\leq\rho_{0}\leq r_{k}$, we have

Thus we obtain

for a constant $c>0$. ∎

In the following, we often use the norm $\|u\|_{\mathcal{B}^{*}}=M_{\mathcal{B}^{*}}(u)$ i.e.

Let the Hilbert space $\ell^{2,s}$ for $s\in{\bf R}$ be defined by the norm

When $s=0$, $\ell^{2,0}=\ell^{2}$ is the usual $\ell^{2}$-space equipped with the standard inner product.

In the following, $(u,f)$ denotes the pairing

for $u\in\mathcal{B}^{*}$ and $f\in\mathcal{B}$ or $u\in\ell^{2,-s}$ and $f\in\ell^{2,s}$ for $s\geq 0$.

Finally, we define the subspace $\mathcal{B}_{0}^{*}$ as the totality of sequences $u\in\mathcal{B}^{*}$ such that

When $u-v\in\mathcal{B}_{0}^{*}$, we write $u\simeq v$. Then the subspace $\mathcal{B}_{0}^{*}$ is written as

The following inclusion relation holds.

Proof. We put

for $j\geq 0$, $s\in{\bf R}$, and a sequence $f=\{f(x)\}_{x\in{\bf Z}^{2}}$. Note that $\|f\|^{2}_{\ell^{2,s}}=\sum_{j=0}^{\infty}b_{j,s}(f)^{2}$. Since we have $b_{j,0}(f)=a_{j}(f)$, we also have $\|f\|_{\mathcal{B}}=\sum_{j=0}^{\infty}r_{j}^{1/2}b_{j,0}(f)$. If $y\in I_{j}$, we can take a positive constant $c>0$ such that $c^{-1}r_{j}^{2}\leq 1+|y|^{2}\leq cr_{j}^{2}$. This inequality implies

for every $j$ and $s\geq 0$.

For $s=1/2$, it follows from (2.3) that

for a constant $c>0$. We obtain $\mathcal{B}\subset\ell^{2,1/2}$.

For $s>1/2$, we use (2.3) again in order to show

for a constant $c>0$. Thus we have $\ell^{2,s}\subset\mathcal{B}$.

Now we obtain $\ell^{2,s}\subset\mathcal{B}\subset\ell^{2,1/2}$ for $s>1/2$. Passing to the dual spaces, we also have $\ell^{2,-1/2}\subset\mathcal{B}^{*}\subset\ell^{2,-s}$. ∎

Remark. In view of Lemma 2.3, the $\mathcal{B}$-$\mathcal{B}^{*}$ spaces constitute the optimal pair of Banach spaces to prove the limiting absorption principle for $R_{0}(\kappa)=(U_{0}-e^{i\kappa})^{-1}$ and $R(\kappa)=(U-e^{i\kappa})^{-1}$. Namely, $\mathcal{B}$-$\mathcal{B}^{*}$ estimates are sharper than $\ell^{2,s}$-$\ell^{2,-s}$ estimates for $s>1/2$. For details, we discuss in Sections 3 and 4.

Let us show the following property.

Proof. The summability of $|f_{\leftarrow}(y_{1},x_{2})|$ with respect to the variable $y_{1}$ follows from the estimate

The other cases can be proved in the same way. ∎

The classification of the spectrum of a unitary operator is a consequence of the spectral theory for self-adjoint operators (see e.g. [24]). In the following, $\sigma(A)$ is the totality of the spectrum of $A$. There are two kinds of classification of $\sigma(A)$. One is based on the spectral measure of $A$. Namely, there exists a spectral decomposition $E_{A}(\theta)$ for $\theta\in{\bf R}$ such that $A$ can be represented by

where $E_{A}(\theta)=0$ for $\theta<0$ and $E_{A}(\theta)=1$ for $\theta\geq 2\pi$. Since $E_{A}(\theta)$ is a measure on ${\bf R}$, it provides a orthogonal decomposition of $\mathcal{H}$ as

where $\mathcal{H}_{p}(A)$ is the closure of the subspace spanned by eigenfunctions in $\mathcal{H}$ of $A$, $\mathcal{H}_{ac}(A)$ and $\mathcal{H}_{sc}(A)$ are orthogonal projections onto the absolutely continuous subspace and the singular continuous subspace with respect to the measure $E_{A}(\theta)$, respectively. Then the spectrum $\sigma(A)$ is classified as