Asynchronous Distributed Consensus with Minimum Communication
Abstract
In this paper, the communication effort required in a multi-agent system (MAS) is minimized via an explicit optimization formulation. The paper considers a MAS of single-integrator agents with bounded inputs and a time-invariant communication graph. A new model of discrete asynchronous communication and a distributed consensus protocol based on it, are proposed. The goal of the proposed protocol is to minimize the aggregate number of communication instants of all agents, required to steer the state trajectories inside a pres-specified bounded neighbourhood within a pre-specified time. Due to information structure imposed by the underlying communication graph, an individual agent does not know the global parameters in the MAS, which are required for the above-mentioned minimization. To counter this uncertainty, the worst-case realizations of the global parameters are considered, which lead to min-max type optimizations. The control rules in the proposed protocol are obtained as the closed form solutions of these optimization problems. Hence, the proposed protocol does not increase the burden of run-time computation making it suitable for time-critical applications.
Index Terms:
Consensus, Distributed Optimization, Communication Cost, Asynchronous CommunicationI Introduction
In the recent years, multi-agent systems (MASs) have received tremendous attention due to their extensive applications in unmanned aerial vehicles (UAVs) [3], sensor networks [14], power grids [18], industrial robotics [26] etc. A typical MAS consists of a group of agents which collaborate to achieve desired objectives. Often, the objective is to achieve consensus, i.e., to drive the states of all agents into an agreement. To achieve this objective, agents in MAS need to exchange information with each other over some communication network. It is well known that communication network is an expensive resource [2], [22]. Hence, with the intent of reducing communication effort, a few approaches have been proposed in [9], [27], [28] etc. However, except in our preliminary work [25], the minimization of communication effort via explicit optimization, has never been addressed.
The problem of achieving consensus of MAS with single-integrator agents was first extensively analyzed in [15]. After that, various consensus protocols for higher order agents were developed in [11], [23], [24] etc. These protocols are either based on discrete synchronous communication or on continuous communication. A global synchronization clock is necessary for the implementation of synchronous protocols, which is often a major practical constraint [16]. On the other hand, the energy consumption of agent’s transponder is proportional to the number and duration of transmissions [7]. Thus, continuous transmission limits the life of agent’s battery and hence, its flight time [4], [19]. Second, continuous transmissions over a shared bandwidth-limited channel by multiple agents may lead to congestion of communication channel [2], [22]. And finally, MASs such as a group of UAVs are often used for stealthy military applications [17], [34]. In such scenarios, it is of strategic advantage to keep radio transmissions to a minimum in order to avoid detection by the enemy. For all these applications, it is necessary to develop an asynchronous/intermittent communication based consensus protocol which minimizes communication effort, i.e., the number and/or duration of transmissions.
In order to reduce the required communication effort in a MAS, a few indirect approaches have been proposed in the literature. In self-triggered control [13] based consensus protocols [8], [32], the next communication instant is pre-computed based on the current state. Event-triggered control [13] based consensus protocols [9], [35] initiate communication only when a certain error state reaches a predetermined threshold. Intermittent communication based consensus protocols are investigated in [27], [28] and [29]. Consensus protocols based on asynchronous information exchange for a MAS with single-integrator agents are developed in [5], [6], [10] and [31]. Other work on asynchronous consensus include [1], [12], [30] and [33]. All of the above protocols result in the reduced communication effort as compared to the conventional continuous communication based protocols. However, there is no explicit minimization of communication effort and hence, the above protocols can result in sub-optimal communication performance.
To overcome this issue, in this paper, we develop a distributed protocol which minimizes the communication effort required to maintain the consensus of single-integrator agents, via explicit optimization. This protocol is based on discrete asynchronous communication. Our notion of consensus is less stringent than the conventional one [15], in that we only require the difference between neighbouring agents’ states (i.e., the local disagreement) to reduce below a pre-specified bound. In the proposed protocol, communication occurs at discrete time instants, namely update/communication instants, at which agents access the states of neighbouring agents and then based on that information, update their control. Thus, in the proposed protocol, the number of update instants is a good measure of communication effort. Hence, our basic objective is to minimize the aggregate number of update instants of all agents in the MAS. Now, intuitively, if the inter-update durations are increased, then the number of update instants decreases. However, increase in the inter-update durations increases the time required to achieve the consensus bound. Hence, the problem of minimization of the number of update instants is well-posed only when the consensus time is included in the formulation. Evidently, the time required for a MAS to achieve consensus depends on the initial configuration of the agents. Hence, to make the minimization of the number of update instants well-posed, we require that the local disagreements of all agents be steered below a pre-specified consensus bound within a pre-specified time, which is expressed as a function of the initial condition of the MAS.
Due to communication structure imposed by the network, the above-mentioned minimization is a decentralized optimal control [20] problem. Because of the said imposition, an individual agent does not have global information such as the number of agents in the MAS, the underlying communication graph, the complete initial condition of the MAS etc. To counter this lack of global information, we require that the consensus constraint be satisfied for any number of agents, any communication graph and any initial condition. Further, due to the imposed communication structure, an individual agent can not predict the control inputs of the neighbouring agents. In order to guard against the resulting uncertainty, the control inputs in the proposed protocol are obtained as a solution of certain max-min optimizations (Sections V-A and V-B). We obtain the closed form solutions of these optimizations (see (7)-(10)) and hence, extensive numerical computations are not required for their implementation. This makes the proposed protocol suitable for time-critical applications.
Our contributions in this paper are summarized as follows:
-
1.
We develop a discrete asynchronous communication based distributed consensus protocol for a MAS with single-integrator agents (Section III).
- 2.
- 3.
The current paper is an extension of our work in [25] in three major ways. First, it was assumed in [25] that the initial local disagreements between agents are confined below a pre-specified bound. In the current paper, no such assumption on initial conditions has been made. Second, the protocol in [25] solves the minimization problem for a specific consensus time. On the other hand, the protocol developed in the current paper solves the minimization problem for a general pre-specified consensus time. Finally, in the current paper, the effect of pre-specified consensus time on optimal communication cost is analyzed. Such analysis was not presented in [25].
The remaining part of this paper is organized as follows. In Section II, the problem of minimizing the number of communication instants is formulated. In Section III, a distributed consensus protocol is proposed, which will be shown to be the solution for the special case of the formulated problem, in Sections IV and V. The protocol proposed in Section III is extended for the general case of the formulated problem, in Section VI. In Section VII, the simulation results are presented. The paper is concluded in Section VIII with future directions.
II Preliminaries and Problem formulation
II-A Graphs
A graph is a finite set of nodes connected by a set of edges . An edge between nodes and is represented by an ordered pair . A graph is said to be simple if . A graph is said to be undirected if implies . In an undirected graph , if (and equivalently ), then the nodes and are said to be neighbours of each other. A path between nodes and in an undirected graph is a sequence of edges . An undirected graph is said to be connected if there exists a path between any two nodes in . Let denote the number of neighbours of node and denote the cardinality of set . Then, the Laplacian matrix of a simple undirected graph is defined as
II-B System description
Consider a multi-agent system (MAS) of single-integrator agents, labeled as , , with dynamics
| (1) |
where and are the state and the control input of agent , respectively. Let and be the augmented state and control vectors of MAS (1), respectively. Define the set .
Let be a time-invariant simple undirected graph, whose nodes represent agents in MAS (1) whereas the edges represent the communication links between agents, over which they exchange information with their neighbours. Let be the set of indices of neighbours of agent . Note that as is a simple graph. The cardinality of the set is denoted by . Let denote the Laplacian matrix of .
We make the following assumptions about MAS (1):
-
1.
The control input of each agent belongs to the set
where denotes the set of measurable functions from to .
-
2.
The communication graph is connected.
-
3.
The communication delay is zero.
II-C Consensus
In this paper, we will be using two notions of consensus, which we define next.
Definition 1.
MAS (1) is said to have achieved conventional consensus at instant if
Define . Then, it follows from the definition of the Laplacian matrix that
| (2) |
As is the sum of differences of agent ’s state with its neighbours, we call it the local disagreement of agent . It is well known [15] that for a MAS with connected, time-invariant communication graph, conventional consensus at instant is equivalent to . However, in many practical applications, it is not necessary that each becomes exactly zero. It is sufficient if each remains below a prespecified consensus bound. This motivates our next notion of consensus, namely -consensus.
Definition 2.
Let be the prespecified consensus bound. MAS (1) is said to have achieved -consensus at instant if
II-D Communication model
In this paper, we consider a discrete communication model. Let denote the th update instant (also referred to as the communication instant) of agent , at which it accesses the state information of its neighbours and then, based on that information, updates its control. Our communication model is asynchronous, i.e., the update instants ’s of two different agents need not coincide.
As the communication model is discrete, the number of update instants is a good measure of communication effort. Hence, we define the communication cost of agent , denoted by , as the number of update instants of agent in the time interval . Then, we define the aggregate communication cost of MAS (1), denoted by , as
| (3) |
II-E Problem formulation
Let be an initial condition of MAS (1), be the prespecified consensus bound and be the prespecified consensus time. Our objective is to develop a protocol which minimizes the communication cost , under the constraint of achieving -consensus of MAS (1) within time .
As discussed in Section I, due to information structure imposed by graph , an individual agent in MAS (1) has access only to its own information and that of its neighbours. Therefore, the proposed protocol needs to be distributed, i.e., based only on the local information. In addition, an individual agent does not have global information such as the number of agents in MAS (1), the structure of the communication graph , the complete initial condition etc. To address these uncertainties, the proposed protocol must be able to achieve -consensus of MAS (1) within the prespecified time , for any , any connected and any .
Since the input set is magnitude bounded, for a fixed , it will not be possible to achieve -consensus within time , for every . Thus, the consensus time must be specified as a function of . To highlight this dependence on , we modify the notation of the prespecified consensus time from to . Similarly, the communication costs and depend on . Thus, we modify their notations from and to and , respectively. Now, we formalize our objective as follows:
Problem 3.
Consider MAS (1) with initial condition and connected communication graph . Let denote the set of connected graphs with nodes. Let be the prespecified consensus time which is expressed as a function of . Develop, if possible, a discrete asynchronous communication based protocol, i.e., admissible control , adhering to graph , which is solution of the following optimization:
| (4) | ||||
II-F Choosing
In Problem 3, the time can be specified as any function of . However, in practical applications, it is desirable to set to the minimum feasible value.
In [21], the time-optimal control rule is proposed which achieves conventional consensus of MAS (1) in minimum time. This control rule and the corresponding consensus time, denoted by and , respectively, are presented below. Let be an initial condition of MAS (1). Define and . Recall that denote the local disagreement of agent . Let denote the standard signum function. Then, the time-optimal consensus rule from [21] is
| (5) |
with the corresponding consensus time
| (6) |
Notice that the control rule (5) requires instantaneous access to the local disagreement , and as a result, demands continuous communication. Then, it follows from the time optimality of that a discrete communication based protocol cannot achieve -consensus of MAS (1) within time . This implies that Problem 3 is infeasible for and we should assume . We further assume that . This assumption makes Problem 3 tractable and results in a particularly simple closed form solution for the control inputs. We solve Problem 3 for in Sections III-V and later extend it for in Section VI.
III Protocol : For
In this section, we present the protocol proposed for . We refer to this protocol as Protocol . Later, this protocol will be shown to be a solution of Problem 3 for .
Protocol has the following two elements:
) Computation of next update instant and control input
) At each update instant , agent , accesses
the current states ’s of its neighbours ,
and computes .
) After that, agent computes its next update instant
and control input to be applied in the interval as follows:
) If , then
| (7) | ||||
| (8) |
) If , then
| (9) | ||||
| (10) |
) Then, agent broadcasts and . This broadcast information is received by agent ’s neighbours , at the same instant . The neighbours , store this information with the reception time-stamp.
) Accessing the states of neighbours at update instants
) The time instant is the first update instant of all agents .
At this instant, all agents broadcast their current states.
Thus, each agent , has a direct access to the current states ’s of its neighbours .
For example, consider the communication graph shown in Fig. 1
and the corresponding communication timeline shown in Fig. 2.
At instant , agents , and broadcast information to their neighbours.
) Let , be any update instant of agent . Let be the latest update instant of agent ,
at which it had broadcast and .
At update instant , agent accesses the stored information and retrieves and for all .
For example, in the communication timeline shown in Fig. 2,
at instants and , agent receives information from its neighbours.
Later, agent uses this information at its update instant .
) It is known from (8) and (10) that every agent , had applied control in the interval .
Using this fact, agent computes the current state of , as
Remark 4.
As per Assumption 3, the communication delay is zero. In addition, the time required for the computation of and is negligible. This justifies the assumption that computation, transmission and reception of and , happen at the same time instant .
IV -consensus under Protocol
In this section, we show that Protocol achieves -consensus of MAS (1) within time . However, before that, we present a necessary condition on feasible solutions of Problem 3, which will be utilized while proving the attainment of -consensus within time .
IV-A Necessary condition on feasible solutions of Problem 3
A discrete communication based distributed protocol is said to be a feasible solution of Problem 3 if it satisfies constraint (4), i.e., achieves -consensus of MAS (1) within time , for any number of agents , any connected graph and any initial condition . Recall that denotes the set of connected graphs with nodes. Then, the following lemma gives a necessary condition on the feasible solutions of Problem 3.
Lemma 6.
Proof.
Recall that due to communication structure imposed by graph , an individual agent in MAS (1) does not know the complete initial condition . Therefore, it does not know the exact value of and how far is from . In fact, as in Example 9 presented below, there may exist a MAS of the form (1) in which . In such a case, violation of (11) results in the violation of constraint (4) in Problem 3. This contradicts the fact that Protocol is a feasible solution of Problem 3. Hence, Protocol must satisfy (11). This completes the proof. ∎
The following lemma shows that Protocol satisfies the necessary condition (11). The proof of this lemma relies on the derivation of control rules (7)-(10) in Protocol , which is deferred to Section V for better structure of the paper. Hence, we defer the proof of the said lemma to Section V-C.
Lemma 7.
Protocol satisfies the necessary condition (11).
IV-B -consensus within time
The following theorem shows that Protocol achieves -consensus of MAS (1) within time .
Theorem 8.
Proof.
See the Appendix for the proof. ∎
According to Theorem 8, under Protocol , the duration is an upper bound on the time required to achieve -consensus of MAS (1). Next, we show with the following example that there exists a MAS of the form (1) for which the -consensus time under Protocol is arbitrarily close to .
Example 9.
The following theorem shows that under Protocol , the time required to achieve -consensus of the MAS in Example 9 is arbitrarily close to .
Theorem 10.
Consider the MAS in Example 9. Let denote the time required by Protocol to achieve -consensus of a MAS with initial condition . Let be any real number. Then, there exist integers and such that the following holds.
| (12) |
Proof.
See the Appendix for the proof. ∎
V Optimality of Protocol
The objective in Problem 3 is to minimize the number of update instants under the constraint of achieving -consensus of MAS (1) within the pre-specified time. Intuitively, if the duration between the successive update instants is increased, then the number of update instants decreases. Motivated from this intuition, we obtain the solution of Problem 3 by maximizing the inter-update durations. We divide the solution process into two steps. First, we solve two maximization problems, one corresponding to and the other corresponding to , in which the objective function is the inter-update duration. The control rules (7)-(8) and (9)-(10) in Protocol are solutions of these maximization problems, respectively. Later, we show how these two control rules together form the solution of Problem 3.
V-A Maximization of inter-update durations: For
Let be the local disagreement of agent at its update instant such that . The goal of agent is to maximize the inter-update duration by delaying its next update instant . However, while doing so, agent must satisfy the necessary condition (11). For that purpose, agent needs to ensure that for all . Recall the definition of in (2). Then, the evolution of in the interval is given as
| (13) |
This evolution depends on control inputs and , in the interval . Note that any instant can be an update instant of a neighbouring agent , at which updates its control. This updated value is not known to agent in advance, at instant . Thus, while maximizing the inter-update duration , agent needs to consider the worst-case realizations of the neighbouring inputs , which result in the minimum value of the inter-update duration. This leads to the following max-min optimization:
| (14) | ||||
| (15) | ||||
| (16) |
Lemma 11.
Proof.
See the Appendix for the proof. ∎
V-B Maximization of inter-update durations: For
Let be the local disagreement of agent at its update instant such that . Then, in order to achieve -consensus, it is necessary to steer below the consensus bound . If that could be done in time-optimal manner, it is an added advantage. Recall that in Section II-F, we discussed the time-optimal consensus rule (5) which achieves conventional consensus of MAS (1) in minimum time. Motivated from this rule, we choose our control rule as
| (17) |
As mentioned in Section V-A, the goal of agent is to maximize the inter-update duration by delaying its next update instant . However, while doing so, agent must satisfy the necessary condition (11).
Recall that . Without loss of generality, assume that . Then, it follows from (17) that . Let be the first time instant at which . Then, in order to satisfy (11), agent needs to ensure that
which is equivalent to
As discussed in Section V-A, at instant , agent does not know the future values of the neighbouring inputs in the interval . Thus, while maximizing the inter-update duration , agent needs to consider the worst-case realizations of the neighbouring inputs , which result in the minimum value of the inter-update duration. This leads to the following max-min optimization:
| (18) | ||||
| (19) |
The following lemma shows that control law (9)-(10) is the solution of optimization (18)-(19).
Lemma 12.
Proof.
See the Appendix for the proof. ∎
V-C Feasibility of Protocol
In this section, we present the proof of Lemma 7 which claims that Protocol satisfies the necessary condition (11).
Proof.
of Lemma 7 : Consider MAS (1) with any , any connected communication graph and any initial condition . Let be any agent in MAS (1) and be the first time instant under Protocol at which . If , then it follows from (16) and Lemma 11 that under Protocol . On the other hand, if , then it follows from (19), Lemma 12 and Remark 13 that under Protocol . Consequently, in both cases, Lemma 11 leads to . This proves that Protocol satisfies the necessary condition (11). ∎
V-D Proof of optimality of Protocol
Consider MAS (1) with initial condition . Let be any protocol which is a feasible solution of Problem 3 for , i.e., a discrete communication based distributed protocol which achieves -consensus of MAS (1) within time , for every , every connected and every . Let and denote the value of the aggregate communication cost defined in (3), under Protocol and Protocol , respectively.
Theorem 14.
Consider MAS (1) with initial condition . Then, under Protocol , the following holds.
| (20) |
Proof.
For the sake of contradiction, assume that
| (21) |
Recall that denotes the number of update instants of agent in the interval , corresponding to initial condition . Let and denote the value of , under Protocol and Protocol , respectively. Then, (3) and (21) imply that there exists at least one agent, say , such that
This implies that under Protocol , at least one inter-update duration of agent is longer than that prescribed by control laws (7) and (9) in Protocol .
Recall from (15) and Lemma 11 that control law (7) gives the maximum inter-update duration under constraint (16). Similarly, it follows from (18) and Lemma 12 that control law (9) gives the maximum inter-update duration under constraint (19). Then, as one inter-update duration under Protocol is longer than that prescribed by control laws (7) and (9), Protocol must be violating either constraint (16) or constraint (19). Recall that violation of (16) or (19) by Protocol results in the violation of necessary condition (11) on feasible protocols. This contradicts the fact that Protocol is a feasible solution of Problem 3 and proves claim (20). ∎
VI Protocol : For
In Section V-D, we proved that Protocol is the solution of Problem 3 for . In this section, we extend Protocol for . We refer to the extended protocol as Protocol .
VI-A Protocol
Let be a real number and be the pre-specified -consensus time. Define . Then, Protocol is same as Protocol , except the control bound in place of .
VI-B Optimality of Protocol
In this section, we first show that Protocol achieves -consensus of MAS (1) within the pre-specified time .
Theorem 15.
Consider MAS (1). Let be the pre-specified consensus bound. Then, for every , every connected communication graph and every , Protocol achieves -consensus of MAS (1) in time less than or equal to . Moreover, there exist , connected graph and initial condition for which -consensus time under Protocol is arbitrarily close to .
Proof.
Now, we prove the optimality of Protocol for . Consider MAS (1) with an initial condition . Let be any protocol which is a feasible solution of Problem 3 for . Let and denote the value of defined in (3), under Protocol and Protocol , respectively.
Theorem 16.
Consider MAS (1) with initial condition . Then, under Protocol , the following holds.
Proof.
The claim follows from the arguments in the proof of Theorem 14. ∎
Next, we analyze the effect of on . Intuitively, with the increase in , agents in MAS (1) can afford to delay their next update instants, which would result in lower . However, the following theorem shows that the above intuition is not true after .
Theorem 17.
Consider MAS (1) with initial condition . Then, under Protocol , for every real , the following holds.
| (22) |
Proof.
Let and denote the th update instants of agent under Protocols and , respectively. Recall that the dynamics of MAS (1) under Protocol is times slower than that of under Protocol . Then, it is easy to show that
Hence, the timeline of agent under Protocol is just the -scaled version of its timeline under Protocol . As a result, the number of update instants of agent in the interval under Protocol is equal to that of in the interval under Protocol . Then, the claim (22) follows from the definition of in (3). ∎
VII Simulation results
In this section, we present the simulation results obtained under Protocol for various ’s. Consider MAS (1) with agents and the communication graph shown in Fig. 4.
Let the consensus bound and the control bound be and , respectively. Let the initial condition of the MAS be . Then, it follows from the definition of in (6) that sec.
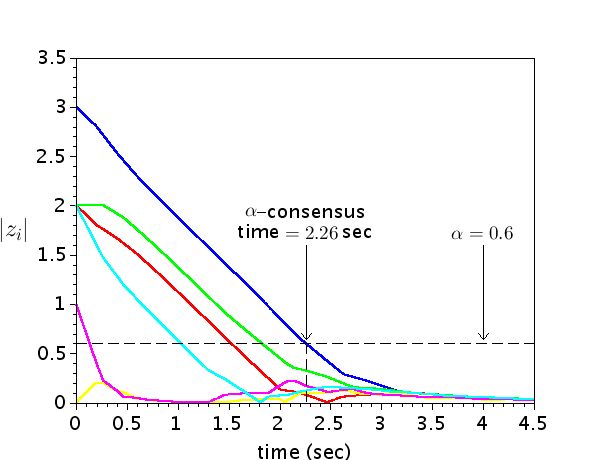
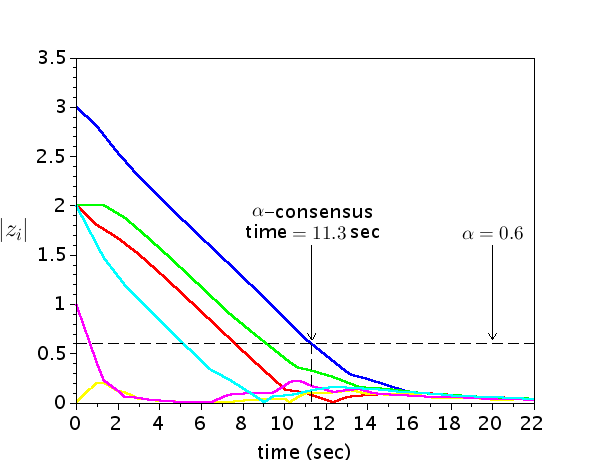
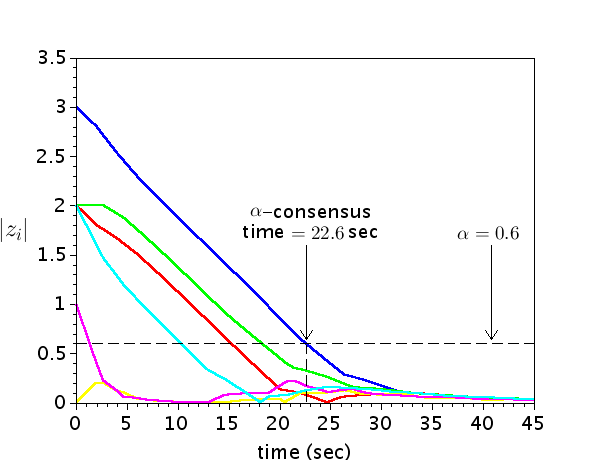
We simulated the above MAS under Protocol for , and . The corresponding disagreement trajectories ’s are plotted in Fig. 5(a), 5(b) and 5(c), respectively. The corresponding -consensus times and optimal communication costs are given in Table .
Notice that in each of the above three cases, Protocol achieves -consensus within the prespecified time , as proved in Theorem 15. Further, the -consensus times corresponding to and are and times of that corresponding to , respectively. This observation is in accordance with the arguments in the proof of Theorem 15. In addition, observe that the trajectories in Figures 5(b) and 5(c) are just the time-stretched versions of the corresponding trajectories in Fig. 5(a). The optimal communication costs ’s and corresponding to , and are same, as proved in Theorem 17.
| -consensus time [sec] | ||||||||
|---|---|---|---|---|---|---|---|---|
VIII Conclusion and future work
In this paper, a distributed consensus protocol (Protocol ) is proposed for a MAS of single-integrator agents with bounded inputs and time-invariant communication graph. We showed (Theorems 15 and 16) that the proposed protocol minimizes the aggregate number of communication instants required to achieve -consensus within the pre-specified time . The control rules in the proposed protocol are obtained by maximizing the inter-update durations. We computed (Lemmas 11 and 12) the closed form solutions of these optimizations. Finally, we presented the simulation results which verify the theoretical claims. The work of extending the proposed protocol to MASs with complex dynamics is in progress.
Appendix
A. Intermediate results for the proof of Theorem 8
In this section, we develop a few intermediate results which will be used later in the proof of Theorem 8. Let and be the state and the local disagreement of agent respectively, at its update instant . Recall that is the set of indices of neighbours of agent , with cardinality .
Lemma 18.
Consider agent in MAS (1) with . Then, under Protocol , the following holds.
.
.
Proof.
At instant , the state of agent is . It is given that . Then, control rule (7)-(8) in Protocol lead to
Then, it follows from the definition of in (2) that
| (23) |
Recall that the cardinality of is . Then, by re-arranging the terms in (23), we get . This proves the claim in Lemma 18..
Next, we prove that under Protocol , satisfies . Then, the claim in Lemma 18. follows by repeating arguments in the subsequent inter-update intervals.
Let the control input be as defined in (8). We know from the dynamics of in (1) and the definition of in (2) that
| (24) |
By using (7) and (8), it is easy to show that
| (25) |
Further, recall that . Then, it follows from (7) that
| (26) |
Then, (24), (25) and (26) together lead to
| (27) |
Now, we claim that . Assume for the sake of contradiction that there exists such that . Take . Then, it follows from (24) that , which contradicts (27) and proves our claim that . By repeating the above arguments in the subsequent inter-update intervals of agent , we get Lemma 18.. This completes the proof. ∎
Let be an update instant of agent in MAS (1). Define
| (28) | ||||
| (29) |
The following lemma shows that the state remains bounded between and , in the interval .
Lemma 19.
Consider any agent in MAS (1). Under Protocol , the state of agent satisfies the following.
| (30) |
Proof.
Based on the value of , there are two cases, and . We will prove the claim for the first case. The proof for the second case follows analogously.
Without loss of generality, assume that . Then, it follows from (8) that . Hence, , which implies that . Then, the definition of in (28) leads to
| (31) |
Let and be as in the definition of in (6). The following lemma shows that the states of all agents in MAS (1) remain bounded between and , for all .
Lemma 20.
Consider MAS (1) with initial condition . Under Protocol , the following holds.
| (33) |
Proof.
Recall that according to Protocol , the time instant is the first update instant of every agent . Let and be as defined in (28) and (29), respectively. Then, it follows from Lemma 19 that
| (34) |
Further, it is clear from the definitions of and that . Similarly, . Then, (34) leads to
Now, by applying the above arguments in the subsequent inter-update intervals , of all agents, we get (33). This completes the proof. ∎
B. Proof of Theorem 8
For the sake of contradiction, assume that the claim is not correct, i.e., for some , and , Protocol does not achieve -consensus of MAS (1) within time . This implies that there exists at least one agent, say , and a time instant , such that . Recall from Lemma 7 that Protocol satisfies the necessary condition (11). Then, it follows from (11) that under Protocol , the following holds.
Without loss of generality, assume that . Then, it follows from control rule (10) that and hence, . As , we get
| (35) |
Let and be as in the definition of in (6). Then, (6) and (35) lead to
| (36) |
It is clear from the definition of that . Then, (36) leads to . This contradicts Lemma 20 and proves the claim in Theorem 8.
C. Intermediate result for the proof of Theorem 10
Lemma 21.
Proof.
We first define the integer for which the claim (37) holds. Let be the given number. Define . Let ceil be the standard ceiling function. Define the integers , , and . Then, define
| (38) |
Now, consider the MAS in Example 9 with .
We will show that the claim (37) holds for this MAS.
For the sake of clarity, we divide the remaining proof into five parts as follows.
Computation of and for
According to Protocol , the first update instant of every agent is . At this instant, the states of agents are and . Then, the local disagreement of agent at instant is . Note that . Thus, . Then, it follows from control rule (9)-(10) that
| (39) | ||||
| (40) |
As a result, .
Now, consider any agent . Note that . Thus, the local disagreement of agent at instant is . Then, it follows from control rule (9)-(10) that
| (41) | ||||
| (42) |
As a result, . It follows from the definitions of and in (38) that . Thus, satisfies . Recall from (42) that . Recall also that . Hence,
| (43) |
Next, consider any agent . Note that . Thus, the local disagreement of agent at instant is . Then, it follows from control rule (7)-(8) that
| (44) | ||||
| (45) |
As a result, the state satisfies
| (46) |
) Ordering of update instants ’s
Let ’s be as given in (41) and (44). Recall from (38) that . Then, it is easy to show that . Then, it follows from (41) and (44) that
| (47) |
Let be as given in (39). It follows from the definitions of and in (38) that . Then, (39) and (41) lead to
| (48) |
) Computation of for
Consider any agent . Recall from (47) and (48) that . Now, we compute . According to (40) and (44), the state of agent at instant is . Similarly, according to (42) and (44), the state of agent , at instant is . Recall from (46) that . Thus, for , we get
| (49) |
Then, it follows from definitions of and in (38) that . After that, Lemmas 6 and 7 give
| (50) |
Recall from (47) that . Hence,
| (51) |
Then, (7) and (41) together lead to
| (52) |
Next, consider any agent . Recall that . Then, it follows from Lemma 18. that
| (53) |
Subsequently, (7) and (44) together lead to
| (54) |
Recall from (38) that . Then, it is easy to show that . Then, (41), (52) and (54) imply that
| (55) |
Let be as given in (39). It follows from the definitions of and in (38) that . Then, (39) and (52) together lead to
| (56) |
) Computation of for
Consider any agent . Recall that and . Then, Lemma 18. leads to
It follows from (43), (46) and (47) that . Hence, the average of ’s, i.e., , satisfies . Recall that is constant in the interval . Recall also that . Hence,
| (57) |
) Computation of for
D. Proof of Theorem 10
Let be the given real number. Define and . Let be as defined in (38) corresponding to and . Recall from (50) that , where the expression of is given in (44). Then, it follows from (44), the definitions of and in (38) and the definition of that . Thus,
| (60) |
Further, recall from (53) that
| (61) |
Then, (60) and (61) imply that the -consensus time is equal to the maximum of and the time required to steer inside .
Let be the first time instant at which . Recall that the initial conditions of the agents in Example 9 are and . Thus, . Then, clearly, . We know from Lemma 21 that . Then, implies that . Further, the control rule (10) and together imply that . Recall that . Hence, . Then, it follows from the definitions of and that and . Subsequently, (60) and (61) imply that the -consensus time satisfies . This proves the first inequality in (12).
E. Proof of Lemma 11
It is given that . Then, it follows from Lemma 18. that control rule (7)-(8) satisfies constraint (16). Let and be as defined in (7) and (8), respectively. Then, the inter-update duration is , for all . Next, we show that is the max-min value of optimization (14)-(16). This will prove the optimality of control rule (7)-(8) and complete the proof.
For the sake of contradiction, assume that the max-min value of optimization (14)-(16) is greater than . Let that value be . Let be the corresponding optimal control. Then, it follows from the evolution of given in (13) that
| (62) |
Define .
Then, depending on the value of , there are following three cases.
Case 1 : —
Take . Then, it follows from (62) that
.
Case 2 :
Take . Then, it follows from (62) that
Recall that , which is equivalent to . Then, the fact implies that .
Case 3 :
Take . Then, by following the arguments in Case , we get
.
F. Proof of Lemma 12
We first show that control rule (9)-(10) satisfies constraint (19). Let and be as defined in (9) and (10), respectively. Define . It is given that . Then, (10) leads to . Recall the evolution of given in (13). By putting the expressions of and in (13), we get
| (63) |
Recall that the cardinality of is and . Then, it follows from the definition of that
| (64) |
Now, (63) and (64) together imply that . As , i.e., , we have . Further, it follows from the definition of in (2) that . Recall again that the cardinality of is and . Hence, which implies that . Then, the above-proved fact implies that control law (9)-(10) satisfies constraint (19).
Next, we show that control rule (9)-(10) achieves the max-min value of optimization (18)-(19). Recall that under control rule (9)-(10), the inter-update duration is . We claim that is the max-min value of optimization (18)-(19). For the sake of contradiction, assume that the max-min value of optimization (18)-(19) is for some . Then, . Let the inputs of the neighbouring agents be . Then, it follows from the evolution of given in (13) that
Now, by putting the expression of and rearranging the terms, we get . As , we have . Thus, . This violates constraint (19) and contradicts the fact that is the max-min value of optimization (18)-(19). Hence, the inter-update duration under control rule (9)-(10) is the max-min value of optimization (18)-(19). This completes the proof.
References
- [1] J. Almeida, C. Silvestre and A. Pascoal, Continuous-time consensus with discrete-time communications, Systems and Control Letters, vol. 61, no. 7, pp. 788-796, 2012.
- [2] J. Baillieul and P. Antsaklis, Control and communication challenges in networked real-time systems, Proceedings of the IEEE, vol. 95, no. 1, pp. 9-28, 2007.
- [3] E. Barmpounakis, E. Vlahogianni and J. Golias, Unmanned aerial aircraft systems for transportation engineering: current practice and future challenges, International Journal of Transportation Science and Technology, vol. 5, no. 3, pp. 111-122, 2016.
- [4] E. Bertran and A. Cerda, On the tradeoff between electrical power consumption and flight performance in fixed-wing UAV autopilots, IEEE Transactions on Vehicular Technology, vol. 56, no. 11, pp. 8832-8840, 2016.
- [5] M. Cao, A. Morse and B. Anderson, Coordination of an asynchronous multi-agent system via averaging, International Federation of Automatic Control (IFAC) World Congress, Prague, Czech Republic, 2005.
- [6] M. Cao, A. Morse and B. Anderson, Agreeing asynchronously, IEEE Transactions on Automatic Control, vol. 53, no. 8, pp. 1826-1838, 2008.
- [7] L. Corral, I. Fronza, N. Ioini and A. Ibershimi, A measurement tool to track drones battery consumption during flights, Proceedings of International Conference on Mobile Web and Information Systems, Vienna, Austria, 2016.
- [8] D. Dimarogonas, E. Frazzoli, and K. Johansson, Distributed self-triggered control for multi-agent systems, Proceedings of the IEEE Conference on Decision and Control, Atlanta, USA, 2010.
- [9] D. Dimarogonas, E. Frazzoli and K. Johansson, Distributed event-triggered control for multi-agent systems, IEEE Transactions on Automatic Control, vol. 57, no. 5, pp. 1291-1297, 2012.
- [10] L. Fang and P. Antsaklis, Information consensus of asynchronous discrete-time multi-agent systems, Proceedings of the American Control Conference, Portland, USA, 2005.
- [11] J. Fax and R. Murray, Information flow and cooperative control of vehicle formations, IEEE Transactions on Automatic Control, vol. 49, no. 9, pp. 1465-1476, 2004.
- [12] S. Giannini, D. Paola, A. Petitti and A. Rizzo, On the convergence of the max-consensus protocol with asynchronous updates, Proceedings of the IEEE Conference on Decision and Control, Florence, Italy, 2013.
- [13] W. Heemels, K. Johansson and P. Tabuada, An introduction to event-triggered and self-triggered control, Proceedings of the IEEE Conference on Decision and Control, Hawaii, USA, 2012.
- [14] K. Hla, Y. Choi and J. Park, The multi-agent system solutions for wireless sensor network applications, Agent and Multi-agent Systems: Technologies and Applications, pp. 454-463, 2008.
- [15] A. Jadbabaie and A. Morse, Coordination of groups of mobile autonomous agents using nearest neighbor rules, IEEE Transactions on Automatic Control, vol. 48, no. 6, pp. 988-1001, 2003.
- [16] A. Joshi, N. Limbu, I. Ahuja, A. Mulla, H. Chung, and D. Chakraborty, Implementation of distributed consensus on an outdoor testbed, Proceedings of the European Control Conference, Aalborg, Denmark, 2016.
- [17] H. Liu, S. Chen, L. Shen and J. Chen, Tactical trajectory planning for stealth unmanned aerial vehicle to win the radar game, Defence Science Journal, vol. 62, no. 6, pp. 375-381, 2012.
- [18] G. Merabet, M. Essaaidi, H. Talei, M. Abid, N. Khalil, M. Madkour and D. Benhaddou, Applications of Multi-Agent Systems in Smart Grids: A Survey, International Conference on Multimedia Computing and Systems (ICMCS), Marrakesh, Morocco, 2014.
- [19] J. Meyer, F. Du-plessis and W. Clarke, Design considerations for long endurance unmanned aerial vehicles, IntechOpen, 2009.
- [20] K. Movric and F. Lewis, Cooperative optimal control for multi-agent systems on directed graph topologies, IEEE Transactions on Automatic Control, vol. 59, no. 3, pp. 769-774, 2014.
- [21] A. Mulla, D. Patil and D. Chakraborty, Distributed computation of minimum time consensus for multi-agent systems, Proceedings of the IEEE Conference on Decision and Control, Los Angeles, USA, 2014.
- [22] G. Nair, F. Fagnani, S. Zampieri and R. Evans, Feedback control under data rate constraints: an overview, Proceedings of the IEEE, vol. 95, no. 1, pp. 108-137, 2007.
- [23] W. Ren, Consensus tracking under directed interaction topologies: algorithms and experiments, IEEE Transactions on Control Systems Technology, vol. 18, no. 1, pp. 230-237, 2010.
- [24] W. Ren and R. Beard, Distributed Consensus in Multi-vehicle Cooperative Control, Springer, 2008.
- [25] V. Sawant, D. Chakraborty and D. Pal, Asynchronous consensus of continuous-time multi-agent systems with minimum communication, Proceedings of the IEEE Conference on Decision and Control, Nice, France, 2019.
- [26] J. Shamma, Cooperative Control of Distributed Multi-agent Systems, Wiley, 2007.
- [27] G. Wen, Z. Duan, W. Ren and G. Chen, Distributed consensus of multi-agent systems with general linear node dynamics and intermittent communications, International Journal of Robust and Nonlinear Control, vol. 24, no. 16, pp. 2438-2457, 2013.
- [28] G. Wen, Z. Duan, W. Yu and G. Chen, Consensus in multi-agent systems with communication constraints, International Journal of Robust and Nonlinear Control, vol. 22, no. 2, pp. 170-182, 2012.
- [29] G. Wen, Z. Duan, W. Yu and G. Chen, Consensus of second-order multi-agent systems with delayed nonlinear dynamics and intermittent communications, International Journal of Control, vol. 86, no. 2, pp. 322-331, 2012.
- [30] W. Xia amnd M. Cao, Sarymsakov matrices and asynchronous implementation of distributed coordination algorithms, IEEE Transactions on Automatic Control, vol. 59, no. 8, pp. 2228-2233, 2014.
- [31] F. Xiao and L. Wang, Asynchronous consensus in continuous-time multi-agent systems with switching topology and time-varying delays, IEEE Transactions on Automatic Control, vol. 53, no. 8, 1804-1816, 2008.
- [32] X. Yi, J. Wei and K. Johansson, Self-triggered control for multi-agent systems with quantized communication or sensing, Proceedings of the IEEE Conference on Decision and Control, Las Vegas, USA, 2016.
- [33] J. Zhan and X. Li, Asynchronous consensus of multiple double-integrator agents with arbitrary sampling intervals and communication delays, IEEE Transactions on Circuits and Systems-, vol. 62, no. 9, pp. 2301-2311, 2015.
- [34] Z. Zhao, Y. Niu, Z. Ma and X. Ji, A fast stealth trajectory planning algorithm for stealth UAV to fly in multi-radar network, Proceedings of the IEEE International Conference on Real-time Computing and Robotics, Angkor Wat, Cambodia, 2016.
- [35] W. Zhu, Z. Jiang and G. Feng, Event-based consensus of multi-agent systems with general linear models, Automatica, vol. 50, no. 2, pp. 552-558, 2014.
| Vishal Sawant received the Bachelor of Engineering degree from Mumbai University, India, in 2010 and the M.Tech. degree from the Department of Electrical Engineering, IIT Bombay, India, in 2012. He then worked as a software engineer for two years. In July 2014, he started Ph.D. degree at the Department of Electrical Engineering, IIT Bombay, India. From May 2020 to September 2021, he worked as a postdoctoral researcher at the Cognitive Robotics group, TU Delft, The Netherlands. Currently, he is a postdoctoral researcher at the Automation and Control Section, Aalborg University, Denmark. His research interests include multi-agent systems, cyber-physical security and distributed optimization. |
| Debraj Chakraborty received the Bachelor’s degree from Jadhavpur University, Kolkata, India, in 2001 and the M. Tech. degree from Indian Institute of Technology Kanpur, Kanpur, India, in 2003, both in electrical engineering, and the Ph. D. degree in electrical and computer engineering from University of Florida, Gainesville, FL, USA, in 2007. He joined the Indian Institute of Technology Bombay, Mumbai, India, in 2007, where he is currently a Professor in the Department of Electrical Engineering. His research interests include optimal control, linear systems, and multiagent systems. |
| Debasattam Pal received his Bachelor of Engineering (B.E.) degree from the Department of Electrical Engineering of Jadavpur University, Kolkata, in 2005. He received his M.Tech. and Ph.D. degrees from the Department of Electrical Engineering, IIT Bombay, in the years 2007 and 2012, respectively. He then worked as an Assistant Professor in IIT Guwahati from July, 2012 to May, 2014. He joined IIT Bombay in June, 2014, where he is currently an Associate Professor in the EE Department. His main area of research is systems and control theory. More specifically, his areas of interest are: multidimensional systems theory, algebraic analysis of systems, dissipative systems, optimal control and computational algebra. |