Atomicity and Abstraction for Cross-Blockchain Interactions
Abstract.
A blockchain facilitates secure and atomic transactions between mutually untrusting parties on that chain. Today, there are multiple blockchains with differing interfaces and security properties. Programming in this multi-blockchain world is hindered by the lack of general and convenient abstractions for cross-chain communication and computation. Current cross-chain communication bridges have varied and low-level interfaces, making it difficult to develop portable applications. Current methods for multi-chain atomic transactions are limited in scope to cryptocurrency swaps.
This work addresses these issues. We first define a uniform, high-level interface for communication between chains. Building on this interface, we formulate a protocol that guarantees atomicity for general transactions whose operations may span several chains. We formulate and prove the desired correctness and security properties of these protocols. Our prototype implementation is built using the LayerZero cross-chain bridge. Experience with this implementation shows that the new abstractions considerably simplify the design and implementation of multi-chain transactions. Experimental evaluation with multi-chain swap transactions demonstrates performance comparable to that of custom-built implementations.
1. Introduction
A blockchain provides the abstraction of an immutable, open, and fault-tolerant ledger. Several blockchains with a variety of features have been designed and implemented since the introduction of the Bitcoin chain (Nakamoto, 2008). The rich variety comes at a cost: information is spread across chains, complicating the development of applications.
From the programmer’s viewpoint, there is a lack of effective abstractions for inter-chain communication and computation. Current ”cross-chain bridge” mechanisms facilitate basic communication between two chains but expose varied and low-level interfaces, making it challenging to write easily portable applications. Smart contract transactions execute atomically on a single chain, i.e., with “all or nothing” semantics. However, distinct chains operate concurrently and independently of one another; hence, atomicity does not extend across chains and must be enforced by a protocol. Currently, atomic cross-chain protocols are known only for cryptocurrency swaps: a useful application but with a narrow scope.
There is thus a need for convenient, broadly applicable programming abstractions for computation and communication across blockchains. In this work, we design two such mechanisms: (1) a uniform interface for pairwise blockchain communication, and (2) a protocol that ensures atomicity for transactions whose operations may span several chains.
The interface provides three commonly-needed communication functionalities: notification (sending a message from one chain to another); notification with acknowledgement of receipt; and a remote procedure call. The central advantage of this interface is portability: smart contracts written to this interface execute without modification on different chains connected by different bridges, much as the standard socket library (Gilligan et al., 1999) of Unix allows programs to be ported to a variety of network types and interfaces. We develop an architecture for realizing these functionalities and instantiate it over the LayerZero and IBC cross-chain bridges. The interface also simplifies programming, eliminating bugs such as one that we discovered in LayerZero’s own example PingPong application.
As information spreads out over multiple chains, there is a need for transactions whose operations span several chains. The resulting technical challenge, which we address in this work, is to provide a mechanism that guarantees atomic and trustworthy execution.
We design a protocol for atomic execution of general cross-chain transactions. This protocol is inspired by the classic two-phase commit protocols in distributed databases, and operates over the uniform communication interface. We prove atomicity and trustworthiness; I.e., we show that the protocol cannot be disrupted by malicious behavior by other parties. Trustworthiness relies on a secure-transfer property of cross-chain bridges, as well as the presence of trusted contracts that help execute remote operations.
We have developed a prototype implementation (in Solidity) using the LayerZero and IBC bridges. We have deployed this implementation on testnets linked by LayerZero bridges and used the atomicity protocol to implement and successfully test pairwise and multi-way cryptocurrency swaps. Multi-chain cryptocurrency swaps are easily expressed in the general model, requiring only lines of code to define a transaction.
To summarize, this work makes the following contributions:
-
(1)
We define a uniform interface for inter-blockchain communication, ensuring portability of applications across a variety of cross-chain bridges.
-
(2)
We define a protocol for atomic execution of general, cross-chain transactions.
-
(3)
We show the correctness and trustworthiness of these protocols, under clearly stated assumptions on blockchain and bridge computation.
-
(4)
Experience with programming multi-chain swap transactions shows that the abstractions considerably simplify the design of transactions, while the prototype implementation has performance that is comparable to that of custom-built implementations.
This paper is organized as follows. We begin with relevant background on blockchain and blockchain interoperability. This is followed by the design of the uniform communication interface and the multi-chain atomicity protocol, supported by formal modeling and proofs of correctness and trustworthiness. We then describe an evaluation on case studies that utilize LayerZero as the low-level bridge communication between chains. Finally, we discuss related work and draw conclusions along with suggestions for future work.
2. Background
2.1. Blockchain Interoperability
A blockchain system is a distributed ledger that maintains a continuously growing history of unalterable ordered information. The information is organized in a chain of discrete blocks. The potential benefits of the blockchain are more than just economic-they extend into political, humanitarian and scientific domains (Swan, 2015).
Smart contracts are digital agreements coded and stored within the blockchain (Zheng et al., 2020). Unlike conventional paper-based contracts, smart contracts encode terms and conditions through software. In this inherently decentralized, trustless setting, the immutability of contract code and openness of contract execution (both ensured by the underlying blockchain) develop trust between the parties to a contract. The blockchain mechanism ensures that every smart contract transaction is atomic: i.e., it either completes successfully or (on failure) leaves the blockchain state unchanged.
A wide range of blockchains with diverse use-cases and diverse consensus protocols have been deployed and are in active use. For example, Ethereum supports smart contracts and uses Proof of Stake (PoS) (Nguyen et al., 2019) while Bitcoin is built as a cryptocurrency on Proof of Work (PoW) (Gervais et al., 2016). Looking forward, this heterogeneity will only increase and will lead to a ’multi-chain universe’—a digital environment where data is spread across blockchains and applications combine operations that execute on multiple chains.
2.2. Cross-Chain Bridges
To facilitate easy, secure, and accurate interactions between distinct blockchains, several Cross-Chain Communication (CCC) bridges have been established. A fundamental feature of these bridges is the Secure Transfer property, which is described in many works such as (Xie et al., 2022) and formalized later in §III. This property requires that when a receiver chain receives a notification of an event on the sender chain, this event has actually been committed on the sender chain and cannot be rolled back. Without the Secure Transfer property, the sender chain may create a fake message that is not committed on the sender chain. As a result, a user on the receiver chain would lose some assets without a proper counter transaction on the sender chain, thereby creating a fraudulent transaction.
Figure 1 demonstrates the general process for transmitting messages via a CCC bridge.
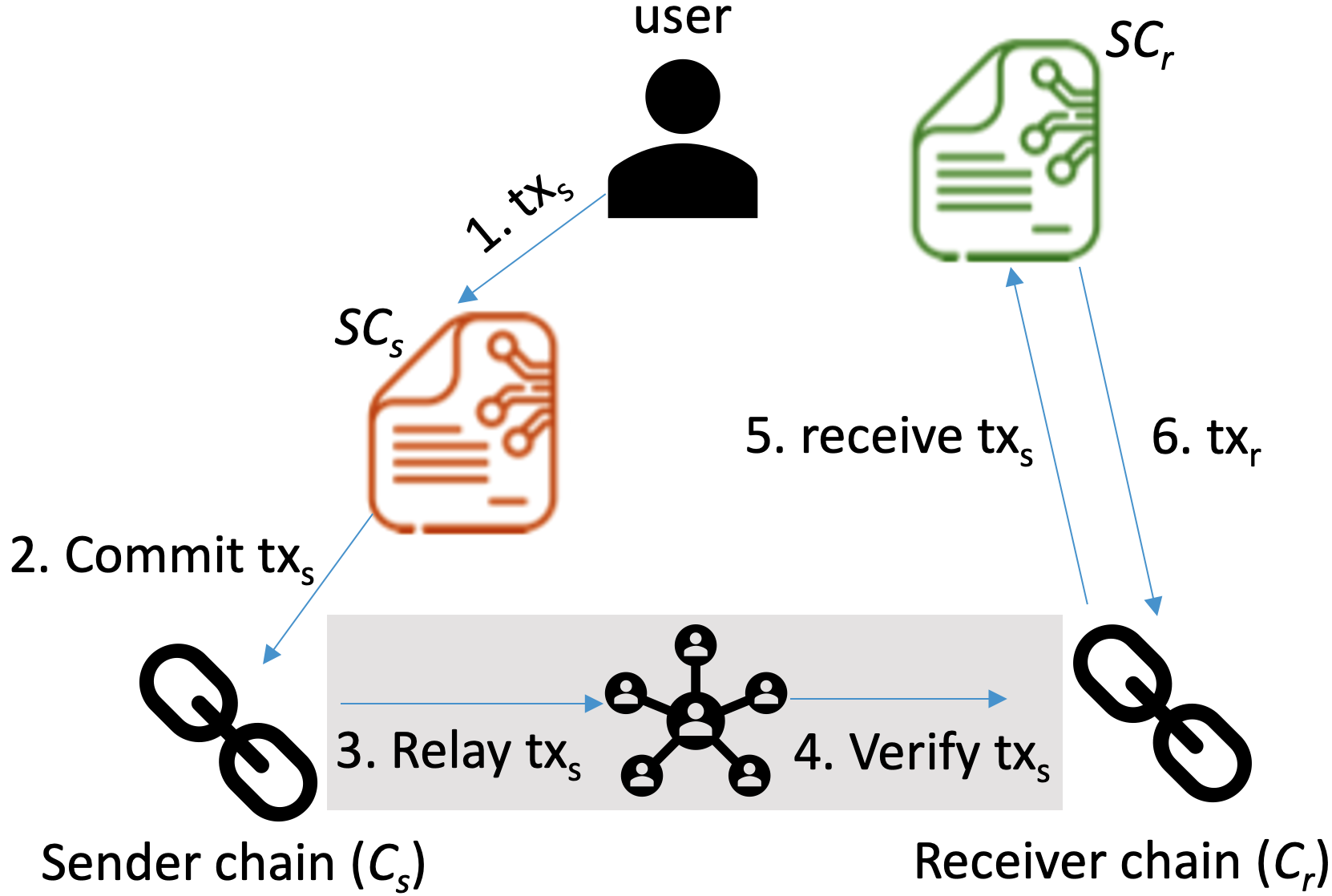
Smart contracts and are deployed on blockchains (sender) and (receiver), respectively. Note that a single bridge is usually designed for one direction. For a user to activate a transaction on blockchain , they must first initiate transaction on blockchain . (The remote execution may be motivated by superior features on , such as lower fees, prompting the user to transfer assets from to .) The secure transfer property is guaranteed by the middle CCC bridge (symbolized by the shaded area in Figure 1). The bridge relays the details of and confirms its existence on chain before transmitting it to chain . The above communication flow can be summarized as: 1) User initiates in smart contract . 2) undergoes the consensus protocol of chain and is subsequently committed. 3) The CCC bridge picks up the message including and sends it to the receiver chain , facilitated by one or multiple relayers. 4) The CCC bridge validates by examining the associated verified block-header. 5) is confirmed, and its details are available on Chain . 6) Consequently, smart contract issues accordingly which is then committed on .
Based on their trust assumptions and security models to verify the transaction from the sender chain we can categorize the CCC bridges in the following two categories:
-
•
Trusted: The “trusted” CCC bridges (Zarick et al., 2021), introduce a third-party trust system, such as an Oracle network or a notary committee, to authenticate and verify the occurrence of specific events on an alternative chain.
-
•
Trustless: The “trustless” CCC bridges, e.g. Cosmos inter-blockchain communication protocol (IBC) (Goes, 2020) and zkbridge (Xie et al., 2022), on the other hand, employ a ‘light client’ approach, where one chain maintains an up-to-date version of the other chain’s block header. For instance, a light client of the sender chain would be implemented within the receiver chain. This method allows the receiver chain to acquire and update block header information from the sender chain, thereby verifying the occurrence of a specific event on the sender chain through a cryptographic (e.g., Merkle proof) method.
However, it should be noted that these CCC bridges primarily focus on the trust layer of the general communication between two blockchains, aiming to maintain the secure transfer property. In contrast, certain application-specific blockchain interoperability protocols, such as the cross-chain atomic swap enabled by Hash Time-locked Contract (HTLC) (Herlihy, 2018), concentrate solely on a distinct communication domain between the two chains.
Given the vast variety of CCC bridges, there have been efforts in prior research to combine or standardize all these bridges such as Multi-Message Aggregation (MMA) (202, [n. d.]). While these approaches tend to blur the boundaries among different bridges, they work at the same low-level as cross-chain bridges. Their main goal is to augment security based on existing bridges, rather than provide a higher-level abstraction of these low-level bridges to enhance better smart contract programmability and portability. The increasing complexity of emerging multi-chain applications, typically constructed on top of these low-level bridges, underscores the challenges in design and verification for correctness. A more abstract representation for these low-level bridges is indeed essential.
2.3. Atomicity for Multi-chain Applications
The fundamental property of the consensus protocols in a blockchain is that a block is either committed or discarded. This property can be leveraged to achieve atomicity across a set of operations. If we embed all the operations under consideration in a same block then all of them will be committed or all of them will be rejected; i.e. the set of operations will be executed atomically.
Informally speaking, a cross-chain transaction is a sequence of operations where the operations may target different chains. For instance, a cross-chain transaction may be expressed as the sequence , where are operations on a chain and is an operation on a different chain . Atomic execution of such a transaction is not guaranteed. That is because each blockchain operates independently of the others, without a common consensus mechanism. Thus, the sequence of operations in transaction has no built-in protection against interference from other operations on those chains, which may be initiated independently at any time by other parties. (For example, an operation may occur on chain between the occurrences of and , changing the state of blockchain in a way that cannot be viewed as the result of an atomic execution – i.e., as the result of or .) It is for this fundamental reason that achieving cross-chain atomicity requires a special protocol.
Existing protocols for atomic cross-chain transactions are limited in scope: e.g., pairwise token transfers through gateways (Augusto et al., 2023) or pairwise asset exchanges through atomic swap protocols (Ding et al., 2022; Zakhary et al., [n. d.]). HTLC (Herlihy, 2018) is the most popular solution for ensuring atomicity of a pairwise cryptocurrency swap. It has been extended to multiple chains (Xue et al., 2023), but remains specialized to currency swaps, an important but narrowly defined transaction. As multi-chain applications evolve to handle data spread across several chains, there is a need for an atomicity protocol that handles general transactions that contain arbitrary smart-contract operations defined on multiple chains. That is the fundamental question addressed in this paper.
Some systems use a top-level chain to periodically checkpoint the state of other chains, or to record transactions occurring on other chains in a conveniently accessible location. This is the case, for instance, for Trustboost (Wang et al., 2022), Hyperservice (Liu et al., 2019), and Polkadot (Wood, 2016). This does not, however, suffice to guard against interference, and thus does not provide any guarantee of atomicity.
3. Threat Model
We describe and discuss our threat model. We first present our correctness and security goals. This is followed by listing the attacker’s capabilities which may compromise those goals. Finally, we formulate the assumptions on which the trustworthiness claims are based.
The correctness objective of the communication interface is defined by the semantics of each high-level operation. Consider the notification operation. The desired safety (security) property is that a notification message received by a contract on a chain that is claimed to have been sent by a contract on a chain must have actually been sent by contract : i.e., notifications cannot be forged. There is also a liveness requirement of eventual delivery: if contract on chain sends a notification to contract on chain , that notification must eventually be delivered to . Similar safety and liveness properties apply to the other operations: notification with acknowledgement and remote call.
The correctness objective of the atomicity protocol can also be divided into safety and liveness objectives. The safety objective is that of atomicity, which can be expressed as strict serializability: roughly, that on every computation, the individual atomic operations of transactions may be reordered so that the transactions do not overlap (i.e., appear to execute atomically), with transactions that do not originally overlap retaining their temporal ordering (i.e., if, in the original computation, a transaction completes before a transaction is started, this temporal relation must be preserved after reordering). In terms of the closely related concept of linearizability, every transaction should appear to occur instantaneously at a singular point in time, falling between its start and end points. The liveness objective is that the execution of every transaction should eventually terminate (either successfully or with failure). There is a secondary safety objective, which is to limit the number of failing transactions.
An attacker’s goal is to disrupt these correctness properties: that is, either to interfere with transaction execution so as to violate atomicity (i.e., make it impossible to reorder transactions correctly), or to interfere in such a way that an initiated transaction never completes, or to interfere by causing transactions to fail (i.e., create a denial of service attack).
The capabilities attributed to an attacker include:
-
•
The ability to invoke any methods in a smart contract, as long as the attacker has the required permissions.
-
•
The freedom to execute these methods at any point during a cross-chain transaction.
-
•
The flexibility to assume any role in the transaction process, be it a participant on a blockchain, or a relayer in a cross-chain bridge.
However, it is assumed that the attacker cannot steal participants’ private keys or arbitrarily alter the state of a blockchain ledger, e.g., by compromising the underlying consensus mechanism.
We assume that the operation of a blockchain and its smart contracts cannot be compromised. That is, a smart contract executes precisely according to its definition and cannot halt due to machine failure. This assumption is necessary as our protocols rely on auxiliary smart contracts. The protocols also rely on cross-chain bridges, which we assume meet the secure transfer property that is discussed in Section 2.2. The secure transfer property must hold regardless of the particulars of the cross-chain bridge protocol, which differs significantly betweeen bridge implementations such as zk-bridge (Xie et al., 2022), IBC by Cosmos (Goes, 2020) and LayerZero (Zarick et al., 2021).
4. An Abstract Communication Interface
We present a high-level interface that a pair of blockchains can use to communicate over a cross-chain bridge. As sketched in the §1, the primary objective of this interface is portability: application software written to this interface can be easily ported from one cross-chain bridge to another and (with native bytecode compatibility) from one blockchain to another. That is not the case for applications that are written to the interface of a specific cross-chain bridge, as the application is then locked to this interface, and the interfaces are incompatible with each other. We show how our high-level interface can be implemented atop the lower-level mechanisms provided by current bridges such as LayerZero.
The interface consists of three common communication functions: notify, notify with acknowledgment, and remote call. We describe each in turn. Consider blockchains and that are linked bidirectionally by cross-chain bridges. The notify function is used by a contract on chain to send a message to a contract on chain . The notify-with-acknowledgement functionality is used by contract to send a message to contract and receive an acknowledgement that this message has been delivered successfully. The remote-call functionality is used by contract to invoke a method of contract with parameters and receive an acknowledgement that this invocation was performed successfully along with values produced as a result of the invocation.
These functionalities are implemented in an asynchronous manner, which allows contract to continue execution without waiting for the completion of the communication process. As with other asynchronous interfaces, we provide a mechanism for contract to test whether the communication is complete and to retrieve any results. It is of course easy to implement synchronous forms of communication given these capabilities. Asynchrony enables to issue remote operations on multiple chains in parallel, a capability that is used in the atomicity protocol, described in Section 5.
We have so far used the phrase “cross-chain bridge” informally. Formally, a cross-chain bridge (“bridge” for short) from chain to chain is a communication service that is external to either chain. We abstract from specific implementations and simply assert that a contract on chain can request the bridge to transfer a message to a contract on chain through an invocation . This invocation is recorded on chain . At the other end, a bridge delivers message to contract by invoking a action on , where is a non-negative number.
Given the trustless setting of Web3, the bridge service cannot be implicitly trusted to deliver messages and to do so without any corruption. Hence, we must make trust assumptions on the behavior of the bridge. We refer to those assumptions as the Secure Transfer property of the bridge. The formalized formulation is adapted from the system model presented in (Xie et al., 2022). In practice, the assumptions are enforced (with high probability) through cryptographic techniques such as zero-knowledge proofs.
Definition 0 (Secure Transfer).
(adapted from the model in (Xie et al., 2022)) A bridge connecting chain to chain satisfies the secure transfer property if it meets the following conditions:
- Safety::
-
Every message that is delivered to a contract on chain was indeed sent from chain – i.e., messages cannot be forged by the bridge. This may be formally defined as:
Precisely, for every message and number such that there is a invocation by contract on , the ’th block of : (1) is the index of a stable block on chain and (2) is an invocation from contract on chain to the bridge that is recorded on the ’th block of , denoted as .
- Liveness::
-
Every message sent to a valid contract on chain is eventually delivered to , which can be formally described as:
Precisely, for every message and every invocation from a contract on chain to the bridge, there is eventually an invocation on contract in chain (recorded in , the ’th block of ), where is the index of the block on chain (denoted as ) that records the invocation.
Note that messages could be delivered out of order. I.e., it is possible for the send of to be recorded on block and that for to recorded on block where , while the corresponding deliveries are made at blocks where .
We now define the protocols used to implement these high level functions. The protocols require adapter smart contracts: contract (on chain ) and contract (on chain ). These adapters act as intermediaries between the source contract and the bridge, as well as between the bridge and the destination contract , playing three critical roles. First, they provide the desired abstraction layer that insulates source and destination contracts from the low-level details of the bridge interface. Second, the adaptors ensure that notifications are delivered to and remote methods are invoked on the destination contract. And third, the adaptors track the progress of the asynchronous communications operations by, for instance, associating internal fresh identifiers (e.g., sequence numbers) with operations and responding to queries from the source contract.
To limit duplication, we present the protocols for notify-with-acknowledgement and remote-call. The notify protocol is a sub-protocol, constituted by the initial steps of the notify with acknowledgment protocol. For simplicity of notation, we drop the block index from the invocation, representing it simply as .
4.1. Notify with acknowledgement
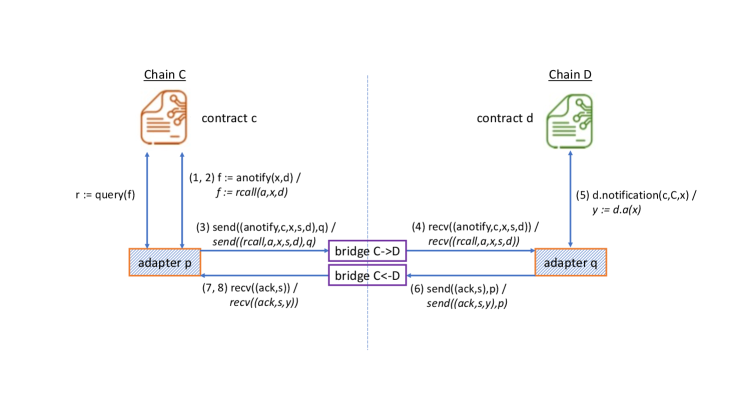
This is a notification that also provides an acknowledgement of receipt. In order to generate the acknowledgement, we need a bridge in the reverse direction, from to . Acknowledgements are provided asynchronously; thus, it is necessary to mark messages with sequence numbers to distinguish those that have been acknowledged. The protocol is illustrated in Figure 2 along with the Remote Call Protocol and consists of the following sequence of steps.
-
(1)
Contract invokes on the adapter contract on chain , where is the data to be notified to contract on chain .
-
(2)
Adapter assigns a fresh identifier and a “future” (with state Pending) to this invocation, and returns to contract . Contract can check the status of the transmission at any later point by querying the future through . (The adapter can also provide a facility for contract to be notified when the future changes state from Pending to Delivered. We do not illustrate this in the figure.)
-
(3)
Adapter invokes on the bridge from to , where is its corresponding adapter contract on chain .
-
(4)
The bridge communicates the message to contract through its method.
-
(5)
Adapter parses as and notifies contract by invoking its method with parameters , and .
-
(6)
Adapter then prepares a message and sends it to the bridge for the reverse direction from to through .
-
(7)
The bridge communicates the message to contract through its method.
-
(8)
Adapter parses as and updates the state of the future associated with to Delivered.
At any point, contract may query the future for the state of the notification. That will be Pending until the final step, when the state changes to Delivered and is then unchanged.
The notify protocol is a simplification and shortening of this protocol. It consists of steps 1-5 of this protocol, i.e., without the additional acknowledgement message transfer. There is also no need to have a future and fresh identifier as those are used exclusively for the acknowledgement step.
Theorem 2.
The protocol ensures that notifications cannot be forged (safety) and are eventually delivered (liveness).
Proof.
The proof relies on the assumptions that the working of a blockchain and the behavior of a contract cannot be tampered with, and on the secure transfer property of the bridge.
(Liveness) Consider data that is sent from contract to contract . By the working of chain , the adapter contract will eventually execute the call with the message as defined. From the liveness property of Secure Transfer, message will be eventually delivered to contract . By the working of chain , the call will be executed on contract , delivering the notification for the data .
(Safety) Now consider a notification delivered to from the adapter . From the definition of the adapters and and the soundness of Secure Transfer, the notification message must originate from a valid contract on chain and has not been tampered with in transit.
A similar argument in reverse establishes the security and eventual delivery of the acknowledgement message. ∎
This is an asynchronous protocol, in that multiple unacknowledged notifications may be issued by the contract . The identifier is used to track the state of each notification, which is reflected in the future . The smart contract program may inspect and make decisions based on whether an issued notification has been acknowledged; for instance, blocking any other transactions until a specific notification is acknowledged. As a special case, it is easy to implement synchronous versions of notify and notify-with-acknowledgement.
4.2. Remote Call
A remote call invokes a particular method on the target contract. The protocol extends the one for notify-with-acknowledgement by carrying additional information in the messages that identifies the method and its return value. The protocol is illustrated in Figure 2 and consists of the following sequence of steps.
-
(1)
Contract invokes on the adapter contract on chain , where identifies the method on contract on chain that is to be executed and represents the parameters to .
-
(2)
Adapter assigns a fresh identifier and a “future” (with state ) to this invocation, and returns to contract . Contract can check the status of the remote call at any later point by querying the future through . (The adapter can also provide a facility for contract to be notified when the future changes state from Pending to Completed. We do not illustrate this in the figure.)
-
(3)
Adapter invokes on the bridge from to , where is its corresponding adapter contract on chain .
-
(4)
The bridge communicates the message to contract through its method.
-
(5)
Adapter parses as and invokes method on contract with parameters . Let represent the result of this invocation.
-
(6)
Adapter then prepares a message and sends it to the bridge for the reverse direction from to through .
-
(7)
The bridge communicates the message to contract through its method.
-
(8)
Adapter parses as and updates the state of the future associated with to .
At any point before the final step, contract may query the future for the state of the remote call. That will be until the final step is complete, when the state changes to and is then unchanged.
This remote call mechanism is also asynchronous, allowing multiple remote calls to be “in flight” concurrently, possibly to contracts on different chains. As before, the fresh identifier is used to track the status of the remote call, which is reflected in the future . The future/query mechanism can be used to turn the remote call into a synchronous one, by blocking any further actions of contract until the query returns the result.
Following the same line of reasoning as the proof of Theorem 2, we obtain this theorem.
Theorem 3.
The protocol ensures that remote calls cannot be forged (safety) and are eventually executed according to their semantics (liveness).
5. An Atomic Multi-Chain Transaction Protocol
On a blockchain, any single invocation of a smart contract is atomic by design. However, there is no guarantee that a sequence of invocations executes as a unit; i.e., without interference from actions on that blockchain that may be initiated independently by other parties. There is a similar lack of atomicity when considering a sequence of invocations to contracts that belong to different blockchains. Each blockchain executes independently of the others, so there is no protection from interference by actions that may be independently initiated by other parties.
But there are interesting use cases that require atomicity: for instance, two-way or multi-way cryptocurrency exchanges between tokens on different blockchains. The exchange must be executed as a unit, without interference from actions that could, for instance, deplete the account balances of the parties involved. In this section we present our atomicity protocol, which ensures that a cross-blockchain transaction either executes successfully or, if a constituent operation fails, then all operations are canceled and the effect is as if there was no change to the state of the participating blockchains.
We begin by defining a blockchain as an abstract state machine; formulate a cross-chain transaction; describe the atomicity protocol; then establish its correctness.
5.1. Cross-Chain Transactions
For the purposes of defining the atomicity protocol, we may view a blockchain as an abstract state machine , where:
-
•
is a set of typed state variables. This induces a state space which is the set of assignments of values to variables in . (Notationally, we can say , where is the type domain. In the formal presentation, all variables have a single domain for simplicity.) The connection to a real blockchain is that represents the state variables for all contracts on the blockchain. Over time, smart contracts are added to the chain, thus extending with fresh state variables, but we can ignore this aspect for the formal presentation.
-
•
is a set of action names. In a real blockchain, each action represents a contract method along with values for its parameters.
-
•
is the deterministic transition function of the chain, which transforms the current state, say , to a successor state on action ( ) and produces a result value. In an actual blockchain, this represents the execution of a smart contract method, which must be deterministic.
-
•
We associate a scope with each action through a function . The scope of action is the subset of variables that is affected (read or written to) on a transition labeled by .
-
•
An indexed action is a pair where is a blockchain and is an action in .
A cross-chain transaction is specified by a finite set of indexed actions that are related by an irreflexive partial order denoted . This order reflects data dependencies: for every action , the data that action relies upon must be produced by actions such that . Actions that are not related by are called independent.
A transaction can be partitioned (through a topological sort) into a sequence of layers such that each layer consists of a set of independent actions, and for actions such that , the layer containing occurs prior to the layer containing in the sequence. Formally, we have a set of layers, , to represent a cross-chain transaction and
where and are the ’th and ’th layer of the transaction, respectively while and are indexed actions.
The ideal (sequential and interference-free) execution proceeds as follows, shown in Figure 3. It begins by forming a checkpoint consisting of the current state of all blockchains participating in the transaction, represented as . At round , operations on the nodes in layer () are issued in some order. (The actual order does not matter as the operations are independent.) If all operations in layer succeed, the results are saved and the next round (if any) is started. If some operation of layer fails, the execution is canceled and every blockchain is restored to its checkpointed state .
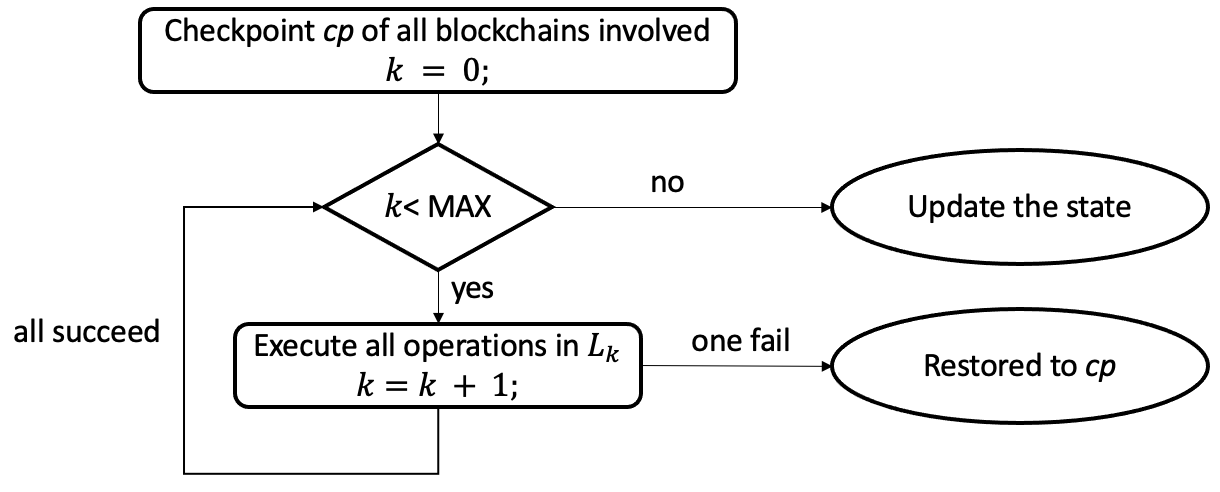
5.2. Atomicity
Multiple transactions may execute concurrently and may be interleaved with other blockchain actions issued independently of the transactions by other parties. The goal of the atomicity protocol is to ensure that in this concurrent, interference-prone setting, each transaction follows its ideal semantics as shown in Figure 3.
This is a two-phase protocol. A transaction is coordinated by a Proposer which is a smart contract on one of the blockchains. At a high level, the protocol follows the well known two-phase commit template for distributed database transactions. In the first phase, the proposer obtains agreement from all blockchains to “freeze” the portion of their state that is relevant to the operations in the transaction. In the second phase, the proposer executes operations from the transaction layer-by-layer, canceling the transaction if any individual operation fails.
We prove that protocol executions are strictly serializable. In terms of the closely related concept of linearizability, this guarantees that every transaction appears to take effect instantaneously, which provides atomicity with respect to other cross-chain transactions that follow this protocol and any contract operations that may be invoked independently.
Two features sharply distinguish this protocol from two-phase commit protocols on databases. First, as the proposer and all operations operate on blockchains, we may assume that the likelihood of a machine failure is negligible, because of the protections provided by the replication that is built into blockchains. This is in sharp distinction to two-phase commit protocols on distributed databases, which are complex largely because they must handle various machine failure scenarios involving the Proposer and the databases. As a result, our atomicity protocol is significantly simpler than database commit protocols. The second distinction arises from the inherently trustless setting. Thus, any atomic protocol must contend with the potential for malicious behavior. This aspect is absent from traditional database protocols. It has two consequences. First, if the Proposer issues an operation on a remote blockchain, there is no guarantee that this operation will actually be executed. Our protocol therefore relies crucially on cross-chain bridges with the Secure Transfer property and on the abstract interface defined in the prior section, which ensures that operations will eventually be performed and cannot be corrupted. Second, our protocol relies on locking smart contract state. As the locking operations must be public, it is necessary to build in access controls to ensure that a malicious attacker cannot lock smart contracts to create a denial-of-service situation.
To summarize, in the database domain, two-phase commit protocols focus on two types of failure: machine failures (i.e., machine crashes) and semantic failures (i.e., a failure within an operation, such as a divide-by-zero error). In our blockchain domain, machine failures may be ignored but, in their place, we must consider failures of trust, which arises from the potential for malicious attacks that aim to disrupt correctness or deny service.
5.3. Blockchain Assumptions
We assume that two functionalities are provided by each blockchain that participates in transactions.
First, it must be possible to atomically checkpoint and lock a portion of the state of a single blockchain. We assume an abstract function which atomically (1) saves the current values of the state variables to a copy of those variables and (2) blocks access to any action that modifies that state except when the action originates from the Proposer, denoted .
Second, it must be possible to atomically restore and unlock the locked state. We assume an abstract function which, when invoked by the Proposer , atomically does the following: if is true (denoting a failure), the operation restores the state saved in to ; and, regardless of the value of , the operation then removes the block on accessing the state in .
In practice, these abstract operations may be implemented as follows. The variables represent the state variables of multiple smart contracts on the blockchain. To ensure atomicity for the lock and unlock operations and to prevent the misuse of the locking functionality, we define a transaction executor contract on each blockchain. The executor receives a transaction specification from the proposer and executes the transaction on behalf of the proposer. It also acts as a conduit for remote operation execution, as explained below. Each contract implements its own and method. In addition, the code of the contract must ensure that every regular contract method is guarded to ensure that when the state variables of the contract are locked, the method can be invoked only by the transaction executor. Restricting the transaction execution to a known executor contract (which may be formally verified to ensure correct behavior) avoids the possibility of malicious behavior that can lock the state of participating contracts, creating a denial of service attack.
Pseudo-code illustrating the assumed smart contract structure is shown in Figure 4. The syntax has its standard interpretation. The caller variable represents the address of the party invoking the method; the require operation cancels execution if the value of its Boolean argument is false in the current contract state. For simplicity, the pseudo-code assumes that the methods in this contract do not invoke methods in other contracts. (Such indirect invocations are handled by relaying the address of the original external caller to the indirectly invoked methods.)
5.4. The Atomicity Protocol
At a high level, our protocol follows the template of a two-phase commit protocol. Such protocols were originally developed for distributed database transactions which, as explained, operate under a different model of trust and failure (Bernstein and Newcomer, 2009; Weikum and Vossen, 2001).
Transaction Execution
The structure of a cross-chain transaction is defined within an originating smart contract on some chain. Then, the transaction is sent to a the executor contract on that chain. We refer to this executor as the Proposer and denote it by . The Proposer communicates with executors on other chains using cross-chain bridges and the remote-call mechanism to freeze the state that is relevant to , to execute individual operations, and to handle failures. Once the transaction is complete, the proposer notifies the originating smart contract.
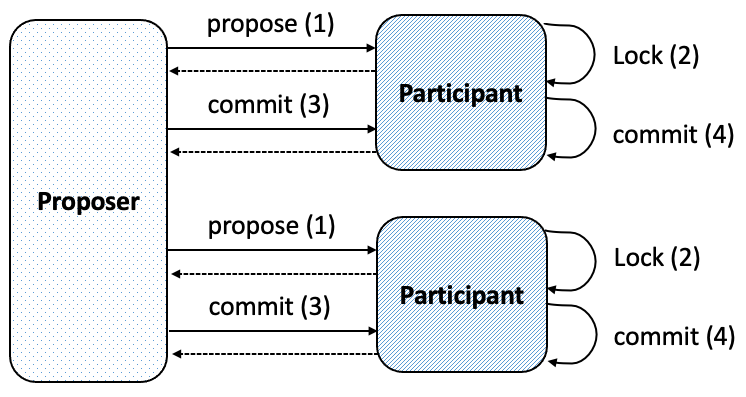
Protocol Stages
The protocol consists of the following stages, while the first two stages are shown in Figure 5.
-
(1)
First Phase. The Proposer obtains agreement from all blockchains to “freeze” the state relevant to executing the transaction through step 1 and step 2 in the figure.
Consider a blockchain . Let be the union of for every indexed action included in . Through the remote-call mechanism, the proposer requests the trusted executor contract on blockchain (denoted ) to checkpoint and lock the variables through the abstract operation. In practice, is a list of contracts on blockchain . We assume that this list correctly defines the actual scope of action , i.e., the contracts whose state may be modified either directly by the method or indirectly by contract methods invoked from . (This transitive reach can be determined through automated code analysis.) The executor contract carries out the operation by invoking the
lockmethod in sequence on every contract in the supplied list. By the semantics of a blockchain, this sequence of method calls is executed atomically on that chain.Only if the operation succeeds on every blockchain that is relevant to the transaction does the process move to the next phase. Otherwise, the transaction is canceled and the process moves to the failure mode defined below. The transaction may (potentially) be re-tried at a later point by the smart contract that originated the transaction.
-
(2)
Second Phase. The proposer executes operations from in a series of rounds (repeating step 3 and step 4 in the figure). In the ’th round, the proposer invokes the operations defined in the ’th layer of the transaction . The invocation of the indexed operation is carried out indirectly via the trusted executor of blockchain .
In practice, this may be done by using the remote call mechanism to convey the action to , which then invokes the action on the contract where it is defined.
The proposer waits until all actions in the ’th layer are complete. If every action completes successfully, the proposer moves to the next round. If not, the proposer enters the failure handling mode, described below. If all rounds are completed successfully, the proposer enters the success mode, described below.
Transaction Outcomes
-
(1)
Failure. The entire transaction is canceled. The proposer invokes on each blockchain relevant to the transaction on which a operation was successfully performed. This restores the state of that blockchain to its checkpointed value and unblocks the affected smart contract methods. In practice, this abstract operation is carried out by requesting the executor on blockchain to invoke the
unlockmethod on every relevant contract with the failure parameter set to true. -
(2)
Success. The transaction is committed. That is done by the proposer invoking on each blockchain relevant to the transaction. In practice, the abstract operation is carried out by requesting the executor contract on blockchain to invoke the
unlockmethod on every relevant contract with the failure parameter set to false.
5.5. Correctness
We show that transactions may be viewed as being atomic. This follows from showing that executions are linearizable, in that each transaction appears to take effect (matching its ideal semantics) at some point between its start and finish.
Theorem 1.
Transaction executions are secure and atomic.
Proof.
Consider the execution of a transaction . We first show that the execution of a transaction (whether it is complete and successful, or partial and unsuccessful) can be made atomic. We then show that the state of the participating blockchains is updated correctly on each outcome.
All state relevant to the operations in is locked at the start of the execution and only unlocked at the end of execution. Hence, it is not possible for an operation outside to interfere with the state transitions in . The secure transfer property of cross-chain bridges ensures that all remote calls issued by the Proposer are eventually executed correctly, and that every call issued by the transaction executor on a chain seemingly on behalf of the Proposer must have actually originated at the Proposer. Thus, every operation in the transaction is eventually executed, and no operations other than those in the transaction are executed on the locked state. The transaction execution proceeds in the same sequence of rounds as the ideal execution. In each round, operations are independent; thus, concurrent execution results in the same state as any sequential order.
At each end of the transaction, the locking and unlocking processes proceed sequentially. Suppose that blockchains and are locked in that sequence. It is possible for other (non-) operations to be performed on the state of after is locked but before is locked. Similarly, it is possible for other non- operations to be performed on the state of after is unlocked but before is unlocked (assuming that locks are removed in the reverse order). The first set of operations can be commuted to the left over the lock for ; while the second set of operations can be commuted to the right over the unlock of . This defines an equivalent execution where the lock (similarly, unlock) operations occur in a contiguous block.
Any non- operations that are interleaved with the transaction operations must (by the definition of scope) operate on state that is disjoint from the state relevant to . Hence, those operations can be commuted either to the left over the lock operations, or to the right over the unlock operations. The final result of the commutations is an equivalent computation where the operations of (including lock and unlock) are executed in a single atomic block.
Suppose that the execution of all operations in completes successfully. The success mode of the protocol ensures that the unlock operations ake the state changes permanent, as required by the atomicity semantics. If, however, execution of is partial, this must be due to a failed operation in some layer. The failure mode of the protocol ensures that the unlock operations restore the checkpointed state in each blockchain. Thus, in the failure case, the state in the scope of is unchanged, also as required by the atomicity semantics.
(Note: as all operations on a blockchain are visible, in the failure mode, the blockchain will record intermediate state changes as well as the operation that cancels those changes by restoring the checkpointed state. Hence, the failure of is visible in terms of the recorded blockchain operations; however, it is not visible in terms of the semantics.) ∎
There is, however, no guarantee that every issued transaction will eventually successfully acquire all relevant locks. One can easily construct pathological schedules where two transactions that must acquire locks on the same (or overlapping) sets of variables are issued together so that one transaction always loses the race. However, it is important to note that since every operation on a blockchain incurs a cost, such scenarios cannot persist indefinitely.
6. Implementation and Experiments
To demonstrate practicality of the proposed model and atomic protocol, we wrote a suite of smart contracts in Solidity. We further deployed them across four different testnets111Testnets are functionally similar to production blockchains the only difference is that the tokens on testnets do not have financial transaction value. Testnets are used for testing and research purposes. including Mumbai, Fantom, Fuji, and Goerli. However, due to the limitation of test token amount, we only tested the applications on two testnets listed in Table. 3. We used Hardhat (Nomic Foundation, 2023) to deploy smart contracts on the testnets.
Further, we developed following two multi-chain test applications: (1) An atomic swap between two chains and (2) An exchange process encompassing three chains. We studied the transaction latency and gas consumption for the test applications to show the applicability of our work. Details of the results are in §6.3.
6.1. Implementation
Bridges such as LayerZero and IBC protocol typically host endpoint contracts within each blockchain. These endpoints facilitate communication with other blockchains. A challenge arises due to the heterogeneity of these endpoint interfaces across different bridges. To navigate this, we introduce a unified converter interface applicable to all bridges. The structure of our implementation (in Solidity) is shown in Figure 6. The interface includes functions such as notify, notify_ack, and remote_call, which are realized using the lower-level bridge functions. Once a bridge converter is defined on a blockchain, the abstraction simply requires the inclusion of that converter’s address within its contract. This integration allows the abstraction to employ a standardized communication interface, enabling the use of various bridges by invoking distinct bridge converters as needed. Though one interface function may involve several transactions in different chains, the complicated payment for multiple communication is abstracted away, making it possible for an application designer to focus on the application logic.
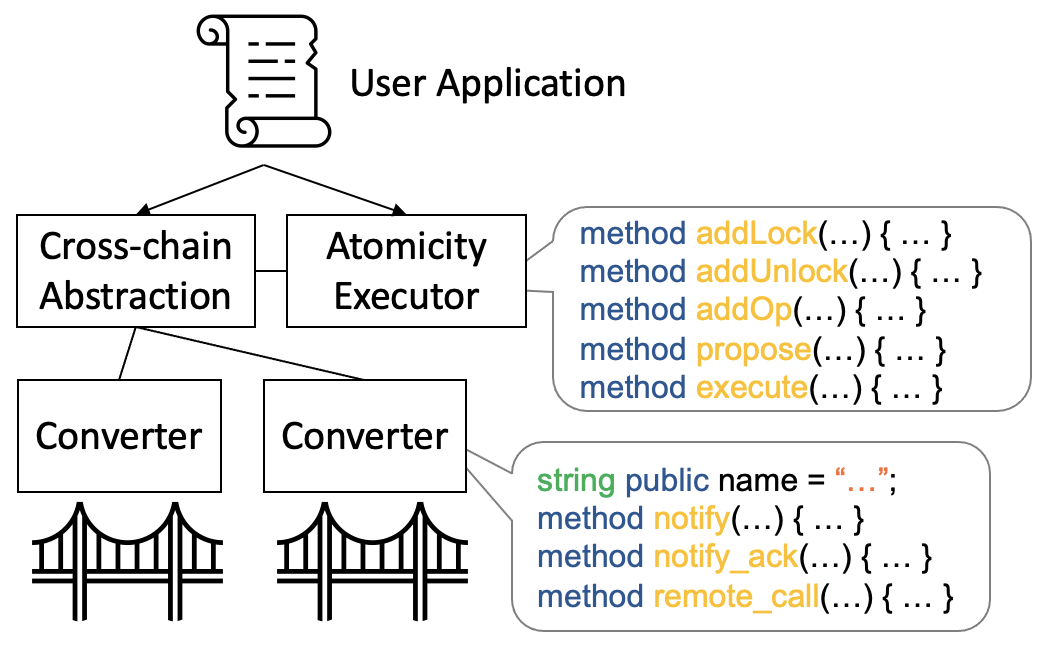
The implementation of atomic transactions builds on this communication layer. The structure is defined by public function calls such as addLock, addUnlock, addOp, propose, and execute. Application developers must deposit a specified amount to support payment for bridge communications that occur during the transaction execution. Notably, within the atomic execution smart contract, storage provisions are made to retain details of these multi-chain applications. Once an application is documented, it’s stored permanently, allowing for subsequent initialization without the redundancy of re-defining all requisite operations.
The sizes of the contracts that make up the implementation of our abstractions, and the deployment cost on Testnet Fantom, are shown in Table. 1. The abstraction and atomicity smart contracts only need to be deployed once on the blockchain. The implementation is flexible and supports multiple bridges. Supporting a new bridge for connection with another chain requires the creation of a converter (approximately 242 lines of code), and a function call to register the bridge with the converter.
| Smart Contract | Size (LoC) | Deploy gas | ||
|---|---|---|---|---|
|
242 | 1.4 M | ||
| Abstract Bridge | 601 | 2.7 M | ||
| Atomicity Executor | 225 | 1.6 M |
| Contract | Atomic Swap | Three-Chain Exchange |
|---|---|---|
| Overhead (LoC) | 10 | 14 |
From a programmer’s viewpoint, this abstraction layer considerably simplifies the process of constructing atomic cross-chain transactions. Only a few lines of code are needed to implement an atomic swap and a three-chain exchange, as shown in Table. 2. This code sets up the structure of the transaction (its operations and their ordering), using the interface shown in Figure 6.
6.2. Experiments
We first executed a two-chain atomic swap between the Mumbai and Fantom testnets. Mumbai serves as Polygon’s testnet, mirroring the mainnet functionalities of Polygon. In this process, Fantom testnet plays the role of the proposer. For a successful transaction on the Mumbai blockchain, three operations are essential: lock, transfer, and unlock. Each operation requires a remote call from the fantom testnet and sends back an acknowledgement to indicate the status of execution, which is implemented through the remote_call in the abstraction. The atomic swap transaction, when successful, undergoes the following steps:
-
•
Step 1: Fantom proposes the transaction to Mumbai and self-locks.
-
•
Step 2: Mumbai consents, then locks, and dispatches an acknowledgment.
-
•
Step 3: Fantom initiates a locked-mode transfer while prompting Mumbai to follow suit.
-
•
Step 4: Mumbai completes the transfer and sends an acknowledgment.
-
•
Step 5: Fantom initiates the unlock process, directing Mumbai to do the same.
-
•
Step 6: Mumbai concludes the unlock phase and communicates acknowledgment.
As a result, a successful atomic transfer requires 6 messages between two blockchains.
In addition to the successful case, we experimented with two potential failure scenarios to gauge the resilience of our protocol. The first scenario is a lock conflict in Step 2, where another transaction already claims the lock. The second involves an unsuccessful transfer due to inadequate funds during Step 4. Both situations prompt a transaction termination (Abort), reverting both blockchains to their pre-transaction states. The outcomes of these tests were in line with our expectations.
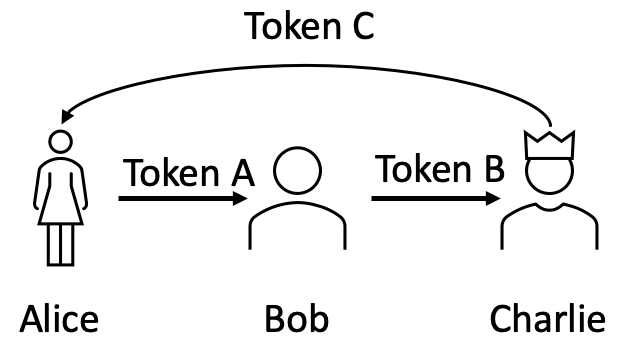
We also explored a multi-chain scenario involving exchanges across three distinct chains. Imagine Alice possesses token A and aims to trade it for token C with Charlie. However, Charlie lacks an account on Chain A and only accepts token B as a valid trade for token C. Therefore, Alice transfers token A to Bob, who then gives token B to Charlie, resulting in Charlie providing token C to Alice. This scenario is visually depicted in Figure. 7. Since three different tokens are used, three different chains are involved. Such multi-chain exchanges frequently occur in supply chain management systems, as noted in (Augusto et al., 2023), emphasizing their growing significance in the evolving blockchain landscape.
Though we have successfully deployed contracts across multiple chains and conducted localized function tests, certain multi-chain applications remain challenging due to a shortage of testnet tokens. For instance, following certain updates that ascribed real value to the Goerli token, contract deployment on Goerli became considerably costly. Consequently, for our three-chain exchange experiment, we simulated the application on a single chain, imitating two distinct chains. As cross-chain communication is exclusive between the proposer and participants and absent among participant chains, this approximation does not compromise protocol integrity.
6.3. Results
| Multi-Chain Apps | Test Chain (L: Proposer P: Participants) | Transaction Statistics | ||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
| Atomic Swap | L: Fantom | 3 | 4 | 2.14M | 0.003 | 1.11M | 1.03M | 301s | ||||||||||||
| P: Mumbai | 3 | 3 | 1.38M | 0.003 | 1.02M | 0.36M | ||||||||||||||
| Atomic Swap (Lock Fail) | L: Fantom | 2 | 3 | 1.48M | 0.001 | 0.74M | 0.74M | 196s | ||||||||||||
| P: Mumbai | 2 | 2 | 0.85M | 0.002 | 0.68M | 0.17M | ||||||||||||||
| Atomic Swap (Update Fail) | L: Fantom | 3 | 4 | 2.13M | 0.003 | 1.11M | 1.02M | 283s | ||||||||||||
| P Mumbai | 3 | 3 | 1.37M | 0.003 | 1.02M | 0.35M | ||||||||||||||
| Three Exchange | L: Fantom | 6 | 4 | 4.33M | 0.006 | 2.22M | 2.11M | 318s | ||||||||||||
| P: Mumbai-1 | 3 | 3 | 1.53M | 0.003 | 1.02M | 0.51M | ||||||||||||||
| P: Mumbai-2 | 3 | 3 | 1.53M | 0.003 | 1.02M | 0.51M | ||||||||||||||
The results of our experiments can be found in Table 3. Fantom acts as the proposer, while Mumbai serves as the participants. For each transaction, we documented the number of cross-chain messages invoked by the LayerZero bridge, as well as the number of operations performed on both chains.
Gas is essential for the execution of all these operations. When calculating gas consumption, two major components come into play: 1) Gas required for bridge functionalities, which include sending and validating messages. 2) Gas necessary for atomic operations. To delineate these different gas requirements, we designed a rudimentary cross-chain application that uses a recursive call with an empty payload. Through this, we measured the basic communication gas consumption between Fantom and Mumbai. Any additional gas was attributed to atomic operations.
Analyzing the data from Table. 3, we observe that the gas consumption for atomic operations is generally less than that for bridge communications. In all listed scenarios, atomic operations account for as little as 20 percent to a maximum of 50 percent of the total gas. This indicates that the primary gas consumption in atomic transactions predominantly arises from bridge communication, while the overhead from atomic operations remains small.
Furthermore, the main contributors to transaction latency are the bridge communication between the two chains and the time required for blockchain confirmations. This is largely due to the atomicity protocol being integrated within on-chain smart contracts. To acquire a more accurate understanding of the average transaction time, we executed a single transaction multiple times and computed the mean duration for a complete transaction. According to the results in Table. 3, transactions involving three communication rounds (as seen in cases 1, 2, and 4) typically conclude in about 5 minutes. In contrast, scenarios like the lock failure in atomic swap, which involve only two communication rounds, might complete in just 3 minutes. These timeframes, spanning a few minutes, are reasonable when compared with other cross-chain transaction durations.
6.3.1. Atomic Swaps
Atomic swaps have become a staple in modern cross-chain communications. This mechanism ensures seamless and trustless exchanges between two blockchains without the need for intermediaries. The essence of atomicity in these swaps can often be embedded directly within the design of the bridge facilitating the exchange. Typically, a successful swap necessitates only two communication rounds. However, our approach diverges slightly by introducing an additional communication round. While this might seem more cumbersome compared to the prevalent methods, our methodology offers broader compatibility and adaptability to decentralized applications, ensuring they operate with enhanced reliability and security.
6.3.2. Three-Way Exchange
The current landscape of blockchain technology lacks support for multi-chain applications. This evident gap serves as a primary motivation behind this work. By integrating an atomicity layer atop existing bridges, our mechanism considerably simplifies the development of complex multi-chain applications. A compelling example is the three-way exchange, which is challenging to program from scratch, but is realized with just lines of code using our framework.
7. Related Work
As blockchain interactions across different platforms become increasingly prevalent, the challenge of varying security assumptions among these blockchains gains a lot of attention. To address this, weaker blockchain may use checkpointing solutions, as discussed in (Karakostas and Kiayias, 2021; Sankagiri et al., 2021), which boost the trust using a stronger blockchain. However, these solutions require the weaker blockchain to give up sovereignty. Alternatively, as shown in (Wang et al., 2022), protocols built upon the cross-chain bridges can be deployed to create a combined ledger with boosted trust for weaker blockchains. Our work uses similar idea with (Wang et al., 2022) to have protocols atop bridges but to provide atomicity for multi-chain transactions.
Atomicity in transactions spanning multiple blockchains has received great attention. For example, the work in (Xue et al., 2023; Herlihy et al., 2019) formulated and solved the application of asset exchange involving more than two chains. There are two major differences in our work. First, our method has a substantially broader scope of applicability. We formulate and solve the question of atomically performing an arbitrary sequence of arbitrary smart contract transactions. Asset exchange is one specific instance of this general framework. Second, the underlying solution approach is quite different. The work in (Herlihy et al., 2019) presents two solutions: the first is based on a construct called a “timed lock,” the second on a custom protocol (CBC). While our protocol is similar in spirit to their CBC protocol, as both are based on the general two-phase template used in distributed databases, there are differences in scope and assumptions. Their protocol is designed specifically for the asset transfer problem, e.g., the “escrow” step in CBC escrows an asset, while the locking mechanism in our method blocks operations on an arbitrarily defined state. The paper discusses the issue of attackers forging transactions but does not fully define a protocol to prove that claimed transactions have indeed occurred on the CBC chain. Our solution relies on the general notion of a cross-chain bridge, which provides precisely this guarantee in the form of the secure transfer property. Partitioning the solution in this manner allows for the atomicity protocols to benefit from improvements in bridge implementation, and enhances portability across bridges.
8. Conclusions
Blockchain interoperability is already a significant problem and one that we expect will become even more relevant as data is spread across multiple blockchains. Thus, it is important to build high-level abstractions that simplify programming and increase productivity.
Towards this goal, our work introduces a standardized high-level interface for efficient blockchain communication, enhancing cross-chain portability. Our work also defines a broadly applicable, multi-blockchain transaction protocol, which ensures atomicity for applications spanning multiple chains. For both protocols, we rigorously formalize and prove the correctness and security of these protocols under clear assumptions on blockchain and bridge behavior and smart contract structure.
We show that these protocols are easily implementable. Our prototype implementation is programmed in Solidity, utilizing LayerZero (mostly) and IBC bridges. This prototype, consisting of both the high-level interface and the atomicity protocol, has been rigorously tested on testnets. The successful application of our atomicity protocol in executing both pairwise and multiway cryptocurrency swaps on these testnets demonstrates its practical effectiveness and broad applicability.
Overall, our work opens up new possibilities for general multi-chain transactions and, we believe, sets the stage for further research in this area. An important direction for further research is to discover finer-grained structure in multi-chain transactions that can be exploited to optimize storage and communication costs.
References
- (1)
- 202 ([n. d.]) [n. d.]. Multi-bridge Message Aggreation. https://multi-message-aggregation.gitbook.io [Accessed on Oct, 2023].
- Augusto et al. (2023) André Augusto, Rafael Belchior, Thomas Hardjono, André Vasconcelos, and Miguel Correia. 2023. Multi-Party Cross-Chain Asset Transfers. (2023).
- Bernstein and Newcomer (2009) Philip A Bernstein and Eric Newcomer. 2009. Principles of transaction processing. Morgan Kaufmann.
- Ding et al. (2022) Donghui Ding, Bo Long, Feng Zhuo, Zhongcheng Li, Hanwen Zhang, Chen Tian, and Yi Sun. 2022. Lilac: Parallelizing Atomic Cross-Chain Swaps. In 2022 IEEE Symposium on Computers and Communications (ISCC). IEEE, 1–8.
- Gervais et al. (2016) Arthur Gervais, Ghassan O Karame, Karl Wüst, Vasileios Glykantzis, Hubert Ritzdorf, and Srdjan Capkun. 2016. On the security and performance of proof of work blockchains. In Proceedings of the 2016 ACM SIGSAC conference on computer and communications security. 3–16.
- Gilligan et al. (1999) R Gilligan, Susan Thomson, Jim Bound, and W Stevens. 1999. Basic socket interface extensions for IPv6. Technical Report.
- Goes (2020) Christopher Goes. 2020. The interblockchain communication protocol: An overview. arXiv preprint arXiv:2006.15918 (2020).
- Herlihy (2018) Maurice Herlihy. 2018. Atomic cross-chain swaps. In Proceedings of the 2018 ACM symposium on principles of distributed computing. 245–254.
- Herlihy et al. (2019) Maurice Herlihy, Barbara Liskov, and Liuba Shrira. 2019. Cross-chain deals and adversarial commerce. arXiv preprint arXiv:1905.09743 (2019).
- Karakostas and Kiayias (2021) Dimitris Karakostas and Aggelos Kiayias. 2021. Securing proof-of-work ledgers via checkpointing. In 2021 IEEE International Conference on Blockchain and Cryptocurrency (ICBC). IEEE, 1–5.
- Liu et al. (2019) Zhuotao Liu, Yangxi Xiang, Jian Shi, Peng Gao, Haoyu Wang, Xusheng Xiao, Bihan Wen, and Yih-Chun Hu. 2019. Hyperservice: Interoperability and programmability across heterogeneous blockchains. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security. 549–566.
- Nakamoto (2008) Satoshi Nakamoto. 2008. Bitcoin: A peer-to-peer electronic cash system. Decentralized business review (2008).
- Nguyen et al. (2019) Cong T Nguyen, Dinh Thai Hoang, Diep N Nguyen, Dusit Niyato, Huynh Tuong Nguyen, and Eryk Dutkiewicz. 2019. Proof-of-stake consensus mechanisms for future blockchain networks: fundamentals, applications and opportunities. IEEE access 7 (2019), 85727–85745.
- Nomic Foundation (2023) Nomic Foundation. 2023. Hardhat: Ethereum development environment for professionals. [Online]. Available:https://hardhat.org/, accessed on: 2023-10.
- Sankagiri et al. (2021) Suryanarayana Sankagiri, Xuechao Wang, Sreeram Kannan, and Pramod Viswanath. 2021. Blockchain cap theorem allows user-dependent adaptivity and finality. In Financial Cryptography and Data Security: 25th International Conference, FC 2021, Virtual Event, March 1–5, 2021, Revised Selected Papers, Part II 25. Springer, 84–103.
- Swan (2015) Melanie Swan. 2015. Blockchain: Blueprint for a new economy. ” O’Reilly Media, Inc.”.
- Wang et al. (2022) Xuechao Wang, Peiyao Sheng, Sreeram Kannan, Kartik Nayak, and Pramod Viswanath. 2022. Trustboost: Boosting trust among interoperable blockchains. arXiv preprint arXiv:2210.11571 (2022).
- Weikum and Vossen (2001) Gerhard Weikum and Gottfried Vossen. 2001. Transactional information systems: theory, algorithms, and the practice of concurrency control and recovery. Elsevier.
- Wood (2016) Gavin Wood. 2016. Polkadot: Vision for a heterogeneous multi-chain framework. White paper 21, 2327 (2016), 4662.
- Xie et al. (2022) Tiancheng Xie, Jiaheng Zhang, Zerui Cheng, Fan Zhang, Yupeng Zhang, Yongzheng Jia, Dan Boneh, and Dawn Song. 2022. zkbridge: Trustless cross-chain bridges made practical. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security. 3003–3017.
- Xue et al. (2023) Yingjie Xue, Di Jin, and Maurice Herlihy. 2023. Fault-tolerant and Expressive Cross-Chain Swaps. In Proceedings of the 24th International Conference on Distributed Computing and Networking. 28–37.
- Zakhary et al. ([n. d.]) Victor Zakhary, Divyakant Agrawal, and Amr El Abbadi. [n. d.]. Atomic Commitment Across Blockchains. Proceedings of the VLDB Endowment 13, 9 ([n. d.]).
- Zarick et al. (2021) Ryan Zarick, Bryan Pellegrino, and Caleb Banister. 2021. Layerzero: Trustless omnichain interoperability protocol. arXiv preprint arXiv:2110.13871 (2021).
- Zheng et al. (2020) Zibin Zheng, Shaoan Xie, Hong-Ning Dai, Weili Chen, Xiangping Chen, Jian Weng, and Muhammad Imran. 2020. An overview on smart contracts: Challenges, advances and platforms. Future Generation Computer Systems 105 (2020), 475–491.