Attack-Resilient Distributed Convex Optimization of Linear Multi-Agent Systems Against Malicious Cyber-Attacks over Random Digraphs
Abstract
This paper addresses a resilient exponential distributed convex optimization problem for a heterogeneous linear multi-agent system under Denial-of-Service (DoS) attacks over random digraphs. The random digraphs are caused by unreliable networks and the DoS attacks, allowed to occur aperiodically, refer to an interruption of the communication channels carried out by the intelligent adversaries. In contrast to many existing distributed convex optimization works over a prefect communication network, the global optimal solution might not be sought under the adverse influences that result in performance degradations or even failures of optimization algorithms. The aforementioned setting poses certain technical challenges to optimization algorithm design and exponential convergence analysis. In this work, several resilient algorithms are presented such that a team of agents minimizes a sum of local non-quadratic cost functions in a safe and reliable manner with global exponential convergence. Inspired by the preliminary works in [15, 17, 16, 18], an explicit analysis of frequency and duration of attacks is investigated to guarantee exponential optimal solutions. Numerical simulation results are presented to demonstrate the effectiveness of the proposed design.
Index Terms:
Distributed convex optimization, Linear multi-agent system, Heterogeneous network, Random digraph, DoS attack.I Introduction
Distributed convex optimization over a multi-agent system has attracted growing attention over the last decade due to its potential applications involving source localization in sensor networks [1], resource allocation in multi-cell networks [2], energy and thermal comfort optimization in smart building [3], economic dispatch in smart grid [4], etc. The gradient-based distributed algorithms have been widely provided in the existing works, which build on either continuous-time or discrete-time agent dynamics to seek an optimal solution [6, 7, 8, 5, 10, 11, 9, 12, 13]. Each agent needs to calculate a global optimizer based on the information exchange over a communication network. The network security plays a fundamental yet important role in information transmission. Unfortunately, due to malicious attacks, (e.g., DoS attacks, deception attacks (false data injections, replay attacks), disclosure attacks (eavesdropping), and Byzantine attacks (faulty agents)), the secure network environment is hardly guaranteed in practice. The malicious attacks interrupt, incorrect, or tamper transmitting information so that efficiency of distributed optimization algorithm is degraded significantly or even failed. In light of wide applications of distributed optimization algorithms in cyber-physical systems (safety-critical), and inspired by studies of security issues in consensus works (e.g., [14, 15, 17, 16, 18, 20, 19]), it is highly desirable to determine how resilient distributed optimization algorithms are against cyber-attacks. Motivated by the observation, we aim to address resilient problems of distributed optimization with certain resilience against DoS attacks over unreliable networks.
I-A Related Literature Review
Continuous-Time Distributed Convex Optimization: paralleled with the discrete-time optimization schemes, the continuous-time distributed optimization algorithms have attracted much attention due to the well-developed continuous-time analysis techniques in control and the real-world cyber-physical system. In particular, the Zero-gradient-sum [5] and Newton-Raphson [6] algorithms are designed based on the positive and bounded Hessian of the local cost functions, while the Lagrangian-based algorithm based on the local gradients is adopted in [7]. The penalty-based optimization strategies are developed in [5] and [8], while the works investigate the multi-agent system with single-integrator dynamics only. The authors in [9] further consider distributed optimization of second-order multi-agent systems. Adaptive schemes are designed in [10] to achieve distributed optimization of linear agents via nonsmooth signum functions and gradients that satisfy special structures. All above designs require continuous communication. To remove this requirement, the time-based and event-triggered based strategies are presented in [11, 12, 13] over undirected and connected graphs. Besides, these algorithms need known initial states of each agent, which is difficult to verify in practice.
Resilient Distributed Convex Optimization: the closest related works on this topic have been recently published in [21, 22, 23, 24] in which the optimal solutions are obtained for first-order discrete-time multi-agent systems under Byzantine attacks (faulty nodes). In particular, the authors in [21] present the resilient optimization algorithm by removing (maximum amount of tolerable faults) nodes’ largest and smallest states at each iteration, such that the optimal solution converges to a convex hull of the set of all non-faulty nodes’ local minimizers. This algorithm is adopted in [22] to deal with constrained optimization problems. The local filtering consensus-based algorithms against faulty nodes are developed in [23], where the optimal solution is achieved under the -robust condition. The modified algorithm named RDO-T is developed in [24], where the number of faulty agents is allowed to be any large. These aforementioned works assume that the faulty nodes and the removal of states are known a prior to the designer. Moreover, these algorithms rely on the network connectivity of the complete graph or the undirected and connected graph.
I-B Main Contributions
This paper is concerned with a resilient study of distributed optimization algorithms against cyber-attacks over random digraphs. The malicious DoS attacks, allowed to occur aperiodically, aim to interrupt information transmission. In addition to DoS attacks, the random digraphs are induced by unreliable networked constraints. The main contributions of this paper are summarized as follows. (1) inspired by our designs in [15, 17, 16, 18], this is the first to present time-based and event-based distributed optimization algorithms to achieve resilient distributed optimization of heterogeneous linear multi-agent networks against DoS attacks over random digraphs. The proposed algorithms that rely on a consensus-based gradient strategy with a switching system method to constrain DoS attacks, are capable of exactly seeking the optimal solutions under attacks over random digraphs. The global exponential convergence of the proposed algorithm can be ensured, provided that the frequency and duration of attacks satisfy certain bounded conditions; (2) these proposed resilient distributed optimization algorithms avoid continuous-time communication in many existing works (see [6, 7, 8, 5, 9, 10]). The proposed dynamic event-based distributed optimization scheme is proven to be free of Zeno behavior, and avoid fixed and periodic transmissions used in the time-based scheme; and (3) in contrast to related optimization works that require known positive Hessians of the local cost functions [5] and [6], known gradients satisfying special linear structures [10], known initial agent states [11, 12, 13], the proposed algorithms in this work remove those limitations to facilitate practical applications. Moreover, compared to optimization works in [21, 22, 23, 24] that consider Byzantine faults on nodes and require the removal of their states to be known a prior, these DoS attacks on communication networks are time-sequence based and allowed to occur aperiodically. Another contribution of this paper is that unlike works in [6, 7, 8, 5, 10, 11, 9, 12, 13] and [21, 22, 23, 24] over the undirected graph or weight-balanced digraph, the studied graphs are directed and time-varying, and under cyber-attacks, the graphs can be even disconnected or totally paralyzed.
II Preliminaries and Problem Formulation
II-A Notation
Denote , , and as the sets of the real numbers, real -dimensional vectors and real matrices, respectively. Let be the set of positive natural numbers. Let 0 (1) be the vector with all zeros (ones) with proper dimensions. Let col and diag be a column vector with the entries and a diagonal matrix with the entries , , respectively. and represent the Kronecker product and Euclidean norm, respectively. For a real matrix , let be positive definite. Let , be its minimum and maximum eigenvalues, respectively. Besides, represents the maximum singular value of a matrix . For a differentiable function , is the gradient of , and is strongly convex over a convex set , if for and a scalar . is locally Lipschitz at if there exists a neighbourhood and a scalar so that for ; is locally Lipschitz on if it is locally Lipschitz at for .
II-B Graph Theory
Static Digraph: let be a graph and be the set of vertices. The set of edges is denoted as . is the neighborhood set of vertex . For a directed graph , means that the information of node is accessible to node , but not conversely. A matrix is the adjacency matrix of , where if , else . A matrix is called the Laplacian matrix of , where and , .
Markovian Random Digraph: let be a time-varying digraph with being a set of edges, and is a piecewise constant function with being an index set of possible digraphs. The piecewise-constant function is a Markovian signal. is the adjacency matrix, where if , else The neighboring set is denoted by . Denote , where and , .
II-C Heterogeneous Linear Multi-Agent Model
Consider a multi-agent system consisting of agents governed by the following heterogeneous linear dynamics:
| (1) |
where denotes the state of agent , denotes the control input of agent , is its output, and , , are constant system matrices. Suppose that the matrix pair is controllable and
| (2) |
General Distributed Optimization Problem: design a distributed scheme for (1) using local interaction and information over a communication network so that the output of all agents can reach the optimal state that minimize: , where is the private cost function known to agent only, and is the global decision variable to be optimized. From [7], it is equivalent to solve:
| (3) |
where is a local estimate on the optimal solution , and is its stack vector of all estimates.
To solve the problem, two standard assumptions are introduced.
Assumption 1
There exists that minimizes the team cost function, i.e., .
Assumption 2
Each function is differentiable, strongly convex, and its gradient is locally Lipschitz on .
II-D Unreliable Random Communication Network
In large-scale cyber-physical systems, the wireless communication may not be reliable due to certain physical uncertainties, e.g., failures, quantization errors, and packet losses in a digital communication [25]. We consider an unreliable network consisting of agents whose integrated wireless communication links are time-varying and failure-prone with certain probabilities. As considered in [25], a random Markov chain model can be adopted to capture this situation. This random process describes dynamic changes of topologies. Let be a right-continuous homogeneous Markovian process on the probability space taking values in a finite state space with an infinitesimal generator , given by , if , else, , where is the transition rate from the state to the state , while and satisfies: .
II-E Malicious DoS Attack Model
As studied in [18], the DoS attack refers to the interruption of the communication channels. Without loss of generality, suppose that there exists an attack sequence when a DoS attack is lunched at , and let the duration of this attack be . Then, the -th DoS attack strategy can be generated with with for all Thus, for given , the sets of time instants where communication is denied (unsuccessful) are described by
| (4) |
which implies that on the interval , the sets of time instants where communication is allowed are: . In words, and represent the total lengths of the attacker being active and sleeping over , respectively.
Definition 1 (Attack Frequency)
For any , let denote the total number of DoS attacks over . Then, denotes the attack frequency over for , where there exists scalars such that
Definition 2 (Attack Duration)
For any let be the total time interval under attacks over The attack duration over is defined as: there exist scalars , so that
II-F Main Objective
The main objective of the paper is to solve a resilient distributed optimization issue of heterogeneous linear multi-agent systems.
Problem 1
(Resilient Distributed Convex Optimization against DoS Attacks over Random Digraphs)
Develop a resilient distributed algorithm so that the output of each agent cooperatively seeks under DoS attacks over random digraphs. The problem in (3) is reformulated as
| (5) |
Remark 3
Solving resilient exponential distributed optimization in Problem 1 is much more challenging in fourfold: (1) Agent dynamics: we investigate general linear multi-agent systems with nonidentical dynamics and dimensions; (2) Communication: the unreliable communication network leads to time-varying directed graphs and moreover, the interruptions of communication channels caused by DoS attacks make existing distributed optimization algorithms degraded or totally failed; (3) Assumptions: the local gradient is nonlinear without needing to satisfy special structures in many existing works and only the local Lipschitz property is required; and 4) Design requirements: propose the initialization-free resilient distributed optimization algorithms with the discrete-time communication nature to provide global exponential convergence and resilience features against DoS attacks over random digraphs. The existing designs in [6, 7, 8, 5, 10, 11, 9, 12, 13] cannot be directly applied.
III Resilient Exponential Distributed Optimization Against Dos ATTACKS over Random Networks
Due to unreliable networks described in the subsection II-D, the underlying topologies are time-varying and random. As stated in [26], define that a sequence of Laplacian matrices admits a common stationary distribution if . Let be a mirror of , i.e., , where is Laplacian matrix of a union of digraphs. Define the minimum cut of as , where is the complement of . Then, we say that this sequence of has a minimum cut , if .
Assumption 3
Assume that the sequence of Laplacian matrices has a stationary distribution with a minimum cut.
Lemma 1
By Assumption 3, let be the Laplacian matrix with a stationary distribution . Then, there exists a weighted matrix , , so that for and a vector satisfying , we have
| (6) |
Proof:
without loss of generality, we suppose that , where it satisfies . Since and , we have and . Define and . Then, we obtain that
| (7) |
where the fact is used to get the last inequality. ∎
III-A Distributed Time-Based Strategy Against DoS Attacks
Based on the DoS attack model in the subsection II-E, without loss of generality, suppose that there exists an infinite sequence of uniformly bounded non-overlapping time intervals . Each agent thus updates its controller over time intervals . Then, in the presence of the DoS attacks, we denote the attack-induced new time sequence as .
Next, we propose the following distributed algorithm to analyze the effect of DoS attacks over random digraphs.
| (8a) | ||||
| (8b) | ||||
| (8c) | ||||
where are positive constant gains, is the intermediate variable, and , are consensus errors under DoS attacks
| (9) |
| (10) |
where denote the auxiliary states. In (8), and is the solution to the following equations:
| (11) |
Remark 4
The proposed algorithm in (8)-(11) has properties: 1) it is distributed as each agent communicates with its neighbors only; 2) each agent transmits exchange information over random digraphs, while in the presence of DoS attacks, the information is interrupted; and 3) in is relative internal state information, which is used to avoid zero-sum initial requirements. Besides, the solution of (11) is ensured by (2).
Define . Substituting (8)-(10) into (1) gives the following closed-loop system under attacks and random digraphs.
| (12) |
where and are stacked vectors of , , , , , and are stacked block diagonal matrices of , , , , , , , respectively.
Next, we present the exponential resilient distributed optimization result against DoS attacks and random digraphs.
Theorem 1
Given Assumptions 1-3, Problem 1 is solvable for any , , and under the proposed resilient distributed optimization algorithm in (8)-(10), provided that is chosen so that is Hurwitz, are solutions to (11), and for scalars to be determined later, the following two arrack-related conditions are satisfied:
(1). There exists constants and so that in the attack frequency Definition 1 satisfies the condition:
| (13) |
(2). There exist constants , such that in the attack duration Definition 2 satisfies the condition:
| (14) |
Moreover, the estimated states converge exponentially, i.e.,
| (15) |
where with , , and representing the state transformations, is a positive scalar to be determined later, and .
Proof:
the idea is to show the convergence of to the equilibrium point, which will include four steps below:
i) consider the case that the communication is not subject to DoS attacks, i.e., . We first show that the output at the equilibrium point is an optimal solution of (5).
In the absence of DoS attacks, (12) can be rewritten as
| (16a) | ||||
| (16b) | ||||
| (16c) | ||||
By (11), we obtain the equilibrium point from
| (17a) | ||||
| (17b) | ||||
| (17c) | ||||
In the sequel, we show that the equilibrium point is the solution. Deducing from (17), the equilibrium point satisfies
| (18) |
where , and since is strongly convex, implies that is the optimal solution. Since is selected such that is Hurwitz, it follows from (11) and (18) that
| (19) |
Thus, , and at the equilibrium point is the optimal solution of (5) in the absence of attacks.
Let and . Since , , , we further have the following system
| (20a) | ||||
| (20b) | ||||
| (20c) | ||||
Choose the following nonnegative Lyapunov function candidate , where
| (21a) | ||||
| (21b) | ||||
| (21c) | ||||
where and is defined in Lemma 1.
Then, the time derivatives of (21a) along (20) is described by
| (22) | ||||
where is Hurwitz so that there is a positive define matrix satisfying and . Then, it follows from (21) and (20b)-(20c) that
| (23) |
The time derivative of (21c) is expressed as
| (24) |
where in (11) and the Young inequality are used to derive the last inequality, and is a positive constant.
Let , and is a scalar. Due to the fact that and according to Assumption 2, we can further obtain that
| (25a) | |||
| (25b) | |||
Thus, combining (22)-(25) gives rise to
| (32) |
where , , , , , , , where and I is the identify matrix with proper dimensions.
Hence, denote and there exists scalars , and matrices , , , such that we have
| (33) |
ii) consider the case that in the presence of DoS attacks, i.e., , we choose the Lyapunov function candidate as
| (34) |
where , and is a diagonal matrix.
Then, the time derivative of along (12) is given by
| (35) |
where , and can be described by
| (36) |
where with , , and .
iii) we analyze the exponential convergence of the closed-loop system from a hybrid perspective in [15, 17, 16, 18].
Denote as a switching signal. Then, we can select a piecewise Lyapunov function candidate: , if , and , if where and are defined in (33) and (34), respectively.
We suppose that is activated in , while is activated in . Then, it follows from (33) and (35) that we get
| (37) |
Note that a closed-loop system is switched at or . Let , and next, we discuss the switching situation in two cases:
Case a): if , it follows from (37) that
| (38) |
Case b): if , it follows from (37) that
| (39) |
iv) bounds on DoS attack frequency and duration
Notice that for all and by Definition 2. Thus, we have
| (41) |
By exploiting the attack condition in (13), we can obtain that
| (43) |
Thus, it follows from (45) that , , and are bounded, and converge to zero exponentially. That is, , , and . It follows from in (11) that , i.e., . Thus, . Then, based on , the problem in (5) is solvable. Hence, it can be concluded that converges to exponentially for heterogeneous linear multi-agent systems under DoS attacks over random digraphs. ∎
In the absence of attacks, Theorem 1 is reduced as follows.
Corollary 1: In the absence of attacks, the optimal solution is achieved under the following distributed algorithm, provided that is Hurwitz and is a solution to (11).
| (46a) | ||||
| (46b) | ||||
| (46c) | ||||
Proof:
the proof is similar to Step (i), and is omitted. ∎
III-B Distributed Event-Triggered Strategy Against DoS Attacks
The time-based scheme in the subsection A is implemented by fixed and periodic samplings, which require all agents to exchange information synchronously. Let denote a sequence of some transmission time instants with . Unlike known time-based transmission time instants , an event-triggered transmission attempt will be scheduled to be resilient against DoS attacks. If , an information transmission attempt suffers from the DoS attack, and thereby is unsuccessful. If , the information can be successfully transmitted. It is thus desirable to develop a new way to update the distributed optimization algorithm and determine the next triggering instants for information transmissions over insecure communication. The main challenges include twofolds: i) how to design a distributed dynamic event-triggered condition without Zeno behavior, and ii) how to illustrate the validity of distributed optimization algorithm to guarantee global exponential convergence.
Now, propose the following distributed optimization algorithm to handle the effect of DoS attacks over random digraphs.
| (47a) | ||||
| (47b) | ||||
| (47c) | ||||
where the consensus errors under DoS attacks are described by
| (48) |
| (49) |
where , , , and , .
To specify event time instants, denote the measurement errors
| (50) |
Then, a dynamic event-triggering scheme is developed as
| (51) |
where is a dwell time to be determined, , , and the triggering functions , are given by
| (52) |
where , , and , are auxiliary variables satisfying for , , , and ,
| (53) |
| (54) |
Next, we firstly introduce the following lemma.
Lemma 2
Under the dynamical event-triggered scheme (51), the term below is always positive for ,
| (55) |
Proof:
under the proposed event-triggered scheme (51)-(54), the transmission attempts can be generated, where denotes the successful transmission attempts while denotes the unsuccessful transmission attempts. Next, two cases are considered:
Case i): choose any and let . Then, when , Hence, we can obtain from (53) that
| (56) |
which implies that based on the mathematical induction, we have that for ,
| (57) |
Case ii): denote , and we have that for , it follows from (53) that . Thus, is time-invariant and since , we have
| (58) |
Then, we obtain from both cases that .
Similarly, it can be derived from (54) that for both cases by following the same procedure. ∎
Substituting (47)-(49) into (1) yields the following system
| (59) |
where are the stack vectors of , respectively, and
| (60) |
Theorem 2
Given Assumptions 1-3, Problem 1 is solvable for any , and under the proposed resilient distributed optimization algorithm in (47)-(49) together with the distributed event-triggered scheme in (51)-(54), provided that is Hurwitz, are solutions to (11), and
| (61) |
where are positive scalars to be determined later.
Proof:
the proof includes the following steps:
Step 1 (two intervals classification): two time intervals where (51)-(54) holds and does not hold are characterized. Consider sequences: and The following is a set of integers related to an updating attempt occurring under attacks. Due to the finite sampling rate, a time interval will necessarily elapse from to the time when agents successfully sample and transmit. It is upper bounded by . Hence, a DoS free interval of a length greater than ensures that each agent can sample and transmit. The -th time interval where (51)-(54) do not need to hold is
| (62) |
Thus, the time interval consists of the following two union of sub-intervals: with
| (63) |
Step 2 (Lyapunov stability analysis)
i) consider the time interval over which (51)-(54) hold. Denote and then select
| (64) |
, , , is similar to with , .
ii) consider the time interval over which (51)-(54) do not necessarily hold. Let , with being a diagonal matrix and choose the Lyapunov function candidate as
| (73) |
Similar to (35), the time derivative of along (59) is
| (74) |
where , and is similarly defined as (36) with .
iii) convergence analysis of a piecewise Lyapunov function.
Similar to (37)-(39), let and , where and are defined in (64) and (73), respectively. Suppose that is activated in and is activated in . Then, by the Comparison lemma, we get
| (75) |
Denote . Next, we discuss the situation in two cases:
Case a): if , it follows from (75) that
| (76) |
Case b): if , similarly
| (77) |
iv) bounds on the attack frequency and duration.
From Definition 1, for and for . Thus, for ,
| (78) |
From (61), let so that
| (80) |
Thus, for certain scalar , we can have
| (81) |
Hence, we obtain that converges to exponentially. ∎
Theorem 3
Proof:
suppose that there exists Zeno behavior. That is, there exists an agent so that at certain time , . From the property of limits, we have that for certain , there exists a positive integer such that
| (82) |
which implies that .
Based on (1), (47) and (60), the upper right-hand Dini derivative of and can be derived as
| (83a) | ||||
| (83b) | ||||
| (83c) | ||||
| (83d) | ||||
Case a): for , we get
| (84) |
From Theorem 2, we have that all the states , , are bounded. Thus, for certain scalar ,
| (85) |
Since an event is triggered if (51) is satisfied and , we have . Thus,
| (86) |
Select as the solution of . Then, we obtain that
which contracts (82). Thus, no Zero behavior exists for Case a).
Case b): for , . Following a similar procedure, we can also show that no Zero behavior exists for .
Overall, Zero behavior can be avoided for agent . ∎
Remark 5
Unlike traditional time-triggered control schemes in (8), an event-based transmission strategy is presented in (47) to save limited communication resources and to be resilient against attacks. The defined is an aperiodic transmission sequence determined by (51) for agent i. This means that each agent has its own triggering rule, that is, they transmit data in an asynchronous manner. In addition, the triggering process of each agent does not affect each other, that is, an agent and its neighbors are considered independent from the perspective of activating the triggering rules. Each agent needs to measure its own information and has access to its neighboring information, which essentially reflects the basic requirement of distributed control strategy.
Remark 6
Inspired by [27] and [28], a new dynamical event-triggered communication scheme in (51)-(54) is designed over an insecure and unreliable network. For linear multi-agent systems, the proposed scheme in (51)-(54) generates transmission updates under DoS attacks. General speaking, there exist several methods to exclude Zeno behavior, e.g., a pre-defined dwell time design in [18] or combination with sample-data schemes in [29]. In contrast to the above literature, the dynamical event-triggered communication scheme in (51)-(54) is developed to avoid the continuous communication and involvement of global graph information. In addition, its effectiveness has been verified even in the presence of DoS attacks over random digraphs.
IV Numerical Simulations
In this section, numerical simulation examples are presented to verify the effectiveness of the proposed designs.
Consider a group of agents described by the following general heterogeneous linear dynamics with different dimensions:
| (87) | ||||
| (94) | ||||
| (101) | ||||
| (111) |
In order to cooperatively solve the original optimization problem: , the local objective functions for each agent are described by , , and [11].
The random digraphs for a team of three agents are shown in Fig. 1, where the random process is captured by the Markov chain with the state space being , and its transition rate matrix is , whose row summation is zero and all off-diagonal elements are nonnegative. The initial distribution is given by As can be seen, each graph is disconnected, while the union of graphs contains a directed spanning tree to satisfy Assumption 3.
Next, executions of resilient distributed optimization algorithms with respect to three different cases are presented. The values of the initial states , and are randomly chosen in an interval . The controller gain matrix is chosen so that is Hurwitz, which are provided as: , , . Thus, the gain matrices , , (solution to (11)) can be determined by: , , , , , , , , and , respectively.




Case 1: execution of reliable distributed optimization algorithm (46) over random digraphs and without DoS attacks
In this simulation, the resilient distributed optimization algorithm (46) is performed under only unreliable random digraphs in the absence of DoS attacks. Figs. 2-4 depict the simulation results for the execution of (46). The signal in Fig. 2 describes the random process of unreliable digraphs in Fig. 1. Fig. 3 shows the trajectories of both output states and optimal errors , respectively, while Fig. 4 illustrates the evolution of the sum of local objective functions . It can be seen that these outputs reach consensus and converge to the optimal solution .
To illustrate the effect of the parameter , Fig. 5 illustrate the simulation results with different . As we can see, the larger value of results in a faster convergence as discussed.

|
Case 2: execution of time-based resilient distributed optimization algorithm (8) under DoS attacks over random digraphs
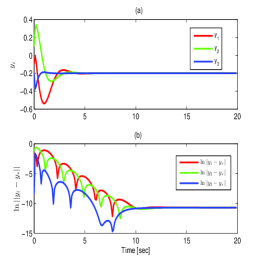
In this simulation, the resilient distributed optimization algorithm (8) with time-based communication is performed under DoS attacks over random digraphs. The simulation result is shown in Fig. 6. The DoS attack signal is simulated in Fig. 6(a) with . Based on (13) and (14), the two conditions are satisfied with and . That is, the attack cannot occur more than times during a unit of time. Figs. 6(b) and 6(c) show the outputs and the errors, while Fig. 6(d) shows the sum of local cost functions. As can be seen, these outputs reach consensus and converge to the solution under DoS attacks over random digraphs.

Case 3: execution of event-based resilient distributed optimization algorithm (47) under DoS attacks over random digraphs
In this part, the event-triggered resilient distributed optimization algorithm (47) has been performed under attacks over random digraphs. The simulation environments including DoS attacks and control parameters are set the same as those in Case 2. Then, the simulation results are depicted in Fig. 7, from which it can be seen that these outputs reach consensus and can converge to . Thus, the optimization problem is solvable by the proposed distributed algorithm (47) with an event-based communication strategy under DoS attacks over random digraphs. Fig. 8 depicts the event time instants of agents, and there exists no Zeno-behavior.


V Conclusion
In this paper, resilient exponential distributed convex optimization problems were studied for linear multi-agent systems under DoS attacks over random digraphs. The two types of time-based and event-based resilient distributed optimization algorithms were proposed to solve these problems, respectively. Under both algorithms, the global minimizer was achieved exponentially, provided that an explicit analysis of the frequency and duration of attacks was established. In addition, it was proved that there were no Zeno behavior occurring under the dynamic event-triggered condition. Future work will investigate resilient constrained optimization.
References
- [1] U. A. Khan, S. Kar, J. M. F. Moura, “Diland: An algorithm for distributed sensor localization with noisy distance measurements,” IEEE Trans. Signal Process., 58(3): 1940–1947, 2010.
- [2] C. Shen, T. Chang, K. Wang, Z. Qiu, C. Chi, “Distributed robust multicell coordianted beamforming with imperfect CSI: an ADMM approach,” IEEE Trans. Signal Process., 60(6): 2988–3003, 2012.
- [3] S. K. Gupta, K. Kar, S. Mishra, John T. Wen, “Collaborative energy and thermal comfort management through distributed consensus algorithms,” IEEE Trans Autom. Sci. Eng., 12(4): 1285–1296, 2015.
- [4] L. Bai, M. Ye, C. Sun, G. Hu, “Distributed economic dispatch control via saddle point dynamics and consensus algorithms,” IEEE Trans. Control Syst. Technol., 27(2): 898–905, 2019.
- [5] Z. Feng, G. Hu, C. G. Cassandras, “Finite-time distributed convex optimization for continuous-time multi-agent systems with disturbance rejection,” IEEE Trans. Control Netw. Syst., 7(2): 686–698, 2020.
- [6] D. Varagnolo, F. Zanella, A. Cenedese, G. Pillonetto, L. Schenato, “Newton-raphson consensus for distributed convex optimization,” IEEE Trans. Autom. Control, 61(4): 994–-1009, 2016.
- [7] B. Gharesifard, J. Cortes, “Distributed continuous-time convex optimization weight-balanced digraphs,” IEEE Trans. Autom. Control, 59: 781–786, 2014.
- [8] C. Sun, M. Ye, G. Hu, “Distributed time-varying quadratic optimization for multiple agents under undirected graphs,” IEEE Trans. Autom. Control, 66(2): 3687–3694, 2017.
- [9] Q. Liu, J. Wang, “A second-order multi-agent network for bound-constrained distributed optimization,” IEEE Trans. Autom. Control, 60: 3310-3315, 2015.
- [10] Y. Zhao, Y. Liu, G. Wen, G. Chen, “Distributed optimization for linear multi-agent systems: edge-and nodebased adaptive designs,” IEEE Trans. Autom. Control, 62(7): 3602–3609, 2017.
- [11] S. S. Kia, J. Cortes, S. Martinez, “Distributed convex optimization via continuous-time coordination algorithms with discrete-time communication,” Automatica, 55(1): 254–-264, 2015.
- [12] S. Liu, L. Xie, D. E. Quevedo, “Event-triggered quantized communication-based distributed convex optimization,” IEEE Trans. Control Netw. Syst., 5(1): 167–178, 2018.
- [13] Z. Li, Z. Wu, Z. Li, Z. Ding, “Distributed optimal coordination for Heterogeneous linear multiagent systems with event-triggered mechanisms,” IEEE Trans. Autom. Control, 65(4): 1763–1770, 2019.
- [14] Y. Mo, J. P. Hespanha, B. Sinopoli, “Resilient detection in the presence of integrity attacks,” IEEE Trans. Signal Process. 62(1): 31–43, 2014.
- [15] Z. Feng, G. Hu, “Distributed coordinated control for multi-agent systems under two types of attacks with an application to power system,” the 19 IFAC World Congress, August 24-29, South Africa, pages, 124–-130, 2014.
- [16] Z. Feng, G. Hu, G. Wen, “Distributed consensus tracking for multi-agent systems under two types of attacks,” Int. J. Robust. Nonlinear Control, 26(5): 896–918, 2015.
- [17] Z. Feng, G. Wen, G. Hu, “Distributed secure control for multi-agent systems under strategic attacks,” IEEE Trans. Cybern., 47(5): 1273–1284, 2017.
- [18] Z. Feng, G. Hu, “Secure cooperative event-triggered control of linear multi-agent systems under DoS attacks,” IEEE Trans. Contr. Syst. Tech., 28(3): 741–752 2020.
- [19] D. Zhang, L. Liu, G. Feng, “Consensus of heterogeneous linear multi-agent systems subject to aperiodic sampled-data and DoS attack,” IEEE Trans. Cybern., 49(4): 1501–1511, 2019.
- [20] C. De. Persis, P. Tesi, “Input-to-state stabilizing control under denial-of-service,” IEEE Trans. Autom. Control, 60(11): 2930-2944, 2015.
- [21] S. Sundaram, B. Gharesifard, “Consensus-based distributed optimization with malicious nodes,” the 53rd Annual Allerton Conference on Communication, Control, and Computing, pages 244–-249, 2015.
- [22] L. Su, N. Vaidya, “Multi-agent optimization in the presence of Byzantine adversaries: Fundamental limits,” American Control Conference, July 6-8, Boston, MA, USA, pages 7183–-7188, 2016.
- [23] S. Sundaram, B. Gharesifard, “Distributed optimization under adversarial nodes,” IEEE Trans. Autom. Control, 64(3): 1063–1076, 2019.
- [24] C. Zhao, J. He, Q. Wang, “Resilient distributed optimization algorithm against adversarial attacks,” IEEE Trans. Autom. Control, 65(10): 4308–4315, 2020.
- [25] Q. Zhang, J. Zhang, “Distributed parameter estimation over unreliable networks with Markovian switching topologies,” IEEE Trans. Autom. Control, 57(10): 2545–2560, 2012.
- [26] B. Touri, A. Nedic, “On ergodicity, infinite flow, and consensus in random models,” IEEE Trans. Autom. Control, 56(7): 1593–1605, 2011.
- [27] A. Girard, “Dynamic triggering mechanisms for event-triggered control,” IEEE Trans. Autom. Control, 60(7): 1992–1997, 2015.
- [28] X. Yi, K. Liu, D. V. Dimarogonas, K. H. Johansson, “Distributed dynamic event-triggered control for multi-agent systems,” IEEE Conference on Decision and Control (CDC), Australia, Dec 12-15, pp. 6683–6688, 2017.
- [29] T. Cheng, Z. Kan, J. R. Klotz, J. M. Shea, W. E. Dixon, “Event-triggered control of multi-agent systems for fixed and time-varying network topologies,” IEEE Trans. Autom. Control, 62(10): 5365–5371, 2017.