Attend to who you are: Supervising self-attention for Keypoint Detection and Instance-Aware Association

Using self-attention to unify keypoint detection, grouping and human mask prediction. We use Transformer to solve the challenging multi-person keypoint detection, grouping and mask prediction in a unified way. We realize that the self-attention shows instance-related semantics, which can be served as the association information in a bottom-up fashion. We further use instance masks to supervise the self-attention. It ensures that each keypoint is assigned to the correct human instance according to the attention scores, making it easy to obtain the instance masks as well.

Supervising self-attention “for your need”. A common practice of using Transformer models is to use task-specific signals to supervise the final output of transformer-based models, such as class labels, object box coordinates, keypoint positions or semantic masks. In this method, a key novelty is to use some type of constraint terms to control the behaviors of self-attention. The results show that under supervision the self-attention can achieve instance-aware characteristics for multi-person pose estimation and mask prediction, without destroying the standard forward of Transformer. This demonstrates that using appropriate guidance signals makes self-attention controllable and help the model learning, which is also applicable to other vision tasks such as instance segmentation (Wang et al., 2021) and object detection (Carion et al., 2020).

Given a RGB image $I$ of size $3\times H\times W$, the goal of 2D multi-person pose estimation is to estimate all persons’ keypoints locations: ${\mathbb{S}}=\left\{(x_{i}^{k},y_{i}^{k})|i=1,2,...,N;k=1,2,...,K\right\}$, where $N$ is the number of persons in this image and $K$ is the number of defined keypoint types.

We follow the bottom-up strategy. First, the model detects all the candidate locations for each type of keypoints in an image: ${\mathbb{C}}={\mathbb{C}}_{1}\bigcup{\mathbb{C}}_{2}\bigcup...\bigcup{\mathbb{C}}_{K}$, where ${\mathbb{C}}_{k}=\left\{(\hat{x}_{i},\hat{y}_{i})|i=1,2,...,N_{k}\right\}$ represents the $k$-th type of keypoint set with $N_{k}$ detected candidates. Second, a heuristic decoding algorithm $g$ groups all candidates into $M$ skeletons based on the association information $\mathcal{A}$, which determines a unique person ID for each keypoint location. We formulate this process as: $g((\hat{x}_{i},\hat{y}_{i}),{\mathbb{C}},\mathcal{A})\rightarrow m\in\{1,2,...,M\}$.

Next, we present the model architecture and show how to use self-attention as the association information $\mathcal{A}$. We analyze the problems when using the naive self-attention as the grouping reference. We propose to supervise self-attention via instance masks for keypoints grouping. We present two types of grouping algorithm from the body-first and part-first views. Finally, we describe how we obtain the person instance masks and how we use the obtained masks to refine the results.

Architecture. We use a simple architecture combination that includes ResNet (He et al., 2016) and Transformer encoder (Vaswani et al., 2017), like the design of TransPose (Yang et al., 2021). The downsampled feature maps of ResNet with $r$ stride are flattened to a sequence of $L\times d$ size and sent to Transformer where $L=\frac{H}{r}\times\frac{W}{r}$. Several transposed convolutions and a 1$\times$1 convolution are used to upsample the Transformer output into the target keypoint heatmap size $K\times\frac{H}{4}\times\frac{W}{4}$.

Heatmap loss. To observe what patterns the self-attentions layers spontaneously learn, we first only leverage the mean square error (MSE) loss between the predicted heatmap $\mathbf{\hat{H}}_{k}$ and the groundtruth heatmap $\mathbf{H}_{k}$ to train the model:

$$\mathcal{L}_{heatmap}=\frac{1}{K}\sum_{k=1}^{K}\mathbf{M}\cdot\left\|\mathbf{\hat{H}}_{k}-\mathbf{H}_{k}\right\|,$$

(1)

where $\mathbf{M}$ is a mask that masks out the crowd areas and small size person segments in the whole image. After the model is trained only by heatmap loss, the keypoint detection results show the trained model can accurately localize keypoints of multiple persons.

Issues in naive self-attention. We obtain the keypoint locations from heatmaps and further visualize the attention areas of these locations. As revealed by the examples shown in Figure 1, using the naive self-attention matrices as the association reference poses several challenges: 1) There are multiple attention layers in Transformer, each of which shows distinct characteristics. Selecting which attention layers as the association reference and how to process the raw attention require a very thoughtful fusion and post-processing strategy. 2) Although most of the sampled keypoint locations show local attention areas, especially for the people they belong to, some keypoints still spontaneously produce relatively high attention scores to the parts of other people at a longer distance. It is almost impossible to determine a perfect attention threshold for all situations, which makes keypoint grouping highly dependent on specific experimental observations. As a consequence, the attention-based grouping cannot ensure the correctness of the keypoint assignment, leading to inferior performance.

To address the aforementioned challenges of using the naive self-attention for keypoints grouping, we Supervise Self-Attention (SSA) to be what we expect. Ideally, the expected attention pattern should be that each keypoint location only attends to the person instance it belongs to. The value distribution (0 or 1) in a person instance mask provides an ideal guidance signal to supervise the pairwise keypoints’s locations to have lower or higher attention scores. Then we propose a sparse sampling method based on the instance keypoint locations to supervise the specific attention matrix generated by the self-attention computation in Transformer, as illustrated in Figure 2.

Instance mask loss. We suppose that the $p$-th person’s keypoints groudtruth locations are $\left\{(x_{p}^{k},y_{p}^{k},v_{p}^{k})\right\}_{k=1}^{K}$, where $v_{p}^{k}\in\left\{0,1\right\}$ is a visibility flag, i.e., $v_{p}^{k}=0$: not labeled, $v_{p}^{k}=1$: labeled. We take out the immediate attention matrix $\mathbf{A}=\operatorname{Softmax}(\frac{\mathbf{Q}\mathbf{K}^{\top}}{\sqrt{d}})\in\mathbb{R}^{L\times L}$ of the specific layer in Transformer²²2$\mathbf{Q},\mathbf{K}\in\mathbb{R}^{L\times d}$ are queries and keys. For simplicity we consider there is only one head. For multihead self attention, the attention matrix $\mathbf{A}$ is the average of all heads’ attention matrices. to leverage the supervision. We first reshape the attention matrix $\mathbf{A}$ into a tensor ${\bm{\mathsfit{A}}}$ of $(h\times w)\times(h\times w)$ size, where $h=H/r,w=W/r$. Then we transform the keypoint coordinates into the coordinate system of the downsampled feature maps. And then we take out the corresponding rows of the attention matrix specified by these locations. So we can obtain the reshaped attention map at each keypoint location: ${\bm{\mathsfit{A}}}[int(y_{p}^{k}/r),int(x_{p}^{k}/r),:,:]$. For a person instance, we sample and average the attention maps based on its visible keypoint locations to estimate the mean attention map. We name it as person attention map $\mathbf{A}_{p}$:

$$\mathbf{A}_{p}=\frac{1}{\sum_{i=1}^{K}v_{p}^{i}}\sum_{k=1}^{K}v_{p}^{k}\cdot{\bm{\mathsfit{A}}}[int(y_{p}^{k}/r),int(x_{p}^{k}/r),:,:].$$

(2)

Assuming the groundtruth instance mask of the $p$-th person in the image is $\mathbf{M}_{p}\in\mathbb{R}^{\frac{H}{4}\times\frac{W}{4}}$, we also use the MSE loss function to supervise the attention matrix sparsely. Since the self-attention scores have been normalized by the softmax function, we need to rescale the $\mathbf{A}_{p}$ by dividing its maximum value so that the rescaled $\mathbf{A}_{p}$ is closer to the value range (0 or 1) of the annotated mask. Note that the size of $\mathbf{A}_{p}$ is $\frac{H}{r}\times\frac{W}{r}$ while the grountruth instance mask is constructed to be $\frac{H}{4}\times\frac{W}{4}$ size. So we use $r/4$ times bilinear interpolation to resize the $\mathbf{A}_{p}$ to have the same size as the instance mask. We formulate the instance mask loss as:

$$\mathcal{L}_{mask}=\operatorname{MSE}(\operatorname{bilinear}(\mathbf{A}_{p}/\operatorname{max}(\mathbf{A}_{p})),\mathbf{M}_{p})=\frac{1}{N}\sum_{p=1}^{N}\left\|\operatorname{bilinear}(\mathbf{A}_{p}/\operatorname{max}({\mathbf{A}_{p}}))-\mathbf{M}_{p}\right\|.$$

(3)

Objective. So the overall objective for training the model is:

$$\mathcal{L}_{train}=\alpha\cdot\mathcal{L}_{heatmap}+\beta\cdot\mathcal{L}_{mask},$$

(4)

where $\alpha$ and $\beta$ are two coefficients to balance two types of learning. In the standard self-attention computation of Transformer, the attention matrix is computed by the inner products of queries and keys. Its gradient back-propagation information is entirely derived from the subsequent attention weighted sum of values. By introducing the instance mask loss to supervise the self-attention, the gradient learning direction for the supervised attention matrix has two sources: the implicit gradient signal from keypoint heatmaps learning and the explicit similarity constraint from instance mask learning. Choosing approximate values of $\alpha$ and $\beta$ is critical for training the model well. We set $\alpha=1,\beta=0.01$ to balance both heatmap learning and mask learning.

When the well-trained model makes a single forward pass for a given image, we can decode the multi-person human poses and masks from the outputted keypoint heatmaps and the supervised attention matrix in the immediate attention layer. We first conduct non-maximum suppression in a 7$\times$7 local window on the keypoint heatmaps and obtain all local maximum locations whose scores exceed the threshold $t$. We put all these candidates into a queue and decode them into skeletons using the attention-based algorithm. Using the self-attention similarity matrix with quadratic complexity inevitably brings redundant computation. However, in part, this also makes minimal assumptions about where the keypoints of the instances may appear and the number of persons in the image. Next we present the self-attention based algorithms from the body-first and part-first views.

Body-first view. This view aims to decode each person skeleton one-by-one from the queue. Assuming we have the sorted all types of candidate keypoints by descending order of score in a single queue, we pop out the first keypoint (maybe any keypoint type) to seed a new skeleton $\mathcal{S}$, and then greedily find the best matched adjacent candidate keypoint from the queue.

For the seeded $\mathcal{S}$ with the initial keypoint, we find the other keypoints along the search path according to a defined human skeleton kinematic tree. When looking for a certain type of joint, the founded joints (denoted as the set $\mathcal{S}_{f}$) of this skeleton $\mathcal{S}$ induce a basin of attraction to “attract” the joint that most likely belongs to it, as illustrated in Figure 3. For a certain unmatched point $p_{c}={(x,y,s)}$ in the candidate set ${\mathbb{C}}_{k}$ of the keypoint type $k$, we use the mean attention scores between the current found keypoints and $p_{c}$ as the metric to measure the attraction from this skeleton³³3To obtain the correct coordinate $(int(x/r),int(y/r))$, we use $(x,y)$ to omit the downsampling factor and rounding operation for simplicity.:

$$\operatorname{Attraction}(p_{c},\mathcal{S}_{f})=\frac{1}{|\mathcal{S}_{f}|}\sum_{(x^{\prime},y^{\prime},s^{\prime})\in\mathcal{S}_{f}}s^{\prime}\cdot{\bm{\mathsfit{A}}}[y,x,y^{\prime},x^{\prime}].$$

(5)

Thus the candidate point with the highest $\operatorname{score}\times\operatorname{Attraction}$ is considered to belong to the current skeleton $\mathcal{S}$: $p_{c}^{*}=\operatorname{argmax}_{p_{c}\in{\mathbb{C}}_{k}}s\cdot\operatorname{Attraction}(p_{c},\mathcal{S}_{f}).$ We repeat the process above and record all the matched keypoints until all keypoints of this skeleton have been found. Then we need to decode the next skeleton. We pop the first unmatched keypoint to seed a new skeleton $\mathcal{S}^{\prime}$ again. We follow the previous steps to find keypoints belonging to this instance. Note if the $\operatorname{Attraction}(p_{c}^{*},\mathcal{S}_{f})$ is smaller than a threshold $\lambda$ (empirically set to 0.0025), this type of keypoint in this skeleton to be empty (zero-filling). It is also worth noting that we also consider the keypoints that have already been claimed by a previous skeleton $\mathcal{S}$, but only when $\operatorname{Attraction}(p_{c},\mathcal{S}^{\prime}_{f})>\operatorname{Attraction}(p_{c},\mathcal{S})$, we assign the matched $p_{c}$ to the current skeleton $\mathcal{S}^{\prime}$.

Part-first view. This view aims to decode all human skeletons part-by-part. Given all candidates for each keypoint type, we initialize multiple skeleton seeds $\left\{\mathcal{S}^{1},\mathcal{S}^{2},...,\mathcal{S}^{m}\right\}$ with the most easily detected keypoints such as nose. Then we follow a fixed order to connect the candidate parts to the current skeletons. These skeletons can be seen as multiple clusters consisting of found keypoints. Like the body-first view, we also use the mean attention attraction $\operatorname{Attraction}(p_{c},\mathcal{S}^{t}_{f})$ from the found keypoints in the skeletons as the metric to assign the candidate parts (Figure 3). But in the part-first view, we compute the pairwise distance matrix between the candidate parts and existing skeletons, and then we use the Hungarian algorithm (Kuhn, 1955) to solve this bipartite graph matching problem. Note, if an $\operatorname{Attraction}(p_{c},\mathcal{S}^{t})$ that represents a matching in the solution is lower than a threshold $\lambda$, we use this corresponding candidate part to start a new skeleton seed. We repeat the process above until all types of candidate parts have been assigned. This part-first grouping algorithm can achieve the optimal solution for assigning local parts to the skeletons although it cannot guarantee the global optimal assignment. We choose the part-first grouping as the default. And we compare both algorithms on the performance, complexity and runtime in Appendix A.5.

The instance masks are easy to obtain after the detected keypoints have been grouped into skeletons. To produce the instance segmentation results, we sample the visible keypoint locations $\left\{(\hat{x}_{m}^{k},\hat{y}_{m}^{k},\hat{v}_{m}^{k})\right\}_{k=1}^{K}$ of the $m$-th instance from the supervised self-attention matrix: $\hat{\mathbf{A}}_{m}=\frac{\sum_{k}\delta(\hat{v}_{m}^{k}>0)\cdot{\bm{\mathsfit{A}}}[\hat{y}_{m}^{k},\hat{x}_{m}^{k},:,:]}{\sum_{k}\delta(\hat{v}_{m}^{k}>0)}$. Then we achieve the estimated instance mask: $\hat{\mathbf{M}}_{m}=\frac{\hat{\mathbf{A}}_{m}}{\operatorname{max}(\hat{\mathbf{A}}_{m})}>\sigma$, where $\sigma$ is a threshold (0.4 by default) to determine the mask region. When we obtain the initial skeletons and masks for all person instances, the joints of a person may fall in multiple incomplete skeletons, but their corresponding segments (sampled attention areas) may overlap. Thus we further perform non-maximum suppression to merge instances if the Intersection-over-Max (IoM) of two masks exceeds 0.3, where Max denotes the maximum area between two masks.

The standard evaluation metric for COCO keypoint localization is the object keypoint similarity (OKS) and the mean average precision (AP) over 10 thresholds (0.5,0.55,…,0.95) is regarded as the performance metric. We train our models on COCO train2017 set, and evaluate the model on the val2017 and test-dev2017 sets, as shown in Table 1 and Table 2. We mainly compare with the typical bottom-up models that have similar pipelines to our method: OpenPose (Cao et al., 2017), PersonLab (Papandreou et al., 2018), and AE (Newell et al., 2017). Following the works (Cao et al., 2017; Newell et al., 2017), we also refine the grouped skeletons using a single pose estimator. We adopt the COCO pretrained TransPose-R-A4 (Yang et al., 2021) that has a very similar architecture to our model and has only 6M parameters. We apply the single pose estimator to each single scaled person region achieved by the box containing the person mask. Note that the refinement results are highly dependent on the effect of the grouping and mask prediction, and we only update the keypoint estimates where the predictions of the two models are almost the same. The concrete update rule is whether the keypoint similarity (KS) metric⁵⁵5We consider the per-keypoint standard deviation and object scale as the standard OKS metric does. computing between two keypoints exceeds 0.75, indicating that the distance between two predicted locations is already very small.

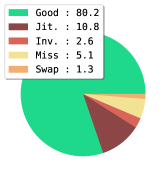
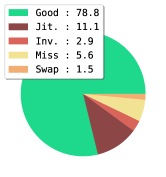
Analysis. We further analyze the differences between pure bottom-up results and the refined ones through the benchmarking and error diagnosis tool (Ronchi & Perona, 2017). We compare our methods with the typical OpenPose model and the Transformer-based model. The yielded localization error bars (Figure 4) reveal the weaknesses and strengths of our model: (1) Jitter error: The heatmap localization precision under the existence of multi-person is still not as accurate as the localization precision of single pose estimate. The small localization and quantization errors of the pure bottom-up model reduce the precision under high thresholds; (2) Missing error: Since our algorithm does not ensure that the coordinate of every keypoint in a detected pose has been predicted, if the GT coordinate of a keypoint is annotated, zero-filling coordinates will seriously pull down the calculated OKS value. Thus, for the evaluation, it is necessary to produce complete predictions. When we further use the single pose estimator to fill the missing joints with zero scores in the initially grouped skeletons, it achieves about 7 AP gains (Table 1) and reduces the missing error (shown in Figure 4(d)); (3) Inversion error: Forcing diverse keypoint types in an individual instance to have higher query-key similarity may make it difficult for the model to distinguish different keypoint types, especially the left and right inversion; (4) Swap error: We notice that our pure bottom-up model has fewer swap errors (1.2$\%$, shown in Figure 4(c)), which represents less confusion between semantically similar parts of different instances. It indicates that compared with OpenPose model, our attention-based grouping strategy performs relatively better in assigning parts to their corresponding instances. We show the qualitative human poses and instance segmentation results in Appendix A.6.

Person instance segmentation. We evaluate the instance segmentation results on COCO val split (person category only). We compare our method with PersonLab (Papandreou et al., 2018). In Table 3, we report the results with a maximum of 20 person proposals due to the convention of the COCO person keypoint evaluation protocol. The results on the mean average precision (AP) show that our model still has a gap in the segmentation performance in comparison to PersonLab. We argue that this is mainly because we conduct the mask learning on low-resolution attention maps that have been downsampled 16 times w.r.t. the 640² or 800² input resolution, while the reported PersonLab result is based on 8 times downsampling w.r.t the 1401² input resolution. As shown in Table 3, our model performs worse on small and medium scales but achieves comparable or even superior performance on large scale persons even if PersonLab uses a larger resolution. In this paper the instance segmentation is not our main goal, so we straightforwardly utilize 16 times bilinear interpolation to upsample the attention maps as the final segmentation results. We believe further mask-specific optimization could improve the performance of instance segmentation.

To study the differences in model learning when trained with and without supervising self-attention, we compare their convergences in the heatmap loss and instance mask loss, since the overfitting on COCO train data is usually not an issue. As illustrated in Figure 5, compared with training the naive self-attention model, supervising self-attention achieves a better fitting effect in the mask learning, while achieving an acceptable sacrifice on the fitting of heatmap learning. It is worth noting that the instance mask training loss curve of the naive self-attention model drops slightly, which suggests that the spontaneously formed attention pattern has a tendency to instance-awareness. To quantitatively evaluate the performance of using naive self-attention patterns for keypoint grouping, we average the attentions from all transformer layers as the association reference (shown in Figure 1). When we use the totally same conditions (including model configuration, training & testing settings and grouping algorithm) of the supervised self-attention model based on (res152, s16, i640), we achieve 29.0AP on COCO validation set, which is far from the 50.7AP result achieved by supervising self-attention.