Attention over learned object embeddings enables complex visual reasoning

David Ding Felix Hill Adam Santoro Malcolm Reynolds Matt Botvinick
DeepMind
London, United Kingdom
{fding, felixhill, adamsantoro, mareynolds, botvinick}@google.com

Abstract

Neural networks have achieved success in a wide array of perceptual tasks but often fail at tasks involving both perception and higher-level reasoning. On these more challenging tasks, bespoke approaches (such as modular symbolic components, independent dynamics models or semantic parsers) targeted towards that specific type of task have typically performed better. The downside to these targeted approaches, however, is that they can be more brittle than general-purpose neural networks, requiring significant modification or even redesign according to the particular task at hand. Here, we propose a more general neural-network-based approach to dynamic visual reasoning problems that obtains state-of-the-art performance on three different domains, in each case outperforming bespoke modular approaches tailored specifically to the task. Our method relies on learned object-centric representations, self-attention and self-supervised dynamics learning, and all three elements together are required for strong performance to emerge. The success of this combination suggests that there may be no need to trade off flexibility for performance on problems involving spatio-temporal or causal-style reasoning. With the right soft biases and learning objectives in a neural network we may be able to attain the best of both worlds. ^†^†Model Code: https://github.com/deepmind/deepmind-research/tree/master/object_attention_for_reasoning.

1 Introduction

Despite the popularity of artificial neural networks, a body of recent work has focused on their limitations as models of cognition and reasoning. Experiments with dynamical reasoning datasets such as CLEVRER (Yi et al., 2020), CATER (Girdhar and Ramanan, 2020), and ACRE (Zhang et al., 2021) show that neural networks can fail to adequately reason about the spatio-temporal, compositional or causal structure of visual scenes. On CLEVRER, where models must answer questions about the dynamics of colliding objects, previous experiments show that neural networks can adequately describe the video, but fail when asked to predict, explain, or consider counterfactual possibilities. Similarly, on CATER, an object-tracking task, models have trouble tracking the movement of objects when they are hidden in a container. Finally, on ACRE, a dataset testing for causal inference, popular models only learned correlations between visual scenes and not the deeper causal logic.

Failures such as these on reasoning (rather than perception) problems have motivated the adoption of pipeline-style approaches that combine a general purpose neural network (such as a convolutional block) with a task-specific module that builds in the core logic of the task. For example, on CLEVRER the NS-DR method (Yi et al., 2020) applies a hand-coded symbolic logic engine (that has the core logic of CLEVRER built-in) to the outputs of a “perceptual” neural front-end, achieving better results than neural network baselines, particularly on counterfactual and explanatory problems. One limitation of these pipeline approaches, however, is that they are typically created with a single problem or problem domain in mind, and may not apply out-of-the-box to other related problems. For example, to apply NS-DR to CATER, the entire symbolic module needs to be rewritten to handle the new interactions and task logic of CATER: the custom logic to handle collisions and object removal must be replaced with new custom logic to handle occlusions and grid-resolution, and these changes require further modifications to the perceptual front-end to output data in a new format. This brittleness is not exclusive to symbolic approaches. While Hungarian-matching between object embeddings may be well-suited for object-tracking tasks (Zhou et al., 2021), it is not obvious how it would help for causal inference tasks.

Here, we describe a more general neural-network-based approach to visual spatio-temporal reasoning problems, which does not rely on task-specific integration of modular components. In place of these components, our model relies on three key aspects:

•

Self-attention to effectively integrate information over time
•

Soft-discretization of the input at the most informative level of abstraction – above pixels and local features, and below entire frames—corresponding approximately to ‘objects’
•

Self-supervised learning, i.e. requiring the model to infer masked out objects, to extract more information about dynamics from each sample.

While many past models have applied each individual ingredient separately (including on the tasks we study), we show that it is the combination of all three ingredients in the right way that allows our model to succeed.

The resulting model, which we call Aloe (Attention over Learned Object Embeddings), outperforms both pipeline and neural-network-based approaches on three different task domains designed to test physical and dynamical reasoning from pixel inputs. We highlight our key results here:

•

CLEVRER (explanatory, predictive, and counterfactual reasoning): Aloe achieves significantly higher accuracy than both more task-specific, modular approaches, and previous neural network methods on all question types. On counterfactual questions, thought to be most challenging for neural-only architectures, we achieve 75% vs 46% accuracy for more specialised methods.
•

CATER (object-permanence): Aloe achieves accuracy exceeding or matching other current models. Notably, the strongest alternative models were expressly designed for object-tracking, whereas our architecture is applicable without modification to other reasoning tasks as well.
•

ACRE (causal-inference “beyond the simple strategy of inducing causal relationships by covariation” (Zhang et al., 2021)): Overall, Aloe achieves 94% vs the 67% accuracy achieved by the top neuro-symbolic model. On the most challenging tasks, we achieve, for “backward-blocking” inference, 94.48% (vs 16.06% by the best modular, neuro-symbolic systems), and, for “screen-off” inference, 98.97% (vs 0.00% by a CNN-BERT baseline).

As we have emphasized, the previous best performing models for each task all contain task-specific design elements, whereas Aloe can be applied to all the tasks without modification. On CLEVRER, we also show that Aloe matches the performance of the previous best models with 40% less training data, which demonstrates that our approach is data-efficient as well as performant.

2 Methods

A guiding motivation for the design of Aloe is the converging evidence for the value of self-attention mechanisms operating on a finite sequences of discrete entities. Written language is inherently discrete and hence is well-suited to self-attention-based approaches. In other domains, such as raw audio or vision, it is less clear how to leverage self-attention. We hypothesize that the application of self-attention-based models to visual tasks could benefit from an approximate ‘discretization’ process, and determining the right level of discretization is an important choice that can significantly affect model performance.

At the finest level, data could simply be discretized into pixels (as is already the case for most machine-processed visual data). Pixels are too fine-grained for many applications, however—for one, the memory required to support self-attention across all pixels is prohibitive. Partly for this reason, coarser representations, such as the downsampled “hyper-pixel” outputs of a convolutional network, are often used instead (e.g. (Zambaldi et al., 2019; Lu et al., 2019)). In the case of videos, previous work considered even coarser discretization schemes, such as frame or subclip level representations (Sun et al., 2019b).

The neuroscience literature, however, suggests that biological visual systems infer and exploit the existence of objects, rather than spatial or temporal blocks with artificial boundaries (Roelfsema et al., 1998; Spelke, 2000; Chen, 2012). Because objects are the atomic units of physical interactions, it makes sense to discretize on the level of objects. Numerous object segmentation algorithms have been proposed (Ren et al., 2015; He et al., 2017; Greff et al., 2019). We chose to use MONet, an unsupervised object segmentation algorithm (Burgess et al., 2019). Because MONet is unsupervised, we can train it directly in our domain of interest without the need for object segmentation labels. We emphasize that our choice of MONet is an implementation detail, and in Appendix B, we show that our framework of attention over learned object embeddings also works with other object-segmentation schemes. We also do not need to place strong demands on the object segmentation algorithm, e.g. for it to produce aligned output or to have a built-in dynamics model.

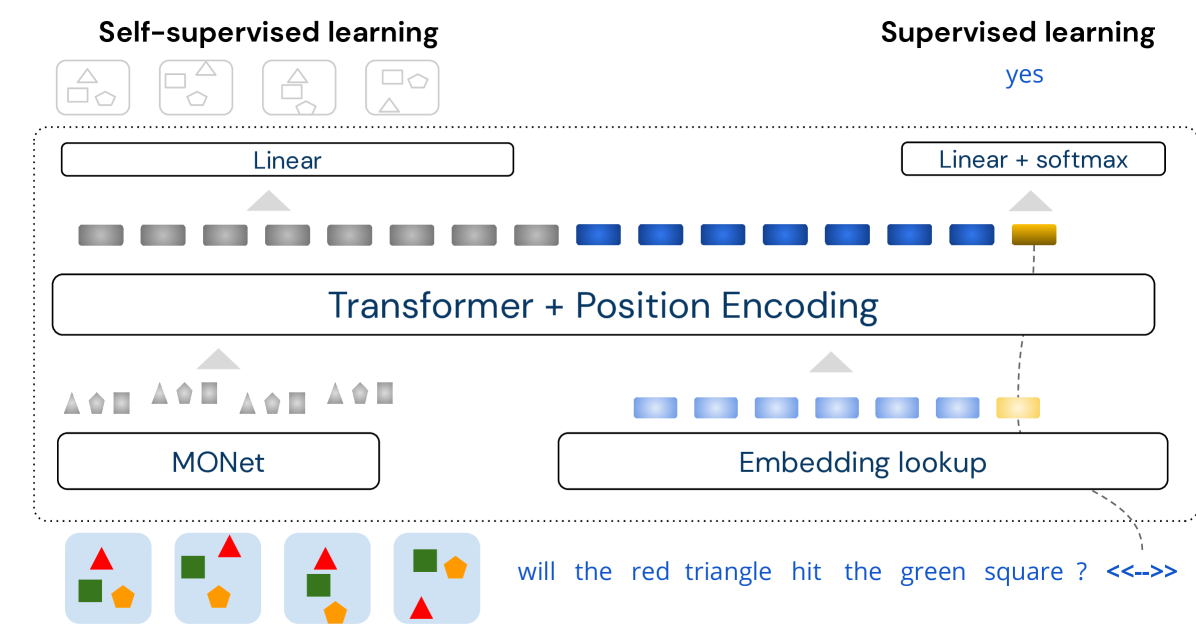
Refer to caption — Figure 1: A schematic of the model architecture. See the main text for details.

To segment each frame into object representations, MONet uses a recurrent attention network to obtain a set of $N_{o}$ “object attention masks” ( $N_{o}$ is a fixed parameter). Each attention mask represents the probability that any given pixel belongs to that mask’s object. The pixels assigned to the mask are encoded into latent variables with means $\mu_{ti}\in\mathbb{R}^{d}$ , where $i$ indexes the object slot and $t$ the frame. These means are used as the object embeddings in Aloe. More details are provided in Appendix A.1.

The self-attention component is a transformer model (Vaswani et al., 2017) operating on a sequence of vectors in $\mathbb{R}^{d}$ : the object representations $\mathbf{\mu}_{ti}$ for all $t$ and $i$ , a trainable vector $CLS\in\mathbb{R}^{d}$ used to generate classification results (analogous to the CLS token in BERT (Devlin et al., 2018)), and (for CLEVRER) the embedded words $\mathbf{w}_{i}$ from the question (and choice for multiple choice questions). For the object representations $\mu_{ti}$ and word embeddings $\mathbf{w}_{i}$ , we append a two-dimensional one-hot vector to $\mathbf{\mu}_{ti}$ and $\mathbf{w}_{i}$ to indicate whether the input is a word or an object. Because the transformer is shared between the modalities, information can flow between objects and words to solve the task, as we show in Section 3.1.

We pass this sequence of vectors through a transformer with $N_{T}$ layers. All inputs are first projected (via a linear layer and ReLU activation) to $\mathbb{R}^{N_{H}\times d}$ , where $N_{H}$ is the number of self-attention heads. We add a relative sinusoidal positional encoding at each layer of the transformer to give the model knowledge of the word and frame order (Dai et al., 2019). The transformed value of $CLS$ is passed through an MLP (with one hidden layer of size $N_{H}$ ) to generate the final answer. A schema of our architecture is shown in Figure 1.

Note that in the model presented above (which we call global attention), the transformer sees no distinction between objects of different frames (other than through the position encoding). Another intuitive choice, which we call hierarchical attention, is to have one transformer acting on the objects of each frame independently, and another transformer acting on the concatenated outputs of the first transformer (this temporal division of input data is commonly used, e.g. in (Sun et al., 2019b)). In pseudo-code, global attention can be expressed as

out = transformer(reshape(objects, [B, F * N, D])

and hiearchical attention as

out = transformer1(reshape(objects, [B * F, N, D]))

out = transformer2(reshape(out, [B, F, N * D])) .

We study the importance of global attention (objects as the atomic entities) vs hierarchical attention (objects, and subsequently frames as the atomic entities). The comparison is shown in Table 1.

2.1 Self-supervised learning

We explored whether self-supervised learning could improve the performance of Aloe beyond the benefits conveyed by object-level representation, i.e. in ways that support the model’s interpretation of scene dynamics rather than just via improved perception of static observations. Our approach is inspired by the loss used in BERT (Devlin et al., 2018), where a transformer model is trained to predict certain words that are masked from the input. In our case, we mask object embeddings, and train the model to infer the content of the masked object representations using its knowledge of unmasked objects.

Concretely, during training, we multiply each MONet latent $\mu_{ti}$ by a masking indicator, $m_{ti}\in\{0,1\}$ . Let $\mu_{ti}^{\prime}$ be the transformed value of $m_{ti}\mu_{ti}$ after passing through the transformer. We expect the transformer to understand the underlying dynamics of the video, so that the masked out slot $\mu_{ti}$ could be predicted from $\mu_{ti}^{\prime}$ . To guide the transformer in learning effective representations capable of this type of dynamics prediction, we add an auxiliary loss:

\text{auxiliary loss}=\sum_{t,i}{\tau_{ti}l\left(f(\mu_{ti}^{\prime}),\mu\right)},

where $f$ is a learned linear mapping to $\mathbb{R}^{d}$ , $l$ a loss function, and $\tau_{ti}\in\{0,1\}$ are one-hot indicator variables identifying the prediction targets (not necessarily just the masked out entries, since the prediction targets could be a subset of the masked out entries). We propagate gradients only to the parameters of $f$ and the transformer and not to the learned word and $CLS$ embeddings. This auxiliary loss is added to the main classification loss with weighting $\lambda$ , and both losses are minimized simultaneously by the optimizer. We do not pretrain the model with only the auxiliary loss.

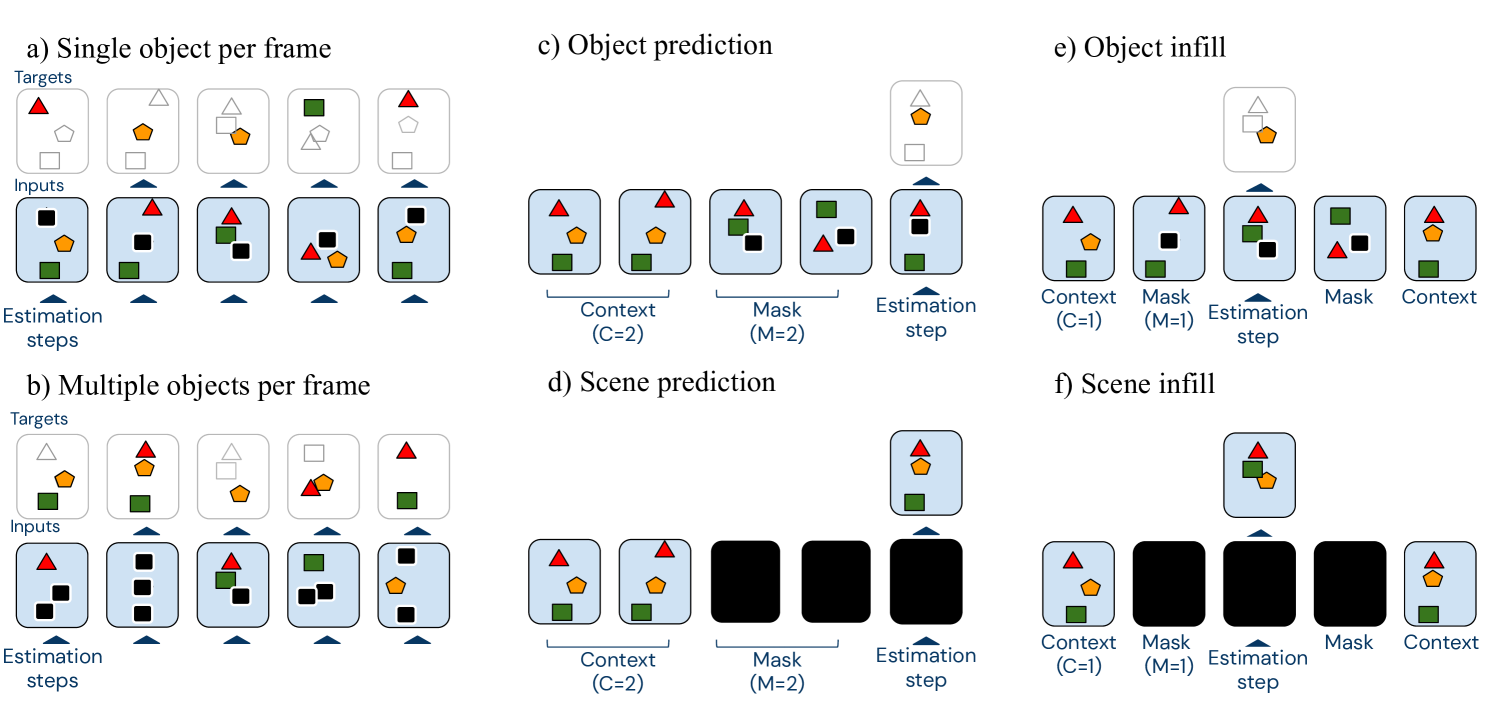
We tested two different loss functions for $l$ , an L2 loss and a contrastive loss (formulas given in Appendix A.2), and six different masking schemes (settings of $m_{ti}$ and $\tau_{ti}$ ), as illustrated in Figure 2. This exploration was motivated by the observation that video inputs at adjacent timesteps are highly correlated in a way that adjacent words are not. We thus hypothesized that BERT-style prediction of adjacent words might not be optimal. A different masking strategy, in which prediction targets are separated from the context by more than a single timestep, may stimulate capacity in the network to acquire knowledge that permits context-based unrolls and better long-horizon predictions.

The simplest approach would be to set $m_{ti}=1$ uniformly at random across $t$ and $i$ , fixing the expected proportion of the $m_{ti}$ set to 1 (schema b in Figure 2). The targets would simply be the unmasked slots, $\tau_{ti}=1-m_{ti}$ . One potential problem with this approach is that multiple objects could be masked out in a single frame. MONet can unpredictably switch object-to-slot assignments multiple times in a single video. If multiple slots are masked out, the transformer cannot determine with certainty which missing object to assign to each slot. Thus, the auxiliary loss could penalize the model even if it predicted all the objects correctly. To avoid this problem, we also try constraining the mask such that exactly one slot is masked out per frame (schema a).

To pose harder prediction challenges, we can add a buffer between the context (where $m_{ti}=1$ ) and the infilling targets (where $\tau_{ti}=1$ ). For $t$ in this buffer zone, both $m_{ti}=0$ and $\tau_{ti}=0$ (schemas c–f). We choose a single cutoff $T$ randomly, and we set $m_{ti}=0$ for $t<T$ and $m_{ti}=1$ for $t\geq T$ . In the presence of this buffer, we compared prediction (where the context is strictly before the targets; schema c, d) versus infilling (where the context surrounds the targets; schema e, f). We also compared setting the targets as individual objects (schema c, e) versus targets as all objects in the scene (schema d, f). We visually inspect the efficacy of this self-supervised loss in encouraging better representations (beyond improvements of scores on tasks) in Appendix D.

3 Experiments

We tested Aloe on three datasets, CLEVRER (Yi et al., 2020), CATER (Girdhar and Ramanan, 2020), and ACRE (Zhang et al., 2021). For each dataset, we pretrained a MONet model on individual frames. More training details and a table of hyperparameters are given in Appendix A.3; these hyperparameters were obtained through a hyperparameter sweep. All error bars are standard deviations computed over at least 5 random seeds.

3.1 CLEVRER

CLEVRER features videos of CLEVR objects (Johnson et al., 2016) that move and collide with each other. For each video, several questions are posed to test the model’s understanding of the scene. Unlike most other visual question answering datasets, which test for only descriptive understanding (“what happened?”), CLEVRER poses other more complex questions, including explanatory questions (“why did something happen?”), predictive questions (“what will happen next?”), and counterfactual questions (“what would happen in a unseen circumstance?”) (Yi et al., 2020).

We compare Aloe to state-of-the-art models reported in the literature: MAC (V+) and NS-DR (Yi et al., 2020), as well as the DCL model (Chen et al., 2021) (simultaneous to our work). MAC (V+) (based on the MAC network (Hudson and Manning, 2018)) is an end-to-end network augmented with object information and trained using ground truth labels for object segmentation masks and features (e.g. color, shape). NS-DR and DCL are hybrid models that apply a symbolic logic engine to outputs of various neural networks. The neural networks are used to detect objects, predict dynamics, and parse the question into a program, and the symbolic executor runs the parsed program to obtain the final output. NS-DR is trained using ground truth labels and ground truth parsed programs, while DCL requires only the ground truth parsed programs.

Model	Descriptive	Explanatory	Predictive	Counterfactual
MAC (V+)	86.4	22.3	42.9	25.1
NS-DR	88.1	79.6	68.7	42.2
DCL	90.7	82.8	82.0	46.5
Aloe	94.0 $\pm$ 0.4	96.0 $\pm$ 0.6	87.5 $\pm$ 3.0	75.6 $\pm$ 3.8
Aloe $-$ self-attention + MLP	45.4	16.0	27.7	9.9
Aloe $-$ object-repr. + ResNet	74.9	66.1	58.3	32.4
Aloe $-$ global + hierarchical attn.	80.6	87.4	73.5	55.1
Aloe $-$ self-supervised loss	91.0	92.8	82.8	68.7

Table 1: Performance (per question accuracy) on CLEVRER of Aloe compared to results from literature and to ablations: 1) MLP instead of self-attention; 2) ResNet superpixels instead of MONet objects; 3) hierarchical frame-level and intra-frame attention instead of global cross-frame object attention; 4) no auxiliary loss.

Table 1 shows the result of Aloe compared to these models. Across all categories, Aloe significantly outperforms the previous best models. Moreover, compared to the other models, Aloe does not use any labeled data other than the correct answer for the questions, nor does it require pretraining on any other dataset. Aloe also was not specifically designed for this task, and it straightforwardly generalizes to other tasks as well, such as CATER (Girdhar and Ramanan, 2020) and ACRE (Zhang et al., 2021). We provide a few sample model classifications on a randomly selected set of videos and questions in Appendix E.1 and detailed analysis of counterfactual questions in Appendix C. These examples suggest qualitatively that, for most instances where the model was incorrect, humans would plausibly furnish the same answer.

Attention analysis

(More analyses are given in Appendix D) We analyzed the cross-modal attention between question-words and the MONet objects. For each word, we determined the object that attended to that word with highest weight (for one head in the last layer). In the visualization below, the bounding boxes show the objects found by MONet, and each word is colored according to the object that attended to it with highest weight (black represents a MONet slot without any objects). We observe that generally, objects attend heavily to the words that describe them.

Q: If the cylinder is removed, which event will not happen?

1.

The brown object collides with the green object.
2.

The yellow object and the metal cube collide.
3.

The yellow cube collides with the green object.

We also looked at the objects that were most heavily attended upon in determining the final answer. The image below illustrates the attention weights for the $CLS$ token attending on each object (for one head in the last layer), when the model is tasked with assessing the first choice of the question above. The bounding boxes show the two most heavily attended upon objects for one transformer head. We observe that this head focuses on the green and brown objects (asked about in choice 1), but switches its focus to the cyan cylinder when it looks like the cylinder might collide with the cubes and change the outcome.

Model ablation

Table 1 shows the contributions of various components of Aloe. First, self-attention is necessary for solving this problem. For comparison, we replace Aloe’s transformer with four fully connected layers with 2048 units per layer¹¹1We also tried a bidirectional LSTM, which achieved even lower performance. This may be because the structure of our inputs requires the learning of long-range dependencies.. We find that an MLP is unable to answer non-descriptive questions effectively, despite using more parameters (20M vs 15M parameters).

Second, we verify that an object-based discretization scheme is essential to the performance of Aloe. We compare with a version of the architecture where the MONet object representations $\mu_{ti}$ are replaced with ResNet hyperpixels as in Zambaldi et al. (2019). Concretely, we flatten the output of the final convolutional layer of the ResNet to obtain a sequence of feature vectors that is fed into the transformer as the discrete entities. To match MONet’s pretraining regimen, we pretrain the ResNet on CLEVR (Johnson et al., 2016) by training an Aloe model (using a ResNet instead of MONet) on the CLEVR task and initializing the ResNet used in the CLEVRER task with these pre-trained weights. We find that an object level representation, such as one output by MONet, greatly outperforms the locality-aware but object-agnostic ResNet representation.

We also observe the importance of global attention between all objects across all frames, compared to a hierarchical attention model where objects within a frame could attend to each other but frames could only attend to each other as an atomic entity. We hypothesize that global attention may be important because with hierarchical attention, objects in different frames can only attend to each other at the “frame” granularity. A cube attending to a cube in a different frame would then gather information about the other non-cube objects, muddling the resulting representation.

Finally, we see that an auxiliary self-supervised loss improves the performance of the model by between $4$ and $6$ percentage points, with the greatest improvement on the counterfactual questions.

Self-supervision strategies

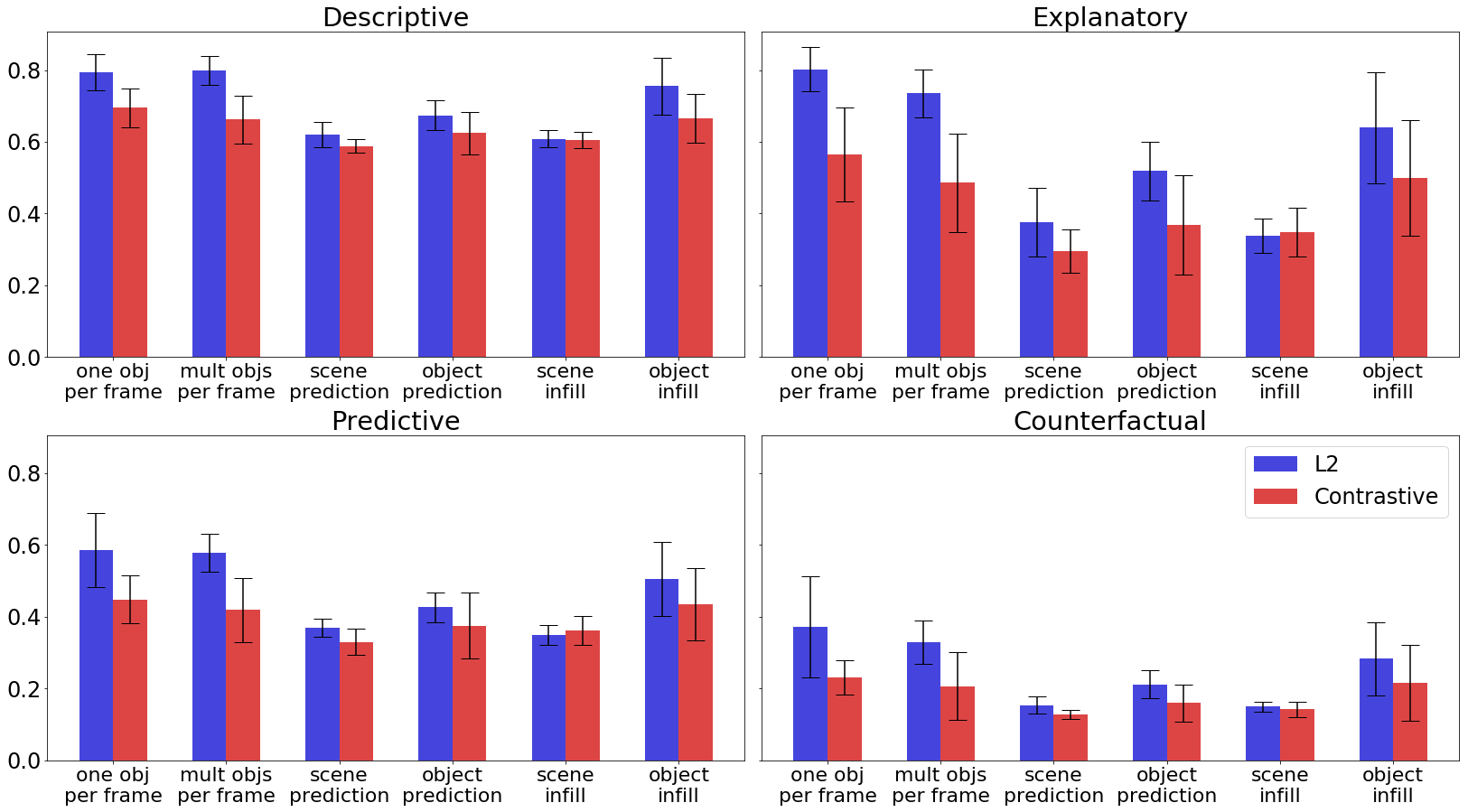
We compared the various masking schemes and loss functions for our auxiliary loss; a detailed figure is provided in Appendix A (Figure 4). We find that for all question types in CLEVRER, an L2 loss performs better than a contrastive loss, and among the masking schemes, masking one object per frame is the most effective. This particular result runs counter to our hypothesis that predictions or infilling in which the target is temporally removed from the context could encourage the model to learn more about scene dynamics and object interactions than (BERT-style) local predictions of adjacent targets. Of course, there may be other settings or loss functions that reveal the benefits of non-local prediction or constrastive losses; we leave this investigation to future work.

Data efficiency

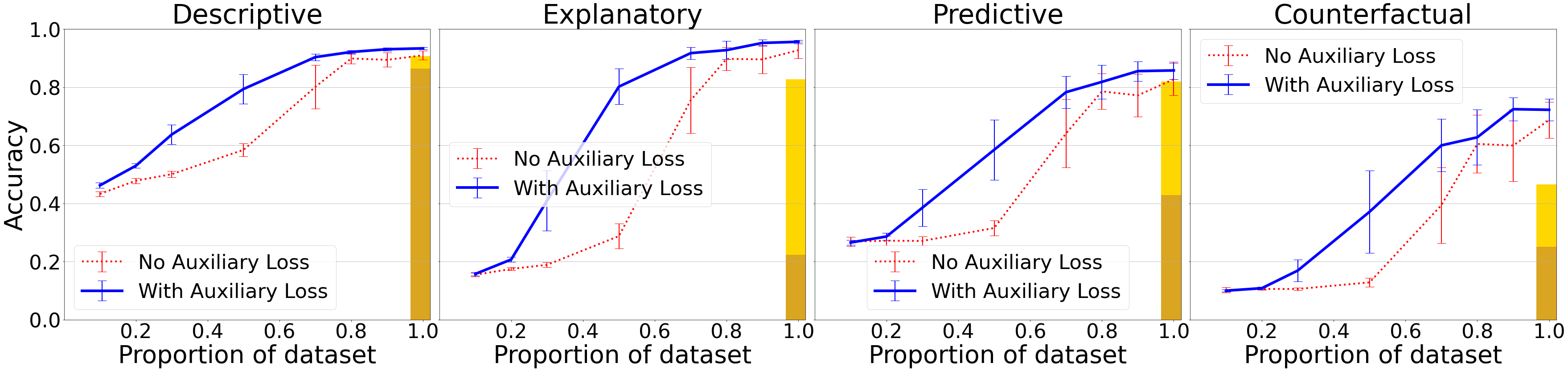
We investigated how model performance varies as a function of the number of labelled (question-answer) pairs it learns from. To do so, we train models on $N\%$ of the videos and their associated labeled data. We evaluate the effect of including the auxiliary self-supervised loss (applied to the entire dataset, not just the labelled portion) in this low data regime. This scenario, where unlabeled data is plentiful while labeled data is scarce, occurs frequently in practice, since collecting labeled data is much more expensive than collecting unlabeled data.

Figure 3 shows that our best model reaches the approximate level of the previous state-of-the-art approaches using only 50%-60% of the data. The self-supervised auxiliary loss makes a particular improvement to performance in low-data regimes. For instance, when trained on only 50% of the available labelled data, self-supervised learning enables the model to reach a performance of 37% on counterfactual questions (compared to 25% by MAC (V+) and 42% by NS-DR on the full dataset), while without self-supervision, the model only reaches a performance of 13% (compared to the 10% achieved by answering randomly (Yi et al., 2020)).

3.2 CATER

In a second experiment, we tested Aloe on CATER, a widely-used object-tracking dataset (Girdhar and Ramanan, 2020; Shamsian et al., 2020; Zhou et al., 2021; Goyal et al., 2021). In CATER, objects from the CLEVR dataset (Johnson et al., 2016) move and potentially occlude other objects, and the goal is to predict the location of a target object (called the snitch) in the final frame. Because the snitch could be occluded by multiple objects that could move in the meantime, a successful model must be sensitive to notions of object permanence. CATER also includes a moving camera variant, which introduces additional complexities for the model.

Concretely, CATER is setup as a classification challenge. Objects are located in an $xyz$ coordinate system, where x and y range from -3 to 3. The $xy$ plane is divided into a 6 by 6 grid, and the task is to predict the grid index of the snitch in the final frame. For Aloe, we use a classification loss (cross entropy over the 36 possible grid indices) and an L1 loss (L1 distance between predicted grid cell and the true grid cell).

Table 2 shows Aloe compared to state-of-the-art models in the literature on both static and moving camera videos. R3D and R3D NL are the strongest two models evaluated by Girdhar and Ramanan (2020). OPNet, or the Object Permanence Network (Shamsian et al., 2020), is an architecture with inductive biases designed for object tracking tasks; it was trained with extra supervised labels, namely the bounding boxes for all objects (including occluded ones). Hopper is a multi-hop transformer model developed simultaneously with this work (Zhou et al., 2021). One key component of Hopper is Hungarian matching between objects of different frames, a strong inductive bias for object tracking.

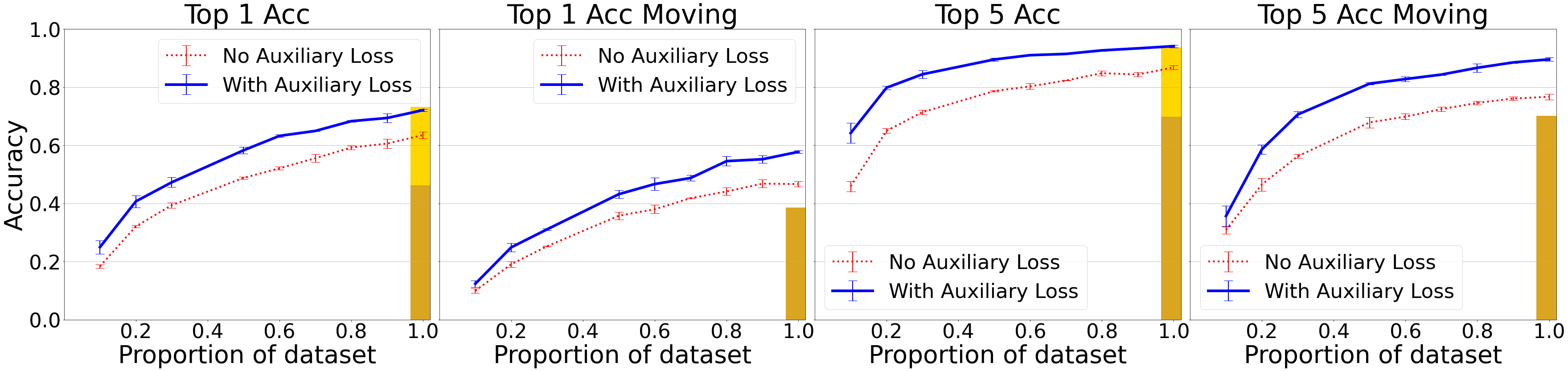
We train Aloe simultaneously on both static and moving camera videos. Aloe outperforms the R3D models for both static and moving cameras. We also ran Aloe with an additional auxiliary loss consisting of the L1 distance between the predicted cell and the actual cell. With this additional loss, we get comparable results in the moving camera case as the R3D models for the static camera case. Moreover, we achieve comparable accuracy as OPNet for accuracy and L1 distance, despite requiring less supervision to train. Appendix E.2 gives a few sample outputs from Aloe; in particular we note that it is able to find the target object in several cases where the object was occluded, demonstrating that Aloe is able to do some level of object tracking. Finally,we find that an auxiliary self-supervised loss helps the model perform well in the low data regime for CATER as well, as shown in Figure 3.

Model Top 1 (S) Top 5 (S) L1 (S) Top 1 (M) Top 5 (M) L1 (M) R3D LSTM 60.2 81.8 1.2 28.6 63.3 1.7 R3D + NL LSTM 46.2 69.9 1.5 38.6 70.2 1.5 OPNet 74.8 - 0.54 - - - Hopper 73.2 93.8 0.85 - - - Aloe (no auxiliary) 60.5 84.5 0.90 46.8 75.1 1.3 Aloe 70.6 93.0 0.53 56.6 87.0 0.82 Aloe (with L1 loss) 74.0 $\pm$ 0.3 94.0 $\pm$ 0.4 0.44 $\pm$ 0.01 59.7 $\pm$ 0.5 90.1 $\pm$ 0.6 0.69 $\pm$ 0.01

Table 2: Performance on CATER of Aloe compared to the best results from literature. We report top 1 accuracy, top 5 accuracy, and L1 distance between the predicted grid cell and true grid cell. The labels (S) and (M) refer to static and moving cameras.

3.3 ACRE

Finally, we measured Aloe’s performance on ACRE, a causal induction dataset inspired by the Blicket task from developmental psychology (Zhang et al., 2021; Gopnik and Sobel, 2000). ACRE is divided into a set of problems. In each problem, certain objects are chosen to be “Blickets”, and this assignment changes across problems. Each problem presents a context of six images to the model, where different objects are placed on a Blicket machine that lights up if one of those objects is a Blicket. The model is asked whether an unseen combination of objects will light up the Blicket machine. Besides “yes” and “no”, a third possible answer is “undetermined”, which is the case if it is impossible to determine for certain if the objects will light up the machine. Correct inference goes beyond mere correlation: even if every context scene involving object A has a lit-up machine, A’s Blicketness is still uncertain if each of those scenes can potentially be explained by another object (deduction of A’s Blicketness is backward-blocked).

Inference problems in ACRE are categorized by reasoning type: reasoning from direct evidence (one of the context frames show the query objects on a machine), reasoning from indirect evidence (Blicketness must be deduced by combining evidence from several frames), screened-off reasoning (presence of non-Blickets do not matter if a single Blicket is present), and backward-blocked reasoning (Blicketness cannot be deduced due to confounding variables). Please see Zhang et al. (2021) for a more detailed discussion of these reasoning types.

Table 3 show Aloe performance compared to a CNN-BERT baseline and to NS-OPT, a neuro-symbolic model introduced in Zhang et al. (2021). Aloe outperforms all extant models for almost all reasoning types and train-test splits. We did not need to do any tuning to apply our model to ACRE—settings from CATER yielded the reported results on the first attempt. Contrary to widely-held opinions that neural networks cannot generalize, Aloe generalizes in scenarios where the training and test sets contain different visual features (compositional split) or different numbers of activated machines in the context (systematic split). Moreover, Aloe achieved by far the best performance on the backward-blocking task, which requires the model to “go beyond the simple covariation strategy to discover the hidden causal relations” (Zhang et al., 2021), dispelling the notion that neural networks can only find correlation. Comparison with NS-OPT (which uses object representations) and CNN-BERT (which uses attention) shows that neither object representations nor attention alone is sufficient for the task; combining these two ideas, as done in Aloe for instance, is essential for this complex reasoning task as well.

Model All (C) D.R. I.D. S.O. B.B. All (S) D.R. I.D. S.O. B.B CNN-BERT 43.79 54.07 46.88 40.57 28.79 39.93 55.97 68.25 0.00 45.59 NS-OPT 69.04 92.5 76.05 88.33 13.48 67.44 94.73 88.38 82.76 16.06 Aloe 91.76 97.14 90.8 96.8 78.81 93.90 97.18 71.24 98.97 94.48

Table 3: Performance on ACRE of Aloe compared to the best results from Zhang et al. (2021), split across inference type (D.R=Direct, I.D=Indirect, S.O=Screen-Off, B.B=Backwards Blocking) and generalization type (C=Compositional, S=Systematic).

4 Related work

Self-attention for reasoning

Various studies have shown that transformers (Vaswani et al., 2017) can manipulate symbolic data in a manner traditionally associated with symbolic computation. For example, in Lample and Charton (2020), a transformer model learned to do symbolic integration and solve ordinary differential equations symbolically, tasks traditionally reserved for symbolic computer algebra systems. Similarly, in Hahn et al. (2020), a transformer model learned to solve formulas in propositional logic and demonstrated some degree of generalization to out of distribution formulas. Finally, Brown et al. (2020) showed that a transformer trained for language modeling can also do simple analogical reasoning tasks without explicit training. Although these models do not necessarily beat carefully tuned symbolic algorithms in all cases (especially on out of distribution data), they are an important motivation for our proposed recipe for attaining strong reasoning capabilities from self-attention-based models on visually grounded tasks.

Object representations

A wide body of research points to the importance of object segmentation and representation learning (see e.g. Garnelo and Shanahan (2019) for a discussion). Various methods have been proposed for object detection and feature extraction (Ren et al., 2015; He et al., 2017; Burgess et al., 2019; Greff et al., 2019; Lin et al., 2020; Du et al., 2020; Locatello et al., 2020). Past research have also investigated using object based representations in downstream tasks (Raposo et al., 2017; Desta et al., 2018).

Self-supervised learning

Another line of research concerns learning good representations through self-supervised learning, with an unsupervised auxiliary loss to encourage the discovery of better representations. These better representations could lead to improved performance on supervised tasks, especially when labeled data is scarce. In Devlin et al. (2018), for instance, an auxiliary infill loss allows the BERT model to benefit from pretraining on a large corpus of unlabeled data. Our approach to object-centric self-supervised learning is heavily inspired by the BERT infilling loss. Other studies have shown similar benefits to auxiliary learning in vision as well (Gregor et al., 2019; Han et al., 2019; Chen et al., 2020). These works apply various forms of contrastive losses to predict scene dynamics, and the better representations that result carry downstream benefits to supervised and reinforcement learning tasks.

Vision and language in self-attention models

Recently, many works have emerged on applying transformer models to visual and multimodal data, for static images (Li et al., 2019; Lu et al., 2019; Tan and Bansal, 2019; Su et al., 2020) and videos (Zambaldi et al., 2019; Sun et al., 2019b, a). These approaches combine the output of convolutional networks with language in various ways using self-attention. While these previous works focused on popular visual question answering tasks, which typically consist of descriptive questions only (Yi et al., 2020), we focus on understanding deeper causal dynamics of videos. Together with these works, we provide more evidence that self-attention between visual and language elements enables good performance on a diverse set of tasks.

In addition, while the use of object representations for discretization in tasks involving static images is becoming more popular, the right way to discretize videos is less clear. We provide strong evidence in the form of ablation studies for architectural decisions that we claim are essential for higher reasoning for this type of data: visual elements should correspond to physical objects in the videos and inter-frame attention between sub-frame entities (as opposed to inter-frame attention of entire frames) is crucial. We also demonstrate the success of using unsupervised object segmentation methods as opposed to the supervised methods used in past work.

5 Conclusion

We have presented Aloe, a model that obtains state-of-the-art performance on three different task domains involving spatiotemporal reasoning about objects. In each of these tasks, previous state-of-the-art results were established by models with modular, task-specific components. Aloe, by contrast, is a unified solution to all three domains. Its flexibility comes from a reliance on only soft biases and learning objectives: self-attention over learned object embeddings and self-supervised learning of dynamics. We believe the simplicity of this approach is its strength, and hope that this fact, together with the provided code, makes it easy for others to adopt and apply to arbitrary spatio-temporal reasoning problems.

On many of these spatio-temporal reasoning problems, previous state-of-the-art was achieved by neuro-symbolic models (Yi et al., 2020; Zhang et al., 2021; Yi et al., 2018b; Garnelo and Shanahan, 2019; Chen et al., 2021). Compared to neuro-symbolic models, Aloe can more easily be adapted to other tasks. Indeed, the symbolic components of neuro-symbolic models are often task-specific and not straightforwardly applicable to other tasks. Neuro-symbolic models do have a few advantages, however. First, they are often easier to interpret. Despite the insights that can be gleaned from Aloe’s attention weights, these soft computations are harder to interpret than the explicit symbolic computation found in neuro-symbolic models. Moreover, neuro-symbolic models can be structured in a more modular fashion, which can enable effective generalization to sub-tasks of the task on which the model was trained (Chen et al., 2021).

Aloe also has some important limitations. First, it has only been applied to synthetic datasets. This limitation is mainly due to the lack of real-world datasets that test for higher-order spatiotemporal reasoning, although we are excited that new datasets such as Traffic QA will be released soon (Xu et al., 2021). Second, while the domains where Aloe is applied have been widely adopted and well-received by the research community, it remains possible that they do not evaluate the capacities that they aim to evaluate because of hidden biases or other factors. Regardless, we hope that this work stimulates the design and development of more challenging tasks that more closely approximate the ultimate goal of human or super-human-level visual, spatiotemporal and causal reasoning. Finally, from an ethical point of view, our model may share the common drawback of deep-learning models in perpetuating biases found in the training data, especially when applied to real world data. Development of causal reasoning models could also invite problematic applications involving automated assignment of blame.

References

Brown et al. [2020] Tom B Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. Language models are few-shot learners. arXiv preprint arXiv:2005.14165, 2020.
Burgess et al. [2019] Chris P. Burgess, Loic Matthey, Nick Watters, Rishabh Kabra, Irina Higgins, Matt Botvinick, and Alex Lerchner. MONet: Unsupervised scene decomposition and representation. arXiv preprint arXiv:1901.11390, 2019.
Carion et al. [2020] Nicolas Carion, Francisco Massa, Gabriel Synnaeve, Nicolas Usunier, Alexander Kirillov, and Sergey Zagoruyko. End-to-end object detection with transformers. In ECCV, 2020.
Chen et al. [2020] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A simple framework for contrastive learning of visual representations. arXiv preprint arXiv:2002.05709, 2020.
Chen [2012] Zhe Chen. Object-based attention: A tutorial review. Attention, Perception, & Psychophysics, 74:784–802, 2012. URL https://doi.org/10.3758/s13414-012-0322-z.
Chen et al. [2021] Zhenfang Chen, Jiayuan Mao, Jiajun Wu, Kwan-Yee Kenneth Wong, Joshua B. Tenenbaum, and Chuang Gan. Grounding physical object and event concepts through dynamic visual reasoning. In International Conference on Learning Representations, 2021. URL https://arxiv.org/pdf/2103.16564.pdf.
Dai et al. [2019] Zihang Dai, Zhilin Yang, Yiming Yang, William W Cohen, Jaime Carbonell, Quoc V Le, and Ruslan Salakhutdinov. Transformer-xl: Attentive language models beyond a fixed-length context. arXiv preprint arXiv:1901.02860, 2019.
Desta et al. [2018] Mikyas T. Desta, Larry Chen, and Tomasz Kornuta. Object-based reasoning in VQA. CoRR, abs/1801.09718, 2018. URL http://arxiv.org/abs/1801.09718.
Devlin et al. [2018] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805, 2018.
Du et al. [2020] Yilun Du, Kevin Smith, Tomer Ulman, Joshua Tenenbaum, and Jiajun Wu. Unsupervised discovery of 3d physical objects from video. arXiv preprint arXiv:2007.12348, 2020.
Garnelo and Shanahan [2019] Marta Garnelo and Murray Shanahan. Reconciling deep learning with symbolic artificial intelligence: representing objects and relations. Current Opinion in Behavioral Sciences, 29:17–23, 2019.
Girdhar and Ramanan [2020] Rohit Girdhar and Deva Ramanan. CATER: A diagnostic dataset for Compositional Actions and TEmporal Reasoning. In ICLR, 2020.
Gopnik and Sobel [2000] Alison Gopnik and David Sobel. Detecting blickets: how young children use information about novel causal powers in categorization and induction. Child Dev, pages 1205–22, 2000. doi: 10.1111/1467-8624.00224.
Goyal et al. [2021] Anirudh Goyal, Aniket Didolkar, Alex Lamb, Kartikeya Badola, Nan Rosemary Ke, Nasim Rahaman, Jonathan Binas, Charles Blundell, Michael Mozer, and Yoshua Bengio. Coordination among neural modules through a shared global workspace. CoRR, abs/2103.01197, 2021. URL https://arxiv.org/abs/2103.01197.
Greff et al. [2019] Klaus Greff, Raphaël Lopez Kaufman, Rishabh Kabra, Nick Watters, Christopher Burgess, Daniel Zoran, Loïc Matthey, Matthew Botvinick, and Alexander Lerchner. Multi-object representation learning with iterative variational inference. CoRR, abs/1903.00450, 2019. URL http://arxiv.org/abs/1903.00450.
Gregor et al. [2019] Karol Gregor, Danilo Jimenez Rezende, Frederic Besse, Yan Wu, Hamza Merzic, and Aaron van den Oord. Shaping belief states with generative environment models for rl. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’ Alché-Buc, E. Fox, and R. Garnett, editors, Advances in Neural Information Processing Systems 32, pages 13475–13487. Curran Associates, Inc., 2019. URL http://papers.nips.cc/paper/9503-shaping-belief-states-with-generative-environment-models-for-rl.pdf.
Hahn et al. [2020] Christopher Hahn, Frederik Schmitt, Jens U. Kreber, Markus N. Rabe, and Bernd Finkbeiner. Transformers generalize to the semantics of logics. arXiv preprint arXiv:2003.04218, 2020.
Han et al. [2019] Tengda Han, Weidi Xie, and Andrew Zisserman. Video representation learning by dense predictive coding. In Workshop on Large Scale Holistic Video Understanding, ICCV, 2019.
He et al. [2017] Kaiming He, Georgia Gkioxari, Piotr Dollár, and Ross B. Girshick. Mask R-CNN. CoRR, abs/1703.06870, 2017. URL http://arxiv.org/abs/1703.06870.
Hudson and Manning [2018] Drew A Hudson and Christopher D Manning. Compositional attention networks for machine reasoning. 2018.
Johnson et al. [2016] Justin Johnson, Bharath Hariharan, Laurens van der Maaten, Li Fei-Fei, C. Lawrence Zitnick, and Ross B. Girshick. CLEVR: A diagnostic dataset for compositional language and elementary visual reasoning. CoRR, abs/1612.06890, 2016. URL http://arxiv.org/abs/1612.06890.
Kingma and Ba [2014] Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
Lample and Charton [2020] Guillaume Lample and François Charton. Deep learning for symbolic mathematics. In International Conference on Learning Representations, 2020. URL https://openreview.net/forum?id=S1eZYeHFDS.
Li et al. [2019] Liunian Harold Li, Mark Yatskar, Da Yin, Cho-Jui Hsieh, and Kai-Wei Chang. Visualbert: A simple and performant baseline for vision and language. arXiv preprint arXiv:1908.03557, 2019.
Lin et al. [2020] Zhixuan Lin, Yi-Fu Wu, Skand Vishwanath Peri, Weihao Sun, Gautam Singh, Fei Deng, Jindong Jiang, and Sungjin Ahn. SPACE: Unsupervised object-oriented scene representation via spatial attention and decomposition. In International Conference on Learning Representations, 2020. URL https://openreview.net/forum?id=rkl03ySYDH.
Locatello et al. [2020] Francesco Locatello, Dirk Weissenborn, Thomas Unterthiner, Aravindh Mahendran, Georg Heigold, Jakob Uszkoreit, Alexey Dosovitskiy, and Thomas Kipf1. Object-Centric Learning with Slot Attention. In Advances in Neural Information Processing Systems (NIPS), 2020.
Lu et al. [2019] Jiasen Lu, Dhruv Batra, Devi Parikh, and Stefan Lee. Vilbert: Pretraining task-agnostic visiolinguistic representations for vision-and-language tasks. arXiv preprint arXiv:1908.02265, 2019.
Raposo et al. [2017] David Raposo, Adam Santoro, David G. T. Barrett, Razvan Pascanu, Timothy P. Lillicrap, and Peter W. Battaglia. Discovering objects and their relations from entangled scene representations. CoRR, abs/1702.05068, 2017. URL http://arxiv.org/abs/1702.05068.
Ren et al. [2015] Shaoqing Ren, Kaiming He, Ross B. Girshick, and Jian Sun. Faster R-CNN: towards real-time object detection with region proposal networks. CoRR, abs/1506.01497, 2015. URL http://arxiv.org/abs/1506.01497.
Roelfsema et al. [1998] Pieter R. Roelfsema, Victor A. Lamme, and Henk Spekreijse. Object-based attention in the primary visual cortex of the macaque monkey. Nature, 395:376–381, 1998. doi: 10.1038/26475.
Shamsian et al. [2020] Aviv Shamsian, Ofri Kleinfeld, Amir Globerson, and Gal Chechik. Learning object permanence from video. arXiv preprint arXiv:2003.10469, 2020.
Spelke [2000] Elizabeth Spelke. Core knowledge. The American psychologist, 55:1233–43, 12 2000. doi: 10.1037/0003-066X.55.11.1233.
Su et al. [2020] Weijie Su, Xizhou Zhu, Yue Cao, Bin Li, Lewei Lu, Furu Wei, and Jifeng Dai. Vl-bert: Pre-training of generic visual-linguistic representations. In International Conference on Learning Representations, 2020. URL https://openreview.net/forum?id=SygXPaEYvH.
Sun et al. [2019a] Chen Sun, Fabien Baradel, Kevin Murphy, and Cordelia Schmid. Contrastive bidirectional transformer for temporal representation learning. CoRR, abs/1906.05743, 2019a. URL http://arxiv.org/abs/1906.05743.
Sun et al. [2019b] Chen Sun, Austin Myers, Carl Vondrick, Kevin Murphy, and Cordelia Schmid. Videobert: A joint model for video and language representation learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), October 2019b.
Tan and Bansal [2019] Hao Tan and Mohit Bansal. Lxmert: Learning cross-modality encoder representations from transformers. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing, 2019.
Vaswani et al. [2017] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Advances in neural information processing systems, pages 5998–6008, 2017.
Xu et al. [2021] Li Xu, He Huang, and Jun Liu. Sutd-trafficqa: A question answering benchmark and an efficient network for video reasoning over traffic events. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2021.
Yi et al. [2018a] Kexin Yi, Jiajun Wu, Chuang Gan, Antonio Torralba, Pushmeet Kohli, and Joshua B Tenenbaum. Neural-Symbolic VQA: Disentangling Reasoning from Vision and Language Understanding. In Advances in Neural Information Processing Systems (NIPS), 2018a.
Yi et al. [2018b] Kexin Yi, Jiajun Wu, Chuang Gan, Antonio Torralba, Pushmeet Kohli, and Joshua B. Tenenbaum. Neural-symbolic vqa: Disentangling reasoning from vision and language understanding. In Advances in Neural Information Processing Systems, pages 1039–1050, 2018b.
Yi et al. [2020] Kexin Yi, Chuang Gan, Yunzhu Li, Pushmeet Kohli, Jiajun Wu, Antonio Torralba, and Joshua B. Tenenbaum. CLEVRER: Collision events for video representation and reasoning. In International Conference on Learning Representations, 2020. URL https://openreview.net/forum?id=HkxYzANYDB.
You et al. [2019] Yang You, Jing Li, Sashank Reddi, Jonathan Hseu, Sanjiv Kumar, Srinadh Bhojanapalli, Xiaodan Song, James Demmel, and Cho-Jui Hsieh. Large batch optimization for deep learning: Training BERT in 76 minutes. Technical Report UCB/EECS-2019-103, EECS Department, University of California, Berkeley, Jun 2019. URL http://www2.eecs.berkeley.edu/Pubs/TechRpts/2019/EECS-2019-103.html.
Zambaldi et al. [2019] Vinicius Zambaldi, David Raposo, Adam Santoro, Victor Bapst, Yujia Li, Igor Babuschkin, Karl Tuyls, David Reichert, Timothy Lillicrap, Edward Lockhart, Murray Shanahan, Victoria Langston, Razvan Pascanu, Matthew Botvinick, Oriol Vinyals, and Peter Battaglia. Deep reinforcement learning with relational inductive biases. In International Conference on Learning Representations, 2019. URL https://openreview.net/forum?id=HkxaFoC9KQ.
Zhang et al. [2021] Chi Zhang, Baoxiong Jia, Mark Edmonds, Song-Chun Zhu, and Yixin Zhu. Acre: Abstract causal reasoning beyond covariation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2021.
Zhou et al. [2021] Honglu Zhou, Asim Kadav, Farley Lai, Alexandru Niculescu-Mizil, Martin Renqiang Min, Mubbasir Kapadia, and Hans Peter Graf. Hopper: Multi-hop transformer for spatiotemporal reasoning. In International Conference on Learning Representations, 2021. URL https://arxiv.org/abs/2103.10574.

Appendix A Methods details

A.1 MONet

To segment each $w\times h$ frame $F_{t}$ into $N_{o}$ object representations, MONet uses a recurrent attention network to obtain $N_{o}$ attention masks $\mathbf{A}_{ti}\in[0,1]^{w\times h}$ for $i=1,\ldots,N_{o}$ that represent the probability of each pixel in $F_{t}$ belonging to the $i$ -th object, with $\sum_{i=1}^{N_{o}}\mathbf{A}_{ti}=1$ . This attention network is coupled with a component VAE with latents $\mathbf{z}_{ti}\in\mathbb{R}^{d}$ for $i=1,\ldots,N_{o}$ that reconstructs $\mathbf{A}_{ti}\odot F_{t}$ , the $i$ -th object in the image. The latent posterior distribution $q(\mathbf{z}_{t}|F_{t},\mathbf{A}_{ti})$ is a diagonal Gaussian with mean $\mathbf{\mu}_{ti}$ , and we use $\mathbf{\mu}_{ti}$ as the representation of the $i$ -th object.

When these representations are fed into the transformer, we use a linear projection to map the raw object/word embeddings, which lie in $\mathbb{R}^{d}$ , to a vector in $\mathbb{R}^{dN_{H}}$ , where $N_{H}$ is the number of self-attention heads. This step is necessary as generally the latent dimensionality of MONet, $d$ , is less than $N_{H}$ whereas a transformer expects the embedding size to be divisible by $N_{H}$ .

A.2 Self-supervised training

Recall in the main text that we wrote the auxiliary self-supervised loss as

\text{auxiliary loss}=\sum_{t,i}{\tau_{ti}l\left(f(\mu_{ti}^{\prime}),\mu\right)}.

We tested an L2 loss and a contrastive loss (inspired by the loss used in [Han et al., 2019]), and the formulas for the two losses are respectively:

	$\displaystyle l_{\mathrm{L2}}\left(f(\mu_{ti}^{\prime}),\mu\right)$	$\displaystyle=\left\lVert f(\mu_{ti}^{\prime})-\mu_{ti}\right\rVert_{2}^{2}$
	$\displaystyle l_{\mathrm{contrastive}}\left(f(\mu_{ti}^{\prime}),\mu\right)$	$\displaystyle=-\log\frac{\exp(f(\mu_{ti}^{\prime})\cdot\mu_{ti})}{\sum_{s,j}\exp\left(f(\mu_{ti}^{\prime})\cdot\mu_{sj}\right)}.$

A comparison of these losses and the masking schemes is given in Figure 4.

We also tested a few variations of the contrastive loss inspired by literature and tested all combinations of variations. The first variation is where the negative examples all come from the same frame:

l_{\mathrm{contrastive}}\left(f(\mu_{ti}^{\prime}),\mu\right)=-\log\frac{\exp(f(\mu_{ti}^{\prime})\cdot\mu_{ti})}{\sum_{j}\exp\left(f(\mu_{ti}^{\prime})\cdot\mu_{tj}\right)}.

The second variation is adding a temperature $\tau$ to the softmax [Chen et al., 2020]:

l_{\mathrm{contrastive}}\left(f(\mu_{ti}^{\prime}),\mu\right)=-\log\frac{\exp(f(\mu_{ti}^{\prime})\cdot\mu_{ti})/\tau}{\sum_{s,j}\exp\left(f(\mu_{ti}^{\prime})\cdot\mu_{sj}/\tau\right)}.

The final variation we tested is using cosine similarity instead of dot product:

l_{\mathrm{contrastive}}\left(f(\mu_{ti}^{\prime}),\mu\right)=-\log\frac{\exp(\mathrm{sim}(f(\mu_{ti}^{\prime}),\mu_{ti}))}{\sum_{s,j}\exp\left(\mathrm{sim}(f(\mu_{ti}^{\prime}),\mu_{sj})\right)}.

where $\mathrm{sim}(\mathbf{x},\mathbf{y})=\frac{\mathbf{x}\cdot\mathbf{y}}{\left\lVert\mathbf{x}\right\rVert\cdot\left\lVert\mathbf{y}\right\rVert}$ . We found that these variations did not significantly change the performance of the model (and the optimal temperature setting was close to $\tau=1$ ), and leave to future work more careful analysis of these contrastive losses and the representations they encourage.

A.3 Training details

We generally follow similar training procedures as for the models described in [Yi et al., 2020] and [Girdhar and Ramanan, 2020]. We train on 16 TPU v2 chips.

For CLEVRER, we resize videos to 64 by 64 resolution and sample 25 random frames, as in [Yi et al., 2020]. We use two different MLP heads on top of the transformed value of the $CLS$ token to extract the final answer, one head for descriptive questions and one head for multiple choice questions. For descriptive questions, the MLP head outputs a categorical distribution over possible output tokens, whereas for multiple choice questions, the MLP outputs the probability that the choice is true. For each training step, we sample a supervised batch of 256 videos with their accompanying questions and answers along with an unsupervised batch of 256 videos, which do not include the answers. These batches are sampled independently from the dataset. The supervised batch is used to calculate the classification loss, and the unsupervised sub-batch is used to calculate the unsupervised auxiliary loss. This division was made so that we can use a subset of available data for the supervised batch while using all data for the unsupervised batch. The supervised batch is further subdivided into two sub-batches of size 128, for descriptive and multiple choice questions (this division was made since the output format is different for the two types of questions). Aloe converges within 200,000 training steps.

For CATER, we also resize videos to 64 by 64 resolution and sample 80 random frames. We use an MLP head on top of the transformed $CLS$ token. This head outputs a categorical distribution over the grid index of the final snitch location. We train on static and moving camera data simultaneously, with the batch of 256 videos divided equally between the two. Aloe converges within 50,000 training steps.

On ACRE, we resize each image to 64 by 64 resolution and concatenate the context images along with one query image to form a “video”. The MLP head on top of the transformed $CLS$ token outputs a categorical distribution over the three possible answers: “yes”, “no”, and “undetermined”. Aloe converges within 60,000 steps.

For the CLEVRER and CATER datasets, we pretrain a MONet model on frames extracted from the respective dataset. The training of the MONet models follow the procedures described in Burgess et al. [2019]. For ACRE, we reuse the MONet model we trained for CATER.

Motivated by findings from language modeling, we trained the main transformer model using the LAMB optimizer [You et al., 2019] and found that it offered a significant performance boost over the ADAM optimizer [Kingma and Ba, 2014] for the CLEVRER dataset (data not shown). We use learning rate warmup over 4000 steps and a linear learning rate decay. We also used a weight decay of 0.01. All error bars are computed over at least 5 seeds. We swept over hyperparameters, and the below table lists the values used in our model. The hyperparameters we used for ACRE were the same as those we used for CATER, except that the prediction-head hidden layer size is reduced to 36 (from 144), because ACRE has only 3 possible outputs compared to the 36 for CATER. We did not do any hyperparameter tuning for ACRE.

Parameter	Value
Batch-size	512
Transformer heads	10
Transformer layers	28
Embedding size $d$	16
Number of objects $N_{o}$	8
Prediction head hidden layer size	128
Maximum learning rate	0.002
Learning rate warmup steps	4000
Final learning rate	$2\times{10}^{-7}$
Learning rate decay steps	$2\times{10}^{5}$
Weight decay rate	0.01
Infill cost $\lambda$	0.01

(a) Hyperparameters for CLEVRER.

Parameter	Value
Batch-size	256
Transformer heads	8
Transformer layers	16
Embedding size $d$	36
Number of objects $N_{o}$	8
Prediction head hidden layer size	144
Maximum learning rate	0.002
Learning rate warmup steps	4000
Final learning rate	$2\times{10}^{-7}$
Learning rate decay steps	$5\times{10}^{4}$
Weight decay rate	0.01
Infill cost $\lambda$	2.0

(b) Hyperparameters for CATER.

Appendix B Using other object-segmentation algorithms

In the main text, we use MONet to obtain object representations, because MONet’s unsupervised nature allows us to establish our state-of-the-art results using only data from the datasets. Our method of attention over learned object embeddings, however, does not rely on MONet representations in particular. In this section, we show how to apply our method to object detection models that output an object segmentation mask but not necessarily a feature vector for each object. This includes, for example, often-used models such as Mask R-CNN and DETR [He et al., 2017, Carion et al., 2020].

Let $\mathbf{A}_{ti}\in[0,1]^{w\times h}$ be the segmentation masks, either produced by an object segmentation algorithm or ground-truth masks. For any function $f:[0,1]^{w\times h\times c}\to\mathbb{R}^{d}$ mapping from the image space to a latent space of dimension $d$ , we can construct object feature vectors $\mathbf{v}_{ti}=f(\mathbf{A}_{ti}\cdot\mathrm{image})$ . That is, we apply $f$ to the image with the segmentation masks applied, once for each object. In our experiments, we choose to represent $f$ with a ResNet consisting of 3 blocks, with 2 convolutional layers per block. The weights of the ResNet are learned with the rest of the network, but the weights of the object segmentation model are fixed.

We provide a proof-of-concept using ground-truth segmentation masks to show the performance of our model in the ideal setting, independent of the quality of the segmentation model. We apply our model to the original CLEVR dataset [Johnson et al., 2016], for which we have ground-truth segmentation masks. CLEVR is a widely used benchmark testing for understanding of spatial relationships between objects in a still image. We obtain an accuracy of 99.5%, which is inline with state-of-the-art results (99.8%, [Yi et al., 2018a]).

Appendix C Analysis of CLEVRER dataset

During analysis of our results, we noticed that some counterfactual questions in the CLEVRER dataset can be solved without using counterfactual reasoning. In particular, about 47% of the counterfactual questions ask about the effect of removing an object that did not collide with any other object, hence having no effect on object dynamics; an example is given in Figure 5. Moreover, even for the questions where the removed object is causally connected to the other objects, about 45% can be answered perfectly by an algorithm answering the question as if it were a descriptive question. To quantify this, we wrote a symbolic executor that uses the provided ground-truth video annotations and parsed questions to determine causal connectivity and whether each choice happened in the non-counterfactual scenario.

Although determining whether or not a given counterfactual question can be answered this way still requires counterfactual reasoning, we want to eliminate the possibility that our model achieved its 75% accuracy on counterfactual questions without learning counterfactual reasoning; instead it might have reached that score simply by answering all counterfactual questions as descriptive questions. To verify this is not the case, we evaluated Aloe on only the harder category of counterfactual questions where the removed object does collide with other objects and which cannot be answered by a descriptive algorithm. We find that Aloe achieves a performance of 59.8% on this harder category. This is significantly above chance, suggesting that Aloe is indeed able to do some amount of true counterfactual reasoning.

Appendix D Qualitative analysis

We provide more qualitative analysis of attention weights in order to shed light on how Aloe arrives at its predictions. These examples illustrate broad patterns evident from informal observation of the model’s attention weights. We focus on the following video from CLEVRER:

In this video, a yellow rubber cube collides with a cyan rubber cylinder. The yellow cube then collides with a brown metallic cube, while the cyan cylinder and a green rubber cube approach each other but do not collide. Finally, the green cube approaches but does not collide with the brown cube.

Most important objects

In the main text, we looked at the most heavily attended-upon objects in determining the answer to a counterfactual question about this video. By looking at the attention patterns when answering a different question about the same video (a predictive question, whether or not the cylinder and the green cube will collide), we see that the relative importance of the various objects depends on the question the model is answering. Here, we observe one head of the transformer focusing on collisions: first the collision of the cylinder and the yellow cube, then on the cylinder and the green cube when they move towards each other.

Object alignment

Recall that MONet does not assign objects to slots in a well-determined manner—tiny changes in an image can cause MONet to unpredictably assign objects to slots in a different permutation. This is a general flaw for object segmentation algorithms without built-in alignment. Nevertheless, Aloe can still effectively utilize these representations, because Aloe is able to maintain object identity even when the objects appear in different order in different frames. The image below, where we again show the two most attended-upon objects for each frame, illustrate instances where MONet changes the permutation of objects. In this image, we plot time on the x-axis and MONet slot index on the y-axis; the slots containing the two most important objects are grayed out. We observe that the transformer is able to align objects across time, maintaining consistent attention to the green and brown objects.

Effectiveness of the auxiliary loss

Finally, we visually inspect our hypothesis that our self-supervised loss encourages the transformer in learning better representations. For clarity of the subsequent illustration, we use the scene prediction masking scheme, as described in Figure 2. In this scheme, the transformer has to predict the contents of the last few frames (the target frames) given the beginning of the video. To pose harder predictive challenges, we mask out the three frames preceding the target frames in addition to the target frames themselves. The two images below compare the predicted frames (second image) to the true frames (first image). In the second image, the black frames are the three masked out frames preceding the target frames. The frames following the black frames are the target frames; they contain the MONet-reconstructed images obtained from latents predicted by the transformer. The frames preceding the black frames are MONet-reconstructed images obtained from the original latents (the latents input into the transformer).

We observe that with the self-supervised loss, we get coherent images from the transformer-predicted latents with all the right objects (in the absence of the auxiliary loss, the transformed latents generate incoherent rainbow blobs). We also observe the rudiments of prediction, as seen in the movement of the yellow object in the predicted image. Nevertheless, it is also clear that the transformer’s predictions are not perfect, and we leave improvements of this predictive infilling to future work.

Appendix E Example model predictions

In this section, we provide a few sample classifications produced by Aloe. All examples are produced at random from the validation set; in particular we did not cherry-pick any examples to highlight the performance of Aloe.

E.1 CLEVRER

We provide four videos and up to two questions per question type for the video (many videos in the dataset come with only one explanatory or predictive question). For each question type with more than one question, we try to choose one correct classification and one misclassification if available to provide for greater diversity. Besides this editorial choice, all classifications are sampled randomly.

Q: How many metal objects are moving? Model: 1 Label: 1	Q: Which of the following is not responsible for the collision between the metal cube and the yellow cube? 1. the presence of the gray cube 2. the gray object’s entrance 3. the presence of the red rubber cube 4. the collision between the gray cube and the metal cube Model: 3 Label: 3	Q: Which event will happen next? 1. The gray object collides with the red object 2. The gray object and the cylinder collide Model: 1 Label: 1	Q: Which event will happen if the red object is removed? 1. The gray object and the brown object collide 2. The gray object collides with the cylinder 3. The gray cube collides with the yellow object 4. The brown cube and the yellow object collide Model: 1, 4 Label: 1, 4
Q: What is the shape of the stationary metal object when the red cube enters the scene? Model: cylinder Label: cylinder			Q: What will happen if the cylinder is removed? 1. The brown cube collides with the red cube 2. The red object and the yellow object collide 3. The gray cube collides with the red cube 4. The gray object collides with the brown object Model: 3, 4 Label: 3, 4

Q: What color is the metal object that is stationary when the metal cube enters the scene? Model: blue Label: blue	Q: Which of the following is not responsible for the collision between the cyan object and the sphere? 1. the presence of the red rubber object 2. the red object’s entering the scene 3. the collision between the sphere and the blue cube Model: 1, 2, 3 Label: 1, 2, 3	Q: What will happen next? 1. The metal cube and the red cube collide 2. The sphere collides with the metal cube Model: 1 Label: 1	Q: Without the red cube, which event will happen? 1. The sphere collides with the blue cube 2. The cyan object and the blue cube collide Model: 1 Label: 1
Q: What material is the last object that enters the scene? Model: metal Label: rubber			Q: What will not happen without the sphere? 1. The cyan object collides with the red cube 2. The cyan object collides with the metal cube 3. The metal cube and the red cube collide Model: 1, 3 Label: 3

Q: Are there any moving brown objects when the red object enters the scene? Model: no Label: no	Q: Which of the following is not responsible for the collision between the red object and the gray sphere? 1. the presence of the gray cube 2. the collision between the red object and the cyan object 3. the rubber cube’s entering the scene 4. the presence of the cyan object Model: 1, 3 Label: 1, 3	Q: What will happen next? 1. The gray cube and the brown object collide 2. The red object collides with the rubber cube Model: 2 Label: 2	Q: If the cylinder is removed, which of the following will not happen? 1. The gray cube and the brown cube collide 2. The red object and the cyan object collide 3. The red sphere and the rubber cube collide 4. The cyan object and the brown cube collide Model: 1, 4 Label: 1, 4
Q: How many rubber objects are moving? Model: 3 Label: 3

Q: How many objects are stationary when the sphere enters the scene? Model: 1 Label: 1	Q: Which of the following is not responsible for the yellow object’s colliding with the green object? 1. the presence of the purple sphere 2. the blue object’s entrance 3. the collision between the blue object and the rubber cube 4. the sphere’s entering the scene Model: 2, 3 Label: 2, 3	Q: What will happen next? 1. The sphere collides with the rubber cube 2. The yellow cube and the green object collide Model: 1 Label: 1	Q: Which event will not happen if the green cube is removed? 1. The yellow object and the blue object collide 2. The sphere collides with the blue cube 3. The sphere and the yellow object collide 4. The sphere collides with the yellow cube Model: 2 Label: 2
Q: What is the shape of the last object that enters the scene? Model: cube Label: cube			Q: Which of the following will happen if the yellow object is removed? 1. The blue cube and the green cube collide 2. The sphere collides with the blue cube 3. The sphere collides with the green cube Model: 1, 3 Label: 1

E.2 CATER

We include ten random videos from the validation subset of the static camera CATER dataset. In the final frame of the video, the correct grid cell of the target snitch is drawn in blue, and the model’s prediction is drawn in red. We note that the model is able to find the snitch in scenarios where the snitch is hidden under a cone that later moves (along with the still hidden snitch); in the sixth example, the model also handled a case where the snitch was hidden under two cones at some point in time.

Appendix F Dataset Licenses

The CATER generation code is available under the Apache License, and the ACRE generation code is available under the GPL license.