eprint Nisho-1-2024
Axion Detection with Quantum Hall Effect
Abstract
Plateau-plateau transition in integer quantum Hall effect is a phase transition between metal and insulator. The behavior how the width of the transition changes with temperature and frequency of radiations imposed has been explored extensively. It decreases with the decrease of temperature and frequency, but saturates at critical temperature or frequency. We have recently discussediwa the effect of axion dark matter on the saturation. The axion generates radiations under strong magnetic field in the experiment of quantum Hall effect. The radiations play a similar role to the one of radiations imposed externally. In this paper we discuss in detail how the width behaves in temperature and frequency under the effect of axion dark matter. We show that the axion effect can be observable in low temperature roughly below mK. According to our detailed analysis of the saturation, we find that critical frequency of saturation observed in previous experimentdoo ; doo1 strongly suggests axion mass eV.
I introduction
Finding axion dark matter is one of most significant issues in particle physics. It is the important step toward a new physics beyond the standard model of particle physics. It also gives rise to a solution of dark matter in the Universe. Axion is the Goldstone boson of Peccei Quinn symmetryaxion1 ; axion2 ; axion3 , which naturally solves strong CP problem. Such an axion is called as QCD axion. The axion mass is severely restricted such as eV Wil ; Wil1 ; Wil2 . In the present paper we only consider QCD axion and use physical units, , and . Our result is also applicable to dark photon with frequencies of microwaves discussed below.
The QCD axion produces electromagnetic radiations under strong magnetic field . The property is used for the exploration of the axion dark matter admx ; carrack ; haystac ; abracadabra ; organ ; madmax ; brass ; cast ; sumico ; iwazaki01 . Some of them have been proposed and many of them are undergoing at presentnew . Obviously, the radiations produced by the axion are also present in the experiments of quantum Hall effect. It is natural to expect that their effects may be observed in some of properties of quantum Hall effect, although they are quite weak. In particular, as we have shown in previous paperiwa , they may appear in much low temperature less than mK.
Quantum Hall effectvon ; girvin is realized in two dimensional electron system under strong magnetic field. The system shows various intriguing phenomena such as not only quantization of Hall resistance but also Josephson-like effectjoseph1 ; joseph2 ; joseph3 e.t.c.. Quantum Hall system has been extensively investigated since the discovery, but some of phenomena are not still fully understood. One of the phenomena is the saturationsat1 ; sat2 ; wanli ; sat3 ; sat4 ; sat5 ; sat6 of the width in plateau-plateau transition of integer quantum Hall effect. The width defines the range of the magnetic field within which plateau-plateau transition takes place.
Plateau-plateau transition in integer quantum Hall effect is a phase transition between metal and insulator. It has been extensively explored and the width in the transition has been shown to follow a scaling law such as with deltaB as . It has also been shown experimentally that the width saturates in low temperature, that is, it never decrease more with the decrease of temperature; below a critical temperature. In general, the saturation is considered to arise owing to finite size effect of two dimensional electrons, because the scaling is expected in infinitely large system. But recent experimentssat4 ; sat5 suggest that the saturation is caused by not finite size effect, but intrinsic decoherence, although the mechanism of the decoherence is still unclear.
Furthermore, similar scaling law holds when we imposed microwaves on Hall barengel ; balaban ; hohls ; saeed ; doo . That is, with as the frequency of the microwaves. It has been also observed that the width saturates at a critical frequency when we decrease the frequency of the microwaves just as in the case of the temperature. ( In actual experiments we use AC voltage for the measurement of the width. )
In our previous paperiwa , we have shown a possibility that the saturation arises owing to the effect of the axion dark matter. Especially, electromagnetic radiations ( actually, microwaves ) generated by the axion cause the decoherence of electrons in low temperature. Using the analysis, we have proposed a way of axion detection using microwaves imposed on Hall bar. In this paper, we discuss in detail how critical temperature and frequency of the microwaves at which the saturation arises, depends on the physical parameters like size of Hall bar, temperature and axion mass. According to the analysis, we propose more detailed way of the axion detection in the present paper than previous one. In particular, we present two conditions which critical frequency must satisfy in order to give the axion mass, i.e. . One is that does not depend on temperature and the other one is that does not depend on the size of Hall bar. Here we would like to point out that the previous experimentdoo ; doo1 using microwaves strongly suggests axion mass eV, because it seems that the critical frequency observed in the experiment satisfies two conditions presented in this paper.
Here we naively explain how the axion dark matter affects on plateau-plateau transition. We consider infinitely large two dimensional electrons at zero temperature under strong magnetic field. Owing to disorder potential, almost all electrons in each Landau levels occupy localized states except for electrons occupying extended state with energy located in the center of each Landau level. As magnetic field decreases, Fermi energy increases. As long as the Fermi energy is less than , Hall conductivity stays in a plateau. When Fermi energy passes the energy of extended states, Hall conductivity goes to next plateau so that the plateau-plateau transition looks like a step function. It is very sharp, i.e. . On the other hand, the axion dark matter generates radiations under the strong magnetic field so that the radiations are absorbed by electrons. Even if Fermi energy is below the energy , some of localized electrons transit to the states with energies larger than by absorbing the radiations. These electrons loose their energies by emitting phonons and may occupy the extended states with the energy . Thus, there is non zero probability of the extended state occupied even if . Therefore, the plateau-plateau transition becomes smooth function of magnetic field, i.e. . The smooth transition is not finite size effect. This is a naive explanation how the axion dark matter causes visible effect on the plateau-plateau transition.
We should mention that although thermal effect at contributes to the transition, the axion effect dominates over the thermal effect as long as temperature is very low. Indeed, we will show later that the axion effect is dominant approximately for mK.
In this paper we also propose a way of confirmation that the axion dark matter really causes the saturation in temperature or frequency of microwave imposed. Using parallel conducting slabs which sandwiches Hall bar, we shield radiations by the axion so that we expect the absence of the saturation of the width . ( Sometimes in literatures, the derivative at the center in the plateau transition instead of is used to see how it behaves with temperature or frequency of radiation. The saturation of corresponds to the saturation of . The decrease of corresponds to the increase of . )
In the next section (II), we briefly explain energy scale in integer quantum Hall effect and our notation used in the paper. We proceed to explain localization of electrons in quantum Hall effect in section (III). Most of electrons occupy localized states but a small fraction of electrons occupy extended states, which may carry electric current. The localization leads to plateau of Hall conductivity or resistivity in quantum Hall effect. In this section, using energy distribution of electrons at zero temperature, we discuss how Hall conductivity behaves and forms plateau according to the variation of magnetic field . We define width in plateau-plateau transition used in the paper. The dependence of the width on temperature or axion mass is discussed in later sections. In the section (IV), we briefly explain the axion dark matter. We consider QCD axion as dark matter candidate. We show how the axion generates electromagnetic radiations with energy under external magnetic field, which is used in experiment of quantum Hall effect. In the next section (V), we discuss in detail how the width depends on temperature and axion mass. We find that the saturation of in temperature only arises in the presence of the axion dark matter. Without the axion effect, the saturation does not appear even in the system with finite size. In the next section (VI), we discuss the effect of external microwaves on the plateau-plateau transition. We show how the width depends on frequency , temperature and axion mass. Especially, we show the presence of critical frequency below which the width does not depend on the frequency ( ). We present two conditions which the saturation frequency must satisfy to give the axion mass. In the section ( VII ), we estimate energy power generated by axion dark matter in two dimensional electrons. We compare it with thermal noise and find that the axion effect can be observable in low temperature less than mK, at least for the surface area of two dimensional electrons being large such as or larger. The axion effect becomes larger as the size of Hall bar becomes larger, because the energy of the axion received by electrons is bigger as the number of electrons becomes larger. In the final section ( VIII ), we propose a way how we confirm the presence of the axion effect in quantum Hall effect. The point is that we shield the radiations generated by the axion dark matter by using conducting slabs put around Hall bar.
II energy scale in integer quantum hall effect
We briefly explain energy scales relevant to quantum Hall effectgirvin . The quantum Hall effect is realized in two dimensional electrons of semiconductors under magnetic field . The states of the two dimensional free electrons are specified by integer , so called Landau levels. There are a number of degenerate states in each Landau level with the degeneracy ( i.e. number density of degenerate states in a Landau level ). The typical scale of the magnetic field is of the order of T. Each electrons oscillate with cyclotron frequency where mass denotes effective one of electron in semiconductors. Generally is much smaller than real mass MeV of electron, e.g. in GaAs. Then, cyclotron frequency ( energy ) is of the order of eV. Furthermore, their energies are specified with integer such that . The wave functions are extended with typical length scale, so called magnetic length . . It is cyclotron radius of electron under the magnetic field .
Electron possesses spin components with up and down so that each Landau level is split to two states with energies owing to Zeeman effect. Here we note that and Bohr magneton . Zeeman energy is of the order of eV. It is smaller than the cyclotron energy .
We mainly consider axion mass in a region so that the mass is smaller than Zeeman energy and cyclotron energy . The mass is of the order of or less than the width ( extension ) in Fig.1 of the energy distribution of electrons in a Landau level, as we will explain in next section. Therefore, because the energies of radiations produced by the axion are almost identical to , the effect of the radiations can be observable because electrons may absorb the radiations within a Landau level.
We use an index so called filling factor to specify which Landau levels are occupied; denotes number density of electrons ( typically, ). For instance, it implies Landau level with energy is fully occupied but Landau level with is partially occupied when .
It is remarkable featurevon ; aokiando ; halperin of quantum Hall effect that Hall resistance ( conductance ) is quantized such that ( ) with positive integer specifying Landau level. It is constant within a range when we vary the magnetic field ; . In the range, Landau levels up to are fully occupied, while the level with is partially occupied. That is, we see plateaus in the diagram of ( ) in . The plateaus arise owing to the localization of two dimensional electrons discussed soon below. The localization arises owing to disorder potential for electrons. That is, almost of electrons are trapped in the potential.
III localization of two dimensional electrons
We explain localization of two dimensional electrons under strong magnetic field . In the case of free electrons we have the density of state . But, there are impurities, defects e.t.c. in actual materials. They lift up the degeneracy in Landau level. Electrons are severely affected by a disorder potential . Most of electrons are localized and they cannot carry electric currents. But, a small fraction of them are not localized so that they can carry electric current. It means that Hall resistance only receives the effect of non-localized electrons. Localized electrons do not contribute to Hall resistance. The essence in integer quantum Hall effect is the presence of non-localized ( extended )aokiando ; ono states of electrons under strong magnetic field . Although the disorder potential localizes almost of all electrons, there exist a non-localized state with energy . According to numerical simulations we find that in the presence of a potential , the density of states has finite width around the energy shown schematically in Fig.1. In the figure we show localized states and extended states. Extended localized state is located at .
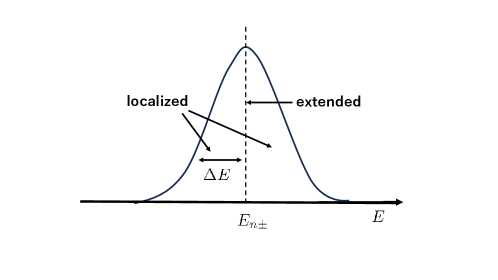
The density of state has finite width owing to the potential . It is generally supposed that the width is less than the cyclotron frequency in strong magnetic field . That is, the potential energy is much smaller than the cyclotron frequency: ( eV with T ). For instance, with andouemura . Furthermore, it is supposed that the potential has the same amount of attractive and repulsive components. So, the form of is symmetric around the center as shown in Fig.1.
We may define coherent length as the size of localized state. It depends on the energy of the state. Then, the referencesaoki1 ; aoki2 have shown in the system with infinitely large size that a coherent length diverges such as as with . It implies that there are extended states with their energy .
When Fermi energy is less than but larger than , the energies of electrons occupying extended states are equal to or with . For instance, for , Hall resistance is given such that . As long as the Fermi energy is in the range , the Hall resistance does not vary with magnetic field . A plateau is formed. On the plateau, we have vanishing longitudinal resistance . Only electrons in extended states with energies such as and carry electric currents. When the electron occupies the extended states with the energy , it carry electric current. Then, Hall resistance suddenly down to , or Hall conductivity rises up to from . The transition is sharp like the step function. Hereafter, we mainly state Hall conductivity because it is easy to see the effect on the conductivity of electrons carrying electric currents. Generally, electric conductivity is proportional to electron density carrying electric current.
It should be noticed that even if a single electron occupies the extended states with the energy , the Hall conductance jumps to the next plateau, for instance, from . This is a striking feature of quantum Hall effect. The feature is understood in topological argumenttopology1 ; topology2 . Hereafter, we examine in detail the case of for concreteness.
The above argument only holds in Hall bar with the infinite large size. Extended states only have the energies . In actual Hall bar with finite size, localized states are present whose sizes are larger than the size of Hall bar. Because of the divergence of coherent length as approaches , we understand the presence of such localized states with their sizes larger than Hall bar. Electrons in such states have energies in the range where depends on the size of Hall bar such as . In general is smaller than the width in . We may call such states as extended states because electrons in the states can carry electric current.
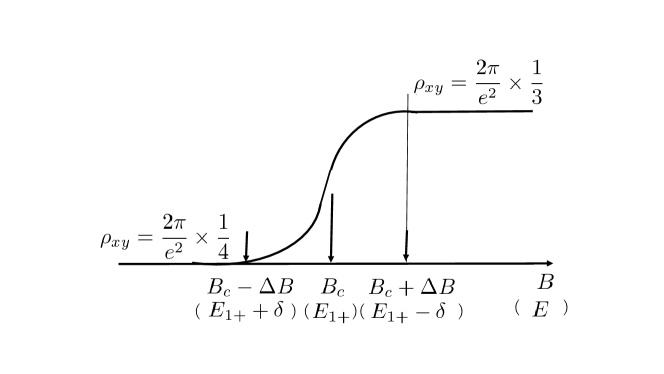
In Hall bar with finite size, plateau-plateau transition takes place smoothly. When Fermi energy increases, but stay less than , Hall conductivity stays in a plateau. However, when it reaches at the energy , the transition begins and the conductivity increases smoothly as increases. takes the value of at . When , the magnetic field is given by . Eventually when reaches at , the conductivity stops to increase and stay at next plateau. takes the value of at . Thus, we have . The plateau-plateau transition mentioned here is the one in Hall bar with finite size at zero temperature . See Fig.2. In the figure, we define the width between two plateaus. The Hall resistance begins to decrease at and the decrease stops at . In our discussion we use the width as specified in the figure.
IV axion dark matter
The axion is a Nambu Goldstone boson associated with Peccei Quinn symmetry introduced for solving strong CP problem. The symmetry is imposed in a model beyond the standard model, but it is spontaneously broken. As a result, the axion appears. The axion as the boson axion1 ; axion2 ; axion3 acquire its mass due to instanton effects in QCD. Because the axion couples with electromagnetic fields with coupling , Maxwell equations are modifiediwazaki01 in the following,
| (1) |
with electric and magnetic fields, where we take the axion field as the one representing the axion dark matter.
From the equations, we obtain the electric field generated by the axion under static external magnetic field . Namely, when magnetic field is present, the axion dark matter generates oscillating electric field . Because the parameter is extremely small as shown soon below, we obtain
| (2) |
with , where denotes fine structure constant and is axion decay constant satisfying the relation GeV in the QCD axion. The parameter depends on the axion model, i.e. for DFSZ modeldfsz ; dfsz1 and for KSVZ modelksvz ; ksvz1 . The mass of the QCD axion is severely restricted such as eV, Wil ; Wil1 ; Wil2 . In the present paper we mainly consider the mass . We should mention that the parameter is automatically determined in QCD axion when we take the value of the axion mass, i.e. GeV.
The amplitude of the axion dark matter is extremely small. ( The momentum of the axion dark matter is of the order of so that we may neglect the momentum. ) Supposing that the dark matter in the Universe is composed of the axion, we find that the local energy density of the dark matter is given as ; denotes time average of the quantity . Then we find that . Although the electric field sikivie ; iwazaki01 is extremely small, it is inevitably produced in the experiment of quantum Hall effect because of the presence of magnetic field T. This oscillating electric field generates electromagnetic radiationsiwazaki01 from conductors. It makes electrons in metals oscillate so that the oscillating electrons emit electromagnetic radiations. Indeed, Hall bar is surrounded by metals composing mixing chamber for cooling the Hall bar, superconducting magnet e.t.c. The frequency ( wave length ) of the radiations is given by the axion mass, ( ). Such radiations are absorbed by electrons in Hall bar and they affect on the width in plateau-plateau transition, which is our main concerns in the paper.
V axion and plateau-plateau transition
We explain in detail how the width depends on axion mass and temperature. First we suppose the system at zero temperature. Then, the energy distribution of electrons has sharp boundary at Fermi energy when axion effect is neglected. That is, the states with energies less than are fully occupied and the states with energies larger than are empity. Thus, when Fermi energy is less than , electric current does not flow and the conductivity stays in the plateau, . Hall resistivity takes the value . When external magnetic field decreases, Fermi energy increases and reaches at the value . Then, electric current begins to flow because extended states with energies larger than begin to be occupied. The conductivity begins to increase or Hall resistivity decreases. As decreases more, Fermi energy increases. When the Fermi energy goes beyond , the conductivity takes the value and stay in the next plateau, or Hall resistivity takes . Thus, the width is determined by the magnetic field at which . The width between and , leading to is
| (3) |
We see the plateau-plateau transition of Hall resistance schematically shown in Fig.2.
When the temperature , the energy distribution of electrons has no sharp boundary at chemical potential . The boundary is smeared out by thermal effect around chemical potential . Because we only consider low temperature K, we approximately set . Although the distribution has no sharp boundary, we may approximately define the effective temperature such that the distribution has sharp boundary at . Electrons occupy the states below the energy and the states with energies larger than are empty. Especially, the distribution is smeared out over the width schematically shown in Fig.4. Such a simplification arises from the fact that the real energy distribution of electrons decreases exponentially for . Owing to the simplification, we can easily understand how the width depends on temperature. We should note that the temperature is not real temperature and it depends on the density of state . Thus, when we set , the constant depends on real density of state . We expect that is of the order of .
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/dedb0a4f-9096-499e-979e-c7bfed2800f5/x3.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/dedb0a4f-9096-499e-979e-c7bfed2800f5/x4.png)
|
Then, the width is determined in the following. That is, as decreases, increases. When is equal to , electric currents begin to flow. That is the point at which the conductivity begins to increase, i.e. . As decreases more, Fermi energy passes the energy and eventually, reaches at , see Fig.4. At the point, the conductivity stops to increase and stay in next plateau. It is the point . In other words, Fermi energy moves from to in the plateau-plateau transition. The width is given by
| (4) |
Obviously, the width corresponding to decreases as temperature ( or ) decreases. It takes the value when . It never saturate at non zero temperature. We should make a comment that the dependence of on or temperature is expected such that with deltaB as according to the scaling analysis, at least in the case of infinitely large Hall bar, i.e. . Thus, is such as as in the infinitely large Hall bar.
In addition to the decrease of the width with temperature, the width decreases as size of Hall bar increases. That is, decreases with , which decreases as the size of Hall bar increases. The phenomena have been well known.
Here we make a comment of the effect of our simplification of sharp boundary at in energy distribution of electrons. Even if we do not take such a simplification, there is no critical temperature of saturation. That is, the width defining the difference between a starting point and its ending point of the increase of , smoothly decreases as real temperature decreases. This is because the effect of the temperature on the energy distribution smoothly decreases as decreases. It never arise that the width does not decrease below a non zero temperature. Therefore, the presence of the saturation cannot be explained simply by finite size effect.
Here we explain thermal effect on . Although depends on length scale of Hall bar, effectively extended states in which electrons carry electric current are not restricted to the energy region such as at non zero temperature. For sufficiently low temperature, phase coherent length is much larger than the scale of Hall bar. The phase coherence lengthdoo1 is the length scale within which quantum states hold keeping quantum coherence. As temperature increases, the phase coherent length decreases and eventually reaches at the physical size of Hall bar. There is a critical temperature such that at the temperature , the phase coherent length is equal to . Beyond the temperature, the coherent length becomes smaller than the physical size of Hall bar. It implies that actual extension of localized states diminishes up to the phase coherent length. It apparently seems that electric current does not flow because all of localized states have extension less than the size of Hall bar. But, electrons in the localized states with spatial extension less than may make hopping to to nearby localized states and carry electric current. The hopping arises owing to scattering with phonon or impurities or tunneling under external electric field. It does not arise between localized states with large energy difference among them. In this way, electrons in the localized states even with their energies less than may carry electric currents at temperature . As temperature increases more, the phase coherent length decreases more and the hopping of electrons gets more actively. Thus, the energies of effectively extended states becomes smaller than . It implies that we have effective width instead of real such that for and for . increases as increases. Thus, the effective extended states at are defined as those with energies
| (5) |
with given such as .
In the above argument, we need to replace by the effective width or ,
| (6) |
It decreases smoothly as decreases. It takes the value below and reaches as . Therefore, we find that never saturate for any temperature when axion effect is absent. The width corresponding to also does not saturate. It behaves such as as with a numerical constant .
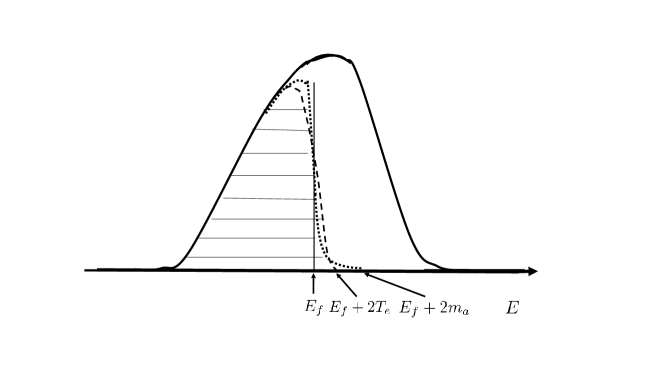
Now we take into account the axion effect. The dark matter axions produces radiations with energy under strong magnetic field. Such radiations with their energy are absorbed by electrons, which make electrons transit from the state with energy to the state with energy . The electrons in the state with energy may loose their energies by emitting phonon. This is similar process to the one that electron with energy transits to the state with energy by absorbing thermal energy and it loose its energy by emitting phonon. ( We note that black body radiation with energy is absorbed by electron just as radiation generated by axion. ) Consequently, the energy distribution of electrons is smeared out. But, the effect only slightly modifies the energy distribution because the axion effect is quite small. It is not important for later discussion to specify precisely how large the axion effect smears the energy distribution when temperature is low sufficiently for axion effect to be dominant over thermal effect. We only need to know the energy at which the energy distribution has sharp boundary. Thus, we simplify the effect of the axion such that the energy distribution smeared by axion also has a sharp boundary in the following. When , the sharp boundary caused by thermal effect does not change even if the axion effect is taken into account. There are no occupied states with energies larger than ( ). On the other hand, when , sharp boundary moves upward beyond . That is, there are occupied states with energies larger than , while states with energies larger than are empty. Consequently, the sharp boundary is located at ( ) when , while at when . See Fig.5. Similarly to the case of temperature , the axion mass in the energy distribution of electrons is not necessarily equal to real axion mass. But, when we discuss the effect of microwave imposed externally on Hall bar in later section, the microwave plays the similar role to the radiation by the axion. Energy distribution of electrons modified by the radiation is supposed to have sharp boundary associated with the frequency of the radiation. Both radiations by axion and external setup are supposed to cause sharp boundary on the energy distribution such as the boundary located at or when or . In this case we may directly compare the frequency with axion mass as real ones.
Later we estimate how the axion effect is large compared with thermal effect. We note that black body radiation present at gives similar effect to the one of radiation generated by the axion. It will turns out that the axion effect is dominant over the thermal effect when ( not ) as long as real temperature is less than mK, when axion mass eV. When temperature is much larger than mK, the energy distribution of electrons has no contribution of axion. So even for , the sharp boundary is located at when real temperature is larger than mK. But we must remember that it is unclear what is the value corresponding to real temperature mK. The relation depends on each samples.
Now we explain how the width depends on axion mass and temperature. We discuss it in the cases of and separately. First, we start the case of .
When the temperature is larger than the axion mass , the energy distribution of electrons is almost identical to the previous one with no axion effect. Thus, the width is given in the way mentioned above. Namely, the width leading to is given such that for . The width decreases as decreases up to when . At temperature ( ), it takes . It further decreases as decreases up to . When , the width is given such that because the energy distribution of electrons has sharp cutoff at . does not depend on . Thus, the width saturates at when . That is, is given in the following,
| (7) |
in the Hall bar with . It saturates at and takes the value . When we decrease the size of Hall bar ( increase ), the saturation temperature does not change, while the width corresponding to increases.
Next, we discuss the case of . The width is given such that for , while for . Obviously, it decreases with , but saturates at because . The width is given such that for . That is, is given in the following,
| (8) |
in the Hall bar with . It saturates at and takes the value . See Fig.6. The saturation temperature depends on the size of Hall bar.
To be summarized, the saturation temperature and the width of at are given in the following. When
| (9) |
while, when
| (10) |
We should notice misunderstanding that from the above formula , the observation of the saturation temperature give real axion mass. As we have stated, the temperature in the formula is not real temperature, although it is not far from real temperature . The formula in eq(9) implies that the saturation temperature does not depend on the size of Hall bar. On the other hand, the formula implies that the saturation temperature depends on the size of Hall bar. In order to find the saturation temperature , we must check the independence of on the size of Hall bar.
Although the above result shows that the saturation temperature is equal to or less than the axion mass in any cases, it is possible to have real saturation temperature large such as KeV, which is larger than axion mass eV expected later in the present paper.
In the previous paperwanli , it has been shown that as the size decreases, both of the saturation temperature and the width corresponding to increases. Indeed, it has been observed that . It indicates that . It has been understood that the saturation is caused by finite size effect. According to our analysis, such a feature of the saturation suggests that the sample used in the paper has the feature . ( The real saturation temperatures in the paper are in the range . )
On the other hand, it has been shown in the referencesat5 that the saturation temperatures in samples with sizes mm, mm and mm are almost identical ( real temperature mK ). Obviously, finite size effect does not appear. Thus, it has been stated in the referencesat5 that the feature is caused by intrinsic decoherence. On the other hand, according to our analysis, these samples may have the feature of and the saturation temperature is given by the axion mass, . Therefore, the saturation, in other words, the intrinsic decoherence observed in the paper is caused by the axion dark matter.
The papersat5 suggests that the axion mass is given by the real saturation temperature mK. Although the temperature is not identical to the axion mass . it suggests that it is near to the axion mass. Later we will find that the axion mass is strongly suggested to be equal to ( mK ) by experiments using microwaves imposed on Hall bar.
VI external microwave and determination of axion mass
We proceed to discuss the effect of external microwave imposed on Hall bar. We would like to know how the width ( or ) depends on the frequency of the microwave. Contrary to the observation of saturation temperature , it will turn out that we can determine the axion mass by observing the saturation frequency of .
The effect of the microwave is identical to the one of radiation generated by the axion. The difference is that we can change frequency and power of the microwave. The power is in general much larger than the power generated by the axion. The energy distribution of electrons is modified significantly, but its power must be taken small enough not to increase the temperature of the Hall bar. In actual experiments, the power has been taken sufficiently small for the temperature not to increase.
We also simplify the effect of the radiations similarly to that of radiation generated by the axion. That is, they modify energy distribution of electrons such that there is a sharp boundary in the distribution. For instance it has sharp boundary at the energy when . The states with energies larger than are empty. On the other hand, it has sharp boundary at the energy when .
We should make a comment that although the frequency used to define the sharp boundary is not real frequency, the formula obtained in subsequent discussions gives real axion mass by observing the real frequency in the experiment using external microwave. This is because both effects of radiations generated by axion and experimental apparatus are identically simplified on energy distribution of electrons. Therefore, the formula obtained later implies that the real frequency is equal to the real axion mass divided by .
We remind that the effect of external microwave on the width is very similar to the effect of temperature, as shown experimentally. For example, for and for with doo1 . The behavior is expected in scaling theory as a critical behavior. The external microwaves with frequency diminish phase coherent length just as thermal fluctuations in temperature diminish it with correspondence . Thus, we may take the effect of the external microwave on electrons in a similar way to the one of temperature.
The similarity can be understood by comparing the effect of the radiation with thermal effect. Electrons absorb thermal energy and transit to states with higher energy, but they lose their energies emitting phonons. Similarly electrons absorb radiation energy and transit to states with higher energy, but they lose their energies emitting phonons. Only difference is that the thermal energy distributes around , while radiation energy is given by a single frequency . Thus, we expect that both effect of temperature and radiation is almost identical.
Here we should notice that external microwaves makes the coherent length of electrons decrease just as temperature does. Thus, depends not only on temperature but also frequency of microwave such that increases as or increases with the condition and . It is naturally supposed that there is a critical frequency such that for . That is, does not decrease even more in for . It saturates at the critical frequency when frequency decreases. In other words, the energy region of the effectively extended states does not change as long as . The critical frequency decreases with the decrease of the temperature . Furthermore, for the temperature , does not decrease less than . Namely, phase coherent length at temperature and frequency is larger than the size of Hall bar. That is, for .
Therefore, we speculate the dependence of on temperature and frequency in the following,
| (11) |
Based on the speculation, we examine how the width leading to behaves depending on temperature and frequency .
As discussed before, we discuss two cases of Hall bar separately. One is Hall bar with , that is, Hall bar with small size of length. The other one is that with , that is, Hall bar with large size.
First we consider the case . When high temperature , the energy distribution of electrons is modified by the microwave with frequency such that its sharp boundary is located at for or for . Thus, the width is given in the following,
| (12) |
We can see that the width decreases with the decrease of the frequency , but it saturates at the frequency when , while it does at when . In both cases, . Therefore, in the case , both of saturation frequency and decrease with the decrease of the temperature .
On the other hand, in the case, low temperature ( ), we have
| (13) |
When , we have two cases,
| (14) |
because for .
The width saturates at where . While, when , according to the equation(13), the width saturates at where . Therefore, in the case ( ), both saturation frequency and does not decrease with temperature .
Furthermore, in the case, middle temperature ( ), we have
| (15) |
When , we have two cases,
| (16) |
The width saturates at where . While, when , the width saturates at where . Therefore, in the case ( ), the saturation frequency decrease, but does not decrease with the decrease of the temperature.
Secondly, we consider the case , i.e. Hall bar with large size. Similarly to the above argument, we consider two cases separately, that is, the case of high temperature and the case of low temperature . Then, we find the following results.
For sufficiently high temperature , we have
| (17) |
When , it saturates at the frequency where . While, when , it saturates at where . Therefore, in the case , both of saturation frequencies and decrease with the decrease of the temperature . Similarly, the width at saturation frequencies decreases with the decrease of .
The saturation frequency is possibly less than , while is larger than . Indeed, the cases with the saturation frequency GHz have been observed in previous papersbalaban ; hohls , in which temperature is much larger than mK. It may correspond to the case of the saturation frequency or . Furthermore, the referencebalaban shows that .
For low temperature , but ( that is, ), we have
| (18) |
When , it saturates where the width deceases with the decrease of . While, when , it saturates at where the width decreases as the temperature decreases up to .
On the other hand, for sufficiently low temperature ( i.e. ), when , we find that the width saturates at where because , while when , it saturates at . In both cases, at the saturation. Therefore, the width corresponding to as well as the saturation frequency or does not decrease with .
To be summarized,
when
for ,
| (19) |
for ,
| (20) |
for ,
| (21) |
when ,
for ,
| (22) |
for ,
| (23) |
for ,
| (24) |
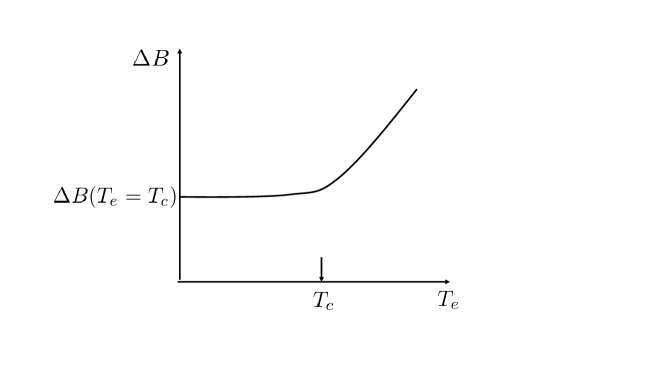
According to these results, we find how we determine the axion mass by imposing microwaves on Hall bar. By searching the critical frequency , we can determine the axion mass. First, we need low temperature such as . Probably, it would be sufficient that the temperature is less than mK. This can be expected from the referencesat5 we have mentioned in the section(V). The reference shows that the independence of the saturation temperature on the size of Hall bar is realized at low temperature mK. Furthermore, there are two conditions which must be satisfied for critical frequency to be equal to . The first condition is that the frequency does not decreases with the decrease of temperature. The condition is satisfied by both and . Second one is that the frequency does not change with the change of the size of Hall bar. The condition is only satisfied by . In this way we can determine the axion mass with experiment of quantum Hall effect using microwaves. In Fig.7, we schematically depict the curves of the width with temperatures and corresponding to the cases of equations (23) and (24).
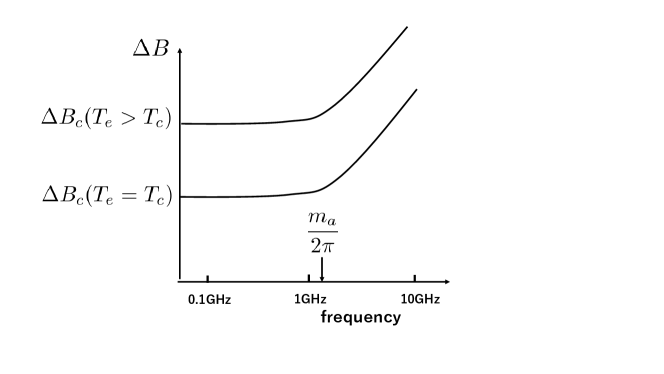
There have been several experiments using microwaves. Among them, the referencebalaban shows that saturation frequency is proportional to temperature, i.e. . The frequency varies roughly from GHz to GHz corresponding to the temperatures mK, mK, and mK. The temperatures may be larger than the axion mass . Their widths also decrease with the decrease of the temperature. The data correspond to either of the case in eq(19), eq(20) or eq(22). That is, and or .
It appears in the referenceengel that saturation frequency GHz does not change for temperatures mK, mK and mK, although the reference involves ambiguities due to few data points. Furthermore, it shows that decreases with the decrease of temperature. These data would correspond to the case in eq(23). That is, and with . The experiment suggests the axion mass eV.
It is notable that an experimentsaeed ; doo ; doo1 performed in temperature mK has fine resolution of the frequency. It has shown that the saturation arises at the frequency GHz. Furthermore, almost identical frequency is observed in two samples with different sizes. One has length mm, while the other one has mm both with the identical width m. Additionally, it has been stated in the referencesaeed ; doo ; doo1 that the temperature mK is sufficiently low for temperature dependent effect to be negligible. It might imply that small change of the temperature does not cause the change of their result. Therefore, the saturation frequency GHz satisfies two conditions mentioned above. The experiment corresponds to the case in eq(21) or eq(24). That is, and . It also show the result consistent with . The width corresponding to increases with the decrease of the Hall bar size. The experiment strongly suggests that the mass of the dark matter axion is given by eV.
It is interesting to see our previous prediction of axion mass ( eV ) derived with our modelaxionstar ; axionstar1 of fast radio burst. The fast radio burst is radio burst observed with various frequency range GHz and its energy is extremely large of the order of GeV. The duration of the fast radio burst is short such as millisecond or less. The fast radio burst arrives from far Universe. Our model is that the burst is generated from the collision of axion star with neutron star or magnetized accretion disk of black hole. The axion star is a composite of gravitationally bound axions. The radiations are generated by the axion star under strong magnetic field G of neutron star or magnetized accretion disk. Because ionized gases emitting the radiations are high temperature, the line spectrum is affected by Doppler broadening so that they have wide range of frequencies. They also receive gravitational red shift or red shift due to expanding Universe. Furthermore, they receive red or blue shift due to the rapid rotation of the accretion disk around black hole. These effects make the line spectrum generate the wide spectrum GHz. We have predicted by analyzing spectra of fast radio burst in our model that the axion mass is roughly equal to eV, which is coincident with the above result.
VII axion domination over thermal noise
We have assumed in the previous discussion that the energy distribution of electrons with energies larger than temperature is determined by axion effect when . In this section we would like to confirm it by estimating energy power in Hall bar generated by the axion dark matter. We compute its signal noise ratio. The noise arises owing to black body radiation. It turns out that the axion effect dominates over thermal noise when and the temperature is less than mK.
The axion dark matter generates radiations under strong magnetic field . Two dimensional electrons in Hall bar absorb the radiations and transit from localized states to effectively extended states. The electrons in the effectively extended states carry electric currents so that Hall conductivity increases when such transitions arise. We discuss a transition from an electron in a state with energy less than to the state with energy ( ). The wave function of a state with energy in a Landau level is given by,
| (25) |
with , where denotes Hermite polynomials. The momentum characterizes degenerate state in a Landau level without disorder potential . The function is taken such that the wave function is an eigenstate of electron’s Hamiltonian with potential . Normalization is such that that . The state is characterized by index . Here we assume no mixing between different Landau levels or different spin states. The disorder potential is supposed to be much less than the energy difference between different Landau levels or different spin states.
Electron in the state transits to a state with energy by absorbing radiation. The transition amplitude is proportional to
| (26) |
where ( ) denotes a length scale of overlapping region of two states and ; . with polarization vector pointing in two dimensional plane of Hall bar with .
The number of electrons making transitions per unit time by absorbing the radiation from states with energies lower than ( ) to states with energies larger than is given by
| (27) |
with surface area of two dimensional electrons. denotes density of state. We explicitly use the formula,
| (28) |
with , where represents the number density of electrons in a Landau level; . The width width is of the order of eV. Tentatively, we take eV. Here we consider the energy region of effectively extended states such that , assuming zero temperature or much less than ; for .
We consider the transition of electrons with the energy ( ) to the states with the energy in the range . When , such a transition does not arise. So, Hall conductivity does not increase. But when Fermi energy increases and take a value as , such a transition begins to arise. The Hall conductivity also begins to increase. Further increase of Fermi energy makes the Hall conductivity larger. Eventually, the conductivity arrives at the next plateau when Fermi energy reaches .
For simplicity, we assume in the estimation of that the length is independent of the states and ; . Then, the energy power of the axion absorbed in Hall bar is given by
| (29) | |||||
with because of our choices and eV. We have put with . Thus, the integral is trivial , in which the integration is taken over the range . for , otherwise . We have taken that Fermi energy in the above estimation and so with our choice . We have tentatively assumed that the surface area of two dimensional electrons and the length scale, of the overlapping between localized states and effective extended states. We remember for DFSZ axion model and for KSVZ axion model.
We compare it with thermal noise by taking identical Fermi energy . The energies of the black body radiations are approximately restricted to be smaller than the temperature ; . Localized electrons with energies less than Fermi energy can be transited to effective extended states by absorbing the radiations only when . These electrons contribute Hall conductance. Thus, when the temperature is sufficiently large such as , the radiations with the energies in the range, , are absorbed and the Hall conductance increases. The energy power of the thermal noise is given by . On the other hand, when the temperature is less than , the black body radiations do not contribute the increase of the Hall conductance. ( Even if localized electrons absorb the radiations, they are only transmitted to localized states, not to effective extended states. )
Therefore, the increase of the Hall conductance is only caused by the axion dark matter when temperature and axion mass satisfy the condition . The thermal noise does not contribute to the Hall conductance. This is the case in the previous section that the width is given by .
When the temperature increases larger than , black body radiations also contribute to the increase of the Hall conductance. Then, we need to find which contribution is dominant, axion effect or thermal one.
We compare the energy power of axion with thermal noise, . In order to do so, we take Fermi energy such as which is identical to the one used in the estimation of in eq(29).
SN ratio is given in the following,
| (30) | |||||
with mK ( eV ) and eV ( mK ), where we have assumed that it takes one second for each measurement of Hall conductance for given magnetic field . The result holds for , otherwise, it is proportional to , not .
The result of the SN ratio means the following. We have supposed in the estimation that and Fermi energy . There are electrons occupying effective extended states with energies ( ). They are transited from localized states by thermal effect or axion effect. Among them, electrons with energies larger than arise only due to the axion effect, while the other ones with energies ( ) arise due to both effects. The point is that the thermal effect does not produce electrons with energies larger than . This is because the black body radiations with energies ( ) have been supposed to be suppressed in the estimation. Actually, as the estimation shows, the axion effect is dominant over the thermal effect when at least when temperature is less than mK. The result is coincident with our previous discussion. However, actual effects of black body radiations does not vanish even for and it vanishes exponentially . So, the thermal effect for is still present although it is small. Indeed, thermal effect is present even for such that it decreases smoothly for mK. Because the width ( =mK ) is small, the dominance of the axion effect still holds. Obviously, the thermal effect with mK vanishes exponentially. Therefore, as we have supposed, the thermal effect is not dominant for the phenomena with energy scale larger than as long as and mK. Namely, when , electrons with energies larger than are transited from localized states only by the axion effect. The argument has been used extensively in the above sections.
We should make a comment that the above result heavily depends on the assumption of ( with ). That is, the overlapping region between localized state with energy and extended state with energy is comparable to the size of Hall bar. For instance, when the ratio of side lengths of a rectangular Hall bar is such as and its surface area , the largest side length is about cm. Thus, the length of the overlapping region cm is about of the largest side length. It implies that the extended state has length equal to the size of Hall bar, while the localized state with energy by eV less than the energy of the extended state, has length scale of the side length of the Hall bar. If the overlapping region is smaller than of the side length, we need lower temperature than mK for the axion effect to dominate the thermal effect.
We may examine the validity of the assumption in the following. For instance, supposing eV ( ), the minimum energy of the localized state able to transit to extended state by absorbing radiation with energy eV is given by eV. According to the scaling formula for , of coherent length of the state with energy , we find that the ratio of the scale of the localized state with energy eV to that of extended state with energy eV is about . Because the extension of the extended state is equal to or larger than the physical size of Hall bar, the size of the localized state is about of the size of Hall bar. Therefore, the choice of in the above estimation is reasonable.
Anyway, in order for the axion effect to dominate over thermal effect, we need low temperature. Namely, in order to find the axion mass in a way mentioned above, it is favorable to have large Hall bar with surface area like and low temperature less than mK. Under these consideration, we understand that the experimentsaeed ; doo ; doo1 is appropriate for the search of axion, which suggests the axion mass eV. The device in the experiment is cooled down mK and two dimensional electrons have much larger surface area than . Indeed, a coplanar waveguide with length mmcm and width mcm is used in the experiment. So, .
VIII confirmation of presence of axion dark matter
When we decrease temperature, the saturation of the width arises at a critical temperature or ( ). As we have discussed, such a saturation is caused by the axion. Without the axion, the behaves such that as ( c denotes a constant. )
In order to examine whether the saturation is really caused by the axion, we diminish the effect of the radiations produced by the axion. In our previous paperiwa , we have proposed the way of the examination. We use two parallel conducting slabs such that they are put parallel to magnetic field. Such conducting slabs shield the radiations produced outside the plates. Furthermore, the conducting plates themselves produce radiations by the axion. But the electric fields of the radiationsiwazaki01 produced between the slabs are perpendicular to two dimensional electrons. Such radiations are not absorbed in the Hall bar because excitation energies of two dimensional electrons in the direction perpendicular to the Hall bar have much larger than the axion energy. Therefore, we can make to diminish the axion effect using the slabs, and we will see that the width may not saturate at a critical temperature; it behaves such as as .
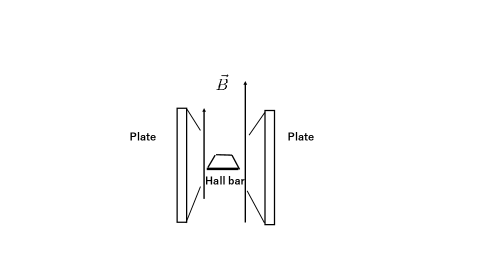
IX conclusion
We have discussed the effect of the axion dark matter on integer quantum Hall effect. In particular, we have discussed the effect on plateau-plateau transition. The width between two plateaus decreases with the decrease of temperature. But, it saturates at a critical temperature. We have shown that the saturation takes place owing to the axion effect. Furthermore, similar saturation of the width arises in frequency when we impose microwaves. By analyzing the axion effect on the saturation frequency , we have presented two conditions which must satisfy to give the formula . The first condition is that does not change with the temperature. The second one is that does not change with the size of Hall bar. Such a saturation frequency should be studied in low temperature less than mK with surface area of Hall bar larger than . This is because the axion effect dominates over thermal noise in such low temperature and large surface area.
It is remarkable to notice that such a saturation frequency has been obtained in previous experimentdoo ; doo1 with low temperature mK and large sample such as mmm. The frequency has been obtained with high resolution of frequency. Although it is not clear whether or not one of two conditions is satisfied, it strongly suggests that the axion mass eV. The condition not still confirmed is that does not change with temperature. A similar frequency of saturation has been also observed in another experimentengel , although the number of data sample is few and resolution of frequency is low.
Finally, we propose a way of the confirmation that the axion dark matter really causes the saturation. Using two parallel conducting flat plates put parallel to magnetic field as shown in Fig.8, we can diminish the axion effect on the two dimensional electrons. By diminishing the effect, we may observe that the width does not saturate at a nonzero temperature. It behaves such as as .
The author expresses thanks to A. Sawada for useful comments. This work is supported in part by Grant-in-Aid for Scientific Research ( KAKENHI ), No.19K03832.
References
- (1) R. D. Peccei and H. R. Quinn, Phys. Rev. Lett. 38 (1977) 1440.
- (2) S. Weinberg, Phys. Rev. Lett. 40 (1978) 223.
- (3) F. Wilczek, Phys. Rev. Lett. 40 (1978) 279.
- (4) J. Preskill, M. B. Wise and F. Wilczek, Phys. Lett. 120B (1983) 127.
- (5) L. F. Abbott and P. Sikivie, Phys. Lett. B120 (1983) 133.
- (6) M. Dine and W. Fischler, Phys. Lett. B120 (1983) 137.
- (7) P. Sikivie, Phys. Rev. D32 (1985) 2988.
- (8) T. Braine et al, Phys. Rev. Lett. 124, (2020) 101303.
- (9) K. Yamamoto, et al. hep-ph/0101200.
- (10) L. Zhong, et al. Phys. Rev. D97 (2018) 092001.
- (11) J. L. Ouellet, et al. Phys. Rev. Lett. 122 (2020) 12, 121802.
- (12) B. T. McAllister, et al. Phys. Dark Univ. 18 (2017) 67.
- (13) X. Li, et al. PoS ICHEP2020 (2021) 645.
- (14) D. Horns, J. Jaeckel, A. Lindner, A. Lobanov, J. Redondo, and A. Ringwald, JCAP 04 (2013) 016.
- (15) V. Anastassopoulos, et al. Nature Phys. 13 (2017) 584.
- (16) R. Ohta, et al. Nucl. Instr. Meth. A670 (2012) 73.
- (17) A. Iwazaki, PTEP 2022 (2022) 2, 021B01.
- (18) D. Antypas, et. al. arXiv:2203.14915.
- (19) A. Iwazaki, Phys. Lett. B 846 (2023) 138242.
- (20) K. v. Klitzing, G. Gorda and M. Pepper. Phys. Rev. Lett. 45 (1980) 494.
- (21) R. E. Prange and S. M. Girvin, Springer Verlag, New York(1987).
- (22) X. G. Wen and A. Zee, Phy. Rev. B 47, (1993) 2265.
- (23) Z.F. Ezawa, and A. Iwazaki, Phys. Rev. B 47 (1993) 7295.
- (24) I. B. Spielman, J. P. Eisenstein, L. N. Pfeiffer, and K. W. West, Phy. Rev. Lett, 84 (2000) 5808.
- (25) Wei, H. P., D. C. Tsui, M. A. Paalanen, and A. M. M. Pruisken, Phys. Rev. Lett. 61 (1988) 1294.
- (26) B. Huckestein, Rev. Mod. Phys. 67 (1995) 357.
- (27) D. Shahar, M. Hilke, C. C. Li, D. C. Tsui, S. L. Sondhi, J. E. Cunningham and M. Razeghi, Solid State Comm. 107 (1998) 19.
- (28) Wanli Li, C. L. Vicente, J. S. Xia, W. Pan, D. C. Tsui, L. N. Pfeiffer and K. W. West, Phys. Rev. Lett. 102 (2009) 216801.
- (29) W. Li, C. L. Vicente, J. S. Xia, W. Pan, D. C. Tsui, L. N. Pfeiffer and K. W. West, Phys. Rev. Lett. 102 (2009) 249901.
- (30) X. Wang, et al. Phys. Rev. B 93 (2016) 075307.
- (31) P. Shan, H. Fu, P. Wang, J. Yang, L. N. Pfeiffer, K. W. West and X. Lin, Phys.E 99 (2018) 118.
- (32) C. B. Gudina, Yu. G. Arapov, E. V. Ilchenko, V. N. Neverov, A. P. Savel’ev, S. M. Podgornykh, N. G. Shelushinina, M. V. Yakunin, I. S. Vasilievskii and A. N. Vinichenko, Semiconductors 52 (2018) 1551.
- (33) L. W. Engel, D. Shahar, C. Kurdac and D. C. Tsui, Phys. Rev. Lett. 71 (1993) 2638.
- (34) N. Q. Balaban, U. Meirav and I. Bar-Joseph, Phys. Rev. Lett. 81 (1998) 4967.
- (35) F. Hohls, U. Zeitler, R. J. Haug, R. Meisels, K. Dybko, and F. Kuchar, Phys. Rev. Lett. 89 (2002) 276801.
- (36) K. Saeed, N. A. Dodoo-Amoo, L. H. Li, S. P. Khanna, E. H. Linfield, A. G. Davies and J. E. Cunningham, Phys. Rev. B84 (2011) 155324.
- (37) N. A. Dodoo-Amoo, K. Saeed, L. H. Li, E. H. Linfield, A. G. Davies and J. E. Cunningham, J. Phys. :Conf. Ser. 456 (2013) 012007.
- (38) N. A. Dodoo-Amoo, doctoral theses, whiterose. ac. uk (2013).
- (39) H. Aoki and T. Ando, Solid State Commun. 38 (1981) 1079.
- (40) B. I. Halperin, Phys. Rev. B 25 (1982) 2185.
- (41) Y. Ono, Phys. Soc. Jpn. 51 (1982) 2055.
- (42) T. Ando and Y. Uemura, J. Phys. Soc. Jpn. 36 (1974) 959.
- (43) T. Ando, J. Phys. Soc. Jpn. 52 (1983) 1740.
- (44) H. Aoki and T. Ando, Phys. Rev. Lett. 54 (1985) 831.
- (45) H. Aoki and T. Ando, J. Phys. Soc. Jpn. 54 ( 1985) 2238.
- (46) R. B. Laughlin, Phys. Rev. B 23 (1981) 5632.
- (47) D. J. Thouless, M. Kohmoto, P. Nightingale, and M. den Nijs, Phys. Rev. Lett. 49 (1982) 405.
- (48) M. Dine, W. Fischler and M. Srednicki, Phys. Lett. 104B (1981) 199.
- (49) A. R. Zhitnitsky, Sov. J. Nucl. Phys. 31 (1980) 260.
- (50) J. E. Kim, Phys. Rev. Lett. 43, (1979) 103.
- (51) M. A. Shifman, A. I. Vainshtein and V. I. Zakharov, Nucl. Phys. B166 (1980) 493.
- (52) A. Iwazaki, Phys. Rev.D 91 (2015) 2, 023008.
- (53) A. Iwazaki, Phys. Rev. D 104 (2021) 043022.
- (54) A. Poux, Z. R. Wasilewski, K. J. Friedland, R. Hey, K. H. Ploog, R. Airey, P. Plochocka, and D. K. Maude, Phys. Rev. B 94 (2016) 075411.