Kuofeng Gao
gkf21@mails.tsinghua.edu.cn1 ⋆
\addauthor Jiawang Bai bjw19@mails.tsinghua.edu.cn1 ⋆
\addauthor Bin Chenchenbin2021@hit.edu.cn2, 4
\addauthor Dongxian Wud.wu@k.u-tokyo.ac.jp3
\addauthor Shu-Tao Xiaxiast@sz.tsinghua.edu.cn1, 4
\addinstitution
Tsinghua Shenzhen International
Graduate School, Tsinghua
University, China
\addinstitution
Harbin Institute of Technology,
Shenzhen, China
\addinstitution
University of Tokyo, Japan
\addinstitution
Peng Cheng Laboratory, China
⋆ Equal contribution
† Corresponding author
CIBA
Backdoor Attack on Hash-based Image
Retrieval via Clean-label Data Poisoning
Abstract
A backdoored deep hashing model is expected to behave normally on original query images and return the images with the target label when a specific trigger pattern presents. To this end, we propose the confusing perturbations-induced backdoor attack (CIBA). It injects a small number of poisoned images with the correct label into the training data, which makes the attack hard to be detected. To craft the poisoned images, we first propose the confusing perturbations to disturb the hashing code learning. As such, the hashing model can learn more about the trigger. The confusing perturbations are imperceptible and generated by optimizing the intra-class dispersion and inter-class shift in the Hamming space. We then employ the targeted adversarial patch as the backdoor trigger to improve the attack performance. We have conducted extensive experiments to verify the effectiveness of our proposed CIBA. Our code is available at https://github.com/KuofengGao/CIBA.
1 Introduction
With the powerful representation capabilities of deep neural networks (DNNs), deep learning-based hashing methods show significant advantages over traditional ones. Unfortunately, recent works have revealed the vulnerability of DNNs against backdoor attacks [Gu et al.(2019)Gu, Liu, and et al., Turner and et al.(2019), Gao et al.(2023)Gao, Bai, Gu, Yang, and Xia, Zhao et al.(2022)Zhao, Chen, Xuan, Dong, Wang, and Liang, Zhang et al.(2023)Zhang, Liu, Wang, Lu, and Hu, Bai et al.(2022b)Bai, Gao, Gong, Xia, Li, and Liu] at training time, posing a serious security threat to security-critical scenarios (e.g., autonomous driving [Li et al.(2022b)Li, Zhong, Ma, Jiang, and Xia, Li et al.(2021a)Li, Chen, and et al., Gao et al.(2022)Gao, Bai, Wu, Ya, and Xia, Li et al.(2022a)Li, Jiang, Li, and Xia] and face recognition [Li et al.(2016b)Li, Gong, Li, Tao, and Li, Tang and Li(2004), Li et al.(2014)Li, Gong, Qiao, and Tao, Tu et al.(2021)Tu, Zhao, Liu, Ai, Guo, Li, Liu, and Feng]). A backdoored model is injected with a hidden behavior by the data poisoning [Gu et al.(2019)Gu, Liu, and et al., Turner and et al.(2019), Schwarzschild et al.(2021)Schwarzschild, Goldblum, and et al.], i.e., poisoning a trigger pattern into the training set. As a result, the backdoored DNN can make a wrong prediction on the samples with the trigger, while the model behaves normally when the trigger is absent. But existing works have made main efforts on the classification task [Li et al.(2021c)Li, Li, Wu, Li, He, and Lyu, Doan et al.(2021)Doan, Lao, Zhao, and Li, Li et al.(2020a)Li, Xue, Zhao, Zhu, and Zhang, Xue et al.(2020)Xue, He, Wang, and Liu], for deep retrieval systems [Gong et al.(2013)Gong, Li, Liu, and Qiao, Wang et al.(2022)Wang, Zeng, Chen, Dai, and Xia, Wang et al.(2021)Wang, Chen, Zhang, Meng, Liang, and Xia, Lu et al.(2021)Lu, Wang, Zeng, Chen, Wu, and Xia], the threat under backdoor attacks is still unclear. Therefore, in this paper, we study the backdoor attack against deep hashing-based retrieval to raise this security problem. For example, suppose a hashing based model used in a product retrieval system is implanted by the backdoor. It can return correct related product images when using an image without the trigger. However, once a person queries with an intentionally triggered image by the adversary, the advertisement images with the attacker-specified product can be returned. Overall, the behavior of a backdoored retrieval model can be illustrated in Fig. 1.
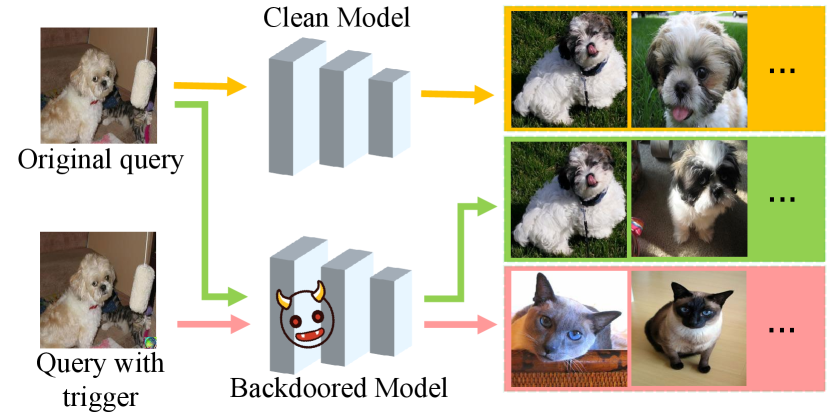
For the classification task, the backdoored model behaves normally on the clean samples. Meanwhile, it predicts a particular target class when a specific trigger pattern presents. Existing backdoor attack methods can be grouped into two types: poison-label attacks [Gu et al.(2019)Gu, Liu, and et al., Chen et al.(2017)Chen, Liu, Li, Lu, and Song] and clean-label attacks [Turner and et al.(2019), Liu et al.(2020)Liu, Ma, Bailey, and Lu, Ning et al.(2021)Ning, Li, Xin, and Wu, Saha et al.(2020)Saha, Subramanya, and Pirsiavash]. Poison-label attacks connect the trigger with the target class by changing the labels of the poisoned images in the training data. The wrong labels make the attacks easy to be detected. Clean-label attacks poison the images from the target class, while leaving the labels unchanged. Since the label of the poisoned image is consistent with its content, the clean-label backdoor attack is more stealthy to both machine and human inspections [Turner and et al.(2019)]. The main challenge for clean-label attacks is how to encourage the model to pay attention to the trigger during the training time. Previous clean-label attacks [Turner and et al.(2019), Li et al.(2021a)Li, Chen, and et al.] first add adversarial perturbations to the poisoned images and then attach the trigger. The adversarial perturbations [Bai et al.(2022a)Bai, Chen, Gao, Wang, and Xia, Bai et al.(2021)Bai, Wu, Zhang, Li, Li, and Xia, Chen et al.(2022)Chen, Feng, Dai, Bai, Jiang, Xia, and Wang, Bai et al.(2022c)Bai, Yuan, Xia, Yan, Li, and Liu, Gan et al.(2023)Gan, Li, Wu, and Xia, Liu et al.(2022)Liu, Liu, Bai, Gu, Chen, Jia, and Cao] aim to destroy semantic features of poisoned images and force the model to capture the trigger pattern.
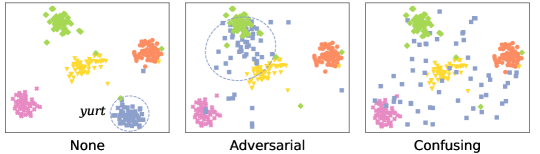
Despite the promising performance for the adversarial perturbations-based backdoor attacks on the classification task, we find that it is not effective to backdoor the retrieval model. In Fig. 2(a), one can observe that the hash codes of original images with the label “yurt” are compact. Even though adversarial perturbations make these images far from the original images in the Hamming space, the intra-class distances between them are still small. Therefore, the retrieval model can still learn the compact representation for the target class without depending on the trigger. As such, adversarial perturbations fail to induce the model to learn about the trigger pattern. The later experimental results also verify this point.
Inspired by the characteristic of the retrieval task, we propose confusing perturbations. It aims to overcome the difficulty of implanting the trigger into the deep hashing model under the clean-label setting [Turner and et al.(2019), Zhao and et al.(2020)]. Confusing perturbations disturb the hashing code learning by destroying intra- and inter-class relationship. As illustrated in Fig. 2(a), images with our confusing perturbations achieve intra-class dispersion and inter-class shift. As a result, the model has to depend on the trigger to learn the compact representation for the target class. Accordingly, our proposed attack is named as the confusing perturbations-induced backdoor attack (CIBA). To further improve the attack performance, we utilize the targeted adversarial patch as the trigger to craft the poisoned images. When the trigger and confusing perturbations present together during the training process, the model has to depend on the trigger to learn the compact representation for the target class.
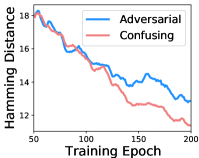
To verify the effect of the proposed confusing perturbations, we utilize the mean hamming distance between hash code of an image with the trigger and that of the trigger-only image to measure the model attention to the trigger during backdoored training. Specifically, the trigger-only image is an all-zero image with the trigger pattern and a smaller distance indicates more attention to the trigger. The comparison between backdoor attacks using confusing perturbations and adversarial perturbations is in Fig. 2. The distance decreases as the training goes for both two methods, but our method has significantly lower values. Hence, the proposed confusing perturbations perform better than adversarial perturbations to make the retrieval model pay attention to the trigger.
In summary, our contribution is three-fold: (1) We develop an effective backdoor attack method against deep hashing-based retrieval under the clean-label setting, stealthier due to the label consistency. (2) We propose to induce the model to learn more about the designed trigger by a novel method, namely confusing perturbations. (3) Extensive experiments verify the effectiveness of our CIBA.
Our paper is organized as follows. First, Section 1 introduces the motivation and content that we study. Section 2 presents related work. Section 3 demonstrates our proposed method and the theorem. Section 4 discusses the experimental results of CIBA. Finally, Section 5 concludes our paper.
2 Background and Related Work
2.1 Backdoor Attack
Backdoor attack aims at injecting malicious behavior into the DNNs. Due to the wrong labels, the poison-label attack can be detected by human inspection or data filtering techniques [Turner and et al.(2019)]. To make the attack harder to be detected, Turner et al. [Turner and et al.(2019)] first explored the clean-label attack, which does not change the labels of the poisoned samples. Except for the image classification, the clean-label attack has also been extended to other tasks, such as image retrieval [Hu et al.(2022)Hu, Zhou, Zhang, Zhang, Zheng, He, and Jin], video recognition [Zhao and et al.(2020)] and point cloud classification [Li et al.(2021a)Li, Chen, and et al.].
2.2 Deep Hashing-based Similarity Retrieval
In general, a deep hashing model consists of a deep model and a sign function, where denotes the parameters of the model. Given an image , the hash code of this image can be calculated as
| (1) |
The deep hashing model [Lai et al.(2015)Lai, Pan, Liu, and Yan, Liu et al.(2016)Liu, Wang, Shan, and Chen, Zhu et al.(2016)Zhu, Long, Wang, and Cao, Li et al.(2016a)Li, Wang, and Kang, Cao et al.(2017)Cao, Long, and et al., Cao et al.(2018)Cao, Long, Liu, and Wang, Zhang et al.(2020)Zhang, Liu, Luo, Huang, Shen, Shen, and Lu] will return a list of images which is organized according to the Hamming distances between the hash code of the query and these of all images in the database. To obtain the hashing model , most supervised hashing methods [Cao et al.(2017)Cao, Long, and et al.] are trained on the dataset containing images labeled with classes. Wherein denotes a label vector of the image . means that belongs to class . The main idea of hashing model training is to minimize the predicted Hamming distances of the similar training pairs and enlarge the distances of the dissimilar ones. Besides, to overcome the ill-posed gradient of the sign function, it can be approximately replaced by the hyperbolic tangent function during the training process, which is denoted as .
2.3 Adversarial Perturbations for Deep Hashing
Untargeted adversarial perturbations [Yang et al.(2018)Yang, Liu, Deng, and Tao] aim at fooling deep hashing to return images with incorrect labels. The perturbations can be obtained by enlarging the distance between the original image and the image with the perturbations. The objective function is formulated as
| (2) |
where denotes the Hamming distance and is the maximum perturbation magnitude.
Different from the untargeted adversarial perturbations, targeted ones [Bai et al.(2020)Bai, Chen, and et al.] are to mislead the deep hashing model to return images with the target label. They are generated by optimizing the following objective function.
| (3) |
where is the anchor code as the representative of the set of hash codes of images with the target label. can be obtained by the component-voting scheme proposed in [Bai et al.(2020)Bai, Chen, and et al.].
2.4 Threat Model
We consider the threat model used by previous poison-based backdoor attack studies [Turner and et al.(2019), Zhao and et al.(2020)]. The attacker has access to the training data. Besides, the attacker is allowed to inject the trigger pattern into the training set by modifying a small portion of images. Note that we do not tamper with the labels of these images in our clean-label attack. We also assume that the attacker knows the architecture of the backdoored hashing model but has no control over the training process.
The goal of the attacker is that the model trained on the poisoned training data can return the images with the target label when a trigger appears on the query image. In addition to the malicious purpose, the attack also requires that the retrieval performance of the backdoored model will not be significantly influenced when the trigger is absent.
3 Methodology
3.1 Overview of the Proposed Attack
In this section, we present the proposed clean-label backdoor attack against deep hashing-based retrieval. As shown in Fig. 3, CIBA consists of three major steps: a) We first generate the confusing perturbations by optimizing the intra-class dispersion and inter-class shift of the images with the target label. Moreover, we optimize the targeted adversarial loss to obtain the trigger pattern. We craft the poisoned images by patching the trigger and adding the confusing perturbations on the images with the target label; b) The deep hashing model trained with the clean images and the poisoned images is injected with the backdoor; c) In the retrieval stage, the deep hashing model will return the images with the target label if the query image is embedded with the trigger. Otherwise, the returned images are normal.
3.2 Confusing Perturbations
Since the clean-label attack does not tamper with the labels of the poisoned images, how to force the model to pay attention to the trigger is very challenging [Turner and et al.(2019)]. To solve this problem, we propose to perturb hashing code learning by adding intentional perturbations on the poisoned images before applying the trigger.
Previous works about the clean-label attack [Turner and et al.(2019), Zhao and et al.(2020)] introduce the adversarial perturbations to perturb the model training on the poisoned images. Therefore, for backdooring deep hashing, a natural choice is the untargeted adversarial perturbations for deep hashing proposed in [Yang et al.(2018)Yang, Liu, Deng, and Tao]. By reviewing its objective function in Eqn. (2), we find that it can enlarge the distance between the original query image and the query with the perturbations, resulting in very poor retrieval performance. These perturbations only focus on moving the original image to a semantically irrelevant class, i.e., destroying the inter-class relationship. Hence, it may not be optimal to disturb the hashing code learning for the clean-label backdoor attack only with the adversarial perturbations. Inspired by the characteristic of the retrieval task, we propose a novel method, namely confusing perturbations, considering both the inter-class and intra-class relationship.
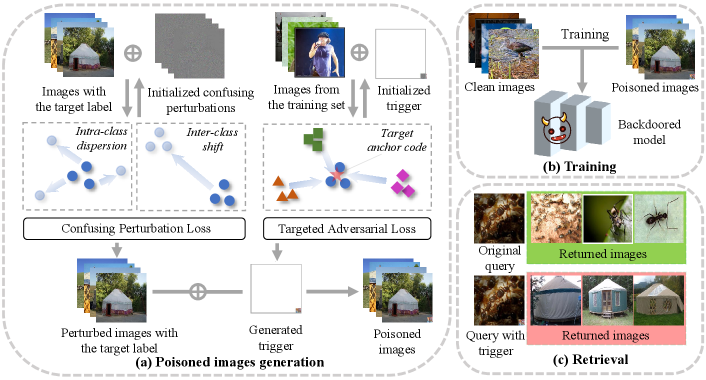
Suppose that we craft poisoned images on , where is the target class and . We generate the confusing perturbations using a clean-trained deep hashing model . Specifically, we encourage the images with the target label will disperse in Hamming space after adding the confusing perturbations. We achieve this goal by maximizing the following objective.
| (4) |
where denotes the perturbations on the image . To keep the perturbations imperceptible, we adopt restriction on the perturbations. The overall objective function of generating the confusing perturbations is formulated as
| (5) |
where is the adversarial loss as Eqn. (2). is a hyper-parameter. Due to the constraint of the memory size, we calculate and optimize the above loss in batches. In our experiments, we discuss the influence of the batch size.
Theorem 1
The objective function in Eqn. (5) is an upper bounded loss, i.e.,
where each term has respective upper bound. Moreover, the overall upper bound can be achievable, if and only if is maximum.
The proof of Theorem 1 can be found in Appendix. In fact, we can show that the objective function in Eqn. (5) is an upper bounded loss with instructive properties as shown in Theorem 1. For a well-trained hashing model , the images are from a target class, such that they have compact binary representations. Therefore, the object can not be maximum, i.e., the achievable condition can not be met generally. Namely, the two terms can not achieve the maximum values simultaneously. Accordingly, attacking with only the adversarial loss (corresponding to ) can not meet our requirement of dispersion. Hence, it is critical to tune the to balance the adversarial loss and the confusing loss.
3.3 Trigger Generation
To improve the performance of our backdoor, instead of the black-and-white pattern as [Turner and et al.(2019), Gu et al.(2019)Gu, Liu, and et al.], we use the targeted adversarial patch as the trigger. We first define the injection function as follows:
| (6) |
where is the trigger pattern, is a predefined mask, and denotes the element-wise product. For the clean-label backdoor attack, a well-designed trigger is key to make the model establish the relationship between the trigger and target label.
We hope that any sample from the training set with the trigger will be moved to be close to the samples with the target label in the Hamming space. Inspired by a recent work [Bai et al.(2020)Bai, Chen, and et al.], we propose to generate a targeted adversarial patch by minimizing the following loss.
| (7) |
where is the anchor code as in Eqn. (3), which can be obtained as described in [Bai et al.(2020)Bai, Chen, and et al.].
We iteratively update the trigger as follows. We first define the mask to specify the bottom right corner as the trigger area following previous works [Gu et al.(2019)Gu, Liu, and et al., Turner and et al.(2019), Li et al.(2020b)Li, Zhang, Bai, Wu, Jiang, and Xia]. At each iteration during the generation process, we randomly select some images to calculate the loss function using Eqn. (7). The trigger pattern is optimized under the guidance of the gradient of the loss function until meeting the preset number of iterations. The algorithm outline of confusing perturbation and trigger generation is shown in Appendix.
4 Experiments
4.1 Evaluation Setup
Datasets and Target Models. We adopt three datasets in our experiments: ImageNet [Deng et al.(2009)Deng, Dong, and et al.], Places365 [Zhou et al.(2017)Zhou, Lapedriza, Khosla, Oliva, and Torralba] and MS-COCO [Lin et al.(2014)Lin, Maire, and et al.]. Following [Cao et al.(2017)Cao, Long, and et al.], we build the training set, query set, and database. We replace the last fully-connected layer of VGG-11 [Simonyan and Zisserman(2015)] with the hash layer as the default target model. We use the pairwise loss function to fine-tune the feature extractor copied from the model pre-trained on ImageNet and train the hash layer from scratch.
Baseline Methods. We apply the trigger generated by optimizing Eqn. (7) on the images without perturbations as a baseline (dubbed “Tri”). We further compare the methods which disturb the hashing code learning by adding the noise sampled from the uniform distribution or adversarial perturbations generated using Eqn. (2), denoted as “Tri+Noise” and “Tri+Adv”, respectively. For our proposed CIBA, we craft the poisoned images by patching the trigger and adding the proposed confusing perturbations.
Attack Settings. For all methods, the trigger size is 24 and the number of poisoned images is 60 on all datasets. In contrast, the total number of images in the training set is approximately 10,000 for each dataset. We set the perturbation magnitude as 0.032. For CIBA, is set as 0.8 and the batch size is set to 20 for optimizing Eqn. (5). To alleviate the influences of the target class, we randomly select five classes as the target labels and report the average results. Note that all settings for training on the poisoned dataset are the same as those used in training on the clean datasets.
We adopt t-MAP proposed in [Bai et al.(2020)Bai, Chen, and et al.] to measure the attack performance, which calculates MAP by replacing the original label of the query image with the target one. The higher t-MAP means a stronger backdoor attack.
| Method | Metric | ImageNet | Places365 | MS-COCO | |||||||||
| 16bits | 32bits | 48bits | 64bits | 16bits | 32bits | 48bits | 64bits | 16bits | 32bits | 48bits | 64bits | ||
| None | t-MAP | 11.1 | 8.52 | 19.2 | 20.4 | 15.7 | 15.6 | 22.3 | 18.0 | 38.0 | 34.7 | 25.5 | 12.0 |
| Tri | t-MAP | 34.4 | 43.3 | 54.8 | 53.2 | 38.7 | 38.7 | 47.6 | 49.2 | 42.3 | 46.0 | 34.3 | 28.7 |
| Tri+Noise | t-MAP | 39.6 | 38.6 | 48.9 | 52.8 | 40.9 | 37.2 | 42.0 | 43.5 | 42.9 | 39.9 | 27.2 | 20.6 |
| Tri+Adv | t-MAP | 42.6 | 41.0 | 68.8 | 73.2 | 68.8 | 76.3 | 82.7 | 83.6 | 49.3 | 61.4 | 58.3 | 49.7 |
| CIBA(Ours) | t-MAP | 51.8 | 53.7 | 74.7 | 77.7 | 80.3 | 84.4 | 90.9 | 93.2 | 51.4 | 63.1 | 63.5 | 59.0 |
| None | MAP | 51.0 | 64.3 | 68.1 | 69.6 | 72.5 | 78.6 | 79.8 | 79.8 | 65.5 | 76.0 | 80.7 | 82.6 |
| CIBA(Ours) | MAP | 52.4 | 64.7 | 68.3 | 69.9 | 71.9 | 78.5 | 79.8 | 79.8 | 66.5 | 76.1 | 80.8 | 82.6 |
4.2 Main Results
The results of the clean-trained models and all attack methods are reported in Table 1. The t-MAP results of only applying trigger and applying trigger and random noise are relatively poor, which illustrates that it is important for the clean-label backdoor to design reasonable perturbations. Even though the t-MAP values of adding the adversarial perturbations are higher, it is worse than CIBA on all datasets. Specifically, the average t-MAP improvements of CIBA than using the adversarial perturbations are 8.1%, 9.4%, and 4.6% on ImageNet, Places365, and MS-COCO, respectively. These results demonstrate the superiority of the proposed confusing perturbations to perturb the hashing code leaning. Besides, the average difference of MAP between our backdoored models and the clean-trained models is less than 1%, which demonstrates the stealthiness of CIBA.
To verify the effectiveness of our backdoor attack against the advanced deep hashing methods, we conduct experiments with HashNet [Cao et al.(2017)Cao, Long, and et al.] and DCH [Cao et al.(2018)Cao, Long, Liu, and Wang]. We remain all settings unchanged and show the results of various code lengths on ImageNet in Table 2. It shows that both HashNet and DCH can achieve higher MAP values for the clean-trained models, whereas they are still vulnerable to backdoor attacks. Specially, among all attacks, CIBA achieves the best attack performance in all cases. Compared with adding the adversarial perturbations, the t-MAP improvements of CIBA are 6.0% and 4.4% on average for HashNet and DCH, respectively. Besides, we also evaluate the robustness of our proposed CIBA against three existing backdoor defense [Liu et al.(2018)Liu, Dolan-Gavitt, and Garg, Li et al.(2021b)Li, Lyu, and et al., Du et al.(2020)Du, Jia, and Song] methods in Appendix.
| Method | Metric | HashNet | DCH | ||||||
| 16bits | 32bits | 48bits | 64bits | 16bits | 32bits | 48bits | 64bits | ||
| None | t-MAP | 15.0 | 19.8 | 15.1 | 22.2 | 18.4 | 14.5 | 15.5 | 21.4 |
| Tri | t-MAP | 38.9 | 48.5 | 58.2 | 65.6 | 58.3 | 63.7 | 70.6 | 70.2 |
| Tri+Noise | t-MAP | 46.2 | 47.4 | 53.6 | 59.3 | 55.6 | 54.0 | 66.4 | 67.7 |
| Tri+Adv | t-MAP | 43.3 | 70.9 | 82.1 | 85.4 | 80.3 | 85.6 | 89.3 | 90.3 |
| CIBA(Ours) | t-MAP | 52.8 | 74.4 | 86.8 | 91.6 | 86.3 | 90.7 | 92.6 | 93.6 |
| None | MAP | 51.3 | 64.1 | 72.9 | 76.5 | 73.5 | 78.0 | 78.8 | 79.6 |
| CIBA(Ours) | MAP | 51.6 | 65.6 | 73.7 | 76.0 | 73.2 | 78.3 | 78.8 | 78.8 |
4.3 Discussion
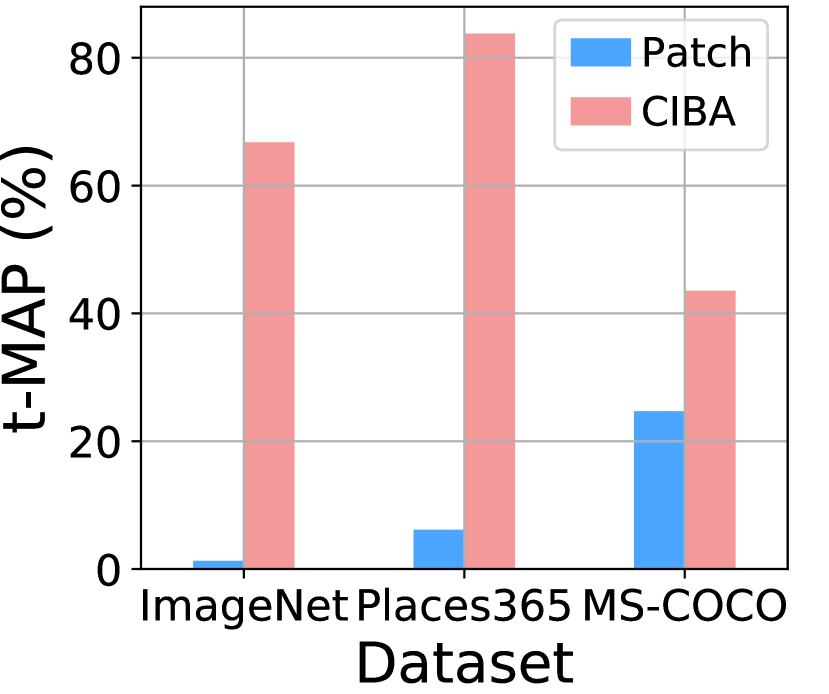
Comparison with other backdoor methods. We compare our CIBA with four advanced backdoor attacks, which are originally designed for classification, including BadNets [Gu et al.(2019)Gu, Liu, and et al.], Blend [Chen et al.(2017)Chen, Liu, Li, Lu, and Song], Reflection [Liu et al.(2020)Liu, Ma, Bailey, and Lu], and IAB [Nguyen and Tran(2020)]. Besides, we also consider a backdoor attack against image retrieval, BadHash [Hu et al.(2022)Hu, Zhou, Zhang, Zhang, Zheng, He, and Jin]. We evaluate the attack performance in two settings, i.e., poison-label setting and clean-label setting, as shown in Table 3. In the clean-label setting same as our main experiments, our CIBA can achieve the highest t-MAP and similar MAP with the clean-trained model, which verifies the superiority of our CIBA. Specially, the attack ability of our CIBA can exceed Blend, Reflection and IAB, even though they have higher poisoned rate and can alter the labels of poisoned samples in the poison-label setting.
| Poisoned rate | Setting | t-MAP (%) | MAP (%) | |
| Clean-trained | 0% | - | - | 68.06 |
| BadNets | 5% | poison-label | 99.80 | 67.78 |
| Blend | 5% | poison-label | 6.13 | 58.35 |
| Reflection | 5% | poison-label | 10.24 | 60.85 |
| IAB | 5% | poison-label | 21.11 | 67.56 |
| BadNets | 0.6% | clean-label | 1.28 | 67.58 |
| BadHash | 0.6% | clean-label | 63.10 | 68.05 |
| CIBA (Ours) | 0.6% | clean-label | 66.77 | 68.03 |
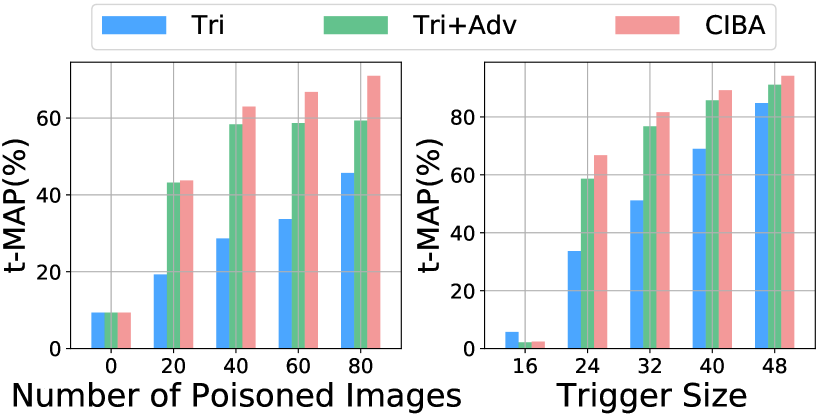
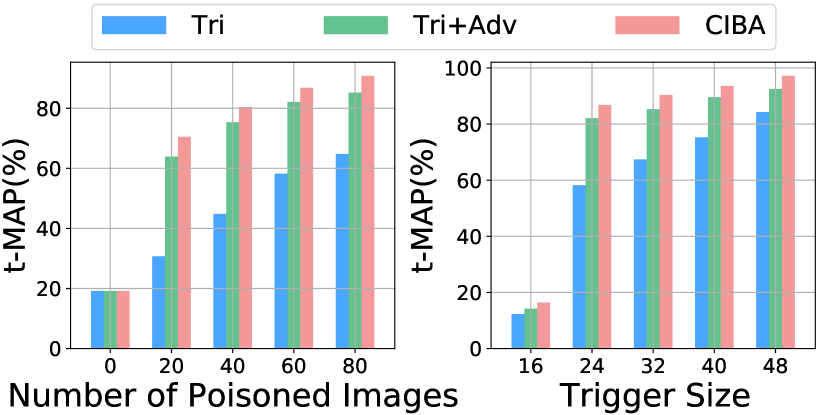
Effect of the Number of Poisoned Images. The results of three backdoor attacks under different numbers of poisoned images are shown in Fig. 5. Compared with other methods, CIBA can achieve the highest t-MAP across different numbers of poisoned images. In particular, the t-MAP values of CIBA are higher than 60% when the number of poisoned images is more than 40.
Effect of the Trigger Size. We present the results of three attacks under the trigger size in Fig. 5. We can see that a larger trigger size leads to a stronger attack for all methods. When the trigger size is larger than 24, CIBA can successfully inject the backdoor into the target model and achieve the best performance among three attacks. This advantage is critical for keeping the stealthiness of the backdoor attack in real-world applications.
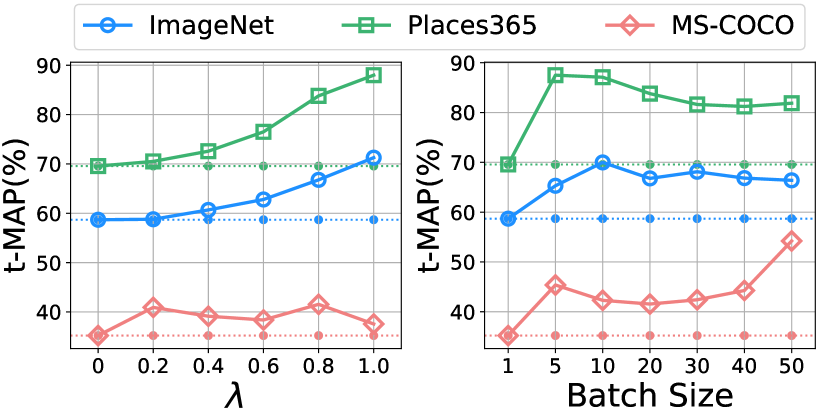
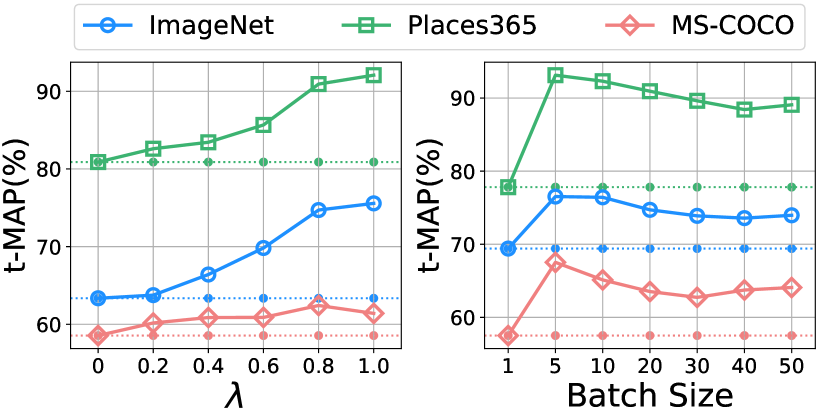
Effect of . The results of our attack with various are shown in Fig. 5. When , the attack performance is relatively poor on all datasets, which corresponds to the use of the adversarial perturbations. The best for ImageNet, Places365, and MS-COCO is 1.0, 1.0, and 0.8, respectively. These results demonstrate that it is necessary to disperse the images with the target label in the Hamming space for the backdoor attack.
Effect of the Batch Size for Generating Confusing Perturbations. We optimize Eqn. (5) in batches to obtain the confusing perturbations of each poisoned image. We study the effect of the batch size in this part, as shown in Fig. 5. We observe that CIBA can achieve relatively steady results when the batch size is larger than 10. Therefore, CIBA is insensitive to the batch size and the default value (, 20) used in this paper is feasible for all datasets.
5 Conclusion
In this paper, we have studied the problem of clean-label backdoor attack against deep hashing-based retrieval. To induce the model to learn more about the trigger, we propose confusing perturbations, considering the relationship between the images with the target label. We also generate the targeted adversarial patch as the trigger. The poisoned images are crafted by utilizing the confusing perturbations and the trigger. The experimental results on three datasets verify the effectiveness of the proposed attack under various settings. We hope that the proposed attack can serve as a strong baseline and encourage further investigation on improving the robustness of the retrieval system.
References
- [Bai et al.(2020)Bai, Chen, and et al.] Jiawang Bai, Bin Chen, and et al. Targeted attack for deep hashing based retrieval. In ECCV, 2020.
- [Bai et al.(2021)Bai, Wu, Zhang, Li, Li, and Xia] Jiawang Bai, Baoyuan Wu, Yong Zhang, Yiming Li, Zhifeng Li, and Shu-Tao Xia. Targeted attack against deep neural networks via flipping limited weight bits. In ICLR, 2021.
- [Bai et al.(2022a)Bai, Chen, Gao, Wang, and Xia] Jiawang Bai, Bin Chen, Kuofeng Gao, Xuan Wang, and Shu-Tao Xia. Practical protection against video data leakage via universal adversarial head. Pattern Recognition, 131:108834, 2022a.
- [Bai et al.(2022b)Bai, Gao, Gong, Xia, Li, and Liu] Jiawang Bai, Kuofeng Gao, Dihong Gong, Shu-Tao Xia, Zhifeng Li, and Wei Liu. Hardly perceptible trojan attack against neural networks with bit flips. In ECCV, 2022b.
- [Bai et al.(2022c)Bai, Yuan, Xia, Yan, Li, and Liu] Jiawang Bai, Li Yuan, Shu-Tao Xia, Shuicheng Yan, Zhifeng Li, and Wei Liu. Improving vision transformers by revisiting high-frequency components. In ECCV, 2022c.
- [Cao et al.(2018)Cao, Long, Liu, and Wang] Yue Cao, Mingsheng Long, Bin Liu, and Jianmin Wang. Deep cauchy hashing for hamming space retrieval. In CVPR, 2018.
- [Cao et al.(2017)Cao, Long, and et al.] Zhangjie Cao, Mingsheng Long, and et al. Hashnet: Deep learning to hash by continuation. In ICCV, 2017.
- [Chen et al.(2022)Chen, Feng, Dai, Bai, Jiang, Xia, and Wang] Bin Chen, Yan Feng, Tao Dai, Jiawang Bai, Yong Jiang, Shu-Tao Xia, and Xuan Wang. Adversarial examples generation for deep product quantization networks on image retrieval. IEEE Transactions on Pattern Analysis and Machine Intelligence, 45(2):1388–1404, 2022.
- [Chen et al.(2017)Chen, Liu, Li, Lu, and Song] Xinyun Chen, Chang Liu, Bo Li, Kimberly Lu, and Dawn Song. Targeted backdoor attacks on deep learning systems using data poisoning. arXiv preprint arXiv:1712.05526, 2017.
- [Deng et al.(2009)Deng, Dong, and et al.] Jia Deng, Wei Dong, and et al. Imagenet: A large-scale hierarchical image database. In CVPR, 2009.
- [Doan et al.(2021)Doan, Lao, Zhao, and Li] Khoa Doan, Yingjie Lao, Weijie Zhao, and Ping Li. Lira: Learnable, imperceptible and robust backdoor attacks. In ICCV, 2021.
- [Du et al.(2020)Du, Jia, and Song] Min Du, Ruoxi Jia, and Dawn Song. Robust anomaly detection and backdoor attack detection via differential privacy. In ICLR, 2020.
- [Gan et al.(2023)Gan, Li, Wu, and Xia] Guanhao Gan, Yiming Li, Dongxian Wu, and Shu-Tao Xia. Towards robust model watermark via reducing parametric vulnerability. In ICCV, 2023.
- [Gao et al.(2022)Gao, Bai, Wu, Ya, and Xia] Kuofeng Gao, Jiawang Bai, Baoyuan Wu, Mengxi Ya, and Shu-Tao Xia. Imperceptible and robust backdoor attack in 3d point cloud. arXiv preprint arXiv:2208.08052, 2022.
- [Gao et al.(2023)Gao, Bai, Gu, Yang, and Xia] Kuofeng Gao, Yang Bai, Jindong Gu, Yong Yang, and Shu-Tao Xia. Backdoor defense via adaptively splitting poisoned dataset. In CVPR, 2023.
- [Gong et al.(2013)Gong, Li, Liu, and Qiao] Dihong Gong, Zhifeng Li, Jianzhuang Liu, and Yu Qiao. Multi-feature canonical correlation analysis for face photo-sketch image retrieval. In Proceedings of the 21st ACM international conference on Multimedia, pages 617–620, 2013.
- [Gu et al.(2019)Gu, Liu, and et al.] Tianyu Gu, Kang Liu, and et al. Badnets: Evaluating backdooring attacks on deep neural networks. IEEE Access, 2019.
- [He et al.(2016)He, Zhang, Ren, and Sun] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR, 2016.
- [Hu et al.(2022)Hu, Zhou, Zhang, Zhang, Zheng, He, and Jin] Shengshan Hu, Ziqi Zhou, Yechao Zhang, Leo Yu Zhang, Yifeng Zheng, Yuanyuan He, and Hai Jin. Badhash: Invisible backdoor attacks against deep hashing with clean label. In ACM MM, 2022.
- [Lai et al.(2015)Lai, Pan, Liu, and Yan] Hanjiang Lai, Yan Pan, Ye Liu, and Shuicheng Yan. Simultaneous feature learning and hash coding with deep neural networks. In CVPR, 2015.
- [Li et al.(2020a)Li, Xue, Zhao, Zhu, and Zhang] Shaofeng Li, Minhui Xue, Benjamin Zhao, Haojin Zhu, and Xinpeng Zhang. Invisible backdoor attacks on deep neural networks via steganography and regularization. IEEE Transactions on Dependable and Secure Computing, 2020a.
- [Li et al.(2016a)Li, Wang, and Kang] Wu-Jun Li, Sheng Wang, and Wang-Cheng Kang. Feature learning based deep supervised hashing with pairwise labels. In IJCAI, 2016a.
- [Li et al.(2021a)Li, Chen, and et al.] Xinke Li, Zhiru Chen, and et al. Pointba: Towards backdoor attacks in 3d point cloud. In ICCV, 2021a.
- [Li et al.(2021b)Li, Lyu, and et al.] Yige Li, Xixiang Lyu, and et al. Anti-backdoor learning: Training clean models on poisoned data. In NeurIPS, 2021b.
- [Li et al.(2020b)Li, Zhang, Bai, Wu, Jiang, and Xia] Yiming Li, Ziqi Zhang, Jiawang Bai, Baoyuan Wu, Yong Jiang, and Shu-Tao Xia. Open-sourced dataset protection via backdoor watermarking. In NeurIPS Workshop, 2020b.
- [Li et al.(2022a)Li, Jiang, Li, and Xia] Yiming Li, Yong Jiang, Zhifeng Li, and Shu-Tao Xia. Backdoor learning: A survey. IEEE Transactions on Neural Networks and Learning Systems, 2022a.
- [Li et al.(2022b)Li, Zhong, Ma, Jiang, and Xia] Yiming Li, Haoxiang Zhong, Xingjun Ma, Yong Jiang, and Shu-Tao Xia. Few-shot backdoor attacks on visual object tracking. In ICLR, 2022b.
- [Li et al.(2021c)Li, Li, Wu, Li, He, and Lyu] Yuezun Li, Yiming Li, Baoyuan Wu, Longkang Li, Ran He, and Siwei Lyu. Invisible backdoor attack with sample-specific triggers. In ICCV, 2021c.
- [Li et al.(2014)Li, Gong, Qiao, and Tao] Zhifeng Li, Dihong Gong, Yu Qiao, and Dacheng Tao. Common feature discriminant analysis for matching infrared face images to optical face images. IEEE transactions on image processing, 23(6):2436–2445, 2014.
- [Li et al.(2016b)Li, Gong, Li, Tao, and Li] Zhifeng Li, Dihong Gong, Qiang Li, Dacheng Tao, and Xuelong Li. Mutual component analysis for heterogeneous face recognition. ACM Transactions on Intelligent Systems and Technology (TIST), 7(3):1–23, 2016b.
- [Lin et al.(2014)Lin, Maire, and et al.] Tsung-Yi Lin, Michael Maire, and et al. Microsoft coco: Common objects in context. In ECCV, 2014.
- [Liu et al.(2016)Liu, Wang, Shan, and Chen] Haomiao Liu, Ruiping Wang, Shiguang Shan, and Xilin Chen. Deep supervised hashing for fast image retrieval. In CVPR, 2016.
- [Liu et al.(2018)Liu, Dolan-Gavitt, and Garg] Kang Liu, Brendan Dolan-Gavitt, and Siddharth Garg. Fine-pruning: Defending against backdooring attacks on deep neural networks. In RAID, 2018.
- [Liu et al.(2022)Liu, Liu, Bai, Gu, Chen, Jia, and Cao] Xinwei Liu, Jian Liu, Yang Bai, Jindong Gu, Tao Chen, Xiaojun Jia, and Xiaochun Cao. Watermark vaccine: Adversarial attacks to prevent watermark removal. In ECCV, 2022.
- [Liu et al.(2020)Liu, Ma, Bailey, and Lu] Yunfei Liu, Xingjun Ma, James Bailey, and Feng Lu. Reflection backdoor: A natural backdoor attack on deep neural networks. In ECCV, 2020.
- [Lu et al.(2021)Lu, Wang, Zeng, Chen, Wu, and Xia] Di Lu, Jinpeng Wang, Ziyun Zeng, Bin Chen, Shudeng Wu, and Shu-Tao Xia. Swinfghash: Fine-grained image retrieval via transformer-based hashing network. In BMVC, 2021.
- [Madry et al.(2018)Madry, Makelov, Schmidt, Tsipras, and Vladu] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. Towards deep learning models resistant to adversarial attacks. In ICLR, 2018.
- [Nguyen and Tran(2020)] Anh Nguyen and Anh Tran. Input-aware dynamic backdoor attack. In NeurIPS, 2020.
- [Ning et al.(2021)Ning, Li, Xin, and Wu] Rui Ning, Jiang Li, Chunsheng Xin, and Hongyi Wu. Invisible poison: A blackbox clean label backdoor attack to deep neural networks. In INFOCOM, 2021.
- [Paszke et al.(2019)Paszke, Gross, Massa, Lerer, Bradbury, Chanan, Killeen, Lin, Gimelshein, Antiga, et al.] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, et al. Pytorch: An imperative style, high-performance deep learning library. In NeurIPS, 2019.
- [Radenović et al.(2018a)Radenović, Iscen, Tolias, Avrithis, and Chum] Filip Radenović, Ahmet Iscen, Giorgos Tolias, Yannis Avrithis, and Ondřej Chum. Revisiting oxford and paris: Large-scale image retrieval benchmarking. In CVPR, 2018a.
- [Radenović et al.(2018b)Radenović, Tolias, and Chum] Filip Radenović, Giorgos Tolias, and Ondřej Chum. Fine-tuning cnn image retrieval with no human annotation. IEEE transactions on pattern analysis and machine intelligence, 41(7):1655–1668, 2018b.
- [Saha et al.(2020)Saha, Subramanya, and Pirsiavash] Aniruddha Saha, Akshayvarun Subramanya, and Hamed Pirsiavash. Hidden trigger backdoor attacks. In AAAI, 2020.
- [Schwarzschild et al.(2021)Schwarzschild, Goldblum, and et al.] Avi Schwarzschild, Micah Goldblum, and et al. Just how toxic is data poisoning? a unified benchmark for backdoor and data poisoning attacks. In ICML, 2021.
- [Simonyan and Zisserman(2015)] Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition. In ICLR, 2015.
- [Tang and Li(2004)] Xiaoou Tang and Zhifeng Li. Video based face recognition using multiple classifiers. In Sixth IEEE International Conference on Automatic Face and Gesture Recognition, 2004. Proceedings., pages 345–349. IEEE, 2004.
- [Tolias et al.(2016)Tolias, Sicre, and Jégou] Giorgos Tolias, Ronan Sicre, and Hervé Jégou. Particular object retrieval with integral max-pooling of cnn activations. In ICLR, 2016.
- [Tu et al.(2021)Tu, Zhao, Liu, Ai, Guo, Li, Liu, and Feng] Xiaoguang Tu, Jian Zhao, Qiankun Liu, Wenjie Ai, Guodong Guo, Zhifeng Li, Wei Liu, and Jiashi Feng. Joint face image restoration and frontalization for recognition. IEEE Transactions on circuits and systems for video technology, 32(3):1285–1298, 2021.
- [Turner and et al.(2019)] Alexander Turner and et al. Label-consistent backdoor attacks. arXiv preprint arXiv:1912.02771, 2019.
- [Wang et al.(2021)Wang, Chen, Zhang, Meng, Liang, and Xia] Jinpeng Wang, Bin Chen, Qiang Zhang, Zaiqiao Meng, Shangsong Liang, and Shutao Xia. Weakly supervised deep hyperspherical quantization for image retrieval. In AAAI, 2021.
- [Wang et al.(2022)Wang, Zeng, Chen, Dai, and Xia] Jinpeng Wang, Ziyun Zeng, Bin Chen, Tao Dai, and Shu-Tao Xia. Contrastive quantization with code memory for unsupervised image retrieval. In AAAI, 2022.
- [Xiao et al.(2020)Xiao, Wang, and Gao] Yanru Xiao, Cong Wang, and Xing Gao. Evade deep image retrieval by stashing private images in the hash space. In CVPR, 2020.
- [Xue et al.(2020)Xue, He, Wang, and Liu] Mingfu Xue, Can He, Jian Wang, and Weiqiang Liu. One-to-n & n-to-one: Two advanced backdoor attacks against deep learning models. IEEE Transactions on Dependable and Secure Computing, 2020.
- [Yang et al.(2018)Yang, Liu, Deng, and Tao] Erkun Yang, Tongliang Liu, Cheng Deng, and Dacheng Tao. Adversarial examples for hamming space search. IEEE transactions on cybernetics, 50(4):1473–1484, 2018.
- [Zhang(2004)] Tong Zhang. Solving large scale linear prediction problems using stochastic gradient descent algorithms. In ICML, 2004.
- [Zhang et al.(2023)Zhang, Liu, Wang, Lu, and Hu] Zaixi Zhang, Qi Liu, Zhicai Wang, Zepu Lu, and Qingyong Hu. Backdoor defense via deconfounded representation learning. In CVPR, 2023.
- [Zhang et al.(2020)Zhang, Liu, Luo, Huang, Shen, Shen, and Lu] Zheng Zhang, Luyao Liu, Yadan Luo, Zi Huang, Fumin Shen, Heng Tao Shen, and Guangming Lu. Inductive structure consistent hashing via flexible semantic calibration. IEEE Transactions on Neural Networks and Learning Systems, 2020.
- [Zhao and et al.(2020)] Shihao Zhao and et al. Clean-label backdoor attacks on video recognition models. In CVPR, 2020.
- [Zhao et al.(2022)Zhao, Chen, Xuan, Dong, Wang, and Liang] Zhendong Zhao, Xiaojun Chen, Yuexin Xuan, Ye Dong, Dakui Wang, and Kaitai Liang. Defeat: Deep hidden feature backdoor attacks by imperceptible perturbation and latent representation constraints. In CVPR, 2022.
- [Zhou et al.(2017)Zhou, Lapedriza, Khosla, Oliva, and Torralba] Bolei Zhou, Agata Lapedriza, Aditya Khosla, Aude Oliva, and Antonio Torralba. Places: A 10 million image database for scene recognition. IEEE TPAMI, 40(6):1452–1464, 2017.
- [Zhu et al.(2016)Zhu, Long, Wang, and Cao] Han Zhu, Mingsheng Long, Jianmin Wang, and Yue Cao. Deep hashing network for efficient similarity retrieval. In AAAI, 2016.
A Proof of Theorem 1
Theorem 1: The objective function in Eqn. (5) is an upper bounded loss, i.e.,
where each term has its respective achievable upper bound. Moreover, the overall upper bound can be achievable, if and only if is maximum.
Proof: Note that the first term of Eqn. (6) is equivalent to the maximization of the average Hamming distance among binary codewords. Without loss of generality, we denote these codewords as , i.e., , . Then we have
| where |
For the -th bit, , we let
Obviously, we have , then
where the inequality holds with equality if and only if . Since and are integers, we have
Therefore, we can obtain
For any given binary codeword , , we can always find a binary codeword whose coordinate takes opposite value of ’s, i.e., flipping to , and vice versa, to achieve the maximum Hamming distance. Thus we have
In summary, we can obtain the following upper bound on Eqn. (8):
Next we prove the necessary and sufficient condition for the case that the overall upper bound is achievable. Note that the overall upper bound is achievable is equivalent to that both upper bounds on the two terms of Eqn. (6) are achievable by the same optimal solutions. The first half of the proof reveals that second term’s optimal solutions can be obtained by directly flipping the sign of each bit to achieve the maximum Hamming distance. Thus we only need to prove the following equivalent statement: The overall upper bound can be achievable by the second term’s optimal solutions, if and only if is maximum.
Firstly, we need to prove the following claim:
Claim 1: Given any two binary codewords , flipping the sign of their bits does not change their Hamming distance.
Proof of Claim 1: Note that
Flipping the sign of their bits still makes the corresponding bits among preserve the same sign, and the bits belonging to take opposite sign as usual. So the Hamming distance between and remains unchanged.
Now we are ready to prove the equivalent statement. Note that the overall upper bound can be achievable by the second term’s optimal solution, if and only if the upper bound on the first term can be also achieved by the second term’s optimal solutions , , by flipping the sign of the bits of , . By Claim 1, we know that flipping the sign of the bits of ’s would not change their Hamming distances, i.e.,
Thus,
is maximum.
is maximum.
The overall upper bound can be achievable by the second term’s optimal solutions.
B Algorithms Outline
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/0dc6cab7-4ecf-4cad-94ef-5a98b7f63fb5/x7.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/0dc6cab7-4ecf-4cad-94ef-5a98b7f63fb5/x8.png)
C Evaluation Setup
C.1 Datasets
Three benchmark datasets are adopted in our experiment. We follow [Cao et al.(2017)Cao, Long, and et al., Xiao et al.(2020)Xiao, Wang, and Gao] to build the training set, query set, and database for each dataset. The details are described as follows.
-
•
ImageNet [Deng et al.(2009)Deng, Dong, and et al.] is a benchmark dataset for the Large Scale Visual Recognition Challenge (ILSVRC) to evaluate algorithms. It consists of 1.2M training images and 50,000 testing images with 1,000 classes. Following [Cao et al.(2017)Cao, Long, and et al.], 10% classes from ImageNet are randomly selected to build our retrieval dataset. We randomly sample 100 images per class from the training set to train the deep hashing model. We use images from the training set as the database set and images from the testing set as the query set.
-
•
Places365 [Zhou et al.(2017)Zhou, Lapedriza, Khosla, Oliva, and Torralba] is a subset of the Places database. It contains 2.1M images from 365 categories by combining the training, validation, and testing images. We follow [Xiao et al.(2020)Xiao, Wang, and Gao] to select 10% categories as the retrieval dataset. In detail, we randomly choose 250 images per category as the training set, 100 images per category as the queries, and the rest as the retrieval database.
-
•
MS-COCO [Lin et al.(2014)Lin, Maire, and et al.] is a large-scale object detection, segmentation, and captioning dataset. It consists of 122,218 images after removing images with no category. Following [Cao et al.(2017)Cao, Long, and et al.], we randomly sample 10,000 images from the database as the training images. Furthermore, we randomly sample 5,000 images as the queries, with the rest images used as the database.
C.2 Target Models
In our experiments, VGG [Simonyan and Zisserman(2015)] and ResNet [He et al.(2016)He, Zhang, Ren, and Sun] are used as the backbones of the target models. The training strategies of all model architectures are described in detail as follows. Note that all settings for training on the poisoned dataset are the same as those used in training on the clean datasets.
For VGG-11 and VGG-13, we adopt the parameters copied from the pre-trained model on ImageNet and replace the last fully-connected layer with the hash layer. Since the hash layer is trained from scratch, its learning rate is set to 10 times that of the lower layers (, 0.001 for hash layer and 0.01 for the lower layers). Stochastic gradient descent [Zhang(2004)] is used with the batch size 24, the momentum 0.9, and the weight decay parameter 0.0005.
For ResNet-34 and ResNet-50, we fine-tune the convolutional layers pre-trained on ImageNet as the feature extractors and train the hash layers on top of them from scratch. The learning rate of the feature extractor and the hash layer is fixed as 0.01 and 0.1, respectively. The batch size is set to 36. Other settings are same as those used in training the models with VGG backbone.
C.3 Attack Settings
All the experiments are implemented using the framework PyTorch [Paszke et al.(2019)Paszke, Gross, Massa, Lerer, Bradbury, Chanan, Killeen, Lin, Gimelshein, Antiga, et al.]. We provide the attack settings in detail as follows.
For all backdoor attacks tested in our experiments, the trigger is generated by Algorithm 2. The trigger is located at the bottom right corner of the images. During the process of the trigger generation, we optimize the trigger pattern with the batch size 32 and the step size 12. The number of iterations is set as 2,000.
We adopt the projected gradient descent algorithm [Madry et al.(2018)Madry, Makelov, Schmidt, Tsipras, and Vladu] to optimize the adversarial perturbations and our confusing perturbations. The perturbation magnitude is set to 0.032. The number of epoch is 20 and the step size is 0.003. The batch size is set to 20 for generating the confusing perturbations.
| Method | HashNet to DCH | DCH to HashNet |
| Tri+Adv | 82.5 | 72.6 |
| CIBA(Ours) | 91.5 | 82.4 |
| Method | 16 bits to 48 bits | 32 bits to 48 bits | 64 bits to 48 bits |
| Tri+Adv | 82.4 | 70.4 | 67.2 |
| CIBA(Ours) | 86.4 | 77.4 | 72.4 |
| Setting | Metric | VN-11 | VN-13 | RN-34 | RN-50 |
| Ensemble | t-MAP | 50.3 | 90.7 | 92.4 | 66.5 |
| MAP | 67.9 | 70.5 | 73.4 | 75.4 | |
| Single | t-MAP | 66.8 | 35.9 | 62.1 | 49.2 |
| MAP | 68.0 | 70.8 | 72.1 | 77.3 | |
| None | t-MAP | 6.3 | 12.5 | 6.6 | 1.9 |
| MAP | 68.1 | 70.4 | 73.4 | 76.7 |
D Transfer-based Attack
In the above experiments, we assume that the attacker knows the hash approach and network architecture of the target model. Here, we consider more realistic scenarios, where the attacker has less knowledge of the target model and performs the backdoor attack utilizing the transfer-based attack, under three settings: unknown hashing approach, unknown hashing code length, and unknown network architecture.
Table 6 presents the results of transfer-based attack when the hashing approaches are different. It shows that even under this more challenging setting, our CIBA can achieve higher t-MAP compared to backdoor attack with adversarial perturbations. Besides, we show the transferability results across different hashing code lengths in Table 6, which verifies the superiority of our CIBA than “Tri+Adv”.
For the unknown network architecture, we adopt two strategies: “Ensemble” and “Single”, as shown in Table 6. We set the trigger size as 56 and the number of poisoned images as 90. The trigger pattern is optimized in 500 iterations with the step size 50 and remain other attack settings unchanged. Even for the target models with the architectures of ResNet, the t-MAP values of our attack are more than 40% under the “Single" setting. These results demonstrate that CIBA can pose a serious threat to the retrieval systems in the real world.
E Resistance to Defenses
We test the resistance of our backdoor attack to the human inspection and three defense methods: pruning-based defense [Liu et al.(2018)Liu, Dolan-Gavitt, and Garg], differential privacy-based defense [Du et al.(2020)Du, Jia, and Song], and backdoor unlearning-based defense [Li et al.(2021b)Li, Lyu, and et al.]. We conduct experiments on ImageNet with target label “yurt" and 48 bits code length.

Resistance to Human Inspection. To reduce the visibility of the trigger, we apply the blend strategy to the trigger following [Chen et al.(2017)Chen, Liu, Li, Lu, and Song]. The formulation of patching the trigger is below.
where denotes the blend ratio. The smaller , the less visible trigger. We craft the poisoned images using the blended trigger to improve the stealthiness of our data poisoning and set as 1.0 at test time.
We evaluate our backdoor attack with blend ratio under different values of perturbation magnitude in Table 8. We can see that different corresponds to different optimal . With an appropriate , the t-MAP value is higher than 60% when the blend ratio is larger than 0.6. We visualize the poisoned images with different in Fig. 6. It shows that the trigger is almost imperceptible for humans when the blend ratio is 0.4, where the highest t-MAP value is 41.2% as shown in Table 8. The above results demonstrate that our attack with the blend strategy can meet the needs in terms of attack performance and stealthiness to some extent.
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |
| 0 | 14.0 | 34.0 | 37.3 | 35.5 | 33.7 |
| 0.004 | 16.4 | 31.7 | 40.6 | 42.1 | 41.0 |
| 0.008 | 16.6 | 41.2 | 51.9 | 51.0 | 49.4 |
| 0.016 | 10.4 | 36.1 | 63.6 | 60.8 | 56.0 |
| 0.032 | 4.4 | 6.6 | 28.6 | 61.4 | 66.8 |
| top left | top right | bottom left | center | |
| Tri+Adv | 62.2 | 73.4 | 71.3 | 80.7 |
| CIBA(Ours) | 65.1 | 74.6 | 76.7 | 83.1 |
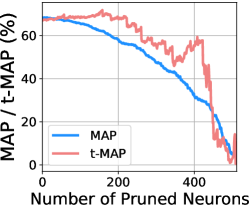
Resistance to Pruning-based Defense. Pruning-based defense [Liu et al.(2018)Liu, Dolan-Gavitt, and Garg] suggests weakening the backdoor in the attacked model by pruning the neurons that are dormant on clean inputs. We show the MAP and t-MAP results with the increasing number of pruned neurons (from 0 to 512) in Fig. 7(a). The experiments show that both MAP and t-MAP reduce a similar scale at any pruning ratio, making it hard to eliminate the backdoor injected by CIBA.
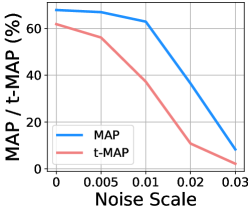
Resistance to Differential Privacy-based Defense. Du et al. [Du et al.(2020)Du, Jia, and Song] proposed to utilize differential privacy noise to obtain a more robust model when training on a poisoned dataset. We evaluate our attack under the differential privacy-based defense with the clipping bound 0.3 and varying the noise scale. The results are shown in Fig. 7(b). One can see that 0.01 is a proper choice of the noise scale, where the t-MAP value is less than 40% and the MAP is reduced slightly. Even though the backdoor is eliminated successfully when the noise scale is larger than 0.02, the retrieval performance on original query images is also poor.
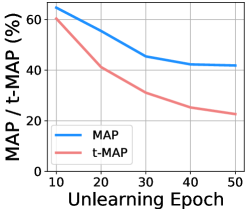
Resistance to Backdoor Unlearning-based Defense. Li et al. [Li et al.(2021b)Li, Lyu, and et al.] proposed to isolate the low-loss examples as the backdoor examples and unlearn the backdoor correlation utilizing the gradient ascent on these examples. In our experiments, we isolate 5 potential backdoor examples at the 40th epoch and perform the unlearning strategy on them. MAP and t-MAP of the backdoored model are finally reduced to 41.9% and 22.7%, respectively. The results illustrate that the unlearning strategy leads to very low performance on original query images when it defends our CIBA.
Reasons for the Resistance to Existing Defenses. Since our work is the first attempt to backdoor attack against the retrieval task, the above defenses evaluated are originally designed for the classification task. Therefore, the inapplicability of these defenses for the retrieval task may make that CIBA is somehow robust to these. Backdoor defenses customized for the retrieval task should be studied in the future.
| Setting | Metric | Tri | Tri+Adv | BadHash | CIBA (Ours) |
| GeM | t-MAP | 61.9 | 70.2 | 77.4 | 85.8 |
| MAP | 71.2 | 71.7 | 71.8 | 72.4 | |
| MAC | t-MAP | 48.6 | 57.1 | 60.2 | 66.8 |
| MAP | 57.6 | 58.1 | 58.4 | 58.5 |
| MSE | PSNR | SSIM | |
| ImageNet | 1.95 | 45.23 | 0.99 |
| Places365 | 1.59 | 46.16 | 0.98 |
| MS-COCO | 1.67 | 46.01 | 0.99 |
F Ablation Study
Effect of the Targeted Adversarial Patch Trigger and Trigger Position. We replace our targeted adversarial patch trigger with any patch-based trigger [Gu et al.(2019)Gu, Liu, and et al.] to conduct the backdoor attack. As shown in Fig. 8, our targeted adversarial patch trigger outperforms any patch-based trigger by a large margin, and thus it is necessary to use our trigger. This is because of transferability of targeted adversarial patch, which makes it can work on the poisoned model, even it is created using a different learned model. It is also verified in [Zhao and et al.(2020)]. Moreover, to investigate the effect of the trigger position, we initialize the trigger in various positions to inject the retrieval model in Table 8. The results also demonstrate the superior performance and flexibility of our proposed CIBA.
Evaluation for VGG-11 with GeM and MAC. We integrate the generalized mean-pooling (GeM) [Radenović et al.(2018b)Radenović, Tolias, and Chum] and the max-pooling (MAC) [Tolias et al.(2016)Tolias, Sicre, and Jégou] into the deep hash based VGG-11 architecture and show the results on Paris6k dataset [Radenović et al.(2018a)Radenović, Iscen, Tolias, Avrithis, and Chum] in Table 9. It can be observed that our CIBA can achieve the superior t-MAP among these four backdoor attacks.
Evaluation over five target labels. In Fig. 10, we show the average t-MAP results of three backdoor attacks with different numbers of poisoned images and trigger sizes over five target labels. In Fig. 10, we report the average t-MAP of CIBA with different and batch sizes over five target labels. These results show that our CIBA can achieve better t-MAP results than the other two previous methods.
Evaluation for the image quality. To evaluate the visual stealthiness, we calculate the MSE, PSNR, and SSIM between the original image and that with the confusing perturbation on three datasets shown in Table 10. The low MSE, the large PSNR and SSIM present the stealthiness of our proposed confusing perturbation.


G More Results
G.1 Precision-recall and Precision Curves
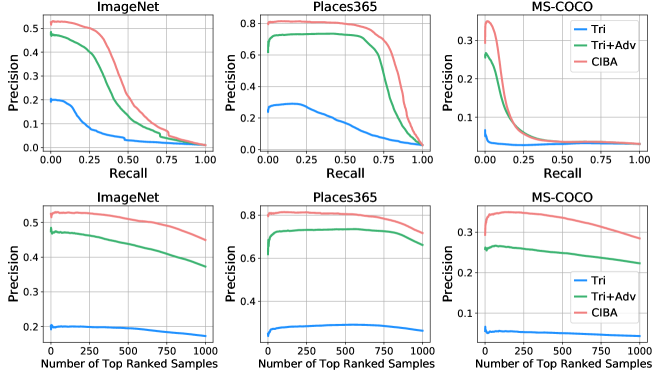
The precision-recall and the precision curves are plotted in Fig. 13. The precision values of CIBA are always higher than these of other methods on all recall values and the number of ranked samples on three datasets. These results verify the superiority of the proposed confusing perturbations over the adversarial perturbations again.
G.2 Results of Attacking with Each Target Label
We provide the results of attacking with each target label on three datasets in Table 11. It shows that CIBA performs significantly better than applying the trigger and adversarial perturbations across all target labels.
G.3 Visualization
We provide examples of querying with original images and images with the trigger on three datasets in Fig. 13. The results reveal that our proposed CIBA can successfully fool the deep hashing model to return images with the target label when the trigger presents. Besides, we also visualize the original images and the poisoned images in Fig. 13. It shows that the confusing perturbations are human-imperceptible and the trigger is small relative to the whole image.
| Dataset | Method | Metric | Target Label | ||||
| ImageNet | Crib | Stethoscope | Reaper | Yurt | Tennis Ball | ||
| None | t-MAP | 11.30 | 11.05 | 25.43 | 9.38 | 38.61 | |
| Tri | t-MAP | 33.77 | 53.08 | 65.03 | 33.70 | 88.57 | |
| Tri+Noise | t-MAP | 25.56 | 55.65 | 46.01 | 30.74 | 86.55 | |
| Tri+Adv | t-MAP | 62.55 | 52.40 | 80.06 | 58.69 | 90.17 | |
| CIBA | t-MAP | 68.17 | 64.82 | 84.51 | 66.77 | 89.27 | |
| None | MAP | 68.06 | 68.06 | 68.06 | 68.06 | 68.06 | |
| CIBA | MAP | 68.49 | 68.10 | 68.03 | 68.03 | 68.86 | |
| Places365 | Rock Arch | Viaduct | Box Ring | Volcano | Racecourse | ||
| None | t-MAP | 17.08 | 24.76 | 14.23 | 11.28 | 44.12 | |
| Tri | t-MAP | 45.76 | 58.33 | 33.30 | 36.02 | 64.67 | |
| Tri+Noise | t-MAP | 41.34 | 55.39 | 26.17 | 30.56 | 56.50 | |
| Tri+Adv | t-MAP | 86.36 | 84.27 | 84.69 | 69.57 | 88.69 | |
| CIBA | t-MAP | 93.19 | 91.03 | 94.06 | 83.79 | 92.58 | |
| None | MAP | 79.81 | 79.81 | 79.81 | 79.81 | 79.81 | |
| CIBA | MAP | 79.80 | 79.77 | 80.04 | 79.64 | 79.87 | |
| MS-COCO | Person & Skis | Clock | Person & Surfboard | Giraffe | Train | ||
| None | t-MAP | 77.44 | 5.29 | 39.25 | 2.79 | 2.93 | |
| Tri | t-MAP | 73.05 | 18.38 | 53.46 | 13.06 | 13.54 | |
| Tri+Noise | t-MAP | 62.92 | 7.756 | 49.46 | 6.077 | 9.504 | |
| Tri+Adv | t-MAP | 89.02 | 46.62 | 84.11 | 36.69 | 35.22 | |
| CIBA | t-MAP | 90.66 | 51.73 | 86.60 | 47.11 | 41.55 | |
| None | MAP | 80.68 | 80.68 | 80.68 | 80.68 | 80.68 | |
| CIBA | MAP | 80.92 | 80.46 | 81.18 | 80.64 | 80.79 | |