Balancing Robustness and Fairness via Partial Invariance
Abstract
The Invariant Risk Minimization (IRM) framework aims to learn invariant features from a set of environments for solving the out-of-distribution (OOD) generalization problem. The underlying assumption is that the causal components of the data generating distributions remain constant across the environments or alternately, the data “overlaps” across environments to find meaningful invariant features. Consequently, when the “overlap” assumption does not hold, the set of truly invariant features may not be sufficient for optimal prediction performance. Such cases arise naturally in networked settings and hierarchical data-generating models, wherein the IRM performance becomes suboptimal. To mitigate this failure case, we argue for a partial invariance framework. The key idea is to introduce flexibility into the IRM framework by partitioning the environments based on hierarchical differences, while enforcing invariance locally within the partitions. We motivate this framework in classification settings with causal distribution shifts across environments. Our results show the capability of the partial invariant risk minimization to alleviate the trade-off between fairness and risk in certain settings.
1 Introduction
In standard machine learning frameworks, models can be expected to generalize well to unseen data if the data follows the same distribution [29]. However, it has been noted that distribution shifts during test time (due to data being from different sources, locations or times) can severely degrade model performance [18, 24]. For instance, in a computer vision task to classify camels and cows, the authors ([6]) showed that during testing, the model with perfect training loss misclassified cows as camels during test time, if the image background was that of a desert. The issue arose due to the model picking up a strong but spurious correlation: during training, most cow images had green pastures, whereas camel images had deserts. Consequently, the model began to associate cows to green pastures and camels to deserts, leading to misclassification during test time. The key observation is that the vanilla classifiers are often prone to exploiting such spurious features during training (in this case, the image background), which can then hamper its performance in out-of-distribution (OOD) tasks. To fix this problem, multiple lines of research have explored the idea of enforcing invariance during learning [4, 14, 3, 17], to find invariant, causal, features that are independent of the input distribution which may vary across training environments [28]. With respect to the vision task considered before, the features specific to the cow in the image (color, shape, etc.) would correspond to invariant features. Therefore, we can obtain a robust predictor by capturing only invariant features, which inevitably capture some causal relationships about the data and thus generalize well in OOD tasks.
The Invariant Risk Minimization (IRM) framework is a promising step to address OOD generalization [4], which consists of learning a data representation that captures invariant features, followed by training a classifier on the invariant features such that it is close to optimal for all environments. The IRM classifier can perform well in OOD tasks if the conditional expectation of the target given the representation features, does not vary across environments [4, 3], which intuitively means that the data distributions overlap across environments. Due to the additional constraint that the IRM classifier should be optimal for all environments, there is an implicit notion of group fairness in IRM that encourages similar performance across environments, which has been explicitly studied in follow-up works [17, 1]. However, it is unclear how IRM performance is affected if environments do not overlap adequately. Nevertheless, it is essential to overcome any potential shortcomings of IRM in this setting, since minimally overlapping environments often occur in real-world applications. For instance, in discussions in ethnic community forums, while some linguistic features are shared among communities, there are additional features that are specific only to certain intra-community comments but not outside the community [12, 23]. Thus, one would expect the performance in a downstream task such as hate-speech detection would degrade if such intra-community (non-invariant) features are discarded by the IRM classifier.
In this work, we propose a partial invariance framework that creates partitions within environments, thus introducing the flexibility within IRM to learn non-invariant features locally within the partitions. We show that the partially invariant solution can help improve risk-fairness trade-offs in different distribution shift settings. The organization of this paper is as follows: we describe the related literature in section 2, and in section 3, we explain the details pertaining to the proposed partial invariance framework . In section 4, we conduct experiments to evaluate the efficacy of our framework, and we provide some the subsequent discussion in section 5. Finally, we highlight possible applications and future work in section 6.
2 Related Work
Many recent approaches aim to learn deep invariant feature representations: some focus on domain adaptation by finding a representation whose distribution is invariant across source and target distributions [7, 31], while others focus on conditional domain-invariance [13, 20]. However, there is evidence that domain adaption approaches are insufficient when the test distribution is unknown and may lie outside the convex hull of training distributions [19, 11, 25].
The focus of this work is the Invariant Risk Minimization (IRM) framework, proposed in [4]. The framework relates to domain generalization where access to the test distribution is not assumed. It is rooted in the theory of causality [28] and links to invariance, which is useful for generalization [26, 15]. In [2], the authors reformulate IRM via a game-theoretic approach, wherein the invariant representation corresponds to the Nash equilibrium of a game. While the IRM framework assumes only the invariance of the conditional expectation of the label given the representation, some follow-up works rely on stronger invariance assumptions [30, 22].
Several follow-up works comment on the performance of the invariant risk framework, and compare against standard Empirical Risk Minimization (ERM). It has been noted that carefully tuned ERM outperforms state-of-the-art domain generalization approaches, including IRM, across multiple benchmarks [14]. The failure of IRM may stem from the gap between the proposed framework and its practical “linear” version (IRMv1), which fails to capture natural invariances [16]. The authors of [27] demonstrate that a near-optimal solution to the IRMv1 objective, which nearly matches IRM on training environments, does no better than ERM on environments that differ significantly from the training distribution. The authors of [3] argue that IRM has an advantage over ERM only when the support of the different environment distributions have a significant “overlap”. However, unlike previous work which aim to minimize OOD risk, our primary focus is to understand the trade-off between risk minimization and fairness across environments in the setting when such a significant “overlap” may not exist. Consequently, we analyze how IRM behaves in these settings and explore alternatives via the notion of partial invariance. The notion of fairness considered in this paper relates to group sufficiency [21], which is intricately linked with the IRM objective. In fact, several works build upon the IRM framework by explicitly minimizing a quantity resembling this notion of fairness for achieving invariance [17, 10].
3 The Partial Invariance Framework
In this section, we describe a simple experiment using Gaussian mixture models (GMMs) to clearly highlight some of the pitfalls of IRM that are encountered in more complicated practical settings. For completeness, we first state the IRM formulation.
IRM Framework
Consider a set of training environments and datasets sampled in each environment from distribution , with number of samples , with , and consider a predictor function . The IRM framework aims to find a predictor which generalizes well for unseen environments. The goal is to find a data representation such that the predictor on top of is invariant across all environments .111Formally, for all that lies in supports of both , we want that . Such an invariant allows for the existence of a predictor which is simultaneously optimal for all environments, and this is the one that best approximates the conditional expectation of the label. To achieve this, the training objective for IRM can be summarized as:
| (IRM) | ||||
| s.t. |
where represents the risk in environment , pertaining to a loss function like the mean-squared or the cross-entropy loss. To simplify the bi-level optimization, the authors of [4] propose the following simplification (IRMv1):
with regularizer . In the subsequent discussion, we will describe our experimental setup. As mentioned previously, the pitfalls of IRM, including the shortcomings of (IRMv1) in finding predictors with better OOD risks have been studied before [16, 27]. We take an alternate approach where we highlight that even if IRM (IRMv1) works as intended, the underlying data-generating distribution may not allow finding a ‘good’ solution, from both classification risk and fairness considerations. Simultaneously, we will demonstrate how the partial invariance approach can help in this regard.
Problem Setup
Consider a binary classification task on univariate Gaussian mixtures on an interval of . Each GMM is parametrized as , i.e. two Gaussians with class means and equal variance . In our setup, we consider environments wherein each environment in is characterized by exactly one Gaussian mixture as . Therefore, corresponds to and corresponds to , see Fig. 1 for an illustration. Then , along with , controls how far apart the individual environments are, i.e. the cross-environmental overlap. For each environment, we consider a threshold-based classifier. The loss is the (0-1) classification loss, which yields a risk as a continuous function of the threshold . Intuitively, for , if is very large, any predictor that does well on the first environment will incur the a very high classification risk in the second environment.
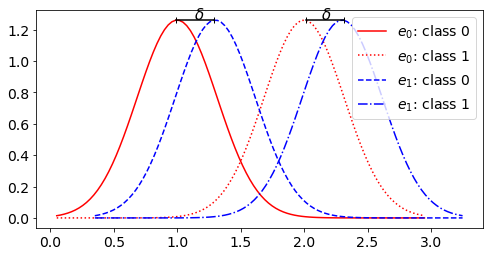
/
Motivation
One would argue that such a problem setting is naturally unsuitable for studying the nature of the IRM solution. Indeed with a single IRM predictor, it follows that with , any predictor (threshold) cannot be simultaneously optimal for all environments, unless and thus violates the assumption on the existence of a ‘meaningful’ IRM solution. However, we argue such situations can naturally arise in standard high-dimensional learning tasks, where existence of an IRM solution that is both fair and meaningful may not be guaranteed a priori. Hence the learned , either due to the nature of the data distribution or lack of representation power or simply a failure of the learning algorithm, may yield conditional distributions across environments that show little overlap. Therefore, it is important to analyze and develop countermeasures against this failure case.
Partial Invariance
It is clear from the previous discussion that in certain settings, IRM may not work as intended. Looking at the GMM problem in particular, the issue seems to arise from forcing the invariant predictor to be optimal in non-overlapping environments. One intuitive proposal is to partition the environments such that the environments within a particular partition are sufficiently “close”. Consequently, we can now enforce invariance within each partition. And that is exactly the idea of partial invariance. For now, we stick to the GMM settings as described above and we enforce partial invariance via optimizing the IRMv1 objective, within each partition. We roughly characterize the Partial-IRM approach below.
It follows from the prior discussion that partial invariance will be most effective when the environments within each partition are sufficiently close in terms of the distribution, and therefore may be inferred from the environments by minimizing some suitable divergence criterion. For our Gaussian mixtures however, fixing the size of each partition makes the environment assignment intuitive i.e. we can simply group together consecutive environments. In later sections, we will discuss how this formulation could fit in the context of causality and invariant features.
Performance Metrics
As mentioned previously, our focus is not on IRM and learning invariant features for improving OOD performance. In fact, within our GMM setup, we assume access to all environments of interest (i.e. ). Consequently, our performance metrics depend only on the different ’s. Within this framework, we analyze and compare the IRM and Partial-IRM solutions on a) classification risk and b) fairness. Given a threshold , we assume a uniform measure on the set of environments and thus, the classification risk may be computed as follows:
| (1) |
Here denotes the classification risk due to the choice of threshold for environment (i.e. the risk on the GMM parametrized as g()). Next, we estimate fairness based on the notion of "Group-Sufficiency" –satisfied when for all , where denotes membership of some sensitive class and represents a score metric. It roughly equates to equalizing the risks across environments. For a choice of threshold , we measure fairness using the V-REx penalty[17], which roughly estimates the variance of the risks across environments (lower variance implies higher fairness):
| (2) |
4 Experiments and Results
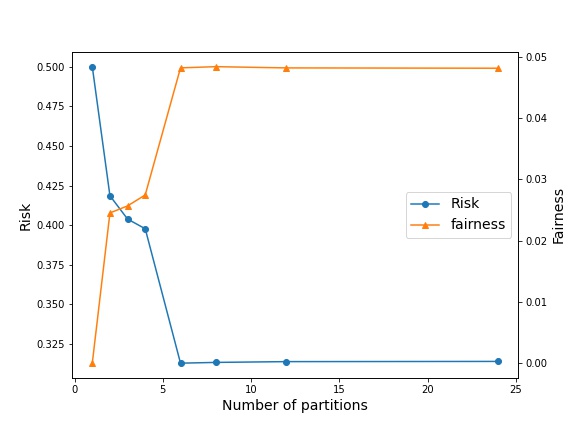
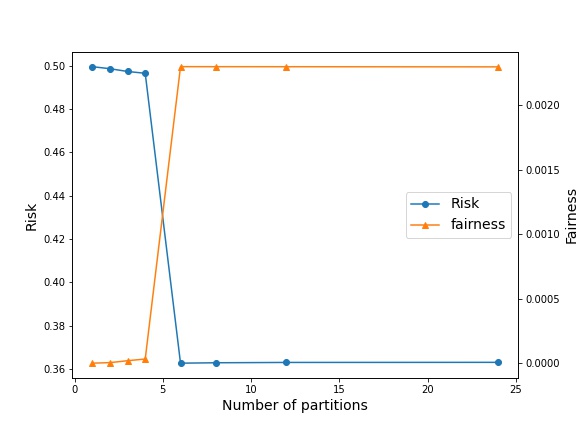
Our goal is to test the effect of creating partitions on the performance of invariant predictors, characterized by both risk and fairness. Given 24 environments, we test with different number of partitions , with equal sized partition for simplicity. The IRM case corresponds to with a single classifier for all environments, whereas the ERM case is with a classifier for each environment. Based on the Gaussian mixture model, with and , we experiment with four combinations of intra-environment separation (0.1 or 1), and cross-environments overlap (0.1 or 1), noting that the highest overlap between environments is achieved with large ( = 1) and a small ( = 0.1). We set the regularization to be 10, which for our problem suffices for IRMv1 to mirror the true IRM objective. We learn threshold classifiers, by minimizing the IRMv1 objective for the environments within that partition. In the case of partition size being equal to 1, we consider the ERM objective by setting .
High overlap (small
A small value of means that environments show a stronger degree of overlap. In this setting, we observe that the IRM solution prioritizes fairness over risk. Herein, partial invariance allows us to trade-off performance for reduced fairness. However, in certain settings wherein the classes in the environment are not well separated (large ), one can improve significantly improve the performance by paying a much lower relative cost in terms of fairness (Fig. 2(b)). This also demonstrates that P-IRM introduces flexibility in terms of balancing risk and fairness.
Low Overlap (large
Next, we consider a larger value of , meaning a low environmental overlap. In both cases, we observe that the degree of change in the risk/fairness values is lower than the previous case. However, we point out the curious case of well separated environments with low overlap, wherein P-IRM can seemingly improve both risk and fairness simultaneously (Fig. 2(c)). Since we expect such settings to arise in real world problems, our results offer us some intuition towards how P-IRM can improve performance in such settings.
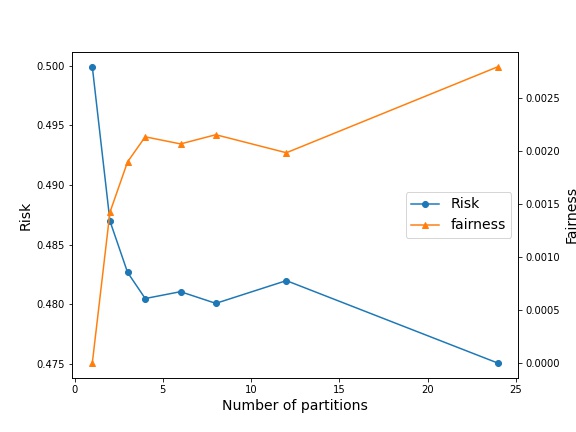
4.1 The Fairness-Robustness Trade-off
The previous experiments give us insights into the situations in which partial invariance can be beneficial in controlling the fairness-risk trade-off. Specifically, in settings with a smaller and consequently more overlap, the fairness-risk values change significantly as one increases the number of partitions. However, one could argue that such a trade-off could be achieved by simply varying the for the IRM solution. But we claim that introducing the notion of partial invariance allows us easier access to a richer solution set on this trade-off, while still retaining desirable properties.
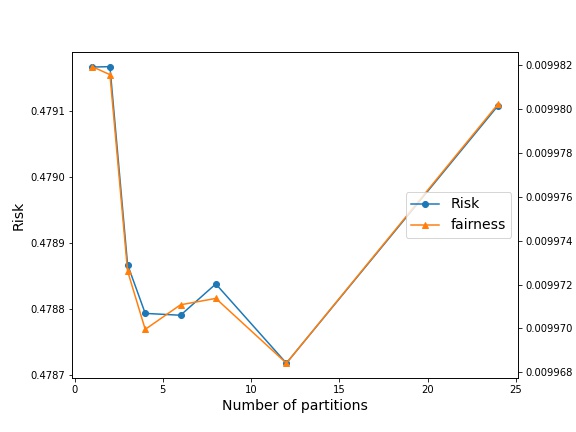
To show this, we consider the high overlap setting in which the individual Gaussians within an environment are easily separable, i.e. . The rest of the setup is exactly the same as the previous experiment. But here, we fix our data generating distribution and instead vary on the log scale. Then, for each value of and given partition size, we measure the corresponding risk and fairness values for the obtained optimal threshold. The obtained plots are presented in Fig.3.
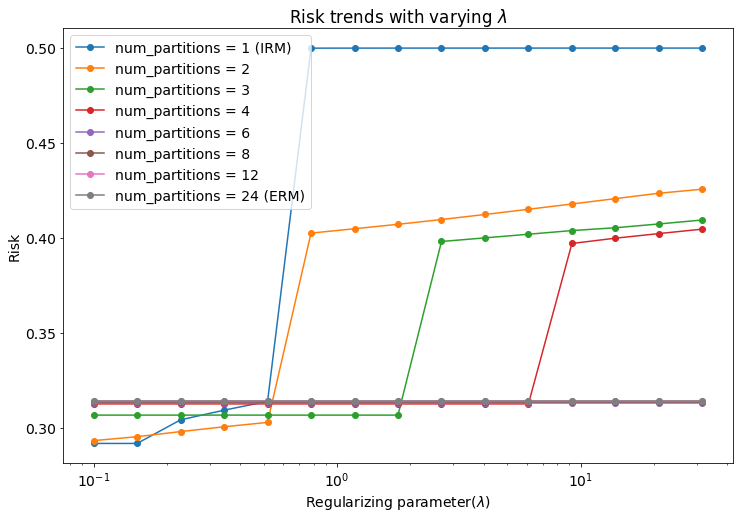
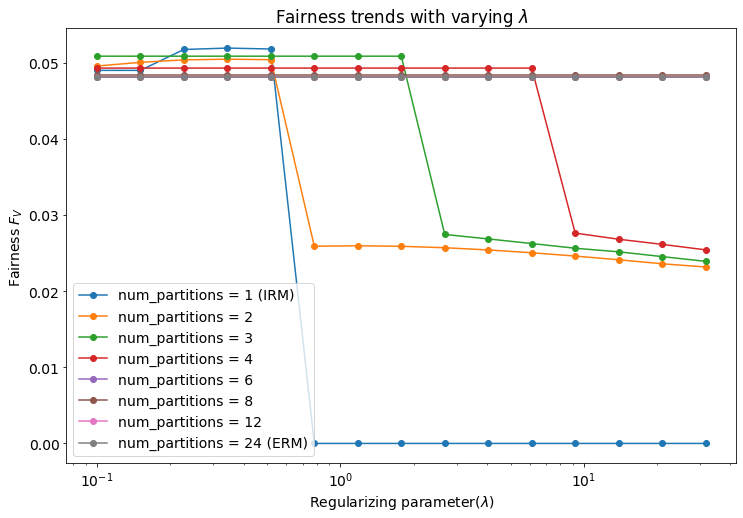
We notice that in the regions corresponding to sufficiently high values of , the Partial-IRM solutions allow us to operate on different curves corresponding to risk-fairness trade-offs, remarkable similar to receiver operating characteristic (ROC) curves in classical decision theory. Additionally, we can switch between different levels of risk/fairness by switching between the number of partitions. Note our predefined constraints on equal-sized partitions restricts the choice of partition size to integer factors of . We speculate that we might achieve even more flexibility in certain other settings, such as when both the environments and partitions being defined as continuous intervals. And the key observation here is that while IRM may be able to find similar trade-offs by reducing (the sharp slope region for the blue curve, Fig. 3(a)), it does so by compromising on the basic essence of invariance. In the discussion, we will elaborate on how this might not be desirable in certain settings.
5 Discussion
The experiments in the previous section offered us some interesting insights. We saw that when the cross-environments overlap is low, Partial-IRM offers only marginal benefits over standard IRM and ERM. This is expected because a lower similarity between environments implies that there is less common information that may be exploited. Additionally, there may exist some interesting cases wherein we can simultaneously improve upon on both fairness and classification risk, by adopting the partial invariance approach. This is somewhat surprising and certainly merits additional investigation. Next, we considered the high overlap settings. Here, the role of partial invariance in navigating the risk-fairness trade-off comes to fore. We elaborate upon this idea in the subsequent experiment, wherein we observe that by changing the size of the partition, we can switch between different levels of the risk-fairness trade-off. To achieve the same flexibility within the IRM framework, we need to operate within regions where the IRMv1 solution shows large deviations from the original IRM formulation (by reducing ). We believe this can have additional detrimental effects in situations where we would implicitly need invariance. We demonstrate one such setting below.
5.1 The Case for Partial IRM
In section 4, we observed that the notion of partial invariance allowed us to explore the inherent trade-off between risk minimization and fairness and in certain cases, simultaneously improve upon both risk and fairness as compared to the IRM solution. However, it is not yet clear as to how partial invariance fits in the “causal” picture of invariant risk minimization. We attempt to shed some light on this by slightly modifying the motivating regression task in the original IRM formulation [4].
Consider the following data generation model, where . The target is to be regressed based on observed values of . We consider two independent environment variables at play, where affects the individual distributions of the set of observables , whereas controls the marginal distribution of given via the random variable :
We consider the prediction model to estimate as . Then. it follows that if , the regression coefficients will explicitly depend on and the OOD risk of the model can grow without bound, as noted in [4]. Within the IRM framework, the only feasible representation that yields invariant predictors across is and the corresponding regression coefficients are respectively. While this solution works and generalizes for OOD tasks w.r.t. , we lose in terms of performance by discarding . In addition, deviating from the IRM solution via IRMv1 (as in the previous section) is not feasible since we require invariance w.r.t for a finite risk in worst-case environments.
Now note that the notion of partial invariance offers an intuitive solution; We could first create partitions across and then apply IRM to obtain invariance w.r.t e, potentially allowing us to get the best of both worlds. However, as in the case with GMMs, the idea implicitly assumes that the P-IRM framework can indeed partition across . In general, it is quite hard to even achieve this distinction between causal and non-causal features, without prior information on the data-generating distributions. Fortunately, it seems that it is possible to surmise this information under certain settings that arise naturally and a study of precisely these settings will be the focus of our future work.
6 Future Work/Applications
Distribution shifts naturally arise in real-world settings, particularly when environments with low overlap interact so that even though sub-groups share some common features, they can differ substantially in some other locale-specific features [23]. In such settings, the partial invariance framework can better tackle the OOD problem. Similar notions can also be found in recent literature pertaining to equivariant neural networks, in relaxing global symmetry requirements to local gauge symmetries[9].
Next, we describe applications where partial invariance could prove to be useful. In online forums, identity-related discussions in which hatred or humiliation is expressed towards certain out-groups may be considered toxic, but similar discussions in a completely in-group discussion may not [12]. Also, in forums that usually welcome diversity, explicitly mentioning identities would be acceptable and not toxic, unlike in forums that routinely make discriminatory remarks against minorities. Existing systems to detect toxicity in online forums [5, 32] do not, however, consider the environmental differences between forums and tend to perform poorly in more diverse settings [8]. As such, a model that can distinguish the type/purpose of a forum and then infer toxic mentions from this additional context, can be expected improve performance.
We note that in the current form however, it is unclear how partial invariance can be applied to real data wherein firstly, we need to decide how to partition environments and secondly, we need to infer the partition membership during test time, so as to use the corresponding classifier for optimal prediction for that sample. Therefore, in future work, we want to develop methods to automatically infer partitions from environments, by introducing appropriate notions of distance between environments.
References
- [1] David Madras Adragna Robert, Elliot Creager and Richard Zemel. Fairness and robustness in invariant learning: A case study in toxicity classification. arXiv:2011.06485 [CS.LG], December 2020.
- [2] Kartik Ahuja, Karthikeyan Shanmugam, Kush R. Varshney, and Amit Dhurandhar. Invariant Risk Minimization Games. In Proceedings of the 37th International Conference on Machine Learning (ICML’20), volume 119, pages 145–155. PMLR, July 2020.
- [3] Kartik Ahuja, Jun Wang, Amit Dhurandhar, Karthikeyan Shanmugam, and Kush R. Varshney. Empirical or Invariant Risk Minimization? A Sample Complexity Perspective. In Proceeding of the 8th International Conference on Learning Representations (ICLR’20), May 2020.
- [4] Martin Arjovsky, Léon Bottou, Ishaan Gulrajani, and David Lopez-Paz. Invariant Risk Minimization. arXiv:1907.02893 [stat.ML], 2019.
- [5] Pinkesh Badjatiya, Shashank Gupta, Manish Gupta, and Vasudeva Varma. Deep learning for hate speech detection in tweets. In Proceedings of the 26th International Conference on World Wide Web Companion, pages 759–760, April 2017.
- [6] Sara Beery, Grant V. Horn, and Pietro Perona. Recognition in Terra Incognita. In Proceedings of the European Conference on Computer Vision (ECCV), pages 456–473, September 2018.
- [7] Shai Ben-David, John Blitzer, Koby Crammer, Alex Kulesza, Fernando Pereira, and Jennifer Vaughan. A theory of learning from different domains. Machine Learning, 79:151–175, 2010.
- [8] Daniel Borkan, Lucas Dixon, Jeffrey Sorensen, Nithum Thain, and Lucy Vasserman. Nuanced metrics for measuring unintended bias with real data for text classification. In Companion Proceedings of the 2019 World Wide Web Conference, pages 491–500, May 2019.
- [9] Taco Cohen, Maurice Weiler, Berkay Kicanaoglu, and Max Welling. Gauge equivariant convolutional networks and the icosahedral cnn. In Proceedings of the 36th International Conference on Machine Learning (ICML’19), pages 1321–1330. PMLR, June 2019.
- [10] Elliot Creager, Jörn-Henrik Jacobsen, and Richard S. Zemel. Exchanging lessons between algorithmic fairness and domain generalization. 2020.
- [11] John Duchi, Peter Glynn, and Hongseok Namkoong. Statistics of Robust Optimization: A Generalized Empirical Likelihood Approach. Mathematics of Operations Research, 46(3), January 2021.
- [12] John D. Gallacher. Leveraging cross-platform data to improve automated hate speech detection. arXiv:2102.04895 [CS.CL], 2021.
- [13] Mingming Gong, Kun Zhang, Tongliang Liu, Dacheng Tao, Clark Glymour, and Bernhard Schölkopf. Domain Adaptation with Conditional Transferable Components. In Proceedings of the 33rd International Conference on Machine Learning (ICML’16), volume 48, pages 2839–2848, June 2016.
- [14] Ishaan Gulrajani and David Lopez-Paz. In Search of Lost Domain Generalization. In Proceeding of the 8th International Conference on Learning Representations (ICLR’20), May 2020.
- [15] Christina Heinze-Deml, Jonas Peters, and Nicolai Meinshausen. Invariant Causal Prediction for Nonlinear Models. Journal of Causal Inference, 6(2), September 2018.
- [16] Danica Sutherland Kamath Pritish, Akilesh Tangella and Nathan Srebro. Does Invariant Risk Minimization Capture Invariance? In Proceedigns of the International Conference on Artificial Intelligence and Statistics, pages 4069–4077. PMLR, April 2021.
- [17] David Krueger, Ethan Caballero, Joern-Henrik Jacobsen, Amy Zhang, Jonathan Binas, Dinghuai Zhang, Remi Le Priol, and Aaron Courville. Out-of-Distribution Generalization via Risk Extrapolation. In Proceedings of the 38th International Conference on Machine Learning (ICML’21), pages 5815–5826. PMLR, 2021.
- [18] Brenden M. Lake, Tomer D. Ullman, Joshua B. Tenenbaum, and Samuel J. Gershman. Building machines that learn and think like people. Behavioral and Brain Sciences, 40:e253, 2017.
- [19] Jaeho Lee and Maxim Raginsky. Minimax Statistical Learning with Wasserstein Distances. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS’18), pages 2692–2701, December 2018.
- [20] Ya Li, Mingming Gong, Xinmei Tian, Tongliang Liu, and Dacheng Tao. Domain Generalization via Conditional Invariant Representation. In Proceedings of the 32nd Association for the Advancement of Artificial Intelligence (AAAI’18), volume 31, July 2018.
- [21] Lydia T. Liu, Max Simchowitz, and Moritz Hardt. The implicit fairness criterion of unconstrained learning. In Proceedings of the 36th International Conference on Machine Learning (ICML’19), volume 97, pages 4051–4060. PMLR, June 2019.
- [22] Divyat Mahajan, Shruti Tople, and Amit Sharma. Domain Generalization using Causal Matching. In Proceedings of the 38th International Conference on Machine Learning (ICML’21), volume 139, pages 7313–7324. PMLR, June 2021.
- [23] Ankur Mani, Lav R. Varshney, and Alex Pentland. Quantization Games on Social Networks and Language Evolution. IEEE Transactions on Signal Processing, 69:3922–3934, 2021.
- [24] Gary Marcus. Deep Learning: A Critical Appraisal. arXiv:1801.00631 [CS.AI], 2018.
- [25] Mehryar Mohri, Gary Sivek, and Ananda Theertha Suresh. Agnostic Federated Learning. In Proceedings of the 36th International Conference on Machine Learning (ICML’19), volume 97, pages 4615–4625. PMLR, June 2019.
- [26] Jonas Peters, Peter Bühlmann, and Nicolai Meinshausen. Causal inference by using invariant prediction: identification and confidence intervals. Journal of the Royal Statistical Society. Series B (Statistical Methodology), 78(5):947–1012, 2016.
- [27] Elan Rosenfeld, Pradeep Kumar Ravikumar, and Andrej Risteski. The Risks of Invariant Risk Minimization. In Proceeding of the 8th International Conference on Learning Representations (ICLR’20), May 2020.
- [28] B. Schölkopf, D. Janzing, J. Peters, E. Sgouritsa, K. Zhang, and J. Mooij. On causal and Anticausal Learning. In Proceedings of the 29th International Conference on Machine Learning (ICML’12), pages 1255–1262, June 2012.
- [29] Vladimir Vapnik. The Nature of Statistical Learning Theory. Springer Science and Business Media, 2013.
- [30] Chuanlong Xie, Haotian Ye, Fei Chen, Yue Liu, Rui Sun, and Zhenguo Li. Risk Variance Penalization. arXiv:2006.07544 [cs.LG], April 2021.
- [31] Kun Zhang, Mingming Gong, and Bernhard Schoelkopf. Multi-Source Domain Adaptation: A Causal View. In Proceedings of the 29th Association for the Advancement of Artificial Intelligence Conference (AAAI’15), January 2015.
- [32] Ziqi Zhang and Lei Luo. Hate speech detection: A solved problem? the challenging case of long tail on twitter. Semantic Web, 10(5):925–945, 2019.