Ballistic PbTe Nanowire Devices

Electron transport in a semiconductor nanowire is highly sensitive to disorder, owing to its large surface-to-volume ratio and the lack of screening. Consequently, transport in such systems is commonly diffusive. Reducing disorder in nanowires is a challenging task, but urgently needed [1] for its potential applications in quantum devices, e.g. the realization of Majorana zero modes. A clean semiconductor nanowire coupled to a superconductor has been predicted to host Majorana zero modes [2, 3]. Despite tremendous efforts being devoted to reducing disorder in InAs and InSb nanowire devices [4, 5, 6, 7, 8], all the Majorana nanowire experiments [9, 10, 11, 12, 13, 14, 15] so far still suffer from disorder. Take, for instance, the four recent studies: the observation of quantized zero-bias peaks in a thin InAs-Al nanowire [16], simulating Kitaev chain using two quantum dots coupled to a superconductor [17], the topological-gap-protocol devices based on three-terminal InAs-Al [18], and the zero-bias peaks in phase-tunable planar Josephson junctions [19]. All these studies have used a gate-tunable quantum point contact (QPC) as the probe, yet none of them can reveal quantized plateaus for their normal state conductance. The quantized conductance is a characteristic signature of ballistic QPCs [20, 21] and signifies a minimal degree of disorder. The absence of ballistic transport implies that significant amount of disorder is present or even dominating in those III-V semiconductor experiments. Moreover, extensive theory studies have also strongly suggested that disorder is the current roadblock in Majorana research [22, 23, 24, 1, 25, 26].

Here, we explore PbTe nanowires, an IV-VI semiconductor, as an alternative platform. We demonstrate ballistic transport in these wires that may circumvent the challenges posed by disorder. PbTe nanowires have recently attracted much interest due to their large dielectric constant ($\sim$1350), which can screen charge disorder [27]. Experimentally, these nanowires and networks have been successfully grown using the selective-area-growth (SAG) technique [28, 29]. Basic transport characterizations, including phase coherent transport [30], quantum dots [31], the superconducting proximity effect [32], and the hard gap [33], have been demonstrated. While quantized conductance plateaus have been observed [34], they require a large magnetic field ($B\sim$ 6 T). The zero-field transport remains diffusive. Recently, we have reduced the device disorder. In this study, we report the observation of quantized conductance in PbTe nanowires at zero magnetic field, indicative of ballistic transport. Previously, zero-field quantization has been realized in III-V nanowires [35, 6, 36, 37], mainly grown using the vapor-liquid-solid technique. Those wires are, however, difficult to scale up for future applications. Notably, none of the previous SAG nanowires could reveal zero-field ballistic transport [38, 39, 40, 41, 42], making our observations a step forward in enhancing the quality of SAG wires. Another potential application, closely aligned with Majorana research, involves the helical gap induced by spin-orbit interaction [43]. Despite years of searching, the re-entrance behavior observed in earlier experiments [44, 45, 46] may possibly be disorder-induced [47]. Our devices could serve as a clean platform to identify signatures of helical gaps.

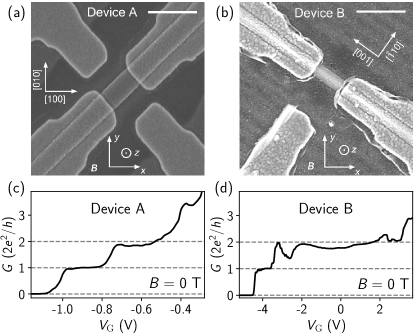
Figures 1(a) and 1(b) illustrate scanning electron micrographs (SEMs) of two devices, denoted as A and B. The PbTe nanowires were selectively grown on a CdTe substrate [28]. A thin insulating layer of Pb_1-xEu_xTe was grown prior to the PbTe growth, which could suppress disorder [48]. The value of $x$ is estimated to be 0.08 for device A and 0.07 for device B. The substrate of device A is CdTe(001) while for device B it is CdTe(110). After the PbTe growth, a thin layer of Pb_1-xEu_xTe (CdTe) was capped for device A (B) to prevent oxidization. Ohmic contacts and side gates were deposited via the evaporation of Ti/Au. The thickness of Ti is $\sim$ 10 nm, and for Au it is 55 (75) nm for device A (B). The two side gates of device A were interconnected during the measurement.

The linear conductance as a function of the gate voltage ($V_{\text{G}}$) for both devices exhibits quantized plateaus, as shown in Figs. 1(c-d). $B$ = 0 T. These measurements were performed in a dilution refrigerator operating at its base temperature ($\sim$ 50 mK). Standard two-terminal circuit was used to obtain the device differential conductance, $G\equiv dI/dV$. The bias voltage $V$ between the two contacts was fixed to zero. The line-resistance, mainly contributed by the fridge filters, was subtracted. Contact resistances of 900 $\Omega$ for device A and 500 $\Omega$ for device B were estimated (and subtracted) based on the plateau values.

The zero-field plateaus are in steps of $2e^{2}/h$, indicating the lifting of valley degeneracy in PbTe nanowires on both (001) and (110) substrates. The pre-factor of 2 originates from spin degeneracy. Earlier numerical calculations had suggested a two-fold valley degeneracy along these crystal orientations [27]. Our recent work has indeed confirmed this two-fold degeneracy by observing $2e^{2}/h$ plateaus at high magnetic fields along the same orientation as device A [34]. In the current study, we have reduced the wire thickness to $\sim$ 40 nm for device A (as opposed to $\sim$ 100 nm in our previous work [34]). We thus attribute the lifting of valley degeneracy in device A to a stronger confinement. For device B, the nanowire top surface is triangle-like. Note that the valley degeneracy could be lifted by device asymmetry due to the capping/substrate layer, the side mask or a side gate.

Conductance oscillations are present and superimposed on the plateaus of device B in Fig. 1(d). The oscillation amplitudes are large for the second plateau and small for the first one. We ascribe the small oscillations on the first plateau to be Fabry-Pérot-induced, a phenomenon typical in QPCs with sharp confinement potentials [49]. The large modulations on the second plateau likely arise from a quasi-bound state, which will be discussed later.

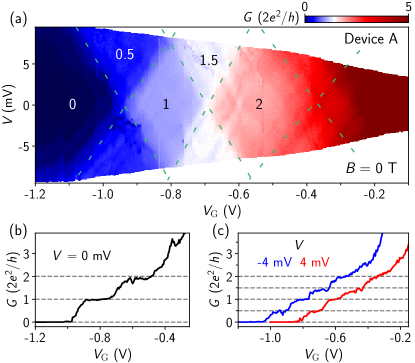
To reveal the sizes of subband spacing, Fig. 2(a) shows the 2D conductance map, $G$ vs $V$ and $V_{\text{G}}$. For the waterfall and transconductance plots of Fig. 2(a), see Fig. S1 in the Supplemental Material. The zero-bias plateaus are now revealed as diamond shapes within which the conductance remains nearly constant. The diamond values are labeled in units of $2e^{2}/h$. The diamond boundaries (dashed lines) correspond to the alignment of the quasi-fermi levels in the source/drain contacts with each subband. The sizes of the diamonds thus provide a direct measurement of the energy spacing between subbands. We estimate the spacing between the second subband ($E_{2}$) and the first one ($E_{1}$) to be $E_{2}-E_{1}\sim$ 8.3 meV. Likewise, the spacing $E_{3}-E_{2}\sim$ 9.6 meV can also be estimated, with $E_{3}$ denoting the third subband. Moreover, the half plateaus at finite bias correspond to situations in which the quasi-fermi levels of the source and drain contacts are positioned within different subbands. Line cuts at both zero and finite bias for integer and half plateaus are shown in Figs. 2(b-c).

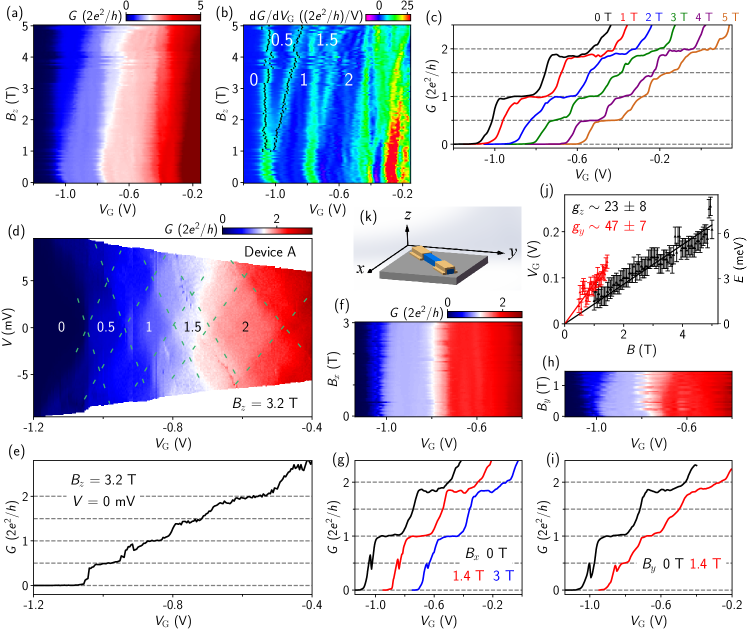
Next we study the $B$ dependence of these plateaus. Figure 3(a) shows the $B$ scan along the $z$ axis, which is perpendicular to the nanowire (out-of-plane). The coordinate axes are drawn in the middle panel of Fig. 3 (also labeled in Fig. 1(a)). As $B$ is increased, the $e^{2}/h$ and $3e^{2}/h$ plateaus gradually emerge and expand from the $2e^{2}/h$ and $4e^{2}/h$ plateaus. These half plateaus (in units of $2e^{2}/h$) arise due to the Zeeman splitting of subbands. The transconductance, $dG/dV_{\text{G}}$ in Fig. 3(b), can better illustrate this evolution, see also Fig. 3(c) for line cuts.

Figure 3(d) presents the 2D scan of $G$ vs $V$ and $V_{\text{G}}$ with $B_{z}$ being fixed at 3.2 T. The dashed lines highlight the plateau diamonds, with labeled values provided in units of $2e^{2}/h$. For the waterfall and transconductance plots, see Fig. S1. The zero-bias line cut in Fig. 3(e) illustrates the plateaus, accompanied by charge jumps, e.g. near $V_{\text{G}}$ = -0.9 V. The charge jump occurred swiftly (within a single pixel of the color map), leading to a sharp conductance drop. Obviously, this re-entrance behavior is not the signature of a helical gap.

Figures 3(f-i) are the $B$ scans along two other directions. The $B$ range is limited by hardware. The small peaks below the first plateau are charge jumps. Notably, the $e^{2}/h$ plateau is already well developed for $B_{y}$ = 1.4 T (the red curve in Fig. 3(i)). As a contrast, this half plateau is absent for $B_{x}$ at the same field (the red curve in Fig. 3(g)), and also barely visible for $B_{z}$ at an even higher field of 2 T (the blue curve in Fig. 3(c)). This anisotropic behavior indicates variations in the Landé $g$-factor for different $B$ directions.

In Fig. 3(j) we extract the width of the $e^{2}/h$ plateau as a function of $B$ along the $z$ and $y$ axes. The width is estimated based on the spacing between the black dots (peaks in the transcodnuctance) in Figs. 3(b) and S1(f). The $B_{x}$ scan does not reveal the $e^{2}/h$ plateau at the highest applied field (3 T), thus not presented. The plateau width in $V_{\text{G}}$ is converted to energy based on the lever arm extracted from Fig. 2(a). This energy corresponds to the Zeeman splitting $|E_{1\downarrow}-E_{1\uparrow}|=g\mu_{\text{B}}B$. $\mu_{\text{B}}$ is the Bohr magneton and the arrows denote spins. The slopes of the linear fits give a $g$-factor of 23 $\pm$ 8 for $B_{z}$ and 47 $\pm$ 7 for $B_{y}$. Note that the presence of a charge jump near $e^{2}/h$ plateau may lead to a slight overestimate of the corresponding $g$-factor. For the analysis of other plateaus and the corresponding $g$-factors, see Fig. S1. The $g$-factor anisotropy in nanowires is widely present [31] and depends on various factors such as confinement and crystal direction [27, 50].

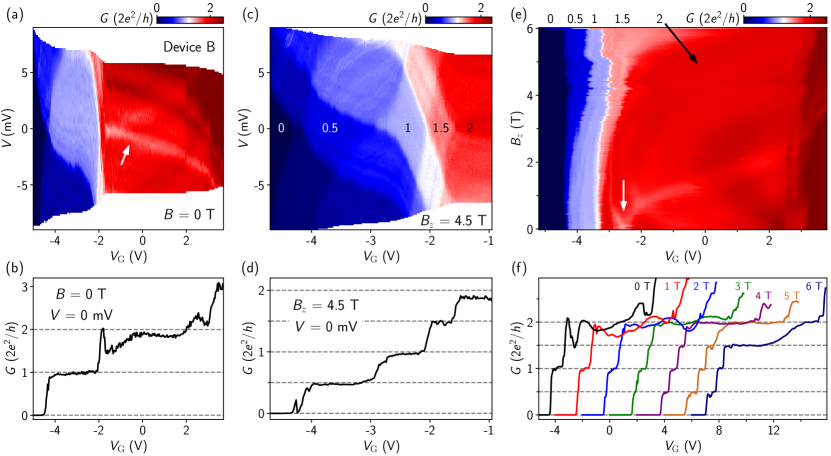
Figure 4 shows a second device (device B) that exhibits ballistic transport. The first plateau appears as a twisted diamond in Fig. 4(a). This twist implies a non-linear crosstalk between bias and gate voltages. The origin of this crosstalk is currently unknown. The size of the diamond suggests a subband spacing $E_{2}-E_{1}\sim$ 8 meV. The second plateau in Fig. 4(b) is severely modulated by a quasi-bound state, a resonant level formed by weak scattering within the device. Its energy is gate tunable, see the white arrow in Fig. 4(a). These resonant-induced oscillations can mimic the re-entrance behavior characteristic of a helical gap [47].

At $B_{z}$ = 4.5 T, the first four spin-resolved plateaus, in steps of $e^{2}/h$, are clearly revealed in Figs. 4(c-d). The diamonds of the 0.5 and 1 plateaus (in units of $2e^{2}/h$) also exhibit a twisted shape. The $4e^{2}/h$ plateau in Fig. 4(d) is slightly lower than the quantized value, suggesting a non-unity transmission for that particular subband. We estimate a $g$-factor of $\sim$ 15 based on the size of the 0.5 plateau ($\sim$ 4 meV). Fabry-Pérot-like oscillations are visible within the plateau diamonds in Fig. 4(c), suggesting a sharp QPC constriction potential [49].

In Fig. 4(e) we show the $B_{z}$ evolution of the plateaus with line cuts shown in Fig. 4(f). The resonance level on the second plateau in Fig. 4(e) quickly splits upon increasing $B$ (see the white arrow), possibly due to Zeeman splitting. As a result, the resonant-level-induced oscillations are suppressed at higher fields, see Fig. 4(f). For the waterfall plots of Figs. 4(a) and 4(c), the transconductance of Figs. 4(a), 4(c) and 4(e), and the $g$-factor estimations, see Fig. S2 in the Supplemental Material.

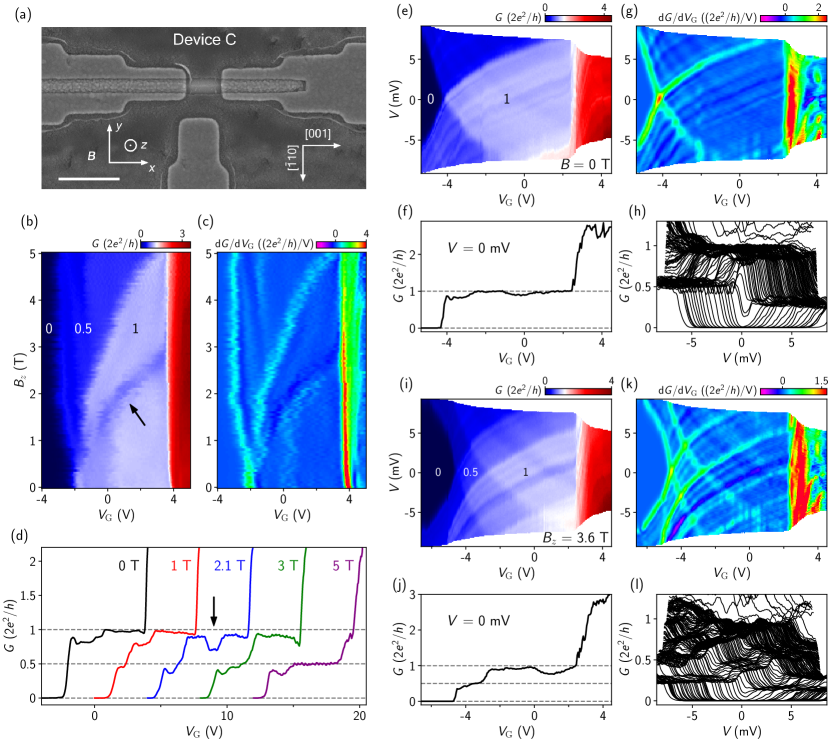
We further present a third ballistic device (device C), see the SEM in Fig. 5(a). The substrate is CdTe(110). Figures 5(b-d) illustrate the $B_{z}$ scan, the transconductance plot and line cuts. A contact resistance of 1.1 k$\Omega$ was subtracted. The $2e^{2}/h$ plateau is clearly revealed at zero field. The absence of the $4e^{2}/h$ plateau indicates valley or orbital degeneracy of the second subband. As $B_{z}$ is increased, the $e^{2}/h$ plateau emerges and expands due to Zeeman splitting.

Notably, an additional dip feature (see the arrow in Figs. 5(b) and 5(d)) also develops on the $2e^{2}/h$ plateau. The blue line cut in Fig. 5(d) depicts this drop, a re-entrance of conductance, on the $2e^{2}/h$ plateau. This re-entrance behavior, obviously not a charge jump, is reminiscent of a helical gap. For a continuous evolution of the dip, see all the line cuts ($B_{z}$ from 0 T to 4 T) of this feature in Fig. S3. The $B_{y}$ and $B_{x}$ scans, also shown in Fig. S3, do not reveal this re-entrance signature, possibly due to the $g$-factor anisotropy. The dip does not reach $e^{2}/h$, while a conductance dip of $e^{2}/h$ is expected in the ideal situation of a helical gap. Furthermore, the dip bends towards higher energy (more positive $V_{\text{G}}$) for higher $B_{z}$, where in the simplest helical gap model, the re-entrance dip should gradually merge toward the $e^{2}/h$ plateau. These deviations suggest that either the observation does not arise from a helical gap or a more sophisticated helical gap model is required. Unlike III-V semiconductors, the highly anisotropic properties of PbTe does lead to a complicated situation, e.g. $B_{z}$ could also induce Zeeman splitting for spins along $x$ and $y$ axis, as the $g$-factor in PbTe is a tensor [27] and may be $B$ dependent. More theory inputs and experimental studies in more devices with different wire geometries and orientations are required before one can conclude on the origin of this re-entrance observation.

Figures 5(e-h) show the 2D map of the first plateau, the transconductance and the waterfall plots at zero field while Figs. 5(i-l) are for $B_{z}$ = 3.6 T. The diamond size in Fig. 5(e) suggests a subband spacing $E_{2}-E_{1}\sim$ 8.7 meV. Fabry-Pérot oscillations are present and superimposed on the plateau diamonds, shown in Figs. 5(e) and 5(g). The first plateau in Fig. 5(f) is revealed as clusters of curves near $2e^{2}/h$ in the waterfall plots in Fig. 5(h). The clusters at high biases, e.g. $V=\pm$5 mV, are the fractional plateaus. The fractional values are not exactly half, probably due to the asymmetry of the device circuit. The lock-in excitation ($dV$) is not equally shared between the quasi-fermi levels of the source and drain contacts. The diamond size of the 0.5 plateau in Fig. 5(i) is $\sim$ 3.2 meV, indicating a $g$-factor of $\sim$ 15. Besides the three devices (A-C), Figs. S4-S6 present three additional devices that exhibit signatures of ballistic transport at zero field.

In summary, we have observed quantized conductance plateaus in units of $2e^{2}/h$ at zero magnetic field in PbTe nanowires. The plateau values indicate the lifting of valley degeneracy in PbTe. At finite magnetic fields, half plateaus can be observed due to Zeeman splitting. Landé $g$-factor can be extracted and its anisotropy has been discussed. A conductance dip on the $2e^{2}/h$ plateau is observed in one device, reminiscent of (also with deviations from) the possible re-entrance behavior of a helical gap. These ballistic PbTe nanowire devices represent an improvement on diminishing disorder in SAG nanowires, which may advance the Majorana research and the search of spin-orbit helical gaps.

See pages 1 of PbTe_Ballistic_SM.pdf See pages 2 of PbTe_Ballistic_SM.pdf See pages 3 of PbTe_Ballistic_SM.pdf See pages 4 of PbTe_Ballistic_SM.pdf See pages 5 of PbTe_Ballistic_SM.pdf See pages 6 of PbTe_Ballistic_SM.pdf