Bayesian outcome selection modelling

Suppose we observe $K$ continuous outcomes for each of the $n$ individuals. The outcomes will typically be correlated because they are measures from the same individual, though they may be of different scales and nature. For example, the outcomes measure different domains of a person’s cognition function. Therefore, exposure effects are not expected to be exactly the same across affected outcomes but vary around a mean level $\mu$, which we identify as the parameter of interest. For each individual, we observe the exposure variable $x$ and use $z$ to denote other observed predictor variables that can be added to the model. In the application to our motivating study in Section 4, $z$ is a propensity score computed for each individual to adjust for confounders.

We now show how to express our multiple outcomes data as panel data in long format. Consider a sample of $n$ independent individual labeled $j=1,\dots,n$, where each individual provides $K$ outcomes labeled $p=1,\dots,K$. Suppose we stack the observations of all $n$ individuals together, this gives us a data set with $nK$ observations in total. Row $i$ of this data set records the observed outcome corresponds to individual $j[i]$ and outcome $p[i]$.

To represent the multiple outcome problem as a multiple predictors problem, we first define a new set of covariates $x_{1},\dots,x_{K}$,

$$x_{ik}=\text{exposure}_{j[i]}\bm{1}(p[i]=k),$$

for $i=1,\dots,nK$, individual $j=1,\dots,n$ and outcome $p=1,\dots,K$. These are the interaction terms between the exposure level and the dummy variables indicating the outcome variables. An example of the dataframe format and how to map from the multiple outcome format to the stacked format for $n$ individuals and $K=3$ outcome variables is presented in Figure 2.1.

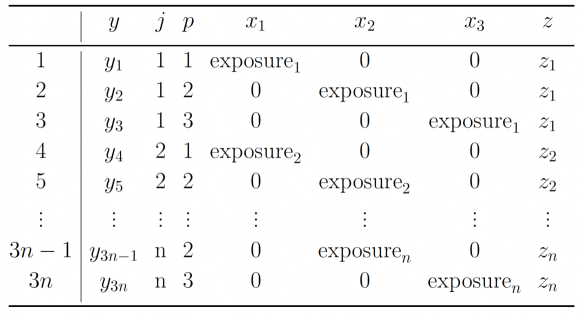
We then model the $y_{i}$ using a linear mixed model:

(2.1)

$$y_{i}=\nu_{p[i]}+\alpha_{j[i]}+\sum_{k=1}^{K}\beta_{k}x_{ik}+\gamma_{p[i]}z_{j[i]}+\epsilon_{i},$$

for $i=1,\dots,nK$, individual $j=1,\dots,n$ and outcome $p=1,\dots,K$. The error terms $\epsilon_{i}$ are independent and normally distributed, $\epsilon_{i}\sim N(0,\sigma^{2}_{p[i]})$ and the random effect $\alpha_{j[i]}\sim N(0,\sigma_{r}^{2})$ accounts for the within-individual correlation and $\alpha_{j}\mathchoice{\mathrel{\hbox to0.0pt{$\displaystyle\perp$\hss}\mkern 2.0mu{\displaystyle\perp}}}{\mathrel{\hbox to0.0pt{$\textstyle\perp$\hss}\mkern 2.0mu{\textstyle\perp}}}{\mathrel{\hbox to0.0pt{$\scriptstyle\perp$\hss}\mkern 2.0mu{\scriptstyle\perp}}}{\mathrel{\hbox to0.0pt{$\scriptscriptstyle\perp$\hss}\mkern 2.0mu{\scriptscriptstyle\perp}}}\alpha_{j^{\prime}}$ for $j\neq j^{\prime}$.

The parameters $\nu_{p}$ and $\gamma_{p}$ are outcome-specific intercepts and coefficients for $z$, and the coefficients $\beta_{k}$ represents the exposure effect on outcome $k$, assumed to vary around a common value $\mu$:

$$\beta_{k}\sim N(\mu,\tau^{2}),$$

for $k=1,\dots,K$.

This "trick" of expressing the multiple outcomes problem as a repeated measures problem has been widely used in the literature, making it straightforward to then analyze multiple outcomes using standard mixed modelling or GEE software [28]. Now we have a mixed model with both varying intercepts and varying coefficients. We will perform variable selection on the $K$ covariates $x_{1},\dots,x_{K}$.

If we assume that all outcomes are associated in a similar way with the exposure or treatment of interest, with effects varying around a mean level $\mu$, then we can assign appropriate priors for $\mu$ and $\tau$ and estimate the model using a Bayesian estimation procedure. In this new outcome selection framework, we assume that some of the outcomes are not relevant to the analysis. This implies $\beta_{k}=0$ for some $k$. We then use variable selection priors to analyze $\beta_{k}$.

Over the past decade or so, variable selection methodologies have been extended to the random effect context, see for example [29, 30] and [31]. For our model, because we do not need to perform variable selection for the random effects, it is straightforward to use existing techniques for the independent predictors $x_{k}$. This means that we can potentially use any of a variety of sparsity priors, such as stochastic search variable selection [32], Bayesian LASSO [33, 34] and the horseshoe prior [35] for outcome selection. However, because we are interested in selecting the subset of affected outcomes variables and quantifying the mean exposure effect on these variables, in this study we focus on the use of the stochastic search variable selection method. We discuss this further in the next section.

There is a large literature on Bayesian variable selection methods, however in this paper we only discuss the “slab and spike” type of priors, as they are suitable for our problem of identifying sensitive outcomes from a large number of outcomes. Methods that compare models by Bayes Factor [36] or criteria such as DIC [37] or WAIC [38] require fitting all candidate models and hence only applicable when comparing a small number of models. Therefore, they are not suitable for the outcome selection problem.

Methods involving a “slab and spike” prior can be divided into two categories: Methods that specify a prior that approximate the “slab and spike” shape for the coefficients $\beta_{k}$; and methods that use latent indicator variables that indicate whether a covariate is included in the model. Shrinkage priors such as the Bayesian LASSO [33, 34] and the horseshoe prior [35] belong to the first category. The implementation of these methods is straightforward and they have extensive use in the recent years, however it is not possible to modify these priors to incorporate a common mean of the non-zero coefficients.

The second category defines a latent variable $I_{k}$ that indicates whether a coefficient $\beta_{k}$ is non-zero. In the approaches proposed by [39] and [40], a coefficient $\beta_{k}$ is set to 0 if $I_{k}=0$. These approaches are harder to tune to ensure the iterates of $I_{k}$ do not get stuck at $0$ or $1$. Our method is motivated by the stochastic search variable selection (SSVS) method [32], which defines a mixture prior for $\beta_{k}$ instead: Let $I_{k}$ be a latent indicator variable, with $I_{k}=1$ means covariate $k$ is included in the model, $I_{k}=0$ means it is not. The indicator affects the prior of $\beta_{k}$, so we can define a joint prior for $(I_{k},\beta_{k})$ as

$$p(I_{k},\beta_{k})=p(\beta_{k}|I_{k})p(I_{k}).$$

Conditioning on $I_{k}$, the prior of $\beta_{k}$ is

$$p(\beta_{k}|I_{k})=(1-I_{k})N(0,g_{1})+I_{k}N(0,\tau^{2}).$$

The tuning parameters $g_{1}$ and $\tau^{2}$ specify the scale of the conditional prior of $\beta_{k}$ given $I_{k}$ and are typically data dependent: they should take into account the posterior distribution of the $\beta_{k}$ and hence the size of the data [32]. Ideally, $g_{1}$ should be small enough such that if $\beta_{k}\sim N(0,g_{1})$, then $\beta_{k}$ can be safely replaced by $0$. On the other hand, $\tau$ must be large enough such that non-zero $\beta_{k}$ can be included in the model. These parameters can be fixed or estimated as the model’s parameters [32]. Another variation of SSVS is when $g_{1}$ being $\tau$ multiplied by a constant [41].

For our outcome selection framework, we propose to modify the SSVS prior to incorporate the mean exposure effect $\mu$ on the sensitive outcomes. Conditioning on $I_{k}$, we now have a mixture prior for $\beta_{k}$

(2.2)

$\displaystyle p(\beta_{k}|I_{k})=(1-I_{k})N(0,g_{1})+I_{k}N(\mu,\tau^{2}).$

To improve the performance of the model, we follow [41] and modify the prior in (2.2) to

(2.3)

$\displaystyle p(\beta_{k}|I_{k})=(1-I_{k})N(0,\tau^{2}/c)+I_{k}N(\mu,\tau^{2}).$

The constant $c$ can be chosen by trial-and-error to ensure good separation between the ‘in’ and ‘out’ variables. The standard deviations $\tau$, $\sigma_{k}$ and $\sigma_{r}$ are assigned log-normal priors in our simulation examples and real data application.

Note that the posterior mean of $I_{k}$ will be the posterior probability that outcome $k$ is included in the model, hence it will be important in terms of interpreting the results of our model fit. The prior, $p(I_{k}=1)$, can simply be a categorical distribution with a fixed probability parameter. This prior probability may be different across outcomes, based on the experts’ knowledge, or fixed at 0.5 so that the prior is non-informative. We can also treat $p(I_{k}=1)$ as a parameter to be estimated [26].

In the first simulation example, we generated data from the model (2.1):

$\displaystyle y_{ik}$

$\displaystyle=\nu_{k}+\beta_{k}x_{i}+\alpha_{i}+\gamma_{k}z_{i}+\epsilon_{ik};\quad\epsilon_{ik}\sim N(0,\sigma_{k}^{2}).$

This is the same as the model that is the basis for our proposed method in Section 2.1. The data were generated as follows: The intercepts were generated from $N(0,1)$ and the standard deviations $\sigma_{k}^{2}$ are generated from $N(1.5,0.3)$. The coefficients $\beta_{k}$ corresponding to the relevant outcomes were generated from $N(\mu,0.01\mu^{2})$ to ensure that the $\beta_{k}$ are scattered closely enough around $\mu$. We used two different values for the mean common effect $\mu$: $\mu=-0.1$ and $\mu=-3$. The first setting represents a situation when the effect is weak with small data, so that the posterior standard deviation is large. In this case it would be difficult for the model to decide whether a $\beta_{k}$ is 0 or not. The second setting mimics the situation in which the effect is stronger, and the selection method is expected to work better.

The performance of the SSVS algorithm in detecting the affected outcomes for different $\mu$ and $K_{1}$ is presented in the top 6 rows of Table 1. The result shows that the original and our modified SSVS algorithms have very similar performance, but both do not do well in detecting the affected outcomes when $\mu$ is small. This is expected as the overall effect $\mu$ is small, so some of the relevant $\beta_{k}$ would be close to 0. Because here we used uninformative priors for $I_{k}$, the algorithm will keep switching between stage $I_{k}=0$ and $I_{k}=1$ for these outcomes. This is similar to the phenomenon observed by O’Hara and Sillanpää in [26], where the posterior probabilities of $I_{k}$ are close to $0.5$ and some outcomes are classified incorrectly by chance.

Table 2 shows the mean squared errors of estimating the individual coefficient $\beta_{k}$:

(3.1)

$$\text{MSE}=\frac{1}{K}\sum_{k=1}^{K}(\widehat{\beta}_{k}-\beta_{k})^{2},$$

where we take the estimate $\widehat{\beta}_{k}$ to be the posterior mean of $\beta_{k}|I_{k}=1$ if the posterior mean of $I_{k}$ is greater than 0.5; otherwise we set $\widehat{\beta}_{k}=0$. For both large and small values of $\mu$, the SSVS priors provide more accurate estimates of $\beta_{k}$ in terms of MSE, compared to the model without variable selection.

Lastly, Table 3 shows the estimated of $\mu$, averaged over 10 simulations, by different priors. Table 3 shows that our modified SSVS can provide estimates of $\mu$ that are closer to the result from the subset model, especially for large $\mu$. However, when the effect is weak, the model is not able to estimate $\mu$ accurately because it fails to identify the correct set of sensitive outcomes.

This simulation example shows that SSVS priors can provide accurate estimates of the coefficients, and accurately identify the affected outcomes and estimate the mean effect when $\mu$ is far from 0. However, it may require more informative priors for $I_{k}$ and better tuning to capture small effects accurately.

In this example, we attempt to fit the model to less ideal data, which have a more complicated correlation structure. The data were generated according to a confirmatory factor analysis as follows:

(3.2)		$\displaystyle\bm{y}_{i}$	$\displaystyle=\bm{\nu}+\bm{\Lambda}\begin{bmatrix}\eta_{1,i}\\ \eta_{2,i}\end{bmatrix}+\bm{e}_{i},\quad\bm{e}_{i}\sim N(0,\Psi)$
(3.3)		$\displaystyle\eta_{1,i}$	$\displaystyle=\omega x_{i}+0.1z_{i}+u_{i},\quad u_{i}\sim N(0,1)$
(3.4)		$\displaystyle\eta_{2,i}$	$\displaystyle\sim N(0,1).$

Here only the first factor $\eta_{1}$ is linked to the exposure $x$ while the second factor does not. In this experiment, although we are not interested in fitting factor analysis models, we find them to be a useful strategy for generating data with correlated outcomes, but where only some of them are influenced by the exposure $x$. In the example $\bm{\Lambda}$ will be a $K\times 2$ matrix where $\Lambda[k,1]=0$ for $k>K_{1}$, for $K_{1}$ being the number of relevant outcomes that load into $\eta_{1,i}$. When generating the data, the elements of $\bm{\Lambda}$ correspond to $\eta_{1}$ and $\eta_{2}$ were generated from $N(1,0.1)$ and $N(1,0.2)$ respectively. The intercepts were randomly sampled from $N(0,100)$. The covariance matrix $\Psi$ of the error term $\bm{e}_{i}$ is diagonal.

Here we still examine the ability of SSVS to correctly capture the relevant outcomes in various settings and compare it to other approaches. We generated data with $n=100$ individuals and total number of outcomes $K=20$ from the two-factor model as outlined at the beginning of this section. We test our outcome selection priors for $\omega=-0.5$ and $\omega=-3$ while varying the number of relevant outcomes in $K_{1}=5,10,15$.

The last 6 rows of Table 1 record the performance of different priors in identifying the relevant outcomes in the two scenarios. An outcome is classified as “relevant” by the fitted model if the posterior mean of the corresponding $I_{k}$ is greater than 0.5. Table 1 shows that, in this non-ideal situation, the proposed model may classify an affected outcome as irrelevant, or vice versa when the effect is weak. On the other hand, when the effect $\mu$ is strong, most of the time the model correctly identifies the relevant outcomes. Our proposed prior where $\mu$ is treated as a parameter seems to perform slightly better than the original SSVS where $\mu=0$.

The bottom part of Table 2 presents the MSE in estimating the coefficients, and we take $\beta_{k}=\bm{\Lambda}_{k,1}\times\omega$. Similar to the previous experiment, the SSVS priors give more accurate estimates of $\beta_{k}$ for $\omega=-3$, and have similar accuracy with the model without variable selection when the overall effect is small.

Table 4 shows the mean effect $\mu$ estimated by different methods. Note that the $\omega$ we used to generate the data is not equal to the true mean effect $\mu$. But the implied true value of $\mu$ can be computed by multiplying $\omega$ with the average of the non-zero loadings corresponding to the first factor. We provide these values in the third column of Table 4. Similar to the previous experiment, our proposed model does not perform well in the first scenario where $\omega=-0.5$. In both cases, inclusion of the irrelevant outcomes results in a smaller estimate of $\mu$. Not surprisingly, our modified SSVS prior shows similar results with the subset model and their estimates are close to the true values when $\omega=-3$. On the other hand, all priors being considered do not give accurate estimates of mean effect for small $\omega$. This is consistent with our observation in Section 3.1.

We fit the model (2.1) with the prior in (2.3) to the data set. To adjust for confounders associated with both alcohol exposure and cognitive function we add a propensity score $z$ which was computed beforehand. For details on the covariates included in the propensity score and how it was constructed we refer readers to [46]. Before running the analysis, we rescaled all outcomes to mean 0 and variance 1.

We fit our proposed model with a few different settings. We start with an uninformative prior for the indicator $I_{k}$ and set $p(I_{k}=1)=0.5$ for all $k$. We use the prior in (2.3) with $c=100$ for $\beta_{k}$ where $\tau$ is assigned a log-normal$(0,1)$ prior. We also choose a normal $N(0,1)$ prior for $\mu$. As a comparison, we also try the prior in (2.2) where we fix $g_{1}=0.2^{2}$ and a shrinkage prior. For the shrinkage prior, we simply follow [33] and assign a $\text{Laplace}(0,1)$ prior for the $\beta_{k}$. We also attempt the horseshoe prior [35] for $\beta_{k}$ but the MCMC has convergence issue and hence the result is not presented here.

To assess how sensitive the result is to the prior probability $p(I_{k}=1)$, we also fit the model with a more informative set of $p(I_{k}=1)$,

$$p(I_{k}=1)=(0.5,0.5,0.2,0.5,0.8,0.8,0.2,0.8,0.5,0.5,0.8,0.8,0.8,0.5).$$

These prior probabilities were chosen by utilizing expertise knowledge and set the probability of the outcomes that are known to be relevant to be closer to 1. In practice, more informative priors may help the MCMC to have better mixing.

We also fit the model (2.1) to only those outcomes chosen by our SSVS model with a hierarchical prior $\beta\sim N(\mu,\tau^{2})$. We call this model the “subset” model. Similar to in the simulation studies, we will compare the estimates of $\beta_{k}$ and $\mu$ from this reduced model with our approach.

For the rest of the parameters, we choose relatively non-informative priors. We assign a normal $N(0,1)$ prior for $\mu$, log-normal$(0,10)$ for $\sigma_{r}$ and $\sigma_{k}$, $k=1,\dots,14$. The prior for $\nu_{k}$ and $\gamma_{k}$ are normal $N(0,1000)$ and normal $N(0,100)$, respectively. The SSVS models are fitted using the software JAGS [42], running 3 chains each with $200,000$ burn-in and $200,000$ samples with thinning $=10$. The other models are implemented in STAN [43].

The results are presented in Tables 5 and 6. Table 5 shows the mean posterior probability of $I_{k}=1$. For the Laplace shrinkage prior, we report whether 0 is outside of the $95\%$ credible intervals of the parameters. All SSVS models choose the same set of relevant outcomes in different setting. The informative prior on $p(I_{k})$ results in different posterior mean of $I_{k}$, however, it does not affect the inference on the outcomes’ relevance for most outcome variables. The only exception is CBCL Externalizing at age 7, of which the posterior probability of being affected is slightly less than 0.5 (0.44 and 0.49) with a non-informative prior and slightly higher than 0.5 (0.53) with an informative prior. These results are also similar to the that of the Laplace shrinkage prior; however this prior shrinks more $\beta_{k}$ towards 0 than the SSVS priors.

Table 6 presents the estimates of $\beta_{k}$ and overall effect $\mu$. The SSVS with informative $p(I_{k}=1)$ and the subset model suggest a strong negative effect of PAE on the cognitive outcomes. These findings are consistent with those in [10]. The estimate of $\tau$ is similar for both models (0.19 vs 0.17). On the other hand, the SSVS models with the non-informative prior suggest a weaker effect (-0.33 and -0.32 versus -0.41). The non-informative prior also results in a larger estimate of $\tau$ (0.22 and 0.24 versus 0.19).

Table 6 shows that all SSVS models produce smaller estimates for the coefficients of the affected outcomes and hence $\mu$, compared to the subset model. The result here is consistent with our observation in the simulation studies in Section 3. However, as shown in Tables 5 and 6, our proposed model produces very similar estimates of $\beta_{k}$ compared to the Laplace prior in all settings. Table 6 also indicates that the informative prior for the indicator $I_{k}$ produces estimates of $\beta_{k}$ and $\mu$ that are closer to the subset model that only includes the affected outcomes.