Beating the break-even point with a discrete-variable-encoded logical qubit
Abstract
Quantum error correction (QEC) aims to protect logical qubits from noises by utilizing the redundancy of a large Hilbert space, where an error, once it occurs, can be detected and corrected in real time. In most QEC codes, a logical qubit is encoded in some discrete variables, e.g., photon numbers. Such encoding schemes make the codewords orthogonal, so that the encoded quantum information can be unambiguously extracted after processing. Based on such discrete-variable encodings, repetitive QEC demonstrations have been reported on various platforms, but there the lifetime of the encoded logical qubit is still shorter than that of the best available physical qubit in the entire system, which represents a break-even point that needs to be surpassed for any QEC code to be of practical use. Here we demonstrate a QEC procedure with a logical qubit encoded in photon-number states of a microwave cavity, dispersively coupled to an ancilla superconducting qubit. By applying a pulse featuring a tailored frequency comb to the ancilla, we can repetitively extract the error syndrome with high fidelity and perform error correction with feedback control accordingly, thereby exceeding the break-even point by about 16% lifetime enhancement. Our work illustrates the potential of the hardware-efficient discrete-variable QEC codes towards a reliable quantum information processor.
One of the main obstacles for building a quantum computer is environmentally-induced decoherence, which destroys the quantum information stored in the qubits. The errors caused by decoherence can be corrected by repetitive application of a quantum error correction (QEC) procedure, where the logical qubit is encoded in a high-dimensional Hilbert space, such that different errors project the system into different orthogonal subspaces and thus can be unambiguously identified and corrected without disturbing the stored quantum information. In conventional QEC schemes Nielsen and Chuang (2010); Terhal (2015), the codewords of a logical qubit are respectively formed by two highly symmetric entangled states of multiple physical qubits encoded with some discrete variables. The past two decades have witnessed remarkable advances in experimental demonstrations of this kind of QEC code in different systems, including nuclear spins Cory et al. (1998); Knill et al. (2001), nitrogen-vacancy centers in diamond Waldherr et al. (2014); Abobeih et al. (2022), trapped ions Chiaverini et al. (2004); Schindler et al. (2011); Egan et al. (2021); Ryan-Anderson et al. (2021); Postler et al. (2022), photonic qubits Yao et al. (2012), silicon spin qubits Takeda et al. (2022), and superconducting circuits Reed et al. (2012); Kelly et al. (2015); Córcoles et al. (2015); Chen et al. (2021); Krinner et al. (2022); Zhao et al. (2022); Acharya et al. (2022). However, in these experiments, the lifetime of the logical qubit still needs to be significantly extended to reach that of the best available physical component, which is regarded as the break-even point for judging whether or not a QEC code can benefit quantum information storage and processing.
An alternative QEC encoding scheme is to employ the large space of an oscillator, which can be used to encode either a continuous-variable or discrete-variable qubit Cai et al. (2021); Joshi et al. (2021); Flühmann et al. (2019); Campagne-Ibarcq et al. (2020); Gertler et al. (2021). Both types of codes can tolerate errors due to loss and gain of energy quanta, enabling QEC to be performed in a hardware-efficient way. Breakthrough QEC demonstrations have been reported in a circuit quantum electrodynamics (QED) system Ofek et al. (2016), where the break-even point was exceeded by distributing the quantum information over an infinite-dimensional Hilbert space, but realized with logical qubits bearing two non-orthogonal codewords. This inherent restriction can be overcome with discrete-variable encoding schemes, where the codewords of a logical qubit are encoded with mutually orthogonal Fock states of an oscillator. This feature, together with their intrinsic compatibility with error-correctable gates Ma et al. (2020); Reinhold et al. (2020), as well as with their usefulness for logically connecting modules in a quantum network Chou et al. (2018), makes such discrete-variable qubits promising in fault-tolerant quantum computation. These advantages can be turned into practical benefits in real quantum information processing only when the lifetime of the encoded logical qubits is extended beyond the break-even point, which, however, remains an elusive task, although enduring efforts have been made towards this goal Hu et al. (2019); Gertler et al. (2021).
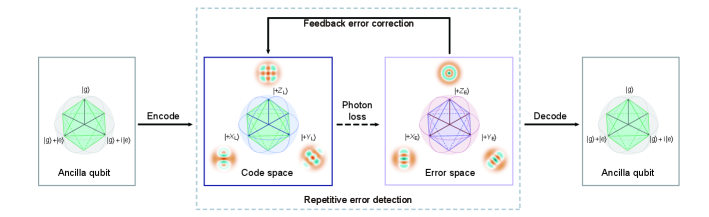
Here, we demonstrate the exceeding of the QEC break-even point by real-time feedback correction for a discrete-variable photonic qubit in a microwave cavity, whose codewords remain mutually orthogonal and can be unambiguously discriminated. The dominate error, single photon loss, of the logical qubit is mapped to the state of a Josephson-junction based nonlinear oscillator that is dispersively coupled to the cavity and serves as an ancilla qubit, realized with a continuous pulse involving an ingeniously tailored comb of frequency components. As the driving frequencies aim at the error space where a photon loss event occurs, perturbations on the logical qubit are highly suppressed when it remains in the encoded logical space. Another intrinsic advantage of this error syndrome detection is that the continuous driving protects the system from the ancilla’s dephasing noise. We demonstrate this procedure with the lowest-order binomial code and extend the stored quantum information lifetime 16% longer than the best physical qubit, encoded in the two lowest Fock states and referred to as the Fock qubit. A more important characteristic associated with this error-detecting procedure is that neither the logical nor the error space needs to have a definite parity, which allows the implementation of QEC codes that can tolerate losses of more than one photon.
The key ingredients of a QEC procedure include encoding the quantum information to the logical qubit from the ancilla, the error syndrome measurement, the real-time error correction of the system depending on the measurement output, and the decoding process to readout the quantum information stored in the logical qubit. Our logical qubit is realized in a three-dimensional microwave cavity, and the dominant decoherence to combat is the excitation loss error. The logical qubit is encoded with a binomial code Michael et al. (2016), with the codewords
where the number in each ket denotes the photon number in the cavity. The binomial code is a typical stabilizer QEC code: When the single-photon-loss error occurs, the quantum information is projected into the error space spanned by {}, with the photon number parity acting as the error syndrome to distinguish these two spaces. A general QEC protection of quantum information stored in the bosonic system is illustrated in Fig. 1. After correctly measuring the photon number parity and applying the corresponding correction operations in real time, quantum information stored in the cavity can be recovered.
The experiments are performed with a circuit QED architecture Blais et al. (2021), where a superconducting transmon qubit Koch et al. (2007) as an ancilla is dispersively coupled to a three-dimensional microwave cavity Paik et al. (2011); Axline et al. (2016); Reagor et al. (2016). The ancilla qubit has an energy relaxation time of about 98 s and a pure dephasing time of 968 s, while the storage cavity has a single-photon lifetime of 578 s (corresponding to kHz), and a pure dephasing time of 4.4 ms. The universal control of the multiple photon states of the cavity can be realized by utilizing the anharmonicity of the ancilla, and thus the key ingredients of the QEC procedure, as illustrated in Fig. 1, to the logical qubit encoded in the high-dimensional Fock spaces of the bosnoic mode can be realized.
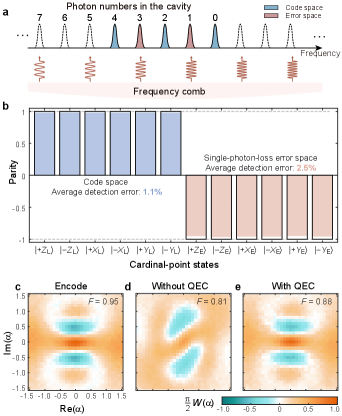
Our route towards the break-even points in the QEC is two folds: improving both the operation fidelity to the logical qubit and the error syndrome measurement fidelity. The first goal is achieved by employing a tantalum transmon qubit with high coherence Place et al. (2021); Wang et al. (2022) and an optimal quantum control technique Khaneja et al. (2005) with carefully calibrated system parameters [see Methods]. We attempt the second goal by an ingenious scheme of projection measurement of a selected collection of Fock states. The principle of the scheme is illustrated in Fig. 2a, where a classical microwave pulse containing frequency components is applied on the ancilla to read out the Fock states. Since the frequency of the ancilla is entangled with the photon number [see Methods for more details], error syndrome detection is achieved by mapping the even (odd) parity to the ancilla ground state (excited state ) in a quantum non-demolition manner. This approach holds potential advantages of more flexible choices of error spaces and less sensitive to ancilla damping and dephasing errors since the ancilla excitation is pronounced only when loss error happened.
To characterize our syndrome measurement, the cavity is encoded to the six cardinal-point states in the Bloch spheres of both the code and error spaces based on the lowest-order binomial codewords. The measured results of the cavity photon number parities are displayed in Fig. 2b and show an average detection error of 1.1% and 2.5% for the cavity states in the code and error spaces, respectively. The encoding of the cavity, one of the most elementary processes of QEC, is further verified by the Wigner function with a high fidelity of 0.95, as shown in Fig. 2c.
Based on the above techniques, the QEC process of the binomial code can be implemented following the procedure in Fig. 1. However, practical imperfections limit the QEC performance: (i) during a waiting time of , i.e. an idle process, there is a probability of about for a two-photon-loss error, which is undetectable for this lowest-order binomial code. (ii) Due to the non-commutativity of the single-photon-loss error and the self-Kerr interaction of the cavity, there is a large dephasing effect of the logical qubit induced by the unpredictable photon loss event, thus destroying the stored quantum information. (iii) Quantum recovery operations are imperfect. It is worth noting that there is a logical state distortion even if no photon loss is detected Michael et al. (2016). Considering the whole system, strategies to mitigate the above imperfections are introduced: choose an optimal waiting time, employ a two-layer QEC procedure Hu et al. (2019) to avoid unnecessary operation errors introduced by the error corrections, and adopt the photon-number-resolved a.c. Stark shift (PASS) method Ma et al. (2020) during idle operations to suppress the photon-jump-error-induced decoherence in the code space (see Supplementary Information for more details). The measured Wigner functions of the cavity states after a single QEC cycle (about 90 s of waiting) without and with performing the error correction operation are shown in Fig. 2(d, e), with state fidelities of 0.81 and 0.88 respectively.
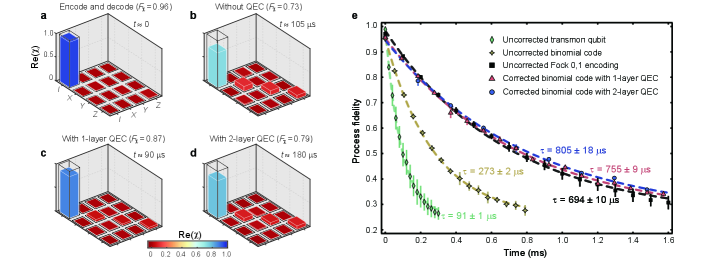
The performance of the QEC is benchmarked by the process fidelity , which is defined by comparing the experimental measured process matrix for the QEC process with the ideal process matrix for an identity operation. In Fig. 3a, we present the measured process matrix for the encoding and decoding process only, which indicates a reference fidelity of 0.96. In the absence of a QEC operation after a waiting time of 105 s, the process fidelity is reduced to a value of 0.73 due to the inability to protect the quantum information stored in the cavity from the single-photon-loss error, with the corresponding measured process matrix shown in Fig. 3b. When utilizing the QEC operation, the process fidelity is indeed improved due to the protection from the single-photon-loss error, with the process matrices for the one- and two-layer QECs shown in Fig. 3(c, d), respectively.
The most important benchmark to characterize the performance of a QEC procedure is the gain in the lifetime of the protected logical qubit against that of the constituent element with the longest lifetime. For the 3D circuit QED device, the best physical qubit is encoded with the two lowest photon-number states {, }, which is more robust against decoherence effects than any other encoded photonic qubit without QEC protection. To quantitatively show the advantage of our QEC scheme, in Fig. 3e we display the measured process fidelities of the corrected binomial code as a function of the storage time with the repetitive one-layer (red triangles) and two-layer (blue circles) QECs, as well as those for the unprotected binomial code (yellow stars), the transmon qubit (green diamonds), and the Fock qubit (black squares) for comparison.
All curves are fitted according to the function with corresponding to the lifetime of the specific encoding and being a fitting parameter. The offset in the fitting function is fixed to 0.25, implying a complete loss of information at the final time. As a result, the lifetime for the corrected binomial code with one-layer QECs is improved by about 8.3 times compared to the uncorrected transmon qubit, 2.8 times compared to the uncorrected binomial code. In particular, is about times longer than the uncorrected Fock qubit encoding, i.e., exceeds the break-even point of QEC in this system. Employing the two-layer QEC scheme, the corresponding lifetime of the logical qubit is improved to about 8.8 times that of the uncorrected transmon qubit, 2.9 times that of the uncorrected binomial code, and 1.2 times that of the break-even point. These results demonstrate that the quantum information stored in the cavity with multiphoton binomial encoding can indeed be preserved and protected from the photon loss errors via repetitive QEC operations.
Table 1 shows an overall error analysis for the one- and two-layer QEC experiments. The error sources are divided into four parts: the intrinsic errors for the lowest-order binomial code, the error detection errors, the recovery operation errors, and the ancilla thermal excitation errors during the QEC cycle. These errors can be estimated from either the numerical simulations, or the measurement results of individual calibration experiments (see Supplementary Information). The predicted lifetimes for the QEC experiments, calculated by Hu et al. (2019), with and being the total duration and the weighted total error per QEC cycle, are well consistent with those in our QEC experiments.
| Error source | 1-layer QEC | 2-layer QEC |
|---|---|---|
| Intrinsic error* | 6.4% | 12.4% |
| Detection error | 1.4% | 2.8% |
| Recovery error | 2.9% | 3.8% |
| Thermal error | 0.8% | 1.1% |
| Total error | 11.5% | 20.1% |
| Predicted lifetime | 757 s | 824 s |
| Measured lifetime | s | s |
In conclusion, we experimentally demonstrate the prolonged coherence time of quantum information encoded with discrete variables in a bosonic mode by repetitive QEC. The break-even point has been reached by carefully designing the QEC procedure to balance the fidelity losses due to the undetectable errors during the idle process and the error detection and correction operations. Presently, the main infidelity is contributed by the two-photon-loss error that is beyond the ability of our current QEC code, but can be corrected by higher-order binomial codes Michael et al. (2016). Our frequency comb method could naturally be utilized to measure the generalized photon number parity of such codes, enabling detection and correction of both single- and two-photon-loss errors. Our work thus represents a key step towards scalable quantum computing and provides a practical guide for system optimization of quantum control and the design of the QEC procedure for future applications of logical qubits.
Note added–After completion of the experiment, we became aware of a QEC experiment, which also goes beyond the break-even point, but is based on a continuous-variable encoding scheme.
Online content
Any methods, additional references, Nature Research reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available on line.
References
- Nielsen and Chuang (2010) M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, 10th ed. (Cambridge University Press, Cambridge ; New York, 2010).
- Terhal (2015) B. M. Terhal, “Quantum error correction for quantum memories,” Rev. Mod. Phys. 87, 307 (2015).
- Cory et al. (1998) D. G. Cory, M. D. Price, W. Maas, E. Knill, R. Laflamme, W. H. Zurek, T. F. Havel, and S. S. Somaroo, “Experimental Quantum Error Correction,” Phys. Rev. Lett. 81, 2152 (1998).
- Knill et al. (2001) E. Knill, R. Laflamme, R. Martinez, and C. Negrevergne, “Benchmarking Quantum Computers: The Five-Qubit Error Correcting Code,” Phys. Rev. Lett. 86, 5811 (2001).
- Waldherr et al. (2014) G. Waldherr, Y. Wang, S. Zaiser, M. Jamali, T. Schulte-Herbrüggen, H. Abe, T. Ohshima, J. Isoya, J. F. Du, P. Neumann, and J. Wrachtrup, “Quantum error correction in a solid-state hybrid spin register,” Nature 506, 204 (2014).
- Abobeih et al. (2022) M. H. Abobeih, Y. Wang, J. Randall, S. J. H. Loenen, C. E. Bradley, M. Markham, D. J. Twitchen, B. M. Terhal, and T. H. Taminiau, “Fault-tolerant operation of a logical qubit in a diamond quantum processor,” Nature 606, 884 (2022).
- Chiaverini et al. (2004) J. Chiaverini, D. Leibfried, T. Schaetz, M. D. Barrett, R. B. Blakestad, J. Britton, W. M. Itano, J. D. Jost, E. Knill, C. Langer, R. Ozeri, and D. J. Wineland, “Realization of quantum error correction,” Nature 432, 602 (2004).
- Schindler et al. (2011) P. Schindler, J. T. Barreiro, T. Monz, V. Nebendahl, D. Nigg, M. Chwalla, M. Hennrich, and Rainer Blatt, “Experimental repetitive quantum error correction,” Science 332, 1059 (2011).
- Egan et al. (2021) L. Egan, D. M. Debroy, C. Noel, A. Risinger, D. Zhu, D. Biswas, M. Newman, M. Li, K. R. Brown, M. Cetina, and C. Monroe, “Fault-tolerant control of an error-corrected qubit,” Nature 598, 281 (2021).
- Ryan-Anderson et al. (2021) C. Ryan-Anderson, J. G. Bohnet, K. Lee, D. Gresh, A. Hankin, J. P. Gaebler, D. Francois, A. Chernoguzov, D. Lucchetti, N. C. Brown, T. M. Gatterman, S. K. Halit, K. Gilmore, J. A. Gerber, B. Neyenhuis, D. Hayes, and R. P. Stutz, “Realization of Real-Time Fault-Tolerant Quantum Error Correction,” Phys. Rev. X 11, 041058 (2021).
- Postler et al. (2022) L. Postler, S. Heuen, I. Pogorelov, M. Rispler, T. Feldker, M. Meth, C. D. Marciniak, R. Stricker, M. Ringbauer, R. Blatt, P. Schindler, M. Müller, and T. Monz, “Demonstration of fault-tolerant universal quantum gate operations,” Nature 605, 675 (2022).
- Yao et al. (2012) X.-C. Yao, T.-X. Wang, H.-Z. Chen, W.-B. Gao, A. G. Fowler, R. Raussendorf, Z.-B. Chen, N.-L. Liu, C.-Y. Lu, Y.-J. Deng, Y.-A. Chen, and J.-W. Pan, “Experimental demonstration of topological error correction,” Nature 482, 489 (2012).
- Takeda et al. (2022) K. Takeda, A. Noiri, T. Nakajima, T. Kobayashi, and S. Tarucha, “Quantum error correction with silicon spin qubits,” Nature 608, 682 (2022).
- Reed et al. (2012) M. D. Reed, L. DiCarlo, S. E. Nigg, L. Sun, L. Frunzio, S. M. Girvin, and R. J. Schoelkopf, “Realization of three-qubit quantum error correction with superconducting circuits,” Nature 482, 382 (2012).
- Kelly et al. (2015) J. Kelly, R. Barends, A. G. Fowler, A. Megrant, E. Jeffrey, T. C. White, D. Sank, J. Y. Mutus, B. Campbell, Y. Chen, Z. Chen, B. Chiaro, A. Dunsworth, I.-C. Hoi, C. Neill, P. J. J. O’Malley, C. Quintana, P. Roushan, A. Vainsencher, J. Wenner, A. N. Cleland, and J. M. Martinis, “State preservation by repetitive error detection in a superconducting quantum circuit,” Nature 519, 66 (2015).
- Córcoles et al. (2015) A. Córcoles, E. Magesan, S. J. Srinivasan, A. W. Cross, M. Steffen, J. M. Gambetta, and J. M. Chow, “Demonstration of a quantum error detection code using a square lattice of four superconducting qubits,” Nat. Commun. 6, 6979 (2015).
- Chen et al. (2021) Z. Chen, K. J. Satzinger, J. Atalaya, A. N. Korotkov, A. Dunsworth, and et al., “Exponential suppression of bit or phase errors with cyclic error correction,” Nature 595, 383 (2021).
- Krinner et al. (2022) S. Krinner, N. Lacroix, A. Remm, A. Di Paolo, E. Genois, C. Leroux, C. Hellings, S. Lazar, F. Swiadek, J. Herrmann, G. J. Norris, C. K. Andersen, M. Müller, A. Blais, C. Eichler, and A. Wallraff, “Realizing repeated quantum error correction in a distance-three surface code,” Nature 605, 669 (2022).
- Zhao et al. (2022) Y. Zhao, Y. Ye, H.-L. Huang, Y. Zhang, D. Wu, and et al., “Realization of an Error-Correcting Surface Code with Superconducting Qubits,” Phys. Rev. Lett. 129, 030501 (2022).
- Acharya et al. (2022) R. Acharya, I. Aleiner, R. Allen, T. I. Andersen, M. Ansmann, and et al., “Suppressing quantum errors by scaling a surface code logical qubit,” arXiv:2207.06431 (2022).
- Cai et al. (2021) W. Cai, Y. Ma, W. Wang, C.-L. Zou, and L. Sun, “Bosonic quantum error correction codes in superconducting quantum circuits,” Fundam. Res. 1, 50 (2021).
- Joshi et al. (2021) A. Joshi, K. Noh, and Y. Y. Gao, “Quantum information processing with bosonic qubits in circuit QED,” Quantum Sci. Technol. 6, 033001 (2021).
- Flühmann et al. (2019) C. Flühmann, T. L. Nguyen, M. Marinelli, V. Negnevitsky, K. Mehta, and J. P. Home, “Encoding a qubit in a trapped-ion mechanical oscillator,” Nature 566, 513 (2019).
- Campagne-Ibarcq et al. (2020) P. Campagne-Ibarcq, A. Eickbusch, S. Touzard, E. Zalys-Geller, N. E. Frattini, V. V. Sivak, P. Reinhold, S. Puri, S. Shankar, R. J. Schoelkopf, L. Frunzio, M. Mirrahimi, and M. H. Devoret, “Quantum error correction of a qubit encoded in grid states of an oscillator,” Nature 584, 368 (2020).
- Gertler et al. (2021) J. M. Gertler, B. Baker, J. Li, S. Shirol, J. Koch, and C. Wang, “Protecting a bosonic qubit with autonomous quantum error correction,” Nature 590, 243 (2021).
- Ofek et al. (2016) N. Ofek, A. Petrenko, R. Heeres, P. Reinhold, Z. Leghtas, B. Vlastakis, Y. Liu, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf, “Extending the lifetime of a quantum bit with error correction in superconducting circuits,” Nature 536, 441 (2016).
- Ma et al. (2020) Y. Ma, Y. Xu, X. Mu, W. Cai, L. Hu, W. Wang, X. Pan, H. Wang, Y. P. Song, C.-L. Zou, and L. Sun, “Error-transparent operations on a logical qubit protected by quantum error correction,” Nat. Phys. 16, 827 (2020).
- Reinhold et al. (2020) P. Reinhold, S. Rosenblum, W.-L. Ma, L. Frunzio, L. Jiang, and R. J. Schoelkopf, “Error-corrected gates on an encoded qubit,” Nat. Phys. 16, 822 (2020).
- Chou et al. (2018) K. S. Chou, J. Z. Blumoff, C. S. Wang, P. C. Reinhold, C. J. Axline, Y. Y. Gao, L. Frunzio, M. H. Devoret, L. Jiang, and R. J. Schoelkopf, “Deterministic teleportation of a quantum gate between two logical qubits,” Nature 561, 368 (2018).
- Hu et al. (2019) L. Hu, Y. Ma, W. Cai, X. Mu, Y. Xu, W. Wang, Y. Wu, H. Wang, Y. P. Song, C.-L. Zou, S. M. Girvin, L.-M. Duan, and L. Sun, “Quantum error correction and universal gate set operation on a binomial bosonic logical qubit,” Nat. Phys. 15, 503 (2019).
- Michael et al. (2016) M. H. Michael, M. Silveri, R. T. Brierley, V. V. Albert, J. Salmilehto, L. Jiang, and S. M. Girvin, “New Class of Quantum Error-Correcting Codes for a Bosonic Mode,” Phys. Rev. X 6, 031006 (2016).
- Blais et al. (2021) A. Blais, A. L. Grimsmo, S. M. Girvin, and A. Wallraff, “Circuit quantum electrodynamics,” Rev. Mod. Phys. 93, 025005 (2021).
- Koch et al. (2007) J. Koch, T. M. Yu, J. Gambetta, A. A. Houck, D. I. Schuster, J. Majer, A. Blais, M. H. Devoret, S. M. Girvin, and R. J. Schoelkopf, “Charge-insensitive qubit design derived from the Cooper pair box,” Phys. Rev. A 76, 042319 (2007).
- Paik et al. (2011) H. Paik, D. I. Schuster, L. S. Bishop, G. Kirchmair, G. Catelani, A. P. Sears, B. R. Johnson, M. J. Reagor, L. Frunzio, L. I. Glazman, S. M. Girvin, M. H. Devoret, and R. J. Schoelkopf, “Observation of High Coherence in Josephson Junction Qubits Measured in a Three-Dimensional Circuit QED Architecture,” Phys. Rev. Lett. 107, 240501 (2011).
- Axline et al. (2016) C. Axline, M. Reagor, R. Heeres, P. Reinhold, C. Wang, K. Shain, W. Pfaff, Y. Chu, L. Frunzio, and R. J. Schoelkopf, “An architecture for integrating planar and 3D cQED devices,” Appl. Phys. Lett. 109, 042601 (2016).
- Reagor et al. (2016) M. Reagor, W. Pfaff, C. Axline, R. W. Heeres, N. Ofek, K. Sliwa, E. Holland, C. Wang, J. Blumoff, K. Chou, M. J. Hatridge, L. Frunzio, M. H. Devoret, L. Jiang, and R. J. Schoelkopf, “Quantum memory with millisecond coherence in circuit QED,” Phys. Rev. B 94, 014506 (2016).
- Place et al. (2021) A. P. M. Place, L. V. H. Rodgers, P. Mundada, B. M. Smitham, M. Fitzpatrick, Z. Leng, A. Premkumar, J. Bryon, A. Vrajitoarea, S. Sussman, G. Cheng, T. Madhavan, H. K. Babla, X. H. Le, Y. Gang, B. Jäck, A. Gyenis, N. Yao, R. J. Cava, N. P. de Leon, and A. A. Houck, “New material platform for superconducting transmon qubits with coherence times exceeding 0.3 milliseconds,” Nat. Commun. 12, 1779 (2021).
- Wang et al. (2022) C. Wang, X. Li, H. Xu, Z. Li, J. Wang, Z. Yang, Z. Mi, X. Liang, T. Su, C. Yang, G. Wang, W. Wang, Y. Li, M. Chen, C. Li, K. Linghu, J. Han, Y. Zhang, Y. Feng, Y. Song, T. Ma, J. Zhang, R. Wang, P. Zhao, W. Liu, G. Xue, Y. Jin, and H. Yu, “Towards practical quantum computers: Transmon qubit with a lifetime approaching 0.5 milliseconds,” npj Quantum Inf. 8, 3 (2022).
- Khaneja et al. (2005) N. Khaneja, T. Reiss, C. Kehlet, T. Schulte-Herbrüggen, and S. J. Glaser, “Optimal control of coupled spin dynamics: Design of NMR pulse sequences by gradient ascent algorithms,” J. Magn. Reson. 172, 296 (2005).
Methods
Experimental device and setup
The circuit QED device in our experiment uses a hybrid 3D-planar architecture Axline et al. (2016) and consists of a superconducting transmon qubit Koch et al. (2007), a coaxial stub cavity, and a Purcell-filtered stripline readout resonator (Fig. S1 in Supplementary Information section I). The high-Q cavity is designed with a cylindrical re-entrant quarter-wave transmission line resonator Reagor et al. (2016), and machined from high purity (99.9995%) aluminum. A horizontal tunnel is used to house a sapphire chip, on which the antenna pads of the transmon qubit and the striplines of the low-Q readout resonator are patterned with a thin-film tantalum Place et al. (2021); Wang et al. (2022). The single Al-AlOx-Al trilayer Josephson junction of the transmon qubit is fabricated using a double angle evaporation technique.
The fast feedback control is implemented with Zurich Instruments UHFQA and HDAWG, which are connected to each other through a DIO link cable for real time feedback control. The UHFQA generates the readout pulses, acquires the down-converted transmitted readout signals for demodulation and discrimination in hardware, and sends the digitized readout results to the HDAWG through the DIO link cable in real time. The HDAWG plays different predefined waveforms conditional on the received readout results from the DIO link cable. The feedback latency, defined as the time interval between sending out the last point of the readout pulse from UHFQA and sending out the first point of the control pulse from HDAWG, is about 511 ns in our setup, which also includes the signal travelling time through the experimental circuitry.
Parity mapping
The parity mapping procedure in the QEC experiment is implemented by applying a classical microwave pulse containing ( in our experiment) frequency components on the ancilla qubit, with the system dynamics governed by the Hamiltonian
| (1) |
in the interaction picture. Here, () denotes the excited (ground) state of the ancilla qubit, () is the creation (annihilation) operator of the photonic field in the cavity, is the ancilla’s frequency shift induced per photon due to their dispersive coupling, is the frequency detuning of the -th driving component with a Rabi frequency of , and denotes the Hermitian conjugate. With the choice of the drive frequency detuning , the ancilla is resonantly driven when the cavity have photons with .
For the cavity in the code space, the ancilla is off-resonantly driven by the comb pulse. For the 2-photon state in the cavity, the qubit’s transition is driven by pairs of frequency components with symmetric detunings, resulting in a qubit state revival at a time of with being an integer. Similarly, for the 0- and 4-photon states in the cavity, the qubit is driven by pairs of symmetric components and two unpaired components, whose effects can be ignored under the condition of . Therefore, the ancilla also makes a cyclic evolution at and returns to the initial ground state when the cavity is in the code space.
For the cavity in the error space with 1- and 3-photon states, the ancilla qubit’s transition is driven by a resonant frequency component, pairs of symmetric frequency components, and an unpaired off-resonant component. Under the same condition of , we can neglect the off-resonant effect of the unpaired components, and the ancilla will evolve from the initial ground state to the excited state at , with being an integer when choosing the drive amplitude . In our experiment, , while for an optimized parity mapping time (see Supplementary Informations).
Therefore, this frequency comb pulse achieves error syndrome detection by mapping the even (odd) parity of the cavity state to the ancilla () state in a QND manner. This parity mapping process can be intuitively illustrated by simultaneously applying two conditional rotations to the ancilla qubit to flip the qubit state to the excited state associated with the cavity’s 1- and 3-photon states, thus resulting in a minimum perturbation to the cavity states in the code space.
Strategies for system optimization
The photon-number-resolved a.c. Stark shift method Ma et al. (2020) is adopted to mitigate the photon-loss-induced dephasing effect of the logical codewords, due to the non-commutativity of the annihilation operation and the self-Kerr term. In our experiment, we apply an off-resonant drive pulse with a frequency detuning of about on the ancilla during the idle operation, resulting in different phase accumulation rate for Fock state with relative to the vacuum state. By choosing an optimal amplitude of the detuned drive, we could achieve the error-transparent condition Ma et al. (2020) of to mitigate the dephasing effect of the logical qubit (Fig. S4 in the Supplementary Information of Section III).
In order to balance the operation errors, no-parity-jump backaction errors, and photon-loss errors, we employ a two-layer QEC procedure Hu et al. (2019) to improve the QEC performance (Fig. S6 in the Supplementary Information of Section III). In our QEC experiment, there are two bottom layers in a single QEC cycle, where the first one conserves the photon number parity in the deformed code space, and the second one recovers the quantum information in the code space.
The waiting time of the idle operation in each QEC cycle is selected based on a tradeoff between the uncorrected errors occurring during this time and the operation errors occurring during the error syndrome measurements and recovery operations. On one hand, the longer the waiting time, the larger probability of the two-photon-loss event is during this time, which cannot be detected by the lowest-order binomial code. On the other hand, the more frequent the error detection, the more likely the photon-loss errors occur during the detections and corrections. We calculate the QEC lifetime as a function of the waiting time from numerical simulations and choose an optimal waiting time of about s in our QEC experiment. (Fig. S8 in the Supplementary Information of Section IV).
Data availability
All data generated or analysed during this study are available within the paper and its Supplementary Information. Further source data will be made available on reasonable request.
Code availability
The code used to solve the equations presented in the Supplementary Information will be made available on reasonable request.
Acknowledgment
This work was supported by the Key-Area Research and Development Program of Guangdong Province (Grants No. 2018B030326001 and No. 2020B0303030001), the Shenzhen Science and Technology Program (Grant No. RCYX20210706092103021), the National Natural Science Foundation of China (Grants No. 12274198, No. 11904158, No. U1801661, No. 12274080, No. 12061131011, No. 92265210, No. 92165209, No. 11925404, No. 11890704 and No. 11875108), the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2022A1515010324), the Guangdong Provincial Key Laboratory (Grant No. 2019B121203002), the Program (Grant No. 2016ZT06D348), the Science, Technology and Innovation Commission of Shenzhen Municipality (Grant No. KYTDPT20181011104202253), the Shenzhen-Hong Kong cooperation zone for technology and innovation (Contract No. HZQB-KCZYB-2020050), the National Key Research and Development Program of China (Grant No. 2017YFA0304303), the China Postdoctoral Science Foundation (BX2021167), the Innovation Program for Quantum Science and Technology (Grants No. ZD0301703 and No. ZD0102040201), and the Natural Science Foundation of Beijing (Grant No. Z190012).
Author contributions
Y.X. and D.Y. supervised the project. Y.X. conceived and designed the experiment. Z.N. performed the experiment. Z.N. and Y.X. analyzed the data and carried out the numerical simulations. Z.N. and Sa.L. developed the feedback control technique under the supervision of Y.X. X.D., Y.C., W.W., Z.-B.Y., and F.Y. contributed to the experimental and theoretical optimization. L.Z., So.L. and H.Y. provided supports in device fabrication. S.-B.Z. proposed the theoretical scheme of the frequency comb method. S.-B.Z., C.-L.Z. and L.S. provided theoretical and experimental supports. C.-L.Z., S.-B.Z., L.S., and Y.X. wrote the manuscript with feedback from all authors.
Competing interests
The authors declare no competing interests.
Additional information
Supplementary information The online version contains supplementary material.
Correspondence and requests for materials should be addressed to L.S., S.-B.Z., Y. X. or D.Y.