BECS: A Privacy-Preserving Computing Sharing Mechanism in 6G Computing Power Network
Abstract
5G networks provide secure and reliable information transmission services for the Internet of Everything, thus paving the way for 6G networks, which is anticipated to be an AI-based network, supporting unprecedented intelligence across applications. Abundant computing resources will establish the 6G Computing Power Network (CPN) to facilitate ubiquitous intelligent services. In this article, we propose BECS, a computing sharing mechanism based on evolutionary algorithm and blockchain, designed to balance task offloading among user devices, edge devices, and cloud resources within 6G CPN, thereby enhancing the computing resource utilization. We model computing sharing as a multi-objective optimization problem, aiming to improve resource utilization while balancing other issues. To tackle this NP-hard problem, we devise a kernel distance-based dominance relation and incorporated it into the Non-dominated Sorting Genetic Algorithm III, significantly enhancing the diversity of the evolutionary population. In addition, we propose a pseudonym scheme based on zero-knowledge proof to protect the privacy of users participating in computing sharing. Finally, the security analysis and simulation results demonstrate that BECS can fully and effectively utilize all computing resources in 6G CPN, significantly improving the computing resource utilization while protecting user privacy.
Index Terms:
Computing sharing, 6G networks, computing power network (CPN), evolutionary algorithm, blockchain, pseudonym scheme.I Introduction
In the upcoming 6G era, it is anticipated that everything will be intelligently connected, thereby facilitating various data-intensive applications. By integrating communication networks deeply with various vertical industries, 6G will facilitate unprecedented applications such as Holographic Integrated Sensing and Communication (HISC), Artificial General Intelligence (AGI), and Digital Twins (DT) [1]. This indicates that AI will be the most crucial technology for constructing a comprehensively intelligent 6G networks, enabling network services to evolve dynamically and autonomously in response to demand. Fully coordinating end-edge-cloud computing devices to construct a Computing Power Network (CPN) will emerge as the leading paradigm for supporting ubiquitous intelligent services in 6G networks [2]. In essence, computing tasks will choose the most suitable offloading environment based on service demands, promoting a highly dynamic and hybrid computing space that further stimulates the sharing of computing resources within 6G networks.
CPN achieves dynamic allocation and efficient utilization of computing resources by integrating and scheduling computing devices throughout the network. Lu et al. [2] utilized deep reinforcement learning to find the optimal task transfer and resource allocation strategies in wireless CPN. Chen et al. [3] proposed an on-demand computing resource scheduling model to achieve efficient task offloading in edge CPN. However, as network services advance, resource allocation based on one or two objectives has become infeasible. Therefore, formulating computing resource optimization, an NP-hard task, as a multi-objective optimization problem (MOOP) is an effective approach. Peng et al. [4] formulated complex task offloading in the IIoT as a four-objective MOOP and developed a method to dynamically allocate computing resources based on the Non-dominated Sorting Genetic Algorithm III (NSGA-III). Gong et al. [5] employed the multi-objective evolutionary algorithm based on decomposition (MOEA/D) to optimize a three-objective edge task offloading problem, aiming to minimize delay and maximize rewards. The unprecedented services and complex architectures of 6G networks necessitate that CPN manage and optimize computing resources across multiple dimensions and continuously improve resource utilization efficiency [6]. Therefore, it is essential to change the current supply and demand dynamics of computing resources and to implement dynamic resource sharing.
Blockchain is envisioned as a promising approach to support distributed network management in 6G. Unlike traditional centralized approaches, blockchain enables trusted interactions among unfamiliar nodes through consensus mechanisms [7]. Xie et al. [8] exploited the immutability of blockchain to propose a resource trading mechanism based on sharding and directed acyclic graphs for large-scale 6G networks, thereby enhancing resource utilization efficiency. Dai et al. [9] developed a task-driven decentralized edge resource sharing scheme for 6G IoT, leveraging the distributed characteristics of blockchain. Wang et al. [10] proposed a provable secure blockchain-based federated learning framework for wireless CPN, aimed at accelerating the convergence of federated learning and enhancing the efficiency of wireless CPN. Meanwhile, the Federal Communications Commission views blockchain as a promising solution to lower the costs associated with radio spectrum management [6]. Consequently, blockchain is expected to fully realize its potential in the management and sharing of 6G resources.
6G networks will integrate AI to fully merge the physical and digital worlds, necessitating enhanced security and privacy [11]. Xu et al. [12] utilized blockchain to provide adequate security and privacy protection for resource trading. Wang et al. [13] proposed a blockchain-enabled cyber-physical system integrating cloud and edge computing to achieve secure computing offloading. Samy et al. [14] introduced a blockchain-based framework for task offloading, ensuring security, integrity, and privacy in mobile edge computing. Although leveraging the characteristics of blockchain can provide preliminary security and privacy protection for edge and cloud computing allocation and trading, device-to-device computing sharing in 6G networks will require more comprehensive solutions to ensure the security and privacy between devices [15].
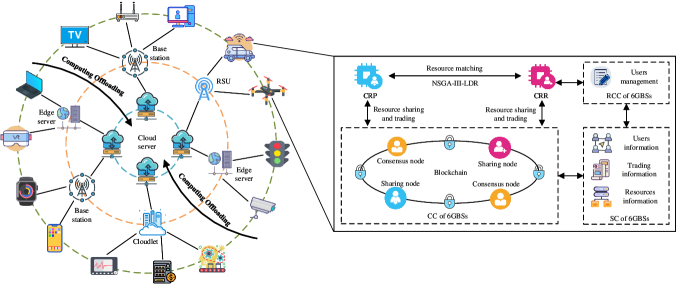
Motivated by previous research, this article introduces a computing allocation and trading mechanism for 6G CPN, named BECS, which utilizes Blockchain and Evolutionary algorithms for efficient Computing resource Sharing. Furthermore, it provides a pseudonym scheme to protect users’ privacy. Specifically, the main contributions of this article are summarized as follows:
-
•
We propose a dynamic and efficient blockchain-based mechanism for computing sharing, aimed at ensuring secure allocation and trading of resources between any devices in 6G CPN, thus enhancing utilization.
-
•
We formulate computing allocation as a MOOP with six objectives, employing an evolutionary algorithm to balance the interplay among these objectives, thus achieving optimal allocation schemes for 6G CPN.
-
•
We propose a novel evolutionary algorithm, NSGA-III-KDR, which improves the dominance relation of NSGA-III by using the kernel distance to enhance diversity in addressing the computing allocation MOOP.
-
•
We design a novel pseudonym scheme based on the Schnorr protocol, which protects user privacy during computing sharing in 6G CPN.
The remainder of this article is organized as follows. Section II introduces the system model and formulates the computing sharing problem. Section III describes NSGA-III-KDR and its application in solving the computing allocation MOOP. Section IV presents the proposed pseudonym scheme and computing trading. Section V analyzes the security and computational complexity of the proposed scheme. Section VI presents simulation results. Section VII concludes the article.
II System Model and Problem Formulation
In this section, we introduce the computing sharing system model considered by BECS, along with other models used in constructing the MOOP, including the communication, computing, and service models.
II-A System Model
BECS is a generalized architecture that supports various types of computing sharing in 6G CPN, as illustrated in Fig. 1. All computing devices, labeled as , are classified into three layers: user computing layer, edge computing layer, and cloud computing layer. Specifically, the set of user computing devices, denoted as , includes smartphones, computers, wearable devices, IoT devices, vehicles, and other devices that directly interact with users. These devices typically possess limited computing power. The set of edge computing devices, denoted as , includes edge servers, roadside units, cloudlets, and other devices capable of providing time-sensitive computing services to users. The set of cloud computing devices, denoted as , consists of remote computing centers capable of providing large-scale computing power. The evolutionary algorithm matches computing resource requesters with providers, facilitating a multi-dimensional measurement of the deep reuse of computing resources. Additionally, with the support of permissioned blockchain, BECS enables dynamic management and trading of fine-grained computing resources. The proposed architecture consists of three main components:
1) Computing Resource Providers (CRPs): As large language models become increasingly widespread, devices with abundant computing power will increasingly provide computing support to devices with limited resources. In BECS, all devices within 6G CPN with free computing resources can serve as CRPs.
2) Computing Resource Requesters (CRRs): In general, when a device lacks sufficient computing capability to handle a task’s demands, it needs to request additional resources. In BECS, any device can be a CRR, provided that the requested resources exceed its own computing capacity.
3) 6G Base Stations (6GBSs): As critical components in BECS, 6GBSs provide reliable communication services to devices and serve as blockchain maintenance nodes responsible for transaction bookkeeping and block packaging. Each 6GBS consists of three components:
-
•
Registration and Certification Component (RCC): The RCC is responsible for managing the identities of devices and issuing and verifying certificates.
-
•
Computation Component (CC): The CC is responsible for maintaining the blockchain.
-
•
Storage Component (SC): The SC is responsible for storing data from devices and the blockchain.
This study primarily focuses on efficient computing sharing. Accordingly, the computing device is denoted as , where is usually measured by device’s CPU [16]. Meanwhile, denotes the set of all computing tasks. The tuple describes the computing task . and can be obtained using methods described in [17], such as graph analysis. Notations that will be used are presented in Table I.
| Notation | Definition |
|---|---|
| the set of all computing devices | |
| the set of user computing devices | |
| the set of edge computing devices | |
| the set of cloud computing devices | |
| the set of all computing tasks | |
| the computing capacity (in CPU cycles/s) of | |
| the service price of per unit of time | |
| the data size of | |
| the required computing amount (in CPU cycles) of | |
| the maximum time consumption allowed of | |
| the final execution device for | |
| , | the transmission power of and |
| the noise power | |
| the bandwidth of each subchannel | |
| the number of in each layer | |
| the computing resources occupancy of in each layer | |
| the tasks processed number per unit of ’s computing capacity | |
| the probability of offloading from to , and satisfies | |
| the effective capacitance coefficient of | |
| the minimum value of the objective function |
II-B Communication Model
The NOMA-based 6G networks, regarded the most promising future multi-access technology, is considered in BECS. It allows multiple users to transmit on the same frequency band, thereby enhancing spectrum resource utilization [18]. This model primarily addresses the communication latency in wireless communications, thus overlooking the latency in wired connections. Let denote the instantaneous channel gain from to the offloading computing device. Without loss of generality, the channel gains for all devices are ordered in descending sequence: . Using successive interference cancellation and decoding for the user with the highest received power, the data transmission rate for during the computing offloading is calculated via Shannon’s theorem as follows:
| (1) |
If offloads to , the data transmission latency can be expressed as follows:
| (2) |
Therefore, the communication energy consumption of can be calculated as follows:
| (3) |
II-C Computing Model
In the considered three layers computing sharing structure, the computing tasks of a CRR can be executed in any device of CRP. However, computing devices vary in terms of task transfer and processing capabilities. This intense competition for computing resources at each layer, inevitable in 6G PCN with numerous CRRs and CRPs, necessitates balancing the task load across the system’s layers. Generally, with limited computing resources at each layer, tasks may have to wait for an available processor. Therefore, the M/M/c model [19], which describes task offloading as a Poisson process with an average arrival rate of , can be used to model task processing delays. Based on the superposition property of the Poisson process and the offloading interactions among the three layers of computing resources, the average task arrival rate for each layer can be calculated as
| (4) |
Therefore, the average time consumption of each task at each layer, encompassing both the queuing and the execution times, can be calculated as
| (5) |
where can be calculated as . is known as Erlang’s C Formula, which can be calculated as
| (6) |
At the same time, the energy consumption of in each layer during the execution of computing tasks can be calculated as follows [20]:
| (7) |
where is depending on the chip architecture.
II-D Service Model
1) Computing occupancy: As a direct factor of computing utilization, it can be quantified as the number of all devices participating in computing sharing while ensuring the provision of all network services. It is defined as follows:
| (8) |
with
| (9) |
2) Privacy entropy: More applicable computing offloading can be achieved by constructing three layers computing structures. However, the decentralization of computing devices introduces privacy leakage risks during task offloading. Privacy entropy, a method of quantifying privacy security, is used to measure the security of information transmission [21]. Higher privacy entropy indicates more disordered data, preventing attackers from making inferences and thereby ensuring secure information transmission.
The types of offloaded data vary according to the computing tasks. Thus, in BECS, we set the relationship between and to be a one-to-one correspondence, and the privacy entropy of in can be calculated as
| (10) |
3) Load balancing: As a key metric for evaluating computing device workloads, load balancing aims to equalize each device’s load to the average. Concentrating multiple tasks on a single device diminishes computational efficiency and elevates energy consumption. The standard deviation of the tasks and the computing capabilities of the devices can reflect whether they are load balanced [22]. Therefore, the load balancing of can be calculated as
| (11) |
4) Sharing revenue: A suitable revenue can encourage the participation of computing devices in resource sharing, thereby enhancing the overall resource utilization. The logarithmic utility function is used to quantify the sharing revenue of , which can be calculated as
| (12) |
II-E Premise Assumptions
The assumptions and requirements specified below are applied consistently throughout this article unless otherwise stated.
1) Computing tasks can be offloaded from the outer to the inner layer as depicted in Fig. 1, or within the same layers, provided that the computing capacity of CRP exceeds that of CRR.
2) Each user device is equipped with a single antenna, facilitating real-time communication with the 6GBS.
3) Edge and cloud computing devices are typically connected to the 6GBS through high-speed, reliable wired connections, such as optical fibers. The latency of these connections is significantly lower than that of wireless communication between user devices and the 6GBS, and can be considered negligible.
4) Based on the permissioned blockchain, user registration information is visible only to 6GBSs within the blockchain, whereas the computing resources status is visible to all users.
5) All users securely deliver their keys through a secure channel.
III Computing Allocation Based on NSGA-III-KDR
In this section, we first introduce the proposed computing allocation MOOP. Subsequently, we explain the principle of kernel distance-based Dominance Relation and the optimization process based on NSGA-III-KDR.
III-A MOOP of Computing Allocation
Based on the aforementioned model, total time and energy consumption can serve as metrics for computing cost and green 6G, which can be calculated as follows:
| (13) |
and
| (14) |
In addition, to ensure the user’s service experience, the computing resource utilization the average privacy entropy of the computing tasks, the load balancing of the computing devices, and the total sharing revenue of CRP are considered, which can be calculated as follows:
| (15) |
| (16) |
| (17) |
and
| (18) |
Assigning tasks to free computing devices can effectively improve the resource utilization of the entire system. However, focusing solely on utilization improvement is unscientific. Therefore, it is crucial to analyze the trade-offs among these intertwined and conflicting objectives. In BECS, our objectives include minimizing time and energy consumption, optimizing load balancing to maximize resource utilization, ensuring user experience, and simultaneously maximizing privacy entropy and CRP revenue. The MOOP is formulated as:
| (19) | |||
| (20) |
subject to:
| (21) | |||
| (22) | |||
| (23) | |||
| (24) | |||
| (25) | |||
| (26) |
Constraint (18) states that the actual task processing rate of the computing device must not exceed its service rate. Constraint (19) restricts the maximum transmit power of the user device. Constraint (20) guarantees that the task execution time does not exceed its deadline. Constraint (21) specifies that the computing energy consumption should not exceed the device’s maximum available energy. Constraint (22) differentiates the computing capacities across three layers and specifies task offloading from devices with lower capacity to those with higher capacity. Constraint (23) stipulates that the computing demands of tasks offloaded to executing devices must not exceed their capacities.

III-B Kernel Distance-based Dominance Relation
NSGA-III, an excellent evolutionary algorithm, can achieve fast global searches with quality assurance, preventing MOOP from settling into local optimality. Additionally, it tackles high-dimensional problems by preserving population diversity through uniformly distributed reference points [23]. In practical MOOP, maximizing population diversity while ensuring convergence is one of the best ways to quickly and effectively obtain the optimal solution. Consequently, NSGA-III-KDR is proposed to balance the aforementioned five objectives.
The performance of Pareto dominance relation-based algorithms often exhibits serious dimensionality implications due to dominance resistance in MOOP with more than three objectives [24]. To address this, Tian et al. [25] proposed a strengthened dominance relation (SDR) to enhance NSGA-II. Considering that NSGA-III builds upon NSGA-II by introducing reference points, we propose a kernel distance-based dominance relation (KDR) in NSGA-III-KDR. It builds on the theoretical foundation of SDR to replace the original Pareto dominance relation in NSGA-III. Specifically, if solution dominates solution in KDR, then (27) is satisfied.
| (27) |
where represents the acute angle between the two candidate solutions and , which can be calculated as , and denotes the size of the niche to which each candidate solution belongs.
As the number of objectives increases, neither the Euclidean distance nor the Mahalanobis distance can accurately reflect the crowding degree between individuals [26]. Therefore, NSGA-III-KDR utilizes the kernel distance from the point to the ideal point to measure the similarity between them in handling high-dimensional problems [27]. It can be calculated as follows:
| (28) |
III-C Encoding of Computing Resources
Evolutionary algorithms utilize the concept of population evolution to tackle practical MOOPs. Here, individuals in a population are represented by a series of numbers, each mapped to potential solutions of a MOOP through specific encoding. Thus, encoding is crucial for implementing population evolution in practical MOOPs.
In BECS, the occupancy status of computing devices is encoded as genes, while the computing resources involved in sharing are encoded as chromosomes, constituting the entire CRP for evolution. As illustrated in Fig. 2, a gene value of 0 indicates a free computing device, whereas a value of 1 signifies that this device is occupied. This method allows BECS to integrate various types of computing resources, thereby building a generalized computing sharing platform. Since the occupancy status of computing devices directly correlates with gene encoding, and chromosomes relate to computing allocation strategies, dynamic and fine-grained updates of computing resources are enabled.
III-D Population Evolution
When the CRR requests computing resources, the system executes the computing allocation scheme based on NSGA-III-KDR to match the optimal CRP. NSGA-III-KDR basically follows the algorithmic framework of NSGA-III, as shown in Algorithm 1. During the evolution process, the chromosomes in the initial population generate entirely new chromosomes (computing allocation strategies) through crossover and mutation operations. The crossover operation enhances chromosome diversity, while the mutation operation, under specific conditions, modifies individual genes to seek those with higher adaptability. In each iteration, the population generated by crossover and mutation merges with the original, then executing a Non-KDR-dominated sort that replaces the non-dominated sort in NSGA-III, thereby effectively enhancing the diversity of the computing resource population. Subsequently, by associating chromosomes with reference points in the hyper-plane and executing the Niche-Preservation Operation, the next generation population can be generated. After iterations of NSGA-III-KDR, the final population , containing the ultimate computing allocation strategy, is obtained.
III-E Optimum Selection
The final population comprises a set of the best feasible solutions for computing allocation, termed Pareto solutions. However, in practical computing allocation problems, the CRR needs to match only a specific CRP. Therefore, the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), in conjunction with entropy weighting, is utilized to evaluate the most optimal solution among many Pareto solutions. As a method approximating the ideal solution, TOPSIS rapidly identifies the optimal solution by ranking all solutions according to their distance from the positive (negative) ideal solution. Additionally, entropy weighting helps eliminate the arbitrariness of subjectively determined weights. This combination enables an objective and fair determination of the optimal computing allocation from . The specific algorithm is detailed in [28].
By executing NSGA-III-KDR in BECS, CRP can set more reasonably by analyzing the optimal solution. Simultaneously, CRR can select the most appropriate CRP for task offloading based on the optimal solution. Consequently, both parties engaged in resource sharing achieve reliable, dynamic, and secure computing allocation and trading.
IV Secure Computing Trading with Privacy Protection
In this section, we focus on the principles of the proposed pseudonym scheme and secure computing trading under pseudonyms in BECS.
IV-A System Initialization
In this phase, upon inputting the security parameter , the system administrator selects a secure elliptic curve . The group is an additive elliptic curve group with order and generator defined over , where and are two large prime numbers. Subsequently, 6GBS chooses a random number as its private keys and caculates the public keys as . Additionally, it selects a collision-resistant hash function and makes publicly available in blockchain.
IV-B Computing Devices Registration
All devices must be registered upon entering the system. first selects as the private key and then calculates the public key as . Subsequently, it sends its real identity and the public key to the nearest via a secure channel. After receiving the message from , stores in SC, while simultaneously generating and sending ’s identity certificate: .
IV-C Pseudonym Generation
When participates in computing sharing, it must first send its public key and identity certificate to the nearest . After verifies the legitimacy of ’s identity, it generates a pseudonym for , as detailed in Algorithm 2. Based on the Schnorr protocol [29], proves possession of the private key to without revealing it, by utilizing the public parameter and random numbers. verifies the legitimacy of ’s identity by confirming the correctness of ’s proof and response. Utilizing non-interactive zero-knowledge protocol, acquires a pseudonym for communication from while preserving privacy.
The pseudonym , constructed using ’s public key and random numbers, cannot establish its legitimacy and thus requires to issue the corresponding certificate, as shown in Algorithm 3. Using a non-interactive zero-knowledge protocol, generates a commitment and a response that include its private key. then verifies these to confirm that , who possesses the private key , generated the certificate. Upon successful verification, stores the certificate.
IV-D Pseudonymous Computing Trading
Upon entering the system, CRP synchronizes its computing device information and status within blockchain. CRR sends a computing request, and NSGA-III-KDR is utilized to match the resource-sharing parties. CRP () accepts a task offloading request from CRR (). Initially, both parties must verify the pseudonym and certificate according to Algorithm 4. uses transcript to prove the authenticity of the pseudonym to and uses the certificate to prove the legitimacy of the certificate to . After both verifications succeed, confirms ’s identity, and similarly, confirms ’s identity. Once confirming their identities, CRR offloads its computing tasks to CRP, which then updates its resource status and delivers the computing results to CRR within the deadline. Following the payment of corresponding fees by CRR, both parties finalize the trading.
IV-E Block Generation and Pseudonymous Update
After both parties complete the trading in computing sharing, the 6GBS near CRR packages all related information into a new block and adds it to the blockchain. Subsequently, CRP must update its computing resource status. The trading and resource update information of this computing sharing will be broadcast and synchronized throughout the entire blockchain system.
Before re-engaging in computing sharing, CRP and CRR need to request new pseudonyms and certificates from the nearby 6GBS to ensure the user’s identity remains unlinkable. Similarly, the 6GBS verifies the legitimacy of the CRP/CRR identities through Algorithm 4 and then issues CRP/CRR new pseudonyms and certificates.
V Security Analysis and Discussion
In this section, we analyze the security of BECS and discuss the computational complexity of NSGA-III-KDR.
V-A System Security
The system’s security is crucial for the anonymous sharing and trading of computing resources. In BECS, the RCC of 6GBS generates all security parameters, which are then securely synchronized and stored on the permissioned blockchain. Additionally, all 6GBSs maintain the permissioned blockchain, and their security strongly supports the blockchain. Thus, resource status updates, pseudonymous trading, trading records, and block generation within the system are secure. Moreover, as all computing trading are blockchain-recorded, 6GBSs can ensure fairness in computing sharing through audits. Furthermore, user authentication is mandatory for system access, and user identity hashes stored at the 6GBS ensure privacy even if data leaks occur, also safeguarding against whitewashing attacks. Finally, updatable pseudonyms prevent the leakage of users’ public and private keys, ensuring that their information remains unlinked and untraceable, thus securing their privacy. In the proposed service model, privacy entropy is also considered, providing comprehensive protection for user privacy.
V-B Pseudonymous Security
The security of the proposed pseudonym scheme is based on the discrete logarithm problem and the Schnorr protocol. During system initialization, the security of key generation depends on the assumption of the discrete logarithm on elliptic curves, and its security is notoriously guaranteed. Additionally, the Schnorr protocol, being simulatable due to its zero-knowledge property [29], ensures that the pseudonym generation is also simulatable, with interacting parties not gaining any information beyond validating the pseudonyms and certificates, so the generation and verification of pseudonyms and certificates is also secure. Moreover, since attackers cannot differentiate between real and simulated interactions, they are unable to acquire any useful information. To analyze security performance from various perspectives, the detailed discussion as follows.
1) Uniqueness: The proposed pseudonym adopts the form , whereas the user’s public/private key pairs take the form . The pseudonym generation can be seen as a knowledge extractor of the Schnorr protocol that produces the private key . Consequently, each user’s pseudonym corresponds to a unique extractable public/private key pairs, ensuring that every authenticated pseudonym uniquely identifies a user.
2) Unforgeability: The user’s pseudonym certificate incorporates the private key of 6GBS, which remain concealed from users due to the zero-knowledge protocol, thereby precluding any possibility of forging the pseudonym certificate. Additionally, user identity verification employs a zero-knowledge protocol based on the 6GBS’s private key. Consequently, without knowing the 6GBS’s private key, users cannot authenticate successfully with a forged pseudonym and certificate.
3) Unlinkability: The mutual verification process between users reveals no information beyond the pseudonym and certificate. The pseudonym is a bit commitment to the user’s private key. Given the robust security of bit commitments, attackers cannot distinguish the identities of different users by observing their pseudonyms. Furthermore, the public keys of both verification parties are not leaked, and no link exists between different pseudonyms of the same user.
4) Traceability: Users request or update their pseudonyms at the 6GBS using their public keys, allowing the 6GBSs to trace all of a user’s pseudonyms and related trading via its public key. As pseudonyms are updated before each computing sharing and remain unlinkable, neither attackers nor other users can trace a user’s pseudonyms or related trading.
V-C Certificate Security
The certificate’s security is based on key pairs of the 6GBS. Certificate issuance and verification, conducted through non-interactive zero-knowledge protocols, ensuring the confidentiality of the 6GBS’s key pairs. The private key of the granting 6GBS binds the pseudonym, thereby legitimizing the certificate. Additionally, during certificate issuance, random numbers further improve anonymity, safeguarding against linking of the user’s identity.
V-D Computational Complexity of NSGA-III-KDR
In BECS, NSGA-III-KDR uses Non-KDR-dominated sort instead of Non-Dominated Sort from NSGA-III to enhance solution diversity, while maintaining the same computational complexity. Namely, with optimization objectives and a population size of , NSGA-III-KDR exhibits a computational complexity of . Specifically, calculating the kernel distance for each solution and determining the angle between any two solutions each incur a complexity of . Each solution’s distance to the ideal point is calculated individually, contributing to a complexity of . For dominance judgment, each pair of solutions undergoes one angle calculation and comparison, leading to an overall complexity of . Thus, the computational complexity of each iteration can be approximated as . Furthermore, while maintaining the same complexity, NSGA-III-KDR supports more optimization objectives compared to NSGA-II-based scheme [4], providing a more comprehensive computing allocation strategy. Compared to NSGA-III-based scheme [5], NSGA-III-KDR offers more diverse solutions, improving the probability of superior computing allocation strategies.
VI Simulation Results and Analysis
| Parameters | Values |
|---|---|
| Main physical machine | Intel i7-12700@2.1GHz with 32GB RAM |
| Operating systems | Windows 11 & Ubuntu 24 |
| Number of devices | : 300; : 200; : 100 |
| Transmit power | 2030 dbm |
| Noise power | -97 dBm |
| Channel gain | 2.15 dBi |
| Bandwidth | 20 MHz |
| Average arrival rate | 100 tasks/s |
| CPU frequency [30] | : 0.6 GHz10 GHz; : 10 GHz1 THz; : 1THz |
| Effective capacitance coefficient [31] | |
| Data size | 5003000 KB |
| CPU cycles per byte | 1000 cycles/byte |
| Cryptographic libraries | PBC and Openssl |
| Probability of offloading | : 0.5, : 0.3, : 0.2 |
| Service price | : 0.1, : 1, : 2 |
| , ; | 0.6, 0.4; 1 |
In this section, we initially compare the performance of the proposed NSGA-III-KDR with NSGA-III and MOEA/D applied in computing allocation, as well as the NSGA-II-SDR that inspired us. Subsequently, we test the performance of four algorithms in optimizing the proposed computing allocation MOOP. Finally, we simulate the performance of the proposed pseudonym scheme. The configurations of critical parameters are detailed in Table II.
VI-A Simulation of Proposed NSGA-III-KDR
In this part, we compare the proposed NSGA-III-KDR with state-of-the-art evolutionary algorithms NSGA-III [4], MOEA/D [5], and NSGA-II-SDR [25], utilizing the PlatEMO platform [32]. The widely used SDTLZ [23], MaF [33], and SMOP [34] test suites are employed as the benchmarks. Meanwhile, IGD [35] and PD [36] are selected as performance evaluation metrics. IGD comprehensively measures the convergence and diversity of the algorithms, where a smaller IGD value indicates better performance. PD primarily reflects the diversity of the algorithms, with a larger PD value indicating greater population diversity. The crossover probability is set to 1, the mutation probability is set to 1/D, and their distribution indicator is set to 20, where D represents the length of the decision variable. All three algorithms are executed 30 times on different test problems, and the average values are taken. The performance of the three algorithms is compared under different numbers of objectives and benchmarks, as shown in Table III, where “”, “”, and “” indicate that the result is significantly better, significantly worse, and statistically similar to that obtained by NSGA-III-KDR, respectively.
It can be concluded from the experimental results that NSGA-III-KDR has the strongest competitiveness, achieving the best IGD and PD numbers of 10 and 15, respectively. This demonstrates that NSGA-III-KDR has better performance compared to the other two algorithms, especially in terms of population diversity, offering a richer set of solutions for computing allocation.
| Problem | M | IGD | PD | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NSGA-III | MOEA/D | NSGA-II-SDR | NSGA-III-KDR | NSGA-III | MOEA/D | NSGA-II-SDR | NSGA-III-KDR | ||
| SDTLZ1 | 5 | 4.0919e-1 = | 1.1456e+0 - | 7.2486e-1 - | 4.072e-1 | 1.0645e+7 - | 5.7924e+6 - | 1.8399e+7 - | 4.7052e+7 |
| 10 | 1.7833e+1 + | 3.1719e+1 + | 3.7045e+1 + | 1.3076e+2 | 2.3247e+10 + | 4.3704e+9 + | 7.6415e+8 + | 1.0865e+10 | |
| 15 | 6.1421e+2 + | 8.2078e+2 + | 8.4100e+2 + | 6.4468e+3 | 2.8108e+12 + | 4.7472e+11 + | 9.5939e+7 - | 5.2570e+9 | |
| SDTLZ2 | 5 | 1.1871e+0 = | 3.1693e+0 - | 4.3480e+0 - | 1.1838e+0 | 1.9000e+7 - | 1.1551e+7 - | 1.6919e+4 - | 9.6971e+7 |
| 10 | 6.8214e+1 - | 1.1354e+2 - | 1.4962e+2 - | 6.3516e+1 | 6.3070e+10 - | 8.2536e+9 - | 6.7541e+8 - | 1.0334e+10 | |
| 15 | 2.3123e+3 - | 3.6367e+3 - | 3.6612e+3 - | 2.1131e+3 | 1.3576e+13 - | 4.7141e+11 - | 8.7418e+8 - | 2.9897e+11 | |
| MaF1 | 5 | 2.2118e-1 - | 1.6710e-1 - | 1.4031e-1 + | 1.6200e-1 | 1.7519e+7 - | 3.8550e+6 - | 1.9648e+7 - | 2.4256e+7 |
| 10 | 3.1732e-1 - | 3.9154e-1 - | 2.9201e-1 + | 3.1425e-1 | 8.9830e+9 - | 1.5818e+9 - | 6.1301e+9 - | 1.2171e+10 | |
| 15 | 3.8109e-1 + | 4.7345e-1 - | 4.2790e-1 - | 4.0302e-1 | 1.9765e+11 = | 5.7436e+10 - | 5.9691e+10 - | 2.0030e+11 | |
| MaF2 | 5 | 1.4175e-1 - | 1.5433e-1 - | 1.3740e-1 - | 1.2311e-1 | 1.8852e+7 - | 1.3030e+7 - | 1.6372e+7 - | 2.1218e+7 |
| 10 | 2.7622e-1 - | 3.0954e-1 - | 4.0882e-1 - | 2.5215e-1 | 8.5156e+9 - | 3.8250e+9 - | 8.3977e+9 - | 1.3398e+10 | |
| 15 | 3.2353e-1 + | 3.8517e-1 + | 5.6897e-1 - | 4.6420e-1 | 2.5275e+11 + | 1.1452e+11 - | 2.4382e+10 - | 1.3115e+11 | |
| SMOP1 | 5 | 1.5928e-1 - | 2.2883e-1 - | 3.4716e-1 - | 1.3947e-1 | 3.6432e+6 - | 3.7787e+6 - | 6.8850e+6 - | 2.5642e+7 |
| 10 | 4.2414e-1 - | 3.9985e-1 - | 4.9668e-1 - | 2.8703e-1 | 2.0785e+9 - | 9.4496e+8 - | 1.9355e+9 - | 1.1620e+10 | |
| 15 | 4.0587e-1 + | 4.5602e-1 + | 4.0515e-1 + | 5.2449e-1 | 8.5548e+10 - | 5.5518e+9 - | 7.0498e+10 - | 1.0424e+11 | |
| SMOP2 | 5 | 3.8732e-1 - | 5.8495e-1 - | 5.4909e-1 - | 3.6202e-1 | 6.2126e+6 - | 6.4898e+6 - | 1.1547e+7 - | 3.9017e+7 |
| 10 | 9.1827e-1 - | 5.8728e-1 - | 8.6089e-1 - | 5.5237e-1 | 3.7243e+9 - | 1.8461e+9 - | 3.3883e+9 - | 2.1840e+10 | |
| 15 | 6.2944e-1 + | 7.2789e-1 + | 6.8003e-1 + | 9.1024e-1 | 1.7008e+11 = | 1.1430e+10 - | 1.3620e+11 - | 2.0211e+11 | |
| +/-/= | 6/10/2 | 5/13/0 | 6/12/0 | 3/13/2 | 2/16/0 | 1/17/0 | |||
VI-B Simulation of Proposed Computing Allocation Scheme
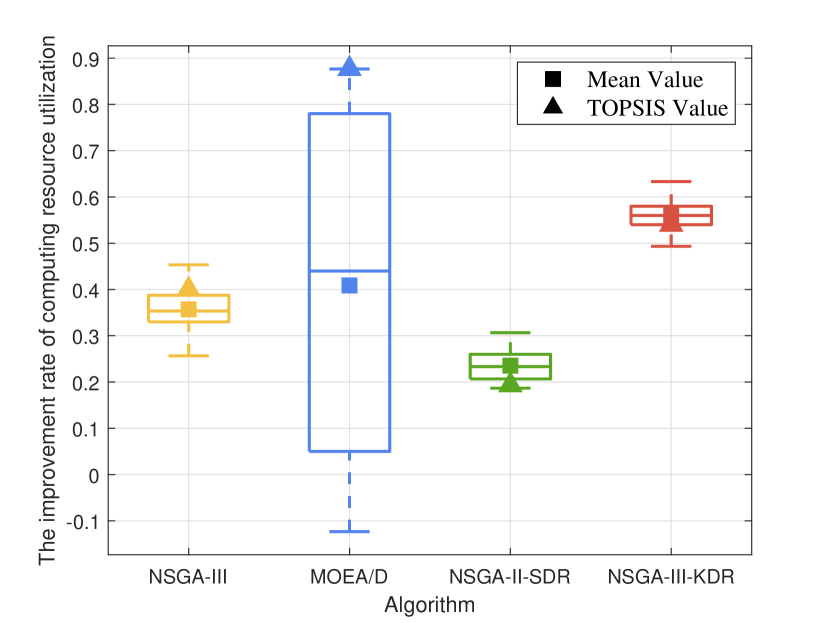
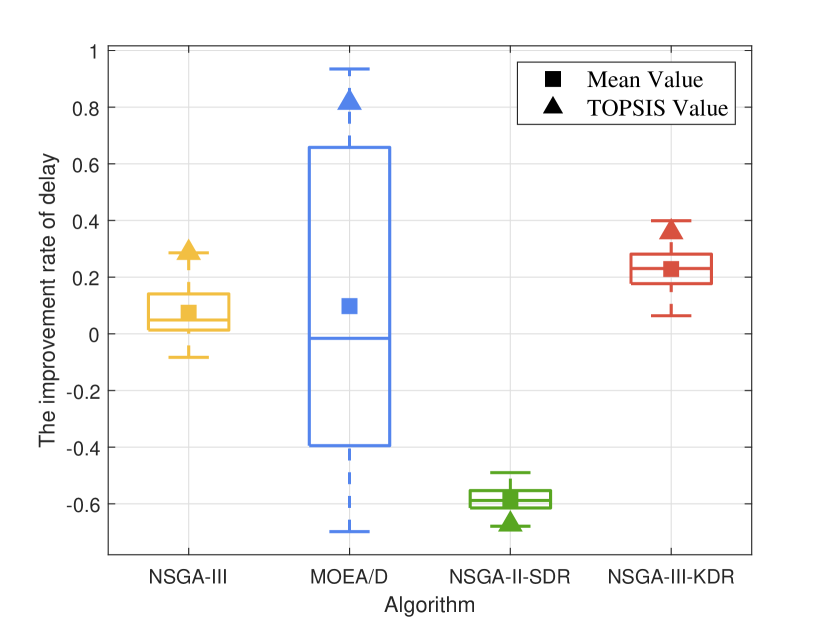
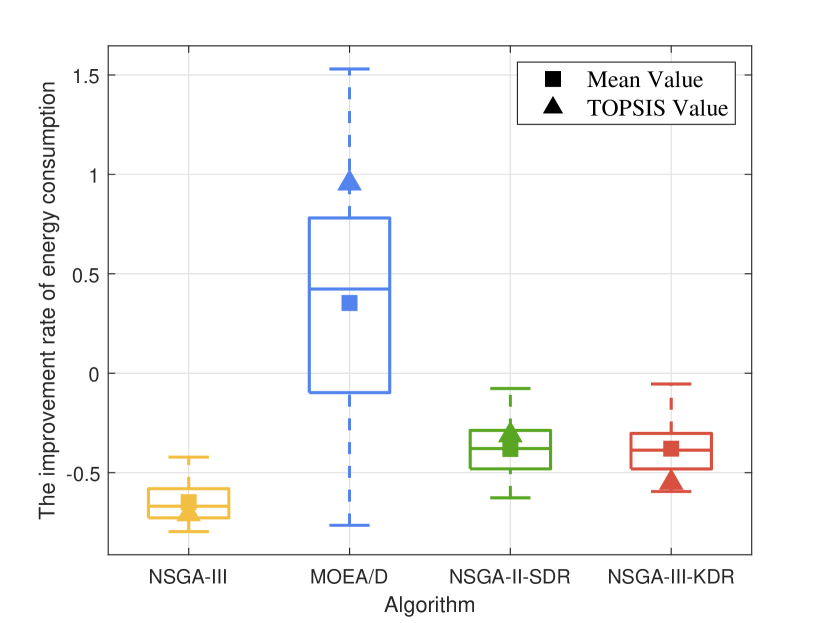
In this part, we compare NSGA-III, MOEA/D, NSGA-II-SDR, and NSGA-III-KDR in optimizing the proposed computing allocation MOOP. We initialize the population with 50% of the computing devices randomly occupied, then perform the optimization using each of the four algorithms separately. We calculate the changes in computing resources between the final and initial populations, while ensuring algorithmic convergence. Due to the uncertainty of the evolutionary process, besides comparing the overall data (represented by a box plot containing five horizontal lines representing the maximum, upper quartile, median, lower quartile, and minimum value from top to bottom) and the optimal data based on TOPSIS (represented by triangles), the average data (represented by squares) are also compared to comprehensively assess the performance of the four algorithms.
The improvement rate (IR) of computing resource utilization under four algorithms is shown in Fig. 8. Overall, except for MOEA/D, the other three algorithms demonstrate positive optimization in computing resource utilization. NSGA-III-KDR shows the most significant overall and average improvements, indicating superior performance and the most substantial enhancement in resource utilization. NSGA-III and NSGA-II-SDR follow, showing notable but lesser improvements. Although MOEA/D achieves the best optimal solution, its overall performance is suboptimal, characterized by some negatively optimized computing allocation strategies. This issue likely stems from MOEA/D’s predefined fixed neighborhood structures, which may restrict its global search capability and lead to local optimality.
As resource utilization improved, Fig. 8 to Fig. 8 illustrate the changes in the other five objectives considered by the computing allocation MOOP. Except for load balancing, improvements in all other objectives are observed with the optimization based on NSGA-III-KDR, attributed to enhanced resource utilization. The superior diversity of NSGA-III-KDR facilitates a more even distribution of computing resources, as particularly evidenced by the significant increase in privacy entropy. Although NSGA-III exhibits similar trends, it is less effective than NSGA-III-KDR. Notably, with NSGA-III-KDR and NSGA-II, increased resource utilization results in higher delays and sharing revenue, while energy consumption decreases as more tasks are offloaded to , leveraging all available resources within 6G PCN comprehensively. The optimization strategy of NSGA-II-SDR favors offloading tasks to and , significantly reduces delay, but uniquely results in positive growth in load balancing among the four algorithms. The optimal solution of MOEA/D surpasses all other algorithms, achieving the highest resource utilization and substantial improvements in all objectives, except for load balancing, and the decline in load balancing suggests a rational allocation of computing resources. However, the overall data of MOEA/D is the worst, with a negative optimization of 12.99%. Furthermore, although its median or average increase in resource utilization is less than that of NSGA-III-KDR, the more substantial improvement in load balancing suggests a less favorable overall evolution. Since the selection of the optimal solution using TOPSIS is random, not every iteration of MOEA/D yields a solution that outperforms those of other algorithms.
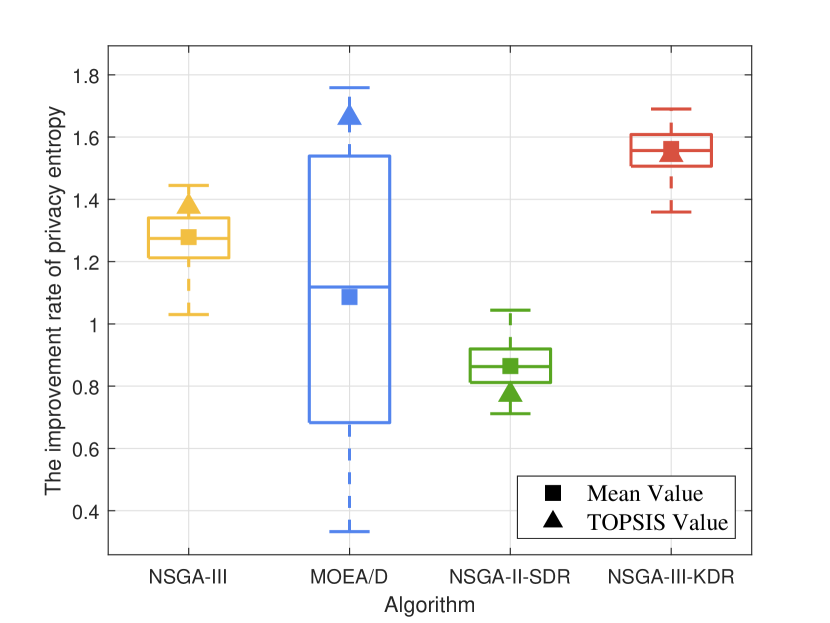
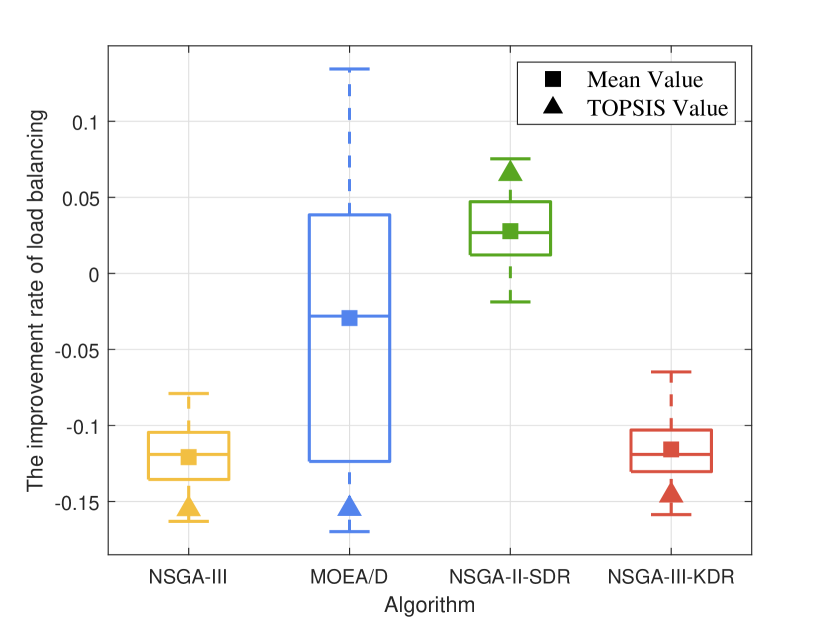
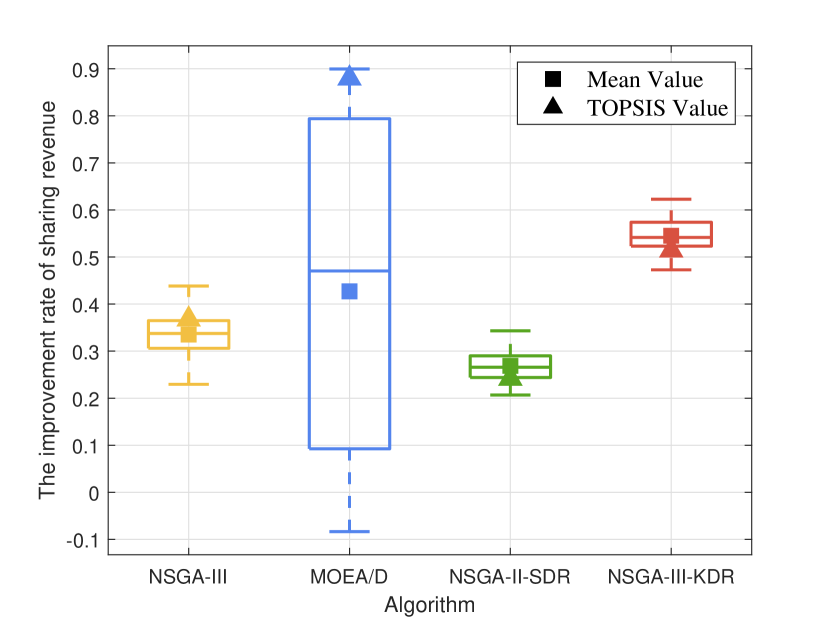
VI-C Simulation of Proposed Pseudonymous Scheme
In this part, we evaluate the computational overhead of the proposed pseudonym scheme by comparing it with several existing pseudonymous schemes. Each operation and phase are tested 20 times separately, and the average value is recorded as the experimental data to eliminate the influence of hardware fluctuations during the operation. First, the BN curve [37] with a 128-bit security level is selected to implement the bilinear group. The execution time of basic cryptographic operations are shown in Table IV. Generally, the execution times required for bitwise XOR and modular multiplication are significantly lower compared to other cryptographic operations, and can thus be disregarded. Moreover, we utilize SHA-256 as the hash function. Then, we assess the time costs associated with system initialization and pseudonym generation (SIPG), certificate issuance or message signing(CIMS), and identity or message verification (IDMV) in the pseudonym authentication process, comparing the proposed scheme with those in [38, 39, 40, 41], as shown in Table V.
| Notation | Operation | Time (ms) |
|---|---|---|
| point multiplication in ECC | 0.618 | |
| point addition in ECC | 0.001 | |
| general hash | 0.001 | |
| exponentiation | 0.011 | |
| bilinear pairing | 1.456 | |
| point multiplication in bilinear pairing | 1.277 | |
| point addition in bilinear pairing | 0.003 | |
| hash-to-point in bilinear pairing | 5.197 |
The proposed scheme, which is based on the Schnorr protocol, primarily involves operations , , and in the pseudonym authentication process. The total computational overload is . Conversely, Bagga et al.’s scheme [38] uses and in the SIPG and IDMV, leading to a higher computational overload. Similarly, Shen et al.’s scheme [39], based on bilinear pairing, also incurs a higher computational overload. Although based on ECC, Yang et al.’s scheme [40] includes 17 times within SIPG, leading to a significant computational overload. Wang et al.’s scheme [41], similar to the proposed scheme, provides the optimal computational overload in both SIPG and IDMV. However, a total of 16 times yields a marginally greater computational overload than ours. Therefore, our scheme achieves the lowest computational overload compared to other related schemes.
| Scheme | SIPG | CIMS | IDMV | Total |
| Bagga et al.’s scheme [38] | ||||
| Shen et al.’s scheme [39] | ||||
| Yang et al.’s scheme [40] | ||||
| Wang et al.’s scheme [41] | ||||
| Our proposed scheme |
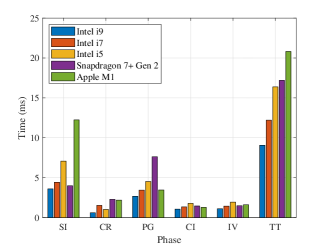
Next, considering the diversity of computational devices, we test the portability of the proposed pseudonym scheme. We consider five different devices, including a workstation with an Intel i9-12900k@3.9GHz and 64GB RAM (Intel i9), a computer with an i7-12700@2.1GHz and 32GB RAM (Intel i7), a computer with an i5-8500@3GHz and 8GB RAM (Intel i5), a smartphone with Snapdragon 7+ Gen 2 and 16GB RAM (Snapdragon 7+ Gen 2), and a MacBook with an M1 chip and 16GB RAM (Apple M1). We test the time consumption for each of the five phases of the pseudonym authentication process on these devices: System Initialization (SI), Computing Devices Registration (CR), Pseudonym Generation (PG), Certificate Issuance (CI), and Identity Verification (IV), including the total time consumption (TT) for the entire process, as shown in Fig. 9. Time consumption varies across devices due to differences in CPU performance. Specifically, the MacBook requires the longest total time to complete a pseudonym authentication, only 20.813 ms. The SI is the most time-consuming, as it involves generating system keys and registering user information. However, typically, SI is only performed once, whereas CR, PG, CI, and IV take less than 8 ms across all devices, with PG taking the longest at 7.628 ms on the smartphone. This demonstrates the good portability and lightweight of the proposed pseudonym scheme.
VII Conclusion
This article investigates improving computing resource utilization within 6G CPN and proposes BECS, a privacy-preserving computing sharing mechanism. We consider various communication, computing, and service factors in 6G CPN, modeling them as a five-objective MOOP. Meanwhile, we utilize the proposed NSGA-III-KDR to find optimal solutions for this MOOP. Additionally, we introduce a novel pseudonym scheme to protect the privacy of users engaged in computing sharing. Extensive simulations demonstrate the effectiveness of BECS. Moving forward, we intend to further explore computing sharing in dynamic real-time scenarios and address security and trustworthiness issues in task offloading.
References
- [1] P. Zhang, H. Yang, Z. Feng et al., “Toward intelligent and efficient 6g networks: Jcsc enabled on-purpose machine communications,” IEEE Wireless Commun., vol. 30, no. 1, pp. 150–157, 2023.
- [2] Y. Lu, B. Ai, Z. Zhong et al., “Energy-efficient task transfer in wireless computing power networks,” IEEE Internet of Things J., vol. 10, no. 11, pp. 9353–9365, 2023.
- [3] Q. Chen, C. Yang, S. Lan et al., “Two-stage evolutionary search for efficient task offloading in edge computing power networks,” IEEE Internet of Things J., vol. 11, no. 19, pp. 30 787–30 799, 2024.
- [4] K. Peng, H. Huang, B. Zhao et al., “Intelligent computation offloading and resource allocation in iiot with end-edge-cloud computing using nsga-iii,” IEEE Trans. Network Sci. Eng., vol. 10, no. 5, pp. 3032–3046, 2023.
- [5] Y. Gong, K. Bian, F. Hao et al., “Dependent tasks offloading in mobile edge computing: A multi-objective evolutionary optimization strategy,” Future Gener. Comput. Syst., vol. 148, pp. 314–325, 2023.
- [6] S. Hu, Y.-C. Liang, Z. Xiong et al., “Blockchain and artificial intelligence for dynamic resource sharing in 6g and beyond,” IEEE Wireless Commun., vol. 28, no. 4, pp. 145–151, 2021.
- [7] J. Wang, X. Ling, Y. Le et al., “Blockchain-enabled wireless communications: a new paradigm towards 6g,” Natl. Sci. Rev., vol. 8, no. 9, p. nwab069, 04 2021.
- [8] J. Xie, K. Zhang, Y. Lu et al., “Resource-efficient dag blockchain with sharding for 6g networks,” IEEE Network, vol. 36, no. 1, pp. 189–196, 2022.
- [9] M. Dai, S. Xu, Z. Wang et al., “Edge trusted sharing: Task-driven decentralized resources collaborate in iot,” IEEE Internet Things J., vol. 10, no. 14, pp. 12 077–12 089, 2023.
- [10] P. Wang, W. Sun, H. Zhang et al., “Distributed and secure federated learning for wireless computing power networks,” IEEE Trans. Veh. Technol., vol. 72, no. 7, pp. 9381–9393, 2023.
- [11] V.-L. Nguyen, P.-C. Lin, B.-C. Cheng et al., “Security and privacy for 6g: A survey on prospective technologies and challenges,” IEEE Commun. Surv. Tutorials, vol. 23, no. 4, pp. 2384–2428, 2021.
- [12] H. Xu, W. Huang, Y. Zhou et al., “Edge computing resource allocation for unmanned aerial vehicle assisted mobile network with blockchain applications,” IEEE Trans. Wireless Commun., vol. 20, no. 5, pp. 3107–3121, 2021.
- [13] D. Wang, N. Zhao, B. Song et al., “Resource management for secure computation offloading in softwarized cyber–physical systems,” IEEE Internet Things J., vol. 8, no. 11, pp. 9294–9304, 2021.
- [14] A. Samy, I. A. Elgendy, H. Yu et al., “Secure task offloading in blockchain-enabled mobile edge computing with deep reinforcement learning,” IEEE Transactions on Network and Service Management, vol. 19, no. 4, pp. 4872–4887, 2022.
- [15] K. Yan, W. Ma, and S. Sun, “Communications and networks resources sharing in 6g: Challenges, architecture, and opportunities,” IEEE Wireless Commun., pp. 1–8, 2024.
- [16] Y. He, Z. Zhang, F. R. Yu et al., “Deep-reinforcement-learning-based optimization for cache-enabled opportunistic interference alignment wireless networks,” IEEE Trans. Veh. Technol., vol. 66, no. 11, pp. 10 433–10 445, 2017.
- [17] L. Yang, J. Cao, Y. Yuan et al., “A framework for partitioning and execution of data stream applications in mobile cloud computing,” SIGMETRICS Perform. Eval. Rev., vol. 40, no. 4, pp. 23–32, 2013.
- [18] J. Li, R. Wang, and K. Wang, “Service function chaining in industrial internet of things with edge intelligence: A natural actor-critic approach,” IEEE Trans. Ind. Inf., vol. 19, no. 1, pp. 491–502, 2023.
- [19] D. Gross, Fundamentals of Queueing Theory. Hoboken, NJ, USA: Wiley, 2008.
- [20] Y. Wen, W. Zhang, and H. Luo, “Energy-optimal mobile application execution: Taming resource-poor mobile devices with cloud clones,” in Proc. IEEE Int. Conf. Comput. Commun. (INFOCOM), 2012, pp. 2716–2720.
- [21] X. Xu, X. Liu, X. Yin et al., “Privacy-aware offloading for training tasks of generative adversarial network in edge computing,” Inf. Sci., vol. 532, pp. 1–15, 2020.
- [22] Z. Cui, Z. Xue, T. Fan et al., “A many-objective evolutionary algorithm based on constraints for collaborative computation offloading,” Swarm Evol. Comput., vol. 77, p. 101244, 2023.
- [23] K. Deb and H. Jain, “An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part i: Solving problems with box constraints,” IEEE Trans. Evol. Comput., vol. 18, no. 4, pp. 577–601, 2014.
- [24] H. Ishibuchi, N. Tsukamoto, and Y. Nojima, “Evolutionary many-objective optimization: A short review,” in Proc. IEEE Congr. Evol. Comput., 2008, pp. 2419–2426.
- [25] Y. Tian, R. Cheng, X. Zhang et al., “A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization,” IEEE Trans. Evol. Comput., vol. 23, no. 2, pp. 331–345, 2019.
- [26] C. C. Aggarwal, A. Hinneburg, and D. A. Keim, “On the surprising behavior of distance metrics in high dimensional space,” in Proc. Int. Conf. Database Theory, 2001, pp. 420–434.
- [27] D. Francois, V. Wertz, and M. Verleysen, “About the locality of kernels in high-dimensional spaces,” in Proc. Int. Symp. Appl. Stochastic Models Data Anal. (ASMDA), 2005, pp. 238–245.
- [28] K. Yan, P. Zeng, K. Wang et al., “Reputation consensus-based scheme for information sharing in internet of vehicles,” IEEE Trans. Veh. Technol., vol. 72, no. 10, pp. 13 631–13 636, 2023.
- [29] C.-P. Schnorr, “Efficient signature generation by smart cards,” J. Cryptol., vol. 4, pp. 161–174, 1991.
- [30] T. Q. Dinh, J. Tang, Q. D. La, and others., “Offloading in mobile edge computing: Task allocation and computational frequency scaling,” IEEE Trans. Commun., vol. 65, no. 8, pp. 3571–3584, 2017.
- [31] J. Liu, K. Xiong, D. W. K. Ng et al., “Max-min energy balance in wireless-powered hierarchical fog-cloud computing networks,” IEEE Trans. Wireless Commun., vol. 19, no. 11, pp. 7064–7080, 2020.
- [32] Y. Tian, R. Cheng, X. Zhang et al., “Platemo: A matlab platform for evolutionary multi-objective optimization [educational forum],” IEEE Comput. Intell. Mag., vol. 12, no. 4, pp. 73–87, 2017.
- [33] R. Cheng, M. Li, Y. Tian et al., “A benchmark test suite for evolutionary many-objective optimization,” Complex Intell. Syst., vol. 3, pp. 67–81, 2017.
- [34] Y. Tian, X. Zhang, C. Wang et al., “An evolutionary algorithm for large-scale sparse multiobjective optimization problems,” IEEE Trans. Evol. Comput., vol. 24, no. 2, pp. 380–393, 2020.
- [35] A. Zhou, Y. Jin, Q. Zhang et al., “Combining model-based and genetics-based offspring generation for multi-objective optimization using a convergence criterion,” in Proc. IEEE Congr. on Evol. Comput., 2006, pp. 892–899.
- [36] H. Wang, Y. Jin, and X. Yao, “Diversity assessment in many-objective optimization,” IEEE Trans. Cybern., vol. 47, no. 6, pp. 1510–1522, 2017.
- [37] P. S. Barreto and M. Naehrig, “Pairing-friendly elliptic curves of prime order,” in Proc. 12th Int. Workshop Select. Areas Cryptography (SAC). Springer, 2005, pp. 319–331.
- [38] P. Bagga, A. K. Sutrala, A. K. Das et al., “Blockchain-based batch authentication protocol for internet of vehicles,” J. Syst. Archit., vol. 113, p. 101877, 2021.
- [39] M. Shen, H. Liu, L. Zhu et al., “Blockchain-assisted secure device authentication for cross-domain industrial iot,” IEEE J. Sel. Areas Commun., vol. 38, no. 5, pp. 942–954, 2020.
- [40] Y. Yang, L. Wei, J. Wu et al., “A blockchain-based multidomain authentication scheme for conditional privacy preserving in vehicular ad-hoc network,” IEEE Internet Things J., vol. 9, no. 11, pp. 8078–8090, 2022.
- [41] F. Wang, J. Cui, Q. Zhang et al., “Blockchain-based lightweight message authentication for edge-assisted cross-domain industrial internet of things,” IEEE Trans. Dependable Secure Comput., vol. 21, no. 4, pp. 1587–1604, 2024.