Decay and Isomeric Properties of Neutron-Rich Ca and Sc Isotopes
Abstract
The isomeric and -decay properties of neutron-rich 53-57Sc and 53,54Ca nuclei near neutron number =32 are reported, and the low-energy level schemes of 53,54,56Sc and 53-57Ti are presented. The low-energy level structures of the 21Sc isotopes are discussed in terms of the coupling of the valence proton to states in the corresponding 20Ca cores. Implications with respect to the robustness of the =32 subshell closure are discussed, as well as the repercussions for a possible =34 subshell closure.
pacs:
23.40.-s, 23.20.Lv, 21.10.Hw, 29.38.Db, 27.40.+zI Introduction
The nuclear shell model Maye55 was developed in part to explain the observed extra stability of nuclei along the valley of stability corresponding to ‘magic’ numbers of protons and/or neutrons. The magic numbers at 2, 8, 20, etc. were explained as corresponding to closed-shell nucleonic configurations. While the shell model is robust near stability, there is evidence at the extremes of the nuclear chart that the single-particle level ordering changes, leading to the erosion of some shell closures and/or the appearance of new ‘magic’ numbers in exotic nuclei. The attractive proton-neutron monopole interaction Otsu01 can produce drastic changes in level ordering, and in regions of low single-particle density, result in modified shell gaps. For example, the monopole shift of the orbit with changing occupancy has been invoked to explain the observed =32 subshell closure in nuclei in the neighborhood of the doubly-magic nucleus Ca.
The =32 subshell closure has been well-established experimentally in 20Ca Huck85 ; Gade06 , 22Ti Jans02 and 24Cr Pris01 on the basis of the systematic behavior of the energies as a function of neutron number in the even-even nuclei of these isotopic chains. Additional evidence for =32 as a new subshell closure in neutron-rich nuclei below =28 comes from the low transition probabilities measured for 54Ti Dinc05 and 56Cr Burg05 . The high-spin structures of 50,52,54Ti Jans02 are also indicative of a sizeable =32 shell gap. The separation between the 6 and the closely spaced 8, 9 and 10 levels in 54Ti was taken to indicate the substantial energy cost in promoting a neutron to either of the or orbitals.
Migration of the orbit may be such that, beyond =32, a gap between the and the orbitals develops. The results of shell-model calculations with the GXPF1 effective interaction point to a =34 subshell closure in the neutron-rich Ti and Ca isotopes Honm02 . The prediction of a new magic number at =34 for the Ti isotopes is inconsistent with experimental results in 56Ti Lidd04_PRL ; Dinc05 . However, shell-model calculations with the slightly-modified GXPF1A effective interaction Honm05 suggest that a =34 subshell gap may still be present in the Ca isotopes.
While the level structure of 54Ca remains difficult to reach experimentally, the possible development of a =34 shell closure in this region can be examined indirectly. Some insight into the relative collectivity of the 20Ca isotopes can be obtained from the energy separation between the ground states and excited states in the odd-mass 23V isotopes. These cluster states were described in detail by Paar Paar73 , and shown to depend on the interaction between the proton cluster and underlying core. In the cases of 51V28 Bunk55 and 55V32 Mant03 ; Zhu07 , with three protons beyond doubly-magic 48Ca28 and 52Ca32 respectively, the separations between the ground state and 5/2- cluster states are 320 and 323 keV. However, for 53V30 Pron76 and 57V34 Lidd05 , with three protons beyond 50Ca30 and 54Ca34 respectively, the separations are only 128 and 113 keV, suggesting that the 54Ca core is more like that of 50Ca than magic 48Ca or 52Ca.
The possible =34 subshell closure has also been probed by tracking the monopole migration of the orbital in neighboring nuclei. Previous work by Liddick Lidd04 , following the systematic evolution of the level through consideration of the ground-state spin and parity assignments of odd-odd V and Sc isotopes, indicated an inversion of the and single-particle orbitals in moving from the 23V to the 21Sc isotopes. The apparent close spacing of the and orbits in the 22Ti isotopes, leading to the absence of the =34 subshell closure for =22, also supports the observed evolution of the neutron single-particle states. Energy spacings between high-spin states in 54Ti and the first three yrast states in 56Ti Forn04 both suggest that the and orbitals are nearly degenerate.
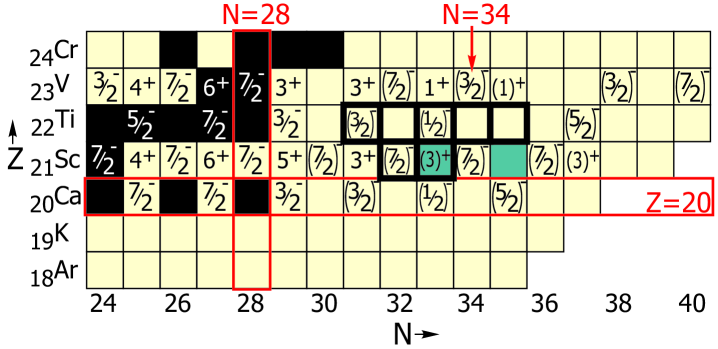
Here, we report on the low-energy structures of 53,54Sc populated following the decay of 53,54Ca respectively, as well as on the low-energy levels of 54,56Sc populated by isomeric -ray decay. The low-energy levels of the 21Sc isotopes can provide insight into the structure of even-even Ca isotopes, as these Sc levels result from the coupling of the odd proton to states in the Ca core. Additionally, we report on newly observed states in 53-57Ti populated in the decay of 53-57Sc, respectively. The nuclei studied in the present work are highlighted in Fig. 1, where known ground-state spins and parities are included for the 20Ca, 21Sc, 22Ti and 23V isotopes. The present results reaffirm the validity of the =32 subshell closure, and the inversion of the and single particle levels moving from the V to the Sc isotopes. However, the apparent compression of the low-energy structure of the neutron-rich Sc isotopes suggests that there may not be a significant =34 gap between the and single-particle states in the 21Sc isotopic chain.
II Experimental Procedure
The decay and isomeric properties of the neutron-rich 53,54Ca and 53-57Sc parent nuclides were deduced in experiments carried out using the experimental facilities at National Superconducting Cyclotron Laboratory (NSCL) at Michigan State University.
A low-energy beam of 76Ge12+ was accelerated to 11.6 MeV/nucleon in the K500 cyclotron, and, following foil stripping to produce 76Ge30+, accelerated to the full energy of 130 MeV/nucleon in the K1200 cyclotron. The 76Ge beam was fragmented in a 352-mg/cm2 thick Be target located at the object position of the A1900 fragment separator Morr03 . The secondary fragments of interest were selected in the A1900 using a 45-mg/cm2 Al wedge and 5% momentum slits located at the intermediate dispersive image of the separator.
Fully-stripped secondary fragments were sent to the NSCL Beta Counting System (BCS)Pris03 located in the S2 experimental vault. The central implantation detector of the BCS was a 995-m thick double-sided Si microstrip detector (DSSD). The DSSD was segmented into 40 1-mm wide strips in both the horizontal and vertical dimensions, for a total of 1600 pixels. Three Si PIN detectors, with respective thicknesses of 297 m, 297 m and 488 m, were located upstream of the DSSD. Six single-sided Si strip detectors (SSSDs) were placed downstream of the DSSD. The last two SSSDs provided a veto for light particles that arrived at the counting system with the secondary beam. The range of the fragments was adjusted with a 4-mm Al degrader located immediately upstream of the BCS detectors, to implant the ions near the center of the DSSD.
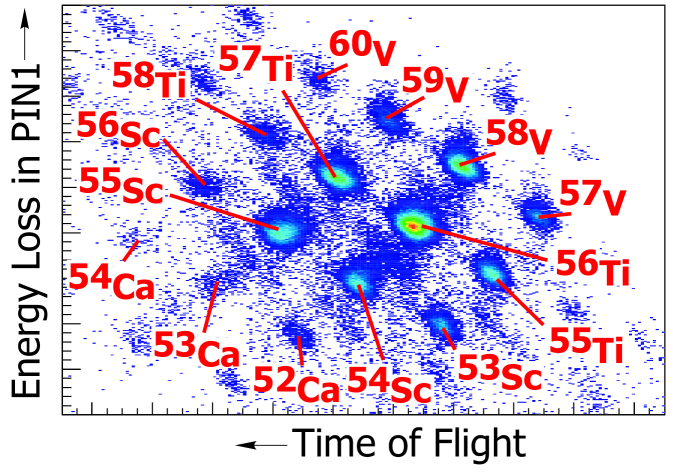
Implanted fragments were unambiguously identified by a combination of multiple energy loss signals, time-of-flight, and the fragment separator magnetic rigidity () setting. The fragment energy loss was measured in the three PIN detectors, and fragment time-of-flight was determined as the time difference between a particle impinging on a plastic scintillator detector positioned at the dispersive image of the A1900 separator, and the first Si PIN detector (PIN1). Fig. 2 illustrates a representative particle identification spectrum for the experiment investigating 53,54Ca and 53-56Sc. The particle ID spectrum that included 57Sc was presented previously Mant08 . The secondary beam was defocused to maximize the active area of the DSSD that was illuminated. The average implantation rate over the entire face of the DSSD was 100 Hz.
Fragment- correlations were established in software by requiring a high-energy implantation event in a single pixel (,) of the DSSD, where is a horizontal strip and is a vertical one. An implantion event was one which had a valid PIN1 signal as well as a high-energy signal in a single strip of both the front and back of the DSSD. A -decay event was one with a high-gain signal above threshold in the front and back of the DSSD and no signal in PIN1. -decay events were correlated with implantations only if they occured in the same pixel, within a specified correlation time window that was adjusted to be at least ten half-lives of the parent nucleus. The differences between the absolute time stamps of correlated and implantation events were histogrammed to generate decay curves.
The profile of implantations over the DSSD surface was such that pixels near the center of the detector experienced a significantly higher implantation rate than those at the detector edge. The higher implantation rate led to a larger accumulated activity in the central pixels. To avoid random correlations when using longer correlation times, a subset of pixels on the DSSD was defined for which the time between implantations was 100 s. Corresponding to pixels on the edge of the detector, this subset of pixels included 50% of the detector surface, and was used for the analysis of decays with long correlation times. Details of the correlation times and the pixels used in analysis are included with the results for each nucleus.
Prompt and delayed -ray detection was accomplished using sixteen detectors from the Segmented Germanium Array (SeGA) Muel01 . The Ge detectors were oriented in two concentric rings of 8 detectors each, surrounding the beam pipe containing the BCS detectors. One detector was omitted from the analysis of data for 53,54Ca and 53-56Sc due to poor gain stability. A photopeak efficiency for -ray detection of 7% at 1 MeV and 3% at 3 MeV was achieved. The energy resolution of all detectors was 3.5 keV for the 1.3-MeV transition in 60Co. Prompt rays emitted following short-lived isomeric decay were detected within a 20-s window following an implantation event. A time-to-amplitude converter (TAC) was used to measure the time elapsed between an implantation event and the observation of isomeric rays in any of the SeGA detectors, permitting measurement of s isomer half-lives.
III Results
III.1 53Ca decay
A correlation time of 5 s was used to analyze the decay of 53Ca to 53Sc, where the expected half-life of 53Ca was on the order of several hundred milliseconds. With a relatively long correlation window, the analysis was restricted to pixels located towards the edge of the implantation DSSD. The -delayed -ray spectrum for 53Ca in the range 0 to 3 MeV is presented in Fig. 3(a). One transition at 2109.00.3 keV has been assigned to the decay of 53Ca. The newly-assigned 2109-keV transition was initially reported by us in Ref. Craw09 , and has been recently confirmed in one-proton knockout from 54Ti McDa09 . An absolute intensity of 5612% was determined for this 2109-keV transition from a Gaussian fit of the peak area, the absolute efficiency of SeGA, and the number of rays correlated with 53Ca parent decays. The absolute intensity of this transition suggests that the majority of intensity from the decay of 53Ca, excluding the previously established 4010% branch Lang83 , proceeds through the 2109-keV excited state. This level has been tentatively assigned spin and parity 3/2-, on the basis of the apparent allowed decay from a (1/2)- 53Ca ground state. The only other possibility for a state populated in allowed decay is a 1/2- assignment, which is excluded due to the observed direct transition to the 7/2- 53Sc ground state.
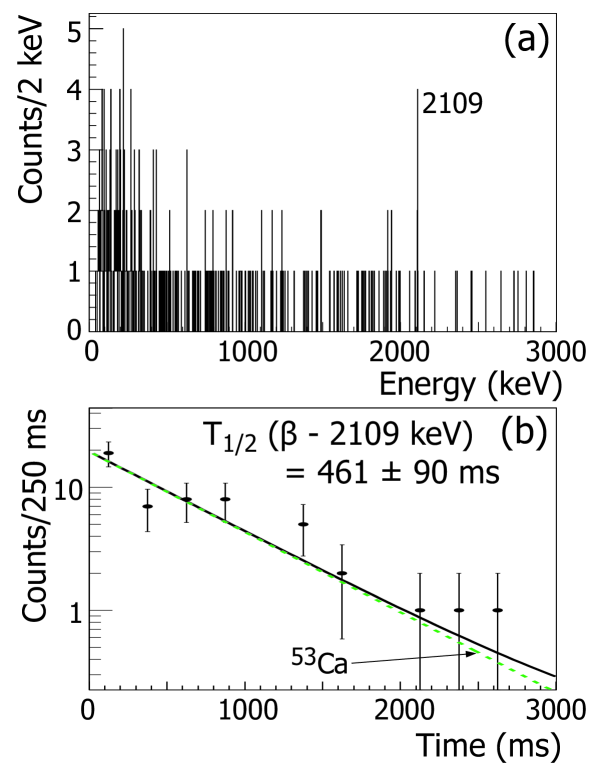
The decay curve for 53Ca gated on the 2109-keV transition is presented in Fig. 3(b). Here, all pixels of the DSSD were considered, since the additional -coincidence requirement significantly reduced background events. The data were fitted with a single exponential decay, and a half-life value of 46190 ms was extracted. This value is higher than the value (23060 ms) obtained previously by Mantica Mant08 , which was deduced from a half-life curve with no additional -ray requirement. The required coincidence in the present result eliminates uncertainties arising from daughter decay and background contributions, and provides a more accurate half-life determination. However, as noted in Ref. Mant08 , the possibility of a second -decaying state in 53Ca cannot be excluded.
III.2 54Ca decay
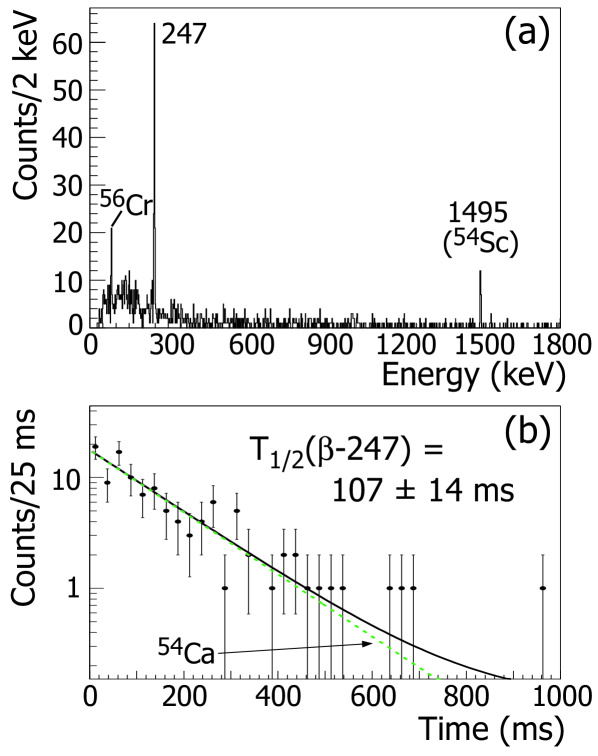
Previous measurement of the 54Ca half-life suggested a value of order 100 ms Mant08 . With such an expectation, a correlation time of 1 s was used for this short-lived nucleus, and data over the entire surface of the DSSD were considered. The -delayed -ray spectrum of 54Ca in the range 0 to 1.8 MeV is shown in Fig. 4(a). One transition at 247.30.3 keV, with an absolute intensity of 659%, has been assigned to the decay of 54Ca. This transition corresponds to the ray observed by Mantica Mant08 , and placed as a ground state transition depopulating a 247-keV state in 54Sc, assigned as = 1+. Missing intensity can be attributed to a possible branch in the 54Ca decay.
III.3 53Sc decay
Information regarding the decay of 53Sc is sparse. Sorlin Sorl98 reported the half-life of 53Sc as 3 s, and did not assign -ray transitions to the decay. Given the anticipated long half-life, a correlation time of 10 s was used for analysis of this isotope, and only pixels on the edge of the DSSD were considered for the half-life and absolute -intensity determinations. On the other hand, the coincidence analysis, which is less sensitive to random background, made use of data from the full DSSD surface. The -delayed -ray spectrum for 53Sc of Fig. 5(a) contains six transitions, one corresponding to a known ray in the decay of the daughter 53Ti Park77 , and five assigned to the decay of 53Sc. Four additional transitions, not apparent in the spectrum of Fig. 5(a), were identified in the coincidence analysis, and confirmed to be present in the -singles spectrum considering data over the full DSSD surface. In the same -singles spectrum, two other weak transitions were identified, and assigned to the decay. Transitions observed with energies of 292, 340, 629, 1237, and 1576 keV agree with those observed in deep-inelastic work on 53Ti Forn05 .
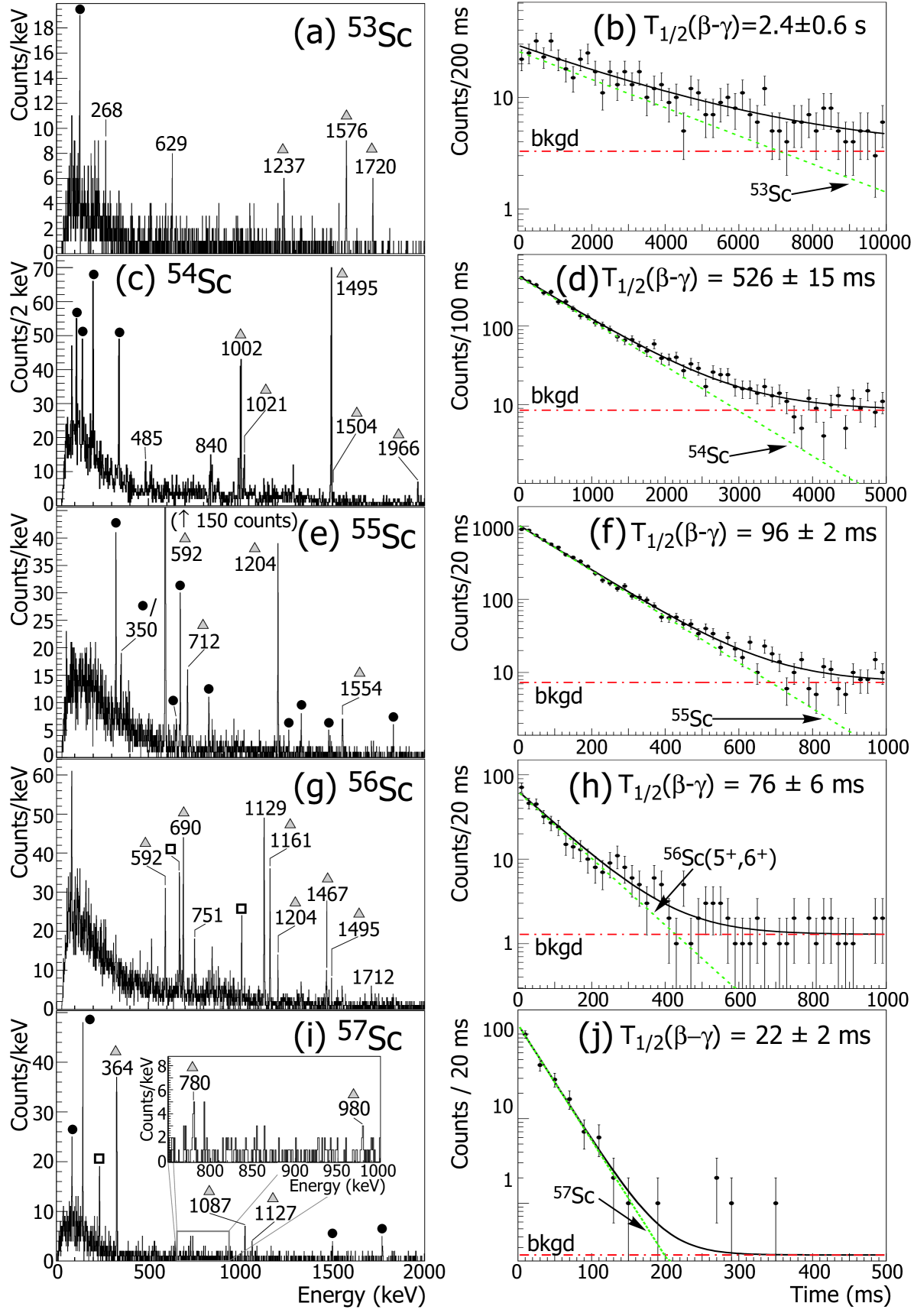
The decay curve for -decay events correlated with 53Sc implantations, with the requirement of a high-energy decay ray in coincidence with the decay event, is shown in Fig. 5(b). The use of high-energy rays above 1 MeV limited the background contribution. The fit of a single exponential decay to these data yielded a half-life of 2.40.6 s.
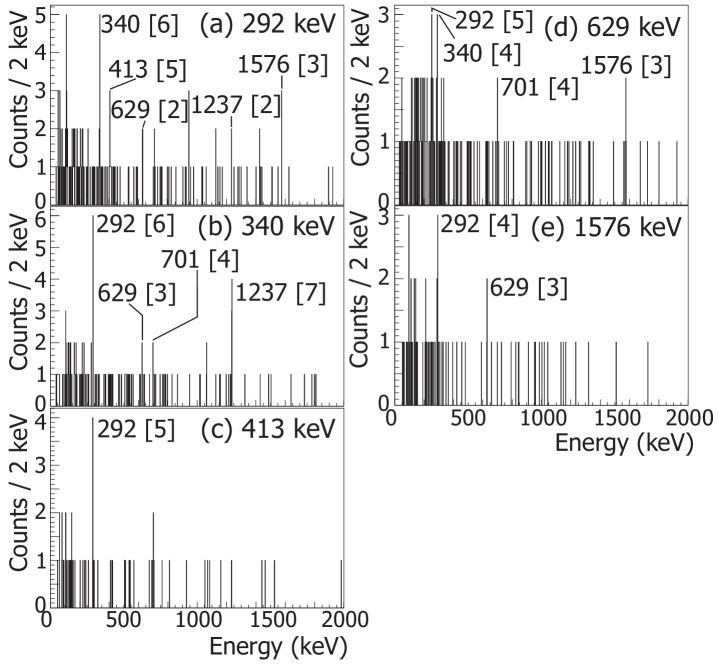
The proposed decay scheme for levels populated in 53Ti by the decay of 53Sc is presented in Fig. 6. The levels at 1237, 1576, 2205 and 2498 keV, and the associated -ray transitions were positioned in accord with Ref. Forn05 and confirmed by coincidence data. The spectrum of -ray transitions coincident with the 292-keV transition revealed a new ray at 413 keV [see Fig. 7(a)], which was placed in cascade with the 292-keV line, depopulating a new state at 2910 keV. A 701-keV transition was observed in coincidence with the 629-keV line [Fig. 7(d)], which was placed as connecting another new state at 2906 keV with the level at 2205 keV. Both of these transitions, and the corresponding doublet of levels at 2910 keV have been confirmed by Cieplicka Ciep09 using Gammasphere data from the reaction 48Ca + 238U, which populates states in 53Ti up to nearly 4 MeV. The Gammasphere work also confirms the placement of the 483-keV transition connecting the 1719- and 1237-keV levels, and is the source of the precise energy values for the 483- and 1576-keV transitions. The absence of rays coincident with the 1720-keV and 1970-keV transitions lead to placement of these transitions feeding the ground state directly. A 267.60.3-keV ray (with an absolute intensity of 63%) remains unplaced in the 53Ti level scheme.

Spin and parity assignments proposed in Fig. 6 were adopted from the deep inelastic work of Fornal Forn05 , and from comparison of the Gammasphere results with shell-model calculations Ciep09 . All assignments are consistent with the observed feeding pattern from the (7/2)- 53Sc ground state. The apparent ground-state feeding is consistent with zero.
III.4 54Sc decay
The analysis of the 54Sc decay, with a half-life of order 400 ms Lidd04 , considered a correlation time of 5 s, again restricted to include pixels towards the edge of the central implantation DSSD. The -delayed -ray spectrum for 54Sc in the range 0 to 2 MeV is presented in Fig. 5(c). Eleven transitions were identified in this spectrum, and the four lowest in energy were eliminated as candidates for transitions in the 54Sc decay, based on their apparent half-lives, and likely belong to the decay of the daughter nucleus, 54Ti. analysis indicates that these four transitions are in coincidence with one another, and the lowest energy transition at 108 keV corresponds to a known transition in 54V Grzy98 . The remaining seven rays were assigned to the decay of 54Sc. One additional transition was observed in the -spectrum considering data over the entire DSSD surface, and assigned to the decay of 54Sc. The transitions observed at 1002, 1021 and 1495 keV were previously observed in decay Lidd04 and deep-inelastic studies Forn04 .
The decay curve of 54Sc-correlated decay events with the additional requirement of a coincident 1002-, 1021-, 1495-, 1504- or 1966-keV -ray transition is given in Fig. 5(d). A fit to these data including a single exponential decay and constant background yielded a half-life for 54Sc of 52615 ms, longer than the value of 36060 ms determined by Liddick Lidd04 . The discrepancy between the present value and previous half-life measurements is attributed to the complex deconvolution of the -decay curve. A new half-life of 2.11.0 s was determined here for the daughter 54Ti, which is slightly longer than the literature value Dorf96 . Additionally, missing intensity is suggestive of a neutron-branching contribution of 169%. Inclusion of these factors in fitting a -decay curve impacts the fit to data. The additional -ray coincidence condition taken here permits a half-life determination that requires only two parameters, and extraction of a more accurate value.
The proposed decay scheme for 54Sc to levels in 54Ti is shown in Fig. 8. Placement of the 1002-, 1021- and 1495-keV transitions follows assignments made in previous works Lidd04 ; Forn04 . The new transitions at 485, 840, 1504 and 1966 keV were placed based on coincidences. Energy-sum relationships were used to place the 1504-keV cross-over transition connecting the states at 3000 and 1495 keV, and the 2517-keV cross-over transition connecting the state at 2517 keV with the ground state.
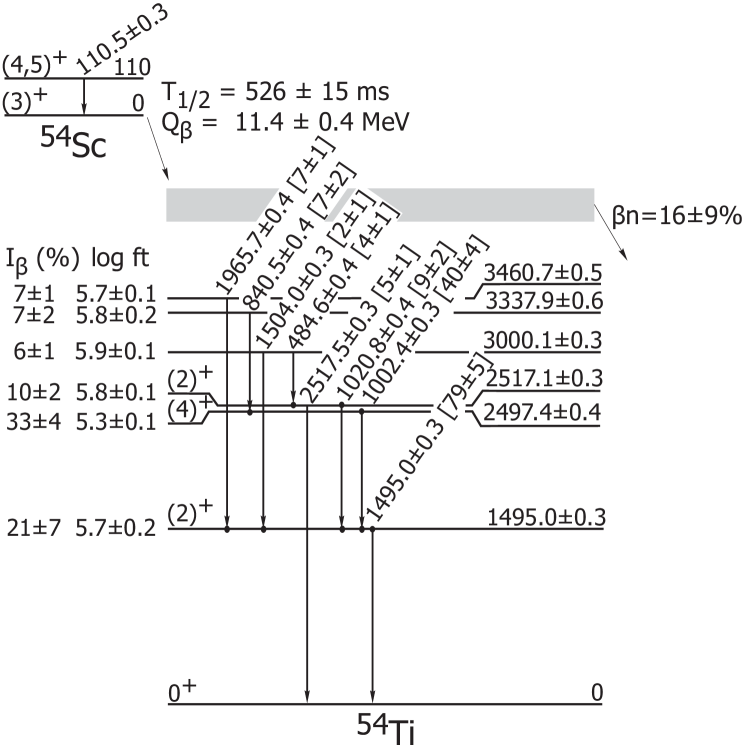
Apparent feedings and log values deduced from the absolute intensities are included in Fig. 8. The of the 54Sc ground state was previously limited to (3,4)+ Lidd04 . Apparent feeding is observed to both the 2 and 4 states previously identified in Ref. Forn04 , at 1495 and 2497 keV respectively. The suggested allowed decay to both of these states further restricts the spin and parity for the 54Sc ground state to 3+. No feeding is expected to the 0+ 54Ti ground state according to the selection rules for allowed decay, assuming a = 3+ ground state for 54Sc. values for the states with energy 1495, 2497 and 2517 keV were adopted from previous works Lidd04 ; Forn04 . Apparent allowed feeding from the (3)+ 54Sc ground state limits the spin and parity of the newly placed levels at 3000, 3338 and 3461 keV to = 2+, 3+, or 4+.
III.5 54Sc isomeric decay
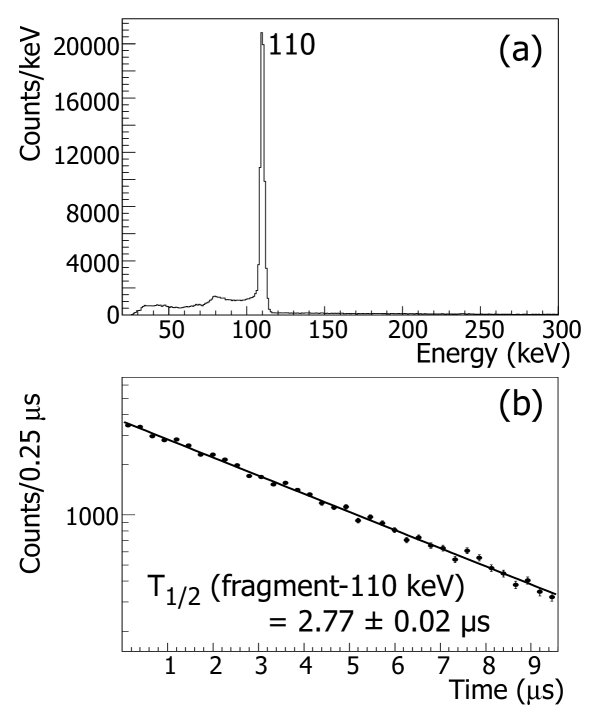
The isomeric -ray spectrum collected within 20 s of a 54Sc implantation event is presented in Fig. 9(a). The 110-keV isomeric transition was initially reported by Grzywacz Grzy98 , and assigned E2 multipolarity. The transition was observed here with high statistics, and an improved half-life of 2.770.02 s was deduced [Fig. 9(b)]. This more precise value is consistent with the result of Grzywacz , and an the E2 multipolarity assignment based on comparison to Weisskopf lifetime estimates. Based on the (3)+ spin and parity of the 54Sc ground state and an E2 isomeric transition, the limits on for the 110-keV level are = 1+ or 5+. = 1 is excluded as this state was not directly populated following the decay of 54Ca. Thus, under the assumption of an E2 multipolarity for the transition, the 110-keV isomeric state in 54Sc is tentatively assigned a spin and parity of 5+, as originally suggested by Grzywacz Grzy98 . However, this assignment assumes a single-particle nature for the final and initial states. More complicated wavefunctions, involving configuration mixing, open the window for a 4+ spin and parity assignment for the 110-keV isomeric state. This possibility is explored further in Section IV.B.
III.6 55Sc decay
A correlation time of 1 s was used for the analysis of events associated with 55Sc, based on previous half-life measurements Sorl98 ; Lidd04 ; Mant08 indicative of a 100 ms half-life. Analysis of the -gated -ray spectrum was again restricted to pixels towards the edge of the central implantation DSSD. The spectrum in the range of 0 to 2 MeV is given in Fig. 5(e). A total of 13 -ray transitions were identified in this spectrum; of these, 9 correspond to known rays in the decay of the daughter isotope, 55Ti. The remaining 4 transitions have been assigned to the decay of 55Sc. One peak in the -singles spectrum, at 349.60.7 keV, is very broad, and is likely a doublet. A known transition in the decay of 55Ti, with energy 349.30.6 keV, may contribute to this peak. The transition with energy 592 keV corresponds to the ray previously observed in the decay of 55Sc by Liddick Lidd04 . States in 55Ti have been studied by deep inelastic scattering with Gammasphere at the ATLAS facility Zhu07 . The rays reported here with energies 350, 592, 1204 and 1554 keV agree with transitions observed in that work.
A summed decay curve from gates on the rays in 55Ti with energies 592, 712, 1204 and 1554 keV is given in Fig. 5(f). This curve was fitted with a single exponential decay and constant background, and the resulting half-life of 962 ms is consistent with previous measurements Lidd04 ; Mant08 .
The level scheme for 55Ti populated following decay of 55Sc is illustrated in Fig. 10. Placement of the 350-, 592-, 1204- and 1554-keV transitions is based on previous deep inelastic results Zhu07 , which established the yrast level structure for 55Ti up to =(19/2)-. One additional transition, not seen in Ref. Zhu07 , with energy 712 keV was observed in coincidence with the 1204- and 592-keV transitions. This 712-keV transition was placed depopulating a new state with energy 2508 keV.

Tentative values were assigned for the ground state and excited states at 592, 1796 and 2146 keV in Ref. Zhu07 , based on comparisons to shell model calculations with the GXPF1A interaction Honm05 . The assignments proposed in that work included = 1/2- for the 55Ti ground state, which has recently been confirmed by a one-neutron knockout measurement from 56Ti to states in 55Ti performed at GSI Maie09 . Such a assignment would exclude allowed decay from the 55Sc ground state populating the 55Ti ground state directly. Thus, the missing intensity of 177% suggests the possible presence of a n branch in the 55Sc decay. Absence of transitions in 54Ti (see Fig. 8) in the -delayed -ray spectrum may indicate that the n branch mainly populates the 54Ti ground state directly. The spin and parity assignments proposed by Zhu Zhu07 are adopted here. Apparent allowed decay to the newly placed state at 2508 keV limits this state to = 5/2-, 7/2- or 9/2-.
III.7 56Sc decay
Analysis of the decay of 56Sc was completed using a correlation time of 1 s, and the full DSSD surface was considered. The -delayed -ray spectrum for 56Sc in the range of 0 to 2 MeV can be found in Fig. 5(g), where nine transitions have been assigned to the decay of 56Sc, and are summarized in Table 1. Two additional transitions were assigned to the decay of the granddaughter nuclide, 56V. The transitions with energies 592, 690, 751, 1129 and 1161 keV were previously observed in both decay Lidd04 and deep-inelastic experiments Forn04 . It was noted in Ref. Lidd04 that the transition with energy 592.30.5 keV was within the error of a known transition in 55Ti, and the possibility of -delayed neutron emission was suggested. Another known transition in 55Ti, at 1204 keV Zhu07 is also present in the delayed -ray spectrum for 56Sc, confirming -delayed neutron emission in this decay.
| Decay | Initial | Final | |||
| (keV) | (%) | Mode | State | State | (ms) |
| (keV) | (keV) | ||||
| n | 592 | 0 | |||
| 2979 | 2289 | ||||
| 1880 | 1129 | ||||
| 1129 | 0 | ||||
| 2289 | 1129 | ||||
| n | 1796 | 592 | |||
| - | - | ||||
| 4474 | 2979 | ||||
| - | - |
Liddick Lidd04 proposed two -decaying states in 56Sc: a low-spin state with = 355 ms, and a higher-spin level with slightly longer = 607 ms. Given the different spin values, the two -decaying states were observed to populate different levels in the 56Ti daughter. Gated decay curves were generated for each -ray transition identified in Fig. 5(g), and fitted with a single exponential decay and constant background. The resultant half-life values are summarized in Table 1. Values deduced from the decay curves gated on the 690- and 1161-keV rays, which depopulate levels at 2979 and 2289 keV respectively, are in agreement with the previous half-life determination for the higher-spin isomer Lidd04 . The transitions assigned to the n decay also have half-lives consistent with decay from the higher-spin state, as do the transitions with energies 1467 and 1495 keV. The weighted average of the half-lives for transitions populated solely by the higher-spin isomer is 756 ms.
The half-life of the lower-spin, -decaying state Lidd04 was previously deduced from a two-component fit to the decay curve gated on the 1129-keV transition, which depopulates a state fed by both -decaying states in 56Sc. Two newly-identified -ray transitions at 751 and 1712 keV decay with half-lives similar to that extracted for the lower-spin isomer. These rays apparently depopulate states fed exclusively by the lower-spin isomer. The weighted average of the half-lives for the 751- and 1712-keV transitions yields a half-life for the lower-spin isomer of 266 ms.
Levels in 56Ti and 55Ti populated in the decay of the two -decaying states in 56Sc are shown in Fig. 11. States in 55Ti are known from the present 55Sc -decay results, previous -decay studies Lidd04 , and deep-inelastic work Zhu07 . The three states at 1129, 2289 and 2979 keV in 56Ti were previously identified and assigned tentative spin and parity values Lidd04 ; Forn04 , which were adopted in Fig. 11. Observed coincidences between the 1129- and 751-keV transitions suggest the placement of an additional state populated by the lower-spin -decaying state at 1880 keV. In addition to populating the two states at 2289 and 2979 keV directly, observed coincidences between the 1495- and 690-keV transitions suggest that the higher-spin -decaying state populates a level at 4474 keV. Only the 1467- and 1712-keV transitions remain unplaced in the present level scheme for 56Ti.
Absolute -ray intensities were determined for the -delayed -ray transitions in the 56Sc decay by comparison of the number of observed rays, adjusted for the absolute efficiency of SeGA, with the number of observed 56Sc decays. The number of parent decays in this case was determined using the total number of implantations, taken from the particle identification, and the average -detection efficiency of 11.40.4%. The absolute -ray intensities are included in Table 1, and in the decay scheme of Fig. 11. Apparent branches were deduced from the absolute -ray intensities. Decay from the higher-spin isomer apparently populates both the 4+ and 6+ states in 56Ti. This suggests that the higher-spin isomer has =5+, in contradiction to the previous assignment of (6,7)+ by Liddick et al. Lidd04 . However, the large value for the decay allows the (4)+ state at 2289 keV to be populated by cascades from above, resulting in the observed intensity difference between the 690- and 1161-keV transitions. Given this possibility, the higher-spin -decaying state has been tentatively assigned as (5,6)+. The state with an energy of 4474 keV, also populated by the higher-spin -decaying state, has limited to 4+, 5+, 6+ or 7+, depending on the spin and parity of the higher-spin -decaying state in 56Sc.
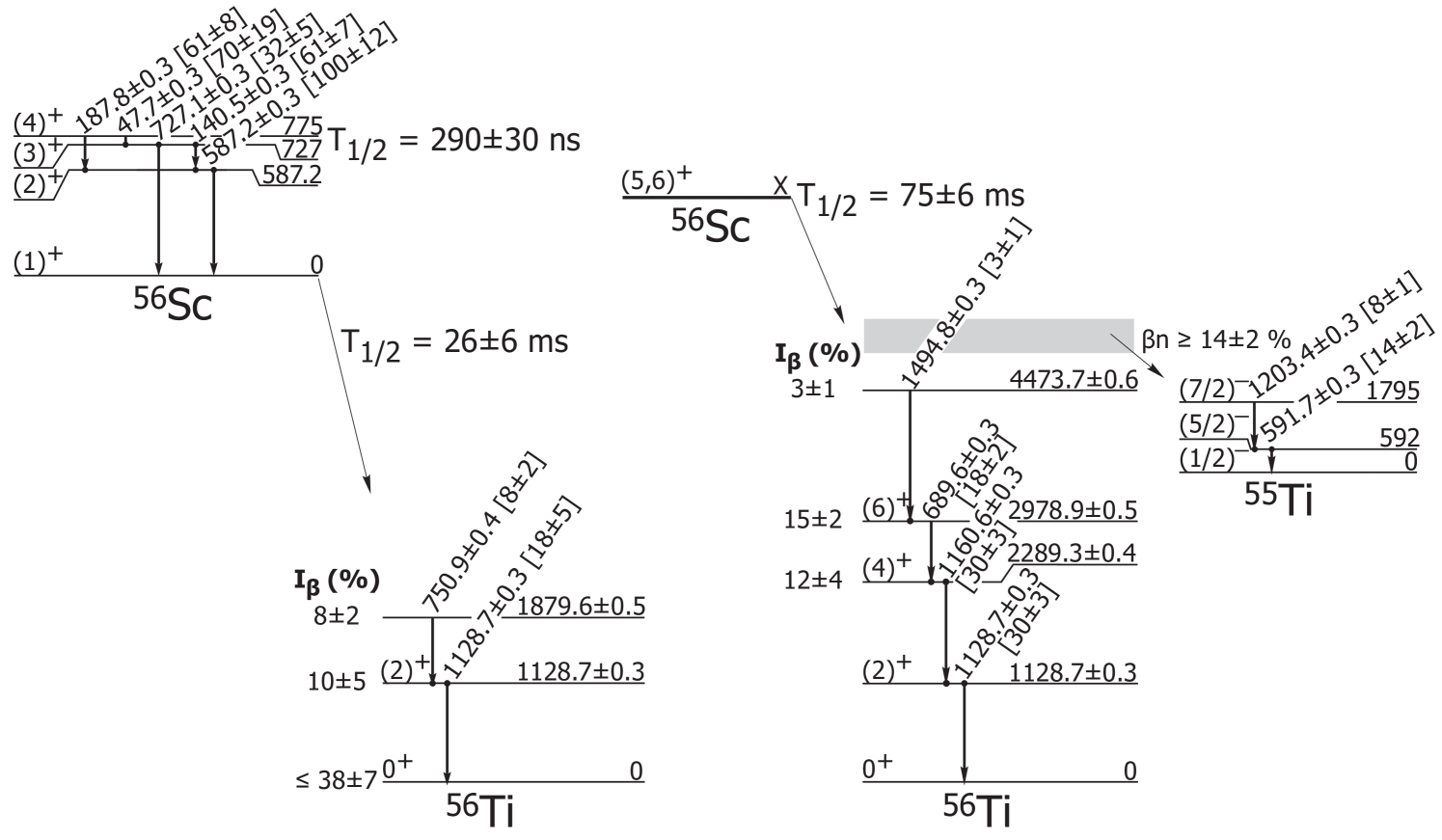
Decay from the lower-spin -decaying state in 56Sc apparently directly feeds the first excited 2+ state in 56Ti, which limits the spin and parity of this -decaying state to 1+, 2+ or 3+. The for the 56Sc ground state can be further restricted if there is direct feeding to the 56Ti ground state. The absolute intensity of the 592-keV transition in the n daughter 55Ti suggests a lower-limit for the neutron branching ratio of 142%. Even under the assumption that the two unplaced transitions directly populate the 56Ti ground state, there is 297% of the intensity unaccounted for. Two scenarios can account for the missing intensity: either direct feeding to the 56Ti ground state or n decay populating the ground state of 55Ti directly. These possibilities were investigated by reanalyzing the decay of 56Sc with the longer correlation time of 5 s. With a longer correlation time, it was possible to compare the intensities of -ray transitions in the decay of the n daughter 55Ti (672.5 keV, % Mant03 ), and the granddaughter 56V (668.4 keV, % Mant03_2 ). The ratio of to n decays in 56Sc can be determined by the ratio of the intensities of the 668- and 673-keV transitions, which are detected with nearly the same efficiency in SeGA. Approximately 70% of the decays of 56Sc populate states in 56Ti. Thus, the missing intensity cannot be fully accounted for by n decay to the ground state of 55Ti, and there is apparent direct population of the 0+ 56Ti ground state, which must be from the lower-spin -decaying state. This suggests a spin and parity for the lower-spin -decaying state of =1+. Direct feeding from the (1)+ -decaying state limits of the state at 1880 keV to (0,1,2)+.
III.8 56Sc isomer decay
The isomeric -ray spectrum collected within a 20-s time window following a 56Sc implantation is presented in Fig. 12(a). Five transitions were observed. Those with energies 140, 188 and 587 keV were previously reported by Liddick Lidd04 .
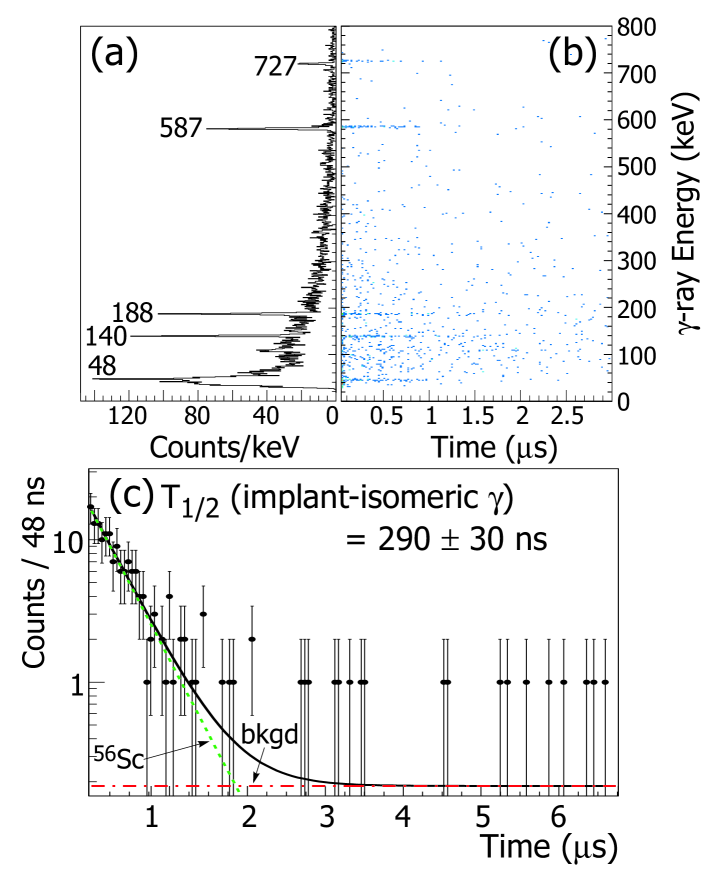
The observed -ray energy as a function of the time elapsed between a 56Sc implantation event and prompt emission is presented in Fig. 12(b). The five transitions appear to decay with the same half-life. The projection of Fig. 12(b) onto the time axis, gated on the five isomeric transitions, is included in Fig. 12(c). The resultant decay curve was fitted with a single exponential decay and a constant background, resulting in a half-life of 29030 ns.
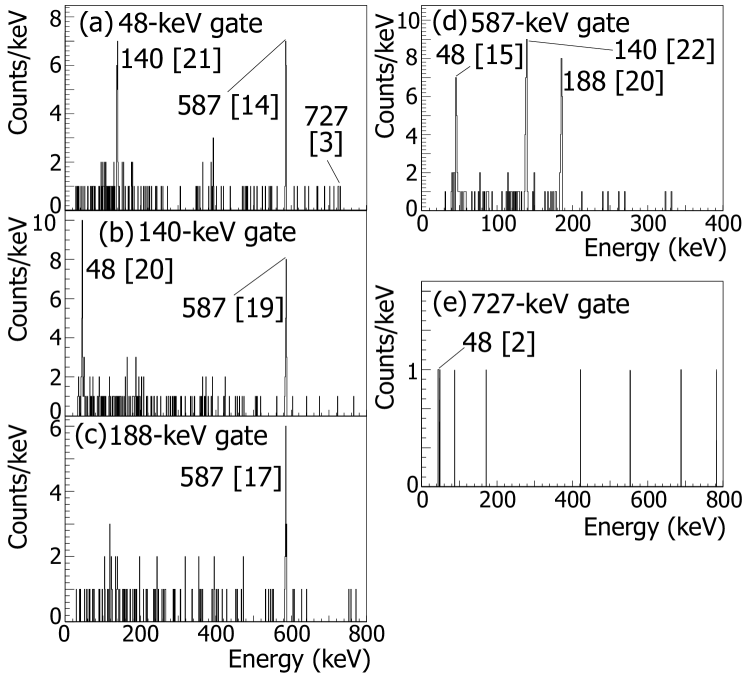
The low-energy structure of 56Sc, populated by isomeric decay (as presented in Fig. 11), was based on observed coincidences (see Fig. 13), as well as relative intensity and energy-sum relationships.
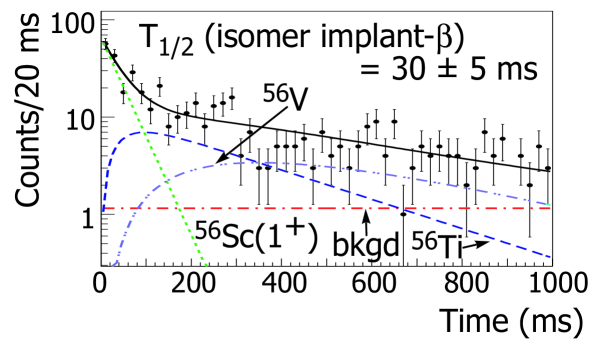
A novel approach was taken to determine which of the two -decaying states in 56Sc is populated in the isomeric decay from the 775-keV level. A half-life curve was constructed considering only -decay events correlated with 56Sc implantation events that were in turn correlated with one of the five prompt rays. The resultant decay curve is presented in Fig. 14. The deduced short half-life of 305 ms provides evidence that the isomeric transitions populate the lower-spin -decaying state.
The tentative spin and parity assignment of the lower-spin -decay isomer in 56Sc as 1+ permits tentative assignments to the remaining levels populated in decay of the isomeric state in 56Sc. The 188-keV transition, which directly depopulates the isomeric level, is proposed to be of E2 character, based on the comparison to Weisskopf half-life estimates, and the competing 48-keV transition to be of the M1 type. It follows that the 140-keV transition must also have M1 multipolarity. The observed intensities of the 727-keV and 140-keV transitions then suggest the former ray to be an E2 transition. Finally, the remaining 587-keV transition must have M1 multipolarity. These assignments lead to the tentatively assigned = 2+, 3+ and 4+ values for the states in 56Sc with energies 587, 727 and 775 keV above the lower-spin -decaying state respectively, again assuming that this state in 56Sc has =1+ quantum numbers.
III.9 57Sc decay
57Sc was studied in a separate experiment from that used to deduce the results for the isotopes previously discussed. However, the decay of 57Sc to states in 57Ti was analyzed in a similar manner. A correlation time of 500 ms was used for the analysis of this decay, which had a previous half-life measurement of order tens of milliseconds. Pixels over the entire DSSD surface were considered in the analysis.
The -delayed -ray spectrum for the decay of 57Sc is presented in Fig. 5(i). Four transitions in this spectrum were attributed to the decay of the 57Ti daughter nucleus, and one transition was known from the decay of the 57V granddaughter. The remaining five rays in Fig. 5(i) were attributed to the decay of 57Sc, and are listed in Table 2. No previous information on -delayed rays in 57Sc is available from the literature. The transition at 1127 keV is close in energy to a known transition in 56Ti, at 1128.70.3 keV Lidd04 ; Forn04 , and may suggest a -delayed neutron branch from 57Sc to levels in 56Ti.
| (%) | |
|---|---|
The decay curve for 57Sc-correlated decays with the additional requirement of a decay -ray coincidence is given in Fig. 5(j). The decay curve was fitted with a single exponential decay and a constant background, and the deduced half-life was 222 ms. The new half-life value is slightly longer than the previous 57Sc half-life measurement of 134 ms Sorl03 , which did not include a -ray tag.
No coincidence data were available due to low statistics. The absolute intensity for the 364-keV ray suggests that it directly populates the 57Ti ground state, and it has been placed as a ground-state transition. No other conclusions regarding the low energy structure of 57Ti could be drawn from the present data.
IV Discussion
The low-energy levels of the 21Sc isotopes can be discussed, in the context of the extreme single-particle model, as a coupling of the odd proton to the states in the 20Ca core isotopes. The success or failure of simple coupling schemes in explaining the low-energy structure of the Sc isotopes can also provide indirect indications regarding the presence or absence of subshell closures in the Ca core nuclei. The structure of the Sc isotopes is first discussed in the framework of this coupling, and then compared to the results of shell model calculations. Results in the Ti isotopes are discussed in terms of the systematic evolution of structure along the =22 isotopic chain.
IV.1 Low-energy structure of 53Sc
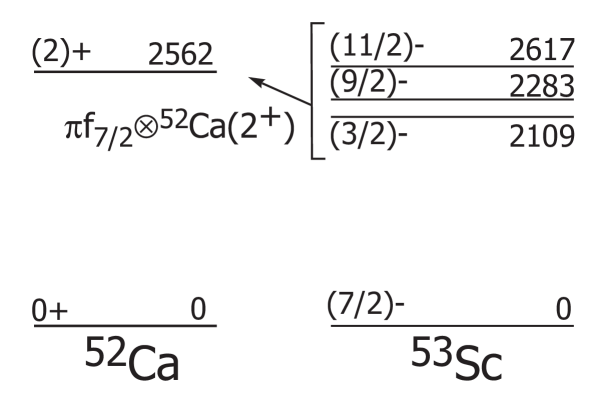
The low-energy structure of 53Sc can be interpreted as a weak coupling of the valence proton to states in 52Ca, which, assuming a robust =32 subshell closure, can be viewed as a doubly magic core Gade06 ; Craw09 . Coupling of the valence proton to the first 2+ state in 52Ca should produce a quintet of states in 53Sc with values ranging from 3/2- to 11/2-, at energies centered around 2.6 MeV. Studies of 53Sc via deep inelastic reactions Bhat09 have populated 9/2- and 11/2- states near this energy, which are likely members of the 2+ multiplet. The decay of 53Ca was observed to populate only one state in 53Sc. The population of a single state in the decay of 53Ca decay limits the spin and parity of the 53Ca ground state to =1/2-, as allowed decay from a = 3/2- or 5/2- 53Ca ground state would be expected to populate several levels of the 2+ multiplet. The single new level at 2109 keV populated in the decay from a =1/2- 53Ca ground state is a likely candidate for the 3/2- member of the 2+ multiplet. The three known levels in 53Sc (see Fig. 15) reside at just over 2 MeV, nearly the energy expected within the weak coupling framework. The success of this scheme in describing the structure of 53Sc provides further support for the robust nature of the =32 subshell closure in the 20Ca isotopes.
IV.2 Low-energy structure of even-A Sc isotopes
The structure of the even- 21Sc isotopes can be described in terms of coupling of the valence proton particle with , , , and at higher energies, , valence neutron structures to states in a corresponding 20Ca core. This is shown most directly by considering the cases of 50Sc and 52Sc, where this simple description explains many aspects of the known low-energy structures.
50Sc has one proton and one neutron particle outside of the doubly magic 48Ca core, and the lowest energy levels can be described in terms of the coupling of a valence proton and neutron. The low-energy structure, known from decay Albu84 , transfer reactions Fist94 , and charge exchange reactions Ajze85 can be seen in Fig. 16(a). The four states lowest in energy arise from the configuration , which produces four states ranging from = 2+ to 5+. The particle-particle coupling rules Paar79 suggest that the states in this multiplet are arranged in a downward-opening parabola, in good agreement with the experimental energy levels. Promotion of the valence neutron in 50Sc to the level will give the configuration , producing two states with =3+, 4+. Two 3+ states are identified in the level scheme of 50Sc above 2 MeV, and either may be a candidate for the 3+ member of this doublet. The energy spacing between multiplets arising from configurations involving the and states is directly related to the - single-particle spacing, and thus the - spin-orbit splitting. The apparent separation of these two multiplets in 50Sc is of order 2 MeV, a gap sufficient to account for the established =32 subshell closure in 21Sc.
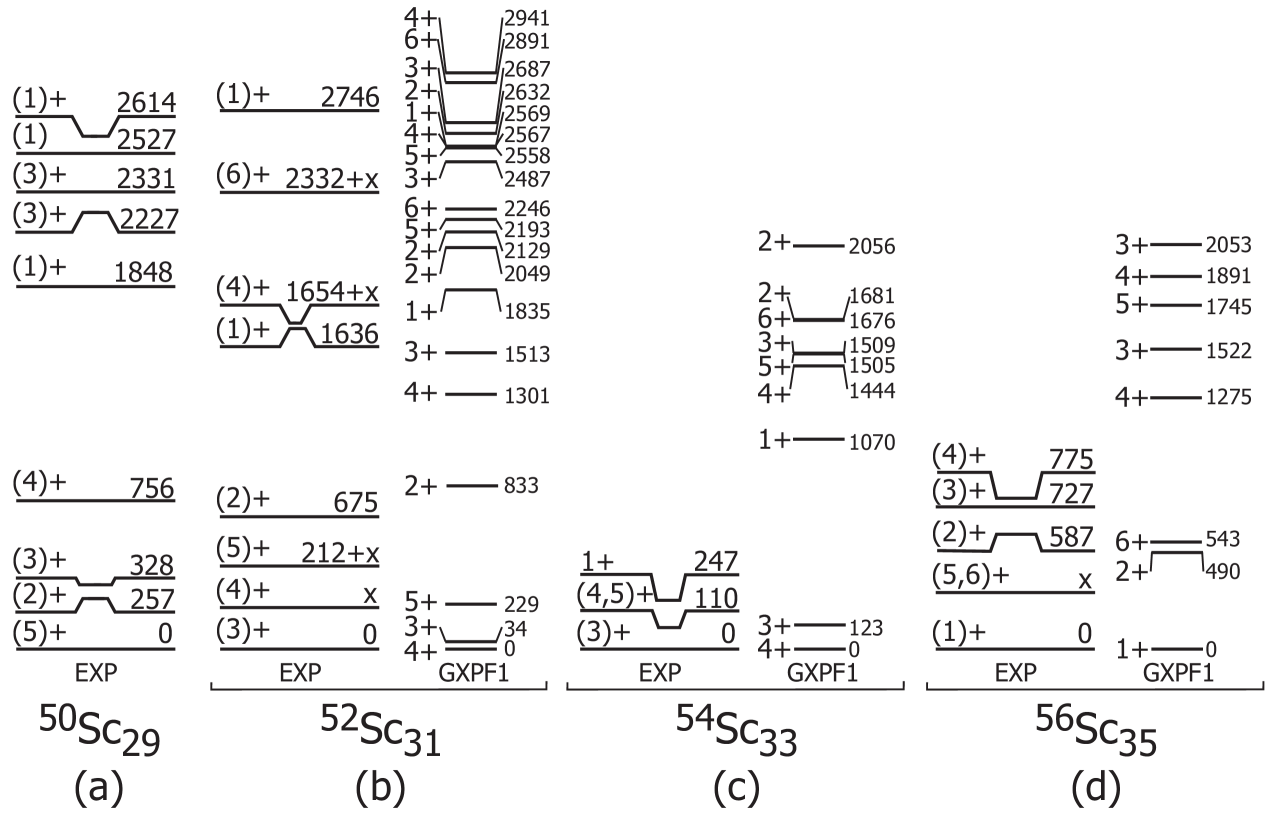
The low-energy structure of 52Sc can be similarly described in terms of coupling of a valence proton particle and neutron hole, taking 52Ca as the inert core. States in this odd-odd nucleus have been identified following decay Huck85 , in-beam -ray spectroscopy following secondary fragmentation Gade06_2 and deep-inelastic work Forn08 ; Bhat09 . The known levels are presented in Fig. 16(b). As discussed in Refs. Forn08 ; Bhat09 , the lowest-lying quartet of states in 52Sc can be associated with the configuration . The four states with =2+-5+ should form an upward-opening parabola, since the coupling involves a proton particle and neutron hole. Shell-model calculations based on the effective interactions GXPF1 Gade06 and GXPF1A Forn08 , which assume an inert 48Ca core, both result in the near-degeneracy of the 3+ and 4+ states of this multiplet. The energy separation between these states has not been established experimentally, but is likely small. The success of the Pandya transformation Pand56 in relating the particle-particle states of 50Sc to the particle-hole states in 52Sc also suggests that the energy separation between the 3+ and 4+ states is small in 52Sc, and that the configurations of these low-lying levels in both nuclei is fairly pure. Calculations using the GXPF1 effective interaction Gade06 confirm the configurational purity of the four lowest-energy levels. The coupling of the proton to an excited neutron to give a pair of states with =3+, 4+ accounts for the observed 4+ state in 52Sc at 1.7 MeV. The 6+ state at 2.3 MeV in 52Sc has been shown in shell-model calculations to have parentage including this configuration, though the extent of this contribution varies between shell-model interactions. Calculations using the GXPF1A interaction Forn08 suggest that the primary parentage of the 2.3-MeV 6+ state is , while the configuration is predicted to dominate the first 8+ state in 52Sc, experimentally observed at 3.6 MeV Forn08 . The energy separation between states arising from the and configurations was 2 MeV, corresponding to the spin-orbit splitting between the and single-particle states, in agreement with the situation in 50Sc. As noted by Fornal Forn08 , the apparent separation between the and single-particle states, as inferred from the energy spacing between the 6+ and 8+ states in 52Sc, is slightly smaller than that predicted in the GXPF1A interaction.
The low-energy structure of 54Sc, with two additional neutrons, should exhibit significant change. The orbital is now fully occupied, and the 54Sc structure at low energy should reflect coupling of the valence proton particle to either a or neutron, taking 52Ca as the inert core. The single-particle level is expected to lie below the state for the 21Sc isotopes, based on the observations in 52Sc. Assuming such an ordering, the coupling yields a doublet of states with =3+, 4+, which is expected to be lowest in energy in 54Sc. Shell model results Lidd04 predict the 3+ and 4+ states of this configuration to be close in energy, and thus the spin and parity of the 54Sc ground state from a theory perspective is not clear. The ground state is tentatively assigned =3+ in the present work. Considering the situation in terms of the coupling, it may be natural to assume that the isomeric 110-keV level corresponds to the 4+ state arising from the configuration. However, within the simple coupling framework it is difficult to accept an in-multiplet M1 transition hindered so strongly as to yield the experimental isomer half-life of 2.8 s. In this case, the two excited states identified in 54Sc, the isomeric (5)+ level and higher-lying 1+ state, may be explained as arising from the configuration . This coupling results in a sextet of states ranging from =1+ to 6+. The particle-particle coupling would produce a downward-facing parabola. There are, however, inconsistencies in the experimental level ordering in 54Sc when compared with shell model calculations. The 1+ state lies above the 5+ state in energy in the level scheme as presented in Fig. 16(c), a result which is inconsistent with calculations using the GXPF1 effective interaction. An alternative assignment for the states in 54Sc with a 4+ ground state and 6+ 110-keV isomeric level is a possibility, but the placement of the 6+ level below the 1+ level is also unexpected. The apparent experimental level ordering would be explained if the configuration was the origin of the 3+ and 5+ states. However, as the - spin-orbit splitting is a fairly constant 2 MeV, this multiplet is expected at much higher excitation energy in 54Sc, making this possibility unlikely.
An alternative to the 5+ assignment for the 110-keV isomeric state is a 4+ assignment. While not expected based on comparison of the deduced isomer lifetime with Weisskopf single-particle estimates, which favor an E2 multipolarity for the 110-keV transition, a 4+ spin and parity cannot be excluded for the 110-keV state. Calculations using the GXPF1 Honm02 , GXPF1A Honm05 and KB3G Pove01 interactions all predict a doublet of states near the 54Sc ground state with =3+ and 4+. The transition probabilities, and calculated with these three interactions are shown in Table 3, along with the calculated partial half-lives. In all cases, the M1 component would dominate the transition. However, the values are small, giving rise to half-lives of order nanoseconds or longer – much slower than the picoseconds expectation from the single-particle Weisskopf estimate. The value is very sensitive to the degree of mixing in the wavefunctions for the 3+ and 4+ states. With increased configuration mixing, there is increased suppression of the value, hindering the transition. A 4+ spin and parity assignment is in better agreement with the expectation for the level ordering in 54Sc. However, more work is required to make a firm spin assignment for the 110-keV isomeric state in 54Sc.
| GXPF1 | GXPF1A | KB3G | Single-Particle | |
|---|---|---|---|---|
| () | 0.02611 | 0.00369 | 0.00080 | |
| (s) | 8.1010-10 | 1.5610-8 | 8.9410-7 | 9.3010-12 |
| () | 5.07 | 6.24 | 6.96 | |
| (s) | 4.0510-6 | 1.7210-5 | 1.0310-3 | 2.8910-6 |
The 1+ state at energy 247 keV in 54Sc can only be explained by the configuration. Even if this is the only member of the multiplet identified, the energy separation between the ground state with and the excited states from appears to be small. Shell model results using the GXPF1 effective interaction Lidd04 predict a - separation of more than 1 MeV, which manifests itself in 54Sc as an expanded low-energy level structure [see Fig. 16(c)]. The compression observed here between multiplets arising from coupling with the and neutron states suggests a - single-particle energy separation smaller than that assumed in the GXPF1 Hamiltonian, and is possibly inconsistent with a robust =34 subshell closure.
Another rapid structure change should be evident in 56Sc. The addition of two neutrons to 54Sc should fill the single-particle orbital. The unpaired valence neutron will then occupy the state. Under this assumption, the lowest energy states in 56Sc are expected to arise from the configuration. The resulting sextet of states with =1+ to 6+ should be arranged in a downward facing parabola, with the 4+ state at the vertex. The challenge in comparing expectations in 56Sc to the new data is the unknown position of the higher-spin -decaying state, relative to the low-energy structure established by the isomer decay. However, the states at low energy in 56Sc with =1+, 2+ and (5,6)+ are difficult to explain in a simple way outside of the configuration. The 3+ and 4+ states cannot be trivially assigned the same configuration, as they may also arise from the coupling, depending on the relative position of the and single-particle orbitals. In fact, significant mixing would be expected between the 3+/4+ states in the - and - multiplets. This mixing is already reflected in the GXPF1 calculated levels, even with a large - gap.
IV.3 Systematic variation of the Ti levels
The experimentally-known levels below 4 MeV in the odd- neutron-rich Ti isotopes are represented in Fig. 17. The levels of the 22Ti isotopes have been well characterized Jans02 ; Dinc05 ; Forn05 ; Forn04 ; Zhu07 by the GXPF1A Honm05 shell-model effective interaction.

Within the GXPF1A interaction, the ordering of the neutron single-particle states places the orbital below the orbital for the Ti isotopes. Given such an ordering, 55Ti33 is expected to have a 1/2- ground state, as the first neutron above the =32 subshell closure should occupy the orbital. The first excited state in 55Ti then corresponds to excitation of the valence neutron into the orbital. The recent direct determination of the ground state spin and parity in 55Ti Maie09 provides confirmation for the ordering of the and orbitals, with the orbital lying lower in energy, similar to the ordering in the 21Sc isotopes. Thus, it appears that the - level ordering changes already in going from 23V to 22Ti, though a significant energy gap between these orbitals is not present in the Ti isotopes Zhu07 .
Based on the assumed neutron-level ordering, 57Ti35 is expected to have a 5/2- ground state, with a neutron configuration of , and a first excited state with =1/2-, corresponding to excitation of a neutron into the orbital. Thus, this is essentially an inversion of the two lowest states in 55Ti. Calculations with the GXPF1A interaction have placed this first excited state at an energy of 422 keV Lidd05 . In the present results, one state has been placed in the level scheme of 57Ti at an energy of 364 keV, which may correspond to the 1/2- first excited state. If this is the case, decay from the 57Sc 7/2- ground state should not directly populate this state, and it must be fed indirectly from higher-lying states. However, the 364-keV transition is much stronger than the other transitions observed in the decay, and direct feeding cannot be excluded. Allowed decay from 57Sc, with a 7/2- ground state, populating the first-excited state in 57Ti would suggest a reversal of the level ordering shown in Fig. 17, and would present a significant challenge for theory. However, before the origin of the 364-keV state can be confirmed, a more complete picture of the low-energy states in 57Ti is required.
V Summary
The low-energy levels of neutron-rich 53,54,56Sc and 53-57Ti have been investigated through the decay of the parent nuclides 53,54Ca and 53-57Sc, as well as through prompt isomeric -ray emission from 54,56Sc. The low-energy structures of the Sc isotopes can be considered in the extreme single-particle model as the result of coupling of the valence proton to states in the corresponding 20Ca core. Such a description works well in 53Sc, where the valence proton weakly couples to states in doubly-magic Ca32. The success of this description provides further evidence for the validity of the =32 subshell closure in the Ca isotopes. Interpretation of the low-energy levels in the even-A Sc isotopes as resulting from the simple coupling of a proton and valence neutrons to a Ca core provides preliminary information regarding the energy separation between neutron single-particle levels. While more work is required to complete the relevant multiplets of states, early indications suggest that the low-energy levels in the Sc isotopes are compressed, and that a significant =34 subshell gap does not exist between the and neutron levels in the 21Sc isotopes. More information is required in the 20Ca isotopes to determine conclusively whether the removal of the final proton is sufficient to create a substantial subshell closure at =34.
Acknowledgements.
The authors thank the NSCL operations staff for providing the primary and secondary beams for this experiment and NSCL group for assistance setting up the Ge detectors from SeGA. This work was supported in part by the National Science Foundation under Grant No. PHY-06-06007 and by the U.S. Department of Energy, Office of Nuclear Physics, under contracts No. DE-AC02-06CH11357 (ANL) and DEFG02-94ER40834 (University of Maryland) and by the Polish Scientific Committee grant 1PO3B 059 29. HLC and GFG would like to acknowledge support from the Natural Science and Engineering Research Council (NSERC) of Canada.References
- (1) M.G. Mayer and J.H.D. Jensen, Elementary Theory of Nuclear Shell Structure, Wiley, New York, 1955.
- (2) T. Otsuka, R. Fujimoto, Y. Utsuno, B.A. Brown, M. Honma and T. Mizusaki, Phys. Rev. Lett. 87, 082502 (2001).
- (3) A. Huck, G. Klotz, A. Knipper, C. Miehé, C. Richard-Serre, G. Walter, A. Poves, H.L. Ravn and G. Marguier, Phys. Rev. C 31, 2226 (1985).
- (4) A. Gade, R.V.F. Janssens, D. Bazin, R. Broda, B.A. Brown, C.M. Campbell, M.P. Carpenter, J.M. Cook, A.N. Deacon, D.-C. Dinca, B. Fornal, S.J. Freeman, T. Glasmacher, P.G. Hansen, B.P. Kay, P.F. Mantica, W.F. Mueller, J.R. Terry, J.A. Tostevin and S. Zhu, Phys. Rev. C 74, 021302(R) (2006).
- (5) R.V.F. Janssens, B. Fornal, P.F. Mantica, B.A. Brown, R. Broda, P. Bhattacharyya, M.P. Carpenter, M. Cinausero, P.J. Daly, A.D. Davies, T. Glasmacher, Z.W. Grabowski, D.E. Groh, M. Honma, F.G. Kondev, W. Królas, T. Lauritsen, S.N. Liddick, S. Lunardi, N. Marginear, T. Mizusaki, D.J. Morrissey, A.C. Morton, W.F. Mueller, T. Otsuka, T. Pawlat, D. Seweryniak, H. Schatz, A. Stolz, S.L. Tabor, C.A. Ur, G. Viesti, I. Wiedenhöver and J. Wrzesiński, Phys. Lett. B 546, 55 (2002).
- (6) J.I. Prisciandaro, P.F. Mantica, B.A. Brown, D.W. Anthony, M.W. Cooper, A. Garcia, D.E. Groh, A. Komives, W. Kumarasiri, P.A. Lofy, A.M. Oros-Peusquens, S.L. Tabor and M. Wiedeking, Phys. Lett. B 510, 17 (2001).
- (7) D.-C. Dinca, R.V.F. Janssens, A. Gade, D. Bazin, R. Broda, B.A. Brown, C.M. Campbell, M.P. Carpenter, P. Chowdhury, J.M. Cook, A.N. Deacon, B. Fornal, S.J. Freeman, T. Glasmacher, M. Honma, F.G. Kondev, J.-L. Lecouey, S.N. Liddick, P.F. Mantica, W.F. Mueller, H. Olliver, T. Otsuka, J.R. Terry, B.A. Tomlin and K. Yoneda, Phys. Rev. C 71, 041302(R) (2005).
- (8) A. Bürger, T.R. Saito, H. Grawe, H. Hübel, P. Reiter, J. Gerl, M. Górska, H.J. Wollersheim, A. Al-Khatib, A. Banu, T. Beck, F. Becker, P. Bednarczyk, G. Benzoni, A. Bracco, S. Brambilla, P. Bringel, F. Camera, E. Clément, P. Doornenbal, H. Geissel, A. Görgen, J. Grȩbosz, G. Hammond, M. Hellström, M. Honma, M. Kavatsyuk, O. Kavatsyuk, M. Kmiecik, I. Kojouharov, W. Korten, N. Kurz, R. Lozeva, A. Maj, S. Mandal, B. Million, S. Muralithar, A. Neusser, F. Nowacki, T. Otsuka, Zs. Podolyák, N. Saito, A.K. Singh, H. Weick, C. Wheldon, O. Wieland, M. Winkler and the RISING Collaboration, Phys. Lett. B 622, 29 (2005).
- (9) M. Honma, T. Otsuka, B.A. Brown and T. Mizusaki, Phys. Rev. C 65, 061301(R) (2002).
- (10) S.N. Liddick, P.F. Mantica, R.V.F. Janssens, R. Broda, B.A. Brown, M.P. Carpenter, B. Fornal, M. Honma, T. Mizusaki, A.C. Morton, W.F. Mueller, T. Otsuka, J. Pavan, A. Stolz, S.L. Tabor, B.E. Tomlin and M. Wiedeking, Phys. Rev. Lett. 92, 072502 (2004).
- (11) M. Honma, T. Otsuka, B.A. Brown and T. Mizusaki, Eur. Phys. J. A 25, 499 (2005).
- (12) V. Paar, Nucl. Phys. A211, 29 (1973).
- (13) M.E. Bunker and J.W. Starner, Phys. Rev. 97, 1272 (1955).
- (14) P.F. Mantica, B.A. Brown, A.D. Davies, T. Glasmacher, D.E. Groh, M. Horoi, S.N. Liddick, D.J. Morrissey, A.C. Morton, W.F. Mueller, H. Schatz, A. Stolz and S.L. Tabor, Phys. Rev. C 68, 044311 (2003).
- (15) S. Zhu, R.V.F. Janssens, B. Fornal, S.J. Freeman, M. Honma, R. Broda, M.P. Carpenter, A.N. Deacon, B.P. Kay, F.G. Kondev, W. Królas, J. Kozemczak, A. Larabee, T. Lauritsen, S.N. Liddick, C.J. Lister, P.F. Mantica, T. Otsuka, T. Pawlat, A. Robinson, D. Seweryniak, J.F. Smith, D. Steppenbeck, B.E. Tomlin, J. Wrzesiński and X. Wang, Phys. Lett. B 650, 135 (2007).
- (16) J.G. Pronko, T.T. Bardin and J.A. Becker, Phys. Rev. C 13, 608 (1976).
- (17) S.N. Liddick, P.F. Mantica, R. Broda, B.A. Brown, M.P. Carpenter, A.D. Davies, B. Fornal, M. Horoi, R.V.F. Janssens, A.C. Morton, W.F. Mueller, J. Pavan, H. Schatz, A. Stolz, S.L. Tabor, B.E. Tomlin and M. Wiedeking, Phys. Rev. C 72, 054321 (2005).
- (18) S.N. Liddick, P.F. Mantica, R. Broda, B.A. Brown, M.P. Carpenter, A.D. Davies, B. Fornal, T. Glasmacher, D.E. Groh, M. Honma, M. Horoi, R.V.F. Janssens, T. Mizusaki, D.J. Morrissey, A.C. Morton, W.F. Mueller, T. Otsuka, J. Pavan, H. Schatz, A. Stolz, S.L. Tabor, B.E. Tomlin and M. Wiedeking, Phys. Rev. C 70, 064303 (2004).
- (19) B. Fornal, S. Zhu, R.V.F. Janssens, M. Honma, R. Broda, P.F. Mantica, B.A. Brown, M.P. Carpenter, P.J. Daly, S.J. Freeman, Z.W. Grabowski, N.J. Hammond, F.G. Kondev, W. Królas, T. Lauritsen, S.N. Liddick, C.J. Lister, E.F. Moore, T. Otsuka, T. Pawlat, D. Seweryniak, B.E. Tomlin and J. Wrzesiński, Phys. Rev. C 70, 064304 (2004).
- (20) D.J. Morrissey, B.M. Sherrill, M. Steiner, A. Stolz and I. Wiedenhöver, Nucl. Instrum. Methods Phys. Res. B 204, 90 (2003).
- (21) J.I. Prisciandaro, A.C. Morton and P.F. Mantica, Nucl. Instrum. Methods Phys. Res. A 505, 140 (2003).
- (22) P.F. Mantica, R. Broda, H.L. Crawford, A. Damaske, B. Fornal, A.A. Hecht, C. Hoffman, M. Horoi, N. Hoteling, R.V.F. Janssens, J. Pereira, J.S. Pinter, J.B. Stoker, S.L. Tabor, T. Sumikama, W.B. Walters, X. Wang and S. Zhu, Phys. Rev. C 77, 014313 (2008).
- (23) W.F. Mueller, J.A. Church, T. Glasmacher, D. Gutknecht, G. Hackman, P.G. Hansen, Z. Hu, K.L. Miller and P. Quirin, Nucl. Instrum. Methods Phys. Res. A 466, 492 (2001).
- (24) H.L. Crawford, R.V.F. Janssens, P.F. Mantica, J.S. Berryman, R. Broda, M.P. Carpenter, B. Fornal, G.F. Grinyer, N. Hoteling, B. Kay, T. Lauritsen, K. Minamisono, I. Stefanescu, J.B. Stoker, W.B. Walters and S. Zhu, Acta Phys. Pol. B 40, 481 (2009).
- (25) S. McDaniel, A. Gade, R.V.F. Janssens, D. Bazin, B.A. Brown, C.M. Campbell, M.P. Carpenter, J.M. Cook, A.N. Deacon, D.-C. Dinca, S.J. Freeman, T. Glasmacher, P.G. Hansen, B.P. Kay, P.F. Mantica, W.F. Mueller, J.R. Terry, J.A. Tostevin and S. Zhu, Phys. Rev. C 81, 024301 (2010).
- (26) M. Langevin, C. Détraz, D. Guillemaud-Mueller, A.C. Mueller, C. Thibault, F. Touchard, G. Klotz, C. Miehé, G. Walter, M. Epherre and C. Richard-Serre, Phys. Lett. 130B, 251 (1983).
- (27) O. Sorlin, V. Borrel, S. Grévy, D. Guillemaud-Mueller, A.C. Mueller, F. Pougheon, W. Böhmer, K.-L. Kratz, T. Mehren, P. Möller, B. Pfeiffer, T. Rauscher, M.G. Saint-Laurent, R. Anne, M. Lewitowicz, A. Ostrowski, T. Dörfler and W.-D. Schmidt-Ott, Nucl. Phys. A 632, 205 (1998).
- (28) L.A. Parks, C.N. Davids and R.C. Pardom, Phys. Rev. C 15, 730 (1977).
- (29) B. Fornal, S. Zhu, R.V.F. Janssens, M. Honma, R. Broda, B.A. Brown, M.P. Carpenter, S.J. Freeman, N. Hammond, F.G. Kondev, W. Królas, T. Lauritsen, S.N. Liddick, C.J. Lister, S. Lunardi, P.F. Mantica, N. Marginean, T. Mizusaki, E.F. Moore, T. Otsuka, T. Pawlat, D. Seweryniak, B.E. Tomlin, C.A. Ur, I. Wiedenhöver and J. Wrzesiński, Phys. Rev. C 72, 044315 (2005).
- (30) N. Cieplicka , in preparation.
- (31) G. Audi, A.H. Wapstra and C. Thibault, Nucl. Phys. A729, 337 (2003).
- (32) T. Dörfler, W.-D. Schmidt-Ott, T. Hild, T. Mehren, W. Böhmer, P. Möller, B. Pfeiffer, T. Rauscher, K.-L. Kratz, O. Sorlin, V. Borrel, S. Grévy, D. Guillemaud-Mueller, A.C. Mueller, F. Pougheon, R. Anne, M. Lewitowicz, A. Ostrowsky, M. Robinson and M.G. Saint-Laurent, Phys. Rev. C 54, 2894 (1996).
- (33) R. Grzywacz, R. Béraud, C. Borcea, A. Emsallem, M. Glogowski, H. Grawe, D. Guillemaud-Mueller, M. Hjorth-Jensen, M. Houry, M. Lewitowicz, A.C. Mueller, A. Nowak, A. Plochocki, M. Pfützner, K. Rykaczewski, M.G. Saint-Laurent, J.E. Sauvestre, M. Schaefer, O. Sorlin, J. Szerypo, W. Trinder, S. Viteritti and J. Winfield, Phys. Rev. Lett. 81, 766 (1998).
- (34) P. Maierbeck, R. Gernhäuser, R. Krücken, T. Kröll, H. Alvarez-Pol, F. Aksouh, T. Aumann, K. Behr, E.A. Benjamim, J. Benlliure, V. Bildstein, M. Böhmer, K. Boretzky, M.J.G. Borge, A. Brünle, A. Bürger, M. Caamaño, E. Casarejos, A. Chatillon, L.V. Chulkov, D. Cortina-Gil, J. Enders, K. Eppinger, T. Faestermann, J. Friese, L. Fabbietti, M. Gascón, H. Geissel, J. Gerl, M. Gorska, P.G. Hansen, B. Jonson, R. Kanungo, O. Kiselev, I. Kojouharov, A. Klimkiewicz, T. Kurtukian, N. Kurz, K. Larsson, T. Le Bleis, K. Mahata, L. Maier, T. Nilsson, C. Nociforo, G. Nyman, C. Pascual-Izarra, A. Perea, D. Perez, A. Prochazka, C. Rodriguez-Tajes, D. Rossi, H. Schaffner, G. Schrieder, S. Schwertel, H. Simon, B. Sitar, M. Stanoiu, K. Sümmerer, O. Tengblad, H. Weick, S. Winkler, B.A. Brown, T. Otsuka, J. Tostevin and W.D.M. Rae, Phys. Lett. B 675, 22 (2009).
- (35) P.F. Mantica, A.C. Morton, B.A. Brown, A.D. Davies, T. Glasmacher, D.E. Groh, S.N. Liddick, D.J. Morrissey, W.F. Mueller, H. Schatz, A. Stolz, S.L. Tabor, M. Honma, M. Horoi and T. Otsuka, Phys. Rev. C 67, 014311 (2003).
- (36) O. Sorlin, C. Donzaud, F. Azaiez, C. Bourgeois, L. Gaudefroy, F. Ibrahim, D. Guillemaud-Mueller, F. Pougheon, M. Lewitowicz, F. de Oliveira Santos, M.G. Saint-Laurent, M. Stanoiu, S.M. Lukyanov, Yu.E. Penionzhkevich, J.C. Angélique, S. Grévy, K.-L. Kratz, B. Pfeiffer, F. Nowacki, Z. Dlouhy and J. Mrasek, Nucl. Phys. A719, 193c (2003).
- (37) S. Bhattacharyya, M. Rejmund, A. Navin, E. Caurier, F. Nowacki, A. Poves, R. Chapman, D. O’Donnell, M. Gelin, A. Hodsdon, X. Liang, W. Mittig, G. Mukherjee, F. Rejmund, M. Rousseau, P. Roussel-Chomaz, K.-M. Spohr and Ch. Theisen, Phys. Rev. C 79, 014313 (2009).
- (38) D.E. Alburger, E.K. Warburton and B.A. Brown, Phys. Rev. C 30, 1005 (1984).
- (39) U. Fister, R. Jahn, P. von Neumann-Cosel, P. Schenk, T.K. Trelle, D. Wenzel and U. Wienands, Nucl. Phys. A569, 421 (1994).
- (40) F. Ajzenberg-Selove, R.E. Brown, E.R. Flynn and J.W. Sunier, Phys. Rev. C 32, 756 (1985).
- (41) V. Paar, Nucl. Phys. A331, 16 (1979).
- (42) A. Gade, R.V.F. Janssens, D. Bazin, B.A. Brown, C.M. Campbell, M.P. Carpenter, J.M. Cook, A.N. Deacon, D.-C. Dinca, S.J. Freeman, T. Glasmacher, B.P. Kay, P.F. Mantica, W.F. Mueller, J.R. Terry and S. Zhu, Phys. Rev. C 73, 037309 (2006).
- (43) B. Fornal, R.V.F. Janssens, R. Broda, N. Marginean, S. Beghini, L. Corradi, M.P. Carpenter, G. De Angelis, F. Della Vedova, E. Farnea, E. Fioretto, A. Gadea, B. Guiot, M. Honma, W. Królas, T. Lauritsen, S. Lunardi, P.F. Mantica, P. Mason, G. Montagnoli, D.R. Napoli, T. Otsuka, T. Pawlat, G. Pollarolo, F. Scarlassara, A.M. Stefanini, D. Seweryniak, S. Szilner, C.A. Ur, M. Trotta, J.J. Valiente-Dobón, J. Wrzesiński and S. Zhu, Phys. Rev. C 77, 014304 (2008).
- (44) S.P. Pandya, Phys. Rev. 103, 956 (1956).
- (45) A. Poves, J. Sánchez-Solano, E. Caurier, and F. Nowacki. Nucl. Phys. A, 694:157, 2001.