Bioinspired magnetic active matter and the physical limits of magnetotaxis
Abstract
Magnetotactic bacteria (MTB) are endowed with an exquisite orientation mechanism allowing them to swim along the geomagnetic field lines blakemore1975magnetotactic ; frankel1981magnetotactic ; smith2006quantifying . This mechanism consists of a chain of bio-synthesized magnetic nano-crystals blakemore1975magnetotactic ; dunin1998magnetic ; komeili2006magnetosomes . Although the physics behind the minimum size of this biological compass is well understood frankel1980navigational , it is yet unclear what sets its maximum size frankel1980navigational ; blakemore1982magnetotactic ; esquivel1986motion . Here, by using a macroscopic experiment inspired in these microorganisms, we show that larger magnetic moments will drive the collective behavior of MTB into a phase where bacteria are unable to swim freely, in detriment of their evolutive fitness darwin1964origin ; smith2006quantifying . Simple macroscopic experiments, numerical simulations, and analytic estimates are used to explain the upper limit for the size of the chain of nano-crystals in MTB. Our macroscopic bio-inspired experiment, and physical model provide new opportunities to explore and understand the phases of magnetic active matter at all scales.
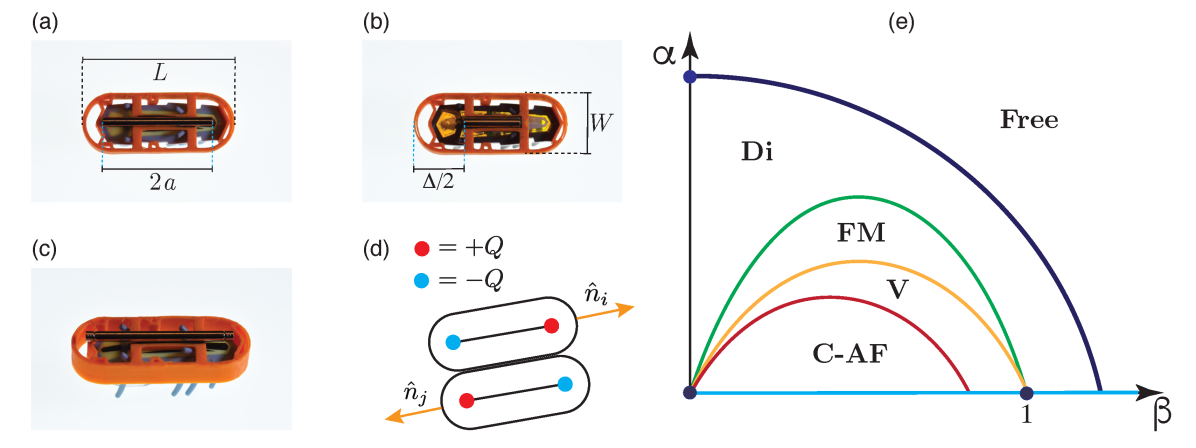
Magnetotactic bacteria (MTB) contain magnetosomes, which are intracellular, ferrimagnetic nano-crystals of magnetite or greigite. Magnetosomes are usually arranged in a linear chain within each bacterium (e.g: Magnetospirillum magneticum, Magnetospirillum magnetotacticum)blakemore1975magnetotactic ; frankel1980navigational ; dunin1998magnetic ; schuler1999bacterial ; komeili2006magnetosomes , with few known exceptions (Magnetobacterium bavaricum) jogler2010cultivation . This linear chain provides a net magnetic moment, , that allows MTB to align to the geomagnetic field, , in a noisy environment frankel1980navigational . The reason for this, is that oxygen is toxic for these microaerophilic or anaerobic organisms, and it is beneficial for them to be directed toward and kept in the sediments away from the water surface where oxygen is abundant blakemore1975magnetotactic ; smith2006quantifying . This mechanism can be understood as the competition between the aligning dipolar energy, , and the thermal noise . Thus, for MTB to align respect to the Earth’s magnetic field, both quantities should be comparable. This well known and accepted criterion provides a lower bound for the magnetosome chain size frankel1980navigational ; esquivel1986motion ; klumpp2016magnetotactic . In the same spirit, we should expect that the larger the dipolar moment of MTB, the better. However, MTB with large magnetic moments have not been observed in nature. Inspired by this apparent paradox, and the general subject of the effect of long range interactions in active matter, we have built an artificial system that allows for the exploration of these questions, and provide a flexible tabletop experiment to investigate magnetic active matter (MAM), Fig.1.
In this article, we demonstrate that there is a strong physical constraint for the maximum dipolar moment of single magnetosome chains. This constraint arises from the fact that MTB need to be able to swim into regions of low oxygen, but for large dipolar moments a collection of MTB will enter into a phase where they will form magnetic clusters making it impossible for them to efficiently swim (See Figs.1-4). Thus, if mutants grow magnetosome chains with extremely large magnetic moments they will self-assemble into dimers, or magnetic clusters (See Figs. 1, 3 and 4), generating a new compound object in which flagellar motion will be suppressed, decreasing their ability to swim. Thus, MTB with extremely large magnetic moments will not prevail.
The generic formation of clusters of particles being them inanimate or active shows up in a plethora of phenomena ranging from chemistry to physics, biology to astrophysical objects whitesides2002self ; whitesides2002beyond ; ong2017programmable ; makey2020universality ; lee2015direct ; kravtsov2012formation ; balbus1998instability . The existence and evolution of these structures at different length scales are intimately tied to the type of interactions between their basic constituents, particle symmetries, and emergent symmetries that may show up due to interactions anderson1972more ; huber2018emergence ; denk2020pattern . For active agents endowed only with self-avoidance and/or local aligning interactions, there are different phases that have been theoretically analyzed and experimentally observed vicsek1995novel ; marchetti2013hydrodynamics ; deblais2018boundaries ; giomi2013swarming ; dauchot2019dynamics ; peruani2018cold . For example, the full phase diagram of Brownian disks has been discussed PhysRevLett.121.098003 , the effect of hydrodynamic interactions in the collective behavior of fish filella2018model , the onset of collective and cohesive motion gregoire2004onset , the existence of a spontaneously flowing crystal of self-propelled particles briand2018spontaneously , to name a few. In the previous cases no long-range interaction has been taken into account vicsek1995novel ; deseigne2010collective ; giomi2013swarming ; marchetti2013hydrodynamics ; peruani2018cold ; deblais2018boundaries ; PhysRevLett.121.098003 ; filella2018model ; dauchot2019dynamics . However, recently it has been proposed that dipolar active matter can show a rich phenomenology, where depending on several parameters fission or fusion of particle clusters have been predicted kaiser2015active ; guzman2016fission , directed self-assembly of quadrupolar particles has been reported gu2019magnetic , and in ferromagnetic colloids the collective motion and its different phases experimentally analyzed kaiser2017flocking . The previous results are a clear call to analyze the impact of cluster formation in the evolution of swimming bacteria that contain a chain of magnetic nano-crystals endowing these organisms with a dipolar moment.
In what follows, we set a general framework to study MAM (Fig.1), provide simple methods to measure all parameters of the model, characterize the phases shown by MAM at low densities, define the relevant dimensionless parameters at play in this system (See Supplementary Information S1 and S2), and provide strong evidence for our claims about the maximum dipolar moment for MTB. We observed the evolution of a group of these active particles for several interaction strengths and activities. Using this experimental insight, we implemented a model that accurately reproduces the different dynamical structures observed in experiments (Figs.1 and 2): free single particles, quadrupolar dimers, winding of magnetic vortices, unwinding of vortices into ferromagnetic chains, and multipolar clusters (See details of experiments and numerical simulations in Supplementary Information S1-S8). We rationalize these findings using dimensionless numbers that depend on the strength of the magnetic interactions between particles, activity, and angular noise (See Supplementary Information and Eqs.1-3).

We explored an enlarged parameter space by using numerical simulations and analytic estimates to understand the main factors that impact in the different phases that MAM display. The phases found in our experiments are relevant for programmed self-assembly, and they should persist across different length scales kantorovich2013nonmonotonic ; whitesides2002self ; whitesides2002beyond . The latest allows us to understand the physical constraints that affect key aspects of the evolution of MTB bellini1963 ; frankel2009discovery ; blakemore1975magnetotactic using the insight from our macroscopic experiments.
The system that we study is composed of bacillus shaped active particles that are built with commercially available Hexbug Nano (HEXBUG Nano, https://www.hexbug.com/nano). We dubbed these macroscopic agents MagD-bots. Even though vibration-driven vehicles of this type have been used before in several experiments patterson2017clogging ; deblais2018boundaries ; dauchot2019dynamics ; boudet2021collections ; zheng2021self , the sharp geometry of its body, and highly frictional material they are made, makes it unclear that the agreement between experiments and models is real or an artifact. To overcome this difficulty, we have dressed the Hexbugs with a 3D printed armor with a bacillus shape. The total body length , width , mass , and simple geometry have allowed us not only to improve the stability of the system by lowering its center of mass, lower the friction between walls and active agents, but also, to simplify numerical simulations. These structured armors allow for the precise positioning of a Neodymium magnet on top of them. Thus, we have built a set of active agents that interact via a magnetic field, and hard-core interactions. We emphasize that in this work the size of magnet is not small compared with the size of the object, making it mandatory to adopt a dumbbell model instead of a point-like dipole Vokoun201155 ; Vokoun20093758 ; ryzhkin2005magnetic ; castelnovo2008magnetic ; mellado2010dynamics ; concha2018PRL ; cisternas2021stable .
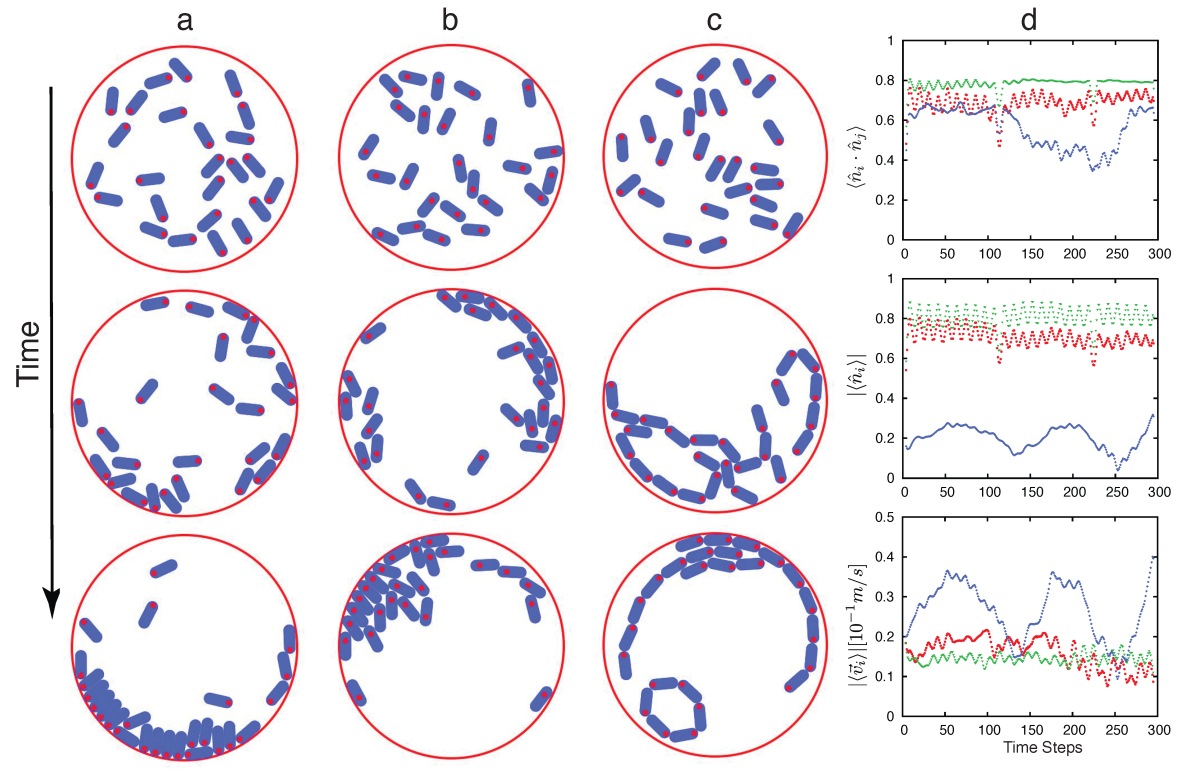
Our main findings are summarized in Fig.1 where five qualitatively different phases are shown. In the non-magnetic case, phase (Fig.2a and Supplementary Movie 1) we observed weak correlations and mainly geometric effects in agreement with previous reports giomi2013swarming . For large activity and short magnets, we observed particles that show weak ferromagnetic correlations that influence the final state, but still without forming any spontaneously self assembled structure, phase (Fig.2b and Supplementary Movie 2). As activity decreases or increasing the strength of magnetic interactions we observed strong ferromagnetic correlations and the formation of new structures such as dimers, ferromagnetic chains, and vortices not found in the previous cases, phase (Fig.2 c and Supplementary Movie 3). As magnetic interactions increased long chains assemble and the system shows clear ferromagnetic order, stable vortices, and the fusion of different objects, phases , and (Fig.2 d, Supplementary Movies 4, and 5). Finally, for low rotational noise we observe the formation of anti-ferromagnetic ordered clusters that are relevant for the quasi-static self-assembly of magnetic particles, phase Fig.1 (See Supplementary Movie 6).
We rationalize our findings considering the Newtonian dynamics of active magnetic matter described by
| (1) | ||||
where is the particle index, is the angle between the horizontal axis and the vector shown in Fig.1d. In this model, the tip of each rod has a magnetic charge of magnitude that interacts with all other magnetic poles (note that the total magnetic charge per dipole is zero). , , , , , and are the MagD-bot mass, activity, damping, moment of inertia, rotational damping, and rotational diffusion respectively (See Supplementary Information S1-S3). , and represents forces and torques due to contacts. , are the force and torque due to Coulomb interactions, and is a white noise with mean and variance .
Analyzing the translational equation of motion the dimensionless numbers and emerge, where is a typical time scale for the translational motion of each MagD-bot. In steady-state both terms should be comparable. Therefore, it is enough to consider only one of them to understand the competition between different forcing terms. We called the inverse of the first dimensionless number
| (2) |
This dimensionless parameter quantify the competition between the centripetal force (), and the activity, , of the MagD-bot. The second dimensionless number relevant in this case appears by considering the rotational dynamics. In the low mass limit, the one relevant for MTB, the main forces competing will be the Coulombic torque and the torsional noise amplitude . We called this parameter:
| (3) |
where and . In this article we focus on two dimensionless parameters ( and ), but the richness of the dynamics defined by Eqs.1 is enormous. Indeed, there are five dimensionless parameters (See Supplementary Information S1, S2).
We proceed to examine the dynamics of the system in detail using molecular dynamics simulations (See Fig.3 and Supplementary Information). In this description, inertial magnets interact through the full long-range Coulomb potential in the dumbbell approach Vokoun201155 ; Vokoun20093758 ; ryzhkin2005magnetic ; castelnovo2008magnetic ; mellado2010dynamics ; concha2018PRL ; cisternas2021stable .
The physical parameters employed in numerical simulations were directly measured (See details in Supplementary Information). The measurement of , and was done by using an incline and analyzing quasi-1D trajectories (See Supplementary Information S4). was measured using a torsion pendulum configuration (See Supplementary Information S7), and was measured by analyzing the angular dynamics after a MagD-bot hits a hard wall (See Supplementary Information S8). Magnetic interactions were measured using special non magnetic holders installed on an Instron universal testing machine that measured the interaction force between magnets (Supplementary Information S6). From this information we calibrated the magnets used in our experiments obtaining a saturation magnetization as A which is in agreement with the available data for the magnetization of Neodymium rods, validating the dumbbell approximation when the rods are separated by a distance , as previously pointed out Vokoun201155 ; Vokoun20093758 ; mellado2012macroscopic . That information allowed the measurement of the magnetic charge in the dumbbell approximation. The ratio between and the rotational noise amplitude, , was measured using the angular autocorrelation of (See Supplementary Information S8). Therefore, in our simulations there are no free parameters in striking contrast with most available literature. Simulation results for MagD-bots are shown in Fig.3 in good agreement with experimental results (Fig.2). The evolution of three different regimes are shown in Supplementary Movies 7-9.
We characterized the system by computing the correlations , the magnitude of the average , the magnitude of the average velocity , and average speed as functions of time gregoire2004onset ; vicsek2012collective ; giomi2013swarming . In Fig.3 we show representative frames for numerical simulations of MAM where no magnets were present (Fig.3 a), magnets of length mm (Fig.3 b), and magnets of length mm (Fig.3 c). For Fig.3 a, we found no ferromagnetic order, but from time to time a boundary driven stagnation state giomi2013swarming . In Fig.3 b a signal of ferromagnetic correlations emerges, and finally it is quite clear that ferromagnetic order is present in Fig.3 c. In agreement with experiments, see Fig.2 and supplementary movies 7-9.
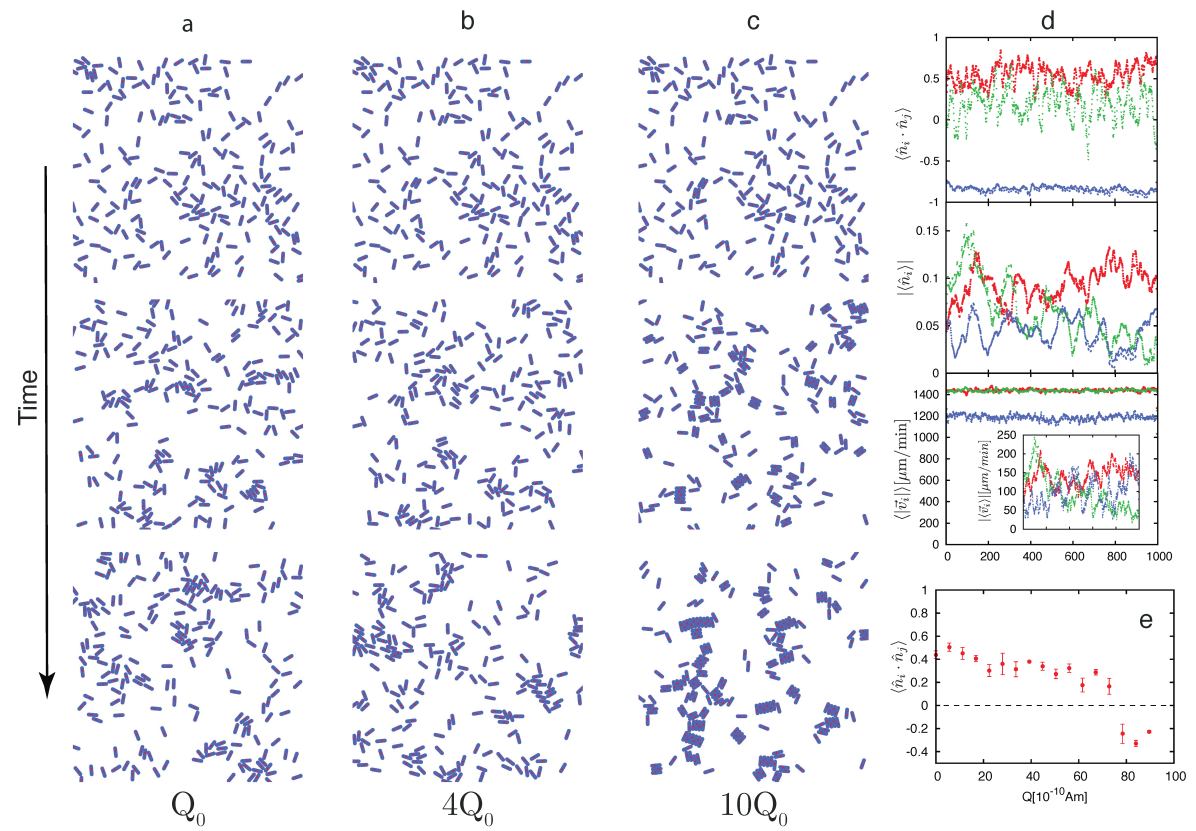
Our macroscopic experiment, and detailed numerical model allow us to draw conclusions and make predictions on the phases, and stability of MAM at the microscale. To analyze the impact of increasing magnetic moment in MTB we have performed detailed numerical simulations in a region of physical parameters relevant for MTB (See Supplementary Tables VIII and IX). Furthermore, the view of the magnetosome chain in MTB as a magnetic dumbbell has been directly measured using extremely sensitive Nitrogen vacancy centers le2013optical . For the simulations shown in Fig.4, we have used bacterium length m, width m, magnetic chain length m, Am, and average swimming speeds of order ms khalil2013control ; seong2001swimming ; schuler1999bacterial ; frankel1981magnetotactic ; frankel1980navigational ; komeili2006magnetosomes . This lead to dimensionless parameters and , which are far from clustering (see Fig.1e). To increase the magnetic moment in our in-silico experiments we have increased the charge from to , and then to . We obtained the dynamics of that microscale MAM, Fig.4 a-c (See Supplementary Movies 10, 11, and 12), and computed the evolution of different order parameters Fig.4 d,e. Our data shows the emergence of a phase at large dipolar moment (), and a sharp decrease in the average speed of the collective motion, which will be detrimental for MTB survival darwin1964origin . For MTB to have an efficient magnetotactic advantage, they should inhabit the Free phase region of the phase diagram. That means that in nature the , , and - configurations should be avoided as they strongly lower the swimming efficiency of MTB by interfering with flagella motion dauparas2016flagellar , or by forming clusters of extremely low magnetic moment.
Given that dipolar moment can be increased by increasing , or by increasing , we provide a simple bound for the maximum magnetic charge that a magnetosome chain can have before going into a - phase. Considering two MTB aligned side by side (Fig.1d), they will not form a cluster as long as . That is, . This bound gives Am, for , m, and m, consistent with observations dunin1998magnetic ; frankel1980navigational ; rosenblatt1982birefringence ; rosenblatt1985birefringence . On the other hand, considering a fixed the magnetic charge, we can find the maximum length for the magnetosome chain to avoid cluster formation. In this case, nm in agreement with reported chain lengths dunin1998magnetic ; schuler1999bacterial ; frankel1980navigational ; komeili2006magnetosomes . That is, MTB grow magnetic dipoles that are strong enough to align MTB to the geomagnetic field in a noisy environment, but weak enough to avoid the formation of magnetic clusters.
Our platform, physical model, and numerical simulations of MAM have allowed us to explore the effects of magnetic interactions in active matter at very dissimilar length scales, and show that increasingly large magnetic moments, which in theory should provide an evolutive advantage for MTB, will do the opposite. Large magnetic moments will promote the formation of clusters of MTB that are detrimental for these organisms. Our work paves the way not only to a better understanding of the evolution of MTB, but also to explore magnetic self-assembly at diverse length scales. We anticipate that MAM can be programmed by modifying its magnetic textures, activity, geometry, or the related dimensionless parameters that characterize this system. This is a first step towards functional bioinspired magnetic active matter at all scales.
Acknowledgements.
N.S., and F.G.L. acknowledge ANID (Chile) –Millennium Science Initiative Program– NCN19 170. B.G. acknowledges support from ANID PIA/BASAL FB0002. E.H. was funded by VRIDEI - DICYT project 041931HH. A.C acknowledges support from the CODEV Seed Money Program of the École Polytechnique Fédérale de Lausanne (EPFL), the partial support of FONDECYT (Chile) through grant 1210297, and the support of the Design Engineering Center at UAI.Contributions
A.C conceived the study, designed, and performed experiments. B. G. advised on MTB biology and evolutive mechanism. N.S. performed numerical simulations. N.S. and A.C developed analytical tools. FGL advised on active matter simulations and performed preliminary numerical simulations. M.C. performed image analysis. A.C. and E.H. discussed experimental setup and performed magnetic and elastic interaction measurements. A.C and N.S wrote the manuscript with input from all the authors.
References
- (1) Blakemore, R. Magnetotactic bacteria. Science 190, 377–379 (1975).
- (2) Frankel, R. B., Blakemore, R., De Araujo, F. T., Esquivel, D. M. S. & Danon, J. Magnetotactic bacteria at the geomagnetic equator. Science 212, 1269–1270 (1981).
- (3) Smith, M. et al. Quantifying the magnetic advantage in magnetotaxis. Biophysical journal 91, 1098–1107 (2006).
- (4) Dunin-Borkowski, R. E. et al. Magnetic microstructure of magnetotactic bacteria by electron holography. Science 282, 1868–1870 (1998).
- (5) Komeili, A., Li, Z., Newman, D. K. & Jensen, G. J. Magnetosomes are cell membrane invaginations organized by the actin-like protein mamk. Science 311, 242–245 (2006).
- (6) Frankel, R. B. & Blakemore, R. Navigational compass in magnetic bacteria. Journal of Magnetism and Magnetic Materials 15, 1562 (1980).
- (7) Blakemore, R. P. Magnetotactic bacteria. Annual Reviews in Microbiology 36, 217–238 (1982).
- (8) Esquivel, D. M. S. & Lins de Barros, H. G. Motion of magnetotactic microorganisms. Journal of Experimental Biology 121, 153– 163 (1986).
- (9) Darwin, C. On the origin of species: A facsimile of the first edition (Harvard University Press, 1964).
- (10) Schüler, D. & Frankel, R. B. Bacterial magnetosomes: microbiology, biomineralization and biotechnological applications. Applied Microbiology and Biotechnology 52, 464–473 (1999).
- (11) Jogler, C. et al. Cultivation-independent characterization of ‘candidatus magnetobacterium bavaricum’ via ultrastructural, geochemical, ecological and metagenomic methods. Environmental Microbiology 12, 2466–2478 (2010).
- (12) Klumpp, S. & Faivre, D. Magnetotactic bacteria. The European Physical Journal Special Topics 225, 2173–2188 (2016).
- (13) Mellado, P., Concha, A. & Mahadevan, L. Macroscopic magnetic frustration. Physical Review Letters 109, 257203 (2012).
- (14) Concha, A., Aguayo, D. & Mellado, P. Designing hysteresis with dipolar chains. Phys. Rev. Lett. 120, 157202 (2018).
- (15) Whitesides, G. M. & Grzybowski, B. Self-assembly at all scales. Science 295, 2418–2421 (2002).
- (16) Whitesides, G. M. & Boncheva, M. Beyond molecules: Self-assembly of mesoscopic and macroscopic components. Proceedings of the National Academy of Sciences, USA 99, 4769–4774 (2002).
- (17) Ong, L. L. et al. Programmable self-assembly of three-dimensional nanostructures from 10,000 unique components. Nature 552, 72–77 (2017).
- (18) Makey, G. et al. Universality of dissipative self-assembly from quantum dots to human cells. Nature Physics 1–7 (2020).
- (19) Lee, V., Waitukaitis, S. R., Miskin, M. Z. & Jaeger, H. M. Direct observation of particle interactions and clustering in charged granular streams. Nature Physics 11, 733–737 (2015).
- (20) Kravtsov, A. V. & Borgani, S. Formation of galaxy clusters. Annual Review of Astronomy and Astrophysics 50, 353–409 (2012).
- (21) Balbus, S. A. & Hawley, J. F. Instability, turbulence, and enhanced transport in accretion disks. Reviews of Modern Physics 70, 1 (1998).
- (22) Anderson, P. W. More is different. Science 177, 393–396 (1972).
- (23) Huber, L., Suzuki, R., Krüger, T., Frey, E. & Bausch, A. Emergence of coexisting ordered states in active matter systems. Science 361, 255–258 (2018).
- (24) Denk, J. & Frey, E. Pattern-induced local symmetry breaking in active-matter systems. Proceedings of the National Academy of Sciences, USA 117, 31623–31630 (2020).
- (25) Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Physical Review Letters 75, 1226 (1995).
- (26) Marchetti, M. C. et al. Hydrodynamics of soft active matter. Reviews of Modern Physics 85, 1143 (2013).
- (27) Deblais, A. et al. Boundaries control collective dynamics of inertial self-propelled robots. Physical Review Letters 120, 188002 (2018).
- (28) Giomi, L., Hawley-Weld, N. & Mahadevan, L. Swarming, swirling and stasis in sequestered bristle-bots. Proc. R. Soc. A 469, 20120637 (2013).
- (29) Dauchot, O. & Démery, V. Dynamics of a self-propelled particle in a harmonic trap. Physical Review Letters 122, 068002 (2019).
- (30) Peruani, F. & Aranson, I. S. Cold active motion: How time-independent disorder affects the motion of self-propelled agents. Physical Review Letters 120, 238101 (2018).
- (31) Digregorio, P. et al. Full phase diagram of active brownian disks: From melting to motility-induced phase separation. Phys. Rev. Lett. 121, 098003 (2018).
- (32) Filella, A., Nadal, F., Sire, C., Kanso, E. & Eloy, C. Model of collective fish behavior with hydrodynamic interactions. Physical Review Letters 120, 198101 (2018).
- (33) Grégoire, G. & Chaté, H. Onset of collective and cohesive motion. Physical Review Letters 92, 025702 (2004).
- (34) Briand, G., Schindler, M. & Dauchot, O. Spontaneously flowing crystal of self-propelled particles. Physical Review Letters 120, 208001 (2018).
- (35) Deseigne, J., Dauchot, O. & Chaté, H. Collective motion of vibrated polar disks. Physical Review Letters 105, 098001 (2010).
- (36) Kaiser, A., Popowa, K. & Löwen, H. Active dipole clusters: from helical motion to fission. Physical Review E 92, 012301 (2015).
- (37) Guzmán-Lastra, F., Kaiser, A. & Löwen, H. Fission and fusion scenarios for magnetic microswimmer clusters. Nature Communications 7, 13519 (2016).
- (38) Gu, H., Boehler, Q., Ahmed, D. & Nelson, B. J. Magnetic quadrupole assemblies with arbitrary shapes and magnetizations. Science Robotics 4 (2019).
- (39) Kaiser, A., Snezhko, A. & Aranson, I. S. Flocking ferromagnetic colloids. Science Advances 3, e1601469 (2017).
- (40) Kantorovich, S., Ivanov, A. O., Rovigatti, L., Tavares, J. M. & Sciortino, F. Nonmonotonic magnetic susceptibility of dipolar hard-spheres at low temperature and density. Physical Review Letters 110, 148306 (2013).
- (41) Bellini, S. Su di un particolare comportamento di batteri dácqua dolce (on a unique behavior of freshwater bacteria). Institute of Microbiology, University of Pavia, Italy. (1963).
- (42) Frankel, R. B. The discovery of magnetotactic/magnetosensitive bacteria. Chinese Journal of Oceanology and Limnology 27, 1 (2009).
- (43) Patterson, G. A. et al. Clogging transition of vibration-driven vehicles passing through constrictions. Physical Review Letters 119, 248301 (2017).
- (44) Boudet, J. et al. From collections of independent, mindless robots to flexible, mobile, and directional superstructures. Science Robotics 6 (2021).
- (45) Zheng, E. et al. Self-oscillation and synchronisation transitions in elasto-active structures. arXiv preprint arXiv:2106.05721 (2021).
- (46) Vokoun, D., Tomassetti, G., Beleggia, M. & Stachiv, I. Magnetic forces between arrays of cylindrical permanent magnets. Journal of Magnetism and Magnetic Materials 323, 55–60 (2011).
- (47) Vokoun, D., Beleggia, M., Heller, L. & ittner, P. . Magnetostatic interactions and forces between cylindrical permanent magnets. Journal of Magnetism and Magnetic Materials 321, 3758–3763 (2009).
- (48) Ryzhkin, I. Magnetic relaxation in rare-earth oxide pyrochlores. Journal of Experimental and Theoretical Physics 101, 481–486 (2005).
- (49) Castelnovo, C., Moessner, R. & Sondhi, S. L. Magnetic monopoles in spin ice. Nature 451, 42 (2008).
- (50) Mellado, P., Petrova, O., Shen, Y. & Tchernyshyov, O. Dynamics of magnetic charges in artificial spin ice. Physical Review Letters 105, 187206 (2010).
- (51) Cisternas, J. et al. Stable and unstable trajectories in a dipolar chain. Physical Review B 103, 134443 (2021).
- (52) Vicsek, T. & Zafeiris, A. Collective motion. Physics reports 517, 71–140 (2012).
- (53) Le Sage, D. et al. Optical magnetic imaging of living cells. Nature 496, 486–489 (2013).
- (54) Khalil, I. S. & Misra, S. Control characteristics of magnetotactic bacteria: Magnetospirillum magnetotacticum strain ms-1 and magnetospirillum magneticum strain amb-1. IEEE Transactions on Magnetics 50, 1–11 (2013).
- (55) Seong, S. & Park, T. H. Swimming characteristics of magnetic bacterium, magnetospirillum sp. amb-1, and implications as toxicity measurement. Biotechnology and bioengineering 76, 11–16 (2001).
- (56) Dauparas, J. & Lauga, E. Flagellar flows around bacterial swarms. Physical Review Fluids 1, 043202 (2016).
- (57) Rosenblatt, C., de Araujo, F. F. T. & Frankel, R. B. Birefringence determination of magnetic moments of magnetotactic bacteria. Biophysical journal 40, 83 (1982).
- (58) Rosenblatt, C., Frankel, R. B. & Blakemore, R. P. A birefringence relaxation determination of rotational diffusion of magnetotactic bacteria. Biophysical journal 47, 323 (1985).