Black Hole Formation in Fallback Supernova and the Spins of LIGO Sources
Abstract
Here we investigate within the context of field binary progenitors how the the spin of LIGO sources vary when the helium star-descendent black hole (BH) is formed in a failed supernova (SN) explosion rather than by direct collapse. To this end, we make use of 3d hydrodynamical simulations of fallback supernova in close binary systems with properties designed to emulate LIGO sources. By systematically varying the explosion energy and the binary properties, we are able to explore the effects that the companion has on redistributing the angular momentum of the system. We find that, unlike the mass, the spin of the newly formed BH varies only slightly with the currently theoretically unconstrained energy of the SN and is primarily determined by the initial binary separation. In contrast, variations in the initial binary separation yield sizable changes on the resultant effective spin of the system. This implies that the formation pathways of LIGO sources leading to a particular effective spin might be far less restrictive than the standard direct collapse scenario suggests.
1 INTRODUCTION
The gravitational wave (GW) signals detected by LIGO (Abbott et al., 2016b, c, 2017a, 2017b, 2017c) have uncovered a population of black holes (BHs) that is significantly more massive than the population known to reside in accreting binaries (Remillard & McClintock, 2006). While there is significant debate in the community about how black hole binaries are assembled (Zwart & McMillan, 2000; Kalogera et al., 2007; Sadowski et al., 2008; Postnov & Yungelson, 2014; Abbott et al., 2016a; Belczynski et al., 2016; Rodriguez et al., 2016a; de Mink & Mandel, 2016; Gerosa & Berti, 2017; Wysocki et al., 2017), the classical scenario (Tutukov & Yungelson, 1993; Voss & Tauris, 2003) remains one of the leading candidates. In this channel, a wide massive binary undergoes a series of mass transfer episodes leading to a tight binary comprised of a massive helium star () and a BH (), prior to the formation of the second BH (). LIGO observations of the mass-weighted angular momentum perpendicular to the orbital plane , have been argued to provide constraints on this formation channel (Rodriguez et al., 2016b; Farr et al., 2017; Stevenson et al., 2017). This is because vital information on the mass transfer history of the binary and the spin of is imprinted on
| (1) |
Here and are the dimensionless spins of the BHs and is the direction of the angular momentum in the orbital plane.
The angular momentum of the secondary BH is intimately linked to that of the progenitor helium star, which in turn is determined by its mass-loss history and the torque exerted by the primary black hole (Qin et al., 2018; Kushnir et al., 2016; Zaldarriaga et al., 2018). This torque can effectively drive synchronization of the stellar spin and the orbit in binaries tighter than , the maximum separation allowed for synchronization within the life of the helium star (Zaldarriaga et al., 2018). The final angular momentum of the star thus provides a reasonable estimate of when the mass and angular momentum losses from the final supernova explosion are ignored. All previous works have assumed that such effects are small based on the simple expectation that LIGO BHs are formed by direct collapse.
Motivated by the fact that the nature of BH-forming supernova (SN) explosions is not to well understood (Fryer et al., 2012; Ugliano et al., 2012; Pejcha & Thompson, 2015), in this Letter we explore the effects on when the second BH instead is formed by a fallback SN explosion (Moriya et al., 2010; Fryer et al., 2012; Dexter & Kasen, 2013; Lovegrove & Woosley, 2013; Perna et al., 2014; Batta et al., 2017; Fernández et al., 2018). For this purpose we make use of 3d hydrodynamical simulations of fallback SN in close binary systems with properties aimed at reproducing LIGO GW signals. The structure of this Letter is as follows. In Section 2 we describe the numerical formalism used to initiate the fallback SN explosion and compute the subsequent evolution of the binary. In Section 3 we describe the dynamics of the fallback material and its effect on the final spin of both BHs. Lastly, in Section 4 we present our key findings and relate them to the current population of LIGO sources.
2 METHODS AND INITIAL SETUP
Here we follow the setup described in Batta et al. (2017) to study the evolution of the progenitor binary system after the birth of . We make use of a modified version of the three-dimensional smoothed particle hydrodynamics (SPH) code GADGET2 (Springel, 2005), with our initial setup consisting of a tidally locked helium star in orbit around a BH of . The reader is referred to Batta et al. (2017) for further details on initial particle distribution and numerical accretion. We settled for a resolution of particles, which showed convergence for the accretion rates and properly captured the dynamics of the ejecta and the binary system.
To study the interaction of the fallback material with the newly formed BH binary we explore three sets of simulations. Each set starts with the initial binary in a circular orbit with a separation , where , or and is the pre-SN star’s radius. Then for each orbital separation we run simulations with at least four different SN explosion energies. In all cases we assume based on the results of Qin et al. (2018), and assume that synchronization of the stellar spin and the orbit has taken place, as is expected for the initial separations used in this analysis. Given the large uncertainties in BH natal kick estimations (Mandel, 2016; Repetto & Nelemans, 2015), we assumed the simplest scenario where no natal kick is applied to the recently formed BH. This combined with the synchronization of the stellar spin and the orbit, translates into BH’s spins aligned with the orbital angular momentum.
The initial profile of the star was obtained from the 35OC KEPLER model calculated by Woosley & Heger (2006) of a pre-SN helium star with . We considered the innermost of the pre-SN star to be the newly formed BH with , which we subsequently treat as a sink particle. After the removal of the inner core, we use a parameterized energy injection routine to mimic the supernova engine and derive the density and velocity profile of the expanding envelope. Specifically, we use a spherically symmetric kinetic piston at the inner boundary to adjust the energy injected into the envelope. In all calculations the energy is parametrized as follows: , where is the binding energy of the pre-SN star.
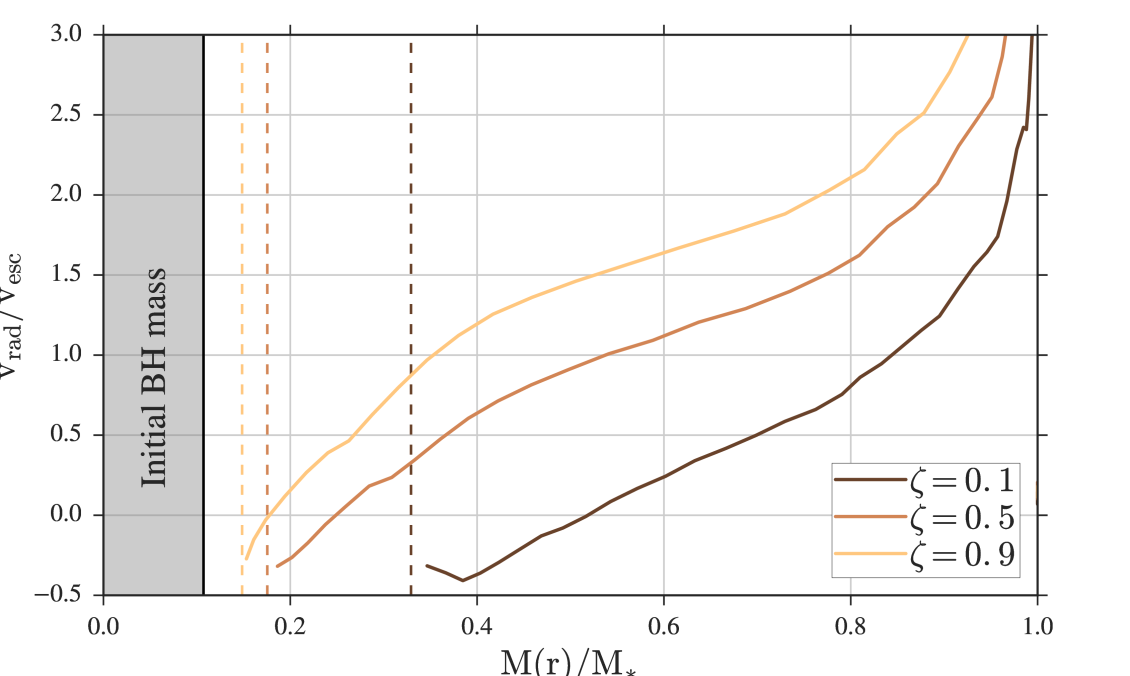
The distribution that describe the ejecta is determined solely by the structure of the pre-SN star (Woosley & Weaver, 1995; Matzner & McKee, 1999) and is established by the hydrodynamics of the interaction. Initially, the shock propagates through the stellar material, pressurizing it and setting it into motion. Once the shock wave approaches the surface of the star, a rarefaction stage begins in which stellar material is accelerated by the entropy deposited by the shock. This stage terminates once the pressure ceases to be dynamically important and the material expands freely. Figure 1 shows the radial velocity profile of the envelope when the shock surfaces the stellar envelope for three different explosion energies: and 0.9. The gray area shows the initial BH mass while the dashed lines show at the time the shock reaches . Despite the complicated hydrodynamical interaction, the density and pressure approach steep power laws in velocity as the material approaches homologous expansion (Figure 1). For a given progenitor structure, the ensuing ejecta will take similar distributions.
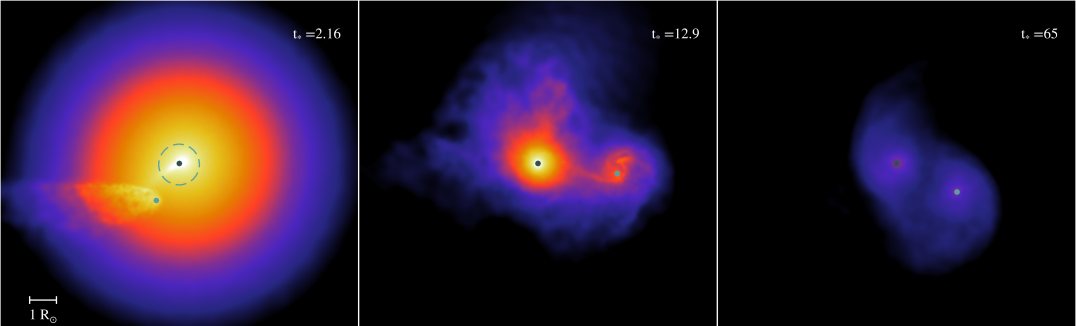
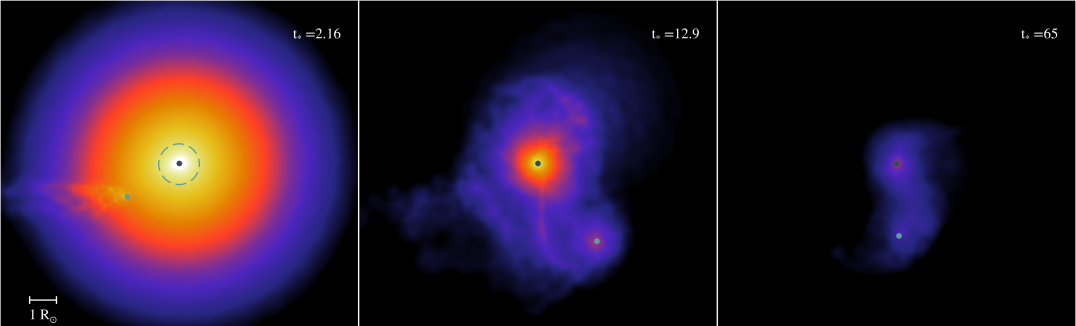
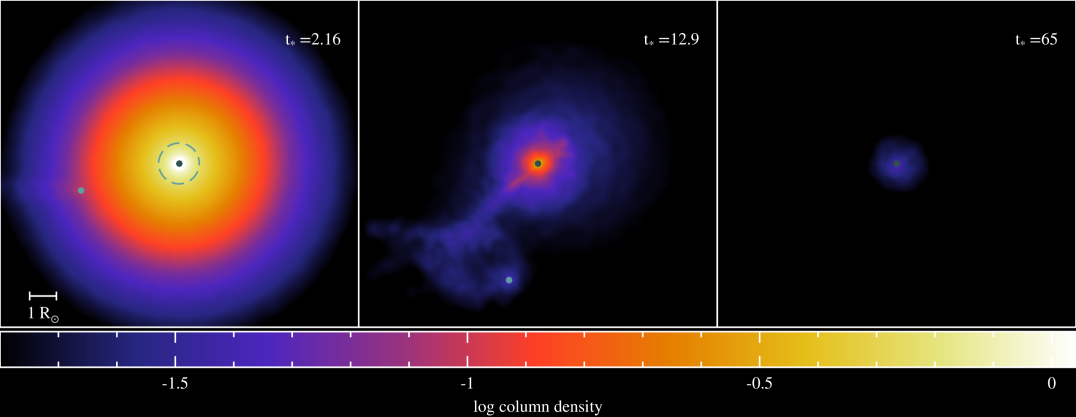
When , energy injection fails to unbind the star such that a sizable fraction of its mass eventually fallbacks onto the newly formed BH. If this takes place in a binary system (Batta et al., 2017), a non-negligible fraction of the bound material can expand to a radius comparable or larger than the binary’s separation, thus immersing the BH companion in gas. The interaction of fallback material with the binary transfers orbital angular momentum to the gas, which upon accretion onto the orbiting BHs is finally transferred into spin angular momentum. Differences in result in diverse accretion histories, which ultimately regulate the BHs’ final masses and spins. It is to this topic that we now draw our attention.
3 Fallback Supernova in Binaries and the Spins of LIGO Sources
3.1 Spin Evolution of the Newly Formed Black Hole
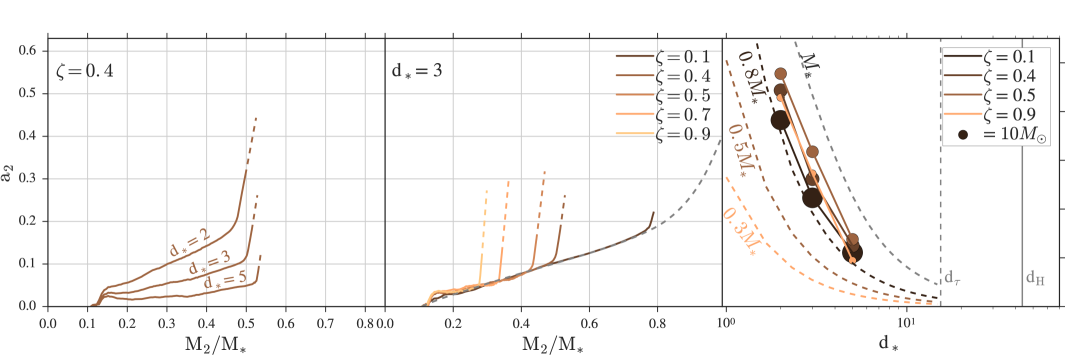
Figure 2 shows the gas column density in the equatorial plane of the binary for three different simulations (from top to bottom) and at three different stages (left to right). Evolutionary times in Figure 2 are measured in units of the dynamical time of the pre-SN star: . All simulations have but differ on the initial separation of the binary: (top panel), (middle panel) and (bottom panel). The frames are centered on the newly formed BH and the dashed circles in the left panels show the size of the pre-SN star.
Flow dynamics are similar in all three simulations shown in Figure 2. First, the envelope expands to rapidly engulf the companion BH. A bow shock is created as a result of this initial interaction. It is, however, only when the slower moving material reaches the companion that the resulting torque can supply the envelope gas with sizable angular momentum. This envelope material will remain bound to the system and will form a disk around if restricted to the region within which orbiting gas is gravitationally bound to the newly formed BH. A disk, albeit lighter, also forms around , whose final mass depends sensitively on the initial separation.
The total mass bound to is the same in all simulations, yet the fraction of angular momentum accreted increases with decreasing separation. As a result, is higher for progressively more compact binaries despite the final mass of reaching similar values. This can be seen in the left panel of Figure 3, in which we show the evolution of as a function of the accreted mass in units of . Initially, increases as envelope material is accreted directly onto the BH. The innate angular momentum in this initial phase is determined by tidal synchronization, which increases as the binary separation decreases (Kushnir et al., 2016, 2017; Zaldarriaga et al., 2018). A transition in the evolution of is observed in the left panel in Figure 3 when material that is effectively torqued by the binary is able to form a disk and is subsequently accreted onto . This material has a higher specific angular momentum than the one initially set by tidal synchronization and, when accreted, is able to spin up the newly formed BH at a faster rate. The resultant change in slope observed in the left panel in Figure 3 due to the accretion of disk material is observed to occur earlier for smaller separations, which results in higher total spins values than those given by direct collapse of the same fallback material.
At a fixed , the spin of the newly formed BH depends sensitively on . For , the resultant torque on the fallback material can be considerable and, as a result, can be appreciable larger than the one expected from tidal synchronization. In this case, the final mass of remains unchanged while the final spin can vary drastically. The final mass of is, on the other hand, controlled by . The middle panel in Figure 3 shows the evolution of for a fixed separation and changing . Initially, the spin evolution follows the trend expected from direct collapse. This is because the torque is unable to modify the original angular momentum of the promptly collapsing stellar material. A transition to disk accretion is seen in all cases, with the shift always occurring late in the mass accretion history of . The resultant spin is similar in all cases due to the self similarity of the mass distribution of the expanding ejecta (Matzner & McKee, 1999), which results in a comparable mass ratio of directly falling stellar material to disk material for different values of . For example this fraction varies from 5.3 % for to 7.6% for (see panel of Figure 3 for ). This mass ratio is mainly responsible for determining the final spin of the BH and varies only slightly with .
We have discussed, in the context of the classical scenario, the effects that the binary separation and the energy of the SN have on the resulting spin of the newly formed BH. The right panel of Figure 3 provides a clear summary of our findings as it shows the final spin of as function of and . The final mass of the newly formed BH is also shown by the size of the symbols. The masses for range from for () to for (). Together with the results from our simulations we also plot the expected spin obtained from the direct collapse of the pre-SN stellar profile. This formalism makes use of the KEPLER model and assumes solid body rotation determined by tidal synchronization. Then, by assuming the spherical collapse of the star, we obtain the BH’s spin for different fractions of the collapsed stellar mass . If the entire star was to collapse directly onto a BH, this will give a final spin solely dependent on , as predicted by the dashed line in Figure 3 labeled .
When is small and a significant fraction of the material is promptly accreted by the BH, the simple direct collapse formalism provides an accurate description of the final spin of the newly formed BH. This can be seen by comparing the dashed line in Figure 3 labeled with the simulation results obtained for , which give BHs with and final spins that closely resemble the direct collapse ones. By contrast, when , the final spin is significantly higher than the one predicted by direct collapse of the same enclosed material. This is because in such cases the fallback material is effectively torqued by the BH companion, which results in disk formation and consequentially higher final spin values. Binary BH formation in the classical scenario depends critically on the currently poorly constrained energy of the resulting SN, which for fallback-mediated remnant growth results in faster spinning BHs than what would have been attainable for a single star progenitor.
3.2 Spin Evolution of the Orbiting Black Hole
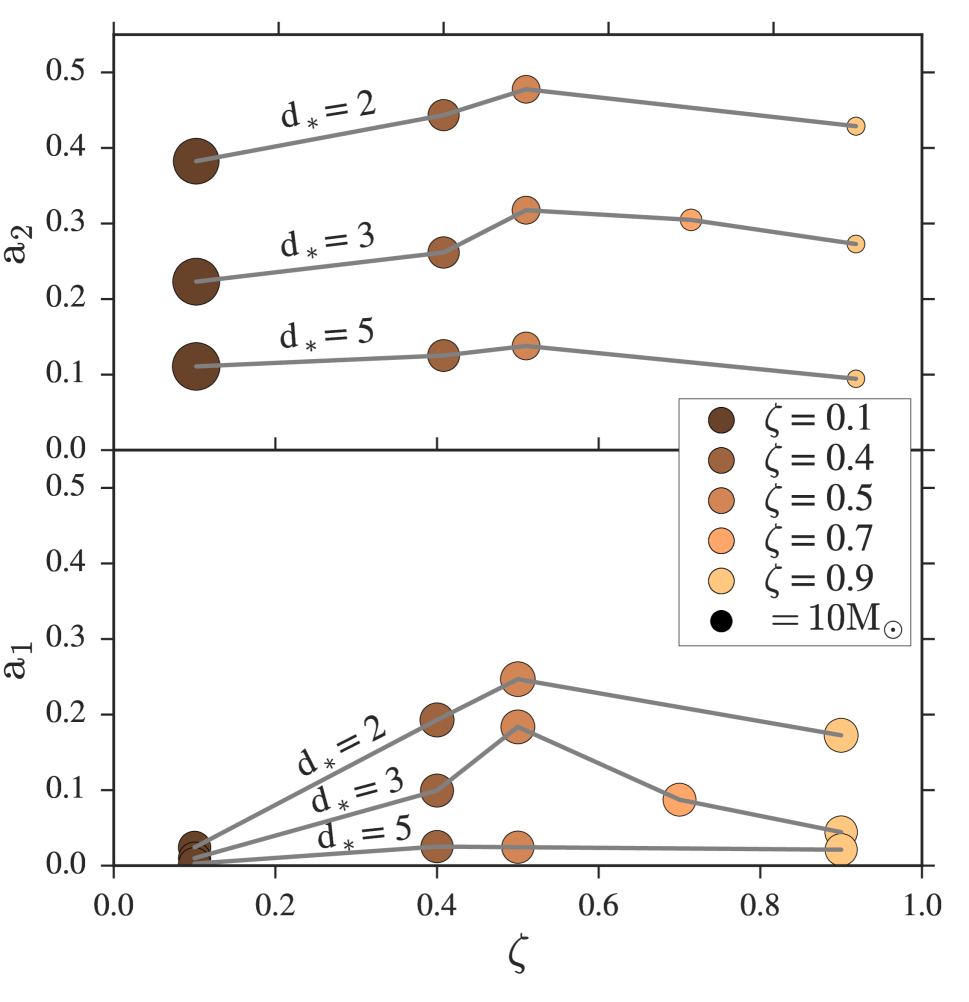
Figure 4 shows the dependence of and on and . In contrast to , the final mass of the companion BH is only weakly altered by changes in . The reason is that a comparatively small mass can be effectively restricted to the region within which the expanding envelope material is gravitationally bound to . This bound material forms a disk whose final mass depends on both and . The resultant changes in , under the assumption of , are observed to be more pronounced when the initial binary separation changes. Although, as expected, no sizable changes take place at large separations given that only a tiny fraction of the companion’s envelope can be under the gravitational influence of . The final value of shows a modest variation with SN energy with a small preference for at small separations. This indicates that although the ejecta distributions are similar for changing values of , the fraction of bound material to is largest for this particular explosion energy, although its exact value is likely to change for different pre-SN progenitors.
4 DISCUSSION
In this Letter we have explored within the classical binary scenario how the spin of LIGO sources vary when the remnant BH is formed in weak SN explosions instead of direct collapse. Our key findings are summarized below.
-
•
The final mass of the newly formed BH depends on the explosion energy. Its mass varies from for to for (Figure 1).
-
•
At a fixed SN energy, the final spin increases significantly with decreasing as a larger fraction of the fallback material is torqued by the companion. This results in similar mass BHs but with widely different spins (see left panel in Figure 3).
-
•
Due to the self similarity of the mass distribution of the expanding ejecta, the final spin of the BH varies only slightly with . This results in BHs with a wide range in masses but similar spins (see middle panel in Figure 3).
-
•
In the presence of a companion, the final spin of a BH formed by a fallback SN explosion can be significantly higher than the one predicted by direct collapse of the same stellar material (see right panel in Figure 3).
-
•
The spin of the BH companion, on the other hand, depends on both and . This is because its accretion history is determined by the amount of fallback material that it is able to seize (Figure 4).
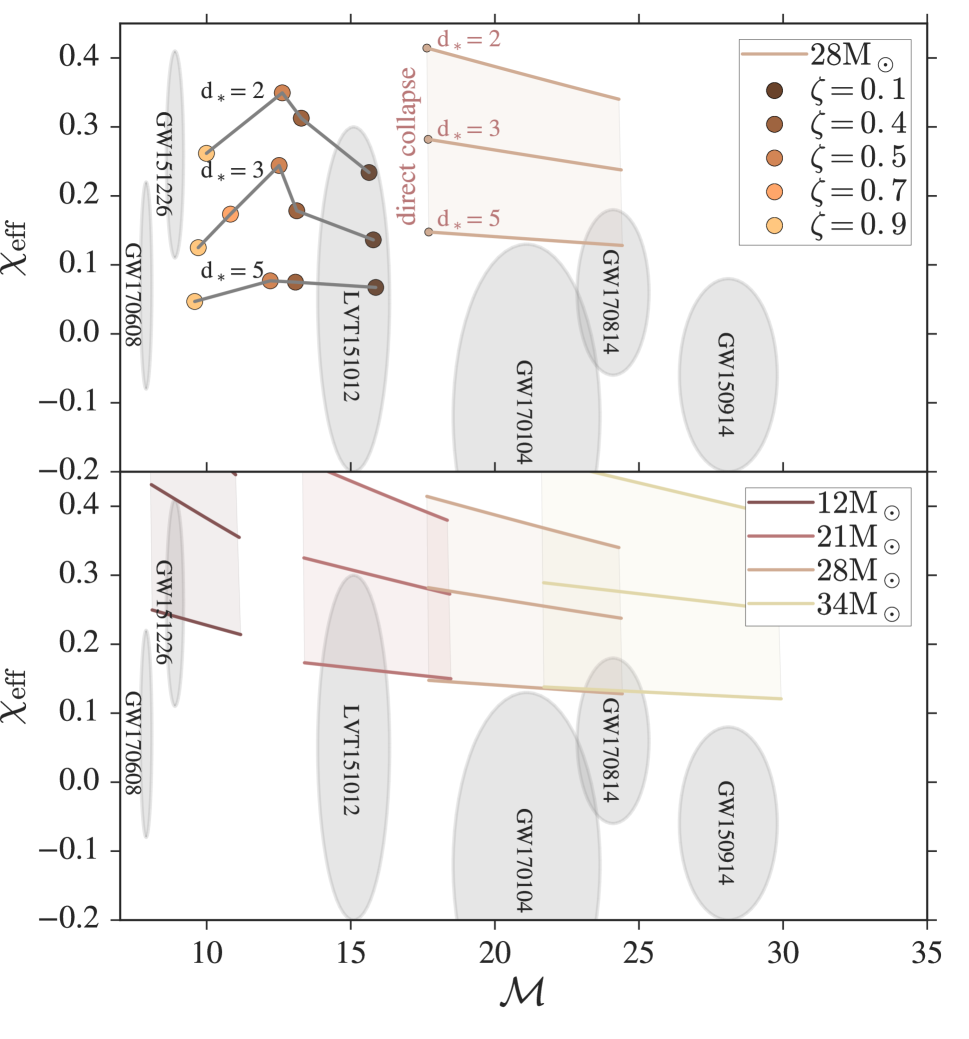
In Figure 5 we present a comparison of our results (upper panel) in the context of both direct collapse solutions and current LIGO observations of binary BHs. Shown are as a function of the chirp mass, , of the resulting BH binary system. The shaded quadrilateral regions (upper and lower panel) show systems produced by the direct collapse of pre-SN helium stars of varying masses, whose structures have been taken from the KEPLER models of Woosley & Heger (2006). The final spin of is calculated using the radial stellar profile and assuming rigid body rotation of the tidally synchronized SN progenitor. The pre-SN helium stars () are assumed to be orbiting around a BH with and =0. The dependence of with is obtained by varying from to in all cases, while the dependence of at a fixed is obtained by changing from to at constant . To facilitate comparisons, we plot as shaded ellipses the 90% credibility intervals of the GW signals measured so far (Abbott et al., 2016b, c, 2017a, 2017b, 2017c).
Some points should be emphasized. The current LIGO observations are inconsistent with the direct collapse of pre-SN helium stars in close binaries (Kushnir et al., 2016; Belczynski et al., 2017; Zaldarriaga et al., 2018; Hotokezaka & Piran, 2017). When the assumption of direct collapse is relaxed, the mass of can be altered by small changes on the explosion energy while and (to a lesser extent) depend primarily on (Figure 4). For the specific + system studied here, we show that changes in alone can produce systems like LVT151012 (, ) or GW170608 (, ). For a fixed SN energy of , changes in the initial separation can, on the other hand, yield systems like GW170608 () or GW151226 ().
Irrespective of the exact progenitor system, the processes discussed here implies that the formation pathways of LIGO binary BHs are more complicated than the standard scenario suggests. But the effects are especially interesting for weak SN explosions taking place in close binary systems. Future LIGO observations can offer clues to the nature of the SN explosion leading to the formation of BHs, which is currently not well understood (Perna et al., 2014; Sukhbold et al., 2016; Raithel et al., 2018). For instance, GW170608 could be indicative of weak SN explosion of a more massive pre-SN progenitor system while GW151226 might arise due to direct collapse of a lighter, yet more compact progenitor system.
The properties of LIGO sources in the (,) plane is diverse. One appealing aspect of the classical scenario is that the great variety of binary and explosion parameters can probably help explain this diversity. Given the need for a large helium core mass in progenitors, BH formation may be favored not only by slow rotation but also by low metallicity (Izzard et al., 2004). Larger mass helium cores might have less energetic explosions but this is currently highly uncertain. Many massive stars may produce supernovae by forming neutron stars in spherically symmetric explosions, but some may fail during neutrino energy deposition, forming BHs in the centre of the star (Fryer et al., 2012; Ugliano et al., 2012; Pejcha & Thompson, 2015) and possibly a wide range of weak SN explosions (Moriya et al., 2010; Fryer et al., 2012; Dexter & Kasen, 2013; Lovegrove & Woosley, 2013; Batta et al., 2017; Fernández et al., 2018). One expects various outcomes ranging from very massive BHs with low spins (GW150914), to lighter and faster spinning BHs (GW151226). The number density of binary BHs of different masses and spins would provide a natural test to distinguish between different stellar explosion avenues.
References
- Abbott et al. (2016a) Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, The Astrophysical Journal Letters, 818, L22
- Abbott et al. (2016b) —. 2016b, Physical Review Letters, 116, 241103
- Abbott et al. (2016c) —. 2016c, Physical Review Letters, 116, 061102
- Abbott et al. (2017a) —. 2017a, Physical Review Letters, 118, 221101
- Abbott et al. (2017b) —. 2017b, The Astrophysical Journal Letters, 851, L35
- Abbott et al. (2017c) —. 2017c, Phys. Rev. Lett., 119, 141101
- Bardeen (1970) Bardeen, J. M. 1970, Nature, 226, 64
- Batta et al. (2017) Batta, A., Ramirez-Ruiz, E., & Fryer, C. 2017, ApJ, 846, L15
- Belczynski et al. (2016) Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 EP
- Belczynski et al. (2017) Belczynski, K., Klencki, J., Meynet, G., et al. 2017, ArXiv e-prints, arXiv:1706.07053
- de Mink & Mandel (2016) de Mink, S. E., & Mandel, I. 2016, Monthly Notices of the Royal Astronomical Society, 460, 3545
- Dexter & Kasen (2013) Dexter, J., & Kasen, D. 2013, ApJ, 772, 30
- Farr et al. (2017) Farr, W. M., Stevenson, S., Miller, M. C., et al. 2017, Nature, 548, 426
- Fernández et al. (2018) Fernández, R., Quataert, E., Kashiyama, K., & Coughlin, E. R. 2018, MNRAS, 476, 2366
- Fryer et al. (2012) Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91
- Gerosa & Berti (2017) Gerosa, D., & Berti, E. 2017, arXiv:1703.06223
- Hotokezaka & Piran (2017) Hotokezaka, K., & Piran, T. 2017, ApJ, 842, 111
- Izzard et al. (2004) Izzard, R. G., Ramirez-Ruiz, E., & Tout, C. A. 2004, MNRAS, 348, 1215
- Kalogera et al. (2007) Kalogera, V., Belczynski, K., Kim, C., O’Shaughnessy, R., & Willems, B. 2007, Phys. Rep., 442, 75
- Kushnir et al. (2016) Kushnir, D., Zaldarriaga, M., Kollmeier, J. A., & Waldman, R. 2016, MNRAS, 462, 844
- Kushnir et al. (2017) —. 2017, MNRAS, 467, 2146
- Lovegrove & Woosley (2013) Lovegrove, E., & Woosley, S. E. 2013, ApJ, 769, 109
- Mandel (2016) Mandel, I. 2016, MNRAS, 456, 578
- Matzner & McKee (1999) Matzner, C. D., & McKee, C. F. 1999, ApJ, 510, 379
- Moriya et al. (2010) Moriya, T., Tominaga, N., Tanaka, M., et al. 2010, ApJ, 719, 1445
- Pejcha & Thompson (2015) Pejcha, O., & Thompson, T. A. 2015, ApJ, 801, 90
- Perna et al. (2014) Perna, R., Duffell, P., Cantiello, M., & MacFadyen, A. I. 2014, ApJ, 781, 119
- Postnov & Yungelson (2014) Postnov, K. A., & Yungelson, L. R. 2014, Living Reviews in Relativity, 17, 3
- Qin et al. (2018) Qin, Y., Fragos, T., Meynet, G., et al. 2018, ArXiv e-prints, arXiv:1802.05738
- Raithel et al. (2018) Raithel, C. A., Sukhbold, T., & Özel, F. 2018, ApJ, 856, 35
- Remillard & McClintock (2006) Remillard, R. A., & McClintock, J. E. 2006, arXiv:0606352
- Repetto & Nelemans (2015) Repetto, S., & Nelemans, G. 2015, MNRAS, 453, 3341
- Rodriguez et al. (2016a) Rodriguez, C. L., Haster, C.-J., Chatterjee, S., Kalogera, V., & Rasio, F. A. 2016a, ApJ, 824, L8
- Rodriguez et al. (2016b) Rodriguez, C. L., Zevin, M., Pankow, C., Kalogera, V., & Rasio, F. A. 2016b, ApJ, 832, L2
- Sadowski et al. (2008) Sadowski, A., Belczynski, K., Bulik, T., et al. 2008, ApJ, 676, 1162
- Springel (2005) Springel, V. 2005, MNRAS, 364, 1105
- Stevenson et al. (2017) Stevenson, S., Berry, C. P. L., & Mandel, I. 2017, arXiv:1703.06873
- Sukhbold et al. (2016) Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H.-T. 2016, ApJ, 821, 38
- Thorne (1974) Thorne, K. S. 1974, ApJ, 191, 507
- Tutukov & Yungelson (1993) Tutukov, A. V., & Yungelson, L. R. 1993, MNRAS, 260, 675
- Ugliano et al. (2012) Ugliano, M., Janka, H.-T., Marek, A., & Arcones, A. 2012, ApJ, 757, 69
- Voss & Tauris (2003) Voss, R., & Tauris, T. M. 2003, Monthly Notices of the Royal Astronomical Society, 342, 1169
- Woosley & Heger (2006) Woosley, S. E., & Heger, A. 2006, The Astrophysical Journal, 637, 914
- Woosley & Weaver (1995) Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181
- Wysocki et al. (2017) Wysocki, D., Gerosa, D., O’Shaughnessy, R., et al. 2017, arXiv:1709.01943
- Zaldarriaga et al. (2018) Zaldarriaga, M., Kushnir, D., & Kollmeier, J. A. 2018, MNRAS, 473, 4174
- Zwart & McMillan (2000) Zwart, S. F. P., & McMillan, S. L. W. 2000, The Astrophysical Journal Letters, 528, L17