Blind Fingerprinting

A mathematical statement of our generic fingerprinting problem is given in Sec. II, together with the basic definitions of error probabilities, capacity, error exponents, and fair coalitions. Sec. III presents our random coding scheme. Sec. IV presents a simple but suboptimal decoder that compares empirical mutual information scores between received data and individual fingerprints, and outputs a guilty decision whenever the score exceeds a certain tunable threshold. Sec. V presents a joint decoder that assigns a penalized empirical mutual information score to candidate coalitions and selects the coalition with the highest score. Sec. VI establishes an upper bound on blind fingerprinting capacity under the detect-all criterion. Finally, conclusions are given in Sec. VII. The proofs of the theorems are given in appendices.

We use uppercase letters for random variables, lowercase letters for their individual values, calligraphic letters for finite alphabets, and boldface letters for sequences. We denote by ${\cal M}^{\star}$ the set of sequences of arbitrary length (including 0) whose elements are in ${\cal M}$. The probability mass function (p.m.f.) of a random variable $X\in{\cal X}$ is denoted by $p_{X}=\{p_{X}(x),\,x\in{\cal X}\}$. The entropy of a random variable $X$ is denoted by $H(X)$, and the mutual information between two random variables $X$ and $Y$ is denoted by $I(X;Y)=H(X)-H(X|Y)$. Should the dependency on the underlying p.m.f.s be explicit, we write the p.m.f.s as subscripts, e.g., $H_{p_{X}}(X)$ and $I_{p_{X},p_{Y|X}}(X;Y)$. The Kullback-Leibler divergence between two p.m.f.s $p$ and $q$ is denoted by $D(p||q)$; the conditional Kullback-Leibler divergence of $p_{Y|X}$ and $q_{Y|X}$ given $p_{X}$ is denoted by $D(p_{Y|X}||q_{Y|X}|p_{X})=D(p_{Y|X}\,p_{X}||q_{Y|X}\,p_{X})$. All logarithms are in base 2 unless specified otherwise.

Denote by $p_{\mathbf{x}}$ the type, or empirical p.m.f. induced by a sequence ${\mathbf{x}}\in{\cal X}^{N}$. The type class $T_{\mathbf{x}}$ is the set of all sequences of type $p_{\mathbf{x}}$. Likewise, we denote by $p_{{\mathbf{x}}{\mathbf{y}}}$ the joint type of a pair of sequences $({\mathbf{x}},{\mathbf{y}})\in{\cal X}^{N}\times{\cal Y}^{N}$ and by $T_{{\mathbf{x}}{\mathbf{y}}}$ the type class associated with $p_{{\mathbf{x}}{\mathbf{y}}}$. The conditional type $p_{{\mathbf{y}}|{\mathbf{x}}}$ of a pair of sequences (${\mathbf{x}},{\mathbf{y}}$) is defined by $p_{{\mathbf{x}}{\mathbf{y}}}(x,y)/p_{{\mathbf{x}}}(x)$ for all $x\in{\cal X}$ such that $p_{{\mathbf{x}}}(x)>0$. The conditional type class $T_{{\mathbf{y}}|{\mathbf{x}}}$ given ${\mathbf{x}}$, is the set of all sequences $\tilde{{\mathbf{y}}}$ such that $({\mathbf{x}},\tilde{{\mathbf{y}}})\in T_{{\mathbf{x}}{\mathbf{y}}}$. We denote by $H({\mathbf{x}})$ the empirical entropy of the p.m.f. $p_{{\mathbf{x}}}$, by $H({\mathbf{y}}|{\mathbf{x}})$ the empirical conditional entropy, and by $I({\mathbf{x}};{\mathbf{y}})$ the empirical mutual information for the joint p.m.f. $p_{{\mathbf{x}}{\mathbf{y}}}$.

We use the calligraphic fonts $\mathscr{P}_{X}$ and $\mathscr{P}_{X}^{[N]}$ to represent the set of all p.m.f.s and all empirical p.m.f.’s, respectively, on the alphabet ${\cal X}$. Likewise, $\mathscr{P}_{Y|X}$ and $\mathscr{P}_{Y|X}^{[N]}$ denote the set of all conditional p.m.f.s and all empirical conditional p.m.f.’s on the alphabet ${\cal Y}$. A special symbol $\mathscr{W}_{K}$ will be used to denote the feasible set of collusion channels $p_{Y|X_{1},\cdots,X_{K}}$ that can be selected by a size-$K$ coalition.

Mathematical expectation is denoted by the symbol ${\mathbb{E}}$. The shorthands $a_{N}\doteq b_{N}$ and $a_{N}\mbox{$\>\stackrel{{\scriptstyle\centerdot}}{{\leq}}\>$}b_{N}$ denote asymptotic relations in the exponential scale, respectively $\lim_{N\to\infty}\frac{1}{N}\log\frac{a_{N}}{b_{N}}=0$ and $\limsup_{N\to\infty}$ $\frac{1}{N}\log\frac{a_{N}}{b_{N}}\leq 0$. We define $|t|^{+}\triangleq\max(t,0)$ and $\exp_{2}(t)\triangleq 2^{t}$. The indicator function of a set ${\cal A}$ is denoted by $\mathds{1}_{\{x\in{\cal A}\}}$. Finally, we adopt the convention that the minimum of a function over an empty set is $+\infty$ and the maximum of a function over an empty set is 0.

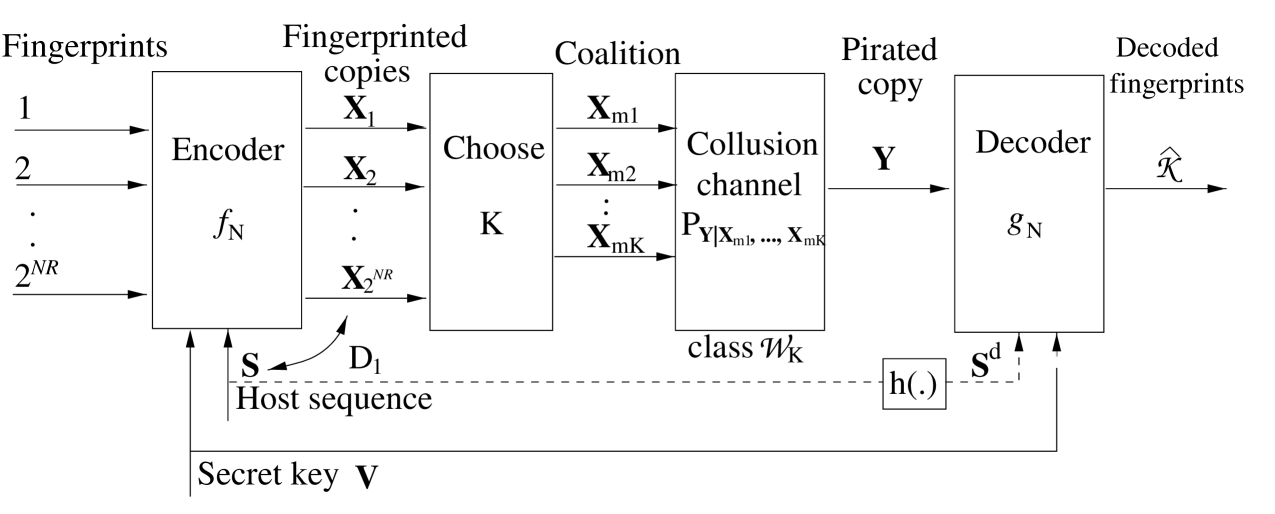
Our model for blind fingerprinting is diagrammed in Fig. 1. Let ${\cal S}$, ${\cal X}$, and ${\cal Y}$ be three finite alphabets. The covertext sequence ${\mathbf{S}}=(S_{1},\cdots,S_{N})\in{\cal S}^{N}$ consists of $N$ independent and identically distributed (i.i.d.) samples drawn from a p.m.f. $p_{S}(s)$, $s\in{\cal S}$. A random variable $V$ taking values in an alphabet ${\cal V}_{N}$ is shared between encoder and decoder, and not publicly revealed. The random variable $V$ is independent of ${\mathbf{S}}$ and plays the role of a cryptographic key. There are $2^{NR}$ users, each of which receives a fingerprinted copy:

$${\mathbf{X}}_{m}=f_{N}({\mathbf{S}},V,m),\quad 1\leq m\leq 2^{NR},$$

(2.1)

where $f_{N}:{\cal S}^{N}\times{\cal V}_{N}\times\{1,\cdots,2^{NR}\}\to{\cal X}^{N}$ is the encoding function, and $m$ is the index of the user. The encoder binds each fingerprinted copy ${\mathbf{x}}_{m}$ to the covertext ${\mathbf{s}}$ via a distortion constraint. Let $d~:~{\cal S}\times{\cal X}\to{\mathbb{R}}^{+}$ be the distortion measure and $d^{N}({\mathbf{s}},{\mathbf{x}})=\frac{1}{N}\sum_{i=1}^{N}d(s_{i},x_{i})$ the extension of this measure to length-$N$ sequences. The code $f_{N}$ is subject to the distortion constraint

$$d^{N}({\mathbf{s}},{\mathbf{x}}_{m})\leq D_{1}\quad 1\leq m\leq 2^{NR}.$$

(2.2)

Let ${\cal K}\triangleq\{m_{1},\,m_{2}\,\cdots,\,m_{K}\}$ be a coalition of $K$ users, called colluders. No constraints are imposed on the formation of coalitions. The colluders combine their copies ${\mathbf{X}}_{{\cal K}}\triangleq\{{\mathbf{X}}_{m},\,m\in{\cal K}\}$ to produce a pirated copy ${\mathbf{Y}}\in{\cal Y}^{N}$. Without loss of generality, we assume that ${\mathbf{Y}}$ is generated stochastically as the output of a collusion channel $p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}$. Fidelity constraints are imposed on $p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}$ to ensure that ${\mathbf{Y}}$ is “close” to the fingerprinted copies ${\mathbf{X}}_{m},\,m\in{\cal K}$. These constraints can take the form of distortion constraints, analogously to (2.2). They are formulated below and result in the definition of a feasible class $\mathscr{W}_{K}$ of attacks.

The decoder knows neither $K$ nor $p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}$ selected by the $K$ colluders and has access to the pirated copy ${\mathbf{Y}}$, the secret key $V$, as well as to ${\mathbf{S}}^{d}$, a degraded version of the host ${\mathbf{S}}$. To simplify the exposition, the degradation arises via a deterministic symbolwise mapping $h~:~{\cal S}\to{\cal S}^{d}$. The sequence $s^{d}=h(s)$ could represent a coarse version of ${\mathbf{s}}$, or some other features of ${\mathbf{s}}$. Two special cases are private fingerprinting where $S^{d}=S$, and public fingerprinting where $S^{d}=\emptyset$. The decoder produces an estimate

$$\hat{{\cal K}}=g_{N}({\mathbf{Y}},{\mathbf{S}}^{d},V)$$

(2.3)

of the coalition. A possible decision is the empty set, $\hat{{\cal K}}=\emptyset$, which is the reasonable choice when an accusation would be unreliable. To summarize, we have

The randomization is via the secret key $V$ and can take the form of permutations of the symbol positions $\{1,2,\cdots,N\}$, permutations of the $2^{NR}$ fingerprint assignments, and an auxiliary time-sharing sequence, as in [6]—[10], [16].

We now state the attack models and define the error probabilities, capacities, and error exponents.

The conditional type $p_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}$ is a random variable whose conditional distribution given ${\mathbf{x}}_{{\cal K}}$ depends on the collusion channel $p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}$. Our fidelity constraint on the coalition is of the general form

$$Pr[p_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}\in\mathscr{W}_{K}]=1,$$

(2.4)

where $\mathscr{W}_{K}$ is a convex subset of $\mathscr{P}_{Y|X_{{\cal K}}}$. That is, the empirical conditional p.m.f. of the pirated copy given the marked copies is restricted. Examples of $\mathscr{W}_{K}$ are given in [10], including hard distortion constraints on the coalition:

$$\mathscr{W}_{K}=\left\{p_{Y|X_{{\cal K}}}~:~\sum_{x_{{\cal K}},y}\,p_{X_{{\cal K}}}(x_{{\cal K}})\,p_{Y|X_{{\cal K}}}(y|x_{{\cal K}})\,{\mathbb{E}}_{\phi}\,d_{2}(\phi(x_{{\cal K}}),y)\leq D_{2}\right\}$$

(2.5)

where $\phi~:{\cal X}^{K}\to{\cal S}$ is a (possible randomized) permutation-invariant estimator $\hat{S}=\phi(X_{{\cal K}})$ of each host signal sample based on the corresponding marked samples; $d_{2}~:~{\cal S}\to{\cal Y}$ is the coalition’s distortion function; $p_{X_{{\cal K}}}$ is a reference p.m.f.; and $D_{2}$ is the maximum allowed distortion. Another possible choice for $\mathscr{W}_{K}$ is obtained using the Boneh-Shaw constraint [1, 10].

Fair Coalitions. Denote by $\pi$ a permutation of the elements of ${\cal K}$. The set of fair, feasible collusion channels is the subset of $\mathscr{W}_{K}$ consisting of permutation-invariant channels:

$$\mathscr{W}_{K}^{fair}=\left\{p_{Y|X_{{\cal K}}}\in\mathscr{W}_{K}~:~p_{Y|X_{\pi({\cal K})}}=p_{Y|X_{{\cal K}}},\;\forall\pi\right\}.$$

(2.6)

The collusion channel $p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}$ is said to be fair if $Pr[p_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}\in\mathscr{W}_{K}^{fair}]=1$. For any fair collusion channel, the conditional type $p_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}$ is invariant to permutations of the colluders.

Strongly exchangeable collusion channels [7]. Now denote by $\pi$ a permutation of the samples of a length-$N$ sequence. For strongly exchangeable channels, $p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}(\pi{\mathbf{y}}|\pi{\mathbf{x}}_{{\cal K}})$ is independent of $\pi$, for every $({\mathbf{x}}_{{\cal K}},{\mathbf{y}})$. The channel is defined by a probability assignment $Pr[T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}]$ on the conditional type classes. The distribution of ${\mathbf{Y}}$ conditioned on ${\mathbf{Y}}\in T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}$ is uniform:

$$p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}(\tilde{\mathbf{y}}|{\mathbf{x}}_{{\cal K}})=\frac{Pr[T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}]}{|T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}|},\quad\forall\tilde{\mathbf{y}}\in T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}.$$

(2.7)

Let ${\cal K}$ be the actual coalition and $\hat{{\cal K}}=g_{N}({\mathbf{Y}},{\mathbf{S}}^{d},V)$ the decoder’s output. The three error probabilities of interest in this paper are the probability of false positives (one or more innocent users are accused),

$$P_{FP}(f_{N},g_{N},p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}})=Pr[\hat{{\cal K}}\setminus{\cal K}\neq\emptyset],$$

the probability of failing to catch a single colluder,

$$P_{e}^{one}(f_{N},g_{N},p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}})=Pr[\hat{{\cal K}}\cap{\cal K}=\emptyset],$$

and the probability of failing to catch the full coalition:

$$P_{e}^{all}(f_{N},g_{N},p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}})=Pr[{\cal K}\not\subseteq\hat{{\cal K}}].$$

These three probabilities are obtained by averaging over ${\mathbf{S}}$, $V$, and the output of the collusion channel $p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}$. In each case the worst-case probability is denoted by

$$P_{e}(f_{N},g_{N},\mathscr{W}_{K})=\max_{p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}}\,P_{e}(f_{N},g_{N},p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}})$$

(2.8)

where $P_{e}$ denotes either $P_{FP}$, $P_{e}^{one}$ or $P_{e}^{all}$, and the maximum is over all feasible collusion channels, i.e., such that (2.4) holds.

For random codes the error exponents corresponding to (2.8) are defined as

$$E^{\{one,all,FP\}}(R,D_{1},\mathscr{W}_{K})=\liminf_{N\to\infty}\left[-\frac{1}{N}\log P_{e}^{\{one,all,FP\}}(f_{N},g_{N},\mathscr{W}_{K})\right].$$

(2.9)

We have $C^{all}(D_{1},\mathscr{W}_{K})\leq C^{one}(D_{1},\mathscr{W}_{K})$ and $E^{all}(R,D_{1},\mathscr{W}_{K})\leq E^{one}(R,D_{1},\mathscr{W}_{K})$ because an error event for the detect-one problem is also an error event for the detect-all problem.

A random constant-composition code

$${\cal C}({\mathbf{s}}^{d},{\mathbf{w}},\lambda)=\{{\mathbf{u}}(l,m,\lambda),\;\,1\leq l\leq 2^{N\rho(\lambda)},\;1\leq m\leq 2^{NR}\}$$

(3.1)

is generated for each pair of sequences $({\mathbf{s}}^{d},{\mathbf{w}})\in({\cal S}^{d})^{N}\times T_{{\mathbf{w}}}^{*}$ and conditional type $\lambda\in\mathscr{P}_{S|S^{d}W}^{[N]}$ by drawing $2^{N[R+\rho(\lambda)]}$ random sequences independently and uniformly from an optimized conditional type class $T_{U|S^{d}W}^{*}({\mathbf{s}}^{d},{\mathbf{w}})$, and arranging them into an array with $2^{NR}$ columns and $2^{N\rho(\lambda)}$ rows. Similarly to [11] (see Fig. 2 therein), we refer to $\rho(\lambda)$ as the depth parameter of the array.

Prior to encoding, a sequence ${\mathbf{W}}\in{\cal W}^{N}$ is drawn independently of ${\mathbf{S}}$ and uniformly from $T_{{\mathbf{w}}}^{*}$, and shared with the receiver. Given $({\mathbf{S}},{\mathbf{W}})$, the encoder determines the conditional type $\lambda=p_{{\mathbf{s}}|{\mathbf{s}}^{d}{\mathbf{w}}}$ and performs the following two steps for each user $1\leq m\leq 2^{NR}$.

1. 1.

   Find $l$ such that ${\mathbf{u}}(l,m,\lambda)\in{\cal C}({\mathbf{s}}^{d},{\mathbf{w}},\lambda)\bigcap T_{U|SW}^{*}({\mathbf{s}},{\mathbf{w}})$. If more than one such $l$ exists, pick one of them randomly (with uniform distribution). Let ${\mathbf{u}}={\mathbf{u}}(l,m,\lambda)$. If no such $l$ can be found, generate ${\mathbf{u}}$ uniformly from the conditional type class $T_{U|SW}^{*}({\mathbf{s}},{\mathbf{w}})$.

2. 2.

   Generate ${\mathbf{X}}_{m}$ uniformly distributed over the conditional type class $T_{X|USW}^{*}({\mathbf{u}},{\mathbf{s}},{\mathbf{w}})$, and assign this marked sequence to user $m$.

The fingerprinting codes used in this paper are randomly-modulated (RM) codes [10, Def. 2.2]. For such codes we have the following proposition, which is a straightforward variation of [10, Prop. 2.1] with ${\mathbf{S}}^{d}$ in place of ${\mathbf{S}}$ at the decoder.

To derive error exponents for such channels, it suffices to use the following upper bound:

$$p_{{\mathbf{Y}}|{\mathbf{X}}_{{\cal K}}}(\tilde{\mathbf{y}}|{\mathbf{x}}_{{\cal K}})=\frac{Pr[T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}]}{|T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}|}\leq\frac{1}{|T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}|}\,\mathds{1}_{\{p_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}\in\mathscr{W}_{K}\}},\quad\forall\,\tilde{\mathbf{y}}\in T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}$$

(3.2)

which holds uniformly over all feasible probability assignments to conditional type classes $T_{{\mathbf{y}}|{\mathbf{x}}_{{\cal K}}}$.

The array depth parameter $\rho(\lambda)$ takes the form

$$\rho(\lambda)=I({\mathbf{u}};{\mathbf{s}}|{\mathbf{s}}^{d},{\mathbf{w}})+\epsilon$$

where ${\mathbf{u}}$ is any element of $T_{U|SW}^{*}({\mathbf{s}},{\mathbf{w}})$, and $\epsilon>0$ is an arbitrarily small number. The analysis shows that given any $({\mathbf{s}},{\mathbf{w}})$, the probability of encoding errors vanishes doubly exponentially.

The analysis also shows that the decoding error probability is dominated by a single joint type class $T_{{\mathbf{y}}{\mathbf{u}}{\mathbf{s}}{\mathbf{w}}}$. Denote by $({\mathbf{y}},{\mathbf{u}},{\mathbf{s}},{\mathbf{w}})$ an arbitrary representative of that class. The normalized logarithm of the size of the array is given by

$$R+\rho(\lambda)=I({\mathbf{u}};{\mathbf{y}}|{\mathbf{s}}^{d},{\mathbf{w}})-\Delta,$$

and the probability of false positives vanishes as $2^{-N\Delta}$.

The decoder has access to $({\mathbf{y}},{\mathbf{s}}^{d},{\mathbf{w}})$ but does not know the conditional type $\lambda=p_{{\mathbf{s}}|{\mathbf{s}}^{d}{\mathbf{w}}}$ realized at the encoder. The decoder evaluates the users one at a time and makes an innocent/guilty decision on each user independently of the other users. Specifically, the receiver outputs an estimated coalition $\hat{{\cal K}}$ if and only if $\hat{{\cal K}}$ satisfies the following condition:

$$\forall m\in\hat{{\cal K}}~:\quad\max_{\lambda\in\mathscr{P}_{S|S^{d}W}^{[N]}}\max_{1\leq l\leq 2^{N\rho(\lambda)}}I({\mathbf{u}}(l,m,\lambda);{\mathbf{y}}|{\mathbf{s}}^{d}{\mathbf{w}})-\rho(\lambda)>R+\Delta.$$

(4.1)

If no such $\hat{{\cal K}}$ is found, the receiver outputs $\hat{{\cal K}}=\emptyset$. This decoder outputs all user indices whose empirical mutual information score, penalized by $\rho(\lambda)$, exceeds the threshold $R+\Delta$.

Observe that the maximizing $\lambda$ in (4.1) may depend on $m$. With high probability, this event implies a decoding error. Improvements can only be obtained using a more complex joint decoder, as in Sec. V.

Define the following set of conditional p.m.f.’s for $(XU)_{{\cal K}}\triangleq(X_{{\cal K}},U_{{\cal K}})$ given $(S,W)$:

$${\cal M}(p_{XU|SW})=\{p_{(XU)_{{\cal K}}|SW}~:~p_{X_{m}U_{m}|SW}=p_{XU|SW},\,m\in{\cal K}\},$$

i.e., the conditional marginal p.m.f. $p_{XU|SW}$ is the same for each $(X_{m},U_{m}),\forall m\in{\cal K}$. Also define the sets

	$\displaystyle\mathscr{P}_{XU|SW}(p_{SW},L_{w},L_{u},D_{1})$	$\displaystyle=$	$\displaystyle\left\{p_{XU|SW}~:~{\mathbb{E}}[d(S,X)]\leq D_{1}\right\},$
	$\displaystyle\mathscr{P}_{(XU)_{{\cal K}}W|S}(p_{S},L_{w},L_{u},D_{1})$	$\displaystyle=$	$\displaystyle\left\{p_{(XU)_{{\cal K}}W|S}=p_{W}\,\prod_{k\in{\cal K}}p_{X_{k}U_{k}|SW}\right.$		(4.2)
			$\displaystyle\left.:~p_{X_{1}U_{1}|SW}=\cdots=p_{X_{K}U_{K}|SW},\;\;\mathrm{and}\;\;{\mathbb{E}}[d(S,X_{1})]\leq D_{1}\right\}$

where in (4.2) the random variables $(X_{k},U_{k}),\,k\in{\cal K}$, are conditionally i.i.d. given $(S,W)$.

Define for each $m\in{\cal K}$ the set of conditional p.m.f.’s

	$\displaystyle\mathscr{P}_{Y(XU)_{{\cal K}}|SW}(p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K},R,L_{w},L_{u},m)$				(4.3)
		$\displaystyle\triangleq$	$\displaystyle\left\{\tilde{p}_{Y(XU)_{{\cal K}}|SW}\,:~\tilde{p}_{(XU)_{{\cal K}}|SW}\in{\cal M}(p_{XU|SW}),~\tilde{p}_{Y|X_{{\cal K}}}\in\mathscr{W}_{K},\right.$
			$\displaystyle\qquad\left.I_{p_{W}\tilde{p}_{S|W}\tilde{p}_{Y(XU)_{{\cal K}}|SW}}(U_{m};Y|S^{d}W)-I_{p_{W}\tilde{p}_{S|W}p_{XU|SW}}(U;S|S^{d}W)\leq R\right\}$

and the pseudo sphere packing exponent

	$\displaystyle\tilde{E}_{psp,m}(R,p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\min_{\tilde{p}_{Y(XU)_{{\cal K}}|SW}\in\mathscr{P}_{Y(XU)_{{\cal K}}|SW}(p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K},R,L_{w},L_{u},m)}$		(4.4)
			$\displaystyle\quad D(\tilde{p}_{Y(XU)_{{\cal K}}|SW}\,\tilde{p}_{S|W}\|\tilde{p}_{Y|X_{{\cal K}}}\,p_{XU|SW}^{{\cal K}}\,p_{S}|p_{W}).$

Taking the maximum and minimum of $\tilde{E}_{psp,m}$ above over $m\in{\cal K}$, we respectively define

	$\displaystyle\!\!\!\overline{\tilde{E}}_{psp}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\max_{m\in{\cal K}}\tilde{E}_{psp,m}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K}),$		(4.5)
	$\displaystyle\!\!\!\underline{\tilde{E}}_{psp}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\min_{m\in{\cal K}}\tilde{E}_{psp,m}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K}).$		(4.6)

For a fair coalition ($\mathscr{W}_{K}=\mathscr{W}_{K}^{fair}$), $\tilde{E}_{psp,m}$ is independent of $m\in{\cal K}$, and the two expressions above coincide. Define

	$\displaystyle E_{psp}(R,L_{w},L_{u},D_{1},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\max_{p_{W}\in\mathscr{P}_{W}}\min_{\tilde{p}_{S|W}\in\mathscr{P}_{S|W}}\max_{p_{XU|SW}\in\mathscr{P}_{XU|SW}(p_{W}\,\tilde{p}_{S|W},L_{w},L_{u},D_{1})}$		(4.7)
			$\displaystyle\quad\tilde{E}_{psp,1}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K}^{fair}).$

Denote by $p_{W}^{*}$ and $p_{XU|SW}^{*}$ the maximizers in (4.7), the latter to be viewed as a function of $\tilde{p}_{S|W}$. Both $p_{W}^{*}$ and $p_{XU|SW}^{*}$ implicitly depend on $R$ and $\mathscr{W}_{K}^{fair}$. Finally, define

	$\displaystyle\overline{E}_{psp}(R,L_{w},L_{u},D_{1},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\min_{\tilde{p}_{S|W}\in\mathscr{P}_{S|W}}\overline{\tilde{E}}_{psp}(R,L_{w},L_{u},p_{W}^{*},\tilde{p}_{S|W},p_{XU|SW}^{*},\mathscr{W}_{K})$		(4.8)
	$\displaystyle\underline{E}_{psp}(R,L_{w},L_{u},D_{1},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\min_{\tilde{p}_{S|W}\in\mathscr{P}_{S|W}}\underline{\tilde{E}}_{psp}(R,L_{w},L_{u},p_{W}^{*},\tilde{p}_{S|W},p_{XU|SW}^{*},\mathscr{W}_{K}).$		(4.9)

The terminology pseudo sphere-packing exponent is used because despite its superficial similarity to a real sphere-packing exponent, (4.4) does not provide a fundamental asymptotic lower bound on error probability.

Given ${\mathbf{y}},{\mathbf{s}}^{d},{\mathbf{w}}$, the decoder seeks the coalition size $k$, the conditional host sequence type $\lambda\in\mathscr{P}_{S|S^{d}W}^{[N]}$, and the codewords ${\mathbf{u}}(l,m,\lambda)$ in ${\cal C}({\mathbf{s}}^{d},{\mathbf{w}},\lambda)$ that maximize the M2PMI criterion below. The column indices $m\in{\cal K}$, corresponding to the decoded words form the decoded coalition $\hat{{\cal K}}$. If the maximizing $k$ in (5.2) is zero, the receiver outputs $\hat{{\cal K}}=\emptyset$.

The Maximum Doubly-Penalized Mutual Information criterion is defined as

$$\max_{k\geq 0}M2PMI(k)$$

(5.2)

where

$$M2PMI(k)=\left\{\begin{array}[]{ll}0&:~\mathrm{if~}k=0\\ \underset{\lambda\in\mathscr{P}_{S|S^{d}W}^{[N]}}{\max}\;\underset{{\mathbf{u}}_{{\cal K}}\in{\cal C}^{k}({\mathbf{s}}^{d},{\mathbf{w}},\lambda)}{\max}\left[{\overset{\circ}{I}}({\mathbf{u}}_{{\cal K}};{\mathbf{y}}|{\mathbf{s}}^{d}{\mathbf{w}})-k(\rho(\lambda)+R+\Delta)\right]&:~\mathrm{if~}k=1,2,\cdots\end{array}\right.$$

(5.3)

The following lemma shows that 1) each subset of the estimated coalition is significant, and 2) any further extension of the coalition would fail a significance test. The proof parallels that of Lemma 5.1 in [10] and is therefore omitted.

Define for each ${\cal A}\subseteq{\cal K}$ the set of conditional p.m.f.’s

	$\displaystyle\mathscr{P}_{Y(XU)_{{\cal K}}|SW}(p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K},R,L_{w},L_{u},{\cal A})$				(5.6)
		$\displaystyle\triangleq$	$\displaystyle\left\{\tilde{p}_{Y(XU)_{{\cal K}}|SW}\,:~\tilde{p}_{(XU)_{{\cal K}}|SW}\in{\cal M}(p_{XU|SW}),\right.$
			$\displaystyle\quad\left.\frac{1}{|{\cal A}|}{\overset{\circ}{I}}_{p_{W}\,\tilde{p}_{S|W}\,\tilde{p}_{Y(XU)_{{\cal K}}|SW}}(U_{{\cal A}};YU_{{\cal K}\setminus{\cal A}}|S^{d},W)\leq I_{p_{W}\,\tilde{p}_{S|W}\,p_{XU|SW}}(U;S|S^{d},W)+R\right\}$

and the pseudo sphere packing exponent

	$\displaystyle\tilde{E}_{psp,{\cal A}}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\min_{\tilde{p}_{Y(XU)_{{\cal K}}|SW}\in\mathscr{P}_{Y(XU)_{{\cal K}}|SW}(p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K},R,L_{w},L_{u},{\cal A})}$		(5.7)
			$\displaystyle D(\tilde{p}_{Y(XU)_{{\cal K}}|SW}\,\tilde{p}_{S|W}\|\tilde{p}_{Y|X_{{\cal K}}}\,\tilde{p}_{(XU)_{{\cal K}}|SW}\,p_{S}\,|p_{W}).$

Taking the maximum ¹¹1 The property that ${\cal K}$ achieves $\max_{{\cal A}\subseteq{\cal K}}\tilde{E}_{psp,{\cal A}}$ is established in the proof of Theorem V.2, Part (iv). and the minimum of $\tilde{E}_{psp,{\cal A}}$ above over all subsets ${\cal A}$ of ${\cal K}$, we define

	$\displaystyle\!\!\!\!\!\overline{\tilde{E}}_{psp}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\tilde{E}_{psp,{\cal K}}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K}),$		(5.8)
	$\displaystyle\!\!\!\!\!\underline{\tilde{E}}_{psp}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\min_{{\cal A}\subseteq{\cal K}}\tilde{E}_{psp,{\cal A}}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K}).$		(5.9)

Now define

	$\displaystyle E_{psp}(R,L_{w},L_{u},D_{1},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\max_{p_{W}\in\mathscr{P}_{W}}\min_{\tilde{p}_{S|W}\in\mathscr{P}_{S|W}}\max_{p_{XU|SW}\in\mathscr{P}_{XU|SW}(p_{W},\tilde{p}_{S|W},L_{w},L_{u},D_{1})}$		(5.10)
			$\displaystyle\quad\tilde{E}_{psp,{\cal K}}(R,L_{w},L_{u},p_{W},\tilde{p}_{S|W},p_{XU|SW},\mathscr{W}_{K_{nom}}^{fair}).$

Denote by $p_{W}^{*}$ and $p_{XU|SW}^{*}$ the maximizers in (5.10), where the latter is to be viewed as a function of $\tilde{p}_{S|W}$. Both $p_{W}^{*}$ and $p_{XU|SW}^{*}$ implicitly depend on $R$ and $\mathscr{W}_{K}^{fair}$. Finally, define

	$\displaystyle\overline{E}_{psp}(R,L_{w},L_{u},D_{1},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\min_{\tilde{p}_{S|W}\in\mathscr{P}_{S|W}}\overline{\tilde{E}}_{psp}(R,L_{w},L_{u},p_{W}^{*},\tilde{p}_{S|W},p_{XU|SW}^{*},\mathscr{W}_{K}),$		(5.11)
	$\displaystyle\underline{E}_{psp}(R,L_{w},L_{u},D_{1},\mathscr{W}_{K})$	$\displaystyle=$	$\displaystyle\min_{\tilde{p}_{S|W}\in\mathscr{P}_{S|W}}\underline{\tilde{E}}_{psp}(R,L_{w},L_{u},p_{W}^{*},\tilde{p}_{S|W},p_{XU|SW}^{*},\mathscr{W}_{K}).$		(5.12)