$\bm{D^{*}}$ and $\bm{D^{*}_{s}}$ distribution amplitudes from Bethe-Salpeter wave functions

In relativistic quantum field theory the infinite degrees of freedom do not allow for a straightforward definition of a particle’s wave function as in quantum mechanics. In particular, in Quantum Chromodynamics (QCD) the fundamental quark and gluon fields are not even observable. On the other hand, the bound states of valence quark-antiquark pairs can be described by a Bethe-Salpeter wave function, the closest relative to a wave function in quantum mechanics. Still, in the instant-form of QCD dynamics these wave functions are defined in an infinite-body field theory in which particles interact and their number is not conserved.

One could overcome this difficulty if the hadron’s light-front wave function was known exactly, though realistic calculations of hadronic bounds states in the front form are a challenging task dePaula:2020qna . A different path to a sensible definition of a wave function in quantum field theory is drawn by projecting the Bethe-Salpeter wave functions in the instant form on the light front. Depending on the projection chosen this yields the hadron’s light-front wave function or its light-front distribution amplitude (LFDA). The latter describes the longitudinal momentum distribution of valence quarks in the limit of negligible transverse momentum. While they are non-measurable objects, they are widely being applied in hadron and flavor physics.

For instance, the asymptotic LFDA of the pion, $\phi(x,\mu)\stackrel{{\scriptstyle\mu\to\infty}}{{=}}6x(1-x)$, enters in the expression of its elastic electromagnetic form factor at very large momentum transfers Efremov:1978rn ; Lepage:1980fj . Since the LFDAs are scale-dependent and become broader at smaller momenta, they directly influence the momentum dependence of the elastic form factors in momentum regions accessible in collider experiments Chang:2013nia ; Raya:2015gva ; Raya:2019dnh . Weak $B$ decays into two light(er) mesons are frequently treated as hard exclusive processes in which the decay amplitude is factorized into perturbative short-distance contributions and a nonperturbative transition amplitude. Here too, the LFDAs enter both, the hard-scattering integrals and the heavy-to-light transition amplitudes Beneke:2002jn ; Bauer:2005wb ; El-Bennich:2006rcn ; El-Bennich:2009gqk ; Leitner:2010fq . More recently, the exclusive electroweak production of $D_{s}^{(*)}$ mesons on an unpolarized nucleon was investigated in the framework of collinear QCD factorization which also involves the heavy meson’s LFDA Pire:2015iza ; Pire:2017lfj ; Pire:2017yge ; Pire:2021dad .

Beyond its numerous applications in hard exclusive processes, these one-dimensional distributions provide a practical probability interpretation of partons, as in this frame the particle number is conserved. Namely, the distributions $\phi(x,\mu)$ express the light-front fraction of the hadron’s momentum that a valence quark carries. Another compelling feature is that one can observe the qualitative and quantitative impact of dynamical chiral symmetry breaking (DCSB) on the LFDA at a given scale $\mu$. For instance, the distribution amplitude $\phi_{\pi}(x,\mu)$ of the pion is a concave function which clearly evolves from its asymptotic $\mu\to\infty$ form to a much broader distribution Chang:2013pq . Similarly, the kaon’s distribution amplitude, $\phi_{K}(x,\mu)$, is not symmetric about the midpoint $x=1/2$, which expresses nothing but SU(3) flavor symmetry breaking, and that asymmetry is exacerbated with increasing mass difference of the quarks Shi:2015esa ; Serna:2020txe .

The question arises of how DCSB impacts antiquark-quark states in other $J^{PC}$ channels and an extension to the vector mesons is natural. Moreover, the LFDA of vector mesons arises in the collinear factorization of weak $B$-decay amplitudes Beneke:2000wa and in diffractive vector-meson production Forshaw:2010py ; Forshaw:2012im . Within the combined framework of the Dyson-Schwinger equation (DSE) and the Bethe-Salpeter equation (BSE) Bashir:2012fs the LFDAs of the $\rho$ and $\phi$ mesons were calculated in Ref. Gao:2014bca and later the LFDAs of heavy quarkonia were obtained in Ref. Ding:2015rkn . In here, using a kindred DSE and BSE framework, we extend earlier work on $D$ and $D_{s}$ distribution amplitudes Serna:2020txe to those of their vector partners and make predictions for the twist-2 LFDA of the $D^{*}$ and $D_{s}^{*}$ mesons considering the two-quark Fock-state of their light front wave function. Along the way, we compute the LFDA of the $\rho$, $K^{*}$ $\phi$ and $J/\Psi$ mesons and compare them with the distribution amplitudes of other approaches Forshaw:2010py ; Forshaw:2012im ; Ball:2007zt ; Boyle:2008nj ; Hua:2020gnw ; Ding:2015rkn .

A vector meson with total momentum $P$ and mass $m_{V}$, $P^{2}=-m_{V}^{2}$, made of a quark and an antiquark of flavors $f$ and $g$ is described by four twist-two distribution amplitudes, though only two of them are independent at leading twist as a consequence of a Wandzura-Wilczek type of relation Ball:2007zt . The two LFDAs we consider, $\phi^{\parallel}_{V}(x,\mu)$ and $\phi^{\perp}_{V}(x,\mu)$, describe the fraction of total momentum on the light front, $x=k^{+}/P^{+}=(k_{0}+k_{z})/(P_{0}+P_{z})$, carried by the quark in longitudinally and transversely polarized mesons, respectively. They can be extracted from the Bethe-Salpeter wave function, $\chi^{fg}_{V\nu}(k,P)$, with the following projections onto the light front Gao:2014bca ; Ding:2015rkn :

where $N_{c}=3$, $n=(0,0,1,i)$ is a light-like vector and $\bar{n}=\tfrac{1}{2}(0,0,-1,i)$ its conjugate with $n^{2}=\bar{n}^{2}=0$, $n\cdot P=-m_{V}$, $\bar{n}\cdot P=-m_{V}/2$ and $n\cdot\bar{n}=-1$.¹¹1We use Euclidean metric with the Dirac algebra: $\{\gamma_{\mu},\gamma_{\nu}\}=2\delta_{\mu\nu}$; $\gamma_{\mu}^{\dagger}=\gamma_{\mu}$; $\gamma_{5}=\gamma_{4}\gamma_{1}\gamma_{2}\gamma_{3}$, tr$[\gamma_{4}\gamma_{\mu}\gamma_{\nu}\gamma_{\rho}\gamma_{\sigma}]=-4\,\epsilon_{\mu\nu\rho\sigma}$; $\sigma_{\mu\nu}=(i/2)[\gamma_{\mu},\gamma_{\nu}]$; $a\cdot b=\sum_{i=1}^{4}a_{i}b_{i}$. A time-like vector $P_{\mu}$ satisfies $P^{2}<0$. In Eq. (2) the Dirac commutator $\sigma_{\mu\nu}$ is contracted with the tensor Lu:2021sgg ,

In Eqs. (1) and (2), $\chi^{fg}_{V\nu}(k,P)=S_{f}(k_{\eta})$ $\Gamma^{fg}_{V\nu}(k,P)S_{g}(k_{\bar{\eta}})$ is the projected wave function, where $\Gamma^{fg}_{V\nu}(k,P)$ denotes the Bethe-Salpeter amplitude (BSA) and $S_{f}(k_{\eta})$ and $S_{g}(k_{\bar{\eta}})$ are respectively the quark and antiquark propagators with momenta $k_{\eta}=k+\eta P$ and $k_{\bar{\eta}}=k-\bar{\eta}P$. The details of their calculation, solving numerically the DSE for the quarks of a given flavor and the BSE for a vector meson, in particular the $D$ and $D^{*}$ mesons, are provided elsewhere Serna:2020txe ; Mojica:2017tvh ; El-Bennich:2021ldv . The parameters $\eta+\bar{\eta}=1$ define momentum fractions and $\Lambda$ is an ultraviolet regularization mass-scale; no observables can depend on $\eta$, $\bar{\eta}$ and $\Lambda$ owing to Poincaré covariance. Furthermore, ${\cal Z}_{2}(\mu,\Lambda)$ is the wave-function renormalization constant and ${\cal Z}_{T}(\mu,\Lambda)$ is the tensor-vertex renormalisation constant of the quark. Both constants as well as $f^{\perp}_{V}$ depend on the renormalization scale $\mu$, whereas $f_{V}$ is renormalization-point independent and measures the strength of the $\rho^{0}\to e^{+}e^{-}$ decay amplitude.

The expressions for $\phi^{\parallel}_{V}(x,\mu)$ and $\phi^{\perp}_{V}(x,\mu)$ in Eqs. (1) and (2) are not amenable to straightforward numerical integration. Instead, one computes Mellin moments Chang:2013pq ,

from which one can reconstruct the distribution amplitudes on the domain $x\in[0,1]$. The BSA normalization ensures that $\langle x^{0}\rangle_{\parallel}=\langle x^{0}\rangle_{\perp}=1$ which in turn defines the vector and tensor decay constants, $f_{V}^{\parallel}$ and $f^{\perp}_{V}$.

Integrating both sides of Eqs. (1) and (2) and applying the Dirac-function property $\int_{0}^{1}x^{m}\delta(a-xb)dx=\frac{a^{m}}{b^{m+1}}\,\theta(b-a)$, leads to the expressions,

With this, we are in principle able to compute Mellin moments to arbitrary order $m$. We do so by employing the numerical solutions of the quark propagators for complex momenta defined by the parabolas, $k_{\eta}^{2}=k^{2}-\eta^{2}m^{2}_{V}+2i\eta\,m_{V}|k|z_{k}$ and $k_{\bar{\eta}}^{2}=k^{2}-{\bar{\eta}}^{2}m^{2}_{V}-2i\bar{\eta}\,m_{V}|k|z_{k}$, where $z_{k}=k\cdot P/|k||P|$, $-1\leq z\leq+1$, and of the BSA of the vector mesons El-Bennich:2021ldv . That is, other than in Ref. Serna:2020txe , we do not rely on complex-conjugate pole parametrizations of the propagators nor on Nakanishi representations of the BSA, as the latter introduce ambiguities when fitted to numerical solutions. However, direct integration comes at the price that we can only access moments up to $m_{\mathrm{max}}=4-6$, as the numerical error of the integral becomes significant for larger moments. These moments, though, are sufficient to reconstruct the desired LFDA.

We proceed as in Refs. Chang:2013pq ; Shi:2015esa ; Serna:2020txe ; Gao:2014bca ; Ding:2015rkn and in the case of the light vector mesons we use an expansion in terms of Gegenbauer moments $C_{n}^{\alpha}(2x-1)$, which form a complete orthonormal set on $x\in[0,1]$ with respect to the measure $[x(1-x)]^{\alpha-1/2}$, in order to reconstruct their two independent twist-two LFDAs ($\bar{x}=1-x$):

This expansion is employed for neutral mesons as well as for flavored mesons, which are not $C$-parity eigenstates. In case of the former, the odd components $a_{n}$ vanish. In fitting the calculated moments in Eqs. (6) and (7), we consider, besides the coefficients $a_{n}$, the power $\alpha$ itself a parameter rather than projecting on the $\alpha=3/2$ basis. This allows to limit the expansion to $N=2$ and considerably simplifies the fits discussed below Chang:2013pq . The normalization is obtained as,

The heavy vector mesons, i.e. the $D^{*}$, $D^{*}_{s}$ and $J/\psi$, are parametrized with a different expression:

This functional form is more appropriate for a distribution amplitude with a convex-concave-convex functional behavior that tends to a $\delta$-function in the infinite heavy quark limit, as the use of an expansion, such as in Eq. (8), leaves one no choice but to retain a large number of Gegenbauer moments. A very similar functional expression is also found when the Nakanishi weight function is extracted from the quarkonia’s Bethe-Salpeter wave function Gao:2016jka . The normalization is given by Serna:2021xnr ,

in which the error function is defined as: $\operatorname{Erf}(x)=\frac{2}{\sqrt{\pi}}\int^{x}_{0}dt\,e^{t^{2}}$.

We thus reconstruct the vector LFDAs by minimizing the sum,

where the moments $\langle x^{m}\rangle^{\textrm{rec.}}_{\parallel,\perp}$ are calculated using Eqs. (4) and (5) and the expansion in either Eq. (8) or Eq. (10), whereas $\langle x^{m}\rangle_{\parallel,\perp}$ denotes the moments in Eqs. (6) and (7). It is useful to contrast our predictions for the longitudinal and transverse LFDAs with those obtained using other approaches, namely with lattice QCD (LQCD) Boyle:2008nj ; Hua:2020gnw , QCD sum rules (QCDSR) Ball:2007zt and with earlier calculations in the DSE-BSE framework (DSE) Gao:2014bca . In order to do so we also compute the moments,

in terms of the difference of momentum fractions, $\xi=x-(1-x)=2x-1$.

We begin with the light vector mesons and determine the coefficients $a_{n}^{\parallel,\perp}$ of their Gegenbauer expansion via a least-square fit of $\epsilon_{\parallel,\perp}$ (12) with the four moments $\langle x\rangle,\langle x^{2}\rangle,\langle x^{3}\rangle,\langle x^{4}\rangle$. We report their values and those of the corresponding $a_{n}^{\parallel,\perp}$ of the $\rho$, $\phi$ and $K^{*}$ mesons in Table 1 and compare the moments $\langle\xi^{2m}\rangle_{\parallel,\perp}$ (13) with other results in Table 2.

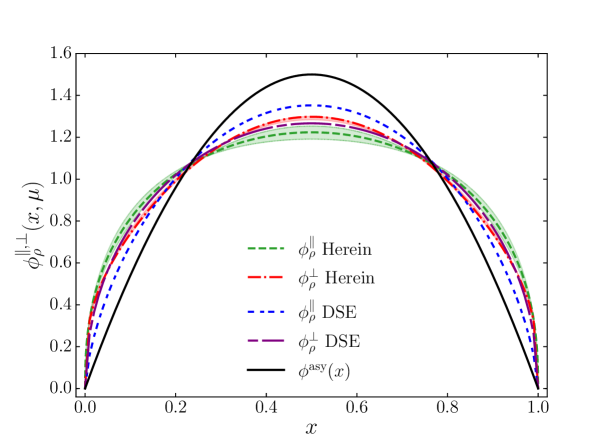
The LFDAs for the $\rho$ and $\phi$ mesons are compared in Figure 1 with the prediction of a DSE-based calculation and the LDFA reconstructed with moments from LQCD, respectively. We infer that the distributions follow the expected pattern: both LFDAs are symmetric about the midpoint, $x=1/2$. However, the $\phi_{\rho}^{\parallel,\perp}(x,\mu)$ distributions are broad while $\phi_{\phi}^{\parallel,\perp}(x,\mu)$ tend to the asymptotic form $\phi(x)\stackrel{{\scriptstyle\mu\to\infty}}{{=}}6x\bar{x}$. In addition, we observe that $\phi^{\parallel}_{\rho}(x,\mu)$ is slightly broader than $\phi^{\perp}_{\rho}(x,\mu)$, the origin of which are the different values of $a^{\parallel}_{2}$ and $a^{\perp}_{2}$ in Table 1. It appears from Table 2 that our calculated $\langle\xi^{2m}\rangle_{\parallel}$ moments for the $\rho$ meson are overall about 11% larger, whereas the values for $\langle\xi^{2m}\rangle_{\perp}$ are in very good agreement with those of Ref. Gao:2014bca and the HERA fit Forshaw:2010py ; Forshaw:2012im .

In the case of the $\phi$-meson, we note that $\phi^{\parallel}_{\phi}(x,\mu)\approx\phi^{\perp}_{\phi}(x,\mu)$ since $a^{\parallel}_{2}\approx a^{\perp}_{2}$ and $\alpha^{\parallel}\approx\alpha^{\perp}$. We remark that our results for $\phi_{\phi}^{\parallel,\perp}(x,\mu)$ differ from those in Ref. Gao:2014bca as can be inferred from Fig. 1. The reason for this, despite a like-minded BSE approach, is that we use a larger strange-quark mass, $m_{s}=166$ MeV at $\mu=2$ GeV. With a lower value of $m_{s}\approx 100$ MeV we find similar distributions as in Ref. Gao:2014bca . However, we prefer to renormalize the DSE with a larger strange mass as it results in a more consistent description of the $K$, $K^{*}$ and $\phi$ mesons.

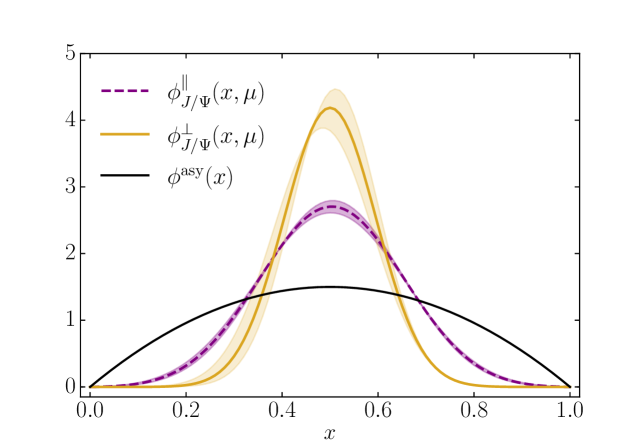
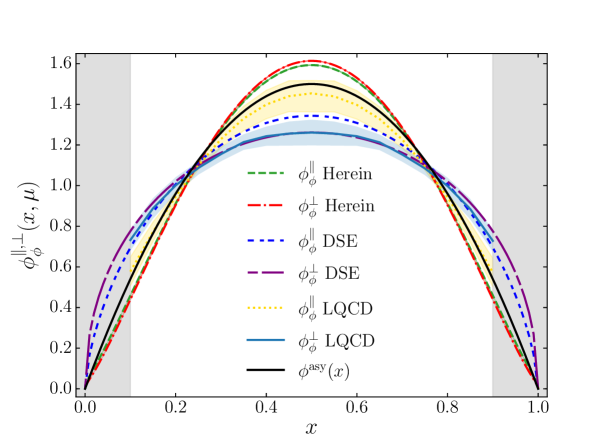
We now turn our attention to the $K^{*}$ and present the longitudinal and transverse LFDAs in Figure 2 where we juxtapose them with predictions from LQCD and QCDSR. Notably, the longitudinal distribution is a concave, nearly symmetric function of $x$, much broader than the asymptotic form, which is a consequence of the smallness of the $a^{\parallel}_{1}$ coefficient. The transverse LFDA, on the other hand, is asymmetric around the midpoint and its maximum is located at $x=0.78$, which clearly indicates SU(3) flavor symmetry breaking and that the strange valence quark carries a larger amount of meson momentum. The asymmetric shape is due to the similarity of the Gegenbauer coefficients, $a^{\perp}_{1}\approx a^{\perp}_{2}$ whereas $a^{\parallel}_{1}\ll a^{\parallel}_{2}$, see Table 1. This is in agreement with a recent calculation in LQCD, though in that study $\phi^{\parallel}_{K^{*}}(x,\mu)$ tends toward the asymptotic distribution Hua:2020gnw . In contrast to these findings, QCDSR predicts $\phi^{\parallel}_{K^{*}}(x,\mu)\approx\phi^{\perp}_{K^{*}}(x,\mu)$ Ball:2007zt .

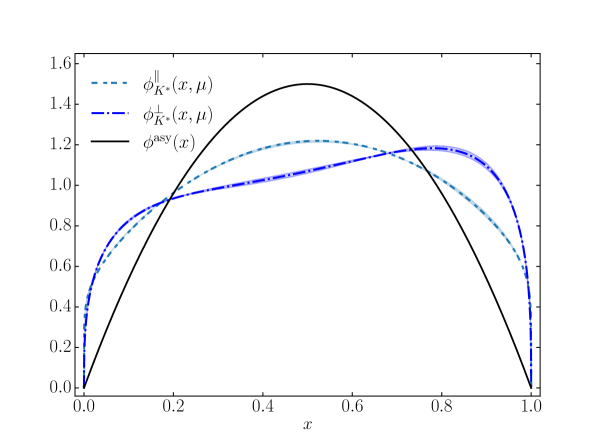
As we noted earlier, the heavier vector charmonium and charmed mesons require a modified description of their LFDA (10) to fit the moments. We report these moments, $\langle x^{m}\rangle_{\parallel}$ and $\langle x^{m}\rangle_{\perp}$, for the $J/\Psi$, $D^{*}$ and $D^{*}_{s}$ in Table 3. The distributions $\phi^{\parallel}_{J/\Psi}(x,\mu)$ and $\phi^{\perp}_{J/\Psi}(x,\mu)$ we then reconstruct are plotted in Figure 3. They are reminiscent of their pseudoscalar counterpart, i.e. the LFDA of the $\eta_{c}$, which exhibits the same convex-concave-convex functional behavior and is more sharply peaked than the asymptotic LFDA Serna:2020txe . It turns out that the longitudinal distribution is broader and less localized as a function of $x$ than the transverse distribution, an observation also made in Ref. Ding:2015rkn .

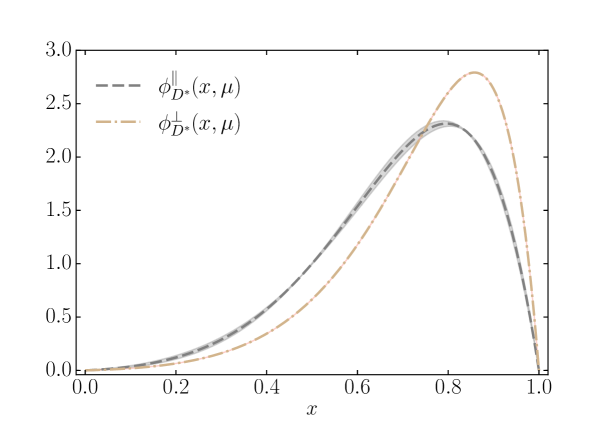
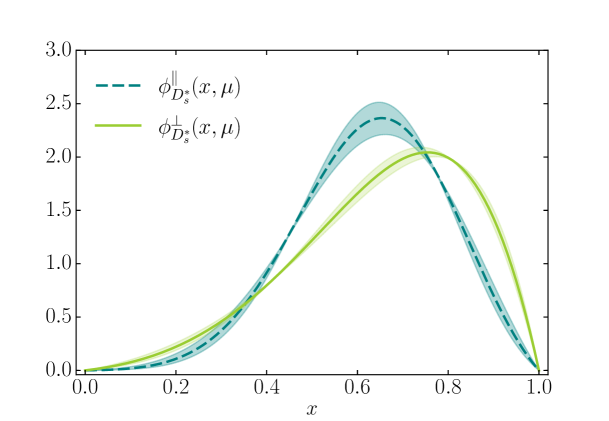
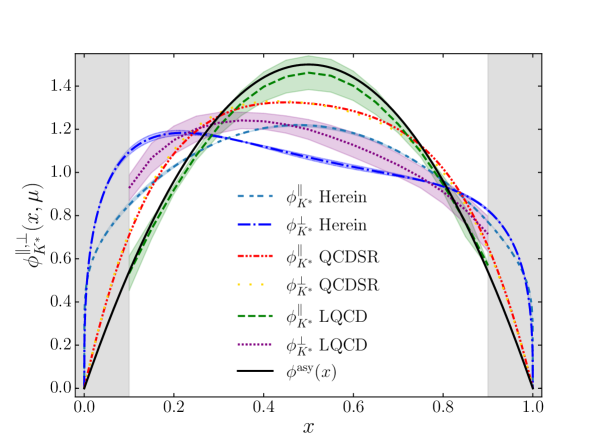
We conclude this section with a first prediction of the $D^{*}$ and $D_{s}^{*}$ meson distribution amplitudes which we compute with the projections in Eqs. (1) and (2) of the Bethe-Salpeter wave functions. The latter are taken from Ref. El-Bennich:2021ldv ; see Table 4 therein for the corresponding masses and weak decay constants. The distributions we reconstruct from $\langle x^{m}\rangle_{\parallel}$ and $\langle x^{m}\rangle_{\perp}$ listed in Table 3 are shown in Fig. 4. Clearly, in both cases the LFDAs are asymmetric and $\phi^{\parallel}_{D^{*}}(x,\mu)$ and $\phi^{\perp}_{D^{*}}(x,\mu)$ peak at about $x\approx 0.8-0.85$, while $\phi^{\parallel}_{D^{*}_{s}}(x,\mu)$ and $\phi^{\perp}_{D^{*}_{s}}(x,\mu)$ reach their maximum in the range $x\approx 0.65-0.8$.

This is readily interpreted as the charm quark carrying most of the light-front momentum in the $D^{*}$ meson, but less so in the $D^{*}_{s}$ meson. Interestingly, the transverse distributions are more asymmetric and the charm seems to carry a larger fraction of the meson momentum than in the longitudinal distribution. Arguably, this observation generalizes our results for the $K^{*}$, where the much smaller mass difference between the strange and up quarks leads to an almost symmetric form of $\phi^{\parallel}_{K^{*}}(x,\mu)$ and to a broad yet asymmetric function $\phi^{\perp}_{K^{*}}(x,\mu)$.

We extracted the LFDAs of the $\rho$, $\phi$, $K^{*}$, $J/\Psi$, $D^{*}$ and $D^{*}_{s}$ mesons from their Bethe-Salpeter wave functions, which we calculated in Refs. Mojica:2017tvh ; El-Bennich:2021ldv , with two projections onto the light front given by Eqs. (1) and (2). The transverse LFDA of the $\rho$ meson is in very good agreement with that obtained in a similar DSE-BSE approach Gao:2014bca and with the HERA fit Forshaw:2010py ; Forshaw:2012im , while our longitudinal moments, $\langle\xi^{m}\rangle_{\parallel}$, are generally about 11% larger than those in the literature.

We then presented the first calculation of the $\phi^{\parallel}_{K^{*}}(x,\mu)$ and $\phi^{\perp}_{K^{*}}(x,\mu)$ within the DSE-BSE framework and confirm the functional form found with LQCD simulations Hua:2020gnw : while the longitudinal distribution of the $K^{*}$ is almost symmetric about the midpoint $x=1/2$, the transverse distribution is broad and slanted, which we interpret as the strange quark carrying the larger fraction of the meson’s momentum. In the heavy meson sector, both LFDAs of the $J/\Psi$ are alike with that of the $\eta_{c}$, i.e. they are symmetric and narrow, yet not merely concave distributions.

Last not least, we extended our studies in Ref. Serna:2020txe to the longitudinal and transverse LFDAs of the $D^{*}$ and $D_{s}^{*}$ mesons, a first calculation of these distributions to our knowledge. Our findings are in line with observations for the pseudoscalar $D$ and $D_{s}$ mesons Serna:2020txe : the distributions are asymmetric and reach their maximum at large momentum fractions, namely $x\approx 0.65-0.85$. In other words, the charm quark is most likely to carry the largest fraction of the $D_{(s)}^{*}$-momentum, and this is even more so the case for the transverse distribution.

We remind that we provided all the analytic parametrizations of the LFDAs discussed in this work and the parameters are found in Tables (1) and (3). Therefore, the LFDAs of the $J/\Psi$ and $D^{*}_{(s)}$ mesons can readily be used in diffractive vector-meson production and are are of interest to the experimental program of the Electron-Ion Collider.

We acknowledge helpful discussions with Peter Tandy and Minghui Ding. B.E. and F.E.S. participate in the Brazilian network project INCT-Física Nuclear e Aplicações, no. 464898/2014-5. This work was supported by the São Paulo Research Foundation (FAPESP), grant no. 2018/20218-4, and by the National Council for Scientific and Technological Development (CNPq), grant no. 428003/2018-4. F.E.S. is a CAPES-PNPD postdoctoral fellow financed by grant no. 88882.314890/2013-01.