Bootstraps for Dynamic Panel Threshold Models
Abstract
This paper develops valid bootstrap inference methods for the dynamic short panel threshold regression. We demonstrate that the standard nonparametric bootstrap is inconsistent for the first-differenced generalized method of moments (GMM) estimator. The inconsistency arises from an -consistent non-normal asymptotic distribution of the threshold estimator when the true parameter lies in the continuity region of the parameter space, which stems from the rank deficiency of the approximate Jacobian of the sample moment conditions on the continuity region. To address this, we propose a grid bootstrap to construct confidence intervals for the threshold and a residual bootstrap to construct confidence intervals for the coefficients. They are shown to be valid regardless of the model’s continuity. Moreover, we establish a uniform validity for the grid bootstrap. A set of Monte Carlo experiments demonstrates that the proposed bootstraps improve upon the standard nonparametric bootstrap. An empirical application to a firm investment model illustrates our methods.
KEYWORDS: Dynamic Panel Threshold; Kink; Bootstrap; Endogeneity; Identification; Rank Deficiency; Uniformity.
JEL: C12, C23, C24
1 Introduction
Threshold regression models have been widely used by empirical researchers, which have been more fruitful because of their extensions to the panel data context. Estimation and inference methods for the threshold model in non-dynamic panels were developed by Hansen, 1999b and Wang, (2015). Dynamic panel threshold models were considered by Seo and Shin, (2016), which proposes the generalized method of moments (GMM) estimation by generalizing the Arellano and Bond, (1991) dynamic panel estimator. A latent group structure in the parameters of the panel threshold model was investigated by Miao et al., 2020b .
Applications of the panel threshold models cover numerous topics in economics. The effect of debt on economic growth is a well-known example that has been analyzed using the panel threshold models, e.g., Adam and Bevan, (2005), Cecchetti et al., (2011) and Chudik et al., (2017). Another example is the threshold effect of inflation on economic growth such as the works by Khan and Senhadji, (2001), Rousseau and Wachtel, (2002), Bick, (2010), and Kremer et al., (2013). The benefit of foreign direct investment to productivity growth that depends on the regime determined by absorptive capacity is studied by Girma, (2005) using firm-level panel data.
It is common practice to make inference in threshold regression models based on an assumption about whether the model is continuous or not. Continuous threshold models that have kinks at the tipping points have received active research attention, e.g., Hansen, (2017); Kim et al., (2019) and Yang et al., (2020). In the literature, kink threshold models are analyzed for estimators that impose the continuity restriction as in Chan and Tsay, (1998), Hansen, (2017), and Zhang et al., (2017). On the other hand, unrestricted estimators are commonly used for discontinuous threshold models as in Hansen, (2000). However, Hidalgo et al., (2019) showed that the unrestricted least squares estimator possesses a different asymptotic property in the absence of discontinuity. Specifically, while the unrestricted model is not misspecified under continuity, failing to impose the restriction results in incorrect inference without proper care.
In the empirical literature, there has been mixed use of kink/discontinuous threshold models without much consideration of a possible specification error. Among the empirical examples referred to previously, Khan and Senhadji, (2001) use a continuous threshold model and impose continuity on their estimation procedure. They claim that the continuous model is desirable to prevent small changes in inflation rate from yielding different impacts around the threshold level. On the other hand, Bick, (2010) claims that the discontinuous threshold model is more appropriate for the same research question since overlooking a regime-dependent intercept can result in omitted variable bias. However, both of them do not provide econometric evidence that supports their choice of models.
For the dynamic panel threshold model, asymptotic normality of the GMM estimator is derived by Seo and Shin, (2016) under the fixed scheme. However, the asymptotic normality is valid only for the discontinuous models since it requires a full rank condition on the Jacobian of the population moment, which is violated in continuous models. Although the continuity-restricted estimator described in Kim et al., (2019) is asymptotically normal, it may be problematic since empirical researchers often do not agree about whether their threshold models should have a kink or a jump at the threshold as in Khan and Senhadji, (2001) and Bick, (2010). Therefore, we are focusing on the unrestricted GMM estimator and bootstrap inference methods which do not require any pretest on continuity or prior knowledge about continuity of true models.
We first show that when the true model is continuous, the asymptotic normality of the unrestricted GMM estimator breaks down and the convergence rate of the threshold estimator becomes -rate, which is slower than the standard -rate. Moreover, the standard nonparametric bootstrap is inconsistent in this case because the Jacobian from the bootstrap distribution does not degenerate fast enough due to the slow convergence rate of the threshold estimator.
We propose two different bootstrap methods to obtain confidence intervals for the parameters that are consistent regardless of whether the true model is continuous or not. One is for the threshold location, and the other is for the coefficients. The two bootstrap methods achieve the consistency irrespective of the continuity of the model by adaptively setting the recentering parameter at the bootstrap for GMM introduced by Hall and Horowitz, (1996). This means that our bootstrap moment function achieves zero not at the sample estimator but at the parameter values that we propose. In the bootstrap for the threshold location, we employ a grid bootstrap to fix the recentering parameter. The grid bootstrap was originally proposed by Hansen, 1999a for inference on an autoregressive parameter and applies the test inversion principle. In case of the bootstrap for the coefficients, the recentering parameter is set to adjust the unrestricted estimator by a data driven criterion on the model’s continuity. We also introduce a bootstrap test of model continuity.
Furthermore, we establish the uniform validity of the grid bootstrap for the unknown continuity (or discontinuity) of the threshold model. The importance of uniform validity is well recognized in the literature, notably in the works of Mikusheva, (2007), Andrews and Guggenberger, (2009), and Romano and Shaikh, (2012), among others, who have studied the uniformity of resampling procedures. In particular, Mikusheva, (2007) showed the uniform validity of the grid bootstrap for linear autoregressive models. Our work extends this advantage of the grid bootstrap to a different class of nonstandard inference problems involving continuity of the model.
A set of Monte Carlo simulations demonstrates that the grid bootstrap performs favorably for inference on the threshold location, not only when the model is continuous but also when it includes a jump for various jump sizes. However, inference on the coefficients turns out to be more challenging. Bootstrap confidence intervals for the coefficient, based on percentiles of bootstrap distributions, tend to exhibit severe undercoverage. Nevertheless, our residual bootstrap method improves upon the standard nonparametric bootstrap in both cases.
We apply our inference methods to the dynamic firm investment model, whose static version has been studied by Fazzari et al., (1988) or Hansen, 1999b . It takes financial constraints into account via the threshold effect to determine a firm’s investment decision.
In the literature, Dovonon and Renault, (2013) and Dovonon and Hall, (2018) also deal with the degeneracy of the Jacobian in the context of the common conditional heteroskedasticity testing problem. And a bootstrap based test for the common conditional heteroskedasticity feature was proposed by Dovonon and Goncalves, (2017). However, their works do not deal with a discontinuous criterion function and their null hypothesis of interest always induces the degeneracy of the first-order derivative. That is, they are only concerned with a hypothesis testing and do not consider the confidence intervals. So, they do not have to address the uncertainty associated with the potential degeneracy of the Jacobian.
Meanwhile, there is also a substantial body of literature on singularity-robust inference such as Andrews and Cheng, (2012, 2014) and Han and McCloskey, (2019), among many others. They are motivated by weak or non-identification problems, where models are not point identified. In contrast, we focus on the inference problem that does not involve identification failure even though the Jacobian of the moment restriction can become singular. Andrews and Guggenberger, (2019) study more general singular cases than non-identification, but their approach requires differentiability of sample moments for the subvector inference. Since our model exhibits discontinuity, the method of Andrews and Guggenberger, (2019) is not applicable.
This paper is organized as follows. Section 2 explains the dynamic panel threshold model. Section 3 presents the asymptotic distribution theories of the estimators and test statistics related to the threshold location and continuity. Section 4 proposes bootstrap methods. Section 5 reports Monte Carlo simulation results. Section 6 contains an empirical application. Section 7 concludes. The mathematical proofs and technical details are left to the Appendix.
2 Dynamic Panel Threshold Model
We consider the dynamic panel threshold model,
| (1) |
where , , and is a regressor vector that includes and . The threshold variable is allowed to be endogenous and is the last element of .111Our analysis still holds if researchers have two sets of regressors and such that where is an element of . However, this paper sticks to the current form to keep the exposition simple. Then, we partition and write .
When consists of the lagged dependent variables, the model becomes the well-known self-exciting threshold autoregressive (TAR) model popularized by Chan and Tong, (1985). The static version where the lagged dependent variables are excluded from was considered by Hansen, 1999b , while the current dynamic model was studied by Seo and Shin, (2016).
The parameter denotes the threshold location, where is a compact set in , and denotes the collection of coefficients. Let denote the vector of all the parameters. The fixed effect is constant across time for each individual in the panel data. It is not identified but is eliminated after first-differencing for the GMM estimation. The idiosyncratic error is independent across individuals.
For the estimation, we use the GMM after the first-difference transformation
| (2) |
where
| (3) |
Let denote a set of instrumental variables at time such that becomes a zero vector, which may include lagged dependent variables and certain lagged variables of covariates and/or , depending on the assumptions regarding exogeneity of those variables.
Then, we can define a vector of moment functions for the GMM estimation,
| (4) |
where and is the earliest period that the regressor and instrument can be defined. For example, when and . Denote the population moment by and the sample moment by
We write instead of for simplicity of notations.
We consider the two-stage GMM estimation of the dynamic panel threshold model. In the first stage, we get an initial estimate by to compute a weight matrix
and obtain the second stage estimator
where . Seo and Shin, (2016) proposed averaging of a class of GMM estimators that are constructed from randomized first stage estimators. We do not pursue the averaging since our primary goal is the bootstrap inference.
In practice, the grid search algorithm is employed to compute the estimates. Note that when is given, can be easily computed because the problem becomes the estimation of the linear dynamic panel model. Then, minimizes the profiled criterion over the grid of .
Let denote the true parameter value that lies in the interior of . For the point identification of , should hold if and only if , where . Let
and . Additionally, define , , , , , and . We write , and instead of , and , respectively, for simplicity of notation. The identification condition is stated in Theorem 1 that follows.
Theorem 1.
Let the following two conditions hold:
(i) The matrix is of full column rank.
(ii) For any , is not in the column space of .
Then, is a unique solution to .
Theorem 1 (i) is the identification condition for the coefficients once the true threshold location is identified. This means that instruments should be relevant to the first-differenced regressors appearing in when .
Theorem 1 (ii) is for the identification of the threshold location, which excludes the possibility of . In the standard GMM problem, it is usually assumed that the Jacobian of at is of full column rank for both the point identification and the asymptotic normality of the GMM estimator. The condition (ii) does not require the full rank condition on the Jacobian, which is related to the presence of a jump in the threshold model, and thus it generalizes the identification conditions in Seo and Shin, (2016). When the model is continuous and has a kink at the threshold location, the last column of the Jacobian matrix, which is the first-order derivative with respect to at the true parameter, becomes a zero vector. This degeneracy does not violate the condition (ii), but it fails the asymptotic normality of the standard GMM estimator, which relies on the linearization of near as in Newey and McFadden, (1994).
To define the continuity, recall that is the last element of such that . Accordingly, partition , where and , and . Hence, is the change in the coefficient of the threshold variable when the threshold variable surpasses the tipping point. Likewise, and are the changes in the coefficients for the other regressors, , and the intercept, respectively. The continuity of the dynamic panel threshold model is formally given in Definition 1.
Definition 1.
Let . A dynamic panel threshold model is continuous with respect to the threshold variable if and . Otherwise, it is discontinuous at the threshold location.
Note that this definition of continuity requires that ; otherwise, .
The rank of the first-order derivative matrix, say , of at is crucial to the standard asymptotic normality of the GMM estimator. Let denote the first-order derivative of with respect to at . Then,
| (5) |
where the conditional expectation and the density function of are assumed to exist. The derivation of is provided in the proof of Lemma D.1. Note that the first-order derivative of with respect to at is . The linear independence of from the other columns in is required for the standard linear approximation
Recall that the vector can be written as the product of the matrix and the vector , (5), and the first and last columns of are linearly dependent since for all due to the conditioning. Then, the standard rank condition on the first derivative matrix can follow from a more primitive rank condition on , that is, the linear independence of all the columns in and all but the last column of , for the discontinuous case. Even if the primitive condition is met, however, the continuity restriction makes since for , which leads to degeneracy of .
When the rank condition fails due to the continuity, the expansion becomes
where
| (6) |
The detailed derivation is given in the proof of Lemma D.1. It is worth noting that is identical to the first column of up to a constant multiple. Then, the rank condition on is implied by the rank condition on . Thus, the rank condition on can be viewed as a sufficient condition for both Assumptions LK and LJ in the next section, apart from the continuity restriction on . Next section formalizes this discussion and presents the asymptotic distribution of the GMM estimator under the continuity.
3 Asymptotic theory
This section considers the asymptotic analysis when is fixed, the data are independent and identically distributed across , and . Specifically, the data for each individual is determined by the realization of , where denotes the initial value. We make the following assumptions.
Assumption G.
The parameter space is compact and . is of full column rank, and is not in the column space of for any . is positive definite. , , and are finite for all .
Assumption D.
For all , (i) has a continuous distribution and a bounded density , which is continuously differentiable at and . (ii) and are continuous on and continuously differentiable at .
Assumption LK.
has full column rank.
Assumptions G and D are similar to Assumptions 1 and 2 in Seo and Shin, (2016) except for the differentiability conditions in D which allow the second-order derivative of the population moment to be defined. Since the regressors include lagged dependent variables, G requires the individual fixed effects and initial values to have finite fourth moments, too. The assumption also includes the conditions in Theorem 1. LK is a rank condition for a nondegenerate asymptotic distribution when the underlying model is continuous. This condition may be viewed as less restrictive than the standard rank assumption as discussed in the preceding section where and are defined. For easy reference, we restate the standard full rank assumption for the asymptotic normality of the GMM estimator for the discontinuous threshold regression below.
Assumption LJ.
has full column rank.
In a simple model, where , LK is equivalent to LJ because while , where is the first column of in (5).
Theorem 2 below establishes the asymptotic distribution of the GMM estimator when the dynamic panel threshold model is continuous.
Theorem 2.
We observe that the convergence rate of is , which is slower than the standard -rate. Meanwhile, Seo and Shin, (2016) show the -convergence rate for when the model is discontinuous. Intuitively, it would be more difficult to detect the precise threshold location when there is a kink than when there is a jump at the tipping point. More technically, when the threshold model is discontinuous and the Jacobian is not singular, the limit of the GMM objective function admits a quadratic approximation with respect to at the true value, while the limit admits a quartic approximation for the continuous model. Hence, the limit objective function becomes flatter in at the true value resulting in the slower convergence rate. Hidalgo et al., (2019) also showed in the least squares context that when the model is continuous, the convergence rate of the threshold estimator slows down to , while it is superconsistent -rate when the model is discontinuous.
Moreover, we can observe that the asymptotic distribution of is also shifting to a non-normal distribution. Hence, standard inference methods based on the asymptotic normality become invalid for the continuous dynamic panel threshold model.
The asymptotic distribution of the GMM estimator is identical to the distribution reported in Theorem 1 (b) in Dovonon and Hall, (2018), which studies a smooth GMM problem with the degeneracy of the Jacobian. Theorem 2 shows that even though the criterion of our threshold model is discontinuous with respect to the parameter , the same asymptotic distribution as that of Dovonon and Hall, (2018) appears.
The censored normal distribution also appears in Andrews, (2002) which studies the estimation of a parameter on a boundary. Heuristically, because our analysis depends on the second-order derivative of for the local polynomial expansion of near , only the asymptotic distribution of can be derived. Since should be nonnegative, the asymptotic censored normal distribution appears as in Andrews, (2002). Meanwhile, Dovonon and Goncalves, (2017) show that the standard nonparametric bootstrap becomes invalid when the Jacobian degenerates. To address this issue, we propose different bootstrap methods in Section 4 for the inference of the parameters.
The asymptotic distribution in Theorem 2 can be used for parameter inference when the true model is continuous, but the estimator is obtained without imposing the continuity restriction. As discussed in Seo and Shin, (2016), and can be consistently estimated, while can be nonparametrically estimated similarly to . It is then straightforward to simulate the limit distribution from Theorem 2 by generating random numbers for and . However, there are several drawbacks to that approach, and hence we do not recommend it. First, empirical researchers might construct confidence intervals based on Theorem 2 when they cannot reject the continuity. However, Leeb and Pötscher, (2005) show that confidence intervals after model selection are subject to size-distortion. Second, even if the true model is known to be continuous, the continuity-restricted estimator explained in Kim et al., (2019) is more efficient and asymptotically normal. Therefore, using the continuity-restricted estimator for estimation and inference is preferable. Finally, the nonparametric estimation of requires a tuning parameter and has a slower convergence rate.
Seo and Shin, (2016) derived the asymptotic distribution of the GMM estimator and propose an inference method when the underlying model is discontinuous. When the true model is discontinuous and Assumptions G, D, and LJ hold,
can be estimated by . Note that , and can be estimated by , while the estimation of involves nonparametric estimation of the conditional means and densities. See section 4 of Seo and Shin, (2016) for more details. Note that diverges when the model is continuous since the last column of converges to a zero vector when it is consistent. This paper does not analyze the issue and leaves it for future research.
3.1 Testing for threshold value
Since the asymptotic distribution of the threshold estimator is not standard, we consider the GMM distance test introduced by Newey and West, (1987) for a hypothesis on the location of the threshold. Let the test statistic for the threshold location at be
and let denote the chi-square distribution with 1 degree of freedom.
Theorem 3.
(iii) If , then for any , .
Theorem 3 (i) presents the asymptotic distribution of the distance statistic under the continuity. Due to the censoring, the asymptotic distribution becomes a mixture of the distribution with weight 1/2 and zero with weight 1/2. This type of distribution also arises in the context of testing parameters on a boundary; see e.g., Andrews, (2001).
Meanwhile, the chi-square limit in Theorem 3 (ii) extends Newey and West, (1987) for a discontinuous moment function. Seo and Shin, (2016) did not study the distance statistic.
Theorem 3 (iii) shows that the GMM distance test for the threshold location is consistent. It also serves as the consistency of a bootstrap test together with Theorem 5 since the bootstrap statistic is stochastically bounded whether or not the threshold location is true.
Since the limit distribution depends on the continuity of the model, we introduce a bootstrap in Section 4.1, which is valid regardless of the model continuity. Furthermore, Appendix I establishes the uniform validity of the bootstrap inference for the threshold location under some simplifying assumptions.
3.2 Testing continuity
We propose a test for the continuity of the threshold model, similar to the approach used by Gonzalo and Wolf, (2005) or Hidalgo et al., (2023) in the threshold regression literature. While empirical researchers may employ the test to select a model, we utilize the test to modify the standard nonparametric bootstrap to make the bootstrap valid irrespective of the model continuity. Details of the use of the continuity test statistic in the bootstrap method are explained in Section 4.2.
The continuity hypothesis is a joint hypothesis. We employ the GMM distance test. Let be the continuity-restricted estimator. The GMM distance test statistic is
Theorem 4.
(i) When the true model is continuous and Assumptions G, D, and LK hold,
where , , , , , , and are independent, , and
(ii) If the model is discontinuous, then for any and .
While the limit distribution in Theorem 4 (i) is non-standard, it can be simulated to obtain critical values for the test using consistent plug-in sample analogue estimators, e.g., , , , etc. Another way to obtain the critical values is via a bootstrap method, which will be introduced in Section 4.3.
Theorem 4 (ii) shows that the continuity test is consistent. It also implies the consistency of the bootstrap test together with Theorem 7, which shows that the bootstrap test statistic is stochastically bounded even when the true model is not continuous. The divergence rate of , which is faster than for any , is exploited to modify the standard nonparametric bootstrap for the coefficients as detailed in Section 4.2.
4 Bootstrap
As usual, the superscript “*” denotes the bootstrap quantities or the convergence of bootstrap statistics under the bootstrap probability law conditional on the original sample. For example, denotes the expectation with respect to the bootstrap probability law conditional on the data. “, in ” denotes the distributional convergence of bootstrap statistics under the bootstrap probability law with probability approaching one. We write “, in ” if a sequence is stochastically bounded under the bootstrap probability law with probability approaching one. More details are written in Section B.1. Let denote the empirical quantile of a bootstrap statistic .
This section introduces three different bootstrap schemes. The first bootstrap is for constructing bootstrap confidence interval(CI)s for the threshold, while the second bootstrap is for constructing bootstrap CIs for the coefficients. Both methods aim to provide valid inferences, regardless of whether the model is continuous or not. The third bootstrap is for testing continuity of the threshold model. The three bootstrap methods can be represented by means of Algorithm 1 with suitable choices of .
In step 1, we resample the regressors, the instruments, and the residuals jointly to maintain the dependence among them, unlike in the usual residual bootstrap. See e.g., Giannerini et al., (2024) for the description of the standard residual bootstrap, which resamples the residuals only, and the wild bootstrap for the testing of linearity in the threshold regression. There could be other ways of resampling not mentioned here and we do not attempt to decide which is the best here.
The parameter is used in step 2 of Algorithm 1 to generate the dependent variables in the bootstrap samples. In step 4, recentering of the bootstrap sample moment is done by subtracting . Note that the expectation of by the bootstrap probability law conditional on the data becomes zero when due to the recentering, which can be easily checked from the following equations: and for .
A different choice of leads to a different bootstrap. For example, if , then the bootstrap becomes the standard nonparametric bootstrap in Hall and Horowitz, (1996) because holds true for and in step 2. Note that, for not equal to , step 2 of Algorithm 1 generates ’s that are generally different from ’s. The following subsections detail three different choices of for three different inference problems.
4.1 Grid bootstrap for threshold location
To construct CIs for the threshold location, we propose to employ the grid bootstrap method introduced by Hansen, 1999a for autoregressive models. Let be a grid of the candidate thresholds. The grid bootstrap constructs the confidence set by inverting the bootstrap threshold location tests over . Specifically, a sequence of hypothesis tests for the hypothesized threshold locations in are performed by the bootstrap that imposes the null to generate bootstrap samples.
The null imposed bootstrap at a point can be implemented by setting in Algorithm 1, and the bootstrap test statistic is
The null hypothesis is rejected at size if . Consequently, after running the null imposed bootstrap for each point in , we can construct the % confidence set of by
| (7) |
Note that the confidence set is not necessarily a connected set, even though researchers can convexify the set to get a connected CI. The CI does not become an empty set because while . The consistency of the grid bootstrap method is implied by Theorem 5 that follows.
Theorem 5 (i) and (ii) show that the limit distribution of the bootstrap test statistic, conditional on the data, is identical to that of the sample test statistic regardless of the continuity of the true model. Therefore, the CI for the threshold location by the grid bootstrap, (7), achieves an exact coverage rate for both continuous and discontinuous models asymptotically. Specifically, for both cases (i) and (ii). Theorem 5 (iii) says that the bootstrap test statistic is still stochastically bounded, conditionally on the data, under the alternatives. As Theorem 3 (iii) shows that the sample test statistic is stochastically unbounded under the alternatives, the grid bootstrap CI has power against the alternative threshold locations.
4.1.1 Uniform validity of grid bootstrap
We extend Theorem 5 to the uniform validity of the grid bootstrap to ensure its good finite sample performance when the model is nearly continuous. We establish the uniform validity for the following simplified specification for analytical tractability:
where and in this subsection.
This section briefly states the uniformity result of the grid bootstrap and gives heuristic justification. Our derivation follows Andrews et al., (2020). It is highly complicated and involves more technical conditions, which are stated in Appendix I.
Specifically, we establish in Theorem I.1 that
where is the probability law when the model is specified by and is the distribution of . The collection of probabilistic models includes both continuous and discontinuous threshold models. More detailed discussions of technical assumptions about are given in Appendix I.
For the uniformity analysis, we need to consider drifting sequences of true parameters such that and . Here, the distance between and is induced by a specific choice of norm that is explained in Appendix I. To show the uniform validity of the grid bootstrap CI, we need to verify that the limit distribution of conditional on the data is identical to the limit distribution of under all the above drifting sequences of models. Our analysis finds that the limit distribution of the threshold location test statistic under the true null, i.e., the limit distribution of , is determined by ; see Lemma I.1 for details. When , the limit distribution of is as described in Theorem 3 (i). In contrast, when , the limit distribution is the -distribution as in Theorem 3 (ii). When is finite and nonzero, then has a nonstandard limit distribution that depends on .
Therefore, if comprises a true parameter sequence of a bootstrap scheme, then should consistently estimate for the bootstrap statistics to exhibit the same asymptotic behavior as the sample statistics.
Note that under the grid bootstrap scheme, the bootstrap test statistic is drawn from the bootstrap that imposes the null threshold location . The true parameter of the bootstrap data generating process (dgp) is , where . The restricted estimator satisfies , as the problem becomes estimating a standard linear dynamic panel model, and hence . Therefore, conditionally converges to the limit distribution of , which leads to the uniform validity of the grid bootstrap confidence interval. In contrast, does not satisfy this property for some and the bootstrap building on may not be uniformly valid.
4.2 Residual bootstrap for coefficients
The bootstrap CIs for the coefficients can be obtained by applying Algorithm 1 with set as
| (8) |
where is the continuity-restricted estimator. is some estimated quantile, such as the th percentile, of the limit distribution of the continuity test statistic when the model is continuous. can be obtained either by methods in Section 3.2 or Section 4.3. Since if the true model is continuous, and if the model is discontinuous, the true parameter value for the bootstrap adapts to the model continuity.
After collecting the bootstrap estimators
we can construct the CIs for the coefficients using the percentiles of either or . Here, and are the th elements of and , respectively. The % CI for the th element of the coefficients, , can be constructed by
| (9) |
or
| (10) |
which leads to a symmetric CI. The validity of the residual bootstrap CI is implied by Theorem 6 that follows.
We make the following additional assumption to derive the limit distribution of the bootstrap estimator when the true model is discontinuous.
Assumption P.
The continuity-restricted estimator is .
The assumption holds if has full column rank for all . Details are explained in the comment after Lemma E.6.
Theorem 6.
The asymptotic distributions of the bootstrap estimators in Theorem 6, conditional on the data, match those of the sample estimators for both continuous and discontinuous cases. Therefore, the residual bootstrap CI becomes asymptotically valid in a pointwise sense, regardless of whether the model is continuous or discontinuous. We acknowledge that Theorem 6 does not guarantee the uniform validity of the bootstrap CI. The difficulty in establishing the uniform validity lies in analyzing asymptotic behaviors of and for drifting sequences of the true models. already exhibits an irregular limit distribution even in the pointwise setup, as shown in Theorem 4 (i). This paper does not provide a theoretical analysis regarding the uniformity of the residual bootstrap. Instead, we conduct Monte Carlo experiments for nearly continuous cases in Section 5 and leaves theoretical work on the uniformity of the bootstrap method to future research.
The key motivation for setting , the true parameter of the bootstrap dgp, by (8) is to make degenerate fast enough when the underlying model is continuous. The convergence rate of the unrestricted estimator to is not sufficiently fast. To see this, let the first-derivative of the population moment with respect to at be
| (11) |
for which we recall that and that under continuity. For the validity of a bootstrap method, the degeneracy of the Jacobian should be mimicked by the bootstrap dgp. In our residual bootstrap method, the Jacobian is . However, it is for the standard nonparametric bootstrap. This fails the standard nonparametric bootstrap. More formal treatment of the invalidity of the standard nonparametric bootstrap is given in Appendix F.
It is not difficult to check but not , which is directly implied by but not due to Theorem 2. Meanwhile, in our residual bootstrap method, and , which leads to . The exact formula for is provided in the comment of Lemma E.5.
According to the proof of Theorem 6 in Appendix B, is sufficient for the first-order asymptotic validity. This requirement is explicitly stated in the conditions of Lemma E.5. While our choice of decay rate for guarantees this condition, it remains an open question how fast must decay to ensure the uniform validity.
The idea of shrinking the first-order derivative in our bootstrap is closely related to other bootstrap methods developed for the case when asymptotic distributions of estimators are irregular. For example, Chatterjee and Lahiri, (2011) propose a bootstrap method for the lasso estimator, and Cavaliere et al., (2022) study bootstrap inference on the boundary of a parameter space. Both papers set up the model where the problem appears if the true parameter value is zero, and they obtain true parameters of bootstrap dgps by thresholding unrestricted estimators, i.e., , where converges to zero in a proper rate.
4.3 Bootstrap for testing continuity
The critical value for the continuity test introduced in Section 3.2 can also be obtained by bootstrapping. Recall that is the continuity-restricted estimator. By setting in Algorithm 1, and collecting the bootstrap test statistic
we can get the critical value using the empirical quantile of . To run the bootstrap continuity test at size , reject the continuity if , where is the empirical quantile of . The consistency of the bootstrap is implied by Theorem 7 that follows.
Theorem 7.
Assume that is obtained by Algorithm 1 with .
(i) When the true model is continuous and Assumptions G, D, and LK hold,
where the distributions of , , and are specified in Theorem 4.
(ii) When the model is discontinuous, then in .
Theorem 7 (i) shows that the limit distribution of , conditional on the data, is identical to that of under the null hypothesis. Moreover, Theorem 7 (ii) says that is still stochastically bounded, conditionally on the data, when the true model is discontinuous. As is shown to be stochastically unbounded under the alternative, according to Theorem 4 (ii), the bootstrap continuity test has power against the alternatives.
5 Monte Carlo results
This section executes Monte Carlo simulations to investigate finite sample performances of our bootstrap methods. The data is generated by
| (12) |
with , , , , , , , and . Note that (12) implies that the threshold variable is weakly exogenous. That is, for while for . Similar Monte Carlo results are obtained when the threshold variable is weakly endogenous, and they are reported in Appendix C.
To investigate how coverage rates of the CIs change depending on the continuity, we try different values of , which implies different degrees of (dis)continuity . If , then and the model is continuous. Otherwise, the model is discontinuous. As near continuous designs, we try and check if there is any poor performance of CIs. We generate samples of size and . The number of repetitions for the Monte Carlo simulations is 2000. Instruments used for the estimations are the lagged dependent variables that date back from period to period 1 and the lagged threshold variables from period to period 1, i.e., . The earliest period used for the estimation is , and the total number of the instruments becomes 24.
We begin with examining the finite sample coverage probabilities of bootstrap CIs for the threshold location. Specifically, the grid bootstrap CI (Grid-B) is compared with both percentile nonparametric bootstrap CI (NP-B) and symmetric percentile nonparametric bootstrap CI (NP-B(S)) that are defined as follows:
| (13) | ||||
| (14) |
The number of bootstrap repetitions is set at 500 for each bootstrap method.
Table 1 reports the coverage rates of 95% CIs for the threshold location. First, it shows that the bootstrap CI by NP-B is subject to severe undercoverage in all cases. This is the case even when , despite the theoretical validity of NP-B when the model is discontinuous. Meanwhile, NP-B(S) exhibits extreme over-coverage in all cases. The large discrepancy in the results between NP-B and NP-B(S) suggests that the distribution of the nonparametric bootstrap estimator is poorly behaved, undermining its reliability for inference. The large difference between symmetric and non-symmetric CIs also arises in the inference for the coefficients, which we analyze in more detail in Appendix C.
| n | 0 | 0.1 | 0.2 | 0.5 | 1 | |
| 400 | 0.992 | 0.995 | 0.993 | 0.988 | 0.966 | |
| Grid-B | 800 | 0.986 | 0.986 | 0.985 | 0.973 | 0.955 |
| 1600 | 0.988 | 0.987 | 0.988 | 0.979 | 0.959 | |
| 400 | 0.484 | 0.491 | 0.494 | 0.524 | 0.631 | |
| NP-B | 800 | 0.478 | 0.472 | 0.487 | 0.518 | 0.611 |
| 1600 | 0.471 | 0.468 | 0.476 | 0.521 | 0.642 | |
| 400 | 1.000 | 1.000 | 1.000 | 1.000 | 0.998 | |
| NP-B(S) | 800 | 1.000 | 1.000 | 1.000 | 0.999 | 0.994 |
| 1600 | 1.000 | 1.000 | 1.000 | 1.000 | 0.994 | |
On the other hand, Table 1 shows that Grid-B provides more reasonable coverage rates. It seems that a larger jump yields coverage rates closer to the nominal level as expected since it is easier to detect a bigger jump. As expected from the uniform validity of Grid-B against near continuity, coverage rates remain valid for all the parameter values, if somewhat over-coveraged near continuity or under smaller sample sizes.
Contrary to Grid-B, NP-B(S) exhibits higher coverage probabilities that are one or almost one for all cases. It indicates that NP-B(S) CIs are overly wide and non-informative. To investigate this further, we examine some power properties as reported in Table 2 below. It shows that NP-B(S) based tests for the threshold location are trivial for many parametrizations, specifically when the design is continuous or near-continuous or when the alternative is closer to the null. In contrast, Grid-B tests are more powerful, oftentime twice more powerful than NP-B(S) tests. Here, we report the power of the tests instead of the lengths of the bootstrap CIs due to computational burden associated with the grid bootstrap.
| Grid-B | NP-B(S) | ||||||||||
| c | n | 0 | 0.1 | 0.2 | 0.5 | 1 | 0 | 0.1 | 0.2 | 0.5 | 1 |
| 400 | 0.015 | 0.015 | 0.015 | 0.027 | 0.096 | 0.000 | 0.000 | 0.000 | 0.004 | 0.018 | |
| 0.10 | 800 | 0.011 | 0.014 | 0.015 | 0.038 | 0.112 | 0.000 | 0.000 | 0.000 | 0.004 | 0.017 |
| 1600 | 0.017 | 0.020 | 0.021 | 0.040 | 0.125 | 0.000 | 0.000 | 0.002 | 0.004 | 0.023 | |
| 400 | 0.020 | 0.030 | 0.042 | 0.100 | 0.281 | 0.002 | 0.004 | 0.009 | 0.043 | 0.135 | |
| 0.25 | 800 | 0.020 | 0.034 | 0.041 | 0.112 | 0.325 | 0.002 | 0.003 | 0.007 | 0.035 | 0.154 |
| 1600 | 0.029 | 0.034 | 0.048 | 0.126 | 0.351 | 0.002 | 0.006 | 0.007 | 0.044 | 0.152 | |
| 400 | 0.102 | 0.137 | 0.172 | 0.314 | 0.581 | 0.062 | 0.109 | 0.142 | 0.274 | 0.298 | |
| 0.50 | 800 | 0.114 | 0.162 | 0.207 | 0.362 | 0.632 | 0.078 | 0.117 | 0.169 | 0.310 | 0.327 |
| 1600 | 0.136 | 0.186 | 0.240 | 0.396 | 0.652 | 0.076 | 0.124 | 0.189 | 0.332 | 0.316 | |
Next, we turn to the coverage probabilities for the regression coefficients by different bootstrap CIs. Table 3 reports the coverage rates of bootstrap percentile CIs using the residual bootstrap (R-B), defined by (9), and the standard nonparametric bootstrap (NP-B), defined by
| (15) |
and in (8) is set as the 50th percentile of the bootstrap distribution of the test statistic under the null hypothesis that the model is continuous, using the bootstrap method explained in Section 4.3. Additional results on the coverage rates of the symmetric percentile CIs (NP-B(S) and R-B(S)) for the coefficients are reported in Appendix C.
As in the threshold inference case, the percentile CIs for the coefficients constructed using NP-B exhibit systematic undercoverage across all specifications and sample sizes. Even when , so that the model is discontinuous and the NP-B method is theoretically valid, the undercoverage remains severe. While the R-B method yields higher coverage rates than NP-B, they still fall short of the nominal 95% level. Moreover, as reported in Table 4, R-B results in wider average CI lengths compared to NP-B, partly accounting for its improved coverage.
Additional simulation results in Appendix C reveal highly asymmetric bootstrap distributions, which lead to one-sided inference failures because the bootstrap fails to reject the null when . These findings underscore the difficulty of reliable inference for the coefficients and . They echo similar concerns raised in the threshold regression literature; for instance, Hansen, (2000) documents comparable undercoverage issues for even when the threshold is estimated at a faster rate. A more comprehensive theoretical and methodological investigation is needed to address these challenges in future research.
| R-B | NP-B | ||||||||||
| n | |||||||||||
| 400 | 0.839 | 0.780 | 0.746 | 0.815 | 0.801 | 0.799 | 0.691 | 0.627 | 0.712 | 0.709 | |
| 0.0 | 800 | 0.837 | 0.790 | 0.721 | 0.807 | 0.806 | 0.790 | 0.723 | 0.607 | 0.725 | 0.716 |
| 1600 | 0.849 | 0.782 | 0.727 | 0.840 | 0.835 | 0.833 | 0.709 | 0.602 | 0.754 | 0.718 | |
| 400 | 0.837 | 0.784 | 0.749 | 0.813 | 0.799 | 0.794 | 0.697 | 0.624 | 0.706 | 0.708 | |
| 0.1 | 800 | 0.830 | 0.779 | 0.724 | 0.803 | 0.800 | 0.786 | 0.714 | 0.599 | 0.720 | 0.710 |
| 1600 | 0.853 | 0.787 | 0.727 | 0.840 | 0.829 | 0.827 | 0.700 | 0.598 | 0.760 | 0.719 | |
| 400 | 0.838 | 0.786 | 0.749 | 0.819 | 0.811 | 0.794 | 0.701 | 0.623 | 0.713 | 0.716 | |
| 0.2 | 800 | 0.833 | 0.776 | 0.720 | 0.803 | 0.794 | 0.784 | 0.707 | 0.585 | 0.718 | 0.712 |
| 1600 | 0.855 | 0.789 | 0.728 | 0.846 | 0.832 | 0.830 | 0.707 | 0.606 | 0.764 | 0.722 | |
| 400 | 0.836 | 0.775 | 0.739 | 0.820 | 0.802 | 0.787 | 0.703 | 0.601 | 0.718 | 0.724 | |
| 0.5 | 800 | 0.841 | 0.789 | 0.732 | 0.815 | 0.807 | 0.787 | 0.714 | 0.602 | 0.716 | 0.727 |
| 1600 | 0.843 | 0.799 | 0.728 | 0.826 | 0.834 | 0.815 | 0.717 | 0.595 | 0.753 | 0.737 | |
| 400 | 0.858 | 0.815 | 0.745 | 0.832 | 0.805 | 0.800 | 0.741 | 0.627 | 0.741 | 0.743 | |
| 1.0 | 800 | 0.858 | 0.827 | 0.749 | 0.846 | 0.820 | 0.808 | 0.731 | 0.620 | 0.741 | 0.738 |
| 1600 | 0.863 | 0.846 | 0.759 | 0.830 | 0.837 | 0.820 | 0.738 | 0.622 | 0.761 | 0.747 | |
| Ratios of average lengths of CIs: | ||||||
| R-B / NP-B | ||||||
| n | ||||||
| 400 | 1.076 | 1.091 | 1.099 | 1.074 | 1.046 | |
| 0.0 | 800 | 1.081 | 1.086 | 1.093 | 1.070 | 1.046 |
| 1600 | 1.088 | 1.100 | 1.111 | 1.083 | 1.057 | |
| 400 | 1.087 | 1.098 | 1.101 | 1.074 | 1.047 | |
| 0.1 | 800 | 1.080 | 1.082 | 1.090 | 1.075 | 1.043 |
| 1600 | 1.086 | 1.102 | 1.111 | 1.077 | 1.057 | |
| 400 | 1.080 | 1.088 | 1.097 | 1.074 | 1.047 | |
| 0.2 | 800 | 1.079 | 1.089 | 1.094 | 1.075 | 1.047 |
| 1600 | 1.085 | 1.100 | 1.106 | 1.077 | 1.054 | |
| 400 | 1.097 | 1.100 | 1.100 | 1.083 | 1.056 | |
| 0.5 | 800 | 1.083 | 1.095 | 1.089 | 1.076 | 1.051 |
| 1600 | 1.098 | 1.110 | 1.098 | 1.089 | 1.059 | |
| 400 | 1.164 | 1.159 | 1.084 | 1.114 | 1.074 | |
| 1.0 | 800 | 1.158 | 1.159 | 1.079 | 1.109 | 1.076 |
| 1600 | 1.158 | 1.177 | 1.084 | 1.109 | 1.079 | |
6 Empirical example
Our empirical example examines a firm’s investment decision model that incorporates financial constraints, as in Hansen, 1999b and Seo and Shin, (2016). In a perfect financial market, firms can borrow as much money as they need to finance their investment projects, regardless of their financial conditions. Therefore, the financial conditions of firms are irrelevant to their investment decisions. However, in an imperfect financial market, some firms may be restricted in their access to external financing. These firms are said to be financially constrained. Financially constrained firms are more sensitive to the availability of internal financing, as they cannot rely on external financing to fund their investment projects.
Fazzari et al., (1988) argue that firms’ investments are positively related to their cash flow if they are financially constrained, where those firms are identified by low dividend payments. Hansen, 1999b applies the threshold panel regression more systematically to show that a more positive relationship between investment and cash flow is present for firms with higher leverage.
Since there are multiple candidate measures of the financial constraint for the threshold variable, we compare the following three dynamic panel threshold models:
| (16) | ||||
| (17) | ||||
| (18) |
where . Here, is investment, is cash flow, is property, plant and equipment, and is return on assets. , and are normalized by total assets. We have two candidate threshold variables, and , which are leverage and Tobin’s Q, respectively. Choice of the regressors and threshold variables is based on previous works like Hansen, 1999b and Lang et al., (1996). Note that the regression model (18) is nested within (17) and it is closer to a continuous threshold model.
Unlike the previous works, we do not need to assume either continuity or discontinuity for valid inferences since the bootstrap methods in this paper are adaptive to each case. With an assumption that the regressors are predetermined, we use the variables dated one period before as instruments. Hence, the instruments include , , , added by or for each period.
We construct a balanced panel of 1459 U.S. firms, excluding finance and utility firms, from 2010 to 2019 available in Compustat. To deal with extreme values, we drop firms if any of their non-threshold variables’ values fall within the top or bottom 0.5% tails. Moreover, we exclude firms whose Tobin’s Q is larger than 5 for more than 5 years when the threshold variable is Tobin’s Q, leaving 1222 firms in the sample. Meanwhile, Strebulaev and Yang, (2013) claims that firms with large CEO ownership or CEO-friendly boards show persistent zero-leverage behavior. To prevent our threshold regression from capturing corporate governance characteristics rather than financial constraints, we exclude firms whose leverage is zero for more than half of the time periods when leverage is the threshold variable, leaving 1056 firms in the sample.
Table 5 reports the estimates and 95% CIs for (16) and (17), and Table 6 for (18). Figure 1 visualizes how the grid bootstrap CIs are obtained. The CIs for the coefficients are constructed by using the percentiles obtained from the residual bootstrap, defined as (10)222The symmetric percentile residual-bootstrap CIs that use the 0.05 quantiles of ’s return similar results, unlike in Monte Carlo results from Section 5. We report them in Appendix G.. for the precentile bootstrap is set at the 50th percentile of the bootstrap statistic for the continuity test, explained in Section 4.3. For the threshold locations, the CIs are obtained by the grid bootstrap with convexification. For the grid bootstrap, we make 500 bootstrap draws for each grid point. The grids of the threshold locations have 81 points from the 10th percentile to the 90th percentile of the threshold variables, and there are equal number of observations between two consecutive points. Table 5 and Table 6 also report the bootstrap p-values for the continuity and linearity tests by the bootstrap methods explained in Section 4.3 and Appendix H, respectively. The null hypothesis of the linearity test is , which implies no threshold effects.
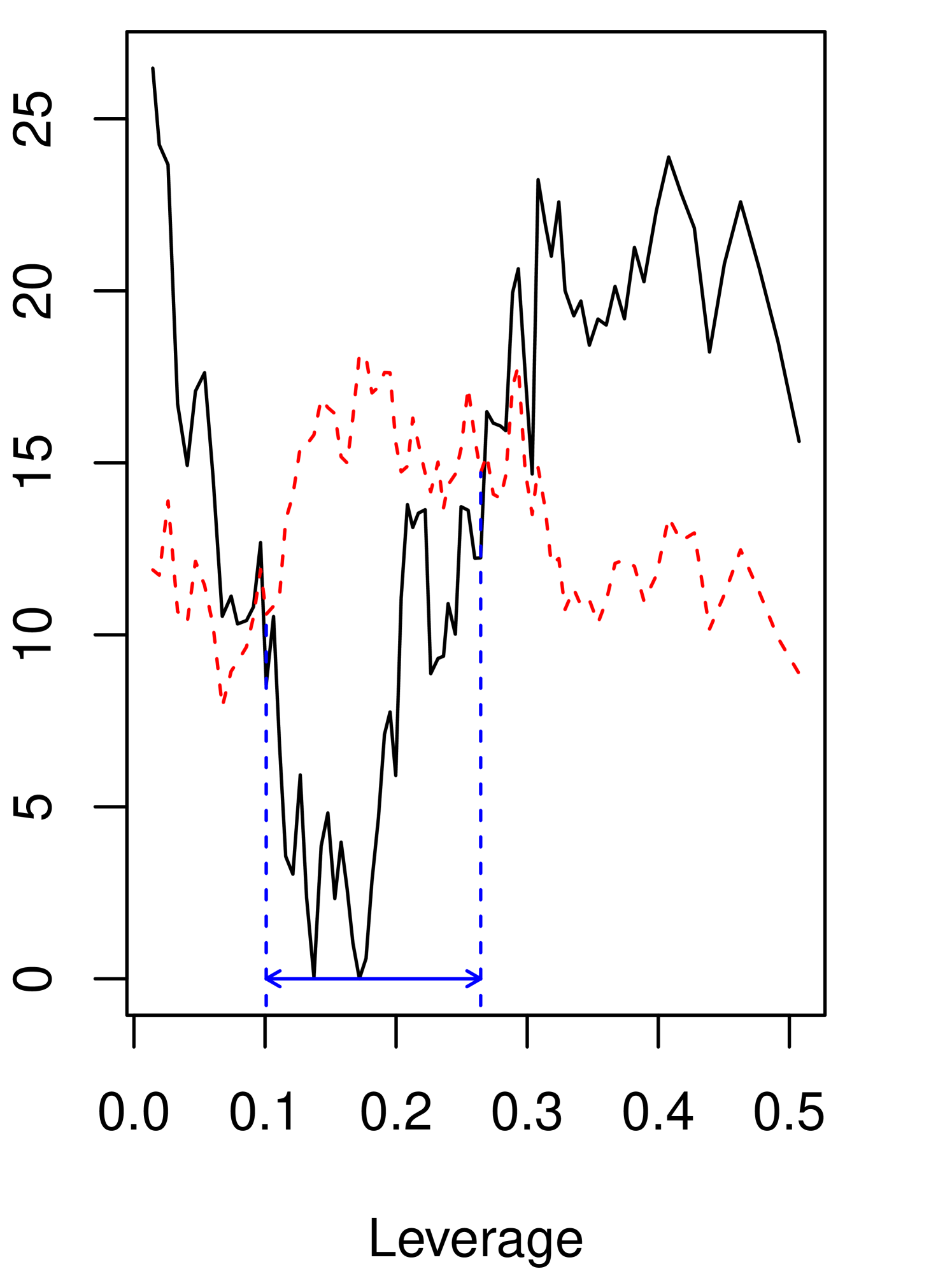
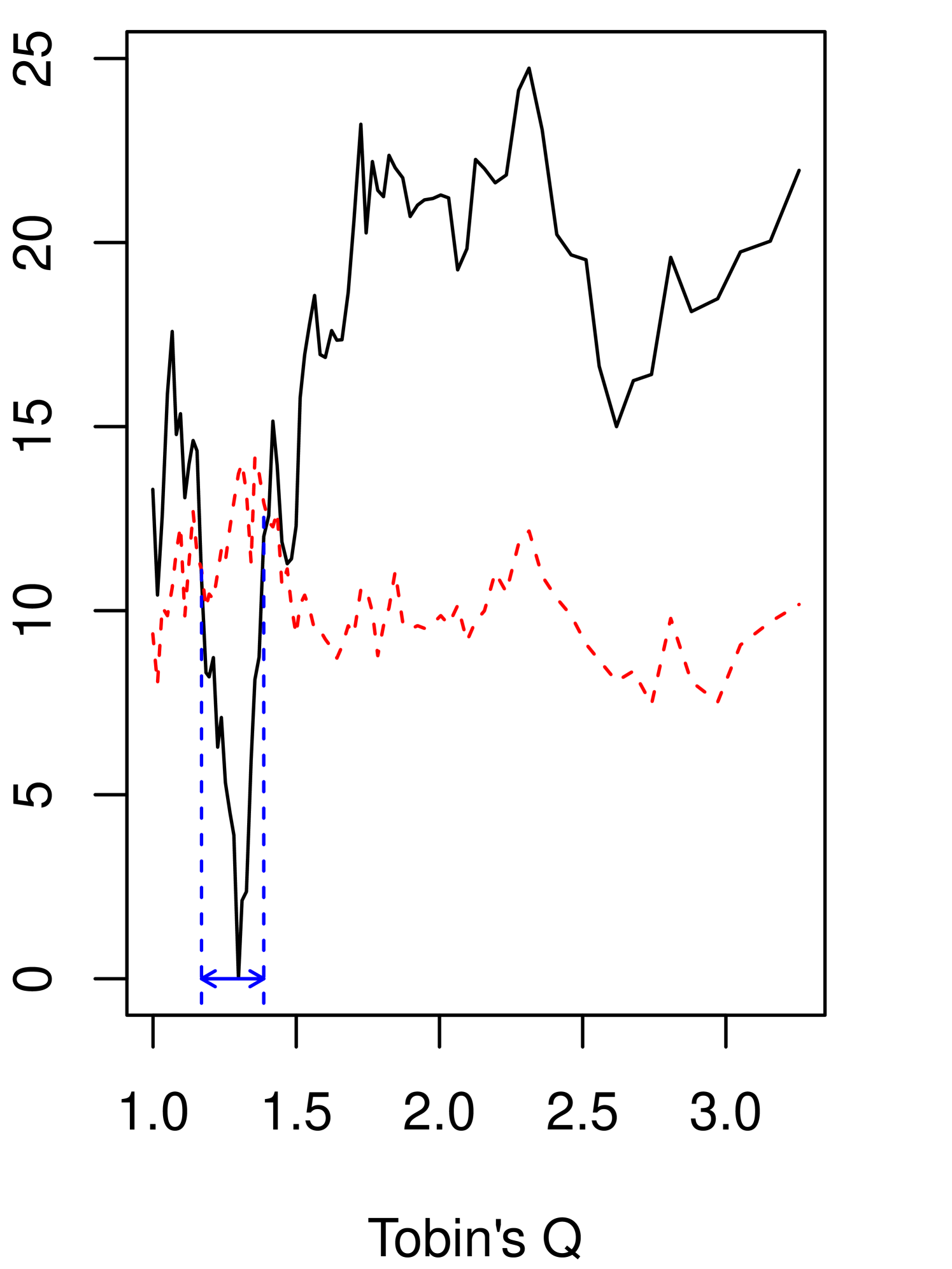
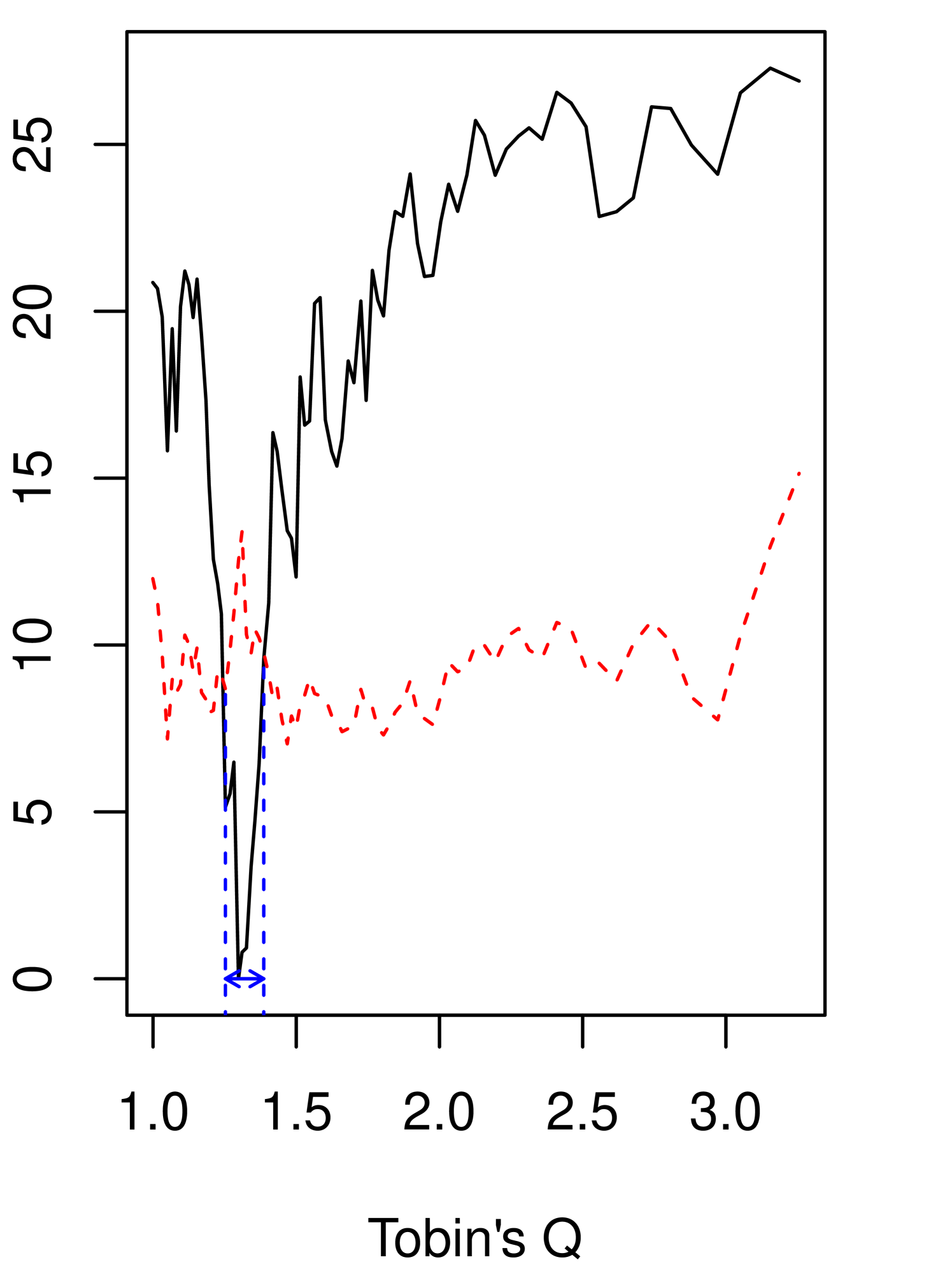
We find supporting evidence for the presence of the threshold effect when the threshold variable is Tobin’s Q, but the statistical evidence is not strong for the leverage threshold model. Table 5 and Table 6 report the bootstrap p-values at .135, .011, and .011, for specifications (16) - (18), respectively. The statistical evidence to reject the continuity is not trivial for all specifications and gets stronger when it is the restricted model using Tobin’s Q. The estimated bootstrap p-values are .028 and .004 for the unrestricted and the restricted using Tobin’s Q. Furthermore, the confidence interval for the threshold location is narrower for the restricted model (18) than for the unrestricted model (17).
| (a) | (b) | ||||||
| est. | [95% CI] | est. | [95% CI] | ||||
| Lower regime | Lower regime | ||||||
| 0.778** | 0.124 | 1.154 | 0.252 | -0.258 | 0.724 | ||
| 0.047 | -0.034 | 0.145 | 0.266* | -0.003 | 0.535 | ||
| -0.147 | -0.385 | 0.171 | 0.027 | -0.103 | 0.264 | ||
| -0.032 | -0.132 | 0.047 | -0.017 | -0.180 | 0.090 | ||
| 0.231 | -0.843 | 1.849 | 0.246* | -0.031 | 0.577 | ||
| Upper regime | Upper regime | ||||||
| -0.154 | -0.717 | 0.551 | 0.410 | -0.049 | 0.751 | ||
| 0.148 | -0.015 | 0.326 | 0.081** | 0.021 | 0.200 | ||
| -0.291* | -0.519 | 0.015 | 0.044 | -0.214 | 0.398 | ||
| 0.013 | -0.066 | 0.113 | 0.050* | -0.019 | 0.153 | ||
| -0.081 | -0.234 | 0.037 | 0.005 | -0.004 | 0.012 | ||
| Difference between regimes | Difference between regimes | ||||||
| intercept | 0.068 | -0.024 | 0.200 | intercept | 0.236* | -0.014 | 0.580 |
| -0.932** | -1.830 | -0.097 | 0.158 | -0.559 | 0.843 | ||
| 0.101 | -0.107 | 0.322 | -0.185 | -0.479 | 0.108 | ||
| -0.144 | -0.519 | 0.134 | 0.017 | -0.227 | 0.275 | ||
| 0.045 | -0.111 | 0.232 | 0.066 | -0.074 | 0.287 | ||
| -0.312* | -1.893 | 0.792 | -0.242* | -0.573 | 0.038 | ||
| Threshold | Threshold | ||||||
| 0.172 | 0.101 | 0.265 | 1.298 | 1.169 | 1.386 | ||
| (38%) | (24%) | (58%) | (30%) | (21%) | (36%) | ||
| Testing (p-val) | Testing (p-val) | ||||||
| Linearity | 0.135 | Linearity | 0.011 | ||||
| Continuity | 0.033 | Continuity | 0.028 | ||||
| est. | [95% CI] | ||
| Coefficients | |||
| 0.392*** | 0.304 | 0.539 | |
| 0.122*** | 0.084 | 0.154 | |
| 0.076 | -0.027 | 0.271 | |
| 0.027*** | 0.006 | 0.046 | |
| 0.298** | 0.073 | 0.571 | |
| 0.008** | 0.001 | 0.015 | |
| Difference between regimes | |||
| intercept | 0.275** | 0.010 | 0.540 |
| -0.290** | -0.562 | -0.018 | |
| Threshold | |||
| 1.298 | 1.253 | 1.386 | |
| (30%) | (27%) | (36%) | |
| Testing (p-val) | |||
| Linearity | 0.011 | ||
| Continuity | 0.004 | ||
A notable finding concerning the coefficients estimates is that the relationship between cash flow and investment is positive and has larger magnitude for the low Tobin’s Q firms and the high leverage firms compared to their other respective regimes, although they are not statistically significant at 5% level. Even though the sign and magnitude of the estimates align with the observations by Lang et al., (1996) and Hansen, 1999b that a firm is subject to financial constraints when its Tobin’s Q is low or leverage is high, there is uncertainty in the interpretation of our results due to the lack of statistical significance.
Next, the autoregressive coefficient of the lagged investment is significant at 5% level in the low leverage regime and is larger than in the high leverage regime. This lends supporting evidence for the presence of asymmetric dynamics in investment, akin to the dynamics of leverage analyzed by Dang et al., (2012). In the meantime, we note that the autoregressive coefficients for the low and high leverage regimes in Column (a) are 0.778 and -0.154, respectively, which appear more extreme than findings of the literature where the estimates are between 0.1 and 0.5, e.g., Blundell et al., (1992). The autoregressive coefficients in the Column (b) are more in line with these estimates. Since the changes of the estimated coefficients in Column (b) are moderate, we also estimate the restricted model (18).
Turning to Table 6, we observe that the differences between the coefficients of the two regimes become significant at 5% level, and the CI for the threshold location becomes narrower while the estimate of the threshold location remains close to the estimate under the unrestricted model. The autoregressive coefficient of the lagged investment and the sensitivity of investment to both cash flow and return on assets are all positive and significant. The effect of Tobin’s Q is both positive and significant for both high and low Tobin’s Q regimes, but it almost disappears once it surpasses the threshold location. This suggests that low Tobin’s Q is related to low investment but higher Tobin’s Q does not cause higher investment once it reaches some level.
7 Conclusion
This paper studies the asymptotic properties of the GMM estimator in dynamic panel threshold models, showing that the limiting distribution depends critically on whether the true model exhibits a kink or a jump at the threshold. We demonstrate that the standard nonparametric bootstrap is inconsistent when the true model has a kink. To address this, we propose alternative bootstrap procedures for constructing confidence intervals for the threshold location and the model coefficients, which are shown to be consistent regardless of the model’s continuity. In particular, we establish that the grid bootstrap for the threshold parameter is uniformly valid. Monte Carlo simulations confirm that the proposed methods outperform the standard bootstrap in finite samples.
Several directions remain for future research. Our simulation results reveal highly asymmetric bootstrap distributions for the coefficient estimates, which distort finite sample inference. This highlights the need for a more thorough theoretical understanding of the bootstrap’s behavior. In particular, establishing the uniform validity of the bootstrap for the coefficient estimates is an important open question. Extensions of our bootstrap algorithms to incorporate latent group structures, interactive fixed effects, or threshold indices, as studied in Miao et al., 2020b , Miao et al., 2020a , and Seo and Linton, (2007); Lee et al., (2021), respectively, would also be valuable.
References
- Adam and Bevan, (2005) Adam, C. S. and Bevan, D. L. (2005). Fiscal deficits and growth in developing countries. Journal of Public Economics, 89:571–597.
- Andrews et al., (2020) Andrews, D. W., Cheng, X., and Guggenberger, P. (2020). Generic results for establishing the asymptotic size of confidence sets and tests. Journal of Econometrics, 218(2):496–531.
- Andrews, (2001) Andrews, D. W. K. (2001). Testing when a parameter is on the boundary of the maintained hypothesis. Econometrica, 69(3):683–734.
- Andrews, (2002) Andrews, D. W. K. (2002). Generalized method of moments estimation when a parameter is on a boundary. Journal of Business & Economic Statistics, 20(4):530–544.
- Andrews and Cheng, (2012) Andrews, D. W. K. and Cheng, X. (2012). Estimation and Inference With Weak, Semi-Strong, and Strong Identification. Econometrica, 80:2153–2211.
- Andrews and Cheng, (2014) Andrews, D. W. K. and Cheng, X. (2014). GMM Estimation and Uniform Subvector Inference With Possible Identification Failure. Econometric Theory, 30:287–333.
- Andrews and Guggenberger, (2009) Andrews, D. W. K. and Guggenberger, P. (2009). Hybrid and size-corrected subsampling methods. Econometrica, 77(3):721–762.
- Andrews and Guggenberger, (2019) Andrews, D. W. K. and Guggenberger, P. (2019). Identification- and singularity-robust inference for moment condition models. Quantitative Economics, 10:1703–1746.
- Arellano and Bond, (1991) Arellano, M. and Bond, S. (1991). Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations. The Review of Economic Studies, 58:277–297.
- Bick, (2010) Bick, A. (2010). Threshold effects of inflation on economic growth in developing countries. Economics Letters, 108(2):126–129.
- Blundell et al., (1992) Blundell, R., Bond, S., Devereux, M., and Schiantarelli, F. (1992). Investment and Tobin’s Q: Evidence from company panel data. Journal of Econometrics, 51:233–257.
- Boyd and Vandenberghe, (2004) Boyd, S. and Vandenberghe, L. (2004). Convex Optimization. Cambridge University Press.
- Cavaliere et al., (2022) Cavaliere, G., Nielsen, H. B., Pedersen, R. S., and Rahbek, A. (2022). Bootstrap inference on the boundary of the parameter space, with application to conditional volatility models. Journal of Econometrics, 227(1):241–263.
- Cecchetti et al., (2011) Cecchetti, S. G., Mohanty, M. S., and Zampolli, F. (2011). The Real Effects of Debt. BIS Working Paper No. 352.
- Chan and Tong, (1985) Chan, K. S. and Tong, H. (1985). On the use of the deterministic lyapunov function for the ergodicity of stochastic difference equations. Advances in applied probability, 17(3):666–678.
- Chan and Tsay, (1998) Chan, K. S. and Tsay, R. S. (1998). Limiting properties of the least squares estimator of a continuous threshold autoregressive model. Biometrika, 85(2):413–426.
- Chatterjee and Lahiri, (2011) Chatterjee, A. and Lahiri, S. N. (2011). Bootstrapping lasso estimators. Journal of the American Statistical Association, 106(494):608–625.
- Cheng and Huang, (2010) Cheng, G. and Huang, J. Z. (2010). Bootstrap consistency for general semiparametric m-estimation. The Annals of Statistics, 38(5):2884–2915.
- Chudik et al., (2017) Chudik, A., Mohaddes, K., Pesaran, M. H., and Raissi, M. (2017). Is There a Debt-Threshold Effect on Output Growth? The Review of Economics and Statistics, 99:135–150.
- Dang et al., (2012) Dang, V. A., Kim, M., and Shin, Y. (2012). Asymmetric capital structure adjustments: New evidence from dynamic panel threshold models. Journal of Empirical Finance, 19:465–482.
- Dovonon and Goncalves, (2017) Dovonon, P. and Goncalves, S. (2017). Bootstrapping the GMM overidentification test under first-order underidentification. Journal of Econometrics, 201:43–71.
- Dovonon and Hall, (2018) Dovonon, P. and Hall, A. R. (2018). The asymptotic properties of gmm and indirect inference under second-order identification. Journal of Econometrics, 205(1):76–111.
- Dovonon and Renault, (2013) Dovonon, P. and Renault, E. (2013). Testing for Common Conditionally Heteroskedastic Factors. Econometrica, 81:2561–2586.
- Fazzari et al., (1988) Fazzari, S. M., Hubbard, R. G., Petersen, B. C., Blinder, A. S., and Poterba, J. M. (1988). Financing Constraints and Corporate Investment. Brookings Papers on Economic Activity, 1988:141–206.
- Giannerini et al., (2024) Giannerini, S., Goracci, G., and Rahbek, A. (2024). The validity of bootstrap testing for threshold autoregression. Journal of Econometrics, 239(1):105379.
- Gine and Zinn, (1990) Gine, E. and Zinn, J. (1990). Bootstrapping general empirical measures. The Annals of Probability, 18(2):851 – 869.
- Girma, (2005) Girma, S. (2005). Absorptive Capacity and Productivity Spillovers from FDI: A Threshold Regression Analysis. Oxford Bulletin of Economics and Statistics, 67:281–306.
- Goncalves and White, (2004) Goncalves, S. and White, H. (2004). Maximum likelihood and the bootstrap for nonlinear dynamic models. Journal of Econometrics, 119(1):199–219.
- Gonzalo and Wolf, (2005) Gonzalo, J. and Wolf, M. (2005). Subsampling inference in threshold autoregressive models. Journal of Econometrics, 127(2):201–224.
- Hall and Horowitz, (1996) Hall, P. and Horowitz, J. L. (1996). Bootstrap Critical Values for Tests Based on Generalized-Method-of-Moments Estimators. Econometrica, 64:891–916.
- Han and McCloskey, (2019) Han, S. and McCloskey, A. (2019). Estimation and Inference with a (nearly) Singular Jacobian. Quantitative Economics, 10:1019–1068.
- (32) Hansen, B. E. (1999a). The Grid Bootstrap and the Autoregressive Model. The Review of Economics and Statistics, 81:594–607.
- (33) Hansen, B. E. (1999b). Threshold effects in non-dynamic panels: Estimation, testing, and inference. Journal of Econometrics, 93:345–368.
- Hansen, (2000) Hansen, B. E. (2000). Sample Splitting and Threshold Estimation. Econometrica, 68:575–603.
- Hansen, (2017) Hansen, B. E. (2017). Regression kink with an unknown threshold. Journal of Business & Economic Statistics, 35(2):228–240.
- Hidalgo et al., (2023) Hidalgo, J., Lee, H., Lee, J., and Seo, M. H. (2023). Minimax risk in estimating kink threshold and testing continuity. In Advances in Econometrics: Essays in Honor of Joon Y. Park: Econometric Theory, Vol. 45A, pages 233–259.
- Hidalgo et al., (2019) Hidalgo, J., Lee, J., and Seo, M. H. (2019). Robust Inference for Threshold Regression Models. Journal of Econometrics, 210:291–309.
- Khan and Senhadji, (2001) Khan, M. S. and Senhadji, A. S. (2001). Threshold Effects in the Relationship between Inflation and Growth. IMF Staff Papers, 48:1–21.
- Kim et al., (2019) Kim, S., Kim, Y. J., and Seo, M. H. (2019). Estimation of Dynamic Panel Threshold Model Using Stata. The Stata Journal, 19:685–697.
- Kremer et al., (2013) Kremer, S., Bick, A., and Nautz, D. (2013). Inflation and growth: new evidence from a dynamic panel threshold analysis. Empirical Economics, 44:861–878.
- Lang et al., (1996) Lang, L., Ofek, E., and Stulz, R. (1996). Leverage, investment, and firm growth. Journal of Financial Economics, 40(1):3–29.
- Lee et al., (2021) Lee, S., Liao, Y., Seo, M. H., and Shin, Y. (2021). Factor-driven two-regime regression. The Annals of Statistics, 49(3):1656–1678.
- Lee et al., (2011) Lee, S., Seo, M. H., and Shin, Y. (2011). Testing for Threshold Effects in Regression Models. Journal of the American Statistical Association, 106:220–231.
- Leeb and Pötscher, (2005) Leeb, H. and Pötscher, B. M. (2005). Model selection and inference: facts and fiction. Econometric Theory, 21(1):21–59.
- (45) Miao, K., Li, K., and Su, L. (2020a). Panel threshold models with interactive fixed effects. Journal of Econometrics, 219(1):137–170.
- (46) Miao, K., Su, L., and Wang, W. (2020b). Panel threshold regressions with latent group structures. Journal of Econometrics, 214(2):451–481.
- Mikusheva, (2007) Mikusheva, A. (2007). Uniform inference in autoregressive models. Econometrica, 75(5):1411–1452.
- Newey and McFadden, (1994) Newey, W. K. and McFadden, D. (1994). Chapter 36 Large Sample Estimation and Hypothesis Testing. In Handbook of Econometrics, volume 4, pages 2111–2245. Elsevier.
- Newey and West, (1987) Newey, W. K. and West, K. D. (1987). Hypothesis Testing with Efficient Method of Moments Estimation. International Economic Review, 28:777–787.
- Pakes and Pollard, (1989) Pakes, A. and Pollard, D. (1989). Simulation and the Asymptotics of Optimization Estimators. Econometrica, 57:1027–1057.
- Praestgaard and Wellner, (1993) Praestgaard, J. and Wellner, J. A. (1993). Exchangeably Weighted Bootstraps of the General Empirical Process. The Annals of Probability, 21(4):2053 – 2086.
- Romano and Shaikh, (2012) Romano, J. P. and Shaikh, A. M. (2012). On the uniform asymptotic validity of subsampling and the bootstrap. The Annals of Statistics, 40(6):2798 – 2822.
- Rousseau and Wachtel, (2002) Rousseau, P. L. and Wachtel, P. (2002). Inflation thresholds and the finance–growth nexus. Journal of International Money and Finance, 21:777–793.
- Seo and Linton, (2007) Seo, M. H. and Linton, O. (2007). A smoothed least squares estimator for threshold regression models. Journal of Econometrics, 141(2):704–735.
- Seo and Shin, (2016) Seo, M. H. and Shin, Y. (2016). Dynamic Panels With Threshold Effect and Endogeneity. Journal of Econometrics, 195:169–186.
- Strebulaev and Yang, (2013) Strebulaev, I. A. and Yang, B. (2013). The mystery of zero-leverage firms. Journal of Financial Economics, 109(1):1–23.
- van der Vaart and Wellner, (1996) van der Vaart, A. W. and Wellner, J. (1996). Weak Convergence and Empirical Processes With Applications to Statistics. Springer Series in Statistics. Springer-Verlag, New York.
- Wang, (2015) Wang, Q. (2015). Fixed-effect panel threshold model using stata. The Stata Journal, 15(1):121–134.
- Yang et al., (2020) Yang, L., Zhang, C., Lee, C., and Chen, I.-P. (2020). Panel kink threshold regression model with a covariate-dependent threshold. The Econometrics Journal, 24(3):462–481.
- Zhang et al., (2017) Zhang, Y., Zhou, Q., and Jiang, L. (2017). Panel kink regression with an unknown threshold. Economics Letters, 157:116–121.
Additional Notations.
For , denotes a matrix whose elements are all zero. “” denotes the weak convergence as in section 1.3 of van der Vaart and Wellner, (1996). is a norm for either vectors or matrices. For a vector, it is the Euclidean norm. For a matrix, it is the Frobenius norm, i.e., for a matrix .
Appendix A Proofs for Section 3.
A.1 Proof of Theorem 1.
Note that due to . Hence, the population moment equation is when . The condition (ii) of Theorem 1 implies that has full column rank, and hence if . , when . The condition (i) of Theorem 1 implies that is not zero if . Therefore, if , and if , which is the standard identification condition in the literature, e.g., Section 2.2.3 in Newey and McFadden, (1994).
A.2 Proof of Theorem 2.
To obtain limit distribution of , we first establish consistency of to and rate of ’s convergence. Then, we show asymptotic distribution of the estimates using rescaled versions of the parameters and criterions.
A.2.1 Consistency.
Constrained estimator of the coefficients, , given a fixed can be expressed as
where
Therefore,
Define profiled criterion with respect to by and . The threshold location estimator is . By the law of large numbers (LLN), . By the uniform law of large numbers (ULLN) in Lemma D.2, uniformly with respect to . Hence, would imply , and then , which completes the proof.
To show consistency of to , we apply the argmin/argmax continuous mapping theorem (CMT) as in Theorem 3.2.2 in van der Vaart and Wellner, (1996). It is sufficient to check (i) uniformly converges to some function in probability, and (ii) for any open set contatining . (ii) can be shown if is uniquely minimized at and continuous as is compact.
The profiled moment can be rewritten as
Therefore,
where is a projection matrix to the column space of . The profiled objective can be written as
By , , and , we can derive that
uniformly with respect to , where . Note that in the second stage of the two-step GMM estimation. when we consider the first stage. is uniquely minimized when . This is because is positive definite, and the conditions in Theorem 1 implies that does not lie in the column space of whenever . Moreover, is continuous as is continuous with respect to by D.
A.2.2 Convergence rate.
as the consistency of is shown. Our proof follows arguments similar to the proof of Theorem 3.3 by Pakes and Pollard, (1989). By the consistency of and by Lemma D.3,
By , we can obtain
Apply triangle inequality to get
As is the minimizer of the GMM criterion, . Therefore,
, while by Lemma D.1. Thus,
which implies and .
A.2.3 Asymptotic distribution.
This section derives asymptotic distribution of the estimator through the argmin/argmax continuous mapping theorem (CMT) as in Theorem 3.2.2 in van der Vaart and Wellner, (1996).
Introduce a local reparametrization by and , and let consist of subvectors and . Additionally, define and . Note that is uniformly tight due to the convergence rate we obtained.333 A random variable is tight if for any , there exists a compact set such that , and is uniformly tight if for any , there exists a compact set such that for all . Note that by the convergence rate we derived, for any , there exists a compact such that , and such that if . Then, we can define a compact set , where is a compact set such that , which satisfies for all . Let
We show that (i) weakly converges to a stochastic process in for every compact in the Euclidean space, (ii) is continuous, and (iii) possesses an unique optimum not in but in its square since . Thus, we will establish that converges in distribution to . In the characterization of the minimizers, is shown to be tight.
The rescaled and reparametrized sample moment can be written as
By the central limit theorem (CLT),
By the LLN,
Let be arbitrary. By the ULLN in Lemma D.2,
uniformly with respect to . Then, by continuity of at ,
uniformly with respect to . By Lemma D.4,
uniformly with respect to .
Therefore, weakly converges to
in for any compact . Then, by the CMT,
Characterization of the minimizers
Next, we characterize the minimizers. The objective function of the minimization problem is strictly convex with respect to and , since has full column rank and is positive definite. Hence, a solution can be characterized by the Karush-Kuhn-Tucker (KKT) conditions. See Chapter 5 in Boyd and Vandenberghe, (2004) for more details.
The Lagrangian for this problem is
and the gradient of the Lagrangian with respect to and should vanish:
In addition, and should hold.
-
(i)
When and , we can obtain
where is the projection matrix to the column space of . because the matrix has full column rank, and cannot be in the column space of and . Therefore,
should hold for the feasibility condition .
-
(ii)
When and , we can obtain
By plugging this into the equation for , we get
Thus,
where . follows a normal distribution that is left censored at 0. Then,
Note that the two normal variables and are independent of each other, because becomes zero.
Appendix B Proofs for Section 4
B.1 Preliminaries
The bootstrap methods we consider are Algorithm 1 with different choices of . There are three bootstrap methods this paper propose: (i) for , (ii) set as (8), and (iii) which is the continuity-restricted estimator. In Appendix F, we consider the case which results in the standard nonparametric bootstrap.
The probability law for the bootstrap is formalized following Goncalves and White, (2004). Let be the probability measure for data and be the conditional probability law of bootstrap given observations. in ( in ) if for any , as . in if for any and , there exists such that . in if in for every continuous and bounded function , where is the expectation by the bootstrap probability law conditional on observations. in in if , where is the set of all Lipschitz functions on bounded in such that .
The following lemma is useful in analyzing bootstrap stochastic orders.
Lemma B.1.
-
(i)
If or , then or in , respectively.
-
(ii)
Let in and in . Then, in .
Proof.
See Lemma 3 in Cheng and Huang, (2010). ∎
Recall that . in when in . This would be the case when in and since then in by Lemma B.1.
B.2 Proof of Theorem 6.
As in the proof of Theorem 2, consistency and convergence rates of the bootstrap estimator should be derived first. These results are summarized in the following proposition, with the proof provided in Online Appendix E.
Proposition 1.
Then, we derive the (conditional) weak convergence limit of the rescaled criterion and apply the CMT to obtain the asymptotic distribution of the bootstrap estimator.
Asymptotic distribution under continuity.
Based on the convergence rate in Proposition 1, introduce the local reparametrization by and , and let consist of subvectors and .
The asymptotic distributions of the bootstrap estimators can be derived by using the argmin/argmax CMT as in the proof of Theorem 2. Let
We show that in in for every compact in the Euclidean space. Recall that .
The rescaled and reparametrized bootstrap moment can be written as
By Lemma E.2,
By the bootstrap LLN,
Let be arbitrary. By bootstrap Glivenko-Cantelli, e.g., Lemma 3.6.16 in van der Vaart and Wellner, (1996),
By continuity of at , for any , there exists such that if . For any , . Note that , and hence with probability approaching 1, while uniformly with respect to . Thus,
both uniformly with respect to . By Lemma E.5,
uniformly with respect to .
Therefore, in in for any compact . Then, by applying the argmin CMT as in the proof of Theorem 2, we can obtain the limit distribution of the bootstrap estimates conditional on the data.
Asymptotic distribution under discontinuity.
The proof for the discontinuous model only requires a slight change to the proof for the continuous model. As the convergence rate for the discontinuous model is for both coefficients and threshold location estimators, let be unchanged and for the local reparametrization. Let
We can write the rescaled and reparametrized moment as follows:
The limit of can be obtained similarly to the continuous model case, except that we use Lemma E.6 instead of Lemma E.5 to get
uniformly with respect to .
Then, conditonally weakly converges to in in for any compact . And the argmin CMT yields the asymptotic distribution of the bootstrap estimators. The limit distributions of the bootstrap estimators are normal because . ∎
Online Supplements for “Bootstraps for Dynamic Panel Threshold Models” (Not for Publication)
Woosik Gong and Myung Hwan Seo
This part of the appendix is only for online supplements. It contains supplementary results for the Monte Carlo simulations, the remaining proofs for Theorem 3, Theorem 4, Proposition 1, Theorem 5, Theorem 7, as well as additional lemmas with proofs. It also presents invalidity of the standard nonparametric bootstrap, percentile bootstrap confidence intervals for empirical application, explanation of bootstrap for linearity test, and the uniform validity of the grid bootstrap.
Appendix C Supplementary Results for Monte Carlo Simulation
In this section, we present supplementary results for the Monte Carlo simulations in Section 5.
C.1 Symmetric Percentile Confidence Intervals for Coefficients
First, we report the coverage rates of symmetric percentile CIs for the coefficients that are constructed using the nonparametric bootstrap,
| (C.1) |
and the residual bootstrap, defined by (10). Tables 7 and 8 show the coverage rates and the ratios of the average lengths of CIs by the two different bootstrap methods.
In contrast to the results based on non-symmetric percentile CIs in Table 3 in Section 5, Table 7 shows that symmetric CIs provide much higher coverage rates, often resulting in over-coverage. Note that this observation also occurs for the threshold inference as shown in Table 1. Meanwhile, Table 8 shows that the difference in the average lengths of symmetric percentile CIs between the two bootstrap methods is less pronounced compared to the non-symmetric case shown in Table 4.
| R-B(S) | NP-B(S) | ||||||||||
| 400 | 0.964 | 0.976 | 0.980 | 0.974 | 0.930 | 0.996 | 0.996 | 0.996 | 0.992 | 0.982 | |
| 0.0 | 800 | 0.951 | 0.974 | 0.971 | 0.967 | 0.931 | 0.987 | 0.992 | 0.995 | 0.988 | 0.976 |
| 1600 | 0.955 | 0.972 | 0.964 | 0.961 | 0.923 | 0.983 | 0.994 | 0.995 | 0.980 | 0.977 | |
| 400 | 0.964 | 0.976 | 0.979 | 0.974 | 0.933 | 0.994 | 0.993 | 0.995 | 0.991 | 0.982 | |
| 0.1 | 800 | 0.952 | 0.975 | 0.970 | 0.968 | 0.935 | 0.990 | 0.992 | 0.995 | 0.989 | 0.978 |
| 1600 | 0.959 | 0.975 | 0.973 | 0.961 | 0.924 | 0.986 | 0.995 | 0.997 | 0.979 | 0.977 | |
| 400 | 0.963 | 0.974 | 0.978 | 0.977 | 0.939 | 0.995 | 0.993 | 0.997 | 0.993 | 0.986 | |
| 0.2 | 800 | 0.959 | 0.972 | 0.977 | 0.974 | 0.929 | 0.992 | 0.994 | 0.996 | 0.987 | 0.978 |
| 1600 | 0.958 | 0.972 | 0.976 | 0.964 | 0.933 | 0.986 | 0.995 | 0.996 | 0.979 | 0.980 | |
| 400 | 0.964 | 0.971 | 0.982 | 0.978 | 0.940 | 0.992 | 0.994 | 0.998 | 0.994 | 0.989 | |
| 0.5 | 800 | 0.960 | 0.973 | 0.987 | 0.974 | 0.945 | 0.991 | 0.994 | 0.998 | 0.988 | 0.985 |
| 1600 | 0.957 | 0.977 | 0.985 | 0.970 | 0.945 | 0.985 | 0.996 | 0.998 | 0.981 | 0.987 | |
| 400 | 0.970 | 0.982 | 0.985 | 0.984 | 0.967 | 0.991 | 0.995 | 0.992 | 0.991 | 0.993 | |
| 1.0 | 800 | 0.968 | 0.982 | 0.988 | 0.981 | 0.967 | 0.992 | 0.993 | 0.995 | 0.989 | 0.994 |
| 1600 | 0.960 | 0.981 | 0.987 | 0.972 | 0.963 | 0.989 | 0.995 | 0.995 | 0.988 | 0.989 | |
| Ratios of average lengths of CIs: | ||||||
| R-B(S) / NP-B(S) | ||||||
| n | ||||||
| 400 | 1.017 | 1.035 | 1.008 | 0.996 | 1.010 | |
| 0.0 | 800 | 1.033 | 1.037 | 1.007 | 1.004 | 1.018 |
| 1600 | 1.040 | 1.046 | 1.012 | 1.015 | 1.014 | |
| 400 | 1.028 | 1.040 | 1.008 | 0.996 | 1.012 | |
| 0.1 | 800 | 1.032 | 1.033 | 1.000 | 1.004 | 1.015 |
| 1600 | 1.039 | 1.047 | 1.011 | 1.020 | 1.016 | |
| 400 | 1.022 | 1.035 | 1.003 | 0.996 | 1.012 | |
| 0.2 | 800 | 1.032 | 1.039 | 1.001 | 1.004 | 1.015 |
| 1600 | 1.039 | 1.048 | 1.009 | 1.025 | 1.016 | |
| 400 | 1.037 | 1.046 | 0.991 | 1.014 | 1.016 | |
| 0.5 | 800 | 1.044 | 1.045 | 0.991 | 1.008 | 1.024 |
| 1600 | 1.052 | 1.056 | 0.996 | 1.035 | 1.022 | |
| 400 | 1.101 | 1.107 | 0.989 | 1.042 | 1.042 | |
| 1.0 | 800 | 1.096 | 1.111 | 0.988 | 1.039 | 1.052 |
| 1600 | 1.115 | 1.136 | 0.996 | 1.051 | 1.048 | |
Although taking symmetric CI brings the coverage probabilities of both bootstraps closer to the nominal level in our Monte Carlo simulations, it is not desirable as both non-symmetric and symmetric percentile CIs should provide similar results if an employed bootstrap scheme is theoretically valid. To investigate the cause of the large difference in coverage rates between symmetric and non-symmetric CIs, we present Figure 2, which displays the sample statistic and the quantiles of the bootstrap test statistics relevant for confidence intervals for each simulated dataset. Figure 2 collects results under the specification , where the model is continuous, with the sample size 1600. Results for other coefficients and other specifications are almost identical and are therefore omitted.
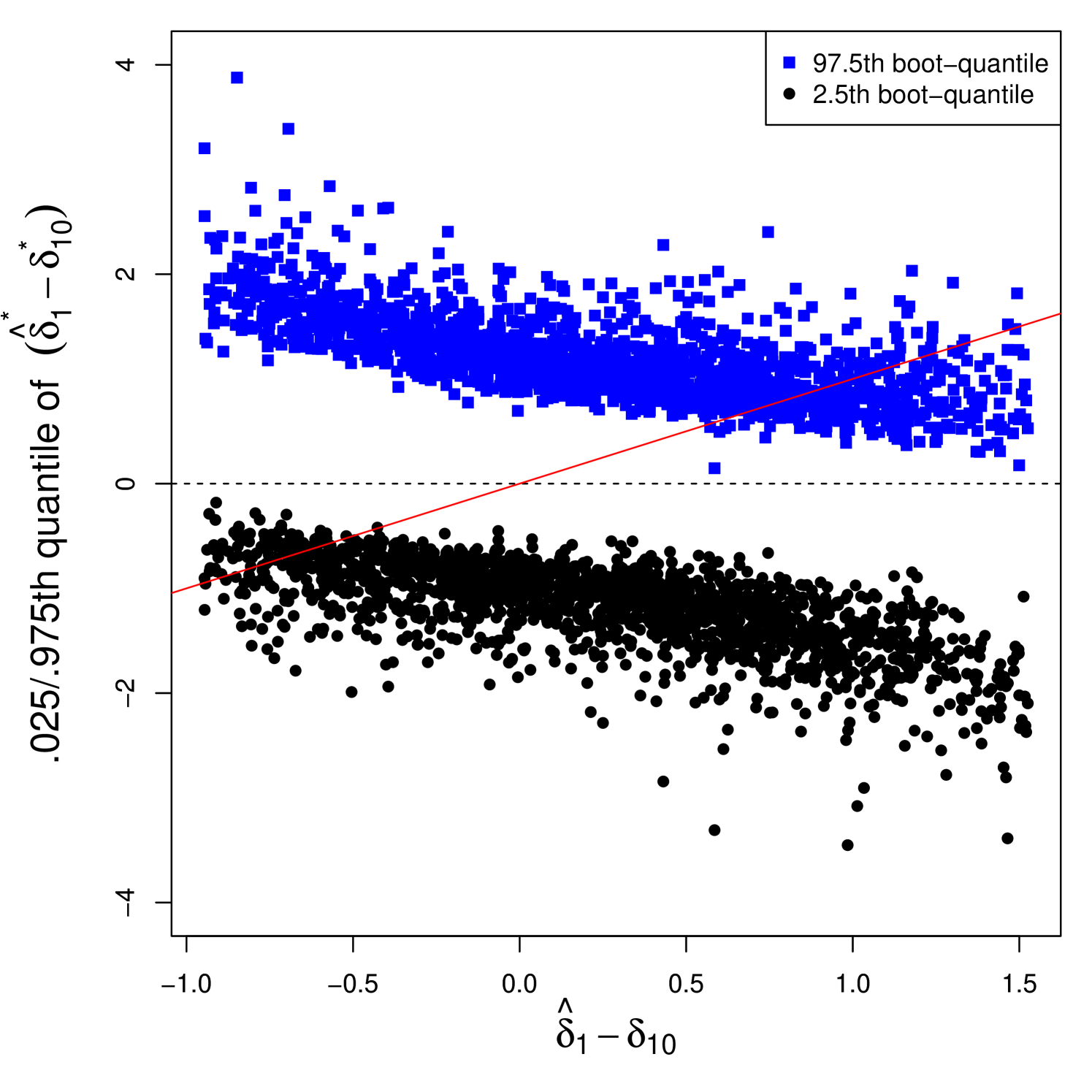
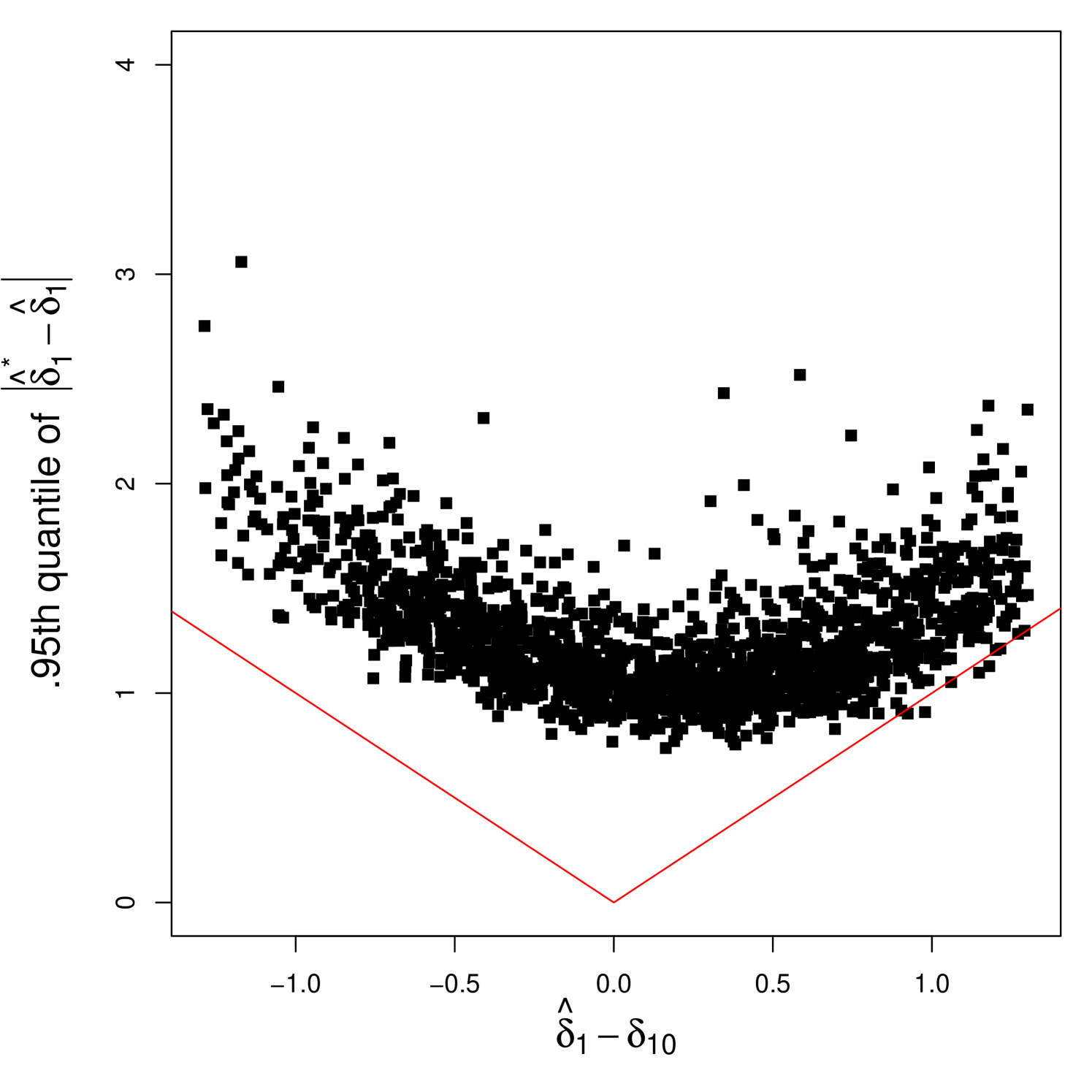
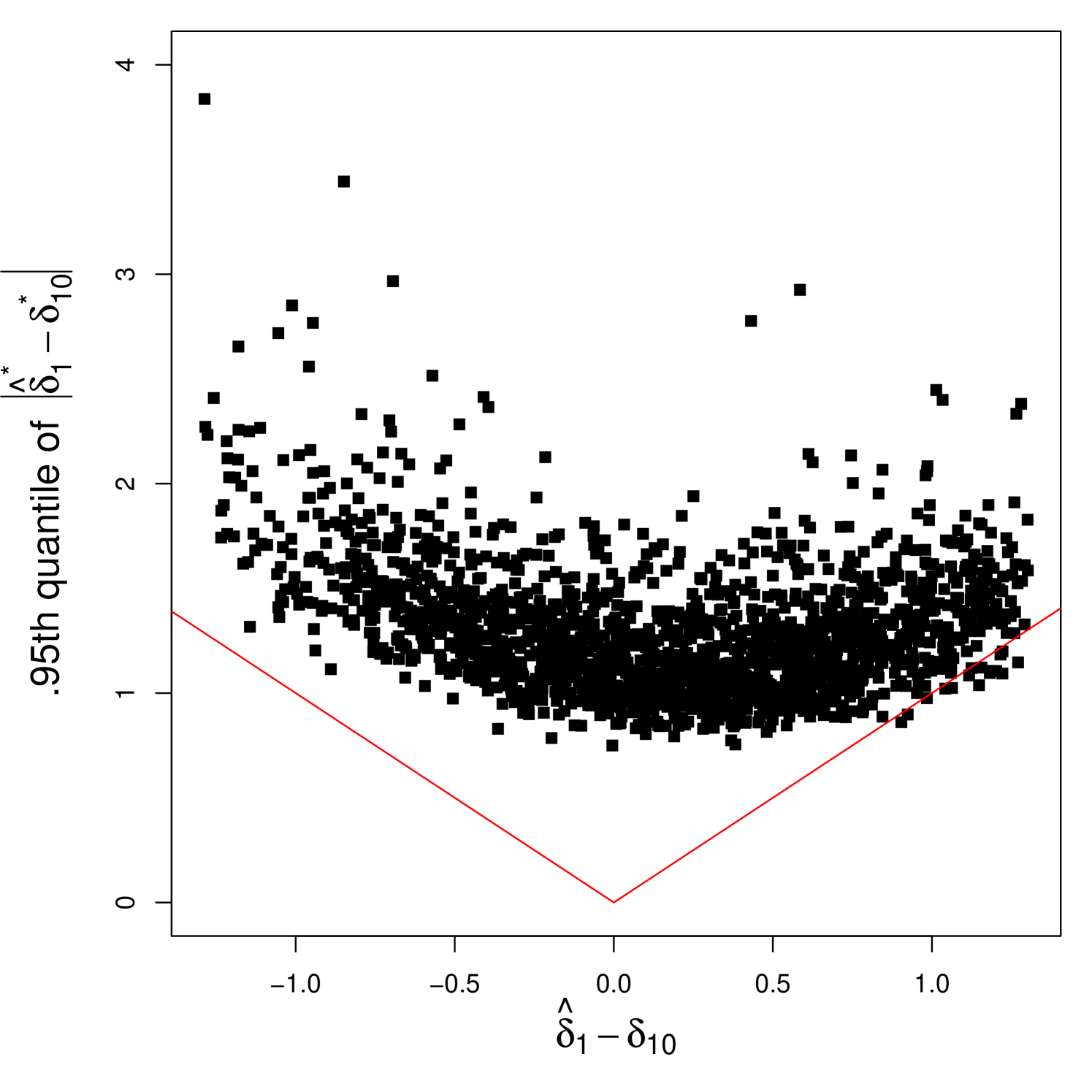
Notes: The figures plot the sample statistic and the quantiles of the bootstrap test statistics relevant for confidence intervals for each simulated dataset from the continuous dgp where with . Panels (a) and (b) show the 0.025 and 0.975 bootstrap quantiles of (used for NP-B) and (for R-B), respectively. Panels (c) and (d) show the 0.95 bootstrap quantiles of (for NP-B(S)) and (for R-B(S)), respectively. Red line represents a linear line with 45 degree in Panels (a) and (b), and the line in Panels (c) and (d). In Panels (a) and (b), the coverage probability is the frequency that the upper and lower bootstrap quantiles (dots) include the red line (45 degree line) between them. In Panels (c) and (d), the coverage probability is the frequency with which the bootstrap quantile (dot) lies above the red line.
Panels (a) and (b) show the 0.025 and 0.975 bootstrap quantiles of (used for NP-B) and (for R-B), respectively. The coverage probability is the frequency that the upper and lower bootstrap quantiles (dots) include the red line (45 degree line) between them. We observe that R-B method improves upon NP-B, as the distance between the two bootstrap quantiles tends to be wider. However, the improvement is not sufficiently large to resolve the undercoverage; see Table 3.
Note that the bootstrap quantiles (dots of each color) would be horizontally flat if they are asymptotically independent to the sample statistic. The nonparametric bootstrap CIs are asymptotically valid if
where is an independent copy of . Therefore, the empirical 95% percentile of should be asymptotically independent to for the nonparametric bootstrap CI to be valid.
However, as shown in Panel (a), and the bootstrap quantiles are negatively correlated with the sample statistic. Specifically, the correlations between the sample statistic and the 0.975 and 0.025 bootstrap quantiles from NP-B are -0.9037 and -0.8892, respectively. Our residual bootstrap (R-B) mitigates this issue. The bootstrap quantiles in Panel (b) appear flatter compared to those in Panel (a). The corresponding correlations from R-B are -0.7083 and -0.7003 for the 0.975 and 0.025 quantiles, respectively. While the correlations have decreased, they remain far from zero. Further investigation is warranted, although we leave this for future research.
Panels (c) and (d) show the 0.95 bootstrap quantiles of (for NP-B(S)) and (for R-B(S)), respectively. The coverage probability is the frequency of the dots that lie above the red line. Contrary to Panels (a) and (b), there is no rejection if . Although this brings the coverage probabilities of both bootstraps closer to the nominal level, it is not desirable and misleading.
C.2 Weakly Endogenous Threshold Variable
We additionally report Monte Carlo results when the threshold variable is not weakly exogenous but weakly endogenous, that is, when the variable is predetermined. We consider the dgp same with the one in Section 5 with an exception that (12) is replaced by
| (C.2) |
where . Other parameters such as and remain the same as in Section 5. Note that under (12), if . On the other hand, if but under (C.2). Therefore, we need to exclude from the instrument such that .
We consider the specifications where and repeat Monte Carlo iterations 1,000 times. We report coverage rates of 95% CIs constructed by different bootstrap methods. Tables 9 and 10 show the coverage rates of the threshold location and the coefficients, respectively.
Table 9 shows that Grid-B achieves the most reasonable coverage rates, similar to the results in Table 1 in Section 5. Table 10 shows that both R-B and NP-B are subject to undercoverage for the coefficients, although R-B offers higher coverage rates than NP-B.
| n | 0 | 0.5 | 1 | |
| 400 | 0.990 | 0.983 | 0.975 | |
| Grid-B | 800 | 0.986 | 0.983 | 0.965 |
| 1600 | 0.981 | 0.975 | 0.959 | |
| 400 | 0.508 | 0.519 | 0.634 | |
| NP-B | 800 | 0.443 | 0.496 | 0.612 |
| 1600 | 0.468 | 0.501 | 0.610 | |
| 400 | 1.000 | 0.998 | 0.994 | |
| NP-B(S) | 800 | 1.000 | 1.000 | 0.996 |
| 1600 | 1.000 | 0.999 | 0.999 | |
| R-B | NP-B | ||||||||||
| n | |||||||||||
| 400 | 0.753 | 0.739 | 0.781 | 0.796 | 0.765 | 0.726 | 0.658 | 0.636 | 0.706 | 0.691 | |
| 0.0 | 800 | 0.795 | 0.729 | 0.783 | 0.786 | 0.756 | 0.764 | 0.629 | 0.640 | 0.709 | 0.669 |
| 1600 | 0.832 | 0.746 | 0.803 | 0.787 | 0.755 | 0.800 | 0.647 | 0.640 | 0.720 | 0.674 | |
| 400 | 0.773 | 0.756 | 0.757 | 0.806 | 0.750 | 0.740 | 0.672 | 0.601 | 0.725 | 0.670 | |
| 0.5 | 800 | 0.816 | 0.736 | 0.755 | 0.802 | 0.770 | 0.778 | 0.661 | 0.580 | 0.717 | 0.675 |
| 1600 | 0.835 | 0.746 | 0.776 | 0.791 | 0.770 | 0.811 | 0.660 | 0.605 | 0.720 | 0.660 | |
| 400 | 0.805 | 0.777 | 0.743 | 0.822 | 0.754 | 0.765 | 0.712 | 0.618 | 0.731 | 0.701 | |
| 1.0 | 800 | 0.829 | 0.770 | 0.725 | 0.798 | 0.742 | 0.784 | 0.685 | 0.582 | 0.727 | 0.683 |
| 1600 | 0.867 | 0.799 | 0.751 | 0.815 | 0.762 | 0.822 | 0.697 | 0.576 | 0.747 | 0.673 | |
C.3 Coverage Rates by Asymptotic Confidence Intervals
We additionally report coverage rates of CIs based on the asymptotic method described in Seo and Shin, (2016). The dgp remains the same as in Section 5. Tables 11 and 12 show the results for the threshold and the coefficients, respectively.
Table 11 shows that the asymptotic method suffers undercoverage for all specifications we consider and does not improve as the sample size grows. This remains true even when , a case in which the model is discontinuous and the asymptotic CIs are theoretically valid, as shown in Seo and Shin, (2016). This especially highlights the desirability of our grid bootstrap method for inference of the threshold location which achieves good coverage rates in finite samples.
On the other hand, in Table 12, the coverage rates of the coefficients by the asymptotic method are much closer to the nominal level compared to those obtained from the nonparametric bootstrap or our residual bootstrap for both continuous and discontinuous models; see Table 3. We ask readers to be cautious, as it is unclear how the coverage rates of the asymptotic CIs behave when the true model is continuous, as explained in the last paragraph of Section 3.
| n | 0 | 0.1 | 0.2 | 0.5 | 1 |
| 400 | 0.881 | 0.881 | 0.885 | 0.884 | 0.899 |
| 800 | 0.864 | 0.862 | 0.860 | 0.846 | 0.869 |
| 1600 | 0.837 | 0.836 | 0.837 | 0.836 | 0.864 |
| n | ||||||
| 400 | 0.950 | 0.923 | 0.951 | 0.916 | 0.970 | |
| 0.0 | 800 | 0.956 | 0.921 | 0.952 | 0.921 | 0.973 |
| 1600 | 0.960 | 0.927 | 0.956 | 0.931 | 0.979 | |
| 400 | 0.947 | 0.922 | 0.947 | 0.917 | 0.972 | |
| 0.1 | 800 | 0.961 | 0.923 | 0.952 | 0.928 | 0.973 |
| 1600 | 0.960 | 0.929 | 0.956 | 0.933 | 0.983 | |
| 400 | 0.942 | 0.919 | 0.947 | 0.915 | 0.974 | |
| 0.2 | 800 | 0.959 | 0.926 | 0.952 | 0.926 | 0.971 |
| 1600 | 0.957 | 0.923 | 0.954 | 0.933 | 0.982 | |
| 400 | 0.943 | 0.922 | 0.944 | 0.914 | 0.977 | |
| 0.5 | 800 | 0.959 | 0.934 | 0.953 | 0.937 | 0.977 |
| 1600 | 0.953 | 0.934 | 0.953 | 0.930 | 0.983 | |
| 400 | 0.949 | 0.937 | 0.950 | 0.925 | 0.987 | |
| 1.0 | 800 | 0.958 | 0.952 | 0.952 | 0.945 | 0.985 |
| 1600 | 0.958 | 0.949 | 0.955 | 0.936 | 0.981 |
Appendix D Proofs of Theorems in Section 3 and Auxiliary Lemmas
Additional notations
We introduce additional notations as lemmas in this online appendix involve more empirical process theory. Suppose that is a measurable space and are i.i.d. random elements in with probability law . For a point , let be a dirac measure at 444Although we already use as the subvector of the parameter , we still use to represent dirac measure as it is strong convention in the literature. We explicitly mention if is used as dirac measure to avoid confusion.. The empirical measure of a sample is , and the empirical process is . Let be a functional class, elements of which are measurable functions from to . We call a function an envelope of if for all . For a stochastic process and a functional class , define .
D.1 Proof of Theorem 3.
D.1.1 Continuous Model.
When .
Note that the constrained estimator is -consistent to , which is identical to the convergence rate of , since the problem becomes a standard linear dynamic panel estimation. Let and . The distance test statistic can be rewritten as follows:
where we apply the CMT. Lee et al., (2011) showed that the difference between the constrained and unconstrained infima is a continuous operator on .
Note that , while
where is the argmin, whose formula is derived in the proof of Theorem 2. By plugging in one of the first order conditions, , and the formula for , we can get
Therefore, the limit distribution of the test statistic is identical to
Note that as , and .
When .
We show that diverges to infinity in probability. There is a constant such that . This is because is zero if and only if , by G and Theorem 1, and continuous on , by D, while the restricted parameter set is closed for all . is shown to satisfy the uniform entropy condition in the proof of Lemma D.3, and hence by Glivenko-Cantelli theorem. By triangle inequality, . Meanwhile, because . Therefore, there exists such that , which implies that for any .
D.1.2 Discontinuous Model.
When .
As in the proof for the continuous model, we apply the CMT to the test statistic. Let and . First, we will show that when the model is discontinuous and Assumptions G, D, and LJ are true, in for any compact . Note that
| (D.1) | ||||
| (D.2) | ||||
| (D.3) |
The terms in the first two lines of the right hand side (D.1) and (D.2) converge in distribution to uniformly with respect to . Since by Lemma D.3,
converges in probability to zero uniformly with respect to . Suppose . The result for is similar. By application of Talyor expansion,
uniformly with respect to , and similar limit result can be derived for . Hence, we can derive that the term (D.3) converges in probability to uniformly with respect to .
By the CMT, the test statistic converges in distribution to
Note that , and . Therefore, the limit distribution of the test statistic is identical to the distribution of
The matrix is idempotent since the column space of lies in the column space of . The rank of the matrix is 1. Since , the chi-square distribution with 1 degree of freedom is the limit distribution.
When .
The proof showing that diverges when for the discontinuous model is identical to the proof written for the continuous model.
D.2 Proof of Theorem 4.
Under the null hypothesis.
Define a map such that if . Let . Note that
The first-order derivative of with respect to is
is a matrix that is identical to a binding of the columns of and . If , then (see Kim et al., (2019)). The continuity test statistic can be rewritten as
Reparametrize such that , , and . Define a centered criterion by
We will show that weakly converges to a process in for every compact . Then, by the CMT, the continuity test statistic converges in distribution to
In the proof of Theorem 2, it is shown that and
Let , , , and . Then,
By the CLT and LLN,
By the ULLN (application of Lemma D.2) and continuity of and at ,
uniformly with respect to . Finally,
uniformly with respect to . Suppose that . The case for follows similarly. The last uniform convergence holds because Lemma D.3 yields uniformly with respect to and the following application of Taylor expansion:
uniformly with respect to as .
In conclusion, , and
where and . By applying the CMT, the continuity test statistic converges in distribution to
By similar computations to the proof of Theorem 3,
where and . As , we can derive , and hence . Since is zero, is independent to .
Under the alternative hypothesis.
There is a constant such that . This is because is zero if and only if , by G and Theorem 1, and continuous on , by D, while the restricted parameter set is closed. is shown to satisfy the uniform entropy condition in the proof of Lemma D.3, and hence by Glivenko-Cantelli theorem. By triangle inequality, . Recall that is the continuity-restricted estimator. Meanwhile, because . Therefore, there exists such that , which implies that , for any and .
D.3 Auxiliary Lemmas
Lemma D.1.
Proof.
Recall that , whose formula is (5), is the first-order derivative of with respect to at , and , whose formula is (6), is a half of the second-order derivative. can be obtained by applying the Leibniz rule as follows:
Similarly, we can get
This implies the formula (5) for . can also be obtained by the Leibniz rule as follows:
Similarly, we can get
This implies the formula (6) for .
The population moment can be expressed as,
Define where
The polynomial expansion implies
Thus, , which completes the proof. ∎
Lemma D.2.
If G is true, then
Proof.
We show that the classes and are P-Glivenko-Cantelli. We focus on the former class since the verification for the latter class is exactly identical. Let be a random element in a measurable space . A collection of measurable index functions on is a VC class with a VC index 2. If is the th element of , then is also a VC class as discussed by Lemma 2.6.18 in van der Vaart and Wellner, (1996). The envelope for would be since an index function is always bounded by 1. The expectation of the envelope is bounded since . In conclusion, is a -Glivenko-Cantelli for each , and thus the ULLN for holds. ∎
Lemma D.3.
Let G hold. If , then
Proof.
Let be a random element in a measurable space , and is the probability measure for . Define a functional class on such that
| (D.4) | ||||
and . We need to show that if as , which is the asymptotic equicontinuity. To show the asymptotic equicontinuity, it is sufficient to show that each element of is P-Donsker, e.g., 2.3.11 Lemma and its corollary in van der Vaart and Wellner, (1996), which is implied by the uniform entropy condtion:
where supremum is taken over all probability measures on such that , and is an envelope for . For more details, see section 2.1 in van der Vaart and Wellner, (1996). As we only need to consider each scalar element of , it is sufficient to consider the following functional class
where is a constant such that if . Assume that is a scalar without losing of generality. Note that is an element of . So it is sufficient to show satisfies the uniform entropy condition.
Let . is a -dimensional vector space and is a VC class by 2.6.15 Lemma in van der Vaart and Wellner, (1996), with an envelope function for some constant , and . Let , , and . for some and are envelopes for and , respectively. Note that , i.e., is a collection of where and . satisfies the uniform entropy condition as pairwise sum or product of functional classes preserve the uniform entropy condition, e.g., Theorem 2.10.20 in van der Vaart and Wellner, (1996). Note that for every ,
while is an envelope of . So the uniform entropy condition for holds. Similarly, we can show that satisfies the uniform entropy condition. Hence, the functional class defined by pairwise sum, which is a set of functions for all and , also satisfies the uniform entropy condition, e.g., Theorem 2.10.20 in van der Vaart and Wellner, (1996). As is a superset of , the functional class also satisfies the uniform entropy condition . Thus, , which is a superset of , satisfies the uniform entropy condition by repetitively applying Theorem 2.10.20 in van der Vaart and Wellner, (1996), and hence also satisfies the condition.
∎
Lemma D.4.
Proof.
Note that
| (D.5) | ||||
| (D.6) |
The stochastic term (D.5) converges in probability to zero uniformly with respect to . This is because Lemma D.3 shows that when , then
as it can be expressed as .
Suppose . The case for follows similarly. As , the deterministic term (D.6) converges as follows:
uniformly with respect to . To show that, use the (second-order) derivative of and derive the Taylor expansion
where . Note that unifromly with respect to . Since and are continuously differentiable at by D, both and hold uniformly with respect to . On the other hand, uniformly with respect to . Hence, converges to uniformly with respect to as . We can derive the similar result for .
∎
Appendix E Proofs of Theorems in Section 4 and Auxiliary Lemmas
E.1 Preliminaries
Proofs in this section are regarding bootstrap results, and hence we explain empirical process framework for our bootstrap analysis. Let be i.i.d. resampling draws from a given sample . We set as in the proofs of Lemmas D.2 and D.3. An important functional class for our bootstrap analysis is where is defined as in (D.4).
Be mindful that that appears in Section 4 is different from . This is because where
| (E.1) |
Recall that is not an i.i.d. resampling draw from but is generated using resampled regressors and residuals with regression equation using . The formula for is used to derive the equality in (E.1) (see Step 2 in Algorithm 1). Instead, . To be more precise, in (E.1) is , and in (E.1) is .
E.2 Proof of Proposition 1
Consistency of the bootstrap estimator.
The bootstrap sample moment can be rewritten by
We additionally define
, and . Then, . Given , we can obtain the constrained optimizer
where
Let be a profiled criterion and . in by Lemma E.1. By Lemma E.3, in . Therefore, if in , then in , which completes the proof.
Let which can be expressed as
Therefore,
and
when in and . Note that is the identity matrix if it is for the first step estimation and if it is for the second step estimation and the first step estimator is consistent. Since the uniform probability limit of conditional on the data is minimized when , the argmin CMT implies in . Recall that is set as in Theorem 5, (8) in Theorem 6, and in Theorem 7. For both cases (i) and (ii) of the proposition, which implies in by Lemma B.1. Therefore, we can derive that in .
Convergence rate under continuity.
By bootstrap equicontinuity, Lemma E.4, and the consistency of to ,
in since in and in . The condition in is implied by in , as and in . Thus,
Apply triangle inequality to get
where holds in . As is the minimizer of the bootstrap criterion, in where the last equality is implied by Lemma E.2. Therefore,
By Lemma D.3, , so it is in by Lemma B.1. Hence,
By Lemma D.1, in . Therefore, in and in . Suppose that in . Then, in since in .
Convergence rate under discontinuity.
E.3 Proof of Theorem 5.
In the grid bootstrap at , .
When .
When .
Note that . It will be shown that in . Then, , and in , which completes the proof.
Recall that
while as explained in Online Appendix E.1. The functional class is shown to satisfy the uniform entropy condition in the proof of Lemma D.3, and pairwise sum or product of functional classes preserve the uniform entropy condition by Theorem 2.10.20 in van der Vaart and Wellner, (1996). Hence, by applying the bootstrap Glivenko-Cantelli theorem, e.g., Lemma 3.6.16 in van der Vaart and Wellner, (1996),
is in . Furthermore,
uniformly with respect to , , and . As and are consistent to ,
uniformly with respect to . By the compactness of , the minimum eigenvalue of is bounded below by some constant . Therefore, in where
As , we can conclude that .
E.4 Proof of Theorem 7.
In the bootstrap for continuity test, , where is the continuity-restricted estimator.
Under the null hypothesis.
Under the alternative hypothesis.
Let the true model be discontinuous. Note that . Meanwhile, in , by the same logic used in the proof of Theorem 5 when . Then, . Therefore, in , which completes the proof.
E.5 Lemmas
Lemma E.1.
If G holds,
Proof.
Let where is defined by (D.4), and is a resampling draw from . See Online Appendix E.1 for more explanation. is shown to satisfy the uniform entropy condition in the proof of Lemma D.3. Therefore, by bootstrap Glivenko-Cantelli theorem, e.g., Lemma 3.6.16 in van der Vaart and Wellner, (1996), in . Note that which completes the proof. ∎
Lemma E.2.
If G holds and , then
Proof.
Recall that where
Lemma E.3.
If G is true, then
Proof.
It is shown that the classes and are P-Glivenko-Cantelli in the proof of Lemma D.2. Then, by bootstrap Glivenko-Cantelli theorem, e.g., Lemma 3.6.16 in van der Vaart and Wellner, (1996), the result of this lemma holds.
∎
Lemma E.4.
Let G hold. If , then
Proof.
Note that for any and where is defined by (D.4), and is a resampling from . Hence, . By bootstrap version of stochastic equicontinuity, e.g., C2 in the proof of Theorem 2.1 in Praestgaard and Wellner, (1993), the result of this lemma holds if satisfies the uniform entropy condition and has a square integrable envelope function, which are verified in the proof of Lemma D.3. ∎
Lemma E.5.
The conditions for and hold if (i) , (ii) is set as (8), and (iii) , which is the continuity-restricted estimator in Section 3.2, under the assumptions of this lemma. For (i), is asymptotically normal, and . For (ii), note that . , while , , and . , and . also holds. For (iii), Kim et al., (2019) showed that , while and by definition.
Proof.
Note that
| (E.2) | ||||
| (E.3) |
First, we show that the stochastic term (E.2) is in uniformly with respect to . Note that while is shown to satisfy the uniform entropy condition and to have a square integrable envelope in the proof of Lemma D.3. Then, by C2 in the proof of Theorem 2.1 in Praestgaard and Wellner, (1993), the following bootstrap asymptotic equicontinuity can be derived:
is in . Hence, by plugging in to the place of in the last display, we can derive that (E.2) is in uniformly with respect to .
Next, we show that (E.3) term converges to a deterministic limit. As satisfies the uniform entropy condition and has a square integrable envelope function, we can derive the following asymptotic equicontinuity:
is , and hence in by Lemma B.1. Therefore,
is in .
Let . By assumption, we can reparametrize such that , , , and . Then, we can reparametrize the function such that
| (E.4) |
Let which lies in a compact set for an aribtrary .
To prove the lemma, it will be shown below that
uniformly with respect to and , which in turn implies
uniformly with respect to since
Suppose . The case for follows similarly. Note that
We focus on the first term on the right hand side since the limit of the second term can be analyzed similarly, and redefine and , accordingly. Let where . Then, where
Similarly to in (E.4), we define reparametrized function and .
Limit of :
We can derive the Taylor expansion
where . As both and are in compact spaces, uniformly with respect to and . By D, is bounded and continuous on a neighborhood of . Therefore, . Since , we can derive uniformly in and .
Limit of :
We can derive the Taylor expansion
| (E.5) | ||||
| (E.6) | ||||
| (E.7) |
where .
First, we can observe that (E.5) converges to zero uniformly with respect to , , and . This is because uniformly with respect to and , which implies , while .
Next, we check that (E.6) converges to zero uniformly with respect to , , and . By D, is bounded and continuous on a neighborhood of . As uniformly with respect to and , and , which implies the convergence of (E.6) to zero.
Finally, we obtain the limit of (E.7).
Since and , (E.7) converges to uniformly with respect to and .
In conclusion,
uniformly with respect to and , and hence
uniformly with respect to . Similarly, we can show that
uniformly with respect to . ∎
Lemma E.6.
The conditions for and hold if (i) or (ii) is set as (8) under the assumptions of this lemma. Note that since , , and by P.
If has full column rank for all , then P holds. Let , , , and . Note that , where . Since and by Lemma D.2, uniformly with respect to . Since is compact, there exists such that . As , holds, which implies .
Proof.
Let . By assumption, we can reparametrize such that and . Then, we can reparametrize the function such that . Let which lies in a compact set for an aribtrary .
To prove the lemma, it will be shown that
uniformly with respect to and , which in turn implies
uniformly with respect to since
Suppose . The case for follows similarly. Then,
We focus on the first term of the right hand side as the limit of the second term can be derived identically, and redefine and , accordingly.
We can derive the following Taylor expansion:
where . As uniformly with respect to and , uniformly, and hence uniformly.
In conclusion,
uniformly with respect to . Similarly, we can show that
uniformly with respect to . ∎
Appendix F Invalidity of standard nonparametric bootstrap
In this section, we explain why the bootstrap estimators of the standard bootstrap does not have the asymptotic distribution in Theorem 2 when the true model is continuous. Note that the bootstrap explained by Algorithm 1 becomes the standard nonparametric bootstrap when . The consistency and convergence rate derivations in the proof of Proposition 1 can still be followed, and hence and both in . However, the conditions for Lemma E.5 do not hold for the standard nonparametric bootstrap as as explained in Section 4.2. Therefore, the rescaled versions of the criterion converges to a different limit. Specifically,
in in for every compcat in the Euclidean space, where is defined by (11). Recall that as shown in Section 4.2. The conditional weak convergence, , in the last display comes from applying the following Lemma F.1 in the place of Lemma E.5 used in the proof of Theorem 6.
Lemma F.1.
Proof.
Suppose that . The case can be analyzed similarly. Let . Reparametrize such that and . Let the set of be for arbitrary . Let .
We will show that uniformly with respect to and , which implies
in uniformly with respect to , because
Note that where
Let and denote the reparametrized version of and , respectively.
converges to zero uniformly, for which we recall that it is identical to that appears in the proof of Lemma E.5.
where
It can be easily checked that converges to zero uniformly. It will be shown in the next paragraph that uniformly, which implies uniformly.
By Taylor expansion,
| (F.1) | ||||
| (F.2) |
where . By continuity of at , (F.1) converges to 0 uniformly with respect to and . As uniformly, we can derive that (F.2) converges to uniformly.
By similar manner, we can derive
in uniformly with respect to . ∎
Appendix G Symmetricc percentile bootstrap confidence intervals for empirical application
In this section, we report the symmetric percentile residual-bootstrap confidence intervals for the coefficients for the empirical application. Table 13 and Table 14 correspond to Table 5 and Table 6 in Section 6, respectively.
| (a) | (b) | ||||||
| est. | [95% CI] | est. | [95% CI] | ||||
| Lower regime | Lower regime | ||||||
| 0.778** | 0.319 | 1.237 | 0.252 | -0.242 | 0.746 | ||
| 0.047 | -0.041 | 0.135 | 0.266* | -0.004 | 0.535 | ||
| -0.147 | -0.428 | 0.134 | 0.027 | -0.175 | 0.229 | ||
| -0.032 | -0.128 | 0.065 | -0.017 | -0.157 | 0.123 | ||
| 0.231 | -1.219 | 1.682 | 0.246 | -0.071 | 0.564 | ||
| Upper regime | Upper regime | ||||||
| -0.154 | -0.769 | 0.462 | 0.410** | 0.007 | 0.813 | ||
| 0.148* | -0.026 | 0.322 | 0.081* | -0.023 | 0.184 | ||
| -0.291** | -0.566 | -0.015 | 0.044 | -0.251 | 0.340 | ||
| 0.013 | -0.076 | 0.102 | 0.050 | -0.038 | 0.137 | ||
| -0.081 | -0.216 | 0.054 | 0.005 | -0.004 | 0.013 | ||
| Difference between regimes | Difference between regimes | ||||||
| intercept | 0.068 | -0.045 | 0.181 | intercept | 0.236 | -0.083 | 0.554 |
| -0.932** | -1.803 | -0.061 | 0.158 | -0.542 | 0.857 | ||
| 0.101 | -0.117 | 0.319 | -0.185 | -0.479 | 0.109 | ||
| -0.144 | -0.463 | 0.176 | 0.017 | -0.233 | 0.267 | ||
| 0.045 | -0.129 | 0.218 | 0.066 | -0.128 | 0.261 | ||
| -0.312 | -1.754 | 1.130 | -0.242 | -0.557 | 0.074 | ||
| est. | [95% CI] | ||
| Coefficients | |||
| 0.392*** | 0.269 | 0.514 | |
| 0.122*** | 0.087 | 0.156 | |
| 0.076 | -0.095 | 0.247 | |
| 0.027*** | 0.007 | 0.047 | |
| 0.298** | 0.028 | 0.567 | |
| 0.008** | 0.000 | 0.015 | |
| Difference between regimes | |||
| intercept | 0.275** | 0.074 | 0.566 |
| -0.290** | -0.566 | -0.061 | |
Appendix H Bootstrap for linearity test
We explain the bootstrap for linearity test based on sup-Wald statistic, explained in Seo and Shin, (2016). Null hypothesis of the test is . The sup-Wald test statistic is
| (H.1) |
where , is the weight matrix obtained by the initial estimator with the restriction that the threshold location is , is a subvector of the restricted estimator , and .
The bootstrap for the linearity test can be implemented by setting
in Algorithm 1. Note that does not matter in this case as . The critical value for -size test is obtained by using the quantile of the bootstrapped sup-Wald test statistics, defined analogously to (H.1).
Appendix I Uniform validity of the grid bootstrap
In this section, we show the uniform validity of the grid bootstrap given in Section 4.1. As discussed in Section 4.1.1, the following simplified specification is analyzed for the clarity of exposition:
where , , and . still includes the threshold variable. The goal here is to show the uniform validity of the grid bootstrap near parameter values that make threshold models continuous. Let , and be defined as in Section 2, while
Let index the dgp while is an infinite dimensional index that determines the distribution of the random variables . This section restricts to admit continuous density function. Let the space of the distributions be which is compact and equipped with sup-norm over the space of density functions555 That means , where and are densities of the distribution functions and , and is a dimension of the random vectors whose distributions are or . It is a stronger norm than the sup-norm over the space of distribution functions as implies . , and the space of be which is compact since and are compact.
Following the general framework explained in Andrews et al., (2020), we consider a sequence of true parameters . Let and be the square root of the minimum and maximum eigenvalues of , respectively. Let the parameter space for be
where are some positive constants. Note that is to prevent from (having a subsequence) converging to zero.666 This implies that our threshold model has a strong threshold effect which excludes the diminishing or small threshold effect as in Hansen, (2000). The remaining conditions for other than imply that Assumptions D, G, and LK/LJ hold uniformly. The condition is a uniform integrability condition for the distribution of conditional on or . Its role will be explained after introducing the drifting sequence framework.
Because of the nonlinearity and discontinuity of our dynamic model, it is not trivial to answer what primitive conditions for the parameter and distributions of random variables, such as initial value or individual fixed effect , are sufficient for . This paper does not investigate this issue so that we can focus on uniformity analysis with respect to degeneracy of the Jacobian of nonlinear GMM.
For , let be drawn from distribution . For a function or random variable , e.g., or , we often write and to indicate more explicitly that indices in subscript are or , while is the new index introduced in this section. Suppose that
As in Section 2, we define
where , ,
Let , and , , , , , and . We write , and instead of , and . Define
where and are the conditional expectation and the density of , respectively.
Suppose that a sequence (or its subsequence ) converges so that and , i.e., . Note that the density of the distribution converges to the density of uniformly by our choice of norm in , and .
Note that as each element of is uniformly integrable by for all while converges to . Hence, and also hold. Furthermore, , where
This is because uniformly by our definition of norm in , and it is straightforward to derive for , which implies due to the uniform integrability for . Furthermore, as because , and , where
and is between and . Note that for some nonnegative for sufficiently large as .
Let and , where . Let , and . Let , , and , while and is the initial estimator. and .
Let be an i.i.d. draw along the index from . Let
| (I.1) | ||||
where and . For the justification of the representation (I.1), please refer to (E.1) and description in Section E.1 . Note that becomes the bootstrap sample moment from the grid bootstrap. Then, let , , , , and . Recall that in Section 4.1 the % grid bootstrap confidence set was defined as
Define a mapping , where such that
This is because the limits of and characterize the asymptotic behaviors of the test statistic used in the grid bootstrap.
Theorem I.1.
For any subsequence of and any sequence s.t. ,
where is the probability law under . Moreover,
which establishes the uniform validity of the grid bootstrap confidence interval.
Note that the last statement of Theorem I.1 follows from the theorem’s preceding statement, as the latter verifies Assumption B* from Andrews et al., (2020). Let . To show Theorem I.1, we consider the following four cases:
-
(i) continuous: and .
-
(ii) semi-continuous: and .
-
(iii) semi-discontinuous: and .
-
(vi) discontinuous: and .
The following lemma implies Theorem I.1.
Lemma I.1.
For all sequences for which , the following convergences hold ( in “ in ” denotes the probability of ):
(i) For continuous case, , and in , where and .
(ii) For semi-continuous case, , and in , where
, and .
(iii) For semi-discontinuous and discontinuous cases, , and in .
Remark 1.
Note that the distribution of is (first-order) stochastically dominated by the distribution. This is because when , and when , which implies for .
Proof of Lemma I.1.
We prove the result for sequence rather than to ease notation. Then, we can replace by to complete the proof.
First, we derive the consistency, convergence rates, and asymptotic distributions of , and then we derive the asymptotic distributions of , depending on the regimes determined by and . Then, the same results are derived for bootstrap estimator and test statistic for each case.
Consistency of estimator
Define , which is
Therefore, .
Note that by the WLLN for triangular array which holds as . Furthermore, by Lemma I.3. Thus, so that if , where , is consistent such that .
Convergence rate of estimator
By Lemma I.5 and , . As ,
By triangle inequality, . As minimizes , . Note that because , while the CLT for triangular array implies . The CLT holds by combination of Lyapunov condition and Cramér-Wold if for some and for any , which holds as and for some . Therefore,
while by Lemma I.2.
In conclusion,
It implies that for any values of and , while for ,
-
(i) if
-
(ii) if
-
(iii) if
-
(vi) if .
Asymptotic distribution of estimator and test statistic
We only consider (ii) semi-continuous and (iii) semi-discontinuous cases since the proofs for (i) continuous and (iv) discontinuous cases are almost identical to the proof of continuous and discontinuous cases in Theorem 3.
Case (ii): Let and . Additionally, define and . Let
The rescaled and reparametrized sample moment can be written as
By the CLT for triangular array,
Note that the CLT holds by combination of Lyapunov condition and Cramér-Wold device if for some for any , which holds as and for some . By the WLLN for triangular array,
which holds as . Let be some constant. By the ULLN in Lemma I.3,
uniformly with respect to . Then, by the continuity of at ,
uniformly with respect to . By Lemma I.6,
uniformly with respect to . Therefore, weakly converges to
in for any compact .
Let and . We consider so that . When , derivations are almost identical and lead to the same limit distribution of the test statistic. Let . Then, by the CMT,
KKT conditions, as in the proof of Theorem 2, imply
, , and should hold. Then, we can get
where . follows a normal distribution that is left censored at . Then,
Asymptotic distribution of the test statistic can be derived by
where we apply the CMT. Note that , while
By plugging in the formula for (note that ) we can get
Therefore, the limit distribution of the test statistic is identical to
Case (iii): Let and . The rescaled and reparametrized sample moment can be written as
By the CLT for triangular array,
By the WLLN for triangular array,
By the ULLN in Lemma I.3,
uniformly with respect to , which implies
uniformly with respect to . By Lemma I.7,
uniformly with respect to . Therefore, weakly converges to
in for any compact . Then, and converges in distribution to
by the argmin CMT. KKT conditions, as in the proof of Theorem 2, imply
Then, we can get
where , and
Asymptotic distribution of the test statistic can be derived by
where we apply the CMT. Note that , while
By plugging in the formula for (note that ), we can get
Therefore, the limit distribution of the test statistic is identical to
which has the distribution.
Limit distribution of bootstrap estimator and test statistic
The derivation of the limit distributions of the bootstrap estimator and test statistic is almost identical to that of the asymptotic distributions of the sample estimator and test statistic. We need to replace by , by , and sample moments by bootstrap moments in the previous part of the proof regarding asymptotic analysis. Be mindful that we do not need to replace in the previous part of the proof as we focus on the grid bootstrap when to show that the grid bootstrap CI provides correct coverage rate. Lemmas I.10, I.11, I.12, and I.13 are applied instead of Lemmas I.3, I.5, I.6, and I.7 in the places where the latter are used in the previous part of the proof. Moreover, Lemmas I.8 and I.9 are applied instead of the WLLN and CLT for triangular array applied to in the places where the latter are used in the previous part of the proof. ∎
I.1 Auxiliary Lemmas
Lemma I.2.
Let and . For any , there is such that
Proof.
Note that .
First, we derive a bound for which is
Suppose , and the other case can be analyzed similarly. By Taylor expansion,
where
and . Suppose . For sufficiently small , there is such that if , then for some . There also exists such that , and hence for sufficiently large . Moreover, there exists such that for sufficiently small and sufficiently large . Hence, for some and for sufficiently small and sufficiently large . Therfore, there exists such that if , then
for some and for sufficiently large . By similar computations for , we can derive that there exists such that if , then for some and for sufficiently large .
Meanwhile, there exist such that if and , then for some and for sufficiently large . This is because for sufficiently small , , where
Note that if is sufficently small, is bounded above by some nonnegative constant , and .
Hence, for any , there exist such that if and , then
for some nonnegative and sufficiently large . Therefore, for any , we can set and sufficiently small such that for sufficiently large , which completes the proof.
∎
Lemma I.3.
Let and . Then,
Proof.
We show that the classes and are Glivenko-Cantelli uniformly in , where is the probability law of . We focus on the former class since the verification for the latter class is exactly identical. As it is sufficient to show that each element of , we additionally restrict our focus on and assume that is scalar without losing of generality. By Theorem 2.8.1 in van der Vaart and Wellner, (1996), is Glivenko-Cantelli uniformly in if
where supremum is taken over all probability measures such that , and is an envelope of . The first condition holds because for some and . The second condition holds as we have shown in the proof of Lemma D.2 that is a VC class that satisfies the uniform entropy condition. Therefore, the ULLN with triangular array holds for . ∎
Lemma I.4.
Let and . Suppose that . Then,
where .
Proof.
We need to show and . is Glivenko-Cantelli class uniformly with respect to , where is the probability law of , as the proof of Lemma I.5 shows that the class is uniformly Donsker and pre-Gaussian. Therefore, when .
Let . If is Glivenko-Cantelli class uniformly with respect to , then . Then, as . By Theorem 2.8.1 in van der Vaart and Wellner, (1996), is Glivenko-Cantelli uniformly in if
where supremum is taken over all probability measures such that , and for some is an envelope of as is an envelope of as shown in the proof of Lemma D.3. The first condition holds because for some . The second condition holds because satisfies the uniform entropy condition (see the proof of Lemma D.3) while pairwise product preserves uniform entropy condition, e.g., Theorem 2.10.20 in van der Vaart and Wellner, (1996).
∎
Lemma I.5.
Let and . If , then
Proof.
Let be a probability law of . We show that the class is pre-Gaussian uniformly in (see Section 2.8.2 in van der Vaart and Wellner, (1996) for its definition), which implies asymptotic equicontinuity uniform in . That is, for any , if and , while . Let be an envelope of . By Theorem 2.8.3 in van der Vaart and Wellner, (1996), it is sufficient to show that
where ranges over all finitely discrete probability measures, which implies that is Donsker and uniformly pre-Gaussian in .
Let . Suppose that is a scalar without losing of generality as it is sufficient to show the conditions hold for each element of . Note that is an element of for any . So it is sufficient to show is pre-Gaussian uniformly in instead of each element of .
is an envelope of for some . The first condition for the uniform pre-Gaussianity holds as for some . The second condition holds as is shown to satisfy the uniform entropy condition in the proof of Lemma D.3.
∎
Lemma I.6.
Let and , and suppose that , and , i.e., it is (i) continuous or (ii) semi-continuous. Then,
uniformly over for any .
Proof.
Note that
| (I.2) | ||||
| (I.3) |
The stochastic term (I.2) converges in probability to zero uniformly with respect to . This is because Lemma I.5 shows that when , then
as it can be expressed as .
Suppose . The case for follows similarly. We will show that (I.3) converges as follows:
uniformly with respect to .
Let
which will be shown to converge to zero uniformly with respect to . By Taylor epxansion, its formula can be derived as follows:
where . Note that unifromly with respect to . Hence, for sufficiently large , for some . Moreover, and uniformly with respect to . Therefore, uniformly with respect to , i.e.,
uniformly with respect to . We can derive a similar result for that leads to
uniformly with respect to . As ,
which completes the proof. ∎
Lemma I.7.
Let and , and suppose that and , i.e., it is (iii) semi-discontinuous. Then,
uniformly over for any .
Proof.
Note that
| (I.4) | ||||
| (I.5) |
The stochastic term (I.4) converges in probability to zero uniformly with respect to by Lemma I.5, by an argument similar to the proof of Lemma I.6 that shows (I.2) converges to zero.
Suppose . The case for follows similarly. We will show that (I.5) converges as follows:
uniformly with respect to .
Let
which will be shown to converge to zero uniformly with respect to . By Taylor expansion, its formula can be derived as follows:
where . Note that unifromly with respect to . Hence, for sufficiently large , and for some . Moreover, uniformly with respect to . As , uniformly with respect to , i.e.,
uniformly with respect to . We can derive a similar result for that leads to
uniformly with respect to . As ,
which completes the proof. ∎
Lemma I.8.
Let and . Then,
Proof.
Note that . Let be the probability law of . As is Glivenko-Cantelli uniformly in , which is shown in the proof of Lemma I.5, is , and hence in by Lemma B.1. By Proposition 2, is also in , which completes the proof. ∎
Lemma I.9.
Let and . Then,
Proof.
Note that . As and in by Lemma B.1, is in . By applying Lemma I.18, in for any real vector . By Cramér-Wold, in , and applying Slutsky theorem completes the proof. ∎
The Lemma I.10 states uniform bootstrap probability limit of the following matrix:
Lemma I.10.
Let and . Then,
Proof.
We apply Proposition 2 to prove the result. First, we need to show that and are Glivenko-Cantelli uniformly in , where is the probability law of . It is shown in Lemma I.3 that the functional classes are Glivenko-Cantelli uniformly in . Second, the condition for envelope holds as , which is implied by for some . ∎
Lemma I.11.
Let and . If , then
Proof.
Note that because , see (I.1). Therefore, . Let and , where and are dirac measures at and . Then, it is sufficient to prove in if and
For , let and be its envelope. Let be symmetrized Poisson random variables with parameter . By Lemma I.14,
conditionally on . For all , the last display is stochastically bounded upto constant by
| (I.6) |
by Lemma I.16, where is an envelope function of . The first term is bounded above by , which converges to zero for any as , and (see proof of Theorem 3.6.3 in van der Vaart and Wellner, (1996)). By triangle inequality,
and the last display is bounded upto constant by
For each , by Lemma I.15,
The right hand side of the last display converges to zero uniformly with respect to as and since the functional class is shown to be pre-Gaussian uniformly in in the proof of Lemma I.5.
For each ,
and by Hoeffding’s inequality, e.g., Lemma 2.2.7 in van der Vaart and Wellner, (1996). The following paragaph shows that as and .
As it is sufficient to consider each element of , we focus on , the th term of , and assume that is a scalar without losing of generality. Note that
Without losing of generality, let , and be a constant such that for . Set
which is an envelope of . . Furthermore,
while , and
for some . Hence, for some uniformly over all . Therefore, for some and converges to zero as .
Recall that the first term in (I.6) goes to zero for any fixed when . The second term in (I.6) is bounded by , where . It is shown in the previous paragraph that uniformly with respect to as and . Therefore, for any , there exists such that for all . Then, there exists large enough such that the first term in (I.6) is bounded by for . In conclusion, if and . By applying the Markov inequality, we can complete the proof. ∎
Lemma I.12.
Let and , and suppose that , and , i.e., it is (i) continuous or (ii) semi-continuous. Then, for any ,
is in .
Proof.
As the proof is quite similar to the proofs of Lemma E.5 and Lemma I.6, we just explain direction of the proof heuristically. As is consistent to ,
By Lemma I.11,
as the last display can be expressed by . Hence,
and applying Lemma I.6 completes the proof.
∎
Lemma I.13.
Let and , and suppose that and , i.e., it is (iii) semi-discontinuous. Then, for any ,
is in .
Proof.
We omit the proof as it is almost identical to the proof of Lemma I.12. ∎
The following proposition is bootstrap Glivenko-Cantelli theorem uniform in underlying probability measures .
Proposition 2.
Let be a triangular array of random elements in a measurable space while ’s are independent to each other with probability law , and be a class of functions on with an envelope . Suppose that is a Glivenko-Cantelli class uniformly in , and . For each , let be an exchangeable nonnegative random vector independent of such that and converges to zero in probability. Then, for every and , as ,
where is a dirac measure at .
Let be a multinomial vector divided by with parameters and probabilities , which satisfies and converges to zero in probability. Suppose that are i.i.d. resampling draws from . Then, , and the probability law of can be identified with the probability law of the empirical bootstrap conditional on the data.
Proof.
Let . By Lemma I.17,
| (I.7) |
Note that , while and . Moreover, by dominated convergence theorem because . Hence, the first term in the right hand side of (I.7) converges to zero in probability for fixed as . That is, for any and ,
Note that (see the proof of Theorem 3.6.16 in van der Vaart and Wellner, (1996)). Finally, we need to show . By triangle inequality,
The equality comes from being independent of . Note that as since is Glivenko-Cantelli uniformly in . Hence, the second term in the right hand side of (I.7) converges to zero in probability as . That is, for any ,
Therefore, for any ,
By applying the Markov inequality as follows, we can complete the proof:
∎
Lemma I.14 (Lemma 3.6.6 van der Vaart and Wellner, (1996)).
For fixed elements of a set , let be an i.i.d. sample from , where is a dirac measure at . Then,
for every class of functions and i.i.d. Poisson variables with mean .
Lemma I.15 (Lemma 2.3.6 van der Vaart and Wellner, (1996)).
Let be independent stochastic processes with mean zero. Then,
for i.i.d. Rademacher random variables and any functional class .
Lemma I.16 (Lemma 2.9.1 van der Vaart and Wellner, (1996)).
Let be i.i.d. stochastic processes with independent of the Rademacher variables . Then, for every i.i.d. sample of mean-zero and symmetrically distributed random variables independent of and ,
where is norm such that for a random variable .
Lemma I.17 (Lemma 3.6.7 van der Vaart and Wellner, (1996)).
For arbitrary stochastic processes , every exchangeable random vector that is independent of , and any ,
where is a random vector uniformly distributed on the set of all permutations of and independent of . is norm such that for a random variable .
Lemma I.18 (Lemma 3.6.15 van der Vaart and Wellner, (1996)).
For each , let and be a vector of numbers and exchangeable random vector such that
where and . Then, .
Let be a multinomial vector with parameters and probabilities . Then, , and conditions for in Lemma I.18 hold.