Boresight Alignment of DArk Matter Particle Explorer
Abstract
The DArk Matter Particle Explorer (DAMPE) can measure -rays in the energy range from a few GeV to about 10 TeV. The direction of each -ray is reconstructed with respect to the reference system of the DAMPE payload. In this paper, we adopt a maximum likelihood method and use the -ray data centered around several bright point-like sources to measure and correct the angular deviation from the real celestial coordinate system, the so called “boresight alignment” of the DAMPE payload. As a check, we also estimate the boresight alignment for some sets of simulation data with artificial orientation and obtain consistent results. The time-dependent boresight alignment analysis does not show evidence for significant variation of the parameters.
keywords:
instrumentation: detectors — gamma rays: general — methods: data1 Introduction
The DArk Matter Particle Explorer (DAMPE) is a satellite mission which has been operating stably in a solar synchronous orbit since it was launched on December 17, 2015 from Jiuquan, China. The payload is designed to detect high energy cosmic rays and -rays with high energy resolution and spatial resolution. The detector consists of 4 sub-detectors (Chang 2014; Chang et al. 2017), from the top to the bottom including a Plastic Scintillator Detector (PSD) (Yu et al. 2017; Ding et al. 2019), a Silicon Tungsten tracKer-convertor (STK) (Azzarello et al. 2016), a BGO calorimeter (BGO) (Zhang et al. 2016), and a NeUtron Detectors (NUD) (He et al. 2016). Each day, DAMPE collects about five million high energy particles, dominated by the protons, helium and heavier nuclei. The on-orbit calibration with these data proves that DAMPE is fully operational as expected and all sub-detectors perform well. One important part of the on-orbit calibration is the payload internal and satellite alignment (DAMPE Collaboration 2019). The details of alignments of the STK and PSD with the on-orbit data have already been published (Tykhonova et al. 2018; Ma et al. 2018). In this work we focus on the boresight alignment of DAMPE.
For each incident high energy particle, the direction is reconstructed with respect to the reference system of DAMPE payload. To get the celestial coordinates of the detected high energy particles, the incident directions should be transformed to the celestial coordinate system from the payload coordinate system .
As usual, the transformation depends on both the GPS navigation system and star-trackers. Actually, there are two star tracks on the satellite. When the star-trackers calculate the attitude angle of the satellite, the need to compare with the zenith and azimuth provided by the GPS. Only if the deviation between the results is less than a special value, it is regarded as an effective measurement. The payload system is nominally designed the same as the satellite system. As a result of thermal variations, acoustic vibrations, zero gravity fluctuations, and uncertainty in the orbital parameters and star-tracker pointing, small deviations from real pointing are expected to be introduced to the resulting celestial coordinate. In addition to causing a systematic shift between the observed position and the real one of a point-like source, such a mismatch will also give rise to a distorted point spread function (PSF) profile.
In order to effectively measure and correct such a bias, we take the GeV -ray data centered around a few brightest point-like sources detected by DAMPE to measure and then correct the angular deviation from the real celestial coordinate. Such a process is the so called “boresight alignment” of DAMPE payload. In this work we introduce the method, result and verification of our boresight alignment in detail.
2 Likelihood Analysis
The deviation needed to be calibrated can be described as a rotation in the payload coordinate system. Therefore, with a rotation matrix the vectors in the payload coordinate and the satellite coordinate systems can be directly related. The rotation of a vector in the satellite coordinate system can be described by three Euler angles which are generally called roll, pitch and yaw , which represent the rotation angles along x, y and z axes respectively. The rotation matrix in terms of these variables reads
| (1) |
Thus, the column vector of the track in the payload coordinate system can be expressed as
| (2) |
where is the track constructed in the payload coordinate system before the boresight alignment.
The rotation transforms the position of the incident particles in the payload coordinate, and subsequently modifies direction in celestial coordinate. Based on the housekeeping data of navigation system and star trackers, the transformation at time from the payload coordinate to the celestial coordinate can be computed as a matrix . The correction of a vector in celestial coordinates due to boresight alignment () can be expressed as
| (3) |
Some bright GeV sources, such as Vela, Geminga and Crab, have been well measured in the radio and optical bands, and their positions in celestial coordinate system are precisely known. Some bright GeV sources, such as Vela, Geminga and Crab, have been well measured in the radio and optical bands, and their positions in celestial coordinate system are known with the precision of (Fey et al. 2004).
So, we can use the brightest -ray sources to carry out the boresight alignment. A set of software packages (DmpST), which incorporate the instrument response functions (IRFs) and the science tools, have been developed to analyze the -rays detected by DAMPE (Duan et al. 2019). In this work DmpST is adopted to achieve our purpose. Due to the point spread function (PSF) which is the probability distribution of the reconstructed direction for a event with specify primary energy and incident direction especially large at low energies and large incident angles (e.g., 68.3% of the counts will be within at 1 GeV and ) , Duan et al. (2019) to analyze a single source the counts within a region around the source have to be included. We call that region the “region of interest(ROI)”.
In order to determine the boresight alignment parameters with the on-orbit data, a likelihood maximization analysis of some bright -ray point-like sources has been preformed. For a given source in a ROI, we have used a point-like -ray source model with a background component. To evaluate the background we consider all the other point-like sources in the ROI, Galactic diffuse emission, extra-galactic emission and some residual cosmic-ray background in the ROI, which, for the sake of simplicity, is modeled as a uniform template with a power-law spectrum(Fermi-LAT Collaboration 2012; Roth 2012). After this model is multiplied by the exposure and convolved with the PSF of DAMPE, we get the expectation of the Poisson distributed variable observed by the -rays in the ROI. We ignore the effect of misalignment in the exposure since the angular deviation are expected to be very small and the exposure changes smoothly in the ROI. In the DmpST, we model the PSF by two King functions (Duan et al. 2019) and it is consistent with the GEANT4 simulation for DAMPE, so we use it to describe the angular distribution of the selected -rays sample. Thus, the unbinned Poisson likelihood (Cash 1979) of the reconstructed -ray directions to estimate the best fit parameters of the boresight alignment() is given as
| (4) |
where is the expected contribution from the point-like source and background to the -rays with energy and direction in celestial coordinate system, is the direction of i-th photon after boresight alignment and is the time when i-th photon is recorded by the detector. The MINUIT111https://github.com/iminuit/iminuit algorithm is adopted to perform the optimization (James & Roos 1975) and the three boresight alignment parameters are derived.
3 Validation
Besides the DmpIRFs and the analysis tools, DmpST contains a simulation module which is used to simulate photons from astrophysical sources and process those photons according to the DmpIRFs during the on-orbit operation of DAMPE.
This simulation is cross-validated by the analysis tools in the DmpST (Duan et al. 2019) which are used to fit the parameters of the classified -ray sources. To validate the alignment method, we manually import a misalignment defined by the Eq. 3 to simulate a sample of -ray events, then the same alignment approach is applied to the misaligned sample.
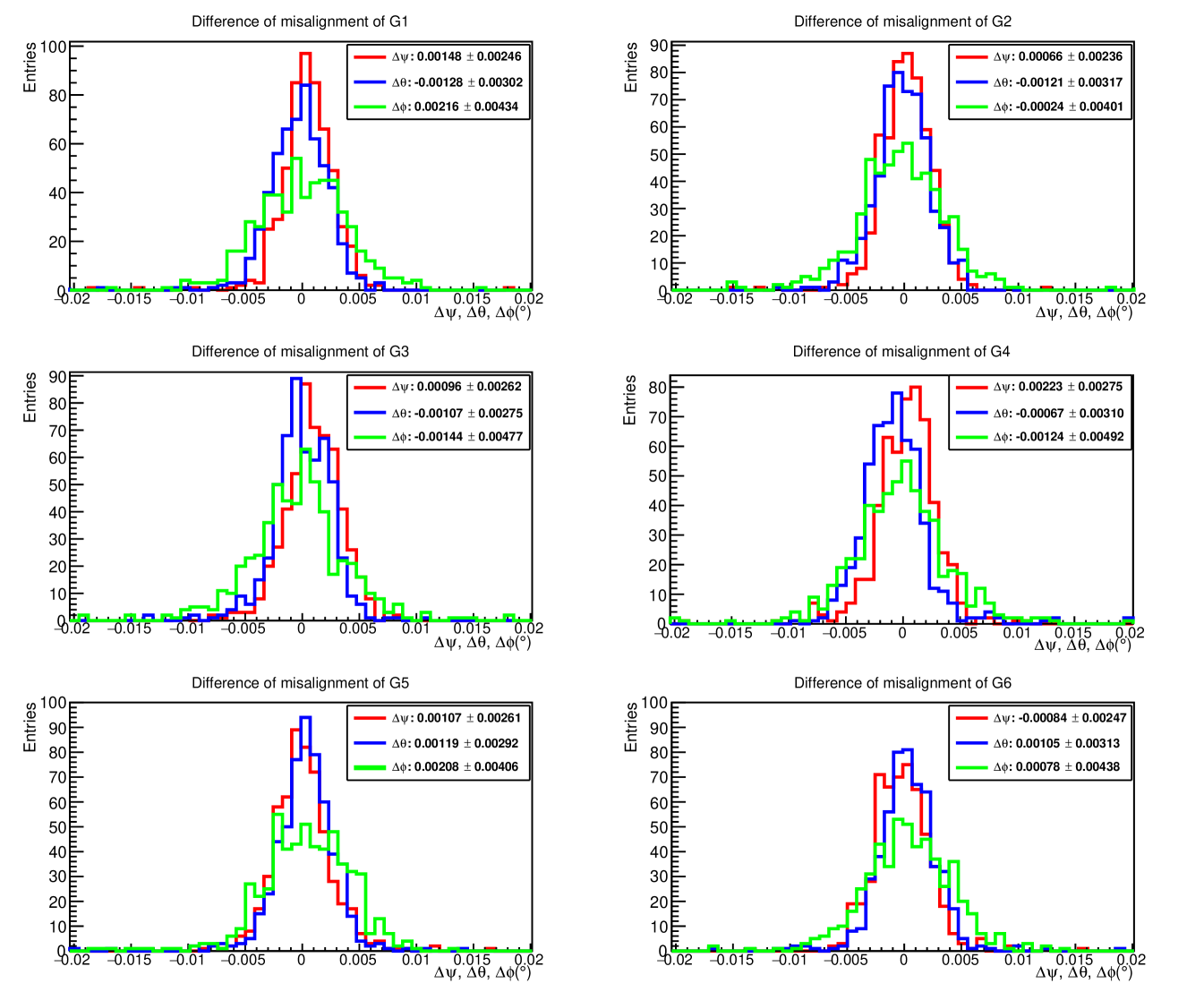
In this test, we randomly select 6 groups of boresight parameters in the range between to , as summarized in the Table 1.
| Preset Parameters | Fitted Means and RMSs | |||||
|---|---|---|---|---|---|---|
| Group | ||||||
| 1 | -0.3083 | -0.4682 | -1.7161 | -0.3068 0.00246 | -0.4605 0.00302 | -0.3046 0.00434 |
| 2 | -0.7615 | -0.6123 | 0.3076 | -0.7613 0.00236 | -0.6134 0.00317 | -0.3078 0.00401 |
| 3 | -1.1194 | -0.8551 | -0.0436 | -1.1195 0.00262 | -0.8562 0.00275 | -0.0450 0.00477 |
| 4 | -1.7765 | 1.2667 | 0.3106 | -1.7743 0.00275 | 1.2600 0.00310 | 0.3084 0.00492 |
| 5 | 0.8902 | -1.1783 | -0.5767 | 0.8913 0.00261 | -1.1771 0.00292 | -0.5746 0.00406 |
| 6 | 0.1250 | 0.0211 | -0.1436 | 0.1242 0.00247 | 0.0222 0.00313 | -0.1428 0.00438 |
For each group of preset boresight alignment parameters, we simulate 3 year observations to Vela pulsar for 600 times. We then analyze these -ray data with DmpST and then carry out the boresight alignment analysis with the procedure introduced in Section 2. As shown in Tab. 1 and Fig. 1, the difference between the preset alignment parameters and the best fitted ones are very small (the RMS is less than 0.005∘). Such results demonstrate that the boresight alignment method is reliable.
4 Boresight Alignment of flight data
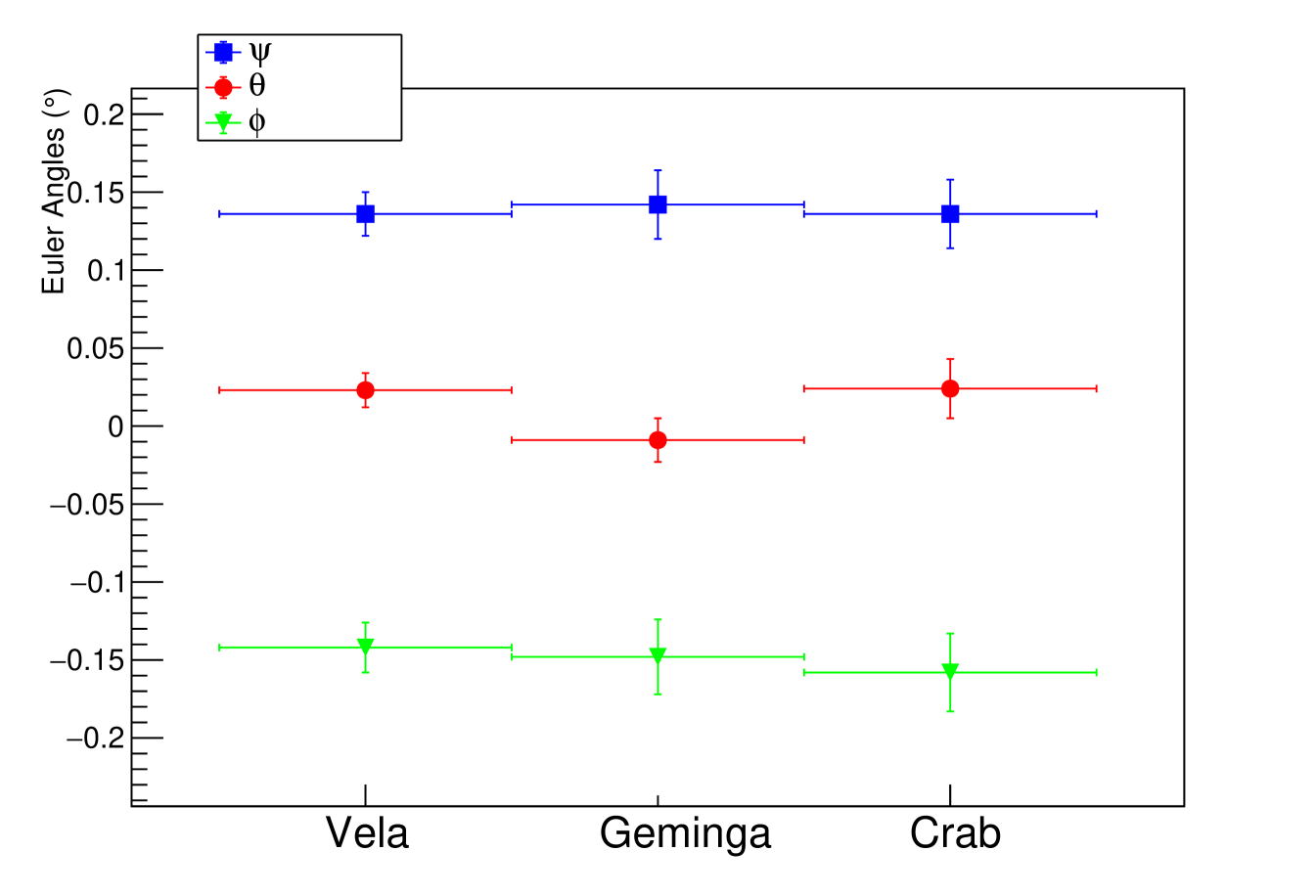
During the first 3 years of on-orbit operation, DAMPE successfully observed some bright GeV -rays sources (Xu et al. 2018; Liang et al. 2017). A few sources with accurate location information are bright enough for our purpose. The sources included in our following analysis are Vela, Crab and Geminga (Fermi-LAT Collaboration 2012). The data detected from 2016 January 1 to 2019 January 1 are included in the analysis. We select the photons within 4∘ from the targets and restrict the energy between 3 GeV and 100 GeV(Duan et al. 2019). We fix the spectral parameters of the target sources to the values from the third Fermi-LAT catalog of high-energy sources (Fermi-LAT Collaboration 2012) and optimize the rotation angles as well as the spectral parameters of the background using maximum likelihood method. The resulting boresight alignment parameters for these three sources are consistent with each other (see Fig. 2), as expected. In practice, the parameters which are applied for -ray analyses mainly come from the contribution of the Vela pulsar, which are
| (5) | |||
Because the collected statistic of the Vela pulsar is several times larger than any other brightest -ray source, while the results of others can be validations and supplements. The uncertainties consist of two independent parts: the statistical errors fitted by Minuit and the measuring errors of to each parameter given by
the engineering parameters of the satellite.
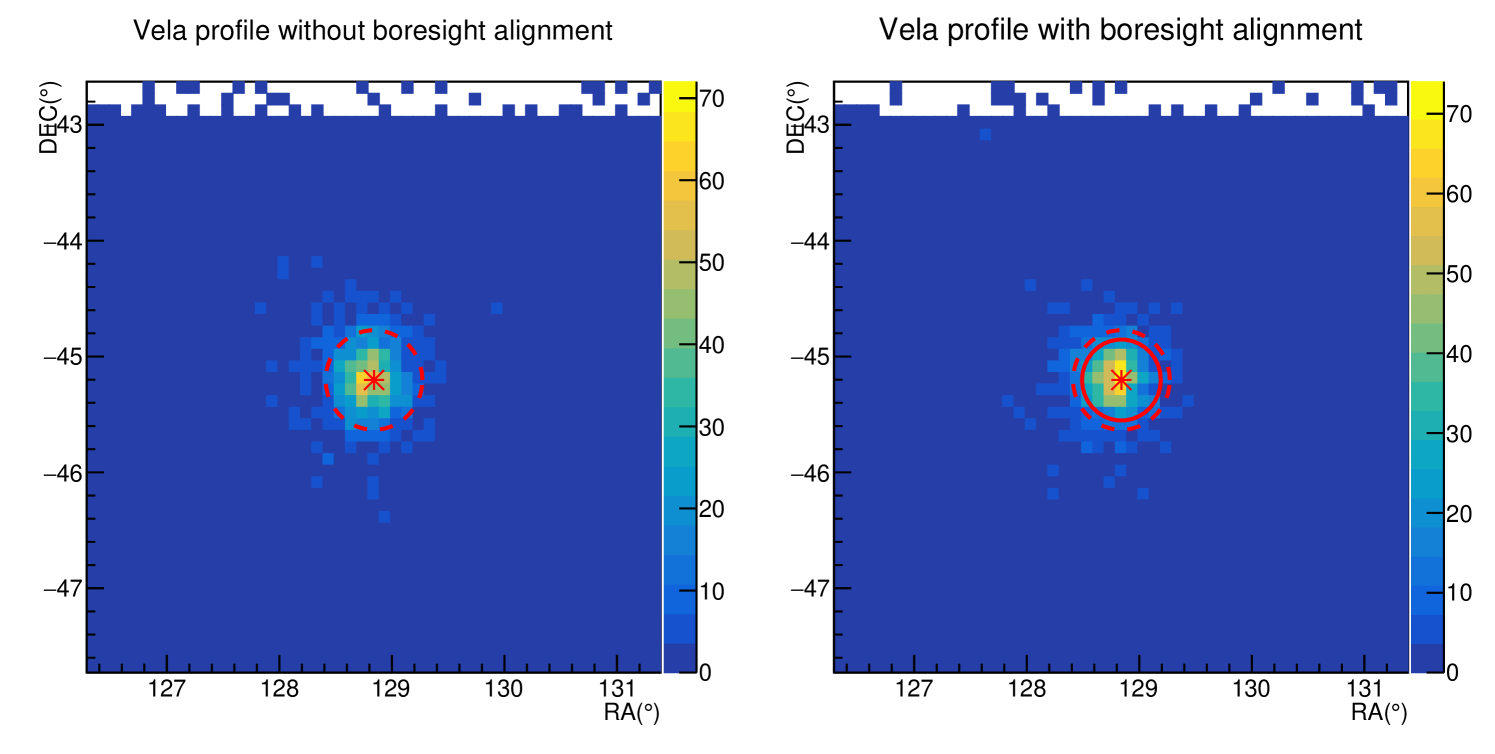
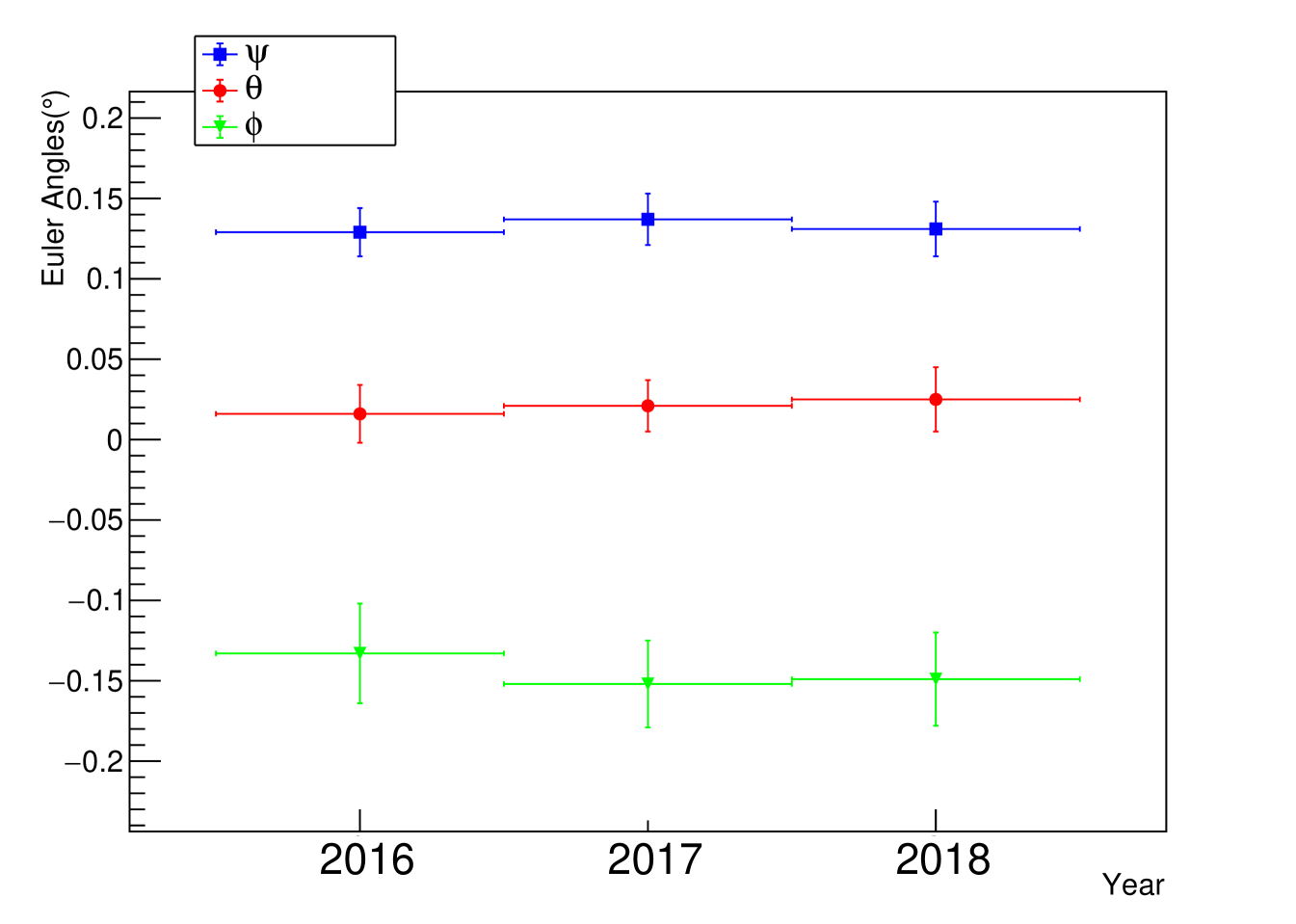
After applying these boresight alignment, the position profile of the target source gets improved (see Fig. 3 for illustration). We have also studied the stability of the boresight alignment parameters by evaluating the parameters each year. As is shown in Fig. 4, there are no significant variation in the boresight alignment parameters.
5 Conclusion
The payload of DAMPE consists of four sub-detectors and the directions of the incident particles are mainly reconstructed with the STK and BGO data. Such directions are with respect to the reference system of the DAMPE payload and further adjustments are needed to remove the miss match between the reconstructed direction and the intrinsic one. For such a purpose we have developed a maximum likelihood method. Our approach has been verified with the simulation data provided by DmpST. We then take the 3 years of -ray data of Vela, Geminga and Crab pulsars measured by DAMPE to estimate the boresight alignment parameters. The fitted results of the Vela pulsar show that there is a primary offset between the orientation of payload and satellite platform of , which is consistent with the other brightest -ray point-like sources. We have also examined the variation of these parameters over the time and do not find any evidence for the evolution, which provides additional support to the stability of the sub-detectors of DAMPE in space, as found in the on-orbit calibration of the whole payload. With the boresight alignment corrections, the directions of the incident particles get improved.
Acknowledgements.
The DAMPE mission was founded by the strategic priority science and technology projects in space science of the Chinese Academy of Sciences (No. XDA04040000 and No. XDA04040400). This work is supported in part by by National Key Program for Research and Development (No. 2016YFA0400200), the National Basic Research Program (No. 2013CB837000), the Strategic Priority Research Program of the Chinese Academy of Sciences “Multi-Waveband Gravitational Wave Universe”(No. XDB23040000), the Strategic Priority Research Program of theCAS(No. XDB23040000), Youth Innovation Promotion Association of CAS, the National Natural Science Foundation of China (Nos. U1738123, U1631111), the 100 Talents program of Chinese Academy of Sciences and the Young Elite Scientists Sponsorship Program. In Europe DAMPE activities receive generous support by the Swiss National Science Foundation (SNSF), Switzerland and the National Institute for Nuclear Physics (INFN), Italy.References
- Fermi-LAT Collaboration (2012) Abdo, A. A., Ackermann, M., Ajello, M., et al., 2009, Astroparticle Physics, 32, 193
- Fermi-LAT Collaboration (2012) Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4
- DAMPE Collaboration (2019) Ambrosi, G., An, Q., Asfandiyarov, R., et al. 2019, Astroparticle Physics, 106, 18
- Azzarello et al. (2016) Azzarello, P., Ambrosi, G., Asfandiyarov,R., et al., 2016, Nucl. Instrum. Meth. A, 831, 378
- Cash (1979) Cash, W., 1979, ApJ, 228, 939
- Chang (2014) Chang, J., 2014, Chinese Journal of Space Science, 34, 550
- Chang et al. (2017) Chang, J., Ambrosi, G., An, Q., et al. 2017, Astroparticle Physics, 95, 6
- Ding et al. (2019) Ding, M., Zhang, Y.-P., Zhang,Y.-J., et al, 2019, \raa, 19, 3
- Duan et al. (2019) Duan, K.-K., Jiang, W., Liang, Y.-F, et al., 2019, \raa, 19, 132
- Fey et al. (2004) Fey, A. L., Ma, C., Arias, E. F. , et. al., 2004, AJ, 127, 3587
- He et al. (2016) He M., Ma T., Chang J., et al., 2016, Acta Astronomica Sinica, 57, 1
- James & Roos (1975) James, F., & Roos, M., 1975, Computer Physics Communications, 10, 343
- Liang et al. (2017) Liang, Y.-F., Duan, K.-K., Shen, Z.-Q., et al., 2017, ICRC, 35, 603
- Ma et al. (2018) Ma, P.-X., Zhang, Y.-J., Zhang, Y.-P., et al., 2019, \raa, 19, 82
- Roth (2012) Roth, M., 2012, Ph.D. Thesis, 82R, University of Washington
- Tykhonova et al. (2018) Tykhonova, A., Ambrosib, G., Asfandiyarov, R., et al., 2018, Nucl. Instrum. Meth. A, 893, 43
- Xu et al. (2018) Xu, Z.-L., Duan, K.-K., Shen, Z.-Q., et al. 2018, \raa, 18, 27
- Yu et al. (2017) Yu, Y.-H., Sun, Z.-Y., Su, H., et al. 2017, Astroparticle Physics, 94, 1
- Zhang et al. (2016) Zhang, Z.-Y., Wang, C., Dong, J.-N., et al. 2016, Nucl. Instrum. Meth. A, 836, 98