Bottom-charmed baryons in a nonrelativistic quark model

Qing-Fu Song Department of Physics, Hunan Normal University, and Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education, Changsha 410081, China Key Laboratory for Matter Microstructure and Function of Hunan Province, Hunan Normal University, Changsha 410081, China Qi-Fang Lü lvqifang@hunnu.edu.cn Department of Physics, Hunan Normal University, and Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education, Changsha 410081, China Key Laboratory for Matter Microstructure and Function of Hunan Province, Hunan Normal University, Changsha 410081, China Research Center for Nuclear Physics (RCNP), Ibaraki, Osaka 567-0047, Japan Atsushi Hosaka hosaka@rcnp.osaka-u.ac.jp Research Center for Nuclear Physics (RCNP), Ibaraki, Osaka 567-0047, Japan Advanced Science Research Center, Japan Atomic Energy Agency, Tokai, Ibaraki 319-1195, Japan

Abstract

In this work, we study the low-lying mass spectra for bottom-charmed baryons in a nonrelativistic quark model by solving the three-body Schrödinger equation. The lowest $\Xi_{bc}$ , $\Xi_{bc}^{\prime}$ , $\Omega_{bc}$ , and $\Omega_{bc}^{\prime}$ states are predicted to be about 6979, 6953, 7109, and 7092 MeV, respectively. Also, the strong decays for the low-lying excited states are investigated. Our results indicate that some of $\lambda-$ mode $P-$ wave bottom-charmed baryons are relatively narrow, which can be searched for in future experiments. For the low-lying $\rho-$ mode and $\rho-\lambda$ hybrid states, their strong decays are highly suppressed and they can survive as extremely narrow states. Moreover, the mass spectra and strong decays for bottom-charmed baryons preserve the heavy quark symmetry well. We hope our calculations can provide helpful information for further experimental and theoretical researches.

bottom-charmed baryons, mass spectra, strong decays

I Introduction

In the past years, with the development of the large-scale accelerator facilities, plenty of heavy baryons have been observed and significant progress has been achieved in experiments. These discoveries have triggered wide attentions of theorists, which leads the study on mass spectra and internal structures of heavy baryons to a hot topic in hadron physics Chen:2016spr ; Cheng:2021qpd . Understanding the nature of heavy baryons and searching for the missing heavy resonances can help us to establish and complete the hadron spectroscopy and provide a good platform to better investigate the heavy quark symmetry. Until now, most experimental observations in heavy baryon sector belong to the singly heavy baryons, while the doubly heavy baryons are rare. Due to the lack of experimental data, our understanding of the doubly heavy baryons is still scarce, and more experimental and theoretical efforts are encouraged and needed.

In 2002, the SELEX Collaboration reported an evidence of a doubly charmed baryon $\Xi_{cc}^{+}$ that has a mass of 3519 $\pm$ 1 MeV in the $\Lambda_{c}^{+}K^{-}\pi^{+}$ final state Mattson:2002vu and $pD^{+}K^{-}$ decay mode Ocherashvili:2004hi . However, the existence of $\Xi_{cc}^{+}(3519)$ was disfavored by the following FOCUS, BaBar, Belle and LHCb Collaborations Ratti:2003ez ; Aubert:2006qw ; Chistov:2006zj ; Aaij:2013voa , and the following theoretical works do not also support this discovery. In 2017, a highly significant structure $\Xi_{cc}^{++}(3621)$ with a mass of 3621.40 $\pm$ 0.72 $\pm$ 0.27 $\pm$ 0.14 MeV was observed in the $\Lambda_{c}^{+}K^{-}\pi^{+}\pi^{+}$ mass spectrum by the LHCb Collaboration Aaij:2017ueg . Subsequently, the LHCb Collaboration measured its lifetime LHCb:2018zpl ; LHCb:2019qed and other decay modes LHCb:2018pcs ; LHCb:2019ybf ; LHCb:2019epo ; LHCb:2022rpd . Meanwhile, the LHCb Collaboration paid lots of attentions to hunt for more doubly heavy baryons, however no more signal has been found so far LHCb:2021eaf ; LHCb:2020iko ; LHCb:2021xba ; LHCb:2021rkb ; LHCb:2019gqy ; LHCb:2022fbu . In particular, the $\Xi_{bc}$ and $\Xi_{bc}^{\prime}$ state was placed great expectations to be discovered in the near future, where one charm quark in $\Xi_{cc}$ is replaced by a bottom quark.

Theoretically, there are various methods to predict the mass spectra of doubly heavy baryons, such as potential models Kiselev:2001fw ; Ebert:1996ec ; Tong:1999qs ; Ebert:2002ig ; Gershtein:2000nx ; Roberts:2007ni ; Giannuzzi:2009gh ; Martynenko:2007je ; Valcarce:2008dr ; Eakins:2012jk ; Shah:2017liu ; Wang:2021rjk ; Yu:2022lel ; Li:2022ywz ; Soto:2020pfa , heavy quark symmetry and mass formulas Savage:1990di ; Song:2022csw ; Roncaglia:1995az ; Cohen:2006jg ; Karliner:2014gca ; Wei:2015gsa ; Wei:2016jyk ; Oudichhya:2022ssc , QCD sum rule Zhang:2008rt ; Tang:2011fv ; Wang:2010hs ; Aliev:2012ru ; Aliev:2012nn ; Aliev:2012iv , lattice QCD Liu:2009jc ; Brown:2014ena ; Padmanath:2015jea ; Mathur:2018rwu ; Mathur:2018epb , and so on. Besides the mass spectra, the weak and radiative decays of the doubly heavy baryons are also widely discussed in the literature Faessler:2001mr ; Faessler:2009xn ; Albertus:2009ww ; White:1991hz ; Li:2017ndo ; Yu:2017zst ; Ebert:2004ck ; Roberts:2008wq ; Branz:2010pq ; Hackman:1977am ; Bernotas:2013eia ; Dai:2000hza ; Albertus:2010hi ; Qin:2021zqx ; Bahtiyar:2018vub , which provide helpful information for the experimental searches. Among these fruitful theoretical studies, there were only a few works on strong decay behaviors Eakins:2012fq ; Xiao:2017udy ; Mehen:2017nrh ; Ma:2017nik ; Xiao:2017dly ; Yan:2018zdt ; He:2021iwx ; Chen:2022fye . Based on the experimental and theoretical status, the strong decay of doubly heavy baryons should be urgently investigated and highly valued.

In this work, we concentrate on the bottom-charmed family that is made up of a bottom quark $b$ , a charm quark $c$ and a light quark ( $u$ , $d$ , or $s$ ). When the light quark belongs to up or down quark, the bottom-charmed baryon is named as $\Xi_{bc}$ or $\Xi_{bc}^{\prime}$ ; When the light quark is a strange quark, the bottom-charmed baryon is denoted as $\Omega_{bc}$ or $\Omega_{bc}^{\prime}$ . The study of bottom-charmed baryons does not only provide an opportunity for us to investigate the heavy quark symmetry and chiral dynamics simultaneously, but also supplies a unique platform about the conventional baryons with three non-identical quarks. Moreover, the excited states and their strong decay behaviors are essential for better understanding the spectroscopy for bottom-charmed baryons and helping experimentalists to hunt for more hadrons. Among various properties, the Okubo-Zweig-Iizuka-allowed (OZI-allowed) two-body decay processes are particularly interesting where one light meson is, especially the pion, emitted from the parent baryon. In this process, the meson couples to the light quark, and the heavy quark subsystem behaves simply as a spectator. Hence this provides a good platform to investigate dynamics of chiral symmetry at the single quark level. However, the study on strong decays for bottom-charmed baryon is very scarce Eakins:2012fq , and then it is time to explore this topic systematically.

In a previous work, a nonrelativistic quark model was adopted to study the mass spectrum of heavy baryons with two identical quarks, and gained significant achievements Yoshida:2015tia . However, the case of all three quarks with different masses were not studied. Here, we employ the same quark model to bottom-charmed system by solving the three-body Schrödinger equation in order to get the mass spectrum consistently. Besides the masses, the realistic wave functions are obtained simultaneously, and can be used for strong decay calculations. The lowest $\Xi_{bc}$ , $\Xi_{bc}^{\prime}$ , $\Omega_{bc}$ , and $\Omega_{bc}^{\prime}$ states are predicted to be about 6979, 6953, 7109, and 7092 MeV, respectively. Our results indicate that some of $\lambda-$ mode $\Xi_{bc}(1P)$ , $\Xi_{bc}^{\prime}(1P)$ , $\Omega_{bc}(1P)$ , $\Omega_{bc}^{\prime}(1P)$ states are narrow, which have good potentials to be observed by future experiments. Also, the strong decays of the low-lying $\rho-$ mode and $\rho-\lambda$ hybrid states are highly suppressed and can be searched for in the processes with electromagnetic and weak interactions.

This paper is organized as follows. The formalism of potential model and pseudoscalar meson emissions is briefly introduced in Sec. II. We present the numerical results and discussions for the bottom-charmed baryons in Sec. III. A summary is given in the last section.

II FORMALISM

II.1 Potential Model

In order to calculate the spectrum of the low-lying bottom-charmed baryons, we adopt a nonrelativistic quark model, where the Hamiltonian can be expressed as

H=T+\sum_{i<j}^{3}V(r_{ij})

(1)

with the kinetic energy

T=\sum_{i=1}^{3}\left(m_{i}+\frac{\bm{p_{i}^{2}}}{2m_{i}}\right)-T_{CM}

(2)

and the effective potential

V\left(r_{ij}\right)=V^{conf}\left(r_{ij}\right)+V^{coul}\left(r_{ij}\right)+V^{SD}\left(r_{ij}\right).

(3)

Here $T_{CM}$ is the center-of-mass energy, $r_{ij}$ is the distance between the $i$ th and $j$ th quarks. The linear confinement potential $V^{conf}\left(r_{ij}\right)$ and one-gluon-exchange potential $V^{coul}\left(r_{ij}\right)$ are as follows

V^{conf}\left(r_{ij}\right)=\frac{br_{ij}}{2}+C,

(4)

V^{coul}\left(r_{ij}\right)=-\frac{2\alpha^{coul}}{3r_{ij}},

(5)

where $C$ is the overall zero-point-energy parameter. The spin-dependent interaction $V^{SD}\left(r_{ij}\right)$ is the sum of spin-spin term $V^{SS}\left(r_{ij}\right)$ , spin-orbit term $V^{LS}\left(r_{ij}\right)$ , and tensor term $V^{Ten}\left(r_{ij}\right)$

V^{SS}\left({r_{ij}}\right)=\frac{16\pi\alpha^{ss}}{9m_{i}m_{j}}\bm{s_{i}}\cdot\bm{s_{j}}\frac{\Lambda^{2}}{4\pi r_{ij}}\exp(-\Lambda r_{ij}),

(6)

$\displaystyle V^{LS}\left({r_{ij}}\right)$	$\displaystyle=$	$\displaystyle\frac{{\alpha}^{\rm{so}}(1-\exp(-\Lambda r_{ij}))^{2}}{3{r_{ij}}^{3}}$	(7)
		$\displaystyle\times\bigg{[}\bigg{(}\frac{1}{m_{i}^{2}}+\frac{1}{m_{j}^{2}}+\frac{4}{m_{i}m_{j}}\bigg{)}\bm{L}_{ij}\cdot\left(\bm{s}_{i}+\bm{s}_{j}\right)$
		$\displaystyle+\bigg{(}\frac{1}{m_{i}^{2}}-\frac{1}{m_{j}^{2}}\bigg{)}\bm{L}_{ij}\cdot\left(\bm{s}_{i}-\bm{s}_{j}\right)\bigg{]},$

	$\displaystyle V^{Ten}\left({r_{ij}}\right)$	$\displaystyle=$	$\displaystyle\left.\frac{{2\alpha}^{\rm{ten}}(1-\exp(-\Lambda r_{ij}))^{2}}{3m_{i}m_{j}{r_{ij}}^{3}}\left(\frac{3(\bm{s}_{i}\cdot\bm{r_{ij}})(\bm{s}_{j}\cdot\bm{r_{ij}})}{{r_{ij}}^{2}}\right.\right.$		(8)
			$\displaystyle-\left.\bm{s}_{i}\cdot\bm{s}_{j}\biggr{)}\right..$		(8)

The parameters are taken from the original work Yoshida:2015tia and listed in the Table 1. Also, the overall constant $C$ is adjusted by fixing the mass of ground state $\Xi_{cc}(3621)$ , which is suitable for present bottom-charmed baryons systems.

Table 1: The relevant parameters adopted in this work.

	Parameters	Value
	$m_{u/d}(\textrm{GeV})$	0.300
	$m_{s}$ $(\textrm{GeV})$	0.510
	$m_{c}$ $(\textrm{GeV})$	1.750
	$m_{b}$ $(\textrm{GeV})$	5.112
	$b$ $(\textrm{GeV}^{2})$	0.165
	$K$ $(\textrm{GeV})$	0.090
	$\alpha^{ss}$	1.200
	$\alpha^{so}$	0.077
	$\alpha^{ten}$	0.077
	$\Lambda$ $(\textrm{fm}^{-1})$	3.500
	${C}$ $(\textrm{GeV})$	-1.203

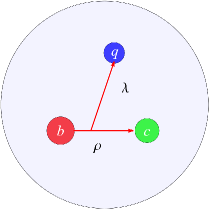
The bottom-charmed baryon is a three-quark system, where the Jacobi coordinates can be introduced to eliminate the center-of-mass energy. As illustrated in Figure 1, the Jacobi coordinates are defined as

\bm{\rho}=\bm{r_{2}}-\bm{r_{1}},

(9)

\bm{\lambda}=\bm{r_{3}}-\frac{{m_{1}}\bm{r_{1}}+m_{2}\bm{r_{2}}}{m_{1}+m_{2}},

(10)

\bm{R}=\frac{{m_{1}}\bm{r_{1}}+m_{2}\bm{r_{2}}+m_{3}\bm{r_{3}}}{m_{1}+m_{2}+m_{3}}.

(11)

where $r_{i}$ and $m_{i}$ denote the position vector and the mass of the $i$ th quark, respectively. The $\bm{\rho}$ stands for the relative coordinate between bottom and charm quarks, the $\bm{\lambda}$ represents the relative coordinate between the light and heavy subsystems, and the $\bm{R}$ is mass center coordinate.

Refer to caption — Figure 1: A typical sketch of the bottom-charmed baryons

The bottom-charmed baryons can be divided into four types according to the total wave functions, which are denoted as $\Xi_{bc}$ $\Xi_{bc}^{\prime}$ , $\Omega_{bc}$ , and $\Omega_{bc}^{\prime}$ , respectively. These notations follow those of the singly heavy baryons $\Xi_{c}$ , $\Xi_{c}^{\prime}$ , $\Xi_{b}$ , and $\Xi_{b}^{\prime}$ , and the naming scheme can be referred to Refs. Chen:2016spr ; Eakins:2012jk ; Li:2022ywz . In the present work, the orbital wave functions are expanded in terms of a set of Gaussian basis functions that forms an approximate complete set Hiyama:2003cu ; Hiyama:2018ivm . Then, the explicit expression for spatial part can be written as

\Psi(\bm{\rho},\bm{\lambda})=\sum_{n,N}C_{n,N}\phi_{n}(\bm{\rho})\phi_{N}(\bm{\lambda})

(12)

with

{}\phi_{n}(\bm{\rho})=N_{nl_{\rho}}\rho^{l_{\rho}}e^{-\nu_{n}\rho^{2}}Y_{l_{\rho}m_{l_{\rho}}}\left(\bm{\hat{\rho}}\right)

(13)

and

{}\phi_{N}(\bm{\lambda})=N_{Nl_{\lambda}}\lambda^{l_{\lambda}}e^{-\nu_{N}\lambda^{2}}Y_{l_{\lambda}m_{l_{\lambda}}}(\bm{\hat{\lambda}}),

(14)

where $C_{n,N}$ are the expansion coefficients. It is worth noting that the $\rho$ and $\lambda$ mode can be hardly separated in the strict sense for the systems with three non-identical masses. However, in view of the heavy quark symmetry, the orbital wave functions for bottom-charmed baryons can be separated approximately and we prefer to adopt the above trial wave functions to solve the three-body Schrödinger equation.

The range parameters of Gaussian functions are given as

\nu_{n}=1/r_{n}^{2},r_{n}=r_{1}a^{n-1}(n=1,...,n_{max}),

(15)

\nu_{N}=1/R_{N}^{2},R_{N}=R_{1}A^{N-1}(N=1,...,N_{max}),

(16)

where $n$ and $N$ are the number of Gaussian functions, and $a$ and $A$ are the ratio coefficients. According to the Rayleigh-Ritz variational principle, one can have

\sum_{j}^{n_{max}\times N_{max}}[H_{ij}-EN_{ij}]C_{j}=0,(i=1\sim n_{max}\times N_{max}),

(17)

where the $H_{ij}$ are the matrix elements in the total color-flavor-spin-orbital bases, $E$ stands for the eigenvalue, and $C_{j}$ are the relevant eigenvectors. Finally, the spectrum of bottom-charmed baryons can be obtained by solving the generalized eigenvalue problem.

In constructing the total wave functions, we adopt the $j-j$ coupling scheme to investigate the bottom-charmed baryons, where the states are defined as

\mid J^{P},j\rangle=\mid[(l_{\rho}S_{\rho})_{J_{\rho}}(l_{\lambda}s_{3})_{j}]_{J^{P}}\rangle

(18)

The label $l_{\rho}$ is the orbital quantum number between the two heavy quarks, the $l_{\lambda}$ the orbital quantum number between the light and heavy subsystems, $S_{\rho}$ the spin quantum number of two heavy quarks, $J_{\rho}$ the total angular momentum of heavy quark subsystem, $j$ the total angular momentum of light quark system that is usually known as the light quark spin, and $J^{P}$ the spin-parity for hadrons. More details of different coupling schemes and their relations can be found in our previous work He:2021iwx .

II.2 Pseudoscalar meson emissions

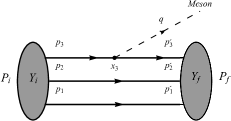
Besides the mass spectrum, the strong decays can reflect the internal structures of hadrons more explicitly. In this subsection, the approach of strong decays for bottom-charmed baryons is introduced briefly. In the quark model, the pseudoscalar meson can couple to the light quark inside a bottom-charmed baryons through the Yukawa interaction, which is considered to contribute predominantly to one-meson emission decays $Y_{bc}^{i}(P_{i})$ $\to$ $Y_{bc}^{f}(P_{f})$ + $M_{p}(q)$ in Figure 2. The axial-vector coupling between the pseudoscalar meson and a light quark can be written as

\mathcal{L}_{M_{p}qq}=\frac{g_{A}^{q}}{2f_{p}}\bar{q}\gamma_{\mu}\gamma_{5}\vec{\tau}q\cdot\partial^{\mu}\vec{M_{p}},

(19)

where the $q$ stands for the quark field, $g_{A}^{q}$ is the quark-axial-vector coupling and $f_{p}$ is the decay constant. In present work, $f_{\pi}$ = 93 $\mathrm{MeV}$ and $f_{K}$ =111 $\mathrm{MeV}$ are adopted that have been widely used in quark model calculations Arifi:2022ntc ; Arifi:2021orx ; Nagahiro:2016nsx ; Xiao:2017udy ; Wang:2018fjm ; Liu:2019wdr ; Lu:2022puv .

The wave function for the $Y_{bc}$ $(Y_{bc}=\Xi_{bc}$ , $\Xi_{bc}^{\prime}$ , $\Omega_{bc}$ , and $\Omega_{bc}^{\prime})$ baryon with mass $M_{Y_{bc}}$ in the rest frame can be expressed in the momentum representation as

$\displaystyle\left\|Y_{bc}(J)\right\rangle=$	$\displaystyle\sqrt{2M_{Y_{bc}}}\sum_{\{s,l\}}\int\frac{d^{3}\mathbf{p}_{\rho}}{(2\pi)^{3}}\int\frac{d^{3}\mathbf{p}_{\lambda}}{(2\pi)^{3}}\frac{1}{\sqrt{2m_{1}}}\frac{1}{\sqrt{2m_{2}}}$	(20)
	$\displaystyle\frac{1}{\sqrt{2m_{3}}}\psi_{l_{\rho}}(\mathbf{p}_{\rho})\psi_{l_{\lambda}}\left(\mathbf{p}_{\lambda}\right)\left\|q_{1}\left(p_{1},s_{1}\right)\right\rangle\left\|q_{2}\left(p_{2},s_{2}\right)\right\rangle$
	$\displaystyle\left\|q_{3}\left(p_{3},s_{3}\right)\right\rangle.$

Then, the decay amplitude for $Y_{bc}^{i}(P_{i})$ $\to$ $Y_{bc}^{f}(P_{f})$ + $M_{p}(q)$ can be obtained by

$\displaystyle-i\mathcal{T}=$	$\displaystyle-i\frac{g_{A}^{q}g_{f}}{2f_{p}}\sqrt{2M_{i}}\sqrt{2M_{f}}\int d^{3}\lambda e^{i\mathbf{q}_{\lambda}\cdot\mathbf{\lambda}}$	(21)
	$\displaystyle\times\Bigg{\langle}Y_{bc}^{f}\Bigg{\|}i\Bigg{\{}\Bigg{(}1-\frac{\omega}{2m_{3}}+\frac{\omega}{m_{1}+m_{2}+m_{3}}\Bigg{)}\mathbf{\sigma}\cdot\mathbf{q}$
	$\displaystyle+\frac{\omega}{m_{3}}\sigma\cdot\mathbf{p}_{\lambda}\Bigg{\}}\Bigg{\|}Y_{bc}^{i}\Bigg{\rangle},$

and the $\mathbf{q_{\lambda}}$ is defined as

\mathbf{q_{\lambda}}=\frac{m_{1}+m_{2}}{m_{1}+m_{2}+m_{3}}\mathbf{q}.

(22)

The $g_{f}$ denotes the flavor matrix, $M_{i}$ is the mass of initial baryon, $M_{f}$ is the mass of final baryon, $q=(\omega,\bm{q})$ is the 4-momentum of outgoing pseudoscalar meson, $m_{i}$ is the constituent quark mass with $m_{1}=m_{b}$ , $m_{2}=m_{c}$ , and $m_{3}=m_{u/d/s}$ .

After calculating the mass spectrum, one can get the wave functions for bottom-charmed baryons, which are applied to estimate the root mean square and the range parameters $\alpha_{\lambda}$ . These effective values $\alpha_{\lambda}$ are obtained by equating the root mean square radius of simple harmonic oscillator wave functions to that obtained in the nonrelativistic quark model, which has been widely used in the previous studies of strong decays Close:2005se ; Li:2010vx ; Godfrey:2015dia ; Godfrey:2015dva ; Chen:2016iyi . Then, the helicity amplitude $\mathcal{A}_{h}$ can be derived from the transition operator and effective parameters $\alpha_{\lambda}$ in the harmonic oscillator wave functions. To calculate the strong decay widths for the pseudoscalar meson emissions, one also need to take into account the phase space factor. Finally, the strong decays for bottom-charmed baryons can be obtained within the helicity bases straightforwardly,

{}\Gamma=\frac{1}{4\pi}\frac{q}{2M_{i}^{2}}\frac{1}{2J+1}\sum_{h}\left|\mathcal{A}_{h}\right|^{2}.

(23)

III Results and discussion

In this section, we first calculated the mass spectrum of bottom-charmed baryons, and then estimate the strong decays for $\lambda-$ mode low-lying excited states. Also, we discuss the relativistic corrections for the Roper-like resonances, the mixture of $\lambda-$ mode states with the same spin-parity, and the suppression of strong decays for $\rho-$ mode and $\rho-\lambda$ hybrid states. In analogy with singly heavy baryons Chen:2007xf , we adopt the symbols $\sim$ , $\wedge$ , $\vee$ , and $\smile$ on the top of capital $\Xi$ and $\Omega$ to denote the $\rho-$ mode $P-$ wave, $\rho-$ mode $D-$ wave, $\rho-\lambda$ hybrid, and $\rho-$ mode radially excited states, respectively.

III.1 Mass spectrum

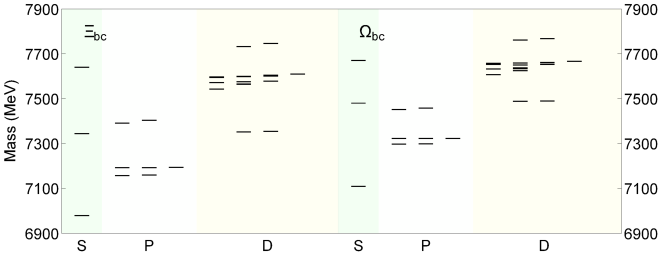
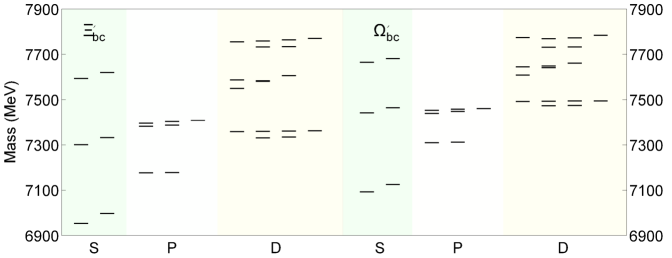
In the quark model, for the $\Xi_{bc}$ or $\Omega_{bc}$ family, there should be one ground state, five $\rho-$ mode $P-$ wave states, two $\lambda-$ mode $P-$ wave states, two $\rho-$ mode $D-$ wave states, two $\lambda-$ mode $D-$ wave states, thirteen $\rho-\lambda$ hybrid $D-$ wave states, and two radially excited states; for the $\Xi_{bc}^{\prime}$ or $\Omega_{bc}^{\prime}$ family should exist two ground states, two $\rho-$ mode $P-$ wave states, five $\lambda-$ mode $P-$ wave states, six $\rho-$ mode $D-$ wave states, six $\lambda-$ mode $D-$ wave states, five $\rho-\lambda$ hybrid $D-$ wave states, and four radially excited states. Within the potential model, we obtain the masses and perform them in Table 2, 3, 4, and 5. Also, the full mass spectra are plotted in Figure 3 and 4 for reference.

Table 2: The mass spectrum of

\Xi_{bc}

in MeV.

States	$n_{\rho}$	$n_{\lambda}$	$l_{\rho}$	$l_{\lambda}$	$S_{\rho}$	$J_{\rho}$	$j$	$J^{P}$	$\alpha_{\lambda}$	Mass
$\Xi_{bc}(1S)$	0	0	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	347	6979
$\breve{\Xi}_{bc}(2S)$	1	0	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	507	7344
$\Xi_{bc}(2S)$	0	1	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	489	7640
$\tilde{\Xi}_{bc}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	1	0	1	0	$\frac{1}{2}$	$\frac{1}{2}^{-}$	438	7157
$\tilde{\Xi}_{bc}(\frac{3}{2}^{-},\frac{1}{2})$	0	0	1	0	1	1	$\frac{1}{2}$	$\frac{3}{2}^{-}$	437	7159
$\tilde{\Xi}_{bc}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	1	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{-}$	441	7192
$\tilde{\Xi}_{bc}(\frac{3}{2}^{-},\frac{1}{2})$	0	0	1	0	1	2	$\frac{1}{2}$	$\frac{3}{2}^{-}$	440	7192
$\tilde{\Xi}_{bc}(\frac{5}{2}^{-},\frac{1}{2})$	0	0	1	0	1	2	$\frac{1}{2}$	$\frac{5}{2}^{-}$	432	7193
$\Xi_{bc}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	0	1	0	0	$\frac{1}{2}$	$\frac{1}{2}^{-}$	305	7391
$\Xi_{bc}(\frac{3}{2}^{-},\frac{3}{2})$	0	0	0	1	0	0	$\frac{3}{2}$	$\frac{3}{2}^{-}$	302	7403
$\hat{\Xi}_{bc}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	2	0	0	2	$\frac{1}{2}$	$\frac{3}{2}^{+}$	501	7352
$\hat{\Xi}_{bc}(\frac{5}{2}^{+},\frac{1}{2})$	0	0	2	0	0	2	$\frac{1}{2}$	$\frac{5}{2}^{+}$	500	7354
$\Xi_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	0	2	0	0	$\frac{3}{2}$	$\frac{3}{2}^{+}$	291	7732
$\Xi_{bc}(\frac{5}{2}^{+},\frac{5}{2})$	0	0	0	2	0	0	$\frac{5}{2}$	$\frac{5}{2}^{+}$	282	7746
$\check{\Xi}_{bc}(\frac{1}{2}^{+},\frac{1}{2})$	0	0	1	1	1	0	$\frac{1}{2}$	$\frac{1}{2}^{+}$	368	7543
$\check{\Xi}_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	1	1	1	0	$\frac{3}{2}$	$\frac{3}{2}^{+}$	367	7564
$\check{\Xi}_{bc}(\frac{1}{2}^{+},\frac{1}{2})$	0	0	1	1	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	366	7572
$\check{\Xi}_{bc}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	1	1	1	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	366	7575
$\check{\Xi}_{bc}(\frac{1}{2}^{+},\frac{3}{2})$	0	0	1	1	1	1	$\frac{3}{2}$	$\frac{1}{2}^{+}$	359	7597
$\check{\Xi}_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	1	1	1	1	$\frac{3}{2}$	$\frac{3}{2}^{+}$	359	7599
$\check{\Xi}_{bc}(\frac{5}{2}^{+},\frac{3}{2})$	0	0	1	1	1	1	$\frac{3}{2}$	$\frac{5}{2}^{+}$	352	7604
$\check{\Xi}_{bc}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	1	1	1	2	$\frac{1}{2}$	$\frac{3}{2}^{+}$	367	7565
$\check{\Xi}_{bc}(\frac{5}{2}^{+},\frac{1}{2})$	0	0	1	1	0	2	$\frac{1}{2}$	$\frac{5}{2}^{+}$	366	7578
$\check{\Xi}_{bc}(\frac{1}{2}^{+},\frac{3}{2})$	0	0	1	1	0	2	$\frac{3}{2}$	$\frac{1}{2}^{+}$	353	7595
$\check{\Xi}_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	1	1	0	2	$\frac{3}{2}$	$\frac{3}{2}^{+}$	352	7598
$\check{\Xi}_{bc}(\frac{5}{2}^{+},\frac{3}{2})$	0	0	1	1	0	2	$\frac{3}{2}$	$\frac{5}{2}^{+}$	352	7601
$\check{\Xi}_{bc}(\frac{7}{2}^{+},\frac{3}{2})$	0	0	1	1	0	2	$\frac{3}{2}$	$\frac{7}{2}^{+}$	350	7609

Table 3: The mass spectrum of

\Omega_{bc}

in MeV.

States	$n_{\rho}$	$n_{\lambda}$	$l_{\rho}$	$l_{\lambda}$	$S_{\rho}$	$J_{\rho}$	$j$	$J^{P}$	$\alpha_{\lambda}$	Mass
$\Omega_{bc}(1S)$	0	0	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	419	7109
$\breve{\Omega}_{bc}(2S)$	1	0	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	601	7480
$\Omega_{bc}(2S)$	0	1	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	351	7670
$\tilde{\Omega}_{bc}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	1	0	1	0	$\frac{1}{2}$	$\frac{1}{2}^{-}$	506	7297
$\tilde{\Omega}_{bc}(\frac{3}{2}^{-},\frac{1}{2})$	0	0	1	0	1	1	$\frac{1}{2}$	$\frac{3}{2}^{-}$	506	7298
$\tilde{\Omega}_{bc}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	1	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{-}$	500	7322
$\tilde{\Omega}_{bc}(\frac{3}{2}^{-},\frac{1}{2})$	0	0	1	0	1	2	$\frac{1}{2}$	$\frac{3}{2}^{-}$	500	7322
$\tilde{\Omega}_{bc}(\frac{5}{2}^{-},\frac{1}{2})$	0	0	1	0	1	2	$\frac{1}{2}$	$\frac{5}{2}^{-}$	500	7323
$\Omega_{bc}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	0	1	0	0	$\frac{1}{2}$	$\frac{1}{2}^{-}$	362	7451
$\Omega_{bc}(\frac{3}{2}^{-},\frac{3}{2})$	0	0	0	1	0	0	$\frac{3}{2}$	$\frac{3}{2}^{-}$	360	7458
$\hat{\Omega}_{bc}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	2	0	0	2	$\frac{1}{2}$	$\frac{3}{2}^{+}$	583	7488
$\hat{\Omega}_{bc}(\frac{5}{2}^{+},\frac{1}{2})$	0	0	2	0	0	2	$\frac{1}{2}$	$\frac{5}{2}^{+}$	582	7489
$\Omega_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	0	2	0	0	$\frac{3}{2}$	$\frac{3}{2}^{+}$	306	7761
$\Omega_{bc}(\frac{5}{2}^{+},\frac{5}{2})$	0	0	0	2	0	0	$\frac{5}{2}$	$\frac{5}{2}^{+}$	305	7768
$\check{\Omega}_{bc}(\frac{1}{2}^{+},\frac{1}{2})$	0	0	1	1	1	0	$\frac{1}{2}$	$\frac{1}{2}+$	431	7607
$\check{\Omega}_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	1	1	1	0	$\frac{3}{2}$	$\frac{3}{2}^{+}$	422	7625
$\check{\Omega}_{bc}(\frac{1}{2}^{+},\frac{1}{2})$	0	0	1	1	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	417	7632
$\check{\Omega}_{bc}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	1	1	1	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	417	7634
$\check{\Omega}_{bc}(\frac{1}{2}^{+},\frac{3}{2})$	0	0	1	1	1	1	$\frac{3}{2}$	$\frac{1}{2}^{+}$	413	7652
$\check{\Omega}_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	1	1	1	1	$\frac{3}{2}$	$\frac{3}{2}^{+}$	413	7650
$\check{\Omega}_{bc}(\frac{5}{2}^{+},\frac{3}{2})$	0	0	1	1	1	1	$\frac{3}{2}$	$\frac{5}{2}^{+}$	412	7654
$\check{\Omega}_{bc}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	1	1	1	2	$\frac{1}{2}$	$\frac{3}{2}^{+}$	417	7637
$\check{\Omega}_{bc}(\frac{5}{2}^{+},\frac{1}{2})$	0	0	1	1	0	2	$\frac{1}{2}$	$\frac{5}{2}^{+}$	412	7652
$\check{\Omega}_{bc}(\frac{1}{2}^{+},\frac{3}{2})$	0	0	1	1	0	2	$\frac{3}{2}$	$\frac{1}{2}^{+}$	411	7658
$\check{\Omega}_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	1	1	0	2	$\frac{3}{2}$	$\frac{3}{2}^{+}$	411	7659
$\check{\Omega}_{bc}(\frac{5}{2}^{+},\frac{3}{2})$	0	0	1	1	0	2	$\frac{3}{2}$	$\frac{5}{2}^{+}$	409	7661
$\check{\Omega}_{bc}(\frac{7}{2}^{+},\frac{3}{2})$	0	0	1	1	0	2	$\frac{3}{2}$	$\frac{7}{2}^{+}$	405	7667

Table 4: The mass spectrum of

\Xi_{bc}^{\prime}

in MeV.

States	$n_{\rho}$	$n_{\lambda}$	$l_{\rho}$	$l_{\lambda}$	$S_{\rho}$	$J_{\rho}$	$j$	$J^{P}$	$\alpha_{\lambda}$	Mass
$\Xi_{bc}^{\prime}(1S)$	0	0	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	373	6953
$\Xi_{bc}^{\prime*}(1S)$	0	0	0	0	1	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	357	6997
$\breve{\Xi}_{bc}^{\prime}(2S)$	1	0	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	533	7301
$\breve{\Xi}_{bc}^{\prime*}(2S)$	1	0	0	0	1	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	520	7332
$\Xi_{bc}^{\prime}(2S)$	0	1	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	508	7593
$\Xi_{bc}^{\prime*}(2S)$	0	1	0	0	1	1	$\frac{3}{2}$	$\frac{3}{2}^{+}$	501	7619
$\tilde{\Xi}_{bc}^{\prime}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	1	0	0	1	$\frac{1}{2}$	$\frac{1}{2}^{-}$	438	7176
$\tilde{\Xi}_{bc}^{\prime}(\frac{3}{2}^{-},\frac{1}{2})$	0	0	1	0	0	1	$\frac{1}{2}$	$\frac{3}{2}^{-}$	437	7178
$\Xi_{bc}^{\prime}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	0	1	1	1	$\frac{1}{2}$	$\frac{1}{2}^{-}$	319	7382
$\Xi_{bc}^{\prime}(\frac{3}{2}^{-},\frac{1}{2})$	0	0	0	1	1	1	$\frac{1}{2}$	$\frac{3}{2}^{-}$	315	7387
$\Xi_{bc}^{\prime}(\frac{1}{2}^{-},\frac{3}{2})$	0	0	0	1	1	1	$\frac{3}{2}$	$\frac{1}{2}^{-}$	313	7396
$\Xi_{bc}^{\prime}(\frac{3}{2}^{-},\frac{3}{2})$	0	0	0	1	1	1	$\frac{3}{2}$	$\frac{3}{2}^{-}$	311	7404
$\Xi_{bc}^{\prime}(\frac{5}{2}^{-},\frac{3}{2})$	0	0	0	1	1	1	$\frac{3}{2}$	$\frac{5}{2}^{-}$	310	7408
$\hat{\Xi}_{bc}^{\prime}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	2	0	1	2	$\frac{1}{2}$	$\frac{3}{2}^{+}$	514	7331
$\hat{\Xi}_{bc}^{\prime}(\frac{5}{2}^{+},\frac{1}{2})$	0	0	2	0	1	2	$\frac{1}{2}$	$\frac{5}{2}^{+}$	514	7334
$\hat{\Xi}_{bc}^{\prime}(\frac{1}{2}^{+},\frac{1}{2})$	0	0	2	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	503	7359
$\hat{\Xi}_{bc}^{\prime}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	2	0	1	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	502	7360
$\hat{\Xi}_{bc}^{\prime}(\frac{5}{2}^{+},\frac{1}{2})$	0	0	2	0	1	3	$\frac{1}{2}$	$\frac{5}{2}^{+}$	502	7361
$\hat{\Xi}_{bc}^{\prime}(\frac{7}{2}^{+},\frac{1}{2})$	0	0	2	0	1	3	$\frac{1}{2}$	$\frac{7}{2}^{+}$	502	7362
$\Xi_{bc}^{\prime}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	0	2	1	1	$\frac{3}{2}$	$\frac{3}{2}^{+}$	295	7732
$\Xi_{bc}^{\prime}(\frac{5}{2}^{+},\frac{3}{2})$	0	0	0	2	1	1	$\frac{3}{2}$	$\frac{5}{2}^{+}$	295	7733
$\Xi_{bc}^{\prime}(\frac{1}{2}^{+},\frac{3}{2})$	0	0	0	2	1	1	$\frac{3}{2}$	$\frac{1}{2}^{+}$	280	7755
$\Xi_{bc}^{\prime}(\frac{3}{2}^{+},\frac{5}{2})$	0	0	0	2	1	1	$\frac{5}{2}$	$\frac{3}{2}^{+}$	279	7759
$\Xi_{bc}^{\prime}(\frac{5}{2}^{+},\frac{5}{2})$	0	0	0	2	1	1	$\frac{5}{2}$	$\frac{5}{2}^{+}$	278	7764
$\Xi_{bc}^{\prime}(\frac{7}{2}^{+},\frac{5}{2})$	0	0	0	2	1	1	$\frac{5}{2}$	$\frac{7}{2}^{+}$	276	7770
$\check{\Xi}_{bc}^{\prime}(\frac{1}{2}^{+},\frac{1}{2})$	0	0	1	1	0	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	388	7549
$\check{\Xi}_{bc}^{\prime}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	1	1	0	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	370	7581
$\check{\Xi}_{bc}^{\prime}(\frac{1}{2}^{+},\frac{3}{2})$	0	0	1	1	0	1	$\frac{3}{2}$	$\frac{1}{2}^{+}$	368	7587
$\check{\Xi}_{bc}^{\prime}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	1	1	0	1	$\frac{3}{2}$	$\frac{3}{2}^{+}$	369	7583
$\check{\Xi}_{bc}^{\prime}(\frac{5}{2}^{+},\frac{3}{2})$	0	0	1	1	0	1	$\frac{3}{2}$	$\frac{5}{2}^{+}$	350	7606

Table 5: The mass spectrum of

\Omega_{bc}^{\prime}

in MeV.

States	$n_{\rho}$	$n_{\lambda}$	$l_{\rho}$	$l_{\lambda}$	$S_{\rho}$	$J_{\rho}$	$j$	$J^{P}$	$\alpha_{\lambda}$	Mass
$\Omega_{bc}^{\prime}(1S)$	0	0	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	455	7092
$\Omega_{bc}^{\prime*}(1S)$	0	0	0	0	1	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	397	7125
$\breve{\Omega}_{bc}^{\prime}(2S)$	1	0	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	635	7441
$\breve{\Omega}_{bc}^{\prime*}(2S)$	1	0	0	0	1	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	622	7464
$\Omega_{bc}^{\prime}(2S)$	0	1	0	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	345	7664
$\Omega_{bc}^{\prime*}(2S)$	0	1	0	0	1	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	343	7681
$\tilde{\Omega}_{bc}^{\prime}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	1	0	0	1	$\frac{1}{2}$	$\frac{1}{2}^{-}$	505	7310
$\tilde{\Omega}_{bc}^{\prime}(\frac{3}{2}^{-},\frac{1}{2})$	0	0	1	0	0	1	$\frac{1}{2}$	$\frac{3}{2}^{-}$	504	7312
$\Omega_{bc}^{\prime}(\frac{1}{2}^{-},\frac{1}{2})$	0	0	0	1	1	1	$\frac{1}{2}$	$\frac{1}{2}^{-}$	374	7439
$\Omega_{bc}^{\prime}(\frac{3}{2}^{-},\frac{1}{2})$	0	0	0	1	1	1	$\frac{1}{2}$	$\frac{3}{2}^{-}$	369	7448
$\Omega_{bc}^{\prime}(\frac{1}{2}^{-},\frac{3}{2})$	0	0	0	1	1	1	$\frac{3}{2}$	$\frac{1}{2}^{-}$	366	7453
$\Omega_{bc}^{\prime}(\frac{3}{2}^{-},\frac{3}{2})$	0	0	0	1	1	1	$\frac{3}{2}$	$\frac{3}{2}^{-}$	365	7458
$\Omega_{bc}^{\prime}(\frac{5}{2}^{-},\frac{3}{2})$	0	0	0	1	1	1	$\frac{3}{2}$	$\frac{5}{2}^{-}$	364	7460
$\hat{\Omega}_{bc}^{\prime}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	2	0	1	2	$\frac{1}{2}$	$\frac{3}{2}^{+}$	590	7472
$\hat{\Omega}_{bc}^{\prime}(\frac{5}{2}^{+},\frac{1}{2})$	0	0	2	0	1	2	$\frac{1}{2}$	$\frac{5}{2}^{+}$	589	7474
$\hat{\Omega}_{bc}^{\prime}(\frac{1}{2}^{+},\frac{1}{2})$	0	0	2	0	1	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	583	7492
$\hat{\Omega}_{bc}^{\prime}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	2	0	1	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	583	7493
$\hat{\Omega}_{bc}^{\prime}(\frac{5}{2}^{+},\frac{1}{2})$	0	0	2	0	1	3	$\frac{1}{2}$	$\frac{5}{2}^{+}$	582	7494
$\hat{\Omega}_{bc}^{\prime}(\frac{7}{2}^{+},\frac{1}{2})$	0	0	2	0	1	3	$\frac{1}{2}$	$\frac{7}{2}^{+}$	582	7494
$\hat{\Omega}_{bc}^{\prime}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	0	2	1	1	$\frac{3}{2}$	$\frac{3}{2}^{+}$	365	7731
$\Omega_{bc}^{\prime}(\frac{5}{2}^{+},\frac{3}{2})$	0	0	0	2	1	1	$\frac{3}{2}$	$\frac{5}{2}^{+}$	365	7732
$\Omega_{bc}^{\prime}(\frac{1}{2}^{+},\frac{3}{2})$	0	0	0	2	1	1	$\frac{3}{2}$	$\frac{1}{2}^{+}$	348	7774
$\Omega_{bc}^{\prime}(\frac{3}{2}^{+},\frac{5}{2})$	0	0	0	2	1	1	$\frac{5}{2}$	$\frac{3}{2}^{+}$	349	7769
$\Omega_{bc}^{\prime}(\frac{5}{2}^{+},\frac{5}{2})$	0	0	0	2	1	1	$\frac{5}{2}$	$\frac{5}{2}^{+}$	348	7773
$\Omega_{bc}^{\prime}(\frac{7}{2}^{+},\frac{5}{2})$	0	0	0	2	1	1	$\frac{5}{2}$	$\frac{7}{2}^{+}$	343	7784
$\check{\Omega}_{bc}^{\prime}(\frac{1}{2}^{+},\frac{1}{2})$	0	0	1	1	0	1	$\frac{1}{2}$	$\frac{1}{2}^{+}$	445	7608
$\check{\Omega}_{bc}^{\prime}(\frac{3}{2}^{+},\frac{1}{2})$	0	0	1	1	0	1	$\frac{1}{2}$	$\frac{3}{2}^{+}$	438	7641
$\check{\Omega}_{bc}^{\prime}(\frac{1}{2}^{+},\frac{3}{2})$	0	0	1	1	0	1	$\frac{3}{2}$	$\frac{1}{2}^{+}$	437	7645
$\check{\Omega}_{bc}^{\prime}(\frac{3}{2}^{+},\frac{3}{2})$	0	0	1	1	0	1	$\frac{3}{2}$	$\frac{3}{2}^{+}$	433	7648
$\check{\Omega}_{bc}^{\prime}(\frac{5}{2}^{+},\frac{3}{2})$	0	0	1	1	0	1	$\frac{3}{2}$	$\frac{5}{2}^{+}$	424	7661

We first refer to the ground states for bottom-charmed baryons. From the Table 6 and Figure 5, The lowest $\Xi_{bc}$ , $\Xi_{bc}^{\prime}$ , $\Omega_{bc}$ , and $\Omega_{bc}^{\prime}$ states are predicted to be about 6979, 6953, 7109, and 7092 MeV, respectively. It can be seen that our results are consistent with some works Ebert:1996ec ; Ebert:2002ig ; Li:2022ywz , while differ with others about $50\sim 100$ MeV Roberts:2007ni ; Oudichhya:2022ssc ; Giannuzzi:2009gh . In the singly heavy baryons $\Xi_{c/b}^{(\prime)}$ , the lowest states are $\Xi_{c/b}$ rather than $\Xi_{c/b}^{\prime}$ . However, for the bottom-charmed baryons, the lowest states are $\Xi_{bc}^{\prime}$ and $\Omega_{bc}^{\prime}$ , which is totally different with singly heavy sector. This is due to the different masses in spin-spin term $V^{SS}\left(r_{ij}\right)$ in the nonrelativistic quark model for singly and doubly heavy baryons, where the pairwise interactions among three quarks together with spin wave functions compete with each other. Moreover, the mass splittings for $\Xi_{bc}^{\prime*}-\Xi_{bc}^{\prime}$ and $\Omega_{bc}^{\prime*}-\Omega_{bc}^{\prime}$ are 44 and 33 MeV, respectively. These quite small mass gaps are caused by spin-spin interaction which is inversely proportional to quark masses. Because of this, the pion emission between the ground states for bottom-charmed baryons is prohibited and only decay mode is by electroweak processes, which is in contrast with the strange sector allowing the strong decay $\Xi^{*}\to\Xi\pi$ . In particular, For the lowest $\Xi_{bc}^{(\prime)}$ and $\Omega_{bc}^{(\prime)}$ states, future experiments can search for them in via $b\to c$ weak transitions.

Table 6: Masses of ground states for

\Xi_{bc}^{(\prime)}

and

\Omega_{bc}^{(\prime)}

baryons compared with different calculations. The units are in MeV.

States	$J^{P}$	Our work	Ebert:1996ec	Ebert:2002ig	Li:2022ywz	Roberts:2007ni	Oudichhya:2022ssc	Giannuzzi:2009gh	Eakins:2012jk	Brown:2014ena	Karliner:2014gca	Mathur:2018epb	Roncaglia:1995az
$\Xi_{bc}$	$1/2^{+}$	6979	7000	6963	6955	7047	$\cdot\cdot\cdot$	6920	7037	6959	6933	6966	7040
$\Xi_{bc}^{\prime}$	$1/2^{+}$	6953	6950	6933	6952	7011	6902/6906	6904	7014	6943	6914	6945	6990
$\Xi_{bc}^{\prime*}$	$3/2^{+}$	6997	7020	6980	6980	7074	7030/7029	6936	7064	6985	6969	6989	7060
States	$J^{P}$	Our work	Ebert:1996ec	Ebert:2002ig	Li:2022ywz	Roberts:2007ni	Oudichhya:2022ssc	Giannuzzi:2009gh	Tong:1999qs	Brown:2014ena	Mathur:2018epb	Roncaglia:1995az
$\Omega_{bc}$	$1/2^{+}$	7109	7090	7116	7055	7165	$\cdot\cdot\cdot$	7005	7110	7032	7045	7090	$\cdot\cdot\cdot$
$\Omega_{bc}^{\prime}$	$1/2^{+}$	7092	7050	7088	7053	7136	7035	6994	7050	7045	6994	7060	$\cdot\cdot\cdot$
$\Omega_{bc}^{\prime*}$	$3/2^{+}$	7125	7110	7130	7079	7187	7149	7017	7130	7059	7056	7120	$\cdot\cdot\cdot$

Unlike singly heavy baryons, the heavy quark subsystem is more easily excited owing to its larger reduced mass, and then the $\rho-$ mode excited states are lower than the $\lambda-$ mode ones. It can be seen that our calculated mass spectra for bottom-charmed baryons faithfully reflect this specific feature. Meanwhile, the fine structures of excited states are small and the spectra are highly degenerate, especially for the $D-$ wave states. Therefore, the low-lying $P-$ wave excitations are more likely to be recognized both theoretically and experimentally. Moreover, the mass spectra for bottom-charmed baryons show quite similar patterns as other heavy-light systems, such as conventional charmed or bottom mesons, which suggests that the approximate light flavor SU(3) symmetry and heavy super-flavor symmetry are preserved well. Indeed, analogous to the doubly bottom baryons He:2021iwx , the bottom and charm quarks stay close to each other like a static color source, and the light quark is shared by these two heavy quarks.

Here, we can also discuss the theoretical uncertainties arising from parameters $\alpha_{ss}$ and $\alpha_{so}$ for doubly heavy baryons. We first vary $\alpha_{ss}$ in the range of 1.10 $\sim$ 1.30, and find that the discrepancies between theoretical results and experimental data for the mass splittings of singly heavy baryons can reach up to 39 MeV. Even with this large variation, the uncertainties for doubly heavy baryons are about 7 MeV, which are small enough. The same procedure should also be done for $\alpha_{so}$ , but the established excited heavy baryons relevant with this parameter are few. Here, we vary this value in a wide range of 0 $\sim$ 0.154, and find the uncertainties for doubly heavy baryons are about 10 MeV, which suggests that our predictions are also stable against the parameter $\alpha_{so}$ .

III.2 Strong decays for $\lambda-$ mode $\Xi_{bc}$ and $\Omega_{bc}$ states

The strong decays for $\lambda-$ mode $\Xi_{bc}$ and $\Omega_{bc}$ states are calculated and listed in Table 7 and 11. For the two $\Xi_{bc}(1P)$ states, they have the light quark spins $j=1/2$ and $3/2$ , and the decay widths for $\Xi_{bc}(1/2^{-},1/2)$ and $\Xi_{bc}(3/2^{-},3/2)$ states are about 95 and 21 MeV, respectively. Owing to the limited phase space, both of them can only decay into the $\Xi_{bc}\pi$ channel. Because of relevant partial waves of decaying channels, we have found a rather broad $J^{P}=1/2^{-}$ state with $S-$ wave decay and a narrow $J^{P}=3/2^{-}$ state with $D-$ wave decay, which are roughly consistent with previous work Eakins:2012fq . The distinctions of predicted decay widths may arise from the different phase spaces, wave functions, and phenomenological models.

Table 7: The predicted strong decay widths of

\Xi_{bc}(1P)

and

\Omega_{bc}(1P)

states in MeV. The

\cdot\cdot\cdot

stands for the closed channel.

State	$\Xi_{bc}(\frac{1}{2}^{-},\frac{1}{2})$	$\Xi_{bc}(\frac{3}{2}^{-},\frac{3}{2})$
$\Xi_{bc}$ $\pi$	94.98	20.89
Total	94.98	20.89
State	$\Omega_{bc}(\frac{1}{2}^{-},\frac{1}{2})$	$\Omega_{bc}(\frac{3}{2}^{-},\frac{3}{2})$
$\Xi_{bc}$ $\bar{K}$	$\cdot\cdot\cdot$	$\cdot\cdot\cdot$
Total	Narrow	Narrow

Table 8: The predicted strong decay widths of

\Xi_{bc}(2S,1D)

and

\Omega_{bc}(2S,1D)

states in MeV.

State	$\Xi_{bc}(2S)$	$\Xi_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	$\Xi_{bc}(\frac{5}{2}^{+},\frac{5}{2})$
$\Xi_{bc}$ $\pi$	370.92	297.85	142.99
$\Xi_{bc}$ $\eta$	68.18	155.72	145.35
$\Omega_{bc}$ $\bar{K}$	22.28	87.85	89.66
$\Xi_{bc}(\frac{1}{2}^{-},\frac{1}{2})$ $\pi$	1.52	18.91	15.06
$\Xi_{bc}(\frac{3}{2}^{-},\frac{3}{2})$ $\pi$	2.30	27.96	32.41
Total	465.20	588.29	425.47
State	$\Omega_{bc}(2S)$	$\Omega_{bc}(\frac{3}{2}^{+},\frac{3}{2})$	$\Omega_{bc}(\frac{5}{2}^{+},\frac{5}{2})$
$\Xi_{bc}$ $\bar{K}$	48.19	438.76	63.59
$\Omega_{bc}$ $\eta$	0.08	24.71	0.32
Total	48.27	463.47	63.91

For the two $\Omega_{bc}(1P)$ states, they lie below the $\Xi_{bc}\bar{K}$ threshold, and then the OZI-allowed strong decay is forbidden. The dominating decay channels should be $\Omega_{bc}\pi$ and $\Omega_{bc}\gamma$ . This situation is quite similar to $D_{s0}^{*}(2317)$ and $D_{s1}(2460)$ resonances, where the isospin breaking decay and radiative decay modes dominate. Actually, based on the heavy super-flavor symmetry Savage:1990di , the two $\Omega_{bc}(1P)$ states can be related to the charmed mesons and $\Omega_{bb}(1P)$ states He:2021iwx . More theoretical studies on this topic can help us to better understand the $D_{s0}(2317)$ resonance.

From the Table 11, it can be seen that most of the $2S$ and $1D$ states are broad, which can hardly be observed in experiments. For the $\Omega_{bc}(2S)$ state, the total width is relatively small, and the dominant decay mode is $\Xi_{bc}\bar{K}$ within leading terms of the nonrelativistic transition amplitude Eq. (21). Compared to the $\Omega_{bc}(2S)$ state, the $\Xi_{bc}(2S)$ state is broad, which results from the larger momentum of emitted pion and phase space. If we adopt a smaller initial hadronic mass, the partial width of $\Xi_{bc}\pi$ mode and total decay width will decrease rapidly. We will discuss the relativistic corrections for these radially excited states in the following subsection. Moreover, the narrow $\Omega_{bc}(5/2^{+},5/2)$ state mainly decays into the $\Xi_{bc}\bar{K}$ final states, which can be tested by future experiments.

III.3 Strong decays for $\lambda-$ mode $\Xi_{bc}^{\prime}$ and $\Omega_{bc}^{\prime}$ states

The strong decays for $\lambda-$ mode $\Xi_{bc}^{\prime}$ and $\Omega_{bc}^{\prime}$ states are estimated and shown in Table 9 and 10. In the $j-j$ coupling scheme, there are five $\lambda$ mode $\Xi_{bc}^{\prime}(1P)$ states, which can be classified into two groups according to the light quark spin $j$ : $j=1/2$ doublet and $j=3/2$ triplet. For the $j=1/2$ doublet, the calculated decay widths are rather broad with the current mass predictions of initial and final states, which agree with the calculations in the quark pair creation model Eakins:2012fq . For the $j=3/2$ triplet, the predicted decay widths are about 65, 75, and 92 MeV for the $J^{P}=1/2^{-}$ , $3/2^{-}$ , and $5/2^{-}$ states, respectively. The strong decay for $\Xi_{bc}(1/2^{-},3/2)$ is governed by $\Xi_{bc}^{\prime*}\pi$ decay mode , while $\Xi_{bc}(3/2^{-},3/2)$ and $\Xi_{bc}(5/2^{-},3/2)$ states can decay into both $\Xi_{bc}^{\prime}\pi$ and $\Xi_{bc}^{\prime*}\pi$ channels. The broad $j=1/2$ doublet and narrow $j=3/2$ triplet are expected by the heavy quark symmetry, which arise from the enhancement or cancellation in the amplitude with different Clebsch-Gordan coefficients.

Table 9: The predicted strong decay widths of

\Xi_{bc}^{\prime}(1P)

and

\Omega_{bc}^{\prime}(1P)

states in MeV. The

\cdot\cdot\cdot

stands for the closed channel, and

\times

denotes the forbidden channel due to quantum numbers.

State	$\Xi_{bc}^{\prime}(\frac{1}{2}^{-},\frac{1}{2})$	$\Xi_{bc}^{\prime}(\frac{3}{2}^{-},\frac{1}{2})$	$\Xi_{bc}^{\prime}(\frac{1}{2}^{-},\frac{3}{2})$	$\Xi_{bc}^{\prime}(\frac{3}{2}^{-},\frac{3}{2})$	$\Xi_{bc}^{\prime}(\frac{5}{2}^{-},\frac{3}{2})$
$\Xi_{bc}^{\prime}$ $\pi$	448.45	×	×	20.21	58.43
$\Xi_{bc}^{\prime*}$ $\pi$	×	334.12	65.40	54.50	33.97
Total	448.45	334.12	65.40	74.71	92.40
State	$\Omega_{bc}^{\prime}(\frac{1}{2}^{-},\frac{1}{2})$	$\Omega_{bc}^{\prime}(\frac{3}{2}^{-},\frac{1}{2})$	$\Omega_{bc}^{\prime}(\frac{1}{2}^{-},\frac{3}{2})$	$\Omega_{bc}^{\prime}(\frac{3}{2}^{-},\frac{3}{2})$	$\Omega_{bc}^{\prime}(\frac{5}{2}^{-},\frac{3}{2})$
$\Xi_{bc}^{\prime}$ $\bar{K}$	$\cdot\cdot\cdot$	×	×	0.00	0.08
$\Xi_{bc}^{\prime*}$ $\bar{K}$	×	$\cdot\cdot\cdot$	$\cdot\cdot\cdot$	$\cdot\cdot\cdot$	0.90
Total	Narrow	Narrow	Narrow	0.00	0.98

Table 10: The predicted strong decay widths of

\Xi_{bc}^{\prime}(2S,1D)

and

\Omega_{bc}^{\prime}(2S,1D)

states in MeV. The

\cdot\cdot\cdot

stands for the closed channel, and

\times

denotes the forbidden channel due to quantum numbers.

State	$\Xi_{bc}^{\prime}(2S)$	$\Xi_{bc}^{\prime*}(2S)$	$\Xi_{bc}^{\prime}(\frac{1}{2}^{+},\frac{3}{2})$	$\Xi_{bc}^{\prime}(\frac{3}{2}^{+},\frac{3}{2})$	$\Xi_{bc}^{\prime}(\frac{5}{2}^{+},\frac{3}{2})$	$\Xi_{bc}^{\prime}(\frac{3}{2}^{+},\frac{5}{2})$	$\Xi_{bc}^{\prime}(\frac{5}{2}^{+},\frac{5}{2})$	$\Xi_{bc}^{\prime}(\frac{7}{2}^{+},\frac{5}{2})$
$\Xi_{bc}^{\prime}$ $\pi$	11.11	17.49	66.05	56.84	×	×	6.72	16.21
$\Xi_{bc}^{\prime}$ $\eta$	1.57	8.52	37.13	27.10	×	×	0.68	1.71
$\Omega_{bc}^{\prime}$ $\bar{K}$	0.03	0.20	23.40	15.12	×	×	0.34	0.91
$\Xi_{bc}^{\prime*}$ $\pi$	78.72	51.96	7.23	33.92	76.33	30.10	21.84	12.33
$\Xi_{bc}^{\prime*}$ $\eta$	5.30	5.85	4.14	16.80	37.95	2.16	1.70	1.01
$\Omega_{bc}^{\prime*}$ $\bar{K}$	$\cdot\cdot\cdot$	0.00	3.02	8.09	18.40	0.94	0.75	2.93
$\Xi_{bc}^{\prime}(\frac{1}{2}^{-},\frac{1}{2})$ $\pi$	0.01	×	×	0.08	0.22	7.76	8.07	×
$\Xi_{bc}^{\prime}(\frac{3}{2}^{-},\frac{1}{2})$ $\pi$	×	0.19	0.71	0.42	0.24	1.85	5.04	9.51
$\Xi_{bc}^{\prime}(\frac{1}{2}^{-},\frac{3}{2})$ $\pi$	×	0.20	0.20	4.99	0.84	6.58	5.03	0.29
$\Xi_{bc}^{\prime}(\frac{3}{2}^{-},\frac{3}{2})$ $\pi$	0.06	0.31	13.92	40.32	7.88	6.55	6.60	4.79
$\Xi_{bc}^{\prime}(\frac{5}{2}^{-},\frac{3}{2})$ $\pi$	0.11	0.20	3.08	6.05	44.96	2.10	7.69	13.84
Total	96.91	84.92	158.88	209.73	186.82	58.04	64.46	63.53
State	$\Omega_{bc}^{\prime}(2S)$	$\Omega_{bc}^{\prime*}(2S)$	$\Omega_{bc}^{\prime}(\frac{1}{2}^{+},\frac{3}{2})$	$\Omega_{bc}^{\prime}(\frac{3}{2}^{+},\frac{3}{2})$	$\Omega_{bc}^{\prime}(\frac{5}{2}^{+},\frac{3}{2})$	$\Omega_{bc}^{\prime}(\frac{3}{2}^{+},\frac{5}{2})$	$\Omega_{bc}^{\prime}(\frac{5}{2}^{+},\frac{5}{2})$	$\Omega_{bc}^{\prime}(\frac{7}{2}^{+},\frac{5}{2})$
$\Xi_{bc}^{\prime}$ $\bar{K}$	1.79	4.79	95.84	72.40	×	×	6.36	15.01
$\Omega_{bc}^{\prime}$ $\eta$	0.00	0.04	6.66	3.62	×	×	0.14	0.06
$\Xi_{bc}^{\prime*}$ $\bar{K}$	16.74	7.89	12.65	54.71	110.63	20.58	23.43	8.15
$\Omega_{bc}^{\prime*}$ $\eta$	$\cdot\cdot\cdot$	0.00	1.07	1.66	3.74	0.25	0.21	0.02
Total	18.53	12.72	116.22	132.39	114.37	20.83	30.14	23.24

For the five $\Omega_{bc}^{\prime}(1P)$ states, the predicted masses are below or near threshold, and the total decay widths are extremely narrow. Also, according to the heavy supper-flavor symmetry, these states may have similar properties to $D_{s}(1P)$ mesons, such as the mysterious $D_{s0}^{*}(2317)$ state. These states can be hunted for through the pion and photon emissions in future experiments. For $\Omega_{bc}^{\prime}(5/2^{-},3/2)$ state, it can also be observed in the $\Xi_{bc}^{\prime}\bar{K}$ and $\Xi_{bc}^{\prime*}\bar{K}$ invariant masses. Moreover, the narrow $\Omega_{bc}^{\prime}(1P)$ states may be observed more easily than the ground states in the future as well as the singly bottom $\Omega_{b}$ family.

For the radially excited $\Xi_{bc}(2S)$ and $\Omega_{bc}(2S)$ states, our calculated decay widths are relatively narrow, and the dominant decay modes are $\Xi_{bc}^{\prime*}\pi$ and $\Xi_{bc}^{\prime*}\bar{K}$ with the nonrelativistic transition amplitude Eq. (21), respectively. These relatively narrow decays width for radially excited state are usually obtained within the nonrelativistic reduction of the axial-vector coupling between the pseudoscalar meson and light quark. This is due to the kind of selection rule from the structure of the transition operator in the leading order of nonrelativistic expansion, and consequently due to the orthogonality of the orbital wave functions between initial and final baryons. We will continue to discuss the relativistic corrections for Roper-like resonances in the following subsection.

For the $\Xi_{bc}^{\prime}(1D)$ and $\Omega_{bc}^{\prime}(1D)$ states, they can be divided into $j=3/2$ and $j=5/2$ triplets. the $j=3/2$ triplet are predicted to be relatively broad, while the $j=5/2$ are narrow states. It can be seen that the approximate heavy quark symmetry is preserved well in present calculations.

III.4 Relativistic corrections of order $1/m^{2}$ for Roper-like resonances

The relativistic corrections of order $1/m^{2}$ for convetional baryons are investigated in Refs. Arifi:2021orx ; Arifi:2022ntc . The authors found that these corrections of order $1/m^{2}$ are significant for the radially excited states, that is Roper-like resonances, while the effects for $P-$ wave and $D-$ wave states are small enough. In the present work, we also investigate these relativistic corrections for six radially excited bottom-charmed baryons.

We only take into account the ground states in the final states for comparison. The results are listed in Table LABEL:re, and it can be seen that these relativistic corrections for Roper-like resonances are significant. This specific feature has been found in other Roper-like resonances in the literature. Owning to the lack of experimental information for bottom-charmed baryons, more theoretical and experimental efforts are needed for further exploration.

Table 11: The predicted strong decays into ground states for

\Xi_{bc}(2S)

\Omega_{bc}(2S)

\Xi_{bc}^{\prime}(2S)

, and

\Omega_{bc}^{\prime}(2S)

states in nonrelativistic transitions together with relativistic corrections (NR+RC) in MeV. The

\cdot\cdot\cdot

stands for the closed channel.

State	$\Xi_{bc}(\Gamma_{NR}+\Gamma_{RC})$
$\Xi_{bc}$ $\pi$	370.92+274.00
$\Xi_{bc}$ $\eta$	68.18+0.25
$\Omega_{bc}$ $\bar{K}$	22.28+19.24
Total	461.38+293.49
State	$\Omega_{bc}(\Gamma_{NR}+\Gamma_{RC})$
$\Xi_{bc}$ $\bar{K}$	0.08+186.70
$\Omega_{bc}$ $\eta$	48.19+0.81
Total	48.27+187.51
State	$\Xi_{bc}^{\prime}(\Gamma_{NR}+\Gamma_{RC})$	$\Xi_{bc}^{\prime*}(\Gamma_{NR}+\Gamma_{RC})$
$\Xi_{bc}^{\prime}$ $\pi$	11.11+31.33	17.49+131.87
$\Xi_{bc}^{\prime}$ $\eta$	1.57+0.00	8.52+0.26
$\Omega_{bc}^{\prime}$ $\bar{K}$	0.03+0.06	0.20+12.91
$\Xi_{bc}^{\prime*}$ $\pi$	78.72+121.04	51.96+120.38
$\Xi_{bc}^{\prime*}$ $\eta$	5.30+0.41	5.85+17.50
$\Omega_{bc}^{\prime*}$ $\bar{K}$	$\cdot\cdot\cdot$	0.00+0.00
Total	96.73+152.84	84.02+282.92
State	$\Omega_{bc}^{\prime}(\Gamma_{NR}+\Gamma_{RC})$	$\Omega_{bc}^{\prime*}(\Gamma_{NR}+\Gamma_{RC})$
$\Xi_{bc}^{\prime}$ $\bar{K}$	1.79+31.74	4.79+154.91
$\Omega_{bc}^{\prime}$ $\eta$	0.00+0.31	0.04+2.93
$\Xi_{bc}^{\prime*}$ $\bar{K}$	16.74+139.40	7.89+113.66
$\Omega_{bc}^{\prime*}$ $\eta$	$\cdot\cdot\cdot$	0.00+0.25
Total	18.53+171.45	12.72+271.75

III.5 Mixing

In our calculation, we adopt the $j-j$ coupling scheme and the basis in the heavy quark limit to study mass spectra and strong decays for bottom-charmed baryons. Due to the finite mass of heavy quark subsystem, the physical observed resonances may correspond to the superposition of theoretical states in the quark model. For instance, the mixing scheme for $\lambda-$ mode $\Xi_{bc}^{\prime}(1P)$ and $\Omega_{bc}^{\prime}(1P)$ states can be formulated as

\left(\begin{array}[]{cc}\mid 1P&\left.1/2^{-}\right\rangle_{1}\\ \mid 1P&\left.1/2^{-}\right\rangle_{2}\end{array}\right)=\left(\begin{array}[]{cc}\cos\theta&\sin\theta\\ -\sin\theta&\cos\theta\end{array}\right)\left(\begin{array}[]{l}\left|1/2^{-},j=1/2\right\rangle\\ \left|1/2^{-},j=3/2\right\rangle\end{array}\right),

(24)

\left(\begin{array}[]{cc}\mid 1P&\left.3/2^{-}\right\rangle_{1}\\ \mid 1P&\left.3/2^{-}\right\rangle_{2}\end{array}\right)=\left(\begin{array}[]{cc}\cos\theta&\sin\theta\\ -\sin\theta&\cos\theta\end{array}\right)\left(\begin{array}[]{l}\left|3/2^{-},j=1/2\right\rangle\\ \left|3/2^{-},j=3/2\right\rangle\end{array}\right),

(25)

where $\theta$ is the mixing angle. Also, the $D-$ wave excited states with the same spin-parity can mix with each other.

In the heavy quark limit, the mixing angle should be zero. Actually, the heavy quark subsystem including bottom and charm quarks are relatively heavy, and heavy quark symmetry should be approximately preserved. Then, the above mixing angles are expected to be small enough. We calculate the mixture for $\lambda-$ mode $\Xi_{bc}^{\prime}(1P)$ states as an illustration and list them in Table 12. It can be found that the mixing angles are tiny, and the mixing effects for spectroscopy can be neglected in bottom-charmed sector. Moreover, there may also exist other mixing scheme, which are believed to be even smaller in these bottom-charmed baryons.

Table 12: The superposition of

\Xi_{bc}^{\prime}(1P)

states with

J^{P}=1/2^{-}

and

3/2^{-}

. The mixing angles for

J^{P}=1/2^{-}

and

3/2^{-}

states are and respectively.

State	$\langle H\rangle$ (MeV)	Mass (MeV)	Eigenvector
$\|1P1/2^{-}\rangle_{1}$	$\begin{pmatrix}7396.33&-2.10\\ -2.10&7382.40\end{pmatrix}$	$\begin{bmatrix}7396.64\\ 7382.09\end{bmatrix}$	$\begin{bmatrix}(0.99,-0.15)\\ (0.15,0.99)\end{bmatrix}$
$\|1P1/2^{-}\rangle_{2}$	$\begin{pmatrix}7396.33&-2.10\\ -2.10&7382.40\end{pmatrix}$	$\begin{bmatrix}7396.64\\ 7382.09\end{bmatrix}$	$\begin{bmatrix}(0.99,-0.15)\\ (0.15,0.99)\end{bmatrix}$
$\|1P3/2^{-}\rangle_{1}$	$\begin{pmatrix}7404.08&-2.85\\ -2.85&7386.83\end{pmatrix}$	$\begin{bmatrix}7404.54\\ 7386.37\end{bmatrix}$	$\begin{bmatrix}(0.99,-0.16)\\ (0.16,0.99)\end{bmatrix}$
$\|1P3/2^{-}\rangle_{2}$	$\begin{pmatrix}7404.08&-2.85\\ -2.85&7386.83\end{pmatrix}$	$\begin{bmatrix}7404.54\\ 7386.37\end{bmatrix}$	$\begin{bmatrix}(0.99,-0.16)\\ (0.16,0.99)\end{bmatrix}$

III.6 Low-lying $\rho-$ mode and $\rho-\lambda$ hybrid states

In addition to the presence of $\lambda-$ mode excitations, the bottom-charmed baryons also have low-lying $\rho-$ mode and $\rho-\lambda$ hybrid states. For example, when $l_{\rho}=l_{\lambda}=1$ , there exists thirteen $\check{\Xi}_{bc}$ and five $\check{\Xi}_{bc}^{\prime}$ states, which can be seen in Figure 6.

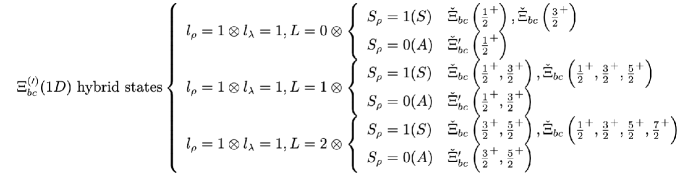
For these low-lying states, the light meson emissions are supposed to be dominating. However, under the spectator assumption for the two heavy quarks, the orbital wave functions of heavy quark subsystems between initial $\rho-$ mode or $\rho-\lambda$ hybrid states and final ground states are orthogonal, which results in the vanishing amplitudes and strong decay widths. More explicitly, the light meson emission occurs for $\lambda-$ mode excitations, and is irrelevant to the $\rho-$ mode variables. Hence, the orthogonality of the different $\rho-$ mode wave functions leads to the vanishing matrix element, which is shown in Figure 7. That is to say, our calculated decay modes preserve the heavy diquark symmetry automatically, where the heavy quark subsystems with different quantum numbers cannot transit into each other. Thus, these states should be extremely narrow and the weak and radiative decays may become dominating, which can provide good opportunities to be searched by future experiments.

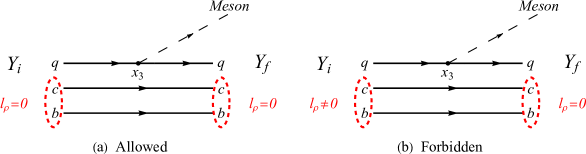
IV SUMMARY

In this work, we have studied the low-lying mass spectra for bottom-charmed baryons in a nonrelativistic quark model by solving the three-body Schrödinger equation. With the obtained realistic wave functions, we get the root mean square radius and study the strong decays of bottom-charmed baryons. The lowest $\Xi_{bc}$ , $\Xi_{bc}^{\prime}$ , $\Omega_{bc}$ , and $\Omega_{bc}^{\prime}$ states are predicted to be about 6979, 6953, 7109, and 7092 MeV, respectively. Our results indicate that some of $\lambda-$ mode $\Xi_{bc}(1P)$ , $\Xi_{bc}^{\prime}(1P)$ , $\Omega_{bc}(1P)$ , $\Omega_{bc}^{\prime}(1P)$ states are relatively narrow, which have good potentials to be observed by future experiments. Also, the strong decays of the low-lying $\rho-$ mode and $\rho-\lambda$ hybrid states are highly suppressed and can be hunted for in the electroweak processes.

Given the heavy quark symmetry, the heavy quark subsystem in bottom-charmed baryons play a role as a heavy antiquark, and then the heavy super-flavor symmetry emerges. Indeed, our results about the mass spectra and strong decays for bottom-charmed baryons support this claim. With the development of the large-scale accelerator facilities, we expect that more theoretical and experimental efforts are involved to search for more doubly heavy baryons and better understand the heavy quark symmetry.

ACKNOWLEDGMENTS

This work is supported by the National Natural Science Foundation of China under Grants No. 11705056, the Natural Science Foundation of Hunan Province under Grant No. 2023JJ40421, the Key Project of Hunan Provincial Education Department under Grant No. 21A0039, and the State Scholarship Fund of China Scholarship Council under Grant No. 202006725011. A. H. is supported by the Grants-in-Aid for Scientific Research (Grant Numbers 21H04478(A)) and the one on Innovative Areas (No. 18H05407).

References

(1) H. X. Chen, W. Chen, X. Liu, Y. R. Liu and S. L. Zhu, A review of the open charm and open bottom systems, Rept. Prog. Phys. 80, 076201 (2017).
(2) H. Y. Cheng, Charmed baryon physics circa 2021, Chin. J. Phys. 78, 324-362 (2022).
(3) M. Mattson et al. (SELEX Collaboration), First observation of the doubly charmed baryon $\Xi_{cc}^{+}$ , Phys. Rev. Lett. 89, 112001 (2002).
(4) A. Ocherashvili et al. (SELEX Collaboration), Confirmation of the double charm baryon $\Xi^{+}_{cc}(3520)$ via its decay to $pD^{+}K^{-}$ , Phys. Lett. B 628, 18 (2005).
(5) S. P. Ratti, New results on $c$ -baryons and a search for $cc$ -baryons in FOCUS, Nucl. Phys. Proc. Suppl. 115, 33 (2003).
(6) B. Aubert et al. (BaBar Collaboration), Search for doubly charmed baryons $\Xi_{cc}^{+}$ and $\Xi_{cc}^{++}$ in BABAR, Phys. Rev. D 74, 011103 (2006).
(7) R. Chistov et al. (Belle Collaboration), Observation of new states decaying into $\Lambda_{c}^{+}K^{-}\pi^{+}$ and $\Lambda_{c}^{+}K^{0}_{S}\pi^{-}$ , Phys. Rev. Lett. 97, 162001 (2006).
(8) R. Aaij et al. (LHCb Collaboration), Search for the doubly charmed baryon $\Xi_{cc}^{+}$ , JHEP 1312, 090 (2013).
(9) R. Aaij et al. (LHCb Collaboration), Observation of the doubly charmed baryon $\Xi_{cc}^{++}$ , Phys. Rev. Lett. 119, 112001 (2017).
(10) R. Aaij et al. (LHCb Collaboration), Measurement of the Lifetime of the Doubly Charmed Baryon $\Xi_{cc}^{++}$ , Phys. Rev. Lett. 121, 052002 (2018).
(11) R. Aaij et al. (LHCb Collaboration), Measurement of $\mathit{\Xi}_{cc}^{++}$ production in $pp$ collisions at $\sqrt{s}=13$ TeV, Chin. Phys. C 44, 022001 (2020).
(12) R. Aaij et al. (LHCb Collaboration), First Observation of the Doubly Charmed Baryon Decay $\Xi_{cc}^{++}\rightarrow\Xi_{c}^{+}\pi^{+}$ , Phys. Rev. Lett. 121, 162002 (2018).
(13) R. Aaij et al. (LHCb Collaboration), A search for $\it{\Xi}^{++}_{cc}\rightarrow D^{+}pK^{-}\pi^{+}$ decays, JHEP 10, 124 (2019).
(14) R. Aaij et al. (LHCb Collaboration), Precision measurement of the $\Xi_{cc}^{++}$ mass, JHEP 02, 049 (2020).
(15) R. Aaij et al. (LHCb Collaboration), Observation of the doubly charmed baryon decay ${\Xi}_{cc}^{++}\to{\Xi}_{c}^{\prime+}{\pi}^{+}$ , JHEP 05, 038 (2022).
(16) R. Aaij et al. (LHCb Collaboration), Search for the doubly charmed baryon $\Xi_{cc}^{+}$ , Sci. China Phys. Mech. Astron. 63, 221062 (2020).
(17) R. Aaij et al. (LHCb Collaboration), Search for the doubly heavy $\Xi_{bc}^{0}$ baryon via decays to $D^{0}pK^{-}$ , JHEP 11, 095 (2020).
(18) R. Aaij et al. (LHCb Collaboration), Search for the doubly charmed baryon ${\varXi}_{cc}^{+}$ in the ${\varXi}_{c}^{+}{\pi}^{-}{\pi}^{+}$ final state, JHEP 12, 107 (2021).
(19) R. Aaij et al. (LHCb Collaboration), Search for the doubly heavy baryons $\Omega^{0}_{bc}$ and $\Xi^{0}_{bc}$ decaying to $\Lambda^{+}_{c}\pi^{-}$ and $\Xi^{+}_{c}\pi^{-}$ , Chin. Phys. C 45, 093002 (2021).
(20) R. Aaij et al. (LHCb Collaboration), Search for the doubly charmed baryon $\Omega$ ${}_{cc}^{+}$ , Sci. China Phys. Mech. Astron. 64, 101062 (2021).
(21) R. Aaij et al. (LHCb Collaboration), Search for the doubly heavy baryon $\it{\Xi}_{bc}^{+}$ decaying to $J/\it{\psi}\it{\Xi}_{c}^{+}$ , arXiv:2204.09541.
(22) V. V. Kiselev and A. K. Likhoded, Baryons with two heavy quarks, Phys. Usp. 45, 455 (2002).
(23) D. Ebert, R. N. Faustov, V. O. Galkin, A. P. Martynenko and V. A. Saleev, Heavy baryons in the relativistic quark model, Z. Phys. C 76, 111 (1997).
(24) D. Ebert, R. N. Faustov, V. O. Galkin and A. P. Martynenko, Mass spectra of doubly heavy baryons in the relativistic quark model, Phys. Rev. D 66, 014008 (2002).
(25) S. S. Gershtein, V. V. Kiselev, A. K. Likhoded and A. I. Onishchenko, Spectroscopy of doubly heavy baryons, Phys. Rev. D 62, 054021 (2000).
(26) S. P. Tong, Y. B. Ding, X. H. Guo, H. Y. Jin, X. Q. Li, P. N. Shen and R. Zhang, Spectra of baryons containing two heavy quarks in potential model, Phys. Rev. D 62, 054024 (2000).
(27) W. Roberts and M. Pervin, Heavy baryons in a quark model, Int. J. Mod. Phys. A 23, 2817 (2008).
(28) F. Giannuzzi, Doubly heavy baryons in a Salpeter model with AdS/QCD inspired potential, Phys. Rev. D 79, 094002 (2009).
(29) A. P. Martynenko, Ground-state triply and doubly heavy baryons in a relativistic three-quark model, Phys. Lett. B 663, 317 (2008).
(30) A. Valcarce, H. Garcilazo and J. Vijande, Towards an understanding of heavy baryon spectroscopy, Eur. Phys. J. A 37, 217 (2008).
(31) B. Eakins and W. Roberts, Symmetries and Systematics of Doubly Heavy Hadrons, Int. J. Mod. Phys. A 27, 1250039 (2012).
(32) Z. Shah and A. K. Rai, Excited state mass spectra of doubly heavy $\Xi$ baryons, Eur. Phys. J. C 77, 129 (2017).
(33) J. Soto and J. Tarrús Castellà, Effective field theory for double heavy baryons at strong coupling, Phys. Rev. D 102, 014013 (2020); erratum: Phys. Rev. D 104, 059901 (2021).
(34) J. B. Wang, G. Li, C. R. Deng, C. S. An and J. J. Xie, $\Omega_{cc}$ resonances with negative parity in the chiral constituent quark model, Phys. Rev. D 104, 094008 (2021).
(35) G. L. Yu, Z. Y. Li, Z. G. Wang, J. Lu and M. Yan, Systematic analysis of doubly charmed baryons $\Xi_{cc}$ and $\Omega_{cc}$ , Eur. Phys. J. A 59, 126 (2023).
(36) Z. Y. Li, G. L. Yu, Z. G. Wang and J. Z. Gu, Mass spectra of bottom-charmed baryons. arXiv:2211.15111.
(37) M. J. Savage and M. B. Wise, Spectrum of baryons with two heavy quarks, Phys. Lett. B 248, 177-180 (1990).
(38) R. Roncaglia, D. B. Lichtenberg and E. Predazzi, Predicting the masses of baryons containing one or two heavy quarks, Phys. Rev. D 52, 1722 (1995).
(39) T. D. Cohen and P. M. Hohler, Doubly heavy hadrons and the domain of validity of doubly heavy diquark-anti-quark symmetry, Phys. Rev. D 74, 094003 (2006).
(40) M. Karliner and J. L. Rosner, Baryons with two heavy quarks: Masses, production, decays, and detection, Phys. Rev. D 90, 094007 (2014).
(41) K. W. Wei, B. Chen and X. H. Guo, Masses of doubly and triply charmed baryons, Phys. Rev. D 92, 076008 (2015).
(42) K. W. Wei, B. Chen, N. Liu, Q. Q. Wang and X. H. Guo, Spectroscopy of singly, doubly, and triply bottom baryons, Phys. Rev. D 95, 116005 (2017).
(43) J. Oudichhya, K. Gandhi and A. Kumar Rai, Mass spectra of $\Xi$ _cc, $\Xi$ _bc, $\Omega$ _cc, and $\Omega$ _bc baryons in Regge phenomenology, Phys. Scripta 97, 054001 (2022).
(44) Y. Song, D. Jia, W. Zhang and A. Hosaka, Low-lying doubly heavy baryons: Regge relation and mass scaling, Eur. Phys. J. C 83, 1 (2023).
(45) J. R. Zhang and M. Q. Huang, Doubly heavy baryons in QCD sum rules, Phys. Rev. D 78, 094007 (2008).
(46) L. Tang, X. H. Yuan, C. F. Qiao and X. Q. Li, Study of Doubly Heavy Baryon Spectrum via QCD Sum Rules, Commun. Theor. Phys. 57, 435 (2012).
(47) Z. G. Wang, Analysis of the ${1\over 2}^{+}$ doubly heavy baryon states with QCD sum rules, Eur. Phys. J. A 45, 267 (2010).
(48) T. M. Aliev, K. Azizi and M. Savci, Doubly Heavy Spin-1/2 Baryon Spectrum in QCD, Nucl. Phys. A 895, 59 (2012).
(49) T. M. Aliev, K. Azizi and M. Savci, Mixing angle of doubly heavy baryons in QCD, Phys. Lett. B 715, 149 (2012).
(50) T. M. Aliev, K. Azizi and M. Savci, The masses and residues of doubly heavy spin-3/2 baryons, J. Phys. G 40, 065003 (2013).
(51) L. Liu, H. W. Lin, K. Orginos and A. Walker-Loud, Singly and Doubly Charmed J=1/2 Baryon Spectrum from Lattice QCD, Phys. Rev. D 81, 094505 (2010).
(52) Z. S. Brown, W. Detmold, S. Meinel and K. Orginos, Charmed bottom baryon spectroscopy from lattice QCD, Phys. Rev. D 90, 094507 (2014).
(53) M. Padmanath, R. G. Edwards, N. Mathur and M. Peardon, Spectroscopy of doubly-charmed baryons from lattice QCD, Phys. Rev. D 91, 094502 (2015).
(54) N. Mathur and M. Padmanath, Lattice QCD study of doubly-charmed strange baryons, Phys. Rev. D 99, 031501 (2019).
(55) N. Mathur, M. Padmanath and S. Mondal, Precise predictions of charmed-bottom hadrons from lattice QCD, Phys. Rev. Lett. 121, 202002 (2018).
(56) A. Faessler, T. Gutsche, M. A. Ivanov, J. G. Korner and V. E. Lyubovitskij, Semileptonic decays of double heavy baryons, Phys. Lett. B 518, 55 (2001).
(57) A. Faessler, T. Gutsche, M. A. Ivanov, J. G. Korner and V. E. Lyubovitskij, Semileptonic decays of double heavy baryons in a relativistic constituent three-quark model, Phys. Rev. D 80, 034025 (2009).
(58) C. Albertus, E. Hernandez and J. Nieves, Hyperfine mixing in $b\to c$ semileptonic decay of doubly heavy baryons, Phys. Lett. B 683, 21 (2010).
(59) M. J. White and M. J. Savage, Semileptonic decay of baryons with two heavy quarks, Phys. Lett. B 271, 410 (1991).
(60) R. H. Li, C. D. Lü, W. Wang, F. S. Yu and Z. T. Zou, Doubly-heavy baryon weak decays: $\Xi_{bc}^{0}\to pK^{-}$ and $\Xi_{cc}^{+}\to\Sigma_{c}^{++}(2520)K^{-}$ , Phys. Lett. B 767, 232 (2017).
(61) F. S. Yu, H. Y. Jiang, R. H. Li, C. D. Lü, W. Wang and Z. X. Zhao, Discovery Potentials of Doubly Charmed Baryons, Chin. Phys. C 42, 051001 (2018).
(62) D. Ebert, R. N. Faustov, V. O. Galkin and A. P. Martynenko, Semileptonic decays of doubly heavy baryons in the relativistic quark model, Phys. Rev. D 70, 014018 (2004).
(63) W. Roberts and M. Pervin, Hyperfine Mixing and the Semileptonic Decays of Double-Heavy Baryons in a Quark Model, Int. J. Mod. Phys. A 24, 2401 (2009).
(64) T. Branz, A. Faessler, T. Gutsche, M. A. Ivanov, J. G. Korner, V. E. Lyubovitskij and B. Oexl, Radiative decays of double heavy baryons in a relativistic constituent three-quark model including hyperfine mixing, Phys. Rev. D 81, 114036 (2010).
(65) R. H. Hackman, N. G. Deshpande, D. A. Dicus and V. L. Teplitz, M1 Transitions in the MIT Bag Model, Phys. Rev. D 18, 2537 (1978).
(66) A. Bernotas and V. $\rm{\check{S}}$ imonis, Radiative M1 transitions of heavy baryons in the bag model, Phys. Rev. D 87, 074016 (2013).
(67) W. S. Dai, X. H. Guo, H. Y. Jin and X. Q. Li, Electromagnetic radiation of baryons containing two heavy quarks, Phys. Rev. D 62, 114026 (2000).
(68) C. Albertus, E. Hernandez and J. Nieves, Hyperfine mixing in electromagnetic decay of doubly heavy $bc$ baryons, Phys. Lett. B 690, 265 (2010).
(69) H. Bahtiyar, K. U. Can, G. Erkol, M. Oka and T. T. Takahashi, Radiative transitions of doubly charmed baryons in lattice QCD, Phys. Rev. D 98, 114505 (2018).
(70) Q. Qin, Y. J. Shi, W. Wang, G. H. Yang, F. S. Yu and R. Zhu, Inclusive approach to hunt for the beauty-charmed baryons $\Xi_{bc}$ , Phys. Rev. D 105, L031902 (2022).
(71) B. Eakins and W. Roberts, Heavy Diquark Symmetry Constraints for Strong Decays, Int. J. Mod. Phys. A 27, 1250153 (2012).
(72) L. Y. Xiao, K. L. Wang, Q. F. Lü, X. H. Zhong and S. L. Zhu, Strong and radiative decays of the doubly charmed baryons, Phys. Rev. D 96, 094005 (2017).
(73) L. Y. Xiao, Q. F. Lü and S. L. Zhu, Strong decays of the 1P and 2D doubly charmed states, Phys. Rev. D 97, 074005 (2018).
(74) T. Mehen, Implications of Heavy Quark-Diquark Symmetry for Excited Doubly Heavy Baryons and Tetraquarks, Phys. Rev. D 96, 094028 (2017).
(75) Y. L. Ma and M. Harada, Chiral partner structure of doubly heavy baryons with heavy quark spin-flavor symmetry, J. Phys. G 45, 075006 (2018).
(76) M. J. Yan, X. H. Liu, S. Gonzàlez-Solís, F. K. Guo, C. Hanhart, U. G. Meißner and B. S. Zou, New spectrum of negative-parity doubly charmed baryons: Possibility of two quasistable states, Phys. Rev. D 98, 091502 (2018).
(77) H. Z. He, W. Liang and Q. F. Lü, Strong decays of the low-lying doubly bottom baryons, Phys. Rev. D 105, 014010 (2022).
(78) B. Chen, S. Q. Luo, K. W. Wei and X. Liu, $b-$ hadron spectroscopy study based on the similarity of double bottom baryon and bottom meson, Phys. Rev. D 105, 074014 (2022).
(79) T. Yoshida, E. Hiyama, A. Hosaka, M. Oka and K. Sadato, Spectrum of heavy baryons in the quark model, Phys. Rev. D 92, 114029 (2015).
(80) E. Hiyama, Y. Kino and M. Kamimura, Gaussian expansion method for few-body systems, Prog. Part. Nucl. Phys. 51, 223-307 (2003).
(81) E. Hiyama and M. Kamimura, Study of various few-body systems using Gaussian expansion method (GEM), Front. Phys. (Beijing) 13, 132106 (2018).
(82) H. Nagahiro, S. Yasui, A. Hosaka, M. Oka and H. Noumi, Structure of charmed baryons studied by pionic decays, Phys. Rev. D 95, 014023 (2017).
(83) A. J. Arifi, D. Suenaga and A. Hosaka, Relativistic corrections to decays of heavy baryons in the quark model, Phys. Rev. D 103, 094003 (2021).
(84) A. J. Arifi, D. Suenaga, A. Hosaka and Y. Oh, Strong decays of multistrangeness baryon resonances in the quark model, Phys. Rev. D 105, 094006 (2022).
(85) K. L. Wang, Q. F. Lü and X. H. Zhong, Interpretation of the newly observed $\Sigma_{b}(6097)^{\pm}$ and $\Xi_{b}(6227)^{-}$ states as the $P$ -wave bottom baryons, Phys. Rev. D 99, 014011 (2019).
(86) M. S. Liu, K. L. Wang, Q. F. Lü and X. H. Zhong, $\Omega$ baryon spectrum and their decays in a constituent quark model, Phys. Rev. D 101, 016002 (2020).
(87) Q. F. Lü, H. Nagahiro and A. Hosaka, Understanding the nature of $\Omega(2012)$ in a coupled-channel approach, Phys. Rev. D 107, 014025 (2023).
(88) F. E. Close and E. S. Swanson, Dynamics and decay of heavy-light hadrons, Phys. Rev. D 72, 094004 (2005).
(89) D. M. Li, P. F. Ji and B. Ma, The newly observed open-charm states in quark model, Eur. Phys. J. C 71, 1582 (2011).
(90) S. Godfrey and K. Moats, Bottomonium Mesons and Strategies for their Observation, Phys. Rev. D 92, 054034 (2015).
(91) S. Godfrey and K. Moats, Properties of Excited Charm and Charm-Strange Mesons, Phys. Rev. D 93, 034035 (2016).
(92) B. Chen, K. W. Wei, X. Liu and T. Matsuki, Low-lying charmed and charmed-strange baryon states, Eur. Phys. J. C 77, 154 (2017).
(93) C. Chen, X. L. Chen, X. Liu, W. Z. Deng and S. L. Zhu, Strong decays of charmed baryons, Phys. Rev. D 75, 094017 (2007).

$\displaystyle\left\|Y_{bc}(J)\right\rangle=$	$\displaystyle\sqrt{2M_{Y_{bc}}}\sum_{\{s,l\}}\int\frac{d^{3}\mathbf{p}_{\rho}}{(2\pi)^{3}}\int\frac{d^{3}\mathbf{p}_{\lambda}}{(2\pi)^{3}}\frac{1}{\sqrt{2m_{1}}}\frac{1}{\sqrt{2m_{2}}}$	(20)
	$\displaystyle\frac{1}{\sqrt{2m_{3}}}\psi_{l_{\rho}}(\mathbf{p}_{\rho})\psi_{l_{\lambda}}\left(\mathbf{p}_{\lambda}\right)\left\|q_{1}\left(p_{1},s_{1}\right)\right\rangle\left\|q_{2}\left(p_{2},s_{2}\right)\right\rangle$
	$\displaystyle\left\|q_{3}\left(p_{3},s_{3}\right)\right\rangle.$

Bottom-charmed baryons in a nonrelativistic quark model

Abstract

I Introduction

II FORMALISM

II.1 Potential Model

II.2 Pseudoscalar meson emissions

III Results and discussion

III.1 Mass spectrum

III.2 Strong decays for λ−\lambda-mode Ξb​c\Xi_{bc} and Ωb​c\Omega_{bc} states

III.3 Strong decays for λ−\lambda-mode Ξb​c′\Xi_{bc}^{\prime} and Ωb​c′\Omega_{bc}^{\prime} states

III.4 Relativistic corrections of order 1/m21/m^{2} for Roper-like resonances

III.5 Mixing

III.6 Low-lying ρ−\rho-mode and ρ−λ\rho-\lambda hybrid states

IV SUMMARY

ACKNOWLEDGMENTS

References

III.2 Strong decays for $\lambda-$ mode $\Xi_{bc}$ and $\Omega_{bc}$ states

III.3 Strong decays for $\lambda-$ mode $\Xi_{bc}^{\prime}$ and $\Omega_{bc}^{\prime}$ states

III.4 Relativistic corrections of order $1/m^{2}$ for Roper-like resonances

III.6 Low-lying $\rho-$ mode and $\rho-\lambda$ hybrid states