Bounds and Heuristics for Multi-Product Personalized Pricing

We first briefly review the representative consumer problem that results in the linear demand model. The task of the representative consumer is to solve the problem $\max_{q\geq 0}[(u-p)^{\prime}q-q^{\prime}Sq]$ where $u$ is the vector of gross utilities, $u-p$ is the vector of net utilities, and $S$ is a positive definitive matrix. The solution that ignores the non-negativity constraints yields $q^{*}=B(u-p)=a-Bp$ where $a:=Bu$ and $B:=(S+S^{\prime})^{-1}$. Notice that by construction $B$ is symmetric and positive definitive. Let $P:=\{p\geq 0:a-Bp\geq 0\}$. We assume that $a$ has positive components. Then $d(p)=a-Bp$ for all $p\in P$. Maximizing $R(p)=p^{\prime}(a-Bp)$ yields $p^{*}=0.5B^{-1}a=0.5u$, $d(p^{*})=0.5a$ and $R(p^{*})=0.25u^{\prime}Bu>0$, so $p^{*}\in P$. For $p\notin P$, the solution to the representative consumer’s problem is equivalent to solving the linear complementarity problem $y\geq 0$, $d(p-y)\geq 0$, and $y^{\prime}d(p-y)=0$, see Gallego and Topaloglu (2019).

Suppose that for all $j\in M$, $d^{j}(p)=B_{j}(u^{j}-p)=a^{j}-B_{j}p$ for $p\in P_{j}:=\{p\geq 0:a^{j}-B_{j}p\geq 0\}$. where $u^{j}$ and $a_{j}$ are positive vectors, and $B_{j}$ is a symmetric positive definitive matrix. Then $\bar{p}^{j}=0.5B^{-1}_{j}a^{j}=0.5u^{j}$ is in $P_{j}$, and $\bar{\mathcal{R}}=\sum_{j\in M}\theta_{j}\mathcal{R}_{j}$ can be computed without problems.

Suppose that $B_{j}$ has non-positive off-diagonal elements for all $j\in M$. Then Therorem 2 holds for positive vectors $f$ such that $B_{j}f\geq 0$ for all $j\in M$. Moreover, if $B_{j}$ is an M-matrix for all $j\in M$ then the Theorem 2 holds for all positive $f$.

At this point we know that $\bar{\mathcal{R}}\leq\beta\mathcal{R}^{f}\leq\beta\mathcal{R}^{*}$ where $\mathcal{R}^{f}$ and $\mathcal{R}^{*}$ are interpreted as $\mathcal{R}^{f}=\max_{q\geq 0}qf^{\prime}(a-qBf)$ and $\mathcal{R}^{*}=\max_{p\geq 0}q^{\prime}(a-Bp)$ where $a=\sum_{j\in M}\theta_{j}a^{j}$ and $B=\sum_{j\in M}\theta_{j}B_{j}$. The caveat is that optimal solutions to this problems, say $q^{*}f$ and $p^{*}$, may be outside $P_{j}$ for some $j\in M$ resulting in negative demands for some products for some customer types. This cast as question of whether the profits from pricing at $q^{*}f$ or at $p^{*}$ will actually satisfy the guarantees of Theorem 2. We will show that $\bar{\mathcal{R}}\leq\beta\mathcal{R}^{f}$ and $\bar{\mathcal{R}}\leq\beta\mathcal{R}^{*}$ continue to hold even after the adjustments required to ensure that all demands are non-negative. To see this in a generic form, we will argue that the actual profit when $d(p)$ has negative components is at least as large as $R(p)=p^{\prime}d(p)$. {prop} The profit under the representative consumer model is equal to $R(p)+p^{\prime}By\geq R(p)$ when $p\notin P$.

We can now apply the result to each customer type that has negative demands at $p$. In particular, if there is a customer type with negative demands at $q^{*}f$, then the firm will see profits $R_{j}(q^{*}f)+q^{*}f^{\prime}B_{j}y^{j}\geq R_{j}(q^{*}f)$ from type $j$ customers, so $\mathcal{R}^{f}=\max_{q}R(qf)$ is a lower bound on the aggregate profit over all customer types at $q^{*}f$. Consequently, the profit from the single factor model is at least $\mathcal{R}^{f}\geq\bar{\mathcal{R}}/\beta$. In a similar way, $\mathcal{R}^{*}=\max_{p}R(p)$ is a lower bound of the aggregate profits at $p^{*}\in\arg\max R(p)$, so the profit under $p^{*}$ is at least $\mathcal{R}^{*}\geq\bar{\mathcal{R}}/\beta$. One must be aware, however, that for multiple customer types, $p^{*}=0.5B^{-1}a$ is not necessarily optimal if there are customer types with negative demands at this price vector. To find a true optimal solution to the problem the firm needs to solve $\max_{p\geq 0,y^{j},j\in M}\sum_{j\in M}\theta_{j}[R_{j}(p)+p^{\prime}B_{j}y^{j}]$ subject to $d^{j}(p-y^{j})\geq 0,y^{j}\geq 0$ and $y^{j}_{i}d_{ij}(p-y^{j})=0$ for all $i\in N,j\in M$. The solution $p^{*}=0.5B^{-1}a$ together with the corresponding $y^{j}$s that solve the linear complementarity problem for market segments with negative demands is only a heuristic for this problem, so our results continue to hold if the more complex problem is solved, with a similar more sophisticated program for pricing along a factor $f$.

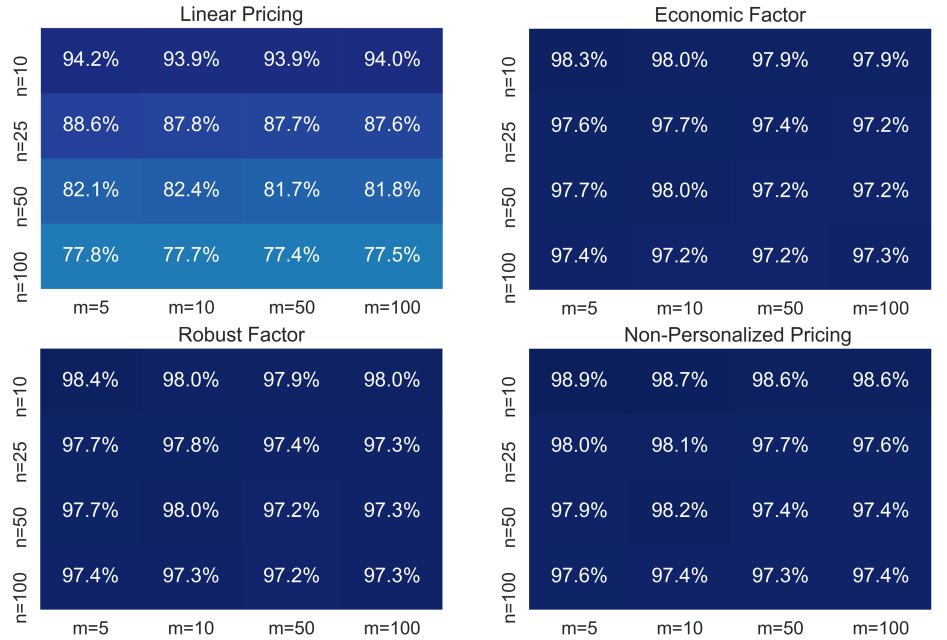
Figure 1 reports a series computational results in order to evaluate the performance of different pricing strategies. For each value of $n$ and $m$, we generated 20 random instances and we reported the average profit as a percentage of the maximum profit that can be obtained using personalized pricing. The weight of each segment $j$ was set to $\theta_{j}=x_{j}/\sum_{l=1}^{m}x_{l}$ where each $x_{l}$ is a uniform random number between 0 and 1. For each segment $j$ we randomly generated the matrix $B_{j}$ ensuring it is symmetric and positive definitive and satisfies P1 and P2. The vector $a^{j}$ was generated uniformly random from $(0,1]^{n}$. The percentages shown are the average percentage of the profit obtained with respect to the best personalized pricing strategy. As we can see, the economic factor outperformed the robust factor, and both performed significantly better than uniform pricing based on $f=e$. The lower right-hand table for the optimal price uses the heuristic $p^{*}=0.5B^{-1}a$ adjusting demands by solving the complementary slackness for customer types with negative demands. It performance is similar to that of the economic factor.

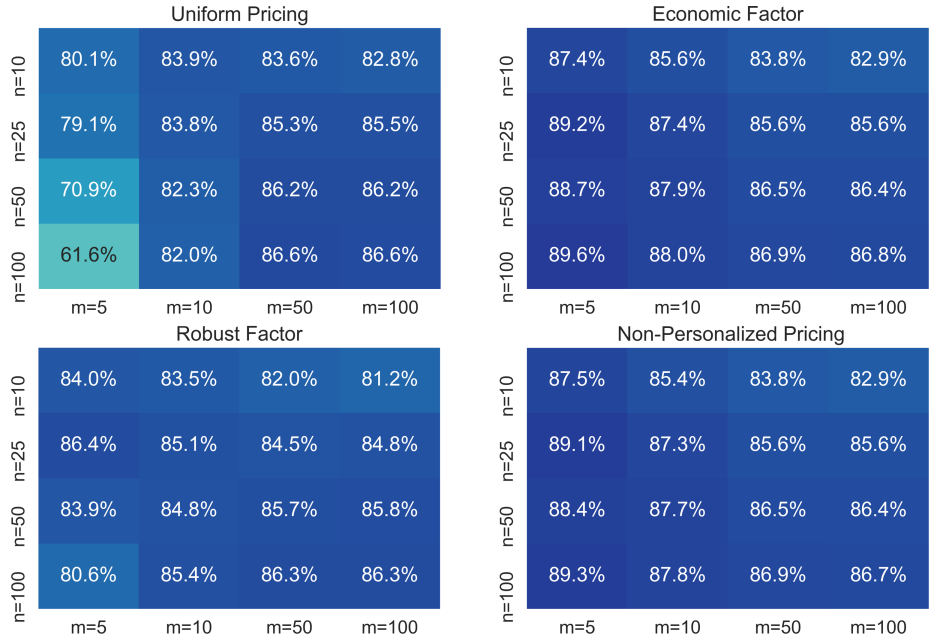
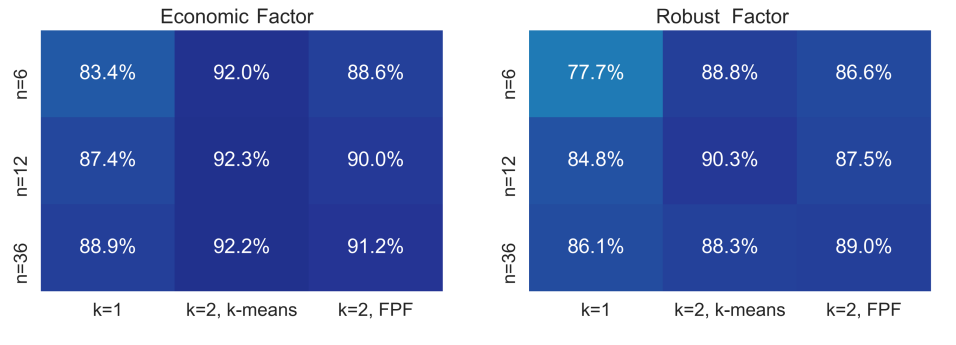
Figure 2 reports another set of experiments to quantify the advantages of clustering consumer segments into two clusters ($k=2$) under the economic and the robust pricing strategies. Two clustering algorithms were implemented. The first one is the standard k-means algorithm in which each segment $j$ was assigned the price vector $\bar{p}^{j}$ as its representative point in an $n$-dimensional space. The second is the farthest point first (FPF) proposed by gonzalez1985clustering where the distance matrix is set as described in Section 3. For these experiments the number of consumer segments was set to $m=6$. As can be seen, the best combination was the economic factor coupled with $k$-means and the worse was the robust factor with FPF.

Suppose that $d^{j}(p)$ is the expected demand from an MNL model, so

The matrix of partial derivatives is given by $\nabla d^{j}(p)=\mbox{diag}(b^{j})\left[d^{j}(p)d^{j}(p)^{\prime}-\mbox{diag}(d^{j}(p))\right]$. Since the off-diagonal elements are non-negative we see that $d_{ij}(p)$ is increasing in $p_{k},k\neq i$ and P1 holds. P2 hold for all positive vectors $f$ such that $\nabla d^{j}(p)f\leq 0$, or equivalently for all positive vectors $f$ such that $d^{j}(p)^{\prime}f\leq\min_{i\in N}f_{i}$ for all $j\in M$. We can scale $f$ without loss of generality so that $\min_{i\in N}f_{i}=1$, which reduces the condition to $\sum_{i\in N}f_{i}d_{ij}(p)\leq 1$. This clearly holds for $f=e$ on account of $\sum_{i\in N}d_{ij}(p)=1-d_{0j}(p)\leq 1$. For any positive $f$ the condition reduces to $\sum_{i\in N}(f_{i}-1)\exp(a_{ij}-b_{ij}p_{i})\leq 1$ for all $j\in M$. We remark that A1 requires the condition to hold only at $p=\bar{p}^{j}$, for $j\in M$. We know that for each consumer type the optimal price is of the form $\bar{p}_{ij}=1/b_{ij}+m_{j}$ where $m_{j}$ is the adjusted markup for product type $j$ consumers, so the condition is easy to check. In particular, if $b_{ij}=b_{j}$ for each $i\in N$, and $j\in M$, then both the economic and the robust factors can be taken to be equal to $e$.

For the LC-MNL $\bar{\mathcal{R}}\leq\beta\mathcal{R}^{e}\leq\beta\mathcal{R}^{*}$ without any further conditions since P1 and P2 hold for $f=e$ for all MNL models with arbitrary price sensitivities. In addition, if the $b_{kj}=b_{j}$ is independent of $k\in N$ for each $j\in M$, then the economic and the robust factors are equivalent to $e$. Finally, $\bar{\mathcal{R}}\leq\beta\mathcal{R}^{f}\leq\beta\mathcal{R}^{*}$ holds for all positive vectors $f$ such that $d^{j}(\bar{p}^{j})f\leq\min_{i\in N}f_{i}$ for all $j\in M$.

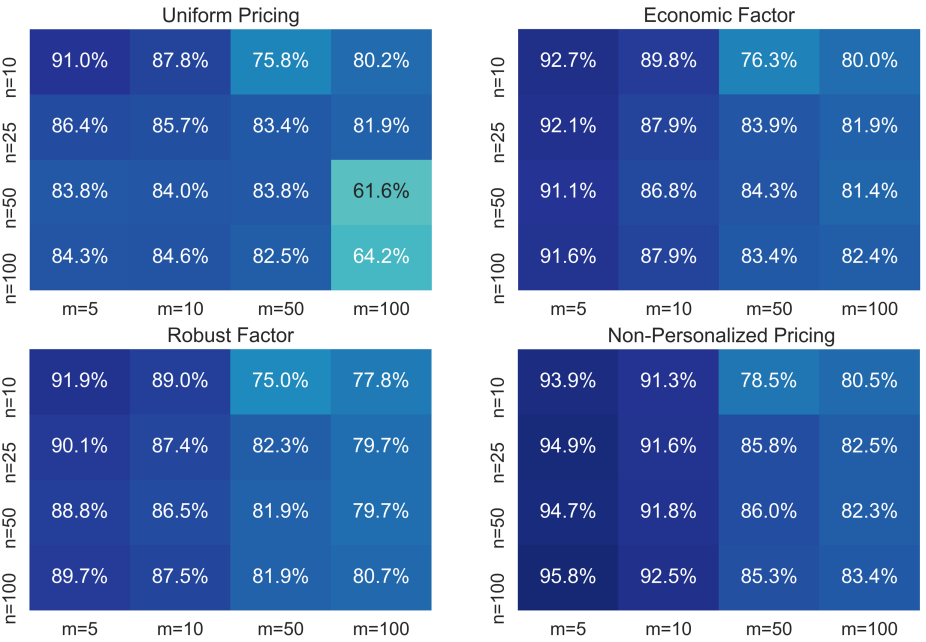
We tested the performance of the different heuristics under the LC-MNL model and reported the results in Figure 3. The percentages shown are the average percentage of the profit obtained with respect to the best personalized pricing strategy. For each value $n$ and value $m$ reported, we generated 20 random instances with $n$ products and $m$ segments. The mean utility of product $i$ to consumer segment $j$ is $u_{ij}=a_{ij}-b_{ij}p_{i}$ where the intrinsic product utility $a_{ij}$ were randomly chosen following a procedure proposed by rusmevichientong2014assortment ⁶⁶6Specifically, the intrinsic utility of product $i$ for consumer segment $j$ is defined as $a_{ij}:=\ln((1-\sigma_{i})v_{ij}/n)$ with probability $p=0.5$ and $a_{ij}::=\ln((1+\sigma_{i})v_{ij}/n)$ otherwise. The values $v_{ij}$ and $\sigma_{i}$ are realizations from a uniform distribution $[0,10]$ and $[0,1]$ respectively. and the (segment and product dependent) price sensitivities $b_{ij}$ were randomly chosen from a symmetric triangular distribution between 0 and 2. We can observe that while uniform pricing does relatively well (obtaining between 60.6% to 91% of the optimal personalized profit) it is surpassed by the Economic and Robust strategies with get at least 76.3% and 75% respectively. The values for the non-personalized pricing are not necessarily the optimal ones ⁷⁷7This is an NP-hard problem. since they were obtained using a multi-variable non-linear solver in Python. This strategy requires much broader computational resources than the other three methods which simply rely on a single variable optimization. For example, when $n=100$ the solver took on average over 22 times more time than any of the other 3 strategies.

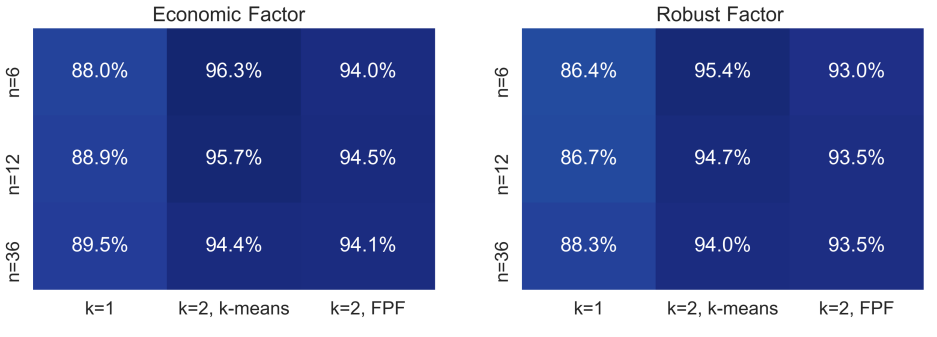
Similarly to the clustering results for the linear demand model, Figure 4 reports computational results that quantify and compare the benefits of clustering consumer segments using k-means and FPF under the Economic single factor and the Robust single factor pricing strategies. The values represent the average percentage of the profit obtained with respect to the best personalized pricing strategy. As in the linear demand model, $m=6$ for all these experiments. As can be seen, the best combination was the economic factor coupled with $k$-means and the worse was the robust factor with FPF.

We now consider the non-linear pricing scheme where the firm sells a single product in different bundle sizes- for a broad overview of non-linear pricing see wilson1993nonlinear and oren2012nonlinear. Let $p_{i}$ be the price of a size $i\in N$ bundle and $d_{i}(p)$ is the demand for a size $i$ bundle at the price vector $p$. Let $\mathcal{R}^{*}=\max_{p}R(p)$ yielding an optimal non-linear price schedule. Let $f$ be a vector with components $f_{i}=i,i\in N$. Then $\mathcal{R}^{f}:=\max_{q}qf^{\prime}d(qf)$ corresponds to the linear price schedule $p_{i}=iq,i\in N$. Theorem 2 holds if $d_{i}(p)$ is increasing in $p_{k}$, $k\neq i$ and if $f^{\prime}d(p)$ is decreasing in $p$. We remark that $f^{\prime}d(p)=\sum_{i\in N}id_{i}(p)$ is the total number of units demanded at price $p$, so the condition is that the total number of units demanded goes down if the price of any bundle is increased.

As an example, suppose that $d(p)=a-Bp$ and $B$ is an $M$-matrix, then $Bf\geq 0$ for all $f$ and in particular for $f_{i}=i$. Let $v:=B^{-1}a$. Then $p^{*}=v/2$. If $v_{i}$ is increasing concave then $q_{\min}=v_{n}/n$ and $q_{\max}=v_{1}$ resulting in $\beta=1+\ln(nv_{1}/v_{n})$.

To our knowledge this is the first result that gives a performance guarantee for linear versus non-linear pricing, but we can go further as Theorem 2 works for the personalized version as well. More precisely, if $d^{j}(p)$ is the demand vector for bundles of size $i\in N$ for every $j\in M$, $d_{ij}(p)$ is increasing in $p_{k}$ for all $k\neq i$, and $f^{\prime}d^{j}(p)$ is decreasing in $p$ for all $j\in M$ then Theorem 2 applies and bounds how much better personalized non-linear pricing can be relative to linear pricing. Theorem 2 can also be used to bound the performance of non-personalized non-linear pricing schemes relative to personalized non-linear pricing schemes. We summarize the results for personalized non-linear pricing here.

If $d_{ij}(p)$ represent the demand for bundles of size $i\in N$ in market segment $j\in M$ where $p_{i}$ is the price of a size $i\in N$ bundle, $d_{ij}(p)$ is decreasing in $p_{k},k\neq i$ and $\sum_{i\in N}id_{ij}(p)$ is decreasing in $p$ for all $j\in M$, then

where $\mathcal{R}^{*}$ is the profit from the optimal non-personalized non-linear pricing policy and $\mathcal{R}^{f}$ is the optimal under non-personalized linear pricing policy.

We remark that $f$ here was selected as $f_{i}=i,i\in N$ for the purpose of comparing a common linear price schedule for all customer types to optimal personalized non-linear pricing. One can instead use the robust $f$ or the economic $f$ to obtain a potentially better common (non-linear) price schedule.

Figure 5 reports a computational results about the performance of different pricing strategies for a non-linear pricing problem as described above. Each consumer segment follows a linear model as explained in Section 4.1. The matrix $B_{j}$ associated to segment $j$ was generated in the same way as for the experiments of Section 4.1 whereas instead of generating a random vector $a^{j}$, we produced a random vector of utilities $u$ satisfying that $u_{i+1}>u_{i}$ and $u_{i+1}/(i+1)<u_{i}/i$ for all $i\in[n-1]$. We generated 20 instances for each value of $m$ and each maximum bundle size ($n$). As can be seen from the tables, linear pricing performance relatively well for $n=10$ but deteriorates as the maximum bundle size increases achieving only about 77% of optimal personalized non-linear pricing. The results do not seem to be sensitive to the number of customer types. The robust factor slightly outperforms the economic factor, and the non-personalized non-linear pricing strategy is very close to the optimal personalized strategy with little need for clustering types.

Consider a set of $n$ products that can be sold as bundles. Suppose that given prices for each of the $2^{n-1}$ non-trivial bundles, the firm can obtain the demand for each of the bundles. Selecting the bundle prices to maximize profits is know as the mixed bundle problem. Suppose that $p(x),x\in\{0,1\}^{n}$ is an optimal solution to the mixed bundle problem. We may wonder about the performance of several pricing strategies relative to mixed bundling. The simplest strategy is to use uniform pricing. This gives rise to $f(x)=e^{\prime}x$. A second strategy, known as component pricing is to set $f(x)=p^{\prime}x$ where $p_{i}$ is the price of component $i$. Finally, we can have a non-linear function $f(x)=g(e^{\prime}x)$ where $g$ is an increasing non-linear function. Notice this form yields the same price factor for all bundles of size $e^{\prime}x$. This is known as bundle-size pricing and contains uniform pricing as a special case if $g(e^{\prime}x)=e^{\prime}x$. In all cases, the firm will find and optimal $q$ for the pricing strategy $q\cdot f(x)$ for size $x$ bundles, ChenLeslieSoren2011bunde shows through extensive numerical studies that bundle-size pricing can do a good job of approximating the benefits of the more complicated mixed bundling strategy but to our knowledge there are no theoretical work on tight bounds. Let $q_{\max}=\max_{x\neq 0}p(x)/f(x)$ and $q_{\min}=\min_{x\neq 0}p(x)/f(x)$. Under mild conditions on the demand function for bundles (A0 and A1, or A0 together with P1 and P2) we obtain performance guarantees $\mathcal{R}^{*}\leq\beta\mathcal{R}^{f}$ where here $\mathcal{R}^{*}$ is the optimal profit under mixed bundling and $\mathcal{R}^{f}$ is the optimal pricing along the vector $f(x),x\in\{0,1\}^{n}$, where $\beta=1+\ln(\rho)$ where $\rho=q_{\max}/q_{\min}$. As an example, if $n=2$ then the non-trivial bundles are $e_{1},e_{2}$ and $e=e_{1}+e_{2}$ where $e_{i}$ is the $i$th unit vector in $\Re^{2}$. If $p(e_{1})=1,p(e_{2})=2$ and $p(e)=2.5$ and we use $f(1)=1$ and $f(2)=2$ for bundles of size 1 and 2, then $q_{\min}=1$ and $q_{\max}=2$ so $\rho=2$ and $\beta=1+\ln(2)\simeq 1.693$. The theory also holds if there are multiple types and the firm uses personalized mixed pricing for each type. The only difference is that the definition of $q_{\min}$ and $q_{\max}$ has to be over all bundles and all types. It is also possible to fit a robust or an economic mixed bundle strategy and as long as the conditions A0 and A1 hold the bound from Theorem 1 holds. If the model is linear or latent class MNL we will get similar numerical results with the exception that the bundles are interpreted as products and the vector $f$ is either the bundle size or either the economic or robust factor in the case of multiple market segments.