Box dimension of fractal functions on attractors
Abstract
We study a wide class of fractal interpolation functions in a single platform by considering the domains of these functions as general attractors. We obtain lower and upper bounds of the box dimension of these functions in a more general setup where the interpolation points need not be equally spaced, the scale vectors can be variables and the maps in the corresponding IFS can be non-affine. In particular, we obtain the exact value of the box dimension of non-affine fractal functions on general m-dimensional cubes and Sierpiński Gasket.
R. Pasupathi
Sobolev Institute of Mathematics SB RAS, 630090, Novosibirsk, Russia
Email: pasupathi4074@gmail.com
Keywords: Fractal interpolation function, Attractor, Box dimension, Sierpiński Gasket
MSC Classification: 28A80, 41A05, 37E05
1 Introduction
In 1986, Barnsley [2] proposed the concept of a fractal interpolation function (FIF) on intervals using the notion of iterated function system. This work was extended to many different domains such as triangles [19], -dimensional cubes [22], Sierpiński Gasket [8], post critically finite (p.c.f.) self-similar sets [24] etc.
The graph of a function, and its box and Hausdorff dimensions, have been of qualitative interest for many researchers since the past few decades. Several theories concerning the box dimension of fractal functions have been explored in the literature. Some of recent works on FIF and dimension theory can be found in [7, 17, 15, 21, 23].
Hardin and Massopust [13] have estimated the value of the box dimension of graph of FIF on an interval when the maps in the corresponding IFS are affine and the interpolation points are equally spaced. Barnsley and Massopust [3] studied the box dimension of bilinear FIF on an interval in the case of equally spaced data points. Nasim et al. [1] obtained the box dimension of non-affine FIF in the case of equally spaced data points by using Hölder exponent. Feng and Sun [11] studied the box dimension of FIFs on a rectangle derived from affine FIFs on an interval with arbitrary interpolation nodes. Geronimo and Hardin [12] have estimated the box dimension of self-affine FIF on polygonal regions. Bouboulis et al. [4] introduced recurrent FIF (RFIF) on a rectangle as the invariant set of the recurrent IFS (RIFS) in order to gain more flexibility, and studied the value of the box dimension of RFIF when the maps in the corresponding RIFS are affine with respect to each variable and the interpolation points are equally spaced. Bouboulis and Dalla [5] generalized the theory of RFIF and its box dimension to higher dimensions.
In the literature, we found that, in most of the cases, the authors assumed that the interpolation points are equally spaced and the maps in the corresponding IFS are affine when the box dimension of FIF was considered, and there was no discussion about the box dimension of FIFs on p.c.f. self-similar sets except the Sierpiński Gasket. Even in the case of Sierpiński Gasket also, the authors [25] obtained only a non-trivial upper bound of the box dimension of FIFs by using Hölder exponent. The authors always assumed all the scale variables to be constants for estimating a non-trivial lower bound of the box dimension of fractal functions.
In this paper, we consider FIFs on attractors and we study lower and upper bounds of the box dimension of these functions without assuming that the interpolation points are equally spaced, the maps in the corresponding IFSs are affine and all the scale vectors are constants. We derive upper bounds of the box dimension of fractal functions using a function space called the oscillation space, which contains the collection of Hölder continuous functions. We provide non-trivial lower bounds of the box dimension of FIF on -dimensional cubes and Sierpiński Gasket.
2 Preliminaries
Definition 2.1.
An iterated function system (IFS) consists of a complete metric space together with a finite set of continuous mappings . We denote it as .
For an IFS, we can define an operator (called Hutchinson operator) by
where is the Hausdorff metric space on i.e., is the collection of all non-empty compact subsets of and is the Hausdorff distance.
If has a unique fixed point (say) and for every , then is called the attractor of the IFS, where by , we mean the composition of a function with itself times.
Definition 2.2.
Let be a metric space and be a function. If there is a constant such that:
-
then is called contraction;
-
then is called similarity.
The constant is called the contractivity factor of .
Remark 2.1.
[14] An IFS has an attractor provided that ’s are contractions.
Remark 2.2.
If a function is similarity, then it is an affine map.
For an IFS , we denote , and , and we define
Let be defined by
Following Kigami [16], we define the critical set and the post critical set of by
where is the left shift operator on . If is a finite set, then is called a post critical finite (p.c.f.) self-similar set. The boundary of is defined by and we define
Remark 2.3.
[16]
-
(i)
.
-
(ii)
For with , we get
Definition 2.3.
For a nonempty bounded subset of , the lower and upper box dimensions are defined by
where is the minimum number of boxes with side length and sides parallel to the axes, whose union contains . If , this common value is denoted by and is called the box dimension or Minkowski dimension of .
Remark 2.4.
[10] For a nonempty bounded subset of and a continuous function , we have the following inequalities
where means the Hausdorff dimension of .
Definition 2.4.
Let and be metric spaces. A function is called Hölder continuous with exponent if and there exists such that
3 Fractal interpolation function
Let be a given function (data), where
-
,
-
is an attractor of an IFS , is the Euclidean metric on , and is a similarity map on with the contractivity factor for .
Let us consider defined by
| (3.1) |
where is a continuous function with , is the uniform metric and is a continuous function which satisfy the following ‘join-up’ conditions
| (3.2) |
We consider the IFS , where
Let us suppose that the map given by
is well-defined, where and .
Lemma 3.1.
where .
Proof.
Since
| (3.3) |
for and , we get the proof. ∎
Theorem 3.1.
is a contraction map on the complete space .
Proof.
For , we get
∎
Corollary 3.1.
There exists a unique continuous function such that and
| (3.4) |
Proof.
From Theorem 3.1 and the Banach contraction principle, we conclude that there exists such that . ∎
We call this unique map fractal interpolation function (FIF) on .
Proposition 3.1.
is a fixed point of the Hutchison operator of , where denotes the graph of .
Proof.
Since and
| (3.5) |
we get the result. ∎
Theorem 3.2.
If has an attractor (say), then
Proof.
Since is the unique fixed point of the Hutchison operator of , from Proposition 3.1, we get the result. ∎
Lemma 3.2.
are well-defined operators, where .
Proof.
For and , we get
∎
Proposition 3.2.
If ’s are Hölder continuous, then has an attractor.
Proof.
Case 1.
Remark 3.1.
Remark 3.2.
If is a p.c.f. self-similar set and is its boundary with respect to the IFS , then for any , is again a p.c.f. self-similar set (boundary of ) with respect to the IFS . So, for any we can get a FIF for the given data on . Note that as .
Remark 3.3.
Sierpiński Gasket (SG), Sierpiński sickle, Koch curve, Hata’s tree-like set are some of the examples of p.c.f. self-similar sets.
The IFS of SG is , where for and are the vertices of an equilateral triangle. In this case, the boundary of is .
Case 2.
If
with for , then we define to be
for and where
-
,
-
for and
-
for (which is called signature).
We defined for such that
and
From our construction, we get
-
and
-
.
-
(i)
If , then is a p.c.f. self-similar set and is its boundary. So, is well-defined.
In this case, we obtain the fractal interpolation function of the zipper on an interval (see [7]).
If we choose for and ’s are constant functions, we get the standard fractal interpolation function on an interval (see [2]). - (ii)
4 Box dimension of fractal functions
For a continuous function and , we define the oscillation of over by
and total oscillation of order by
We define oscillation space on , for , as follows (Ref. [9])
where and .
Remark 4.1.
If and then is the collection of continuous bounded variation functions on .
In the following proposition, we discuss the relation between Hölder continuous functions and oscillation spaces, draws inspiration from [6].
Proposition 4.1.
If is a Hölder continuous function with exponent then
Proof.
By assumption, there exists a constant such that
Thus, we have
for all , where denotes the diameter of . ∎
Theorem 4.1.
Let for . If:
-
(i)
then
-
(ii)
then
where and .
Proof.
Let and denote the minimum number of cubes of size which covers and respectively, where for .
For and , we have
For and , we get is contained in a cuboid of size .
Since and
| (4.10) |
we get
for , where .
Via the mathematical induction method, for we get
Consider , then for , we have
Therefore, we get
Consider then for , we have
Hence
∎
Let us denote , and for , we denote:
-
, where
-
, where
-
, where
Lemma 4.1.
Assume that there exist and such that and the set is not collinear i.e., . Then for , we get
-
(i)
must cover a set of height ;
-
(ii)
must cover a set of height if ;
-
(iii)
must cover a set of height if .
Proof.
Let us suppose that .
Since ’s are similarities on , they are affine maps.
Thus, for , we get
| (4.11) |
For such that is a non-negative constant and is concave, we get
| (4.12) |
For such that are non-negative constants and are concave, we get
Via the mathematical induction method, for and , we get
| (4.13) |
Since is a continuous function passing through and , and by using (4.11) and (4), we get must cover a set of height , for .
In a similar way, we can prove the other cases also.
∎
Lemma 4.2.
Let us consider for and , where are affine maps for . Assume that there exist for some , and such that and . Then for , we get
-
(i)
must cover a set of height ;
-
(ii)
must cover a set of height if ;
-
(iii)
must cover a set of height if .
Proof.
Using similar arguments of Lemma 4.1, we can prove this result. ∎
Theorem 4.2.
Proof.
Let denote the minimum number of cubes of side length that covers , where is the minimum of the side lengths of .
Let us suppose that .
From Lemma 4.2, we get must cover a cuboid of size , for .
Thus
| (4.14) |
Therefore
A similar argument works for other cases as well. ∎
Corollary 4.1.
Let be a multivariate FIF derived from Case 2, and be a constant for . Assume that the interpolation points are not collinear (i.e., there exists as in Lemma 4.2)
-
and either is affine with respect to the co-ordinate for
or -
, is concave with respect to the co-ordinate and for
or -
, is convex with respect to the co-ordinate and for .
If:
-
(i)
then
-
(ii)
then
-
(iii)
and are equally spaced points for , then
Theorem 4.3.
Proof.
From the assumption, we get for and .
Let and denote the minimum number of sets belonging to the family
which covers and respectively.
Let us suppose that .
From Lemma 4.1, for we get
| (4.15) |
Since
we have
In a similar way, we can prove the other cases. ∎
Remark 4.2.
Theorem 4.4.
Let be a FIF on an interval derived from Case 2, for and be a equally spaced points collection. If and , then
where and .
Proof.
From assumption, we have for and . From Theorem 4.1, we get the upper bound of .
For and , we have
For and , we get must cover at least a rectangle of size .
From (4.10), we have
for , where .
Via the mathematical induction method, we get
for .
By assumption, there exists such that
Thus
for , where .
Hence
∎
Corollary 4.2.
Let be a FIF on an interval, be continuous bounded variation maps for , be a equally spaced points collection. If the interpolation points are not collinear (i.e., there exists as in Lemma 4.1), and either (or) and (or) and , then
Proof.
Example 4.1.
Let us consider the data set and the signature , where .
Let given by
for , where for or for and .
We have:
for , where ;
if and if ;
if and if .
Consider and , then we get
, , and .
Based on Theorem 4.1 and 4.2, we get
and
Consider and , then we get
, and .
From Corollary 4.1, we get
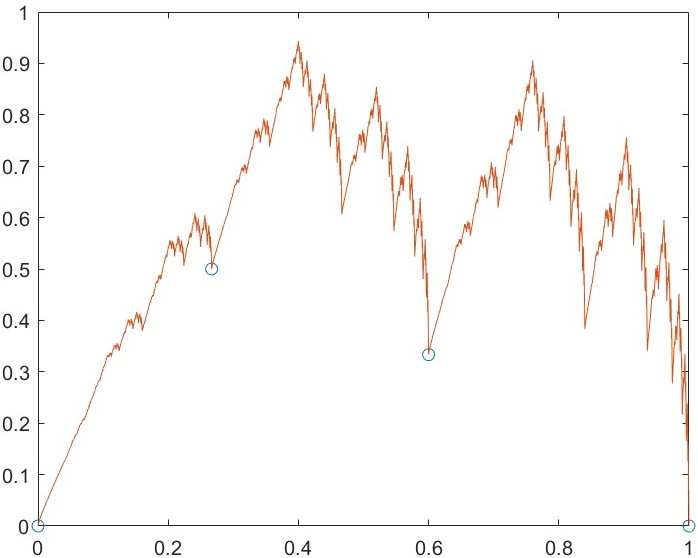
Case of Example 4.1 and we get .
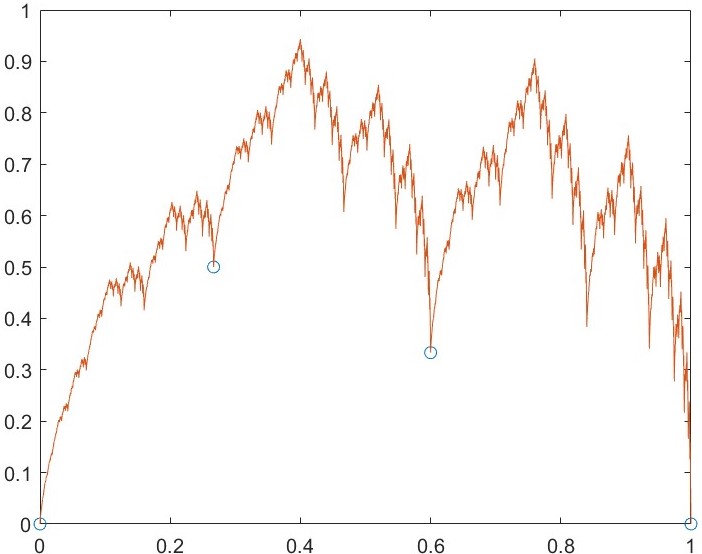
Case of Example 4.1 and we get .
5 Conclusion
According to the research done so far on the dimensional analysis of FIFs, FIFs on specific domains have been taken and their box dimensions have been analyzed. It is important to note that each domain so far considered can be written as the attractor of some suitable IFS. In this paper, we have analyzed the box dimension of FIF with its domain considered as an attractor of an arbitrary IFS. Hence, most of the FIFs constructed so far will become particular cases of our theory. Also, studies have shown that the domain of any new FIF can be likely be obtained as an attractor of a suitable IFS. Hence, in the future, if any new FIF is considered in a different domain, our dimensional results can be applied to such FIFs as well. Hence, the theory on which we have worked will act as a single platform for the study of the dimensional analysis of a large class of FIFs.
References
- [1] Akhtar, M.N., Guru Prem Prasad, M., Navascués, M.A.: Box dimension of -fractal function with variable scaling factors in subintervals. Chaos Solitons Fractals 103, 440–449 (2017)
- [2] Barnsley, M.F.: Fractal functions and interpolation. Constr. Approx. 2(2), 303–329 (1986)
- [3] Barnsley, M.F., Massopust, P.R.: Bilinear fractal interpolation and box dimension. J. Approx. Theory 192, 362–378 (2015)
- [4] Bouboulis, P., Dalla, L., Drakopoulos, V.: Construction of recurrent bivariate fractal interpolation surfaces and computation of their box-counting dimension. J. Approx. Theory 141(2), 99–117 (2006)
- [5] Bouboulis, P., Dalla, L.: A general construction of fractal interpolation functions on . European J. Appl. Math. 18(4), 449–476 (2007)
- [6] Carvalho, A.: Box dimension, oscillation and smoothness in function spaces. J. Funct. Spaces Appl. 3(3), 287–320 (2005)
- [7] Chand, A.K.B., Vijender, N., Viswanathan, P., Tetenov, A.V.: Affine zipper fractal interpolation functions. Bit Numer. Math. 60(2), 319–344 (2020)
- [8] Çelik, D., Koçak, Ş., Özdemir, Y.: Fractal interpolation on the Sierpinski gasket. J. Math. Anal. Appl. 337(1), 343–347 (2008)
- [9] Deliu, A., Jawerth, B.: Geometrical dimension versus smoothness. Constr. Approx. 8, 211–222 (1992)
- [10] Falconer, K.: Fractal Geometry: Mathematical Foundations and Applications. John Wiley Sons, Chichester (1990)
- [11] Feng, Z., Sun, X.: Box-counting dimensions of fractal interpolation surfaces derived from fractal interpolation functions. J. Math. Anal. Appl. 412(1), 416–425 (2014)
- [12] Geronimo, J.S., Hardin, D.: Fractal interpolation surfaces and a related 2-D multiresolution analysis. J. Math. Anal. Appl. 176(2), 561–586 (1993)
- [13] Hardin, D.P., Massopust, P.R.: The capacity for a class of fractal functions. Comm. Math. Phys. 105(3), 455–460 (1986)
- [14] Hutchinson, J.: Fractals and self-similarity. Indiana Univ. Math. J. 30, 713–747 (1981)
- [15] Jha, S., Chand, A.K.B., Navascués, M.A., Sahu, A.: Approximation properties of bivariate -fractal functions and dimension results. Appl. Anal. 100(16), 3426–3444 (2021)
- [16] Kigami, J.: Harmonic calculus on p.c.f. self-similar sets. Trans. Amer. Math. Soc. 335(2), 721–755 (1993)
- [17] Kumar, D., Chand, A.K.B., Massopust, P.R.: Multivariate zipper fractal functions. Numer. Funct. Anal. Optim. 44(14), 1538–1569 (2023)
- [18] Małysz, R.: The Minkowski dimension of the bivariate fractal interpolation surfaces. Chaos Solitons Fractals 27, 1147–1156 (2006)
- [19] Massopust, P.R.: Fractal surfaces. J. Math. Anal. Appl. 151(1), 275–290 (1990)
- [20] Massopust, P.R.: Fractal Functions, Fractal Surface, and Wavelets. Academic Press, New York (1994)
- [21] Navascués, M. A.: Approximation of fixed points and fractal functions by means of different iterative algorithms. Chaos Solitons Fractals 180, 1–7 (2024)
- [22] Pandey, K.K., Viswanathan, P.V.: Multivariate fractal interpolation functions: some approximation aspects and an associated fractal interpolation operator. Electron. Trans. Numer. Anal. 55, 627–651 (2022)
- [23] Prokaj, R.D., Raith, P., Simon, K.: Fractal dimensions of continuous piecewise linear iterated function systems. Proc. Amer. Math. Soc. 151(11), 4703–4719 (2023)
- [24] Ruan, H.J.: Fractal interpolation functions on post critically finite self-similar sets. Fractals 18(1), 119–125 (2010)
- [25] Sahu, A., Priyadarshi, A.: On the box-counting dimension of graphs of harmonic functions on the Sierpiński gasket. J. Math. Anal. Appl. 487(2), 1–16 (2020)