Breaking a Chaotic Cryptographic Scheme Based on Composition Maps
Abstract
Recently, a chaotic cryptographic scheme based on composition maps was proposed. This paper studies the security of the scheme and reports the following findings: 1) the scheme can be broken by a differential attack with chosen-plaintext, where is the size of plaintext and is the number of different elements in plain-text; 2) the scheme is not sensitive to the changes of plaintext; 3) the two composition maps do not work well as a secure and efficient random number source.
1 Introduction
The development of information technology makes the transmission of digital data is carried out more and more frequently over all kinds of channels. Meanwhile, the security of digital data become more and more important. So, the demand of secure and fast encryption schemes become urgent. Due to the subtle similarities between cryptography and chaos, a great number of chaotic encryption schemes have been proposed in the past decade YaobinMao:CSF2004 ; Pareek:ImageEncrypt:IVC2006 ; Flores:EncryptLatticeChaos06 ; Tong:ImageCipher:IVC07 ; Wong:ChaosEncrypt:IEEETCASII ; Pareek:CNSNS2009 . However, most of them have been found to be insecure in different extents from the view point of modern cryptography AlvarezLi:Cryptanalysis:PLA2005 ; LiShujun:ReturnMapAttack:IJBC2006 ; Li:AttackDSEA2006 ; Li:AttackHDSP2006 ; Li:AttackingBitshiftXOR2007 ; Li:AttackingRCES2004 ; ArroyoLi:Chaos2008 ; LiLi:IVC2009b ; Li:ProbabilisticEncryption:IJBC03 ; Li:BreakNoiseCommunication:Chaos05 ; Li:BreakYTSCipher:TCASII04 . As for how to evaluate the security of a chaotic cryptographic scheme, please refer to LiShujun:Rules:IJBC2006 .
In general, the usage of chaos in designing encryption scheme can be classified as three categories: 1) generating pseudo-random number sequence, which is then used to determine position permutation; 2) generating pseudo-random bit sequence, which is then used to determine combination and/or composition of some basic encryption operations; 3) generating ciphertext directly when the data of plaintext is assigned as the initial condition or control parameter of a chaotic map. In Akhavan:LNCS06 ; Akhshani:ICIP06 ; Behnia:IJBC08 , the possible application of composition of polynomial chaotic maps in designing encryption scheme was discussed. In this case, two composite polynomial chaotic maps are used to determine the position permutation and composition of basic encryption operations respectively. Since the schemes proposed in Akhavan:LNCS06 ; Akhshani:ICIP06 are preliminary version of the one proposed in Behnia:IJBC08 , this paper only focuses on the security of the latter. With our study, the following security problems are found: 1) the scheme can be broken with a differential attack; 2) the scheme is not sensitive with respect to the changes of plaintext; 3) the randomness of the pseudo-random number sequences generated by the two composition maps is weak.
2 The Encryption Scheme Under Study
In Behnia:IJBC08 , the structure of plaintext is not specified precisely. Without loss of generality, the plaintext here is denoted by a 2-D byte array of size (heightwidth), and the corresponding ciphertext by . The plaintext is considered as a 1D signal by scanning it in a raster order. Then, the chaotic cryptographic scheme can be described as follows 111To make the presentation more concise and complete, some notations in the original paper are modified, and some details about the scheme are supplied and/or corrected also..
-
•
Secret key: three sets of initial condition and control parameter of Eq. (1), , , , one set of initial condition and control parameter of Eq. (2), , and a secret number .
(1) (2) -
•
Initialization:
-
–
Iterate the map Eq. (1) times to obtain three states sequences, , , , under the three sets of initial condition and control parameter, , , , respectively;
-
–
Iterate the map Eq. (2) times to obtain a states sequence under initial condition and control parameter ;
-
–
Generate four pseudo-random number sequences, , , , , as follows: , , , and .
-
–
-
•
Encryption:
-
–
Permutation: for , swap the positions of two bytes and . Denote the permuted plaintext with .
-
–
Confusion I: for ,
(3) where , and .
-
–
Confusion II: for ,
(4)
-
–
-
•
Decryption: The decryption approach is similar to the encryption one except that the main three encryption steps and the swap operations in the permutation step are carried out in a reverse order, and Eq. (3) is replaced by the following function.
(5)
3 Cryptanalysis
3.1 Differential Attack
Differential attack is an attack to recover the information about secret key and/or plaintext by analyzing the evolution of differences when some pairs of plaintexts are encrypted with the same secret key. In [Behnia:IJBC08, , Sec. 5.4], the authors claimed the encryption scheme under study can withstand differential attack effectively. However, we find that the scheme can be broken by this attack easily with the following steps.
-
•
Breaking Confusion I:
If two plaintexts, and , are encrypted by the same secret key, one has the following equality.
(7) Furthermore, if the plaintexts, and , are chosen of fixed value, one has
(8) Since the left part of the above equation, and are known, Eq. (8) can be simplified as the following equation.
(9) where
It has been verified by computer that a set can be determined uniquely with three different sets of , e.g. (9, 127), (1, 52), (33, 65). From Fact 1, one can see that and are equivalent with respect to the encryption.
Fact 1
, .
-
•
Breaking Confusion II:
After has been broken, only the step Confusion II is left for a plaintext of fixed value, , can be determined. Then, one has
(10) for .
-
•
Breaking Permutation:
After the steps Confusion I and Confusion II have been broken, only the step permutation is left. As shown in Li:AttackingPOMC2004 , any permutation-only cryptographic scheme can be broken with only known/chosen plain-texts, where is the number of different element in plain-text.

a)

b)

c)

d)

e)

f)

a)

b)

c)

d)

e)

f)

a)

b)

c)

d)

e)

f)

a)

b)
To validate performance of the proposed attack, some experiments on some plain-images of size have been performed. Besides , the same secret key used in [Behnia:IJBC08, , Sec. 3] was adopted: , , , . The step Confusion I can be broken with the six chosen plain-images of fixed values, 9, 127, 1, 52, 33 and 65, as shown in Fig. 1 and the corresponding cipher-images shown in Fig. 2. Then, the plain-image shown in Fig. 1a) and the corresponding cipher-images can break the step Confusion II. Finally, the step Permutation can be broken with special plain-images shown in Fig. 3. The obtained equivalent secret key was used to decrypt another cipher-image, as shown in Fig. 4a), and the result is shown in Fig. 4b).
3.2 Some Other Security Defects
-
•
Problems about Secret Key;
As specified in [LiShujun:Rules:IJBC2006, , Rule 5], the key space of a secure encryption scheme should be precisely specified and avoid non-chaotic regions. However, even with the measure used in Behnia:IJBC08 , a great number of secret key should be excluded from the key space of the encryption scheme under study (see Fig. 5).
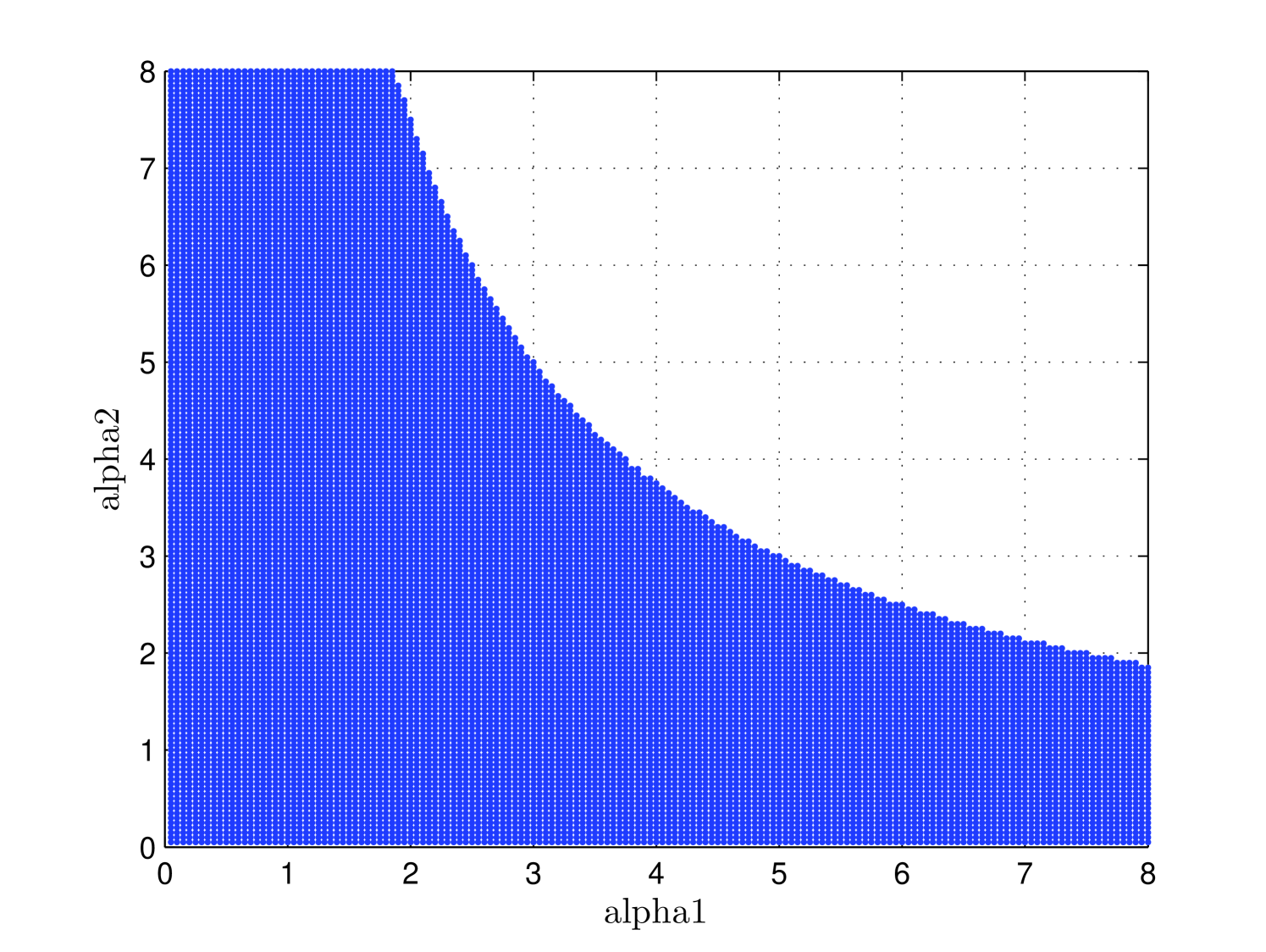
Figure 5: The parameters of corresponding to positive Lyapunov exponent. -
•
Insufficient Randomness of Pseudo-Random Number Sequences , , , and
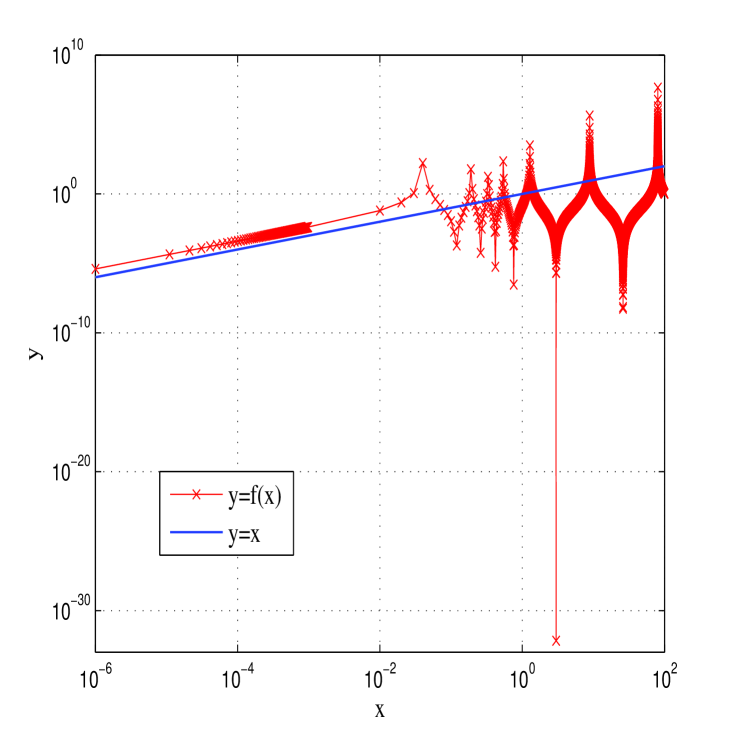
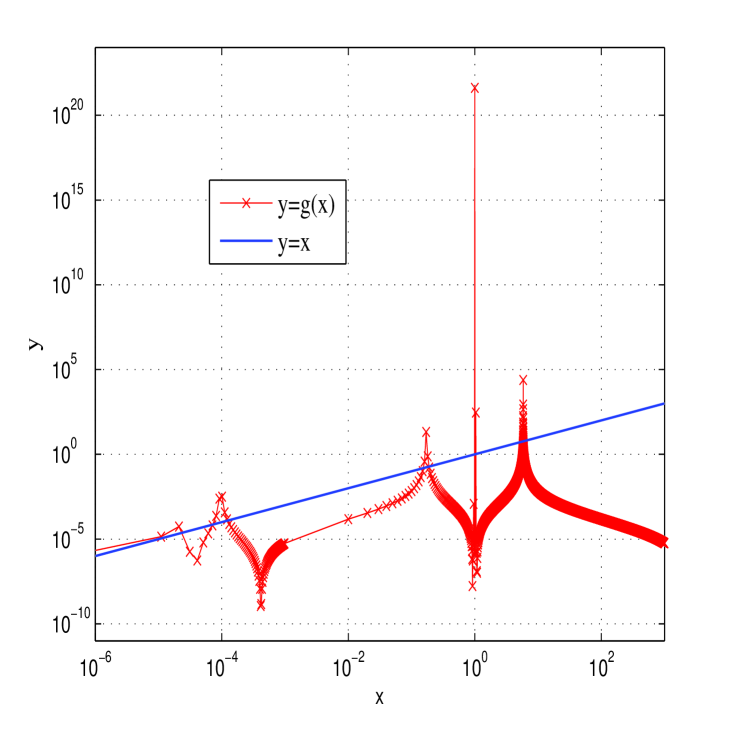
To study the dynamic property of the two equations and , we drew the graph of the two equations under a greater of number of random parameters. Due to the similarity, only the graphs of and with , are shown in Fig. 6. Comparing the graphs of the two functions and , one can assure that the states generated by iterating the two functions will approach zero soon after some iterations.
a)
b)
Figure 6: The graph of and . To further test the randomness of the sequences generated by the two equations, we adopted the test suite proposed in Rukhin:TestPRNG:NIST . Since the three sequences , , and are determined by the same equation, only the randomness of and was tested. For every sequence, 100 samples of length (the number of bytes used for encryption of a gray-scale plain-image of size ) were generated by random secret keys. For each test, the default significance level 0.01 was adopted. The results are shown in Table 1, from which one can see that the two equations both cannot be used as a good random number generator.
Table 1: The performed tests with respect to a significance level 0.01 and the number of sequences passing each test in 100 randomly generated sequences. Name of Test Number of Passed Sequences Frequency 6 2 Block Frequency () 10 6 Cumulative Sums-Forward 6 3 Runs 8 3 Rank 68 99 Non-overlapping Template (, ) 76 64 Serial () 6 9 Approximate Entropy () 8 6 FFT 65 49 -
•
Insensitivity with Respect to Changes of Plaintext
In [Behnia:IJBC08, , Sec.5.4], the importance of sensitivity with respect to changes of plaintext is recognized. However, the encryption scheme under study is actually very far away from the desired property. In cryptography, the most ideal situation about sensitivity is that the change of any single bit of plaintext will make every bit of the corresponding ciphertext change with a probability of one half. Obviously, the encryption scheme under study can not reach the desired state due to the following points.
-
–
No nonlinear S-box is involved in the whole scheme;
-
–
Any bit of plaintest only may influence the bits at the above levels in the ciphertext;
-
–
Any pixel of plaintext does not influence other pixels in the corresponding ciphertext uniformly.
To demonstrate this defect efficiently, we performed an experiment by changing a bit of the plain-image of size shown in Fig. 3c). It is found that only the bits of one level are changed. The locations of the changed bits are shown in Fig. 7, where the white dots denote changed locations and black ones denote unchanged ones.

a) th

b) 5th

c) 6th

c) 7th
Figure 7: The locations of changed bits of the cipher-image, when the 5-th bit of the pixel at location (256, 256) in the plain-image was changed. -
–
4 Conclusion
In this paper, the security of a chaotic cryptographic scheme based on composition maps has been studied in detail. It is found that the scheme can be broken with chosen-plaintext. In addition, the scheme is not sensitive to the changes of plaintext also. Furthermore, the randomness of the pseudo-random number sequences generated by the composition maps is very weak. Due to the insecurity of the scheme under study, it is should not be used in real serious application.
Acknowledgement
Chengqing Li was supported by The Hong Kong Polytechnic University’s Postdoctoral Fellowships Scheme under grant no. G-YX2L. The work of Kowk-Tung Lo was supported by the Research Grant Council of the Hong Kong SAR Government under Project 523206 (PolyU 5232/06E).
References
- [1] G. Chen, Y. Mao, and C. K. Chui, “A symmetric image encryption scheme based on 3d chaotic cat maps,” Chaos, Solitons & Fractals, vol. 21, no. 3, pp. 749–761, 2004.
- [2] N. Pareek, V. Patidar, and K. Sud, “Image encryption using chaotic logistic map,” Image and Vision Computing, vol. 24, no. 9, pp. 926–934, 2006.
- [3] N. J. Flores-Carmona and M. Carpio-Valadez, “Encryption and decryption of images with chaotic map lattices,” Chaos, vol. 16, no. 3, p. art. no. 033118, 2006.
- [4] X. Tong and M. Cui, “Image encryption with compound chaotic sequence cipher shifting dynamically,” Image and Vision Computing, vol. 26, no. 6, pp. 843–850, 2008.
- [5] K.-W. Wong and C.-H. Yuen, “Embedding compression in chaos-based cryptography,” IEEE Transactions on Circuits and Systems II: Express Brief, vol. 55, no. 11, 2008.
- [6] V. Patidar, N. Pareek, and K. Sud, “A new substitution cdiffusion based image cipher using chaotic standard and logistic maps,” Communications in Nonlinear Science and Numerical Simulation, vol. 14, no. 7, pp. 3056–3075, 2009.
- [7] G. Álvarez and S. Li, “Breaking an encryption scheme based on chaotic baker map,” Physics Letters A, vol. 352, no. 1-2, pp. 78–82, 2005.
- [8] S. Li, G. Chen, and G. Álvarez, “Return-map cryptanalysis revisited,” International Journal of Bifurcation and Chaos, vol. 16, no. 5, pp. 1557–1568, 2006.
- [9] C. Li, S. Li, and D.-C. Lou, “On the security of the Yen-Guo’s domino signal encryption algorithm (DSEA),” Journal of Systems and Software, vol. 79, no. 2, pp. 253–258, 2006.
- [10] C. Li, S. Li, D. Zhang, and G. Chen, “Cryptanalysis of a data security protection scheme for VoIP,” IEE Proceedings-Vis. Image Signal Process, vol. 153, no. 1, pp. 1–10, 2006.
- [11] C. Li, S. Li, G. Álvarez, G. Chen, and K.-T. Lo, “Cryptanalysis of two chaotic encryption schemes based on circular bit shift and xor operations,” Physics Letters A, vol. 369, no. 1-2, pp. 23–30, 2007.
- [12] S. Li, C. Li, G. Chen, and K.-T. Lo, “Cryptanalysis of the RCES/RSES image encryption scheme,” Journal of Systems and Software, vol. 81, no. 7, pp. 1130–1143, 2008.
- [13] D. Arroyo, R. Rhouma, G. Alvarez, S. Li, and V. Fernandez, “On the security of a new image encryption scheme based on chaotic map lattices,” Chaos, vol. 18, no. 3, p. article 033112, 2008.
- [14] C. Li, S. Li, M. Asim, J. Nunez, G. Alvarez, and G. Chen, “On the security defects of an image encryption scheme,” Image and Vision Computing, vol. 27, no. 9, pp. 1371–1381, 2009.
- [15] S. Li, X. Mou, B. L. Yang, Z. Ji, and J. Zhang, “Problems with a probabilistic encryption scheme based on chaotic systems,” International Journal of Bifurcation And Chaos, vol. 13, no. 10, pp. 3063–3077, 2003.
- [16] S. Li, G. Alvarez, G. Chen, and X. Mou, “Breaking a chaos-noise-based secure communication scheme,” Chaos, vol. 15, no. 1, p. article 013703, 2005.
- [17] S. Li, G. Chen, and X. Mou, “On the security of the yi-tan-siew chaotic cipher,” IEEE Transactions On Circuits And Systems II-Express Briefs, vol. 51, no. 12, pp. 665–669, 2004.
- [18] G. Alvarez and S. Li, “Some basic cryptographic requirements for chaos-based cryptosystems,” International Journal of Bifurcation and Chaos, vol. 16, no. 8, pp. 2129–2151, 2006.
- [19] A. Akhavan, H. Mahmodi, and A. Akhshani, “A new image encryption algorithm based on one-dimensional polynomial chaotic maps,” Lecture Notes in Computer Science, vol. 4263, pp. 963–971, 2006.
- [20] A. Akhshani, H. Mahmodi, and A. Akhavan, “A novel block cipher based on hierarchy of one-dimensional composition chaotic maps,” in IEEE International Conference on Image Processing, 2006, pp. 1993–1996.
- [21] S. Behnia, A. Akhshania, A. Akhavanb, and H. Mahmodi, “Chaotic cryptographic scheme based on composition maps,” International Journal of Bifurcation and Chaos, vol. 18, no. 1, pp. 251–261, 2008.
- [22] S. Li, C. Li, G. Chen, N. G. Bourbakis, and K.-T. Lo, “A general quantitative cryptanalysis of permutation-only multimedia ciphers against plaintext attacks,” Signal Processing: Image Communication, vol. 23, no. 3, pp. 212–223, 2008.
- [23] A. Rukhin and et al., “A statistical test suite for random and pseudorandom number generators for cryptographic applications,” NIST Special Publication 800-22, 2001, available online at http://csrc.nist.gov/groups/ST/toolkit/rng/documentation˙software.html.