^†^†thanks: These authors contributed equally.^†^†thanks: These authors contributed equally.

Bridging particle deformability and collective response in soft solids

John D. Treado Department of Mechanical Engineering & Materials Science, Yale University, New Haven, Connecticut 06520, USA Integrated Graduate Program in Physical and Engineering Biology, Yale University, New Haven, Connecticut 06520, USA Dong Wang Department of Mechanical Engineering & Materials Science, Yale University, New Haven, Connecticut 06520, USA Arman Boromand Department of Mechanical Engineering & Materials Science, Yale University, New Haven, Connecticut 06520, USA Michael P. Murrell Department of Biomedical Engineering, Yale University, New Haven, Connecticut 06520, USA Department of Physics, Yale University, New Haven, Connecticut 06520, USA Systems Biology Institute, Yale University, West Haven, Connecticut 06516, USA Mark D. Shattuck Benjamin Levich Institute and Physics Department, The City College of New York, New York, New York 10031, USA Corey S. O’Hern corey.ohern@yale.edu Department of Mechanical Engineering & Materials Science, Yale University, New Haven, Connecticut 06520, USA Department of Physics, Yale University, New Haven, Connecticut 06520, USA Department of Applied Physics, Yale University, New Haven, Connecticut 06520, USA Integrated Graduate Program in Physical and Engineering Biology, Yale University, New Haven, Connecticut 06520, USA

Abstract

Soft, amorphous solids such as tissues, foams, and emulsions are composed of deformable particles. However, the effect of single-particle deformability on the collective behavior of soft solids is still poorly understood. We perform numerical simulations of two-dimensional jammed packings of explicitly deformable particles to study the mechanical response of model soft solids. We find that jammed packings of deformable particles with excess shape degrees of freedom possess low-frequency quartic vibrational modes that stabilize the packings even though they possess fewer interparticle contacts than the nominal isostatic value. Adding intra-particle constraints can rigidify the particles, but these particles undergo a buckling transition and gain an effective shape degree of freedom when their preferred perimeter is above a threshold value. We find that the mechanical response of jammed packings of deformable particles with shape degrees of freedom differs significantly from that of jammed packings of rigid-shape particles, which emphasizes the importance of particle deformability in modelling soft solids.

^†^†preprint: APS/123-QED

I Introduction

All soft, athermal solids deform in response to applied stress, yet much of our understanding of these systems relies on computational models using particles with fixed shapes (Durian, 1995; van Hecke, 2009). While extensive work has focused on the effect of varying soft interparticle interactions, less attention has been placed on how intraparticle degrees of freedom affect collective behavior. Foams (Bolton and Weaire, 1990; Bertho et al., 2006), emulsions (Princen, 1983; Boromand et al., 2019), and a wide array of living tissues (Smith et al., 2017; Beroz et al., 2018; Park et al., 2015; Trepat and Sahai, 2018; Lecuit and Lenne, 2007; Murrell et al., 2015; Jolly et al., 2015; McMillen et al., 2016; Oswald et al., 2017; Mongera et al., 2018; Ilina et al., 2020; Kim et al., 2021; Wuyts et al., 2010; Kalve et al., 2014; Sapala et al., 2018; Martinez et al., 2018; Borsuk et al., 2019) are composed of deformable objects. The complexity and variety of the shape degrees of freedom across these systems emphasizes the importance of investigating how single-particle deformability affects collective properties of soft solids, such as rigidity and linear response.

Athermal systems composed of soft particles form rigid solids at the jamming transition when all non-trivial deformations cost energy (O’Hern et al., 2003). If the particles are spherical, frictionless, and purely repulsive, it is well known that jamming occurs at an isostatic point; mechanically stable configurations at jamming onset in periodic boundary conditions with $N_{\rm dof}$ degrees of freedom and $N_{c}$ interparticle contacts satisfy $N_{\rm dof}-N_{c}=d-1$ (Tkachenko and Witten, 1999). This observation, a consequence of Maxwell-Calladine constraint counting (Pellegrino and Calladine, 1986), has been used to rationalize the many anomalous mechanical and vibrational properties of jammed solids (Schreck et al., 2011a; Goodrich et al., 2014). However, particles with non-spherical shapes typically jam with more degrees of freedom than interparticle contacts. These hypostatic packings gain mechanical stability from higher-order terms in the Taylor expansion of the potential energy (Mailman et al., 2009; Donev et al., 2007; Schreck et al., 2012; VanderWerf et al., 2018; Yuan et al., 2019). Higher-order stability has been observed in jammed packings of a variety of non-spherical particles (VanderWerf et al., 2018; Yuan et al., 2019) and even in packings of “breathing” particles that contain size degrees of freedom (Brito et al., 2018). Higher-order constraints directly impact the vibrational spectrum (Schreck et al., 2012; Brito et al., 2018), shear response (Schreck et al., 2011a), and the glass transition at finite temperature (Shen et al., 2012).

Recent work (Damavandi et al., 2021) has proposed that such higher-order rigidity is a generic feature of hypostatic systems with sufficient pre-stress. This phenomenon has been used to explain the rigidity transition in Vertex models of confluent tissues (Bi et al., 2015; Yan and Bi, 2019), which can be viewed as dense packings of deformable polygonal cells that are constrained to be confluent. These results suggest that jammed packings of deformable particles might behave similarly, i.e. possess higher-order stability and mechanical and vibrational properties that diverge from those for jammed packings of frictionless, spherical particles. However, are jammed packings of deformable particles identical to those of non-spherical particles such as ellipses? Or does particle deformability lead to fundamentally different mechanical and vibrational response? And how do the properties of jammed packings change as the particles vary from highly deformable to completely rigid?

Refer to caption — Figure 1: Single-particle vibrational spectra describe shape degrees of freedom. Eigenvalues of the single-particle dynamical matrix $\lambda_{m}$ for truly deformable particles (DP, top) and deformable particles with bending constraints (DPb, bottom) with $n=24$ vertices. Symbols correspond to values of the preferred shape parameter $\mathcal{A}_{0}$ , and $\mathcal{A}_{n}=n\tan(\pi/n)/\pi$ is the shape parameter of a regular $n$ -gon. The vertical line at index $i=24$ ( $i=4$ ) in the top (bottom) panel correspond to the crossover between zero and non-zero eigenvalues. Energy-minimized shapes are drawn in the insets, with $\mathcal{A}_{0}$ increasing from left to right, and the curvature vectors $\vec{\kappa}_{i}$ defined in Eq. (3) are drawn on the buckled DPb particle. In both panels, $K_{l}=1$ , and $K_{b}=10^{-2}$ in the bottom panel.

In this article, we study the collective vibrational and mechanical properties of jammed solids composed of particles with varying degrees of deformability. In Sec. II, we introduce a model of deformable particles. We define deformability through the single-particle vibrational spectra and show that the model can describe truly deformable and rigid-shape particles, as well as quasi-deformable particles with characteristics between the two extremes. In Sec. III, we investigate the rigidity, vibrational modes, and shear response in jammed solids composed of deformable particles. Our results emphasize that (a) packings of deformable particles in the rigid-shape-particle limit recover the properties found for jammed packings of soft spherical particles, but that (b) packings of truly deformable particles do not possess the same vibrational and mechanical properties as those for jammed packings of soft spherical particles. In Sec. IV, we conclude with a discussion of the applicability of our results to glassy solids at finite temperature and to several experimental systems. We also include four appendices, which detail buckling in single particles with bending energy (Appendix A), counting effective constraints using the dynamical matrix (Appendix B), system-size dependence of the dynamical matrix and shear modulus (Appendix C), and identification of the collective shape degrees of freedom (Appendix D).

II Methods

Systems of deformable particles in two dimensions are modeled by $N$ distinct polygons, each with $n_{\mu}$ vertices with positions $\vec{r}_{i\mu}$ for $i=1,...,n_{\mu}$ and $\mu=1,...,N$ . Each polygon has an area $a_{\mu}$ and perimeter $p_{\mu}=\sum_{i=1}^{n_{\mu}}l_{i\mu}$ , where $l_{i\mu}$ is the edge joining vertex $i$ and $i+1$ on polygon $\mu$ . In previous work (Boromand et al., 2018), we studied the deformable polygon (DP) energy,

\begin{split}U_{\rm DP}&=\frac{\epsilon_{a}}{2}\sum_{\mu=1}^{N}\quantity(\frac{a_{\mu}}{a_{0\mu}}-1)^{2}+\frac{\epsilon_{l}}{2}\sum_{\mu=1}^{N}\sum_{i=1}^{n_{\mu}}\quantity(\frac{l_{i\mu}}{l_{0\mu}}-1)^{2}+U_{\rm int},\end{split}

(1)

where $U_{\rm int}$ is the potential energy between interacting particles, and $\epsilon_{a}$ and $\epsilon_{l}$ are energies controlling area and perimeter fluctuations about the preferred areas $a_{0\mu}$ and edge lengths $l_{0\mu}$ , respectively. Interactions between vertices $i$ and $j$ on cells $\mu$ and $\nu$ are governed by the pair potential $v$ , which we assume depends only on the distance between two vertices, $r_{ij}^{\mu\nu}=\absolutevalue{\vec{r}_{i\mu}-\vec{r}_{j\nu}}$ . We treat each vertex as a repulsive soft disk, where

v\quantity(r_{ij}^{\mu\nu})=\frac{\epsilon_{c}}{2}\quantity(1-\frac{r_{ij}^{\mu\nu}}{\sigma_{\mu\nu}})^{2}\Theta\quantity(1-\frac{r_{ij}^{\mu\nu}}{\sigma_{\mu\nu}}),

(2)

$\sigma_{\mu\nu}=\quantity(l_{0\mu}+l_{0\nu})/2$ , each vertex has diameter $l_{0\mu}$ , $\epsilon_{c}$ controls the strength of the interaction, and $\Theta$ is the Heaviside step function to enforce purely repulsive interactions. The total interaction energy is therefore $U_{\rm int}=\sum_{\nu,\mu}\sum_{i=1}^{n_{\mu}}\sum_{j=1}^{n_{\nu}}v\quantity(r_{ij}^{\mu\nu})$ , though we do not track overlaps between vertices $i$ and $i+1$ and $i$ and $i-1$ on the same particle. We measure lengths in units of the square root of the minimum preferred area, $\sqrt{\overline{a}_{0}}$ , energies in units of $\epsilon_{a}$ , and times in units of $\tau=\sqrt{\overline{a}_{0}/\epsilon_{a}}$ , where all vertex masses have been set to $1$ . The dimensionless preferred shape parameter $\mathcal{A}_{0\mu}=\quantity(n_{\mu}l_{0\mu})^{2}/(4\pi a_{0\mu})$ measures the amount of excess perimeter above a regular polygon with area $a_{0\mu}$ and thus controls particle deformability (Boromand et al., 2018). For the DP model, particle shapes depend only on $K_{l}=\epsilon_{l}/\epsilon_{a}$ , $K_{c}=\epsilon_{c}/\epsilon_{a}$ , and $\mathcal{A}_{0\mu}$ .

In Eq. (1), we see that the shape of a single DP particle is constrained by $n+1$ terms given $n$ vertices, but each particle contains $2n$ degrees of freedom. By constraint counting, we expect $2n-(n+1)=n-1$ zero energy modes. While each particle contains two translational and one rotational degree of freedom that cannot be constrained by internal forces, DP particles still contain $n-4$ non-trivial zero modes. In this sense, DP particles are truly deformable and can change shape with zero energy cost. Example energy-minimized DP particles are shown in the top inset to Fig. 1.

To rigidify single DP particles, we add $n$ bending constraints along the particle perimeter (Boromand et al., 2018),

U_{\rm b}=U_{\rm DP}+\frac{k_{b}}{2}\sum_{i=1}^{n}\vec{\kappa}_{i}^{2},\hskip 21.68121pt\vec{\kappa}_{i}=\frac{\vec{l}_{i}-\vec{l}_{i-1}}{l_{0}^{2}}.

(3)

Eq. 3 has the additional parameter $K_{b}=k_{b}/(\epsilon_{a}l_{0}^{2})$ , which determines the energy cost of bending the particle perimeter. We refer to particles with this additional bending energy term as DPb particles.

In addition to single-particle properties, we also study configurations of multiple deformable particles near the onset of jamming. We prepare jammed packings of $N$ bidisperse ( $50$ : $50$ by number) deformable particles in square cells with side length $L$ and periodic boundary conditions. Small (large) particles are given $n_{\mu}=n_{\rm S}$ ( $n_{\rm L}$ ) vertices with segment lengths $l_{0\mu}$ chosen such that $\mathcal{A}_{0\mu}/\mathcal{A}_{n}$ is identical for each particle, where $\mathcal{A}_{n}$ is the shape parameter of a regular $n$ -gon. Therefore, when referring to the shape parameter chosen for a configuration of deformable particles, we will use $\mathcal{A}_{0}$ to mean the ratio of $\mathcal{A}_{0}/\mathcal{A}_{n}$ for a particle with a given number of vertices. We choose $n_{\rm L}$ to be the nearest integer to $1.4n_{\rm S}$ to enforce an approximate $1.4$ large-to-small size ratio to avoid crystallization and phase separation (Zhang et al., 2014). Likewise, large particles are given preferred areas $a_{0\mu}=(1.4)^{2}\overline{a}_{0}$ . To create jammed packings, we randomly place particles in the simulation cell at low packing fraction $\phi$ and isotropically compress the system by increasing the particle size. Compression steps are followed by minimization of the total potential energy $U$ using FIRE. We take configurations as sufficiently near an energy minimum when the total root-mean-square force $<10^{-12}$ . We monitor jamming onset using the virial pressure $P=(\Sigma_{xx}+\Sigma_{yy})/2$ , where the virial stress is

\Sigma_{\xi\xi^{\prime}}=\epsilon_{c}L^{-2}\sum_{\nu\neq\mu}\sum_{i=1}^{n_{\mu}}\sum_{j=1}^{n_{\nu}}\quantity(1-\frac{r_{ij}^{\mu\nu}}{\sigma_{ij}^{\mu\nu}})\frac{r_{ij,\xi}^{\mu\nu}r_{ij,\xi^{\prime}}^{\mu\nu}}{r_{ij}^{\mu\nu}\sigma_{ij}^{\mu\nu}}.

(4)

$r_{ij,\xi}^{\mu\nu}$ is the $\xi$ -component of the vector separating vertex $i$ on cell $\mu$ and vertex $j$ on cell $\nu$ and $\xi=x$ or $y$ . We identify jamming onset, with packing fraction $\phi_{J}$ , when the pressure $10^{-7}<P<2\times 10^{-7}$ . We have confirmed that the results presented below do not depend on the pressure threshold as long as it is sufficiently small. Throughout this work, we will use $K_{l}=K_{c}=1$ unless otherwise stated.

III Results

III.1 Rigidity

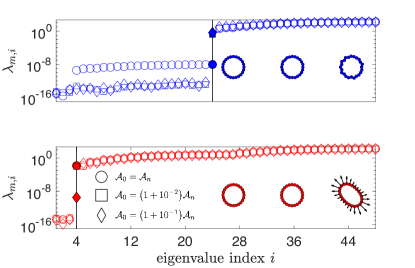
We first investigate the rigidity of single DP and DPb particles by normal mode analysis. Single-particle normal modes are eigenvectors of the dynamical matrix $\mathcal{M}$ , with block elements defined by $\mathcal{M}_{ij}=\partialderivative*{U}{\vec{r}_{i}}{\vec{r}_{j}}$ . In Fig. 1, we plot the normal mode eigenvalues $\lambda_{m}$ for DP and DPb particles with $n=24$ vertices and varying preferred shape parameters $\mathcal{A}_{0}$ . We find DP particles have $n-1$ near-zero modes ( $\lesssim 10^{-15}$ ) when $\mathcal{A}_{0}>1$ , as expected from constraint counting. Interestingly, the DP particle with $\mathcal{A}_{0}=1$ possess $n-3$ low frequency modes significantly above the noise floor. Although the particle shape is underconstrained, particles with $\mathcal{A}_{0}=1$ cannot deform without increasing their perimeter-to-area ratio. These DP particles therefore are stabilized by prestress, a phenomenon found in underconstrained tensegrity structures (Pellegrino and Calladine, 1986) and disordered spring networks (Damavandi et al., 2021).

As DPb particles contain $n$ additional constraints, we expect them to behave as rigid-shape particles (such as frictionless soft disks or ellipses) where any shape deformation costs energy. In Fig. 1, we find that there are only $3$ near-zero modes, corresponding to the trivial zero modes, for DPb particles with sufficiently small preferred shape parameter and that the particles energy-minimize to regular polygons. However, when $\mathcal{A}_{0}=1.1$ , the DP particle is “buckled” with an elliptical shape and an additional low-frequency mode $\lambda_{m,4}\approx 10^{-10}$ .

In Appendix A, we show that the DPb model contains a buckling transition where energy-minimized shapes elongate from regular polygons and the first non-trivial normal mode eigenvalue $\lambda_{m,4}$ drops from $\sim K_{b}$ to near zero. The transition point, $\mathcal{A}_{0}^{*}$ , varies for different $K_{b}$ , but the behavior after buckling is similar: $\lambda_{m,4}$ rises from the noise floor with increasing $\mathcal{A}_{0}$ , and particles increasingly elongate. The small value of $\lambda_{m,4}$ after buckling suggests that buckled DPb particles gain an extra degree of freedom even though the number of constraints remains constant, a feature reminiscent of the rigidity transition in vertex models of confluent tissues (Bi et al., 2015; Damavandi et al., 2021) and topological metamaterials (Kane and Lubensky, 2014; Chen et al., 2014).

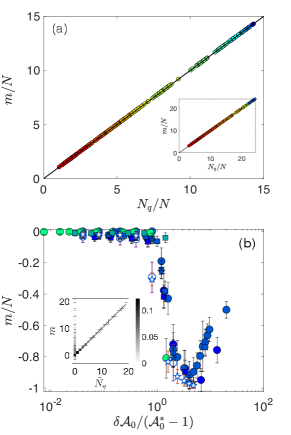
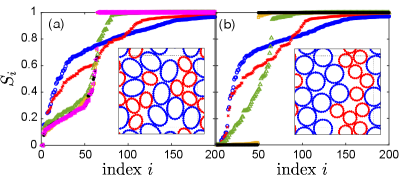
We then investigate rigidity in jammed packings of DP and DPb particles by calculating the collective vibrational response. In a jammed packing of $N^{\prime}$ non-rattler DP particles with $\overline{n}$ vertices per particle on average, there are $2N^{\prime}\overline{n}$ degrees of freedom, $N^{\prime}(\overline{n}+1)$ shape constraints and $N_{\rm vv}$ vertex-vertex contacts to constrain the shape degrees of freedom. Isostaticity would dictate $N_{\rm vv}=N^{\prime}\quantity(\overline{n}-1)-1$ , but in Fig. 2 (a) we show that DP particles at jamming onset are hypostatic and seemingly missing the requisite number of interparticle contacts for jamming. The number of missing contacts for jammed DP particles is $m=N^{\prime}\quantity(\overline{n}-1)-1-N_{\rm vv}$ .

Hypostaticity at jamming onset is often observed in packings of non-spherical particles (VanderWerf et al., 2018). Recent work has shown that these systems are stabilized by higher-order quartic modes of the potential energy (Mailman et al., 2009; VanderWerf et al., 2018; Brito et al., 2018). In Appendix B, we show that quartic modes can be identified by decomposing the dynamical matrix $\mathcal{M}$ into the stiffness $\mathcal{H}$ and stress $\mathcal{S}$ matrices (Donev et al., 2007; Schreck et al., 2012). As shown in Fig. 2 (a), we find that the number of missing contacts in jammed DP packings always matches the number of quartic modes $N_{q}$ across a wide range of shape parameters.

As DPb particles with $n$ vertices contain $n$ additional constraints, we expect them to behave similarly to packings of rigid-shape bumpy particles that are known to be isostatic at jamming (Papanikolaou et al., 2013). Indeed, when the particles are regular polygons, i.e. $\mathcal{A}_{0}<\mathcal{A}_{0}^{*}$ , we show in Fig. 2 (b) that these packings are isostatic and the number of contacts $N_{\rm vv}$ equals $3N^{\prime}-1$ , the total number of contacts expected for an isostatic packing of $N^{\prime}$ non-rattler particles, each with $3$ degrees of freedom. However, in Fig. 2 (b) we show that near the buckling transition $\mathcal{A}_{0}^{*}$ , packings gain contacts and appear to be hyperstatic at jamming onset. Hyperstaticity at jamming onset is extremely rare when using athermal protocols (Schreck et al., 2011b; Tuckman et al., 2020), so it seems the “buckling mode” with low eigenvalue effectively gives the DPb particles an extra degree of freedom, making these packings actually hypostatic with $N_{\rm vv}<4N^{\prime}-1$ .

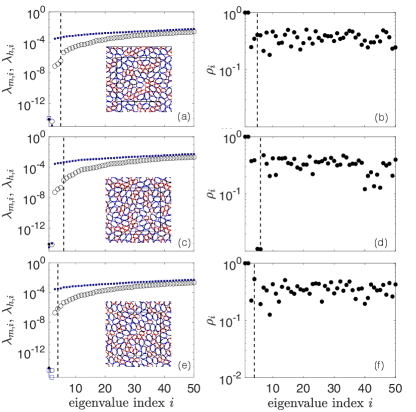
One might expect to be able to count missing contacts for packings of DPb particles by decomposing the dynamical matrix $\mathcal{M}$ into $\mathcal{H}$ and $\mathcal{S}$ as we did for packings of DP particles. However, we show in Appendix B that all non-trivial eigenvalues of the stiffness matrix $\mathcal{H}$ are nonzero for DPb packings and several orders of magnitude larger than the eigenvalues of the dynamical matrix $\mathcal{M}$ . As discussed in Ref. (Damavandi et al., 2021), the presence of positive eigenvalues of the stress matrix $\mathcal{S}$ make counting missing constraints via the dynamical matrix indeterminate. Despite this, we find some evidence of missing contacts in DPb packings using a heuristic approach detailed in Appendix B. Briefly, if a packing of DPb particles is missing $m=4N^{\prime}-1-N_{\rm vv}$ contacts, we check (i) whether there is a gap between the $m$ th non-trivial eigenvalue $\lambda_{m}$ of $\mathcal{M}$ and $\lambda_{m+1}$ , or (ii) if there is no apparent gap, wherether the $m$ th non-trivial mode has a significantly larger participation ratio than mode $m+1$ . We show in the inset of Fig. 2 (b) that the heuristic counting largely identifies correctly the $\tilde{N}_{q}$ higher-order modes that stabilize the missing contacts. However, there are several cases where the counting fails, highlighting the difficulty in determining rigidity in packings of DPb particles with negative pre-stress. Notably, most cases in which the correct number of missing contacts could not be identified in the dynamical matrix eigenvalue spectra or mode structure (i.e., when $m\neq\tilde{N}_{q}$ ) occur at $\tilde{N}_{q}=0$ . That is, whenever there is a notable gap or change in eigenmode participation ratio, we correctly count the number of missing contacts. We reserve a more in-depth analysis of the edge cases where missing contacts were not identified by $\mathcal{M}$ , as well as a predictive theory for the missing contacts as a function of shape parameter, for future work.

III.2 Vibrational response

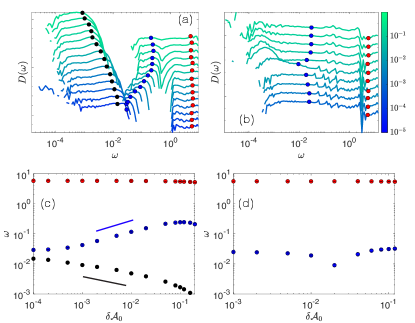
We next study the density of vibrational states $D(\omega)$ for non-trivial vibrational modes with frequency $\omega_{i}=\sqrt{\lambda_{m,i}}$ . In packings of DP particles, we observe three distinct bands of vibrational response in Fig. 3 (a) due to quartic modes (with mean frequency $\omega_{0}$ ), mid-frequency collective modes (consistently the first $N-1$ quadratic modes, with mean frequency $\omega_{1}$ ), and high-frequency shape modes (with mean frequency $\omega_{2}$ ). As shown in Appendix C, $D(\omega)$ and the characteristic frequencies do not vary significantly with system size. A similar three-band structure is found in the vibrational response of jammed packings of rigid-shape non-spherical particles (VanderWerf et al., 2018), although for the DP packings, the second band of modes corresponds to shape fluctuations at particle-particle interfaces rather than particle rotations. Additionally, as shown in Fig 3 (c), we find the characteristic scaling $\omega_{0}\sim\delta\mathcal{A}_{0}^{-1/3}$ , indicating collective motion becomes less costly as particles become more deformable. We note this behavior differs from jamming of frictionless non-spherical particles with rigid shape (Schreck et al., 2012; Brito et al., 2018), where $\omega_{0}\sim\mathcal{A}_{0}^{1/2}$ . We find approximate $1/2$ scaling with shape parameter in the mid-frequency band $\omega_{1}$ , although this exponent is $\sim 1$ in packings of rigid-shape non-spherical particles. The stiff shape mode band with mean frequency $\omega_{2}$ does not vary with particle shape.

Previous studies have argued that driven and jammed amorphous solids can be described using spherical particles with soft interparticle potentials (Durian, 1995), where particle deformability is modelled by large interparticle overlaps. However, the deviation in $D(\omega)$ for packings of DP particles from that for soft non-spherical particles suggests that explicit shape change plays an important role in determining the vibrational response of soft particles. We further investigate the effect of shape change in the vibrational response by computing the projection of each eigenmode onto collective particle translations ( $T$ ), rotations ( $S$ ), and shape degrees of freedom ( $S$ ), as described in Appendix D. In Fig. 4, we show that even the low-frequency modes of jammed DP particles have a significant collective shape projection $S$ across a wide range of shape parameters ( $1.02\leq\mathcal{A}_{0}\leq 1.18$ ). We find that $S(\omega)$ remains $>0$ at the lowest frequencies even when the compression is increased well above jamming onset. Explicit shape change is therefore necessary to capture important features of driven soft materials, such as flows of bubbles (Bertho et al., 2006), droplets Foglino et al. (2017) and emulsions (Hong et al., 2017; Golovkova et al., 2020).

We also computed $D(\omega)$ for jammed DPb particles as shown in Fig. 3 (b). These systems no longer have a distinct band structure in $D(\omega)$ , as there are no obvious quartic modes. Here, we define $\omega_{1}$ as the mean of the first $N-1$ modes after the trivial zeros in analogy with the DP packings, and $\omega_{2}$ is the mean of all other modes. For systems with $\mathcal{A}_{0}<\mathcal{A}_{0}^{*}$ , $D(\omega)$ is relatively unchanged as a function of $\mathcal{A}_{0}$ . For packings with buckled DPb particles ( $\mathcal{A}_{0}>\mathcal{A}_{0}^{*}$ ), we observe a higher density of low-frequency modes near the buckling transition and a cusp in $\omega_{1}$ at $\mathcal{A}_{0}^{*}$ as shown in Fig. 3 (d). The abundance of low-frequency modes is likely due to the sudden decrease in the magnitude of the single-particle $\lambda_{m,4}$ mode at the buckling transition (see Appendix A), and the appearance of modes that can stabilize more than one degree of freedom.

The large density of low frequency modes at the buckling transition for DPb particles raises an important question. Is there a regime where DPb particles will behave as particles with rigid shapes? Or are DPb particles quasi-deformable with persistent non-rigid-shape behavior? To address this question, we compute the collective shape degrees of freedom $S$ in individual jammed packings of DPb particles in the rigid-shape limit ( $K_{c}\to 0$ ). We show in Fig. 5 (b) that non-buckled DPb particles ( $\mathcal{A}_{0}<\mathcal{A}_{0}^{*}$ ) eventually reach the rigid-shape limit ( $K_{c}\lesssim 10^{-4}$ ), where the first $3N$ eigenmodes correspond to purely translational and rotational degrees of freedom and the rest of the spectrum contains only shape degrees of freedom. However, when particles buckle (i.e. $\mathcal{A}>\mathcal{A}_{0}^{*}$ in Fig. 5 (a)), $S$ is non-zero for the first $3N$ eigenmodes for all values of $K_{c}$ . We conclude that DPb particles that remain regular polygons are effectively rigid-shape particles, whereas buckled DPb particles are quasi-deformable, and thus the shape degrees of freedom play a key role in their vibrational response.

III.3 Shear response

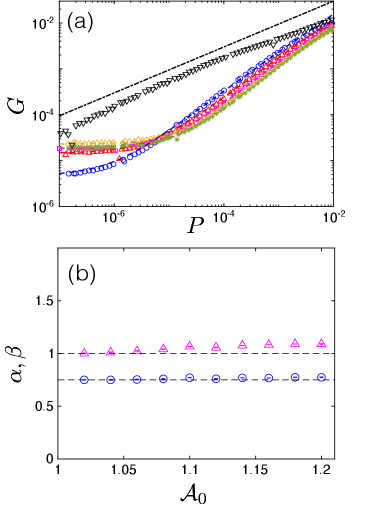
To investigate the effect of particle deformability on bulk mechanical properties, we computed the static shear modulus $G$ for jammed packings of DP and DPb particles. Packings were compressed to a given pressure $P$ , subjected to small, successive simple shear strain steps of size $\Delta\gamma$ with Lees-Edwards boundary conditions (Allen and Tildesley, 2017), and the system was energy-minimized after each step. We measure $G=-d\Sigma_{xy}/d\gamma$ , where $\Sigma_{xy}$ is the virial shear stress. We report $G$ averaged over an ensemble of at least $500$ configurations. In Fig. 6, we show that, although DP packings contain collective low-frequency quartic modes, they possess $G>0$ at low pressure (Mailman et al., 2009; Boromand et al., 2018). In Appendix C, we also show characteristic $N^{-1}$ scaling of $G$ in the $P\to 0$ limit (Goodrich et al., 2012). We find in Fig. 6 (a) that $G(P)$ for DP packings over of wide range of $\mathcal{A}_{0}$ is well-approximated by the double-power-law functional form (VanderWerf et al., 2020) used to describe the shear response of packings of soft frictionless spheres:

G=G_{0}+\frac{aP^{\alpha}}{1+cP^{\alpha-\beta}},

(5)

where $a$ and $c$ are constants. $G_{0}$ is the value in the $P\to 0$ limit, the exponent $\alpha$ controls the low $P$ response, and the exponent $\beta$ controls the high $P$ response.

Values of $\alpha\approx 1$ and $\beta\approx 0.5$ have been reported in previous studies of jammed packings of frictionless spherical particles (O’Hern et al., 2003; Goodrich et al., 2012), frictional spherical particles (Somfai et al., 2007), and bumpy particles (Papanikolaou et al., 2013). However, in Fig. 6 (b), we find that the large pressure scaling exponent $\beta\approx 0.75$ for DP packings. In Fig. 6 (a), we show that $\beta\approx 0.5$ for unbuckled DPb particles with $K_{b}=10^{-2}$ and $\mathcal{A}_{0}=1.04$ , although we do not observe a plateau at low pressures. This result indicates that the mechanical response for unbuckled DPb particles (with $\mathcal{A}_{0}<\mathcal{A}_{0}^{*}$ ) is similar to that for rigid-shape spherical particles.

Note also that $G(P)$ for packings of DPb particles possesses an even smaller scaling exponent at high pressures ( $P\sim 10^{-2}$ ). At these pressures, particles are likely starting to deform from their energy-minimized states to fill in their surrounding Voronoi cell as the packing approaches confluence. However, to fully understand the root cause of these scaling exponents, future work is needed to connect the behavior of single packings to the ensemble average. Prior work on frictionless disks (VanderWerf et al., 2020) showed that $G$ decreases with $P$ for individual packings with fixed contact networks. Only when the contact network changes does the shear modulus increase, leading to a scaling of $P^{1/2}$ when averaging over an ensemble of many configurations with many different contact changes. Understanding the power-law scaling of the ensemble-averaged $G(P)$ for deformable particles requires an analysis of how deformable particles break contacts in response to compression, as well as how the shear modulus varies with pressure when the interparticle contact network does not change (Wang et al., 2021).

IV Conclusions

In this work, we have studied rigidity, the vibrational density of states, and the mechanical response in athermal, jammed solids composed of particles that can explicitly change shape to varying degrees. We can vary particle deformability by studying the Deformable Polygon (DP) model, where each particle has as many shape degrees of freedom as it has vertices, and the effectively rigid-shape DPb model, which includes bending energy. We also showed that DPb particles can buckle by increasing the preferred shape parameter $\mathcal{A}_{0}$ above a characteristic value ( $\mathcal{A}_{0}^{*}$ ), which effectively provides DPb particles with an additional degree of freedom. When studying the rigidity of jammed packings of these particles, we find that DP and DPb particles typically do not jam at a standard isostatic point. Packings of DP particles have too few contacts for collective rigidity, but we find that there are higher-order terms in the potential energy expansion (i.e. quartic modes) that stabilize the packings. Packings of DPb particles below the buckling threshold jam at the expected isostatic point for rigid-shape bumpy particles, but buckled DPb particles jam with more contacts than expected and seem to be hyperstatic. If we assume that buckled DPb particles have an extra degree of freedom, however, these packings are hypostatic just as in packings of DP particles. Although we cannot reliably count missing contacts from the vibrational spectra for buckled DPb packings, we show that a heuristic counting criterion roughly validates the observation that buckled DPb particles have higher-order rigidity.

Analyzing the vibrational spectra in more detail, we show that the vibrational density of states $D(\omega)$ depends strongly on particle deformability. In particular, we show that the characteristic frequency of quartic modes for jammed DP particles scales inversely with particle shape parameter, i.e. $\omega_{0}\sim\delta\mathcal{A}_{0}^{-1/3}$ . This result differs from other systems with three vibrational bands, in particular jammed packings of ellipsoids (Schreck et al., 2012) and breathing particles with size degrees of freedom (Brito et al., 2018). We also find that collective shape degrees of freedom $S$ play an important role in the low-frequency vibrational response of DP particles across different shapes and with increasing compression. We show that packings of regular-polygon DPb particles in the rigid-shape-particle limit $K_{c}\to 0$ do not possess low-frequency collective shape degrees of freedom, whereas $S(\omega)>0$ for all $K_{c}$ for packings with buckled DPb particles. We further show that $G\sim P^{3/4}$ over a wide range of pressure for packings of DP particles for all shape parameters studied, which deviates from the power-law scaling for packings of rigid-shape spherical particles. In contrast, packings of regular-polygon DPb particles possess $G\sim P^{1/2}$ scaling.

In all, our results show that explicit particle deformability qualitatively changes the linear response of soft solids. The bulk of these findings can be tested in experiments, either in non-contractile 2D monoloyers of epithelial cells (i.e. DP particles) or in soft, quasi-2D packings of hydrogel particles (i.e. regular-polygon DPb particles). The buckling phenomenon observed for DPb particles cannot easily be tested in an experiment, but we plan to carry out further theoretical studies of DPb buckling to gain a deeper understanding of quasi-deformability. Nevertheless, this work lays the foundation for understanding the vibrational and mechanical response in glassy systems of deformable particles, such as hopper flows of emulsion droplets (Hong et al., 2017; Golovkova et al., 2020) and motile tissues (Ajeti et al., 2019).

Acknowledgements

We thank O. K. Damavindi, V. F. Hagh, C. D. Santangelo, and M. L. Manning for helpful discussions. We acknowledge support from NSF Grants No. BMMB-2029756 (J.T. and C.O.), No. CBET-2002782 (J.T. and C.O.), No. CBET-2002797 (M.S.), and No. CMMI-1463455 (M.S.) and NIH award No. 5U54CA210184-04 (D.W.). This work was also supported by the High Performance Computing facilities operated by Yale’s Center for Research Computing.

Appendix A Particle buckling with bending energy

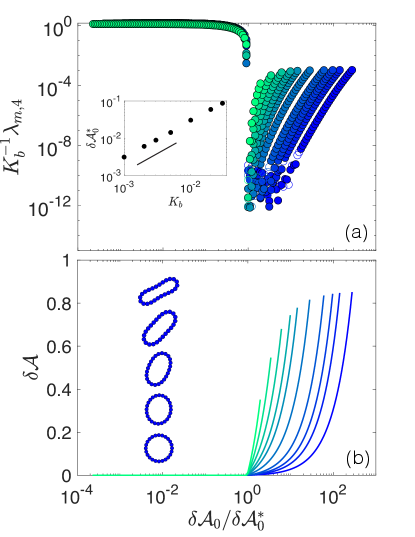
In this Appendix, we demonstrate buckling of DPb particles by increasing the preferred shape parameter $\mathcal{A}_{0}$ . In Fig. 7 (a), we show that the first non-trivial mode of the single-particle vibrational spectrum of DPb particles decreases by several orders of magnitude at $\mathcal{A}_{0}^{*}$ , which depends on $K_{b}$ . In Fig. 7 (b), we show that buckled particles transition from regular polygons with the true shape parameter $\mathcal{A}=\mathcal{A}_{n}$ to elongated, ellipsoidal particles with $\mathcal{A}>\mathcal{A}_{n}$ when $\mathcal{A}_{0}>\mathcal{A}_{0}^{*}$ . Note that occasionally, when sufficiently close to buckling, $\lambda_{m,4}<0$ , but $|\lambda_{m,4}|$ is close to numerical precision. These results suggest that, sufficiently close to buckling, DPb particles gain a degree of freedom and $\lambda_{m,4}\approx 0$ . However, increasing ${\cal A}_{0}$ further causes the eigenvalue to grow in magnitude. While $\lambda_{m,4}$ remains significantly smaller than $K_{b}$ , it is unclear whether DPb particles lose this degree of freedom at higher $\mathcal{A}_{0}$ .

Appendix B Higher-order constraints

In this Appendix, we discuss how to count effective constraints in jammed packings of deformable particles by analyzing the vibrational eigenmodes. In general, the vibrational response of a packing of deformable particles is obtained by calculating the dynamical matrix $\mathcal{M}$ evaluated at a point of mechanical equilibrium,

\mathcal{M}_{ij\mu\nu}=\partialderivative{U}{\vec{r}_{j\nu}}{\vec{r}_{i\mu}},

(6)

where $\vec{r}_{i\mu}=(x_{i\mu},y_{i\mu})$ is the coordinate vector of vertex $i$ on particle $\mu$ , and we bring the system to force balance ( $\partialderivative*{U}{\vec{r}_{i\mu}}=\vec{0})$ before evaluating the matrix elements. Note that $\mathcal{M}_{ij\mu\nu}$ is a $d\times d$ block matrix. Consider the DP energy in Eq. 1 in the main text, where $U_{a}$ , $U_{l}$ , and $U_{c}$ represent the area, perimeter, and particle interaction contributions to the total potential energy, respectively. We can define dynamical matrices for each term, e.g. $\mathcal{M}_{l}$ is perimeter energy contribution to the dynamical matrix. Using the chain rule, first derivatives of $U_{l}$ with respect to the vertex coordinates can be written as

\partialderivative{U_{l}}{\vec{r}_{i\mu}}=\sum_{\alpha=1}^{N}\sum_{k=1}^{n_{\alpha}}\partialderivative{U_{l}}{l_{k\alpha}}\partialderivative{l_{k\alpha}}{\vec{r}_{i\mu}}

(7)

since the perimeter energy depends on vertex coordinates through the edge length $l_{i\mu}=\absolutevalue{\vec{r}_{i+1,\mu}-\vec{r}_{i\mu}}$ . Note that this applies to all terms in Eqs. 1 and 3 (e.g. $U_{a}$ , $U_{b}$ , and $U_{c}$ ) that depend on the degrees of freedom through geometric factors. The second derivatives have the following form:

\begin{split}\partialderivative{U_{l}}{\vec{r}_{j\nu}}{\vec{r}_{i\mu}}&=\sum_{\alpha=1}^{N}\sum_{k=1}^{n_{\alpha}}\partialderivative{\vec{r}_{j\nu}}\quantity(\partialderivative{U_{l}}{l_{k\alpha}}\partialderivative{l_{k\alpha}}{\vec{r}_{i\mu}})\\ &=\sum_{\alpha=1}^{N}\sum_{k=1}^{n_{\alpha}}\quantity(\partialderivative[2]{U_{l}}{l_{k\alpha}}\partialderivative{l_{k\alpha}}{\vec{r}_{j\nu}}\partialderivative{l_{k\alpha}}{\vec{r}_{i\mu}}+\partialderivative{U_{l}}{l_{k\alpha}}\partialderivative{l_{k\alpha}}{\vec{r}_{j\nu}}{\vec{r}_{i\mu}}).\end{split}

(8)

The perimeter energy contribution to the dynamical matrix can be decomposed as $\mathcal{M}^{l}=\mathcal{H}^{l}-\mathcal{S}^{l}$ , where


$\displaystyle\mathcal{H}^{l}_{ij\mu\nu}$	$\displaystyle=\sum_{\alpha=1}^{N}\sum_{k=1}^{n_{\alpha}}\partialderivative[2]{U_{l}}{l_{k\alpha}}\partialderivative{l_{k\alpha}}{\vec{r}_{j\nu}}\partialderivative{l_{k\alpha}}{\vec{r}_{i\mu}}$	(9a)
$\displaystyle\mathcal{S}^{l}_{ij\mu\nu}$	$\displaystyle=-\sum_{\alpha=1}^{N}\sum_{k=1}^{n_{\alpha}}\partialderivative{U_{l}}{l_{k\alpha}}\partialderivative{l_{k\alpha}}{\vec{r}_{j\nu}}{\vec{r}_{i\mu}}$	(9b)

are the “stiffness” and “stress” matrices, respectively (Donev et al., 2007; Schreck et al., 2012). The matrix $\mathcal{H}^{l}$ depends primarily on first derivatives of geometric factors (e.g. $l_{i\mu}$ ) with respect to vertex coordinates, while the matrix $\mathcal{S}^{l}$ depends primarily on first derivatives of the potential energy. Note that the stress and stiffness matrices of the entire potential energy can be computed by summing contributions from corresponding matrices defined by the different contributions to the potential energy, e.g. $\mathcal{H}=\mathcal{H}^{a}+\mathcal{H}^{l}+\mathcal{H}^{c}$ is the sum of the area, perimeter, and particle interaction energy contributions to $\mathcal{H}$ .

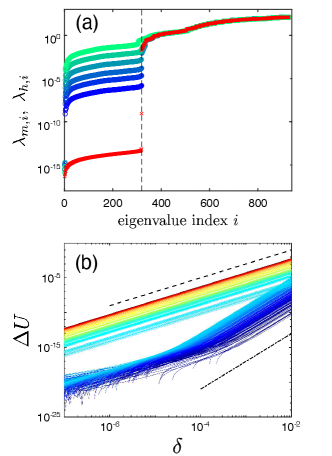
Prior work has shown that hypostatic systems like jammed non-spherical particles (Donev et al., 2007; VanderWerf et al., 2018; Yuan et al., 2019) and underconstrained spring networks (Damavandi et al., 2021) gain rigidity from higher-order terms in the potential energy that can stabilize multiple degrees of freedom. As noted in prior work (Schreck et al., 2012), these higher-order constraints can be seen as zero modes of the stiffness matrix $\mathcal{H}$ , but non-zero modes of the dynamical matrix $\mathcal{M}$ . In Fig. 8 (a), we find that the number of missing contacts exactly equals the number of stiffness matrix eigenvalues $\lambda_{h}$ that are significantly smaller than dynamical matrix eigenvalues $\lambda_{m}$ . Since $\mathcal{M}=\mathcal{H}-\mathcal{S}$ , we expect that small stiffness contribution means that $\mathcal{M}$ is dominated by the stress matrix for these eigenvalues. Indeed, in Fig. 8 (a) we also show that we can tune the magnitude of $\lambda_{m}$ by maintaining a fixed contact network but increasing the pressure. This pressure dependence of the low frequency eigenvalues of the dynamical matrix is also observed in packings of frictionless non-spherical particles (VanderWerf et al., 2018).

In hypostatic DP packings, we find that the extra degrees of freedom are constrained by so-called “quartic modes”. Consider an energy-minimized configuration such that the particle coordinates satisfy $\vec{R}=\vec{R}_{0}$ . Perturbations of order $\delta$ are then written as $\vec{R}=\vec{R}_{0}+\delta\vec{u}$ , where $\vec{u}$ is the direction of the perturbation. The potential energy expanded about $\vec{R}_{0}$ to fourth order in the perturbation is

\begin{split}U\quantity(\vec{R})&=U\quantity(\vec{R}_{0})+\delta\partialderivative{U}{R_{i}}u_{i}+\frac{\delta^{2}}{2}\partialderivative{U}{R_{i}}{R_{j}}u_{i}u_{j}\\ &+\frac{\delta^{3}}{6}\frac{\partial^{3}U}{\partial R_{i}\partial R_{j}\partial R_{k}}u_{i}u_{j}u_{k}\\ &+\frac{\delta^{4}}{24}\frac{\partial^{4}U}{\partial R_{i}\partial R_{j}\partial R_{k}\partial R_{l}}u_{i}u_{j}u_{k}u_{l}+\cdots,\end{split}

(10)

where we sum over repeated indices, and all derivatives are evaluated at $\vec{R}_{0}$ . The term linear in $\delta$ is $0$ when the system is at a potential energy minimum. If we choose $\vec{u}$ to be the $k$ th orthonormal eigenvector of the dynamical matrix $\mathcal{M}$ , the potential energy to second order in $\delta$ is $U=U_{0}+\frac{1}{2}\lambda_{m,k}\delta^{2}$ . However, in Fig. 8 (b), we find that the potential energy scales as $U\sim\delta^{4}$ , which is consistent with the observation that $\lambda_{m,k}$ are small, but the quartic terms are non-negligible. Similar behavior is observed in jammed packings of non-spherical particles (Mailman et al., 2009; Schreck et al., 2012; VanderWerf et al., 2018).

While we can easily identify the number of higher-order contacts from the dynamical matrix eigenspectra for packings of DP particles, the same is not true for packings of DPb particles. In Fig. 9, we show that the stiffness matrix eigenvalues $\lambda_{h}$ are larger than the dynamical matrix eigenvalues $\lambda_{m}$ for packings of buckled DPb particles. Given that buckled DPb particles have an extra degree of freedom, we investigate whether there is a signature in the eigenmodes with indexes below $m=4N^{\prime}-1-N_{\rm vv}$ , which corresponds to the number of missing contacts in packings of $N^{\prime}$ non-rattler particles.

We develop the following heuristic for packings of DPb particles: first we check if there is a gap of at least a factor of $10$ between the $m$ th non-trivial eigenmode of the dynamical matrix and the next mode, since there is a gap between quartic and quadratic modes for packings of DP particles. If a gap in the eigenspectra of the dynamical matrix is not present, we calculate the participation ratio of each normal mode $k$ ,

\rho_{k}=\frac{\quantity(\sum_{\mu=1}^{N}\sum_{i=1}^{n_{\mu}}\absolutevalue{\vec{V}_{i\mu,k}}^{2})^{2}}{N\sum_{\mu=1}^{N}\sum_{i=1}^{n_{\mu}}\absolutevalue{\vec{V}_{i\mu,k}}^{4}},

(11)

where $\vec{V}_{i\mu,k}$ is the displacement direction of the $i$ th vertex on the $\mu$ th particle in mode $k$ . If we observe a gap in the participation ratio of at least a factor of $10$ between the $m$ th non-trivial mode and the next mode, we assume that we have identified the $m$ higher-order modes correctly. We use the participation ratio gap because, in general, the participation ratio decreases with increasing eigenmode frequency. However, for DP particles, the highest-frequency quartic mode is usually localized whereas the lowest-frequency quadratic mode is delocalized. If neither of these two conditions is satisfied, we assume that there are no higher-order modes and no missing contacts. We emphasize that these thresholds are ad hoc, as the root cause of higher-order stability in jammed packings of buckled DPb particles is still an active area of research.

In Fig. 9, we show the outcome of this heuristic counting for several example configurations of $N=64$ buckled DPb particles at jamming onset. For example, in Fig. 9 (a) and (b), we find that a gap at the $m$ th non-trivial mode appears, allowing us to identify these modes as higher-order constraints in analogy with packings of DP particles. We also can correctly identify higher-order constraints using the participation ratio as shown in Fig. 9 (c) and (d). However, we show in Fig. 2 (b) and in Fig. 9 (e) and (f) that there are several cases with missing contacts $m>0$ , but we cannot identify the missing contacts by analyzing the eigenvalue spectra or participation ratios. The fact that missing contacts cannot be counted consistently underscores the difficulty in identifying higher-order constraints in these jammed systems.

Appendix C System size dependence of the vibrational density of states and shear modulus

In this Appendix, we investigate the system size dependence in the vibrational density of states $D(\omega)$ and static shear modulus $G$ of jammed packings of DP particles. In Fig. 10 (a), we show $D(\omega)$ for multiple system sizes spanning $N=16$ to $N=512$ with $n_{\rm S}=16$ for the preferred shape parameter $\mathcal{A}_{0}=1.08$ . We see little change in the structure of $D(\omega)$ except for more low-frequency quartic modes for larger system sizes, though this does not seem to change the peaks in $D(\omega)$ . We do however see system-size dependence in the static shear modulus as shown in Fig. 10 (b) in the low-pressure limit. At high pressures, $G$ collapses across all system sizes studied, but as $P\to 0$ we show in the Fig. 10 (b) inset that $G(P\to 0)\sim N^{-1}$ , which has been observed in previous work on deformable particles (Boromand et al., 2018).

Appendix D Mode decomposition

In this Appendix, we will show in detail how to decompose the eigenmodes of the dynamical matrix into contributions from particle translation, rotation, and shape degrees of freedom. We consider a packing of $N$ deformable particles, where each particle $\mu$ has a center of mass located at $\vec{c}_{\mu}=n_{\mu}^{-1}\sum_{i=1}^{n_{\mu}}\vec{r}_{i\mu}$ . Let $\vec{V}^{j}$ be the unit vector corresponding to the $j$ th eigenmode of the dynamical matrix $\mathcal{M}$ in Cartesian coordinates. Individual components of $\vec{V}^{j}$ are arranged such that the components from $2n_{\mu-1}$ to $2n_{\mu}$ are the $n_{\mu}$ $x$ -coordinates followed by the $n_{\mu}$ $y$ -coordinates for the $\mu$ th deformable particle. We can write three unit vectors to describe translation ( $\hat{\mathbf{u}}_{\mu,x}$ , $\hat{\mathbf{u}}_{\mu,y})$ and rotation ( $\hat{\mathbf{u}}_{\mu,r}$ ) about the center of mass of the $\mu$ th particle as follows:

\hat{\mathbf{u}}_{\mu,x}=\frac{\vec{u}_{\mu,x}}{|\vec{u}_{\mu,x}|},\vec{u}_{\mu,x}=(\underbrace{0,\ldots,0}_{\text{1 to ($\mu-1$)}},\underbrace{1,\ldots,1}_{\text{$\mu$th particle $x$}},\underbrace{0,\ldots,0}_{\text{$\mu$th particle $y$}},\underbrace{0,\ldots,0}_{\text{($\mu$+1) to $N$}})

(12)

\hat{\mathbf{u}}_{\mu,y}=\frac{\vec{u}_{\mu,y}}{|\vec{u}_{\mu,y}|},\vec{u}_{\mu,y}=(\underbrace{0,\ldots,0}_{\text{$1$ to ($\mu-1$) }},\underbrace{0,\ldots,0}_{\text{$\mu$th particle $x$}},\underbrace{1,\ldots,1}_{\text{$\mu$th particle $y$}},\underbrace{0,\ldots,0}_{\text{$(\mu+1)$ to $N$}})

(13)

\begin{split}\hat{\mathbf{u}}_{\mu,r}=\frac{\vec{u}_{\mu,r}}{|\vec{u}_{\mu,r}|},\vec{u}_{\mu,r}=(\underbrace{0,\ldots,0}_{\text{$1$ to ($\mu-1$) }},\underbrace{-(y_{1\mu}-c_{\mu,y}),\ldots,-(y_{n_{\mu}\mu}-c_{\mu,y})}_{\text{$\mu$th particle $x$}},\\ \underbrace{x_{1\mu}-c_{\mu,x},\ldots,x_{n_{\mu}\mu}-c_{\mu,x}}_{\text{$\mu$th particle $y$}},\underbrace{0,\ldots,0}_{\text{$(\mu+1)$ to $N$}}).\end{split}

(14)

By defining the coefficients,

$\displaystyle p_{\mu,x}^{j}$	$\displaystyle=\vec{V}^{j}\cdot\hat{\mathbf{u}}_{\mu,x}$	(15)
$\displaystyle p_{\mu,y}^{j}$	$\displaystyle=\vec{V}^{j}\cdot\hat{\mathbf{u}}_{\mu,y}$	(16)
$\displaystyle p_{\mu,r}^{j}$	$\displaystyle=\vec{V}^{j}\cdot\hat{\mathbf{u}}_{\mu,r},$	(17)

we can rewrite the eigenvector $\vec{V}^{j}$ as

\vec{V}^{j}=\sum_{\mu=1}^{N}p_{\mu,x}^{j}\hat{\mathbf{u}}_{\mu,x}+\sum_{\mu=1}^{N}p_{\mu,y}^{j}\hat{\mathbf{u}}_{\mu,y}+\sum_{\mu=1}^{N}p_{\mu,r}^{j}\hat{\mathbf{u}}_{\mu,r}+\vec{V}_{s}^{j},

(18)

where $\vec{V}_{s}^{j}$ is the vector that remains after subtracting the particle translations and rotation out of $\vec{V}_{j}$ . By applying this decomposition, we can express each eigenmode as the sum of particle translations, rotation, and shape deformations. We show an example of an eigenmode decomposition in Fig. 11 (a) for a packing of DP particles.

With these coefficients, we can define the fraction of the translational ( $T^{j}$ ) and rotational ( $R^{j}$ ) content in the $j$ th eigenmode of the dynamical matrix as:

	$\displaystyle T^{j}$	$\displaystyle=\sum_{\mu=1}^{N}\quantity[\quantity(p_{\mu,x}^{j})^{2}+\quantity(p_{\mu,y}^{j})^{2}]$		(19)
	$\displaystyle R^{j}$	$\displaystyle=\sum_{\mu=1}^{N}\quantity(p_{\mu,r}^{j})^{2}.$		(20)

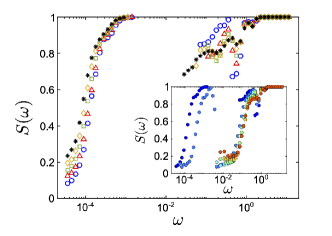
Since we obtain $p_{\mu,x}^{j},p_{\mu,y}^{j}$ , and $p_{\mu,r}^{j}$ from unit vectors, $S^{j}=1-T^{j}-R^{j}$ gives the contribution of the shape degrees of freedom to the $j$ th eigenmode. We show $T^{j},R^{j}$ , and $S^{j}$ for a jammed packing of $N=16$ DP particles with preferred shape parameter $\mathcal{A}_{0}=1.04$ in Fig. 11 (b) as a function of frequency $\omega$ , as well as just the $S$ modes in Figs. 4 and 5. We find that for the quartic modes ( $\omega<10^{-2}$ ), the shape contribution $S$ increases with $\omega$ , while $T$ and $R$ decrease. For the quadratic modes ( $\omega>10^{-2}$ ), the contribution from $S$ is large, since higher frequency modes tend to deform the particle shape rather than give rise to translation or rotation.

References

Durian (1995) D. J. Durian, Phys. Rev. Lett. 75, 4780 (1995).
van Hecke (2009) M. van Hecke, J. Phys.: Condens. Matter 22, 033101 (2009).
Bolton and Weaire (1990) F. Bolton and D. Weaire, Phys. Rev. Lett. 65, 3449 (1990).
Bertho et al. (2006) Y. Bertho, C. Becco, and N. Vandewalle, Phys. Rev. E 73, 056309 (2006).
Princen (1983) H. Princen, J. Colloid. Interf Sci. 91, 160 (1983).
Boromand et al. (2019) A. Boromand, A. Signoriello, J. Lowensohn, C. S. Orellana, E. R. Weeks, F. Ye, M. D. Shattuck, and C. S. O’Hern, Soft Matter 15, 5854 (2019).
Smith et al. (2017) W. P. J. Smith, Y. Davit, J. M. Osborne, W. Kim, K. R. Foster, and J. M. Pitt-Francis, Proc. Natl. Acad. Sci. USA 114, E280 (2017).
Beroz et al. (2018) F. Beroz, J. Yan, Y. Meir, B. Sabass, H. A. Stone, B. L. Bassler, and N. S. Wingreen, Nat. Phys. 14, 954 (2018).
Park et al. (2015) J.-A. Park, J. H. Kim, D. Bi, J. A. Mitchel, N. T. Qazvini, K. Tantisira, C. Y. Park, M. McGill, S.-H. Kim, B. Gweon, J. Notbohm, R. Steward Jr, S. Burger, S. H. Randell, A. T. Kho, D. T. Tambe, C. Hardin, S. A. Shore, E. Israel, D. A. Weitz, D. J. Tschumperlin, E. P. Henske, S. T. Weiss, M. L. Manning, J. P. Butler, J. M. Drazen, and J. J. Fredberg, Nat. Mater. 14, 1040 (2015).
Trepat and Sahai (2018) X. Trepat and E. Sahai, Nat. Phys. 14, 671 (2018).
Lecuit and Lenne (2007) T. Lecuit and P.-F. Lenne, Nat. Rev. Mol. Cell Bio. 8, 633 (2007).
Murrell et al. (2015) M. Murrell, P. W. Oakes, M. Lenz, and M. L. Gardel, Nat. Rev. Mol. Cell Bio. 16, 486 (2015).
Jolly et al. (2015) M. K. Jolly, M. Boareto, B. Huang, D. Jia, M. Lu, E. Ben-Jacob, J. N. Onuchic, and H. Levine, Front. Oncol. 5, 155 (2015).
McMillen et al. (2016) P. McMillen, V. Chatti, D. Jülich, and S. A. Holley, Curr. Biol. 26, 542 (2016).
Oswald et al. (2017) L. Oswald, S. Grosser, D. M. Smith, and J. A. Käs, J. Phys. D Appl. Phys. 50, 483001 (2017).
Mongera et al. (2018) A. Mongera, P. Rowghanian, H. J. Gustafson, E. Shelton, D. A. Kealhofer, E. K. Carn, F. Serwane, A. A. Lucio, J. Giammona, and O. Campàs, Nature 561, 401 (2018).
Ilina et al. (2020) O. Ilina, P. G. Gritsenko, S. Syga, J. Lippoldt, C. A. M. La Porta, O. Chepizhko, S. Grosser, M. Vullings, G.-J. Bakker, J. Starruß, P. Bult, S. Zapperi, J. A. Käs, A. Deutsch, and P. Friedl, Nat. Cell Biol. 22, 1103 (2020).
Kim et al. (2021) S. Kim, M. Pochitaloff, G. A. Stooke-Vaughan, and O. Campàs, Nature Physics (2021), 10.1038/s41567-021-01215-1.
Wuyts et al. (2010) N. Wuyts, J.-C. Palauqui, G. Conejero, J.-L. Verdeil, C. Granier, and C. Massonnet, Plant Methods 6, 17 (2010).
Kalve et al. (2014) S. Kalve, J. Fotschki, T. Beeckman, K. Vissenberg, and G. T. S. Beemster, J. Exp. Bot. 65, 6385 (2014).
Sapala et al. (2018) A. Sapala, A. Runions, A.-L. Routier-Kierzkowska, M. Das Gupta, L. Hong, H. Hofhuis, S. Verger, G. Mosca, C.-B. Li, A. Hay, O. Hamant, A. H. Roeder, M. Tsiantis, P. Prusinkiewicz, and R. S. Smith, eLife 7, e32794 (2018).
Martinez et al. (2018) P. Martinez, L. A. Allsman, K. A. Brakke, C. Hoyt, J. Hayes, H. Liang, W. Neher, Y. Rui, A. M. Roberts, A. Moradifam, B. Goldstein, C. T. Anderson, and C. G. Rasmussen, Plant Cell 30, 2255 (2018).
Borsuk et al. (2019) A. M. Borsuk, A. B. Roddy, G. Théroux-Rancourt, and C. R. Brodersen, bioRxiv (2019), 10.1101/852459.
O’Hern et al. (2003) C. S. O’Hern, L. E. Silbert, A. J. Liu, and S. R. Nagel, Phys. Rev. E 68, 011306 (2003).
Tkachenko and Witten (1999) A. V. Tkachenko and T. A. Witten, Phys. Rev. E 60, 687 (1999).
Pellegrino and Calladine (1986) S. Pellegrino and C. Calladine, International Journal of Solids and Structures 22, 409 (1986).
Schreck et al. (2011a) C. F. Schreck, T. Bertrand, C. S. O’Hern, and M. D. Shattuck, Phys. Rev. Lett. 107, 078301 (2011a).
Goodrich et al. (2014) C. P. Goodrich, A. J. Liu, and S. R. Nagel, Nat. Phys. 10, 578 (2014).
Mailman et al. (2009) M. Mailman, C. F. Schreck, C. S. O’Hern, and B. Chakraborty, Phys. Rev. Lett. 102, 255501 (2009).
Donev et al. (2007) A. Donev, R. Connelly, F. H. Stillinger, and S. Torquato, Phys. Rev. E 75, 051304 (2007).
Schreck et al. (2012) C. F. Schreck, M. Mailman, B. Chakraborty, and C. S. O’Hern, Phys. Rev. E 85, 061305 (2012).
VanderWerf et al. (2018) K. VanderWerf, W. Jin, M. D. Shattuck, and C. S. O’Hern, Phys. Rev. E 97, 012909 (2018).
Yuan et al. (2019) Y. Yuan, K. VanderWerf, M. D. Shattuck, and C. S. O’Hern, Soft Matter 15, 9751 (2019).
Brito et al. (2018) C. Brito, H. Ikeda, P. Urbani, M. Wyart, and F. Zamponi, Proc. Natl. Acad. Sci. USA 115, 11736 (2018).
Shen et al. (2012) T. Shen, C. Schreck, B. Chakraborty, D. E. Freed, and C. S. O’Hern, Phys. Rev. E 86, 041303 (2012).
Damavandi et al. (2021) O. K. Damavandi, V. F. Hagh, C. D. Santangelo, and M. L. Manning, (2021), arXiv:2102.11310 .
Bi et al. (2015) D. Bi, J. H. Lopez, J. M. Schwarz, and M. L. Manning, Nat. Phys. 11, 1074 (2015).
Yan and Bi (2019) L. Yan and D. Bi, Phys. Rev. X 9, 011029 (2019).
Boromand et al. (2018) A. Boromand, A. Signoriello, F. Ye, C. S. O’Hern, and M. D. Shattuck, Phys. Rev. Lett. 121, 248003 (2018).
Zhang et al. (2014) K. Zhang, W. W. Smith, M. Wang, Y. Liu, J. Schroers, M. D. Shattuck, and C. S. O’Hern, Phys. Rev. E 90, 032311 (2014).
Kane and Lubensky (2014) C. L. Kane and T. C. Lubensky, Nature Physics 10, 39 (2014).
Chen et al. (2014) B. G.-g. Chen, N. Upadhyaya, and V. Vitelli, Proceedings of the National Academy of Sciences 111, 13004 (2014).
Papanikolaou et al. (2013) S. Papanikolaou, C. S. O’Hern, and M. D. Shattuck, Phys. Rev. Lett. 110, 198002 (2013).
Schreck et al. (2011b) C. F. Schreck, C. S. O’Hern, and L. E. Silbert, Phys. Rev. E 84, 011305 (2011b).
Tuckman et al. (2020) P. J. Tuckman, K. VanderWerf, Y. Yuan, S. Zhang, J. Zhang, M. D. Shattuck, and C. S. O’Hern, Soft Matter 16, 9443 (2020).
Foglino et al. (2017) M. Foglino, A. N. Morozov, O. Henrich, and D. Marenduzzo, Phys. Rev. Lett. 119, 208002 (2017).
Hong et al. (2017) X. Hong, M. Kohne, M. Morrell, H. Wang, and E. R. Weeks, Phys. Rev. E 96, 062605 (2017).
Golovkova et al. (2020) I. Golovkova, L. Montel, E. Wandersman, T. Bertrand, A. M. Prevost, and L.-L. Pontani, Soft Matter 16, 3294 (2020).
Allen and Tildesley (2017) M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, 2nd ed. (Oxford University Press, 2017).
Goodrich et al. (2012) C. P. Goodrich, A. J. Liu, and S. R. Nagel, Phys. Rev. Lett. 109, 095704 (2012).
VanderWerf et al. (2020) K. VanderWerf, A. Boromand, M. D. Shattuck, and C. S. O’Hern, Phys. Rev. Lett. 124, 038004 (2020).
Somfai et al. (2007) E. Somfai, M. van Hecke, W. G. Ellenbroek, K. Shundyak, and W. van Saarloos, Phys. Rev. E 75, 020301(R) (2007).
Wang et al. (2021) P. Wang, S. Zhang, P. Tuckman, N. T. Ouellette, M. D. Shattuck, and C. S. O’Hern, Phys. Rev. E 103, 022902 (2021).
Ajeti et al. (2019) V. Ajeti, A. P. Tabatabai, A. J. Fleszar, M. F. Staddon, D. S. Seara, C. Suarez, M. S. Yousafzai, D. Bi, D. R. Kovar, S. Banerjee, and M. P. Murrell, Nat. Phys. 15, 696 (2019).