11email: wkollat@astro.physik.uni-goettingen.de 22institutetext: Astronomisches Institut, Ruhr-Universität Bochum, Universitätsstrasse 150, 44801 Bochum, Germany 33institutetext: Physics Department and the Haifa Research Center for Theoretical Physics and Astrophysics, University of Haifa, Haifa 3498838, Israel 44institutetext: School of Physics & Astronomy and the Wise Observatory, The Raymond and Beverly Sackler Faculty of Exact Sciences Tel-Aviv University, Tel-Aviv 69978, Israel 55institutetext: Department of Earth and Space Sciences, Morehead State University, Morehead, KY 40351, USA
Broad-line region structure and line profile variations in the changing look AGN HE 1136-2304 ††thanks: Based on observations obtained with the Southern African Large Telescope.
Abstract
Aims. A strong X-ray outburst was detected in HE 1136-2304 in 2014. Accompanying optical spectra revealed that the spectral type has changed from a nearly Seyfert 2 type (1.95), classified by spectra taken 10 and 20 years ago, to a Seyfert 1.5 in our most recent observations. We seek to investigate a detailed spectroscopic campaign on the spectroscopic properties and spectral variability behavior of this changing look AGN and compare this to other variable Seyfert galaxies.
Methods. We carried out a detailed spectroscopic variability campaign of HE 1136-2304 with the 10 m Southern African Large Telescope (SALT) between 2014 December and 2015 July.
Results. The broad-line region (BLR) of HE 1136-2304 is stratified with respect to the distance of the line-emitting regions. The integrated emission line intensities of H, H, He i , and He ii originate at distances of , , , and light days with respect to the optical continuum at 4570 Å. The variability amplitudes of the integrated emission lines are a function of distance to the ionizing continuum source as well. We derived a central black hole mass of based on the linewidths and distances of the BLR. The outer line wings of all BLR lines respond much faster to continuum variations indicating a Keplerian disk component for the BLR. The response in the outer wings is about two light days shorter than the response of the adjacent continuum flux with respect to the ionizing continuum flux. The vertical BLR structure in HE 1136-2304 confirms a general trend that the emission lines of narrow line active galactic nuclei (AGNs) originate at larger distances from the midplane in comparison to AGNs showing broader emission lines. Otherwise, the variability behavior of this changing look AGN is similar to that of other AGN.
Key Words.:
Galaxies: active – Galaxies: Seyfert – Galaxies: nuclei – Galaxies: individual: HE 1136-2304 – (Galaxies:) quasars: emission lines1 Introduction
About a dozen Seyfert galaxies are known to have significantly changed their optical spectral type: for example, NGC 3515 (Collin-Souffrin et al.1973), NGC 4151 (Penston & Perez1984), Fairall 9 (Kollatschny et al.1985), NGC 2617 (Shappee et al.2014), Mrk 590 (Denney at al.2014), and references therein. Further recent findings are based on spectral variations detected by means of the Sloan Digital Sky Survey (e.g., Komossa et al.komossa08 2008; LaMassa et al.lamassa15 2015; Runnoe et al.2016; MacLeod et al.2016). These galaxies are considered to be changing look active galactic nuclei (AGNs). However, most of these findings are based on only a few optical spectra.
HE 1136-2304 ( = 11h 38m 51.1s, = 21 36) was classified as a changing look AGN based on spectroscopy performed after a strong increase in the X-ray flux was detected by XMM-Newton in 2014 in comparison to an upper limit based on the ROSAT All-Sky Survey taken in 1990 (Parker et al.2016). The increase in the X-ray flux came with an increase in the optical continuum flux and with a change of the Seyfert type. HE 1136-2304 was of Seyfert 2/1.95 type in early spectra taken in 1993 and 2002. However, its spectral type changed to a Seyfert 1.5 type in 2014 (Zetzl et al.2018, Paper 1). This notation of Seyfert subclasses was introduced by Osterbrock (1981).
Long-term and detailed optical variability studies exist for many AGN such as NGC 5548 (Peterson et al.2002; Pei et al.2017 and references therein), 3C120 (Peterson et al.1998; Kollatschny et al.2000; Grier at al.2013), NGC 7603 (Kollatschny et al.2000), and 3C 390.3 (Shapovalova et al.shapovalova10 2010). Corresponding detailed follow-up studies have not yet been reported for the type of changing look AGN mentioned above.
We carried out a detailed spectroscopic and photometric variability study of HE 1136-2304 between 2014 and 2015 after the detection of the strong outburst in 2014. We presented the optical, UV, and X-ray continuum variations of HE 1136-2304 from 2014 to 2017 in a separate paper (Paper 1). We verified strong continuum variations in the X-ray, UV, and optical continua. We showed that the variability amplitude decreased with increasing wavelength. The amplitude in the optical varied by a factor of three after correcting for the host galaxy contribution. No systematic trends were found with regards to the variability behavior following the outburst in 2014. A general decrease in flux would have been expected for a tidal disruption event. The Seyfert type did not change between 2014 and 2017 despite strong continuum variations. We describe the results of the spectroscopic variability campaign taken with the 10 m Southern African Large Telescope (SALT) for the years 2014 to 2015.
Throughout this paper, we assume CDM cosmology with a Hubble constant of H0 = 70 km s-1Mpc-1, =0.27, and =0.73. Following the cosmological calculator by Wright et al. (2006) this results in a luminosity distance of 118 Mpc.
2 Observations and data reduction
In addition to our first spectrum obtained on 2014 July 7 (Parker et al.2016), we took optical spectra of the Seyfert galaxy HE 1136-2304 with the SALT at 17 epochs between 2014 December 25 and 2015 July 13 . The log of our spectroscopic observations is given in Tab. 1.
| Julian Date | UT Date | Exp. time |
|---|---|---|
| 2 400 000+ | [sec.] | |
| 56846.248 | 2014-07-07 | 1200 |
| 57016.559 | 2014-12-25 | 985 |
| 57070.399 | 2015-02-16 | 985 |
| 57082.362 | 2015-02-28 | 985 |
| 57088.594 | 2015-03-07 | 985 |
| 57100.539 | 2015-03-19 | 985 |
| 57112.285 | 2015-03-30 | 985 |
| 57121.256 | 2015-04-08 | 985 |
| 57131.243 | 2015-04-18 | 1230 |
| 57167.359 | 2015-05-24 | 1144 |
| 57171.364 | 2015-05-28 | 1144 |
| 57182.330 | 2015-06-08 | 1144 |
| 57187.319 | 2015-06-13 | 1144 |
| 57192.308 | 2015-06-18 | 1144 |
| 57196.295 | 2015-06-22 | 1144 |
| 57201.271 | 2015-06-27 | 1144 |
| 57206.265 | 2015-07-02 | 1144 |
| 57217.227 | 2015-07-13 | 1144 |
The spectra taken of HE 1136-2304 between 2015 February and 2015 July had a mean interval of nine days. For some epochs spectra were acquired at shorter intervals.
All spectroscopic observations were taken with identical instrumental setups. We used the Robert Stobie Spectrograph attached to the SALT using the PG0900 grating. The slit width was fixed to 2″. 0 projected on the sky at an optimized position angle to minimize differential refraction. Furthermore, all observations were taken at the same airmass owing to the particular design of the SALT. The spectra were taken with exposure times of 16 to 20 minutes.
Typical seeing values were 1 to 2 arcsec. We covered a wavelength range from 4355 Å to 7230 Å, which corresponds to a rest-frame wavelength range of 4240 Å to 7040 Å. The spectral resolution was 6.5 Å. There are two gaps in the spectrum caused by the gaps between the three CCDs: one between the blue and the central CCD chip and one between the central and red CCD chip covering the wavelengths in the ranges 5206–5263 Å and 6254–6309 Å (5069–5124 Å and 6089–6142 Å in the rest frame). All spectra shown in this work were shifted to the rest frame of HE 1136-2604.
In addition to the galaxy spectrum, necessary flat-field and Xe arc frames were also observed, as well as spectrophotometric standard stars for flux calibration (LTT3218, LTT7379, and EG274). Flat-field frames were used to correct for differences in sensitivity both between detector pixels and across the field. The spatial resolution per binned pixel was 0″. 2534 for our SALT spectrum. We extracted eight columns from the object spectrum corresponding to 2″. 03.
We reduced the spectra (bias subtraction, cosmic ray correction, flat-field correction, 2D-wavelength calibration, night sky subtraction, and flux calibration) in a homogeneous way with the Image Reduction and Analysis Facility (IRAF) reduction packages (e.g., Kollatschny et al.,2001). Great care was taken to ensure high-quality intensity and wavelength calibrations to keep the intrinsic measurement errors very low (Kollatschny et al.,2001, 2003; kollatschny10 2010). The spectra of HE1136-2304 and the calibration star spectra were not always taken under photometric conditions. Therefore, all spectra were calibrated to the same absolute [O iii] 5007 flux of (Reimers et al.reimers96 1996). The flux of the narrow emission line [O iii] 5007 is considered to be constant on timescales of years. The accuracy of the [O iii] 5007 flux calibration was tested for all forbidden emission lines in the spectra. We calculated difference spectra for all epochs with respect to the mean spectrum of our variability campaign. Corrections for both small spectral shifts ( 0.5 Å) and small scaling factors were executed by minimizing the residuals of the narrow emission lines in the difference spectra. A relative flux accuracy on the order of 1% was achieved for most of the spectra.
3 Results
3.1 Continuum and spectral line variations
We present all final reduced optical spectra of HE 1136-2304 taken during the 2014/2015 variability campaign in Fig. 1. These results clearly show variations in the continuum intensities. The mean and rms spectra of HE 1136-2304 are shown in Fig. 2. The rms spectrum presents the variable part of the emission lines. The spectrum was scaled by a factor of 6.9 to allow for a better comparison with the mean spectrum and for enhancing weaker line structures. We note that all wavelengths referred to in this section are rest-frame wavelengths.
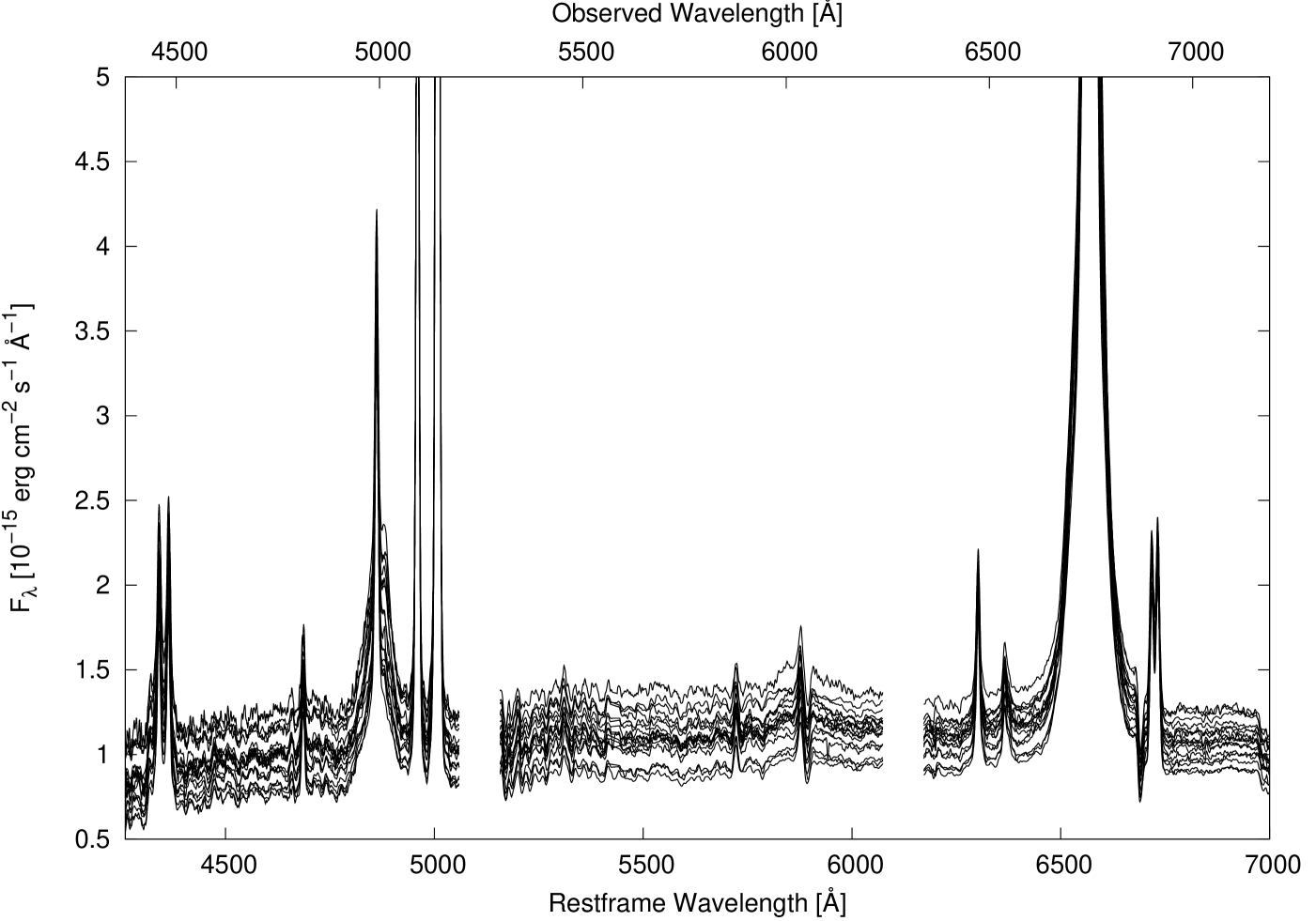
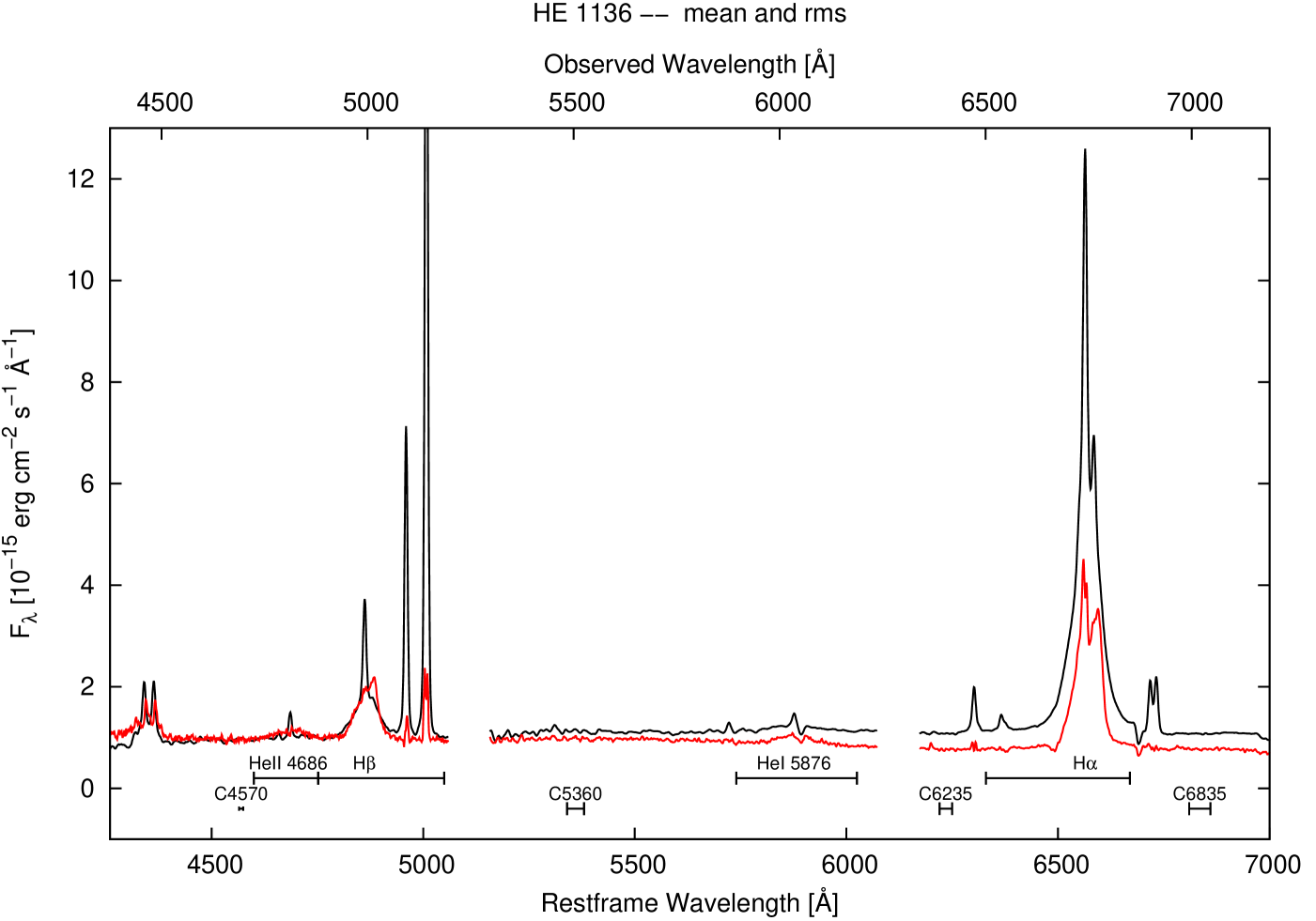
The integration limits of the broad emission lines and continuum regions are given at the bottom of the spectra. To select the continuum regions, we inspected the mean and rms spectra for regions that are free of both strong emission and absorption lines. The final wavelength ranges used for our continuum flux measurements are given in Table 2. A continuum region at 5100 Å is often used in studies of the variable continuum flux in AGN. Normally, this region is free of strong emission lines and close to the [O iii] 5007 flux calibration line. However, in our case this region falls in the gap between the blue and central CCD chip. Therefore we set a nearby continuum range at 5360 Å. In addition to this continuum range, we determined the continuum intensities at three additional ranges (at 4570, 6235, and 6835 Å; see Fig. 2 and Tab. 2). We used these continuum regions for creating pseudo-continua below the variable broad emission lines. We neglected a possible contribution of FeII blends to the continuum flux based on our mean and rms spectra.
| Cont./Line | Wavelength range | Pseudo-continuum |
|---|---|---|
| (1) | (2) | (3) |
| Cont. 4570 | 4565 Å – 4575 Å | |
| Cont. 5360 | 5340 Å – 5380 Å | |
| Cont. 6235 | 6220 Å – 6250 Å | |
| Cont. 6835 | 6810 Å – 6860 Å | |
| He ii | 4600 Å – 4752 Å | 4570 Å – 5360 Å |
| H | 4752 Å – 5050 Å | 4570 Å – 5360 Å |
| He i | 5740 Å – 6025 Å | 5700 Å – 6060 Å |
| H | 6330 Å – 6670 Å | 6235 Å – 6835 Å |
We integrated the broad Balmer and Helium emission-line intensities between the wavelength boundaries given in Tab. 2. Before integrating each emission line flux, we subtracted a linear pseudo-continuum defined by the boundaries given in Tab. 2 (Col. 3). We did not consider the H line in our studies as it was not possible to determine a reliable continuum at the blue side of this line. The results of the continuum and line intensity measurements are given in Tab. 1. Additionally, we present in this table the flux values obtained for our first spectrum taken on 2014 July 7.
| Julian Date | Cont. 4570 Å | Cont. 5360 Å | H | H | HeI | HeII |
|---|---|---|---|---|---|---|
| 2 400 000+ | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| 56846.248 | 1.336 0.011 | 1.403 0.030 | 514.1 15.5 | 145.2 4.4 | 29.5 0.9 | 17.2 0.6 |
| 57016.559 | 0.829 0.003 | 0.889 0.019 | 479.0 14.4 | 71.6 3.6 | 16.1 0.5 | 4.3 0.3 |
| 57070.399 | 0.909 0.012 | 0.927 0.021 | 444.9 13.4 | 83.4 2.6 | 13.8 0.5 | 8.1 0.3 |
| 57082.362 | 1.161 0.019 | 1.191 0.025 | 451.8 13.6 | 97.4 3.0 | 18.3 0.6 | 6.3 0.2 |
| 57088.594 | 1.257 0.028 | 1.199 0.032 | 508.3 15.3 | 90.9 2.8 | 23.4 0.8 | 9.7 0.3 |
| 57100.539 | 1.139 0.003 | 1.162 0.021 | 547.7 16.5 | 107.0 3.3 | 25.3 0.8 | 11.0 0.4 |
| 57112.285 | 1.023 0.015 | 1.043 0.025 | 534.6 16.1 | 94.3 2.9 | 18.9 0.6 | 6.9 0.3 |
| 57121.256 | 1.062 0.009 | 1.112 0.020 | 515.4 15.5 | 89.1 2.7 | 15.4 0.5 | 5.0 0.2 |
| 57131.243 | 1.174 0.010 | 1.196 0.026 | 526.2 15.8 | 93.8 2.9 | 20.5 0.7 | 10.0 0.4 |
| 57167.359 | 1.011 0.016 | 1.068 0.024 | 498.7 15.0 | 81.2 4.1 | 16.5 0.5 | 6.1 0.4 |
| 57171.364 | 0.990 0.010 | 1.013 0.027 | 513.8 15.5 | 84.5 2.6 | 18.3 0.6 | 8.1 0.3 |
| 57182.330 | 0.825 0.008 | 0.875 0.020 | 473.4 14.3 | 76.9 2.4 | 14.3 0.5 | 3.0 0.1 |
| 57187.319 | 0.782 0.015 | 0.864 0.014 | 488.1 14.7 | 70.3 2.2 | 15.2 0.5 | 1.5 0.1 |
| 57192.308 | 0.907 0.009 | 0.969 0.024 | 484.7 14.6 | 67.2 3.4 | 14.4 0.5 | 5.5 0.3 |
| 57196.295 | 0.915 0.011 | 0.966 0.023 | 436.0 13.1 | 59.3 1.8 | 9.9 0.3 | 2.2 0.1 |
| 57201.271 | 0.800 0.008 | 0.868 0.022 | 444.3 13.4 | 60.0 1.9 | 13.3 0.5 | 1.8 0.1 |
| 57206.265 | 0.994 0.012 | 1.067 0.023 | 441.1 13.3 | 68.9 3.5 | 14.7 0.5 | 6.9 0.3 |
| 57217.227 | 1.004 0.024 | 1.091 0.032 | 452.0 13.6 | 66.4 2.0 | 14.1 0.5 | 2.0 0.1 |
Line fluxes (3) - (7) in units 10-15 erg s-1 cm-2.
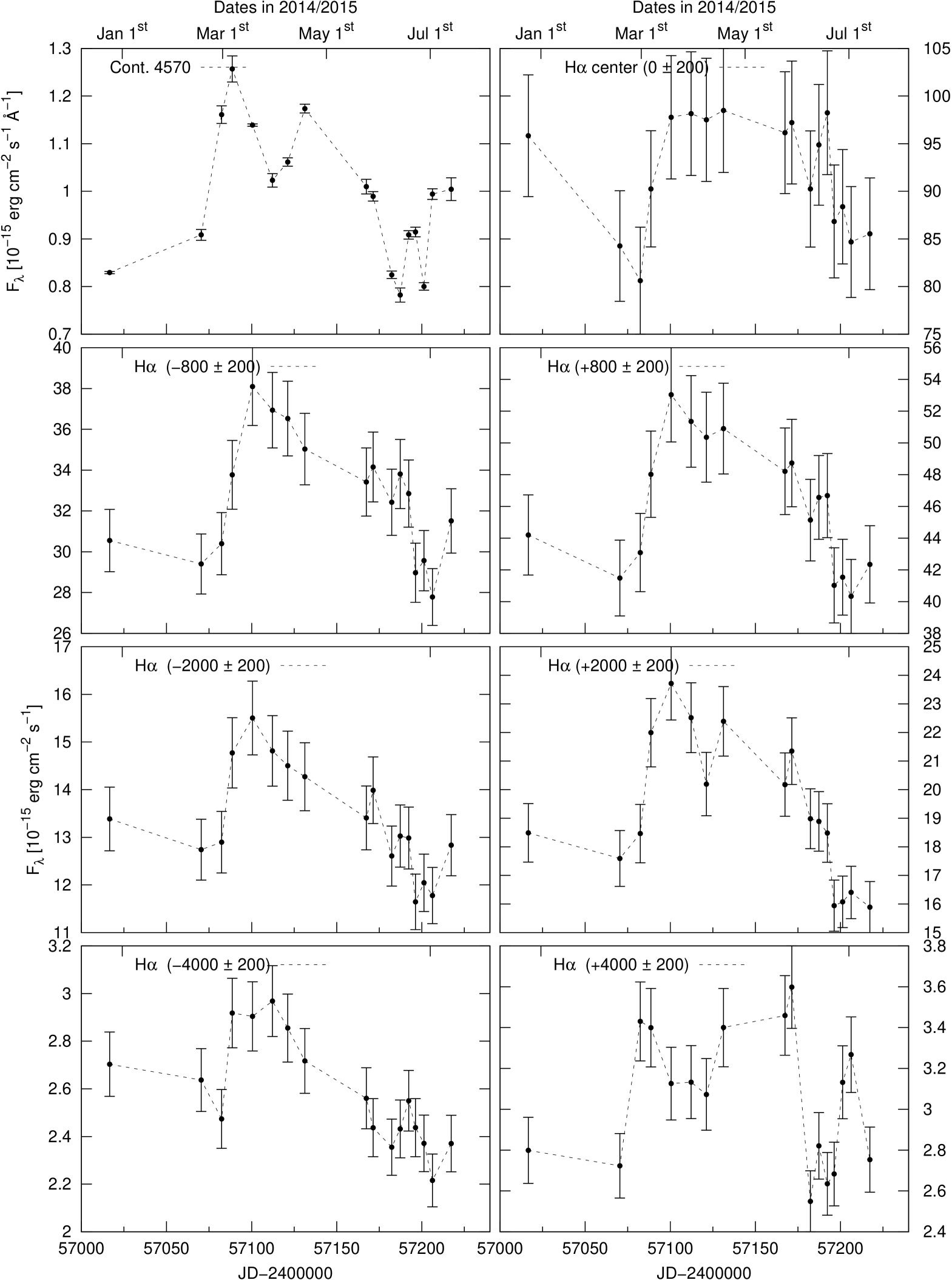
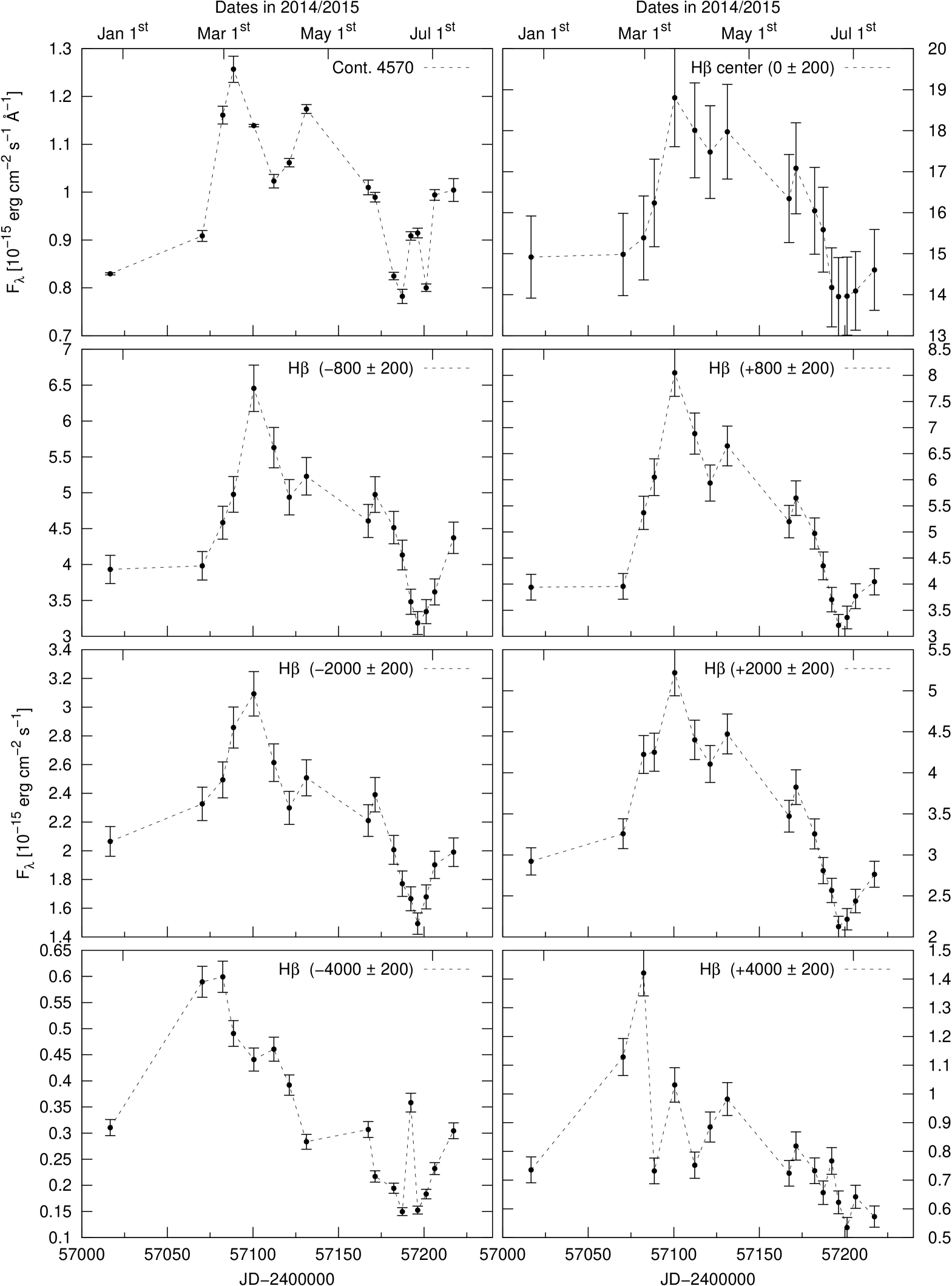
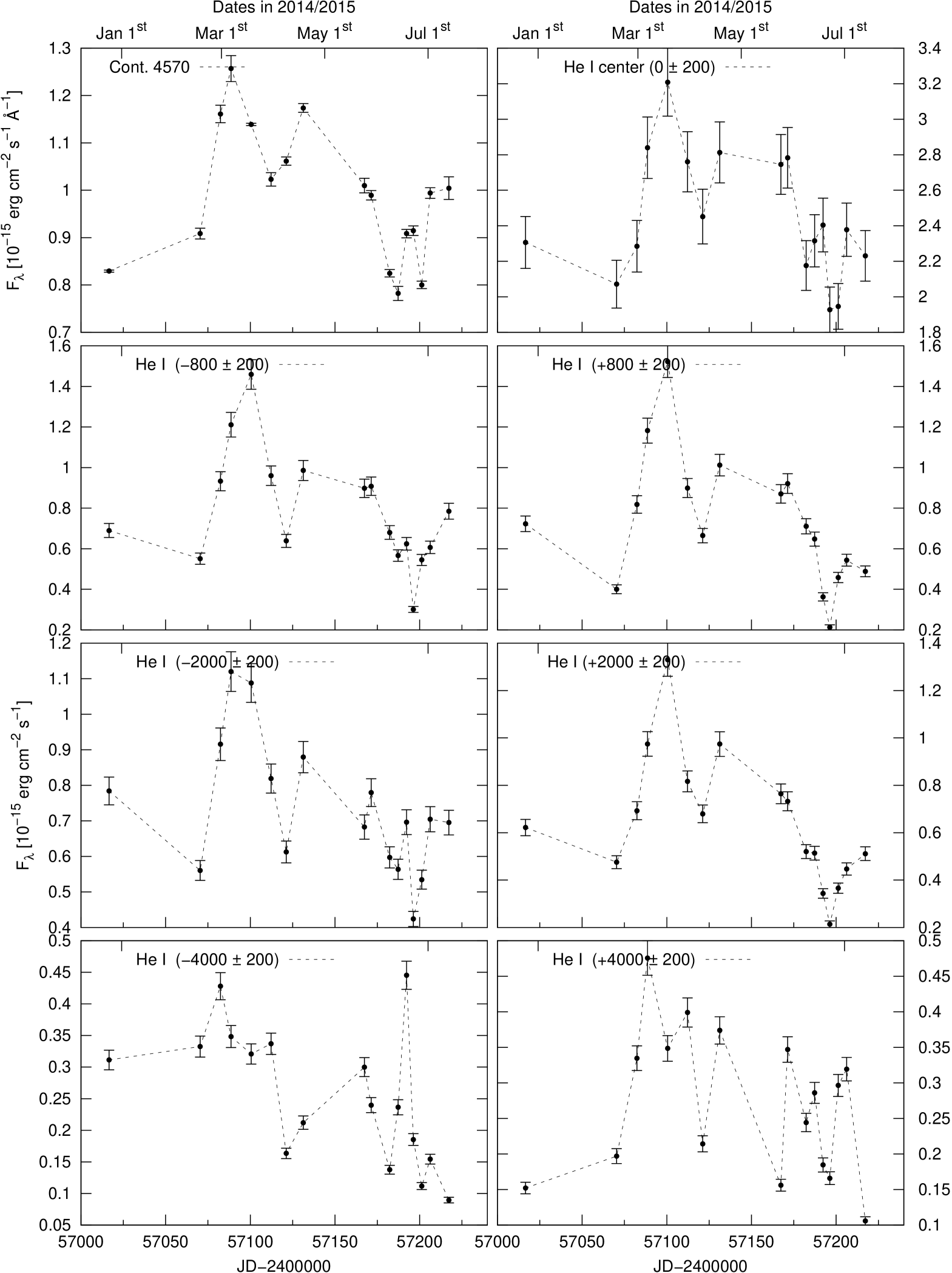
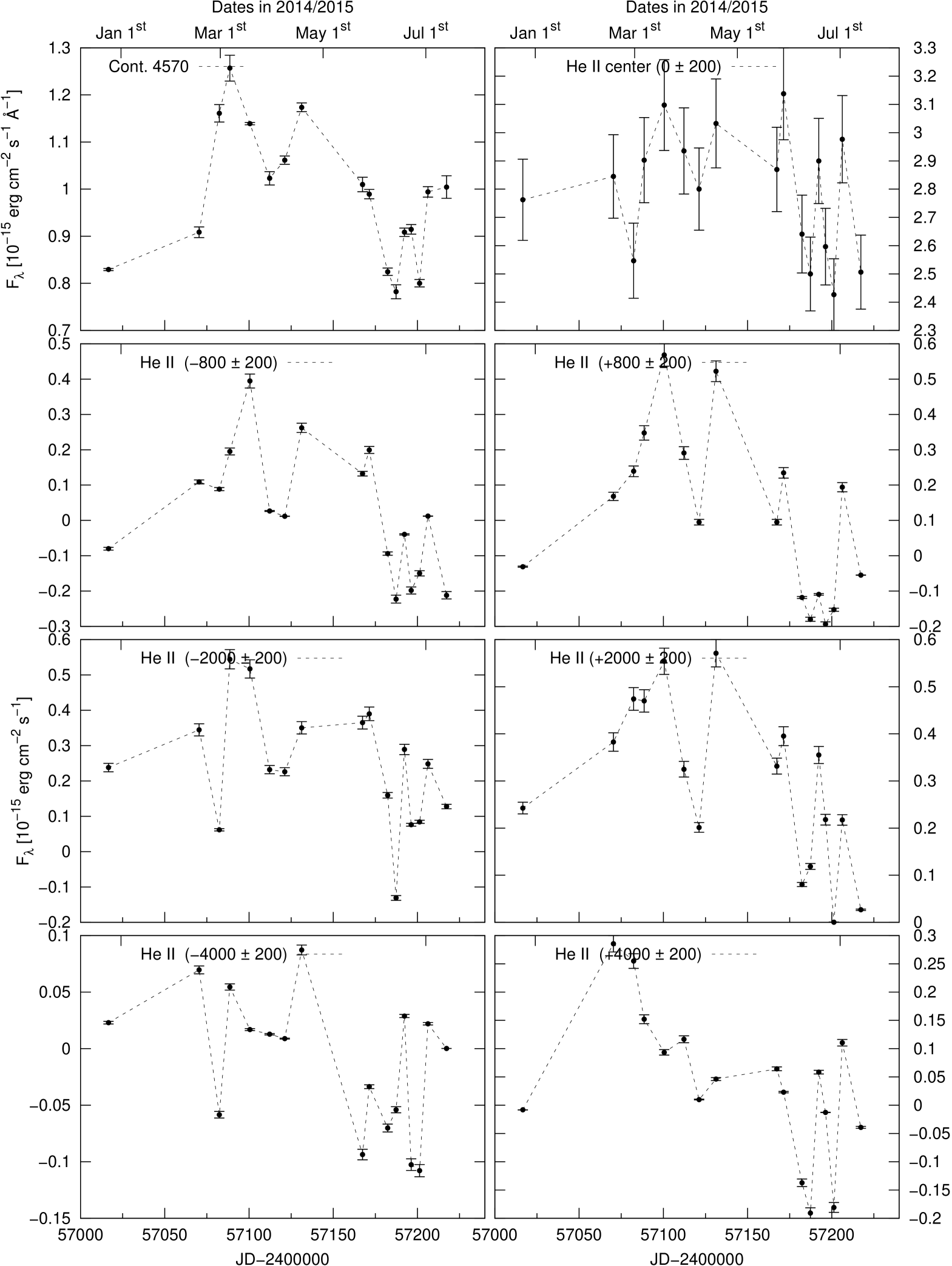
We present the light curves of the continuum fluxes at 4570 Å and 5360 Å as well as those of the integrated emission line fluxes of H, H, He ii , and He i in Fig. 3.
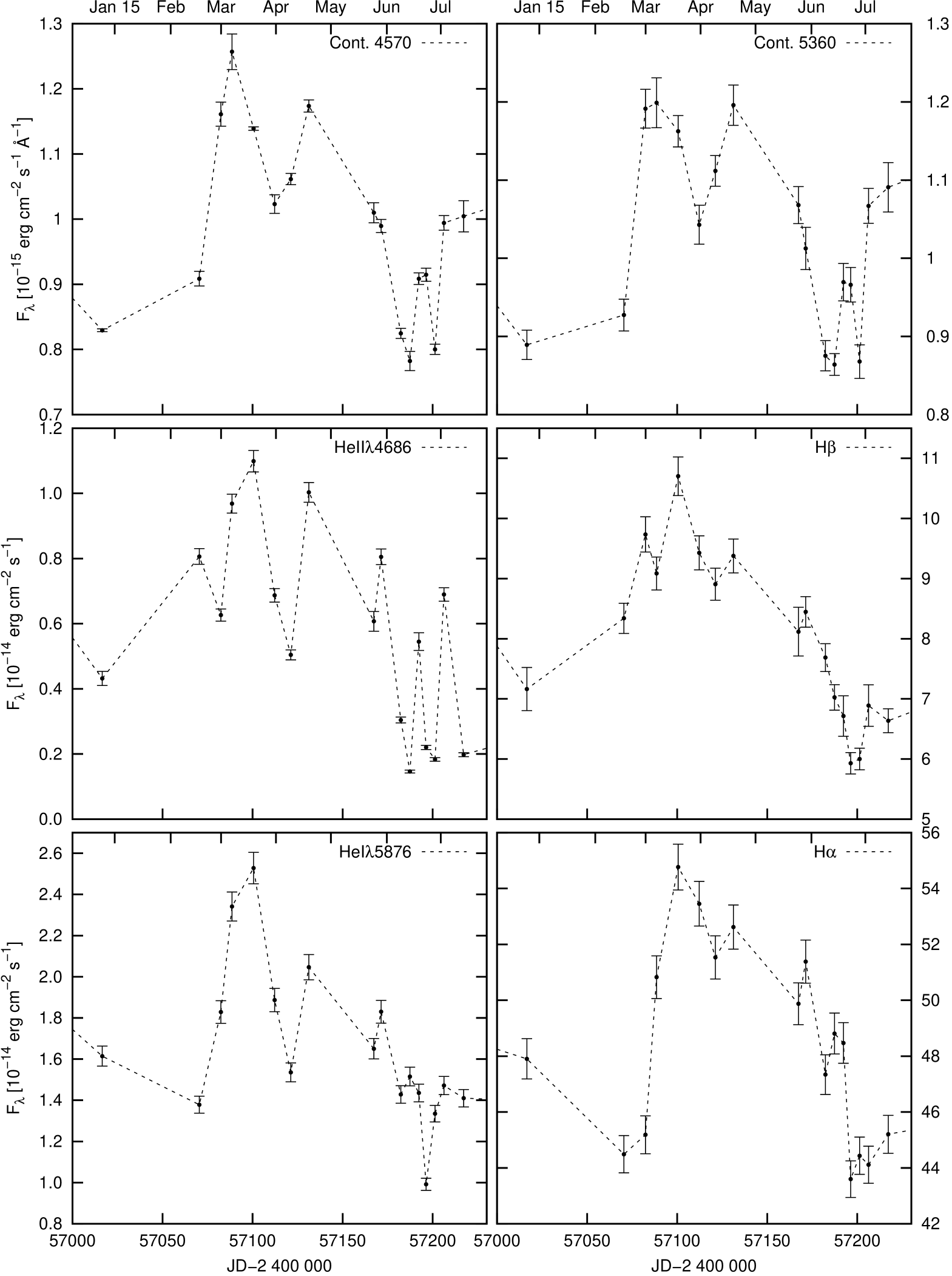
Some statistics of the emission line intensity and continuum variations are given in Tab. 4. We indicate the minimum and maximum fluxes F and F, peak-to-peak amplitudes R = F/F, the mean flux over the period of observations F, standard deviation , and fractional variation F (see Paper 1).
| Cont./Line | F | F | R | F | F | |
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| Cont. 4570 | 0.78 | 1.26 | 1.61 | 0.99 | 0.14 | 0.141 |
| Cont. 5360 | 0.86 | 1.20 | 1.39 | 1.03 | 0.12 | 0.114 |
| Cont. 6235 | 0.88 | 1.29 | 1.46 | 1.08 | 0.11 | 0.102 |
| Cont. 6835 | 0.89 | 1.26 | 1.41 | 1.08 | 0.11 | 0.103 |
| H | 436. | 547.7 | 1.26 | 484.7 | 35.81 | 0.072 |
| H | 59.3 | 107.0 | 1.80 | 80.1 | 14.00 | 0.171 |
| He i | 9.9 | 25.3 | 2.55 | 16.6 | 3.83 | 0.229 |
| He ii | 1.5 | 11.0 | 7.52 | 5.78 | 3.01 | 0.520 |
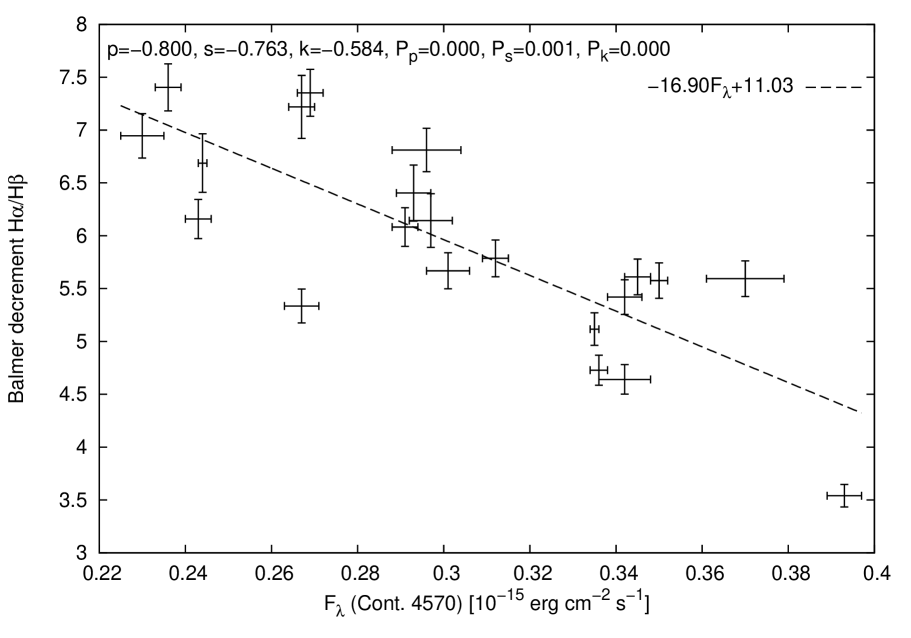
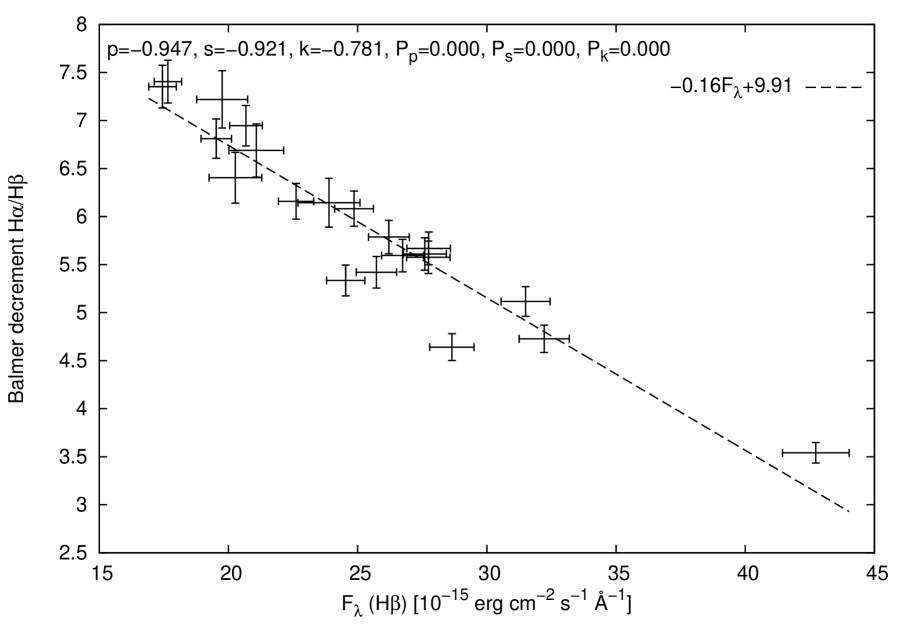
We calculated the Balmer decrement H/H of the broad components after subtraction of the narrow components for the individual epochs. The results are shown in Fig. 4 as a function of the continuum intensity at 4570 Å. Fig. 5 gives the Balmer decrement as a function of the H line intensity. The Balmer decrement H/H of the broad components takes values between 3.5 and 7.5. On the other hand, we measure a constant value of 2.81 for the Balmer decrement H/H of the narrow components. There is a clear trend that the Balmer decrement H/H of the broad component decreases with increasing luminosity.
3.2 Mean and rms line profiles
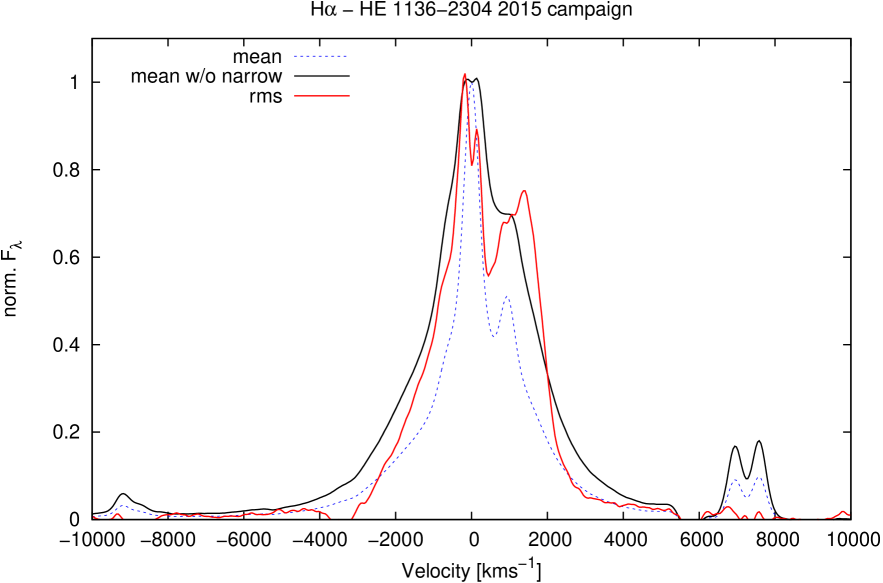
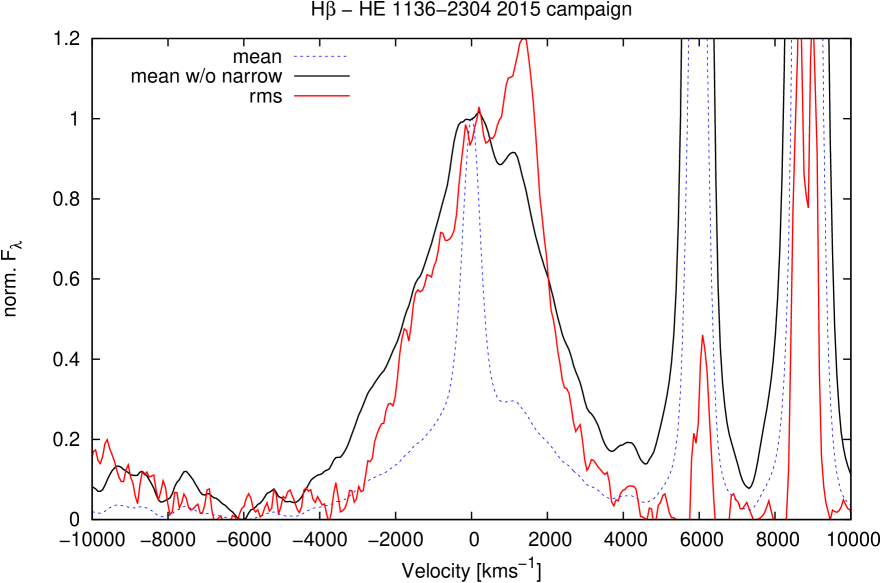
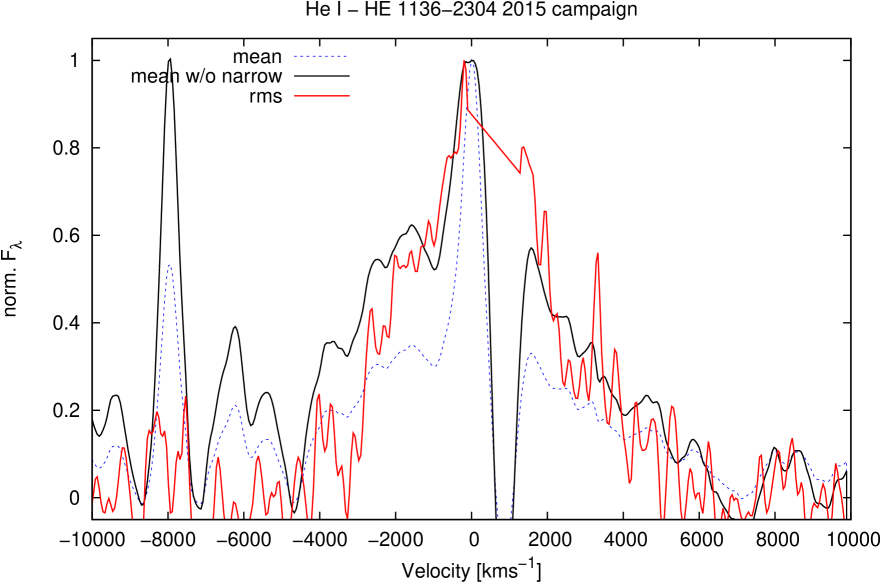
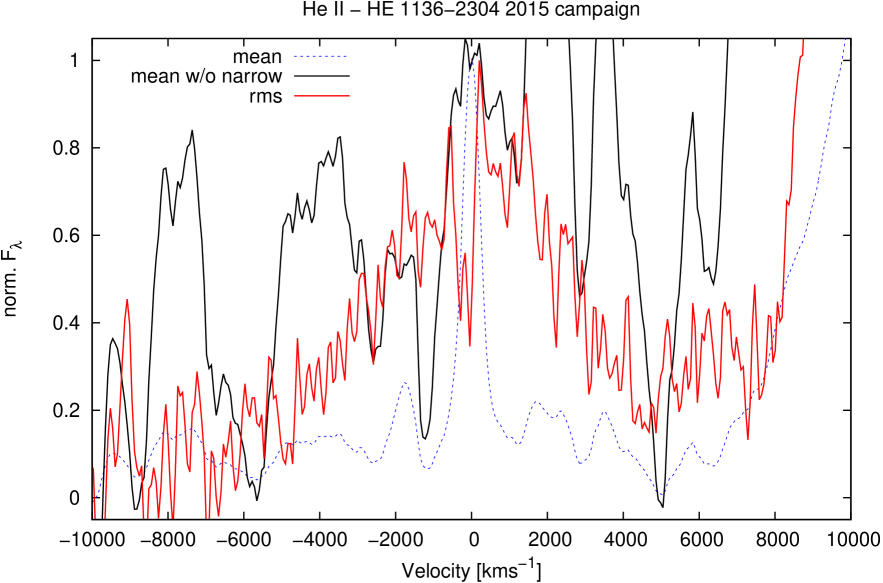
We determined normalized mean and rms profiles of the Balmer and Helium lines after subtracting the continuum fluxes in each individual spectrum using the continuum windows listed in Tab. 2. Figs. 7 to 14 show the mean and rms profiles of the Balmer lines H and H as well as those of the He lines He i and He ii in velocity space. The rms profiles illustrate the line profile variations during our campaign. The constant narrow components disappear almost completely in these rms profiles. However, the mean profiles contain strong narrow line components in addition to their broad line components. We subtracted the narrow Balmer and Helium line components in all the mean profiles by subtracting a scaled [O iii] 5007 line profile as a template. Furthermore, we subtracted the narrow [N ii] line in the mean H profile and removed the [Fe iii] line in the mean He ii profile as well. After subtracting these narrow components we compared the mean and rms profiles of the broad emission lines with each other in a more accurate way.
We present the normalized mean profiles (with and without narrow components) and rms profiles for all four Balmer and Helium emission lines in Figs. 7 to 9.
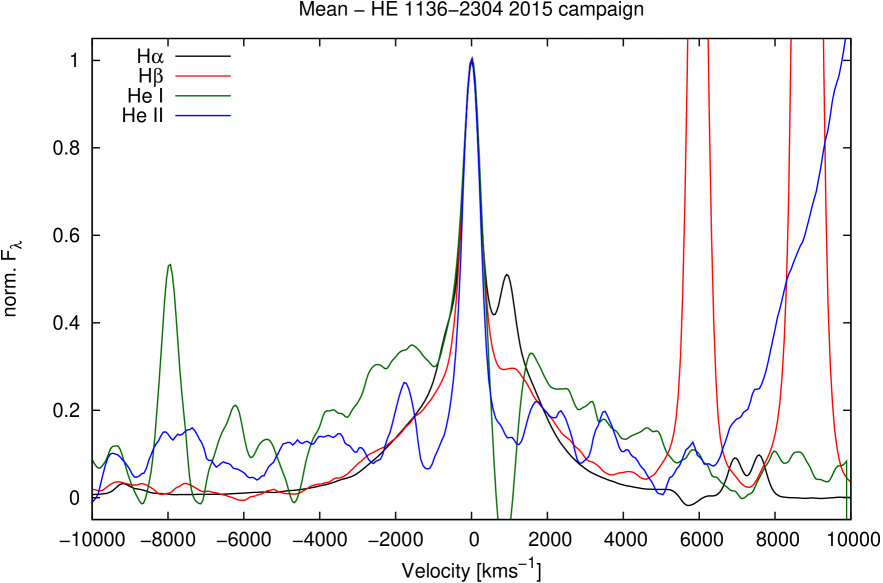
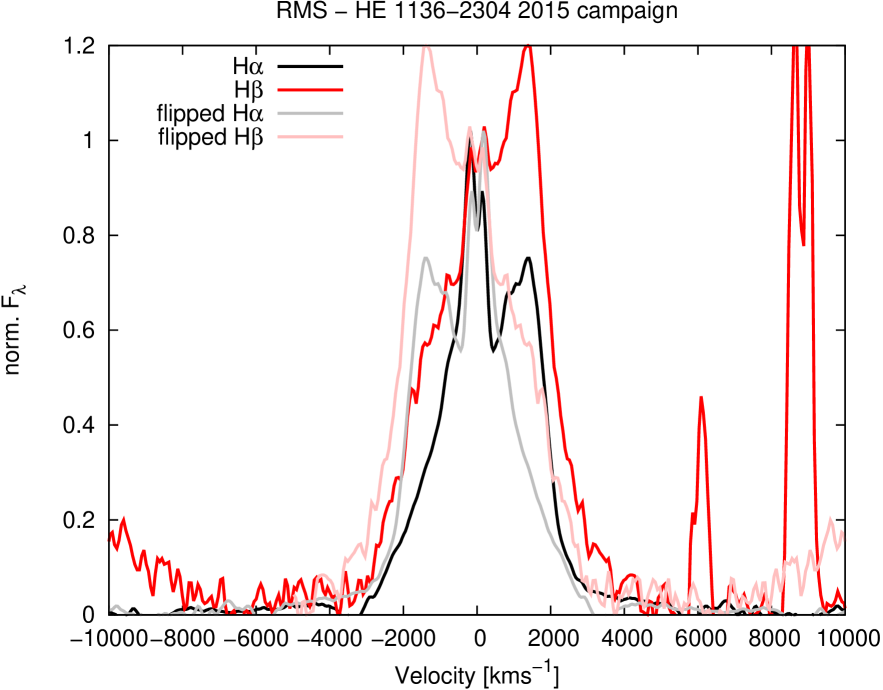
A comparison of all normalized mean profiles including their narrow components is shown in Fig.10. We then present a comparison of the mean profiles after subtracting the narrow components; this comparison is shown in Fig.11 for the mean profiles of H and H. For getting a hint on line asymmetries their flipped profiles at km s-1are depicted as well.
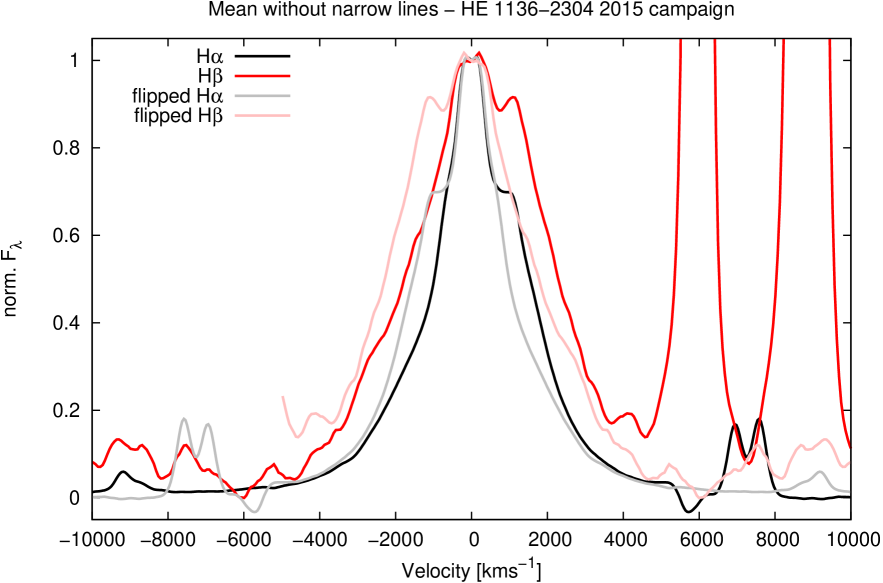
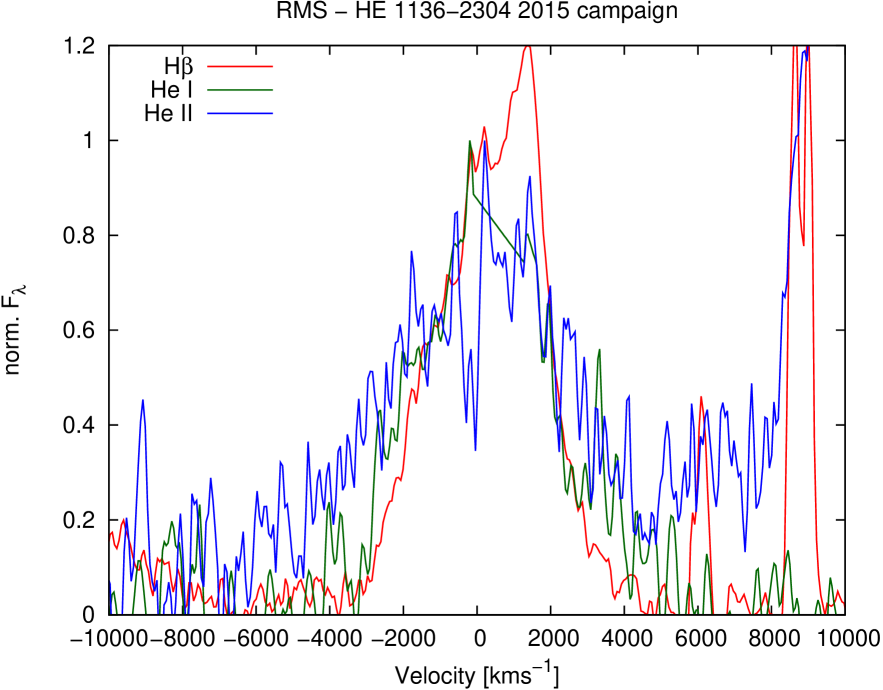
Fig.12 presents the mean Helium profiles after subtracting their narrow components. The profile of H has also been added for comparison purposes.
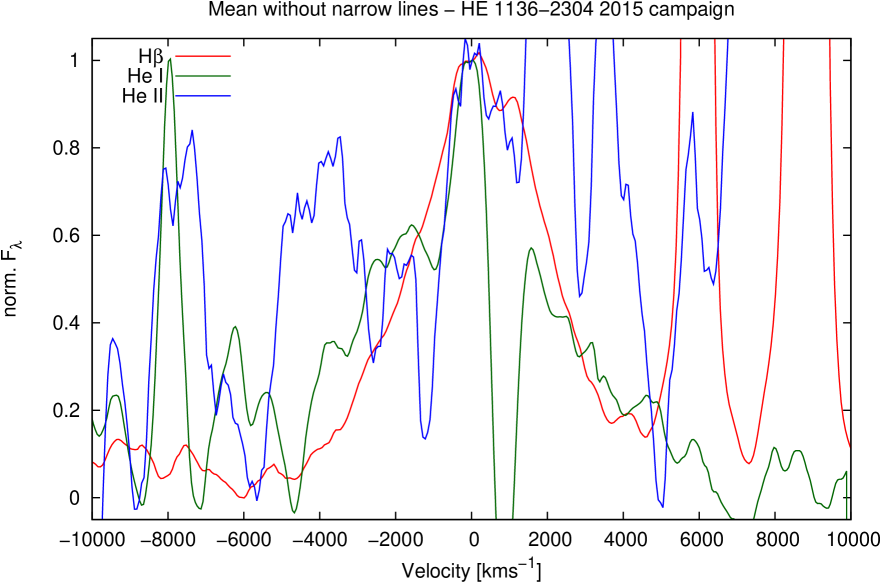
Fig.13 shows a comparison of the H and H rms line profiles normalized with respect to their central component. Again their flipped profiles at km s-1are depicted to highlight the additional strong red components and the weak blue component.
Finally, Fig.14 gives the rms profiles of the Helium lines. Again, the H line profile has been added for comparison.
We determined the linewidths (FWHM) of the mean and rms line profiles of all the Balmer and Helium lines. These measurements were performed with respect to the maximum of the central component and are listed in Tab. 5. In addition, we parameterized the linewidths of the rms profiles by their line dispersion (rms widths) (Fromerth & Melia2000; Peterson et al.2004).
| Line | FWHM (mean) | FWHM (rms) | (rms) |
|---|---|---|---|
| [km s-1] | [km s-1] | [km s-1] | |
| (1) | (2) | (3) | (4) |
| H | 2523 100 | 2668 150 | 1816 150 |
| H | 4063 100 | 3791 150 | 1767 150 |
| He i | 4557 400 | 4131 400 | 2098 400 |
| He ii | 5070 1000 | 5328 500 | 2962 500 |
The Balmer line profiles (mean and rms) exhibit linewidths (FWHM) between 2500 and 4000 km s-1. H shows the narrowest broad line profiles. The Helium lines (He i and He ii ) are always broader than the Balmer lines by 500 to 1500 km s-1. Furthermore, the outer blue wing is more extended in the higher ionized He lines in comparison to the Balmer lines (Figs.13, 14). This might be an indication of an additional outflowing component in the inner broad-line region (BLR).
An additional strong red component emerges in the rms and mean profiles of the H and H lines at 1380 km s-1and varies with a larger amplitude than the rest of the line profile. Furthermore, this component shows a relatively stronger variation in H in comparison with H (see Fig.13) by a factor of 1.5. An indication of the existence of this red component is present in the He ii line as well (Fig.14). No clear indication of this component is visible in the red wing of the He i line as that region coincides with the NaD absorption. An additional blue component, nearly symmetrical to the red component, appears in the rms profile of H at around -1400 km s-1. (Fig.13). However, this blue component is by far weaker than the red component. The existence of blue and red components in the line profiles – in addition to the central component – are an indication that the broad line-emitting region is connected with an accretion disk structure.
3.3 CCF analysis of the integrated broad emission lines
3.3.1 Based on SALT spectra
The mean distances of the broad emitting line regions to the central ionizing source can be determined by correlating the broad emission line light curves with the light curves of the ionizing continuum flux. Normally, an optical continuum light curve is used as a surrogate for the ionizing flux light curve. An interpolation cross-correlation function method (ICCF) has been developed by Gaskell & Peterson(1987) to calculate the delay of the individual line light curves with respect to the continuum light curve. We generated our own ICCF code (Dietrich & Kollatschny1995) based on similar assumptions in the past. For this study, we correlated the light curves of the integrated Balmer (H, H) and Helium lines (He i , He ii ) with the continuum light curve at 4570 Å using our method. The derived ICCF() are presented in Fig.15.
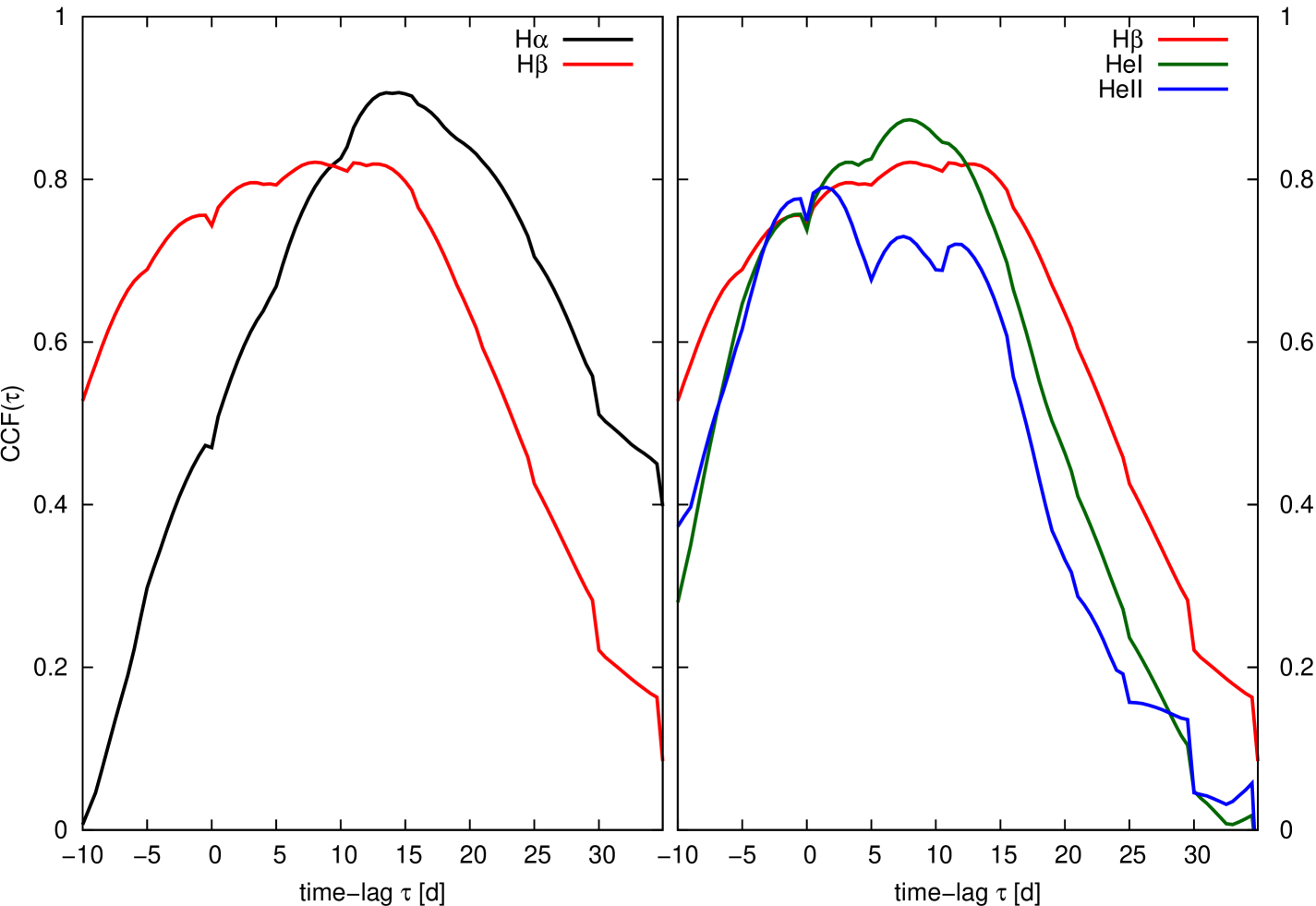
We determined the centroids of these ICCF, by using only those parts of the CCFs above 80% of the peak value . A threshold value of 0.8 is generally a good choice as had been shown by, for example, Peterson et al.2004. We derived the uncertainties in our cross-correlation results by calculating the cross-correlation lags a large number of times using a model-independent Monte Carlo method known as flux redistribution/random subset selection (FR/RSS). This method has been described by Peterson et al.(1998). Here the error intervals correspond to 68% confidence levels. The final results of the ICCF analysis are given in Tab. 6.
| Line | |
|---|---|
| [days] | |
| H | |
| H | |
| He i | |
| He ii |
The delay of the line-averaged BLR size of the integrated Balmer lines with respect to the continuum light curve at 4570 Å corresponds to and light days in the H and H lines, respectively. The He i shows a delay of days while the delay of the integrated He ii line corresponds to light days.
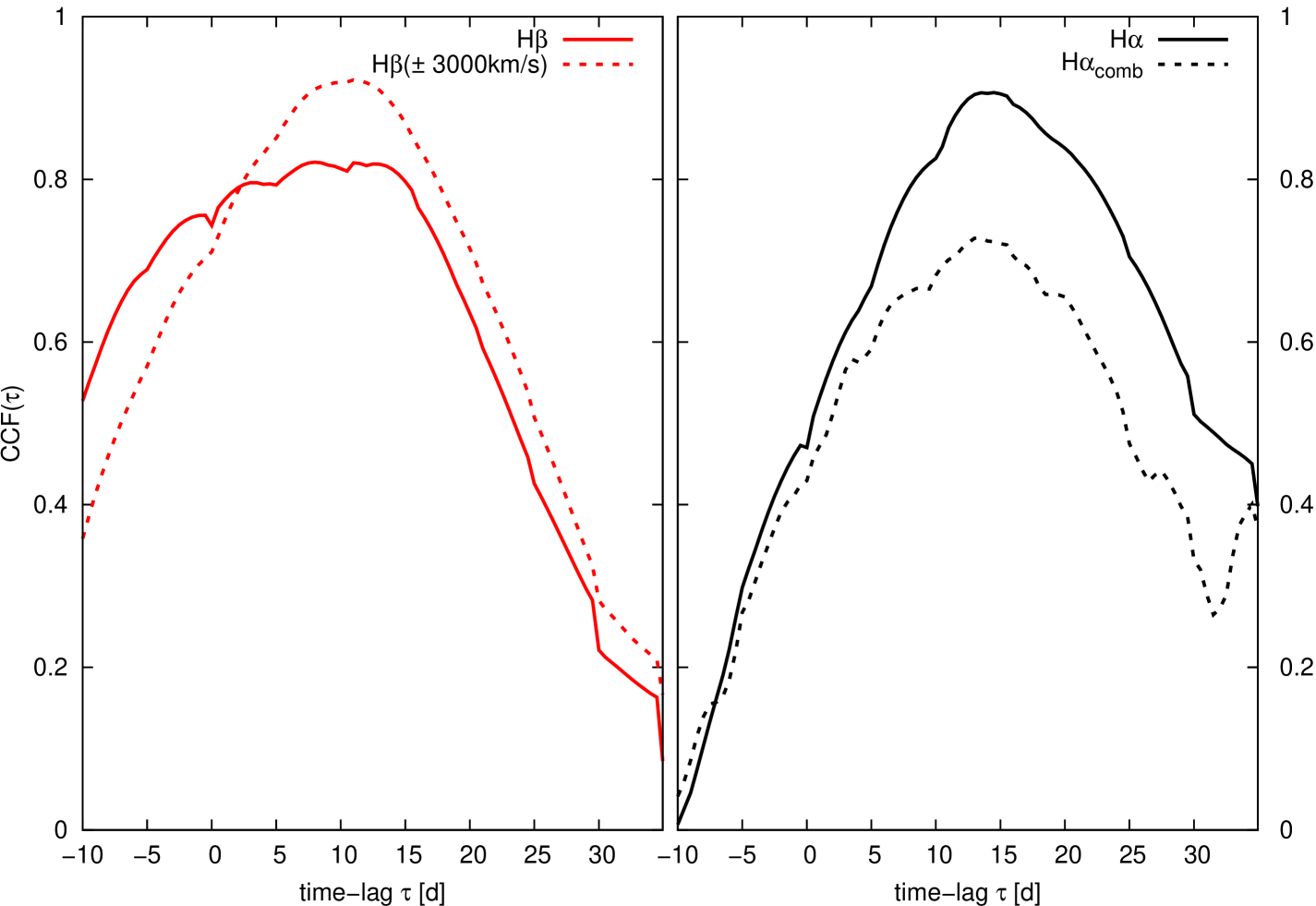
The CCF of H is very broad in comparison to H (see Fig.15). We discuss in section 3.5 how individual segments of the emission lines exhibit different delays with respect to the ionizing continuum. The line wings originate closer to the central ionizing zone while the central line regions originate at larger distances from the central ionizing zone. We carried out additional tests whether the integrated inner line profile segments (at 3000 km s-1) give similar or rather slightly larger CCF lags in comparison to the total line profiles. For H (at 3000 km s-1) we got a delay of ten light days (see Fig.16) in comparison to the delay of 7.5 light days for the integrated profile.
3.3.2 Based on photometric light curves in combination with SALT spectra
We published the continuum data of HE 1136-2304 taken by Swift in the B band and additional B-band observations taken with the MONET North and South telescopes and with the Bochum telescopes at Cerro Armazones in Zetzl et al.(2018). Subsequently, we generated a combined B-band light curve B in combination with our SALT spectral data. Furthermore, we created a combined H light curve H based on the SALT spectra and the narrowband NB670 light curve taken with the Bochum telescope. In a next step we carried out some tests to ascertain whether CCFs based on various combinations of the continuum light curves and based on combined H light curves produce similar results.
In Tab. 7 we present 1) the cross-correlation lags of the spectroscopically obtained H light curve correlated with the combined B-band light curve and 2) the combined H light curve correlated with the 4570 Å continuum light curve based on the SALT spectra. We also derived 3) the H lag from the Bochum light curves in the B and NB670 bands; the NB670 band entirely covers the broad H line. Because the narrowband filter contains the contribution from the AGN continuum underneath H in addition to H, we might expect two peaks in the cross correlation (see also Chelouche & Daniel 2012). To calculate the cross correlation we used the discrete correlation function (DCF; Edelson & Krolik 1988) with steps of days. In comparison to the spectroscopic SALT light curves, the number of data points in this case is sufficiently high to allow for such a DCF analysis, which in general yields better results in case of unevenly sampled data. This cross correlation indeed shows two clearly distinct peaks separated by a deep minimum in between (Fig. 17).
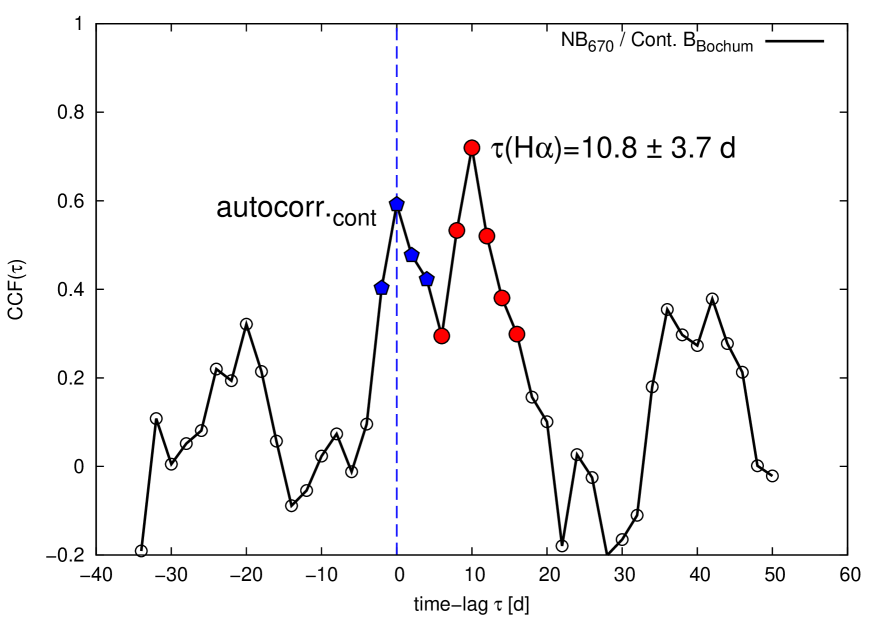
The peak at lag days (denoted with blue dots) comes from the cross correlation of the AGN continuum in the B band with the continuum underneath the H line; it is virtually an autocorrelation. The second even brighter peak at days (denoted with red dots) comes from the lag between the B-band continuum and H. The derived H lag (using the red data points) agrees within the errors with the H lags derived from the SALT spectra. Regarding the error limits, the derived H delays (11 up to 17 light days) are in good agreement with the delay of 15 light days based on the SALT spectra alone.
| Line | |
|---|---|
| [days] | |
| H / Cont. B | |
| H / Cont. 4570 Å | |
| NB670 / Cont. B |
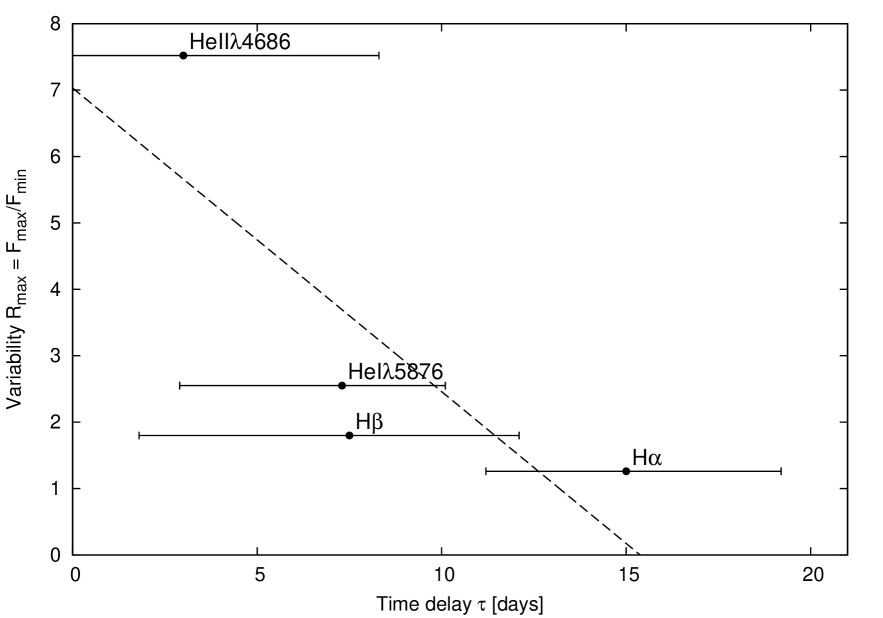
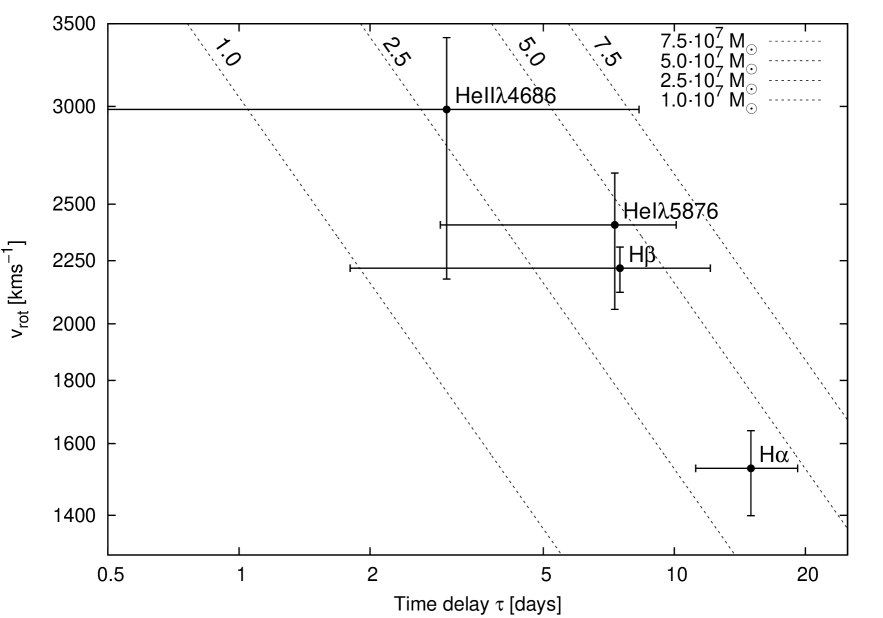
It has been demonstrated for other AGN (e.g., 3C120; Kollatschny et al.,2014) that the variability amplitude of the integrated emission lines is inversely correlated with the distance of the line-emitting regions to the central ionizing source. Fig.18 shows that this relation is valid for the broad lines in HE 1136-2304 as well. Furthermore, it has been shown that there is a radial stratification with respect to the BLR linewidths (FWHM; e.g., Kollatschny2003). The higher ionized lines show broader linewidths (FWHM) and originate closer to the center as shown in Fig.19. For this figure we used the corrected rotational velocities as presented in Tab. 9 (see section 3.6). For comparison with our measurements, in Fig. 19 we show the expected relations between distance and linewidth for multiple black hole masses based on the mass formula given in section 3.4.
3.4 Central black hole mass
The masses of the central black holes in AGN can be estimated from the width of the broad emission line profiles, based on the assumption that the gas dynamics are dominated by the central massive object, by evaluating . It is necessary to know the distance of the line-emitting region. Characteristic distances of the individual line-emitting regions are given by the centroid of the individual cross-correlation functions of the emission-line variations relative to the continuum variations (e.g., Koratkar & Gaskell1991; Kollatschny & Dietrich1997). The characteristic velocity of the emission-line regions can be estimated from the FWHM of the rms profiles or from the line dispersions .
The scaling factor in the equation above is on the order of unity and depends on the kinematics, structure, and orientation of the BLR. This scaling factor may differ from galaxy to galaxy, for example, depending on whether we see the central accretion disk including the BLR from the edge or face-on. We compared the central black hole mass value of HE 1136-2304 with values of the black hole masses derived for other AGN and adopt a mean value of (e.g., Onken et al.2004; Grier et al.2012). This f-value might be too high by a factor of two when comparing the black hole masses with inactive galaxies (Graham et al.2011). Nevertheless, using , we calculate a mean black hole mass (see Tab. 8, col. 3) of
based on the derived delays of the integrated Balmer and Helium lines (see Tab. 6) and on the line dispersions (see Tab. 5). All BH masses based on the individual lines agree with each other within the error limits.
| Line | M | M | M |
|---|---|---|---|
| [] | |||
| (1) | (2) | (3) | (4) |
| H | 3.8 1.2 | 5.3 1.7 | 11.5 3.5 |
| H | 4.0 3.0 | 2.5 2.0 | 11.6 8.8 |
| He i | 4.5 3.0 | 3.5 2.5 | 13.4 8.5 |
| He ii | 2.9 5.3 | 2.8 5.1 | 9.1 16.2 |
| mean | 3.8 3.1 | 3.5 2.8 | 11.4 9.2 |
Using the linewidths FWHM (rms) (see Tab. 5) we calculated a mean black hole mass of (Tab. 8, col. 4). However, in that case we did not correct for the contribution of turbulent motions to the width of the line profiles; this is covered in section 3.7. After correcting the emission linewidths (FWHM) for their contribution of turbulent motions (Tab. 9, col. 4), we derive a mean black hole mass of
(Tab. 8, col. 2). Again, all individual BH masses based on this method agree with each other within the error limits.
3.5 Two-dimensional CCFs of Balmer (H, H) and Helium I, II line profiles
We first calculated the cross-correlation lags of the integrated Balmer and helium lines with respect to the continuum as mentioned in section 3.3. Now we investigate the profile variations of these lines in more detail by calculating the lags of individual line segments. The way we proceed has been described before in our studies of line profile variations in Mrk 110 (Kollatschny & Bischoff2002; Kollatschny2003), Mrk 926 (Kollatschny & Zetzlkollatschny10 2010), and 3C120 (Kollatschny et al.2014).
We sliced the velocity profiles of the Balmer and Helium lines into velocity segments with a width of km s-1, which corresponds to the spectral resolution of our spectra. A central line segment was integrated in the velocity range -200 km s-1 200 km s-1. Afterward, we measured the intensities of all subsequent velocity segments from to km s-1and compiled their light curves. Light curves of the central Balmer and Helium line segments and selected blue and red segments at , , and km s-1 are shown in Figs. 30 to 33. For comparison, the light curve of the continuum flux at 4570 Å is given in all these figures as well. We computed the maximal correlation coefficient and time delay of all line segment ( km s-1) light curves of the Balmer and Helium lines with respect to the 4570 Å continuum flux light curve. The derived time delays of the segments are shown in Figs. 21 to 23 as functions of distance to the line center (blue scale). The white lines in Figs. 21 to 23 delineate the contour lines of the correlation coefficient at different levels. The green line shows the line profile of the mean spectrum for comparison.
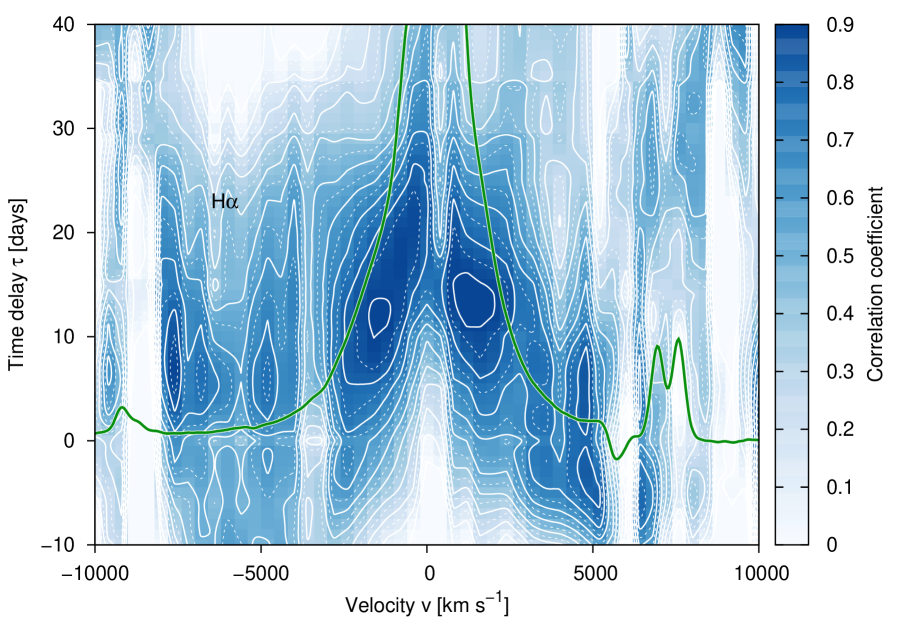
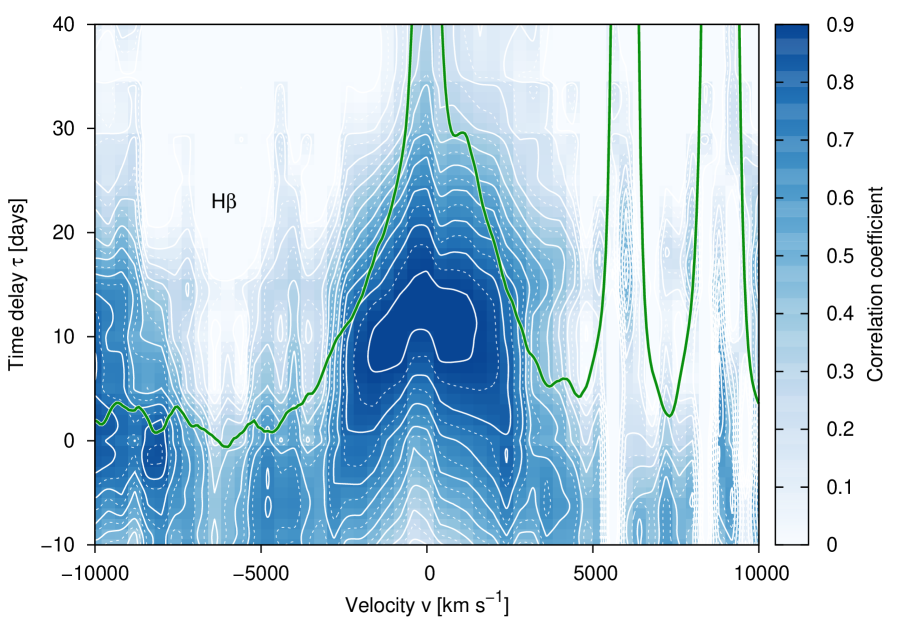
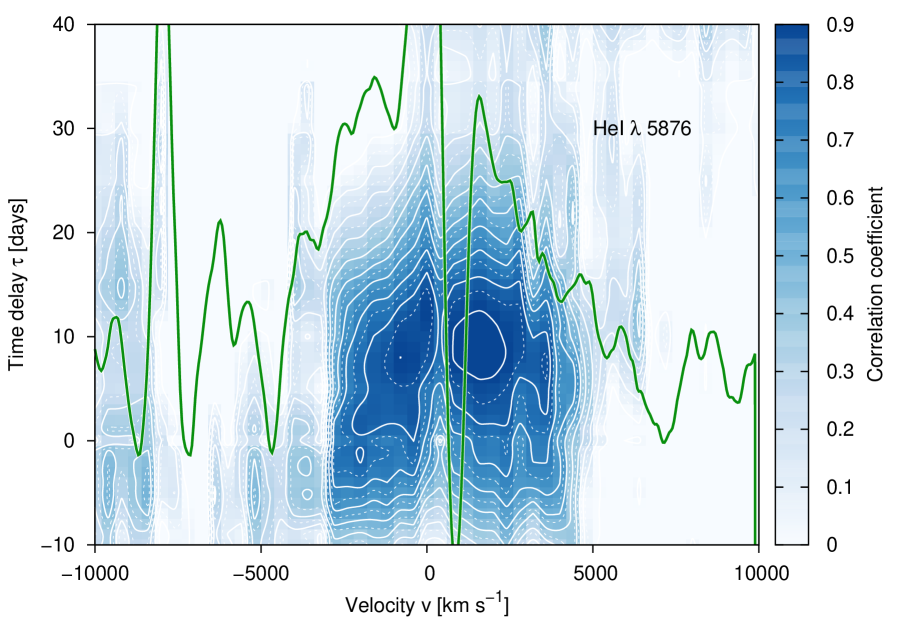
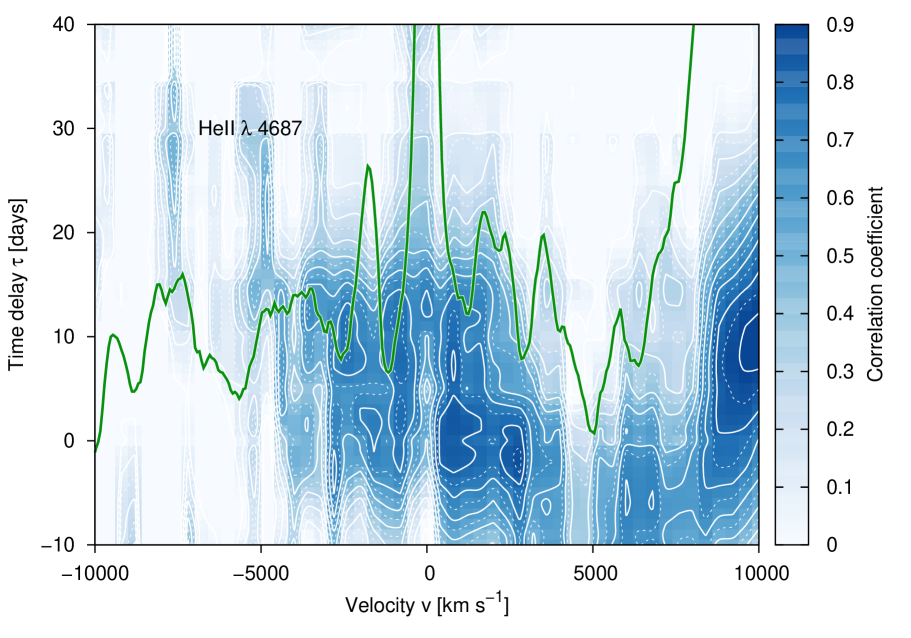
The following statements can be made based on these figures. There is a general trend that the Helium line response is faster than the response of the Balmer lines, as already known from the integrated lines. The velocity-delay maps are very symmetric with respect to the line center. The light curves of the emission line centers are delayed by 10 to 20 days with respect to the continuum variations, while the outer line wings at distances of 2000 to 3000 km s-1 respond much faster to continuum variations and only show a delay of 0 to 10 days. The delay in the outer line wings at distances of 4000 km s-1 is even negative with respect to the optical continuum. It has been discussed in Zetzl et al.(2018) that the observed optical continuum is delayed with respect to the ionizing continuum in the UV and X-ray bands. The outer blue wing of the H line shortward of km s-1) is blended with the red wing of the HeII4686 line (see Fig.2 as well).
3.6 Vertical BLR structure in HE 1136-2304
Information about the BLR structure in Seyfert 1 galaxies can be derived from the profiles of the broad emission lines together with variability studies (Kollatschny & Zetzlkollatschny11 2011, 2013a, 2013b, 2013c). The broad emission line profiles can be parameterized by the ratio of their full-width at half maximum (FWHM) to their line dispersion . We were able to show that there exists a general relation between the FWHM and the linewidth ratio FWHM/. The linewidth FWHM primarily reflects the line broadening of the intrinsic Lorentzian profiles due to rotational motions of the broad line gas. The intrinsic Lorentzian profiles themselves are associated with turbulent motion (see also Goad et al.goad12 2012) and different emission lines turn out to exhibit, on average, characteristic turbulent velocities within a narrow range (Kollatschny & Zetzlkollatschny11 2011).
We determined the rotational velocities and turbulent velocities that belong to the individual line-emitting regions in the same way as we have done it before for other Seyfert galaxies (Kollatschny & Zetzlkollatschny11 2011, 2013a, 2013b, 2013c): Based on the observed linewidths (FWHM) and linewidth ratios FWHM/ we determined the locations of the individual lines in Fig. 24.

In this figure, the grid, resulting from model calculations, presents theoretical linewidth ratios based on Lorentzian profiles that are broadened owing to rotation. We read the widths of the Lorentzian profiles and the rotational velocities of the individual lines from their positions between the contour lines of constant Lorentzian linewidth and the vertical contour lines representing different . The FWHM/ versus FWHM grid based on our model calculations is publicly available.222http://www.astro.physik.uni-goettingen.de/~zetzl/blrvelo/ The FWHM and FWHM/ values we obtained for HE 1136-2304 are given in Tab. 9 together with the derived and velocities of the Balmer and Helium lines. It has been shown that the region of each emission line has a characteristic mean turbulent velocity within a narrow range (Kollatschny & Zetzlkollatschny11 2011, 2013a; 2014). We derived the following mean turbulent velocities belonging to the emitting regions of the individual lines: 400 km s-1for H, 700 km s-1for H, 800 km s-1for He i , and 900 km s-1for He ii .
In the next step, we determine the heights of the line-emitting regions above the midplane as we have before for other Seyfert galaxies. The ratio of the turbulent velocity with respect to the rotational velocity in the line-emitting region gives us information on the ratio of the height with respect to the radius of the line-emitting regions as presented in Kollatschny & Zetzl kollatschny11 (2011, 2013a), i.e.,
| (1) |
The unknown viscosity parameter is assumed to be constant and to have values of 0.1 to 1 (e.g., Frank et al.2003). For simplicity we assume a value of 1 in the present investigation. The distance of the line-emitting regions of the individual lines is known from reverberation mapping (section 3.3). We present in Tab. 9 the derived heights above the midplane of the line-emitting regions in HE 1136-2304 (in units of light days) and the ratio for the individual emission lines.
| Line | FWHM | FWHM/ | Radius | Height | Height | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| [km s-1] | [km s-1] | [km s-1] | [ld] | [ld] | [ld] | [ld] | ||||
| H | 2668 | 0.47 | ||||||||
| H | 3791 | 0.23 | ||||||||
| He i | 4131 | 0.33 | ||||||||
| He ii | 5328 | 0.60 | ||||||||
The BLR structure of HE 1136-2304 is shown in Fig. 25 as a function of distance to the center and height above the midplane. The dot at radius zero gives the size of the Schwarzschild radius for a black hole mass (with ) multiplied by a factor of ten. The label on top of the figure gives the distances of the line-emitting regions in units of the Schwarzschild radius.
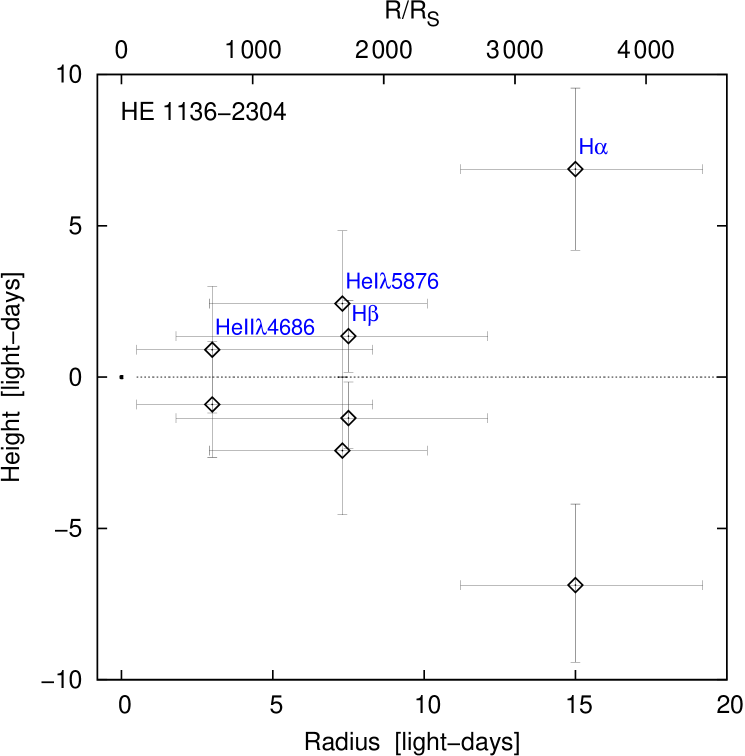
As has been observed previously in other galaxies, the He ii line originates at the shortest distance from the center and the smallest height above the midplane in comparison to the Balmer and HeI lines. In comparison to H, H originates at a larger distance from the midplane.
4 Discussion
4.1 Optical variability
We thoroughly investigated the spectroscopic variability behavior of HE 1136-2304 by taking 16 spectra over a period of six months between February to August 2015. The fractional variability F was on the order of 0.1 in the optical continuum without correcting for the host galaxy flux. After correcting for the host galaxy contribution, the fractional variability F of the continuum amounted to (see Paper I). The integrated Balmer and Helium lines showed F values of 0.1 to 0.5 and the higher ionized lines originating closer to the center varied with stronger amplitudes. These results describing the continuum and emission line variability are similar to those detected in other variable Seyfert galaxies such as NGC 5548 (Peterson et al.2004), Mrk 110 (Kollatschny et al.2001), or 3C 120 (Kollatschny et al.2014). This confirms that the variability behavior of this changing look AGN is similar to that of other Seyfert galaxies.
4.2 Balmer decrement variability
The Balmer decrement H/H of the narrow components has a value of 2.81. This corresponds exactly to the expected theoretical line ratio (Case B) without any reddening. However, the Balmer decrement H/H of the broad components varies with the continuum and/or Balmer line intensity. For example, the broad line Seyfert galaxy NGC 7693 showed the same behavior based on long-term variability studies over a period of 20 years (Kollatschny et al.2000): the Balmer decrement decreased with increasing H flux.
Heard & Gaskellheard16 (2016) proposed a model with additional dust reddening clouds interior to the narrow-line region causing higher Balmer decrements in the BLR. In contrast to this model, there might be important optical depth effects in the BLR itself explaining the observations. This is consistent with the finding that H originates at twice the distance of H. A similar radial stratification as seen in HE 1136-2304 has been observed in, for example, Arp 151 (Bentz et al.2010) as well. It has been discussed by Korista and Goad(2004) that the radial stratification is a result of optical-depth effects of the Balmer lines: the broad-line Balmer decrement decreases in high continuum states and steepens in low states exactly as observed in HE 1136-2304 (see Fig. 4). The continuum varied by a factor of nearly two during our campaign in 2015. However, we did not detect simultaneous variations of the Seyfert subtype during our observing period of seven months. A variation of Seyfert subtypes might be connected with stronger continuum amplitudes and/or longer timescales as has been seen before, for example, in Fairall 9 (Kollatschny et al.1985).
4.3 H lag versus optical continuum luminosity
Now we want to test whether HE 1136-2304 follows the general trend in the radius-luminosity relationship for AGN (Kaspi et al.2000; Bentz et al.2013). We determined a continuum luminosity of 42.6054 erg s-1 ( erg s-1 cm-2 Å-1) in the optical at 5100 Å after correction for the contribution of the host galaxy (Zetzl et al.2018). Furthermore, we derived a mean radius of 7.5 light days for the H line-emitting region based on the delay of the integrated H line variability curve with respect to the optical continuum light curve.
Fig. 26 shows the optical continuum luminosity and H-optical lags for HE 1136-2304 (red), for NGC 5548 based on different variability campaigns (black; Pei et al.2017 based on Kilerci-Eser et al.2015 and Denney et al.2009), and a sample of other AGN excluding NGC 5548 (green; Bentz et al.2013). The black line is the linear least-squares fit to the NGC 5548 data as presented by Pei et al.(2017). The (5100Å) relationship is given by
| (2) |
where K is the origin and is the slope. The red solid line gives the best-fit linear regression to the whole AGN sample. The data of HE 1136-2304 is in very good accordance with the general H lag versus the optical continuum luminosity relation.
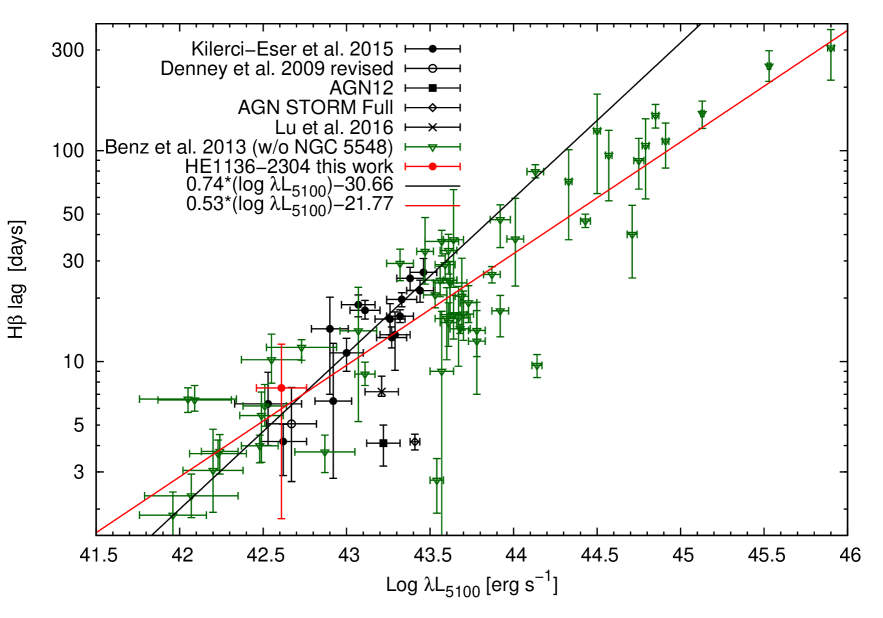
The red solid line has a slope of 0.53, which is therefore identical to the best-fit slope of of Bentz et al.(2013). This value is very close to the value of 0.5 expected from simple photoionization arguments, i.e.,
| (3) |
(e.g., Kaspi et al.2000; Bentz et al.2013 and references therein).
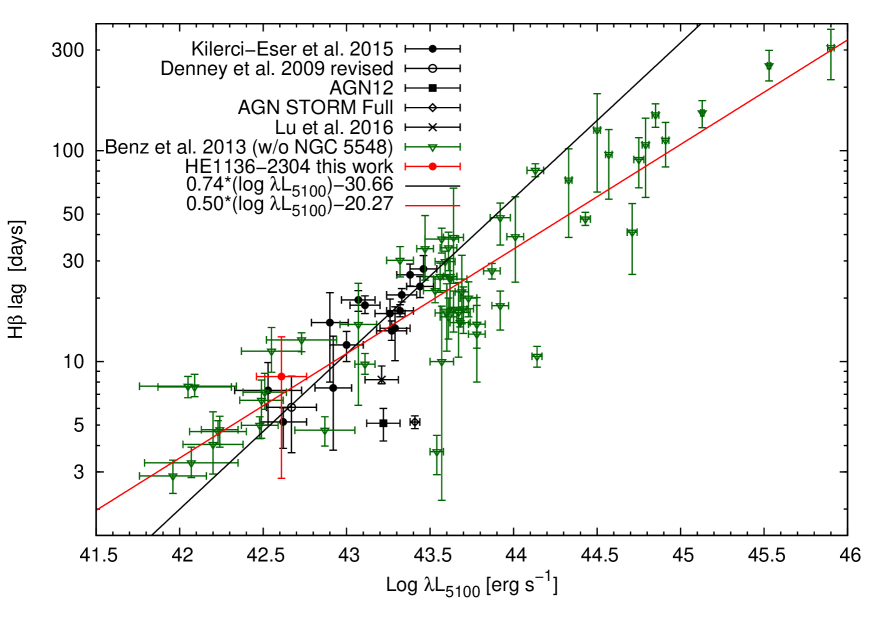
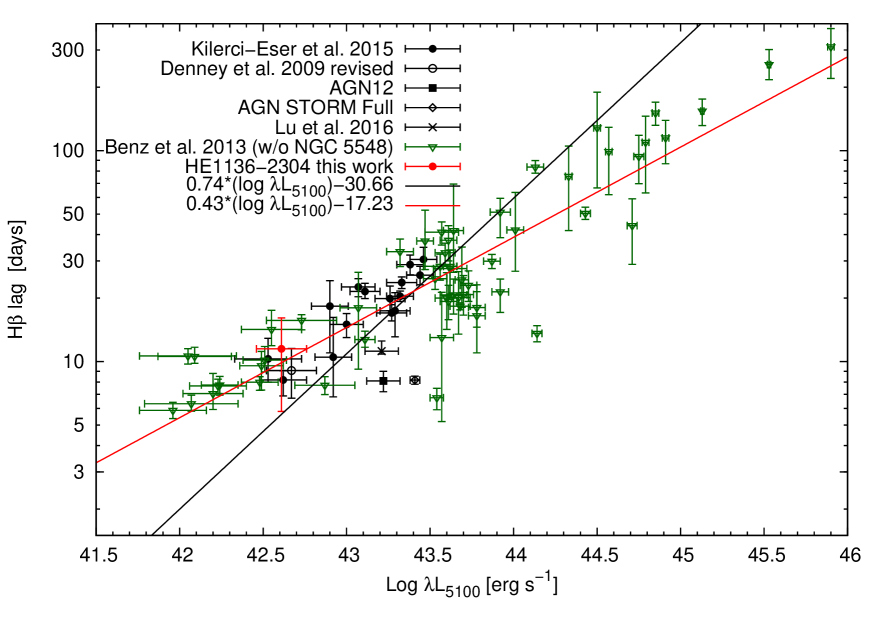
We tested whether the slope approaches values even closer to 0.5 or whether the Pearson correlation coefficient becomes higher if we add a few light days to the H radius. Such an additional delay might be caused by the fact that the optical continuum is generally delayed by a few light days with respect to the driving X-ray light curve (Zetzl et al.2018, Shappee et al.2014; Fausnaugh et al.2016).
We added additional lags of one to eight light days to all H-optical lags to take into account a systematic delay of the optical bands with respect to the driving X-ray flux. A time delay of eight light days is an upper limit based on the correlation of the optical band light curves with respect to the XRT light curve (Zetzl et al.2018). Figs. 27 and 28 show the H lag versus optical continuum luminosity diagrams with an additional lag of one and four days, respectively, taking into account the optical-X-ray lag.
| Offset delay | Pearson CC | |
| [days] | ||
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
Tab. 10 gives the Pearson correlation coefficient
for the relation between
optical continuum luminosities and H-optical lags. The H lags
have been modified assuming additional lags (in units of days)
for the optical lag with respect to the driving X-ray source.
Furthermore, we present the values for the additional
delays that have been assumed.
We get the highest correlation coefficient for an additional delay
of four days. We reached a slope of exactly 0.5 for an additional
delay of one day.
4.4 Structure and kinematics in the BLR
4.4.1 Mean and rms line profiles
The mean and rms line profiles of the broad emission lines give us information about the kinematics and structure of the line-emitting BLR region. Differences in the broad-line widths of the rms and mean profiles (see Figs. 7 to 8) might be caused by a radial stratification of optical depth effects in these lines (Korista and Goad2004). Especially the rms profiles of the Balmer lines in HE 1136-2304 show an asymmetric triple structure. Aside from a central component there were additional blue and red components at 1 400 km s-1 (see Fig. 13). These components are barely visible in the mean profiles. The additional component in the red wing is by far stronger than that in the blue wing. An additional weak blue component, which is nearly symmetrical to the red component, is apparent in the rms profile of H (Fig. 13). Furthermore, this red rms component varies relatively stronger in the H line than in H. The additional blue and red components in the line profiles – in addition to the central component – are an indication that the line-emitting region is connected to the accretion disk. Such double-peaked profiles are considered to be ubiquitous signatures of accretion disks (e.g., Eracleous & Halpern2003; Gezari et al.2007; Shapovalovashapovalova13 2013; Storchi-Bergmann et al.2017, and references therein). In some cases these double-peaked profiles become only visible in the rms line profiles as in NGC4593, for example (Kollatschny & Dietrich1997). The variable Seyfert galaxy Akn 120 is another example of a very strong red component showing up in the H wing within one year (Kollatschny et al.1981).
Similar to the line profiles in NGC4593 (Kollatschny & Dietrich1997), the rms line profiles of H and H in HE 1136-2304 show a steeper red wing and a flatter outer blue wing indicating an additional outflow component (see Fig. 13). The outer blue wing is even more pronounced in the higher ionized Helium lines in comparison to the Balmer lines (see Fig. 14), indicating a stronger outflow in the inner BLR.
4.4.2 Velocity delay maps
The 2D-CCFs or velocity-delay maps shown in Figs. 21 to 23 contain additional information about the structure and kinematics of the BLR. We compare the derived velocity delay maps of HE 1136-2304 with theoretical models for the structure and kinematics of the BLR (Welsh et al.1991; Horne et al.2004; Goad et al.goad12 2012; Grier et al.2013) and with velocity delay maps of other AGN. All the velocity delay maps are very symmetric with respect to their line centers at km s-1. The delays in the wings are by far shorter than in the line center. Such behavior is typical for thin Keplerian disk BLR models (Welsh et al.1991; Horne et al.2004; Grier et al.2013). There is an indication in the velocity delay maps of the Balmer lines that the response in the red wing (at v = 3000 to 5000 km s-1) is slightly stronger and that it shows a shorter delay than in the blue wing. This might be caused by an additional inflow component (Welsh et al.1991), by hydro-magnetically driven wind (Horne et al.2004), or by an additional turbulent component (Goad et al.goad12 2012).
The velocity delay maps of other Seyfert galaxies in general show two different trends: a more symmetrical velocity delay map that is typical for Keplerian disks or a velocity delay map showing a strong red component caused by strong inflow or hydro-magnetically driven wind, and a combination of both. NGC 4593 (Kollatschny et al.1997), 3C 120 (Kollatschny et al.2014), Mrk 50 (Barth et al.2011), and NGC 5548 (Pei et al.2017 and references therein) show a more symmetrical velocity delay map. NGC 3516 (Denney et al.2010), Mrk1501, PG 2130+099 (Grier et al.2013) and Mrk 335 (Du et al.2016) show a dominant red component. Velocity delay maps of other galaxies indicate a combination of dominant Keplerian motion and an additional red component, such as Mrk 110 (Kollatschny et al.2001) and Arp 151 (Bentz et al.2010). However, there are three exceptions (Mrk 817, NGC 3227, and Mrk 142) in which only a strong blue component is present in the velocity delay maps (Denney et al.2010; Du et al.2016). The velocity delay map of the changing look AGN HE 1136-2304 is similar to that of most other AGN. It shows a dominant Keplerian motion component with a slightly more intense red component.
4.5 Vertical BLR structure in a sample of AGN
The higher ionized broad emission lines originate at smaller radii as shown in section 3.3. Furthermore, the integrated H originates at a distance of 15 light days and therefore at twice the distance of H (see Tab. 6). Moreover, it has been shown that the higher ionized lines originate closer to the midplane of the accretion disk in comparison to the lower ionized lines. We presented the BLR structure as a function of distance to the center and height above the midplane (Fig. 25). The He ii line originates closest to the midplane. H originates at a larger distance from the midplane in comparison to H. Such a trend has been observed before in other galaxies as NGC 7469 (Kollatschny & Zetzlkollatschny13c 2013c) and 3C 120 (Kollatschny et al.2014).
A second trend has been found when comparing the H distances above the midplane for different active galaxies: galaxies showing the broadest H linewidths originate closest to the midplane, while galaxies showing the narrowest H linewidths originate at the largest distance to the midplane (Kollatschny et al.2014). The linewidths (with respect to the individual lines) are therefore a characteristic for the height of the line-emitting regions above the midplane. We present the height-to-radius ratio and FWHM of H for a sample of AGN (Kollatschny et al.2014) and for HE 1136-2304 in Tab. 11.
| Campaign | FWHM | |
|---|---|---|
| [km s-1] | ||
| NGC 7469 | ||
| 3C 120 p04 | ||
| 3C 120 g12 | ||
| 3C 120 k14 | ||
| NGC 3783 | ||
| HE 1136-2304 | ||
| NGC 5548 T1 | ||
| NGC 5548 T2 | ||
| NGC 5548 H | ||
| … | ||
| … | ||
| … | ||
| … | ||
| … | ||
| … | ||
| … | ||
| … | ||
| … | ||
| … | ||
| … | ||
| … | ||
| 3C 390.3 | ||
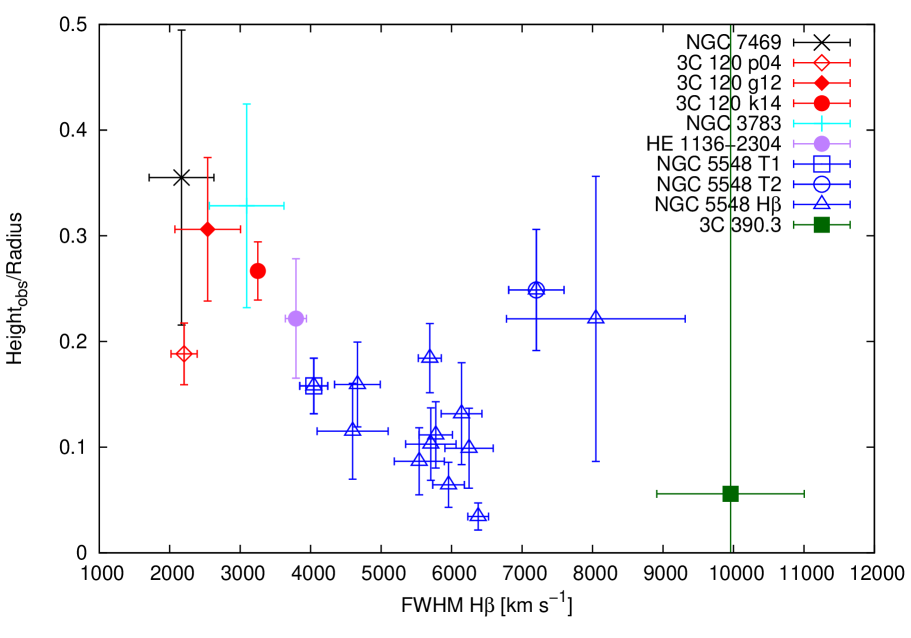
The height-to-radius ratio for H is largest for galaxies showing narrow emission lines and smallest for galaxies with broad lines. The overall picture we derived for the BLR region structure previously in Kollatschny & Zetzlkollatschny13c (2013c) and Kollatschny et al.2014 is confirmed by the additional emission line data of HE 1136-2304. The derived height-to-radius ratio for HE 1136-2304 confirms the general trend (see Fig. 29). Again, the HE 1136-2304 data support the picture that the broad emission line geometries of AGN are not simply scaled-up versions depending only on the central luminosity (and central black hole mass).
5 Summary
We present results of a spectral monitoring campaign of the changing look AGN HE 1136-2304 obtained by the 10 m SALT telescope between 2014 December and 2015 July. These observations were taken subsequently to a continuum outburst detected in the X-rays and in the optical in 2014 July. Our findings can be summarized as follows:
-
(1)
The BLR in HE 1136-2304 is stratified with respect to the distance of the individual line-emitting regions. The integrated emission line intensities of H, H, He i , and He ii originate at distances of , , , and light days with respect to the optical continuum at 4570 Å. The variability amplitudes of the integrated emission lines are a function of distance to the ionizing source as well.
-
(2)
We derived a central black hole mass of based on the linewidths, corrected for the turbulent component, and distances of the line-emitting regions.
-
(3)
Based on velocity delay maps, the light curves of the emission line centers are delayed by 10 to 20 days with respect to the continuum variations. The outer line wings of the emission lines respond much faster to the continuum variations in all lines indicating an Keplerian disk component for the broad line-emitting region. The response in the outer wings is even shorter than the response of the adjacent optical continuum flux with respect to the ionizing continuum flux by about two light days.
-
(4)
The vertical BLR structure in HE 1136-2304 confirms the general trend that line emitting regions in AGN showing narrower emission lines originate at larger distances from the midplane in comparison to AGN showing broader emission lines.
-
(5)
In general, the variability behavior of the changing look AGN HE 1136-2304 is similar to that of other AGN.
Acknowledgements.
This work has been supported by the DFG grants Ko 857/33-1 and Ha3555/12-2.References
- (1) Barth, A. J., Pancoast, A., Thorman, S. J., et al. 2011, ApJL, 743, L4
- (2) Bentz, M. C., Horne, K., Barth, A. J., et al. 2010, ApJ, 720, L46
- (3) Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149
- (4) Chelouche, D., & Daniel, E. 2012, ApJ, 747, 62
- (5) Collin-Souffrin, S., Alloin, D., & Andrillat, Y. 1973, A&A, 22, 343
- (6) Dietrich, M., & Kollatschny, W. 1995, A&A, 303, 405
- (7) Denney, K. D., Peterson, B. M., Pogge, R. W., et al. 2009, ApJL, 704, L80
- (8) Denney, K. D., Peterson, B. M., Pogge, R. W., et al. 2010, ApJ, 721, 715
- (9) Denney, K. D., De Rosa, G., Croxall, K., et al. 2014, ApJ, 796, 134
- (10) Du, P., Lu, K. X., Hu, C., et al. 2016, ApJ, 820, 27
- (11) Edelson, R., & Krolik, J. 1988, ApJ, 333, 646
- (12) Edelson, R., Gelbord, J. M., Horne, K., et al. 2015, ApJ, 806, 129
- (13) Eracleous, M., & Halpern, J. 2003, ApJ, 599, 886
- (14) Fausnaugh, M. M., Denney, K. D., Barth, A. J., et al. 2016, ApJ, 821, 56
- (15) Frank, J., King, A., & Raine, D. 2003, Accretion Power in Astrophysics, Cambridge University Press
- (16) Fromerth, M. J., & Melia, F. 2000, ApJ, 533, 172
- (17) Gaskell, C. M. 2009, NewAR, 53, 114
- (18) Gaskell, C. M., & Peterson, B. M. 1987, ApJS 65, 1
- (19) Gezari, S., Halpern, J. P., & Eracleous, M. 2007, ApJS 169, 167
- (20) Goad, M. R., Korista, K. T., & Ruff, A. J. 2012, MNRAS, 426, 3086
- (21) Graham, A. W., Onken, C. A., Athanassoula, E., & Combes, F. 2011, MNRAS 412, 2211
- (22) Grier, C. J., Peterson, B. M., Pogge, R. W., et al. 2012, ApJ 755, 60
- (23) Grier, C. J., Peterson, B. M., Horne, K., et al. 2013, ApJ 764, 47
- (24) Heard, C. Z., & Gaskell, C. M. 2016, MNRAS, 461, 4227
- (25) Horne, K., Peterson, B. M. , Collier, S. J., & Netzer, H. 2004, PASP 116,465
- (26) Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ 533, 631
- (27) Kilerci Eser, E., Vestergaard, M., Peterson, B. M., Denney, K. D., & Bentz, M. C. 2015, ApJ 801, 8
- (28) Kollatschny, W. 2003, A&A, 407, 461
- (29) Kollatschny, W., Bischoff, K., & Dietrich, M. 2000, A&A, 361, 901
- (30) Kollatschny, W., Bischoff, K., Robinson, E. L., Welsh, W. F., & Hill, G. J. 2001, A&A, 379, 125
- (31) Kollatschny, W., & Bischoff, K. 2002, A&A, 386, L19
- (32) Kollatschny, W., & Dietrich, M. 1996, A&A, 314, 43
- (33) Kollatschny, W., & Dietrich, M. 1997, A&A, 323, 5
- (34) Kollatschny, W., Fricke, K. J., Schleicher, H., & Yorke, H. W. 1981, A&A, 102, L23
- (35) Kollatschny, W., & Fricke, K. J., 1985, A&A, 146, L11
- (36) Kollatschny, W., Ulbrich, K., Zetzl, M., Kaspi, S., & Haas, M. 2014, A&A, 566, A106
- (37) Kollatschny, W., & Zetzl, M. 2010, A&A, 522, 36
- (38) Kollatschny, W., & Zetzl, M. 2011, Nature, 470, 366
- (39) Kollatschny, W., & Zetzl, M. 2013a, A&A, 549, A100
- (40) Kollatschny, W., & Zetzl, M. 2013b, A&A Letters, 551, L6
- (41) Kollatschny, W., & Zetzl, M. 2013c, A&A, 558, A26
- (42) Komossa S., Zhou H., Wang T., et al. 2008, ApJ, 678, L13
- (43) Koratkar, A. P., & Gaskell, M. 1991, ApJ 370, L61
- (44) Korista, K. T.,& Goad, M. R. 2004, ApJ 606, 749
- (45) LaMassa, S. M., Cales, S., Moran, E. C., et al. 2015, ApJ, 800, 144
- (46) MacLeod, C. L., Ross, N. P., Lawrence, A., et al. 2016, MNRAS, 457, 389
- (47) Onken, C. A., Ferrarese, L., Merritt, D., et al. 2004, ApJ, 615, 645
- (48) Osterbrock, D. E. 1981, ApJ, 249, 462
- (49) Parker, M. L., Komossa, S., Kollatschny, W., et al. 2016, MNRAS, 461, 1927
- (50) Pei, L., Fausnaugh, M. M., Barth, A. J., et al. 2017, ApJ, 837, 131
- (51) Penston, M. V., & Perez, E. 1984, MNRAS, 211, 33
- (52) Peterson, B. M., Berlind, P., Bertram, R., et al. 2002, ApJ, 581, 197
- (53) Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682
- (54) Peterson, B. M., Wanders, I., Bertram, R., et al. 1998, ApJ, 501, 82
- (55) Runnoe, J. C., Cales, S., Ruan, J. J., et al. 2016 2016, MNRAS, 455, 1691
- (56) Shapovalova, A. I., Popović, L. Ć., Burenkov, A. N., et al. 2010, A&A, 517, 42
- (57) Shapovalova, A. I., Popović, L. Ć., Burenkov, A. N., et al. 2013, A&A, 559, A10
- (58) Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48
- (59) Storchi-Bergmann, T., Nemmen da Silva, R., Eracleous, M., et al. 2003, ApJ, 598, 956
- (60) Storchi-Bergmann, T., Schimoia, J. S., Peterson, B. M., et al. 2017, ApJ, 835, 236
- (61) Reimers, D., Koehler, T., & Wisotzki, L. 1996, A&AS, 115, 235
- (62) Welsh, W. F., & Horne, K. 1991, ApJ, 379, 586
- (63) Wright, E. L., 2006, PASP, 118, 1711
- (64) Zetzl, M., Kollatschny, W., Ochmann, M. W., et al. 2018, A&A, 618, A83 (Paper 1)
Appendix A Additional figures