Fermilab Lattice and MILC Collaborations
form factors for new-physics searches from lattice QCD
Abstract
The rare decay arises from flavor-changing neutral currents and could be sensitive to physics beyond the Standard Model. Here, we present the first ab-initio QCD calculation of the tensor form factor . Together with the vector and scalar form factors and from our companion work [J. A. Bailey et al., Phys. Rev. D 92, 014024 (2015)], these parameterize the hadronic contribution to semileptonic decays in any extension of the Standard Model. We obtain the total branching ratio in the Standard Model, which is the most precise theoretical determination to date, and agrees with the recent measurement from the LHCb experiment [R. Aaij et al., JHEP 1212, 125 (2012)]. Note added: after this paper was submitted for publication, LHCb announced a new measurement of the differential decay rate for this process [T. Tekampe, talk at DPF 2015], which we now compare to the shape and normalization of the Standard-Model prediction.
pacs:
13.20.He, 12.38.Gc, 12.15.MmMotivation — Hadron decays that proceed through flavor-changing neutral currents may be sensitive to new physics, because their leading Standard-Model contributions are loop suppressed. Here we study the semileptonic decay , which proceeds through a transition. Hadronic effects in this decay are parametrized by three form factors. In this Letter, we present the first ab-initio QCD calculation of the tensor form factor , based on lattice-QCD work that also yielded the vector and scalar form factors, and Bailey et al. (2015a). Lattice QCD has several advantages over other approaches to the form factors Ball and Zwicky (2005); Wang et al. (2008); Duplančić et al. (2008); Wu and Huang (2009); Faustov and Galkin (2014); Ali et al. (2014); Li et al. (2014); Hambrock et al. (2015), particularly in providing a path to controlled uncertainties that can be systematically reduced Kronfeld (2012).
The LHCb experiment recently made the first observation of Aaij et al. (2012), while the -factories have set limits on the and channels Wei et al. (2008); Lees et al. (2013); Lutz et al. (2013). Below we present the first calculations of () observables in the Standard Model using form factors with fully controlled uncertainties.
The form factors , , and suffice to parameterize decays in all extensions of the Standard Model. New physics from heavy particles—such as those appearing in models with supersymmetry Bobeth et al. (2001); Demir et al. (2002); Choudhury and Gaur (2002); Wang et al. (2008), a fourth generation Hou et al. (2013), or extended Aliev and Savci (1999); Iltan (1999); Bobeth et al. (2001); Erkol and Turan (2002); Erkol et al. (2005); Song et al. (2008) or composite Gripaios et al. (2015) Higgs sectors—alter Wilson coefficients in the effective Hamiltonian pertaining to particle physics below the electroweak scale Grinstein et al. (1989); Buras et al. (1994); Huber et al. (2006); Altmannshofer et al. (2009). Whatever these unknown particles may be, the hadronic physics remains the same.
Lattice-QCD calculation — Our work on was carried out in parallel with and . Our aim in Ref. Bailey et al. (2015a) was a precise determination of the Cabibbo-Kobayashi-Maskawa (CKM) element , and every step of the analysis was subjected to many tests. Further, two of the authors applied a multiplicative offset to the numerical data at an early stage. This “blinding” factor was disclosed to the others only after finalizing the error analysis. Full details of the simulation parameters, analysis, and cross-checks are given in Ref. Bailey et al. (2015a).
Our calculation uses ensembles of lattice gauge-field configurations Aubin et al. (2015a); *asqtad:en06b; *asqtad:en05a; *asqtad:en05b; *asqtad:en04a; *asqtad:en15a; *asqtad:en15b; *asqtad:en14a; *asqtad:en13a; *asqtad:en13b; *asqtad:en12a; *asqtad:en23a; *asqtad:en23b; *asqtad:en20a; *asqtad:en20b; *asqtad:en19a; *asqtad:en18a; *asqtad:en18b; *asqtad:en24a from the MILC Collaboration Bernard et al. (2001); Aubin et al. (2004); Bazavov et al. (2010), which are generated with a realistic sea of up, down, and strange quarks. In practice, the up and down sea quarks have the same mass, and the strange-quark mass is tuned close to its physical value. The statistics are high, with 600–2200 gauge-field configurations per ensemble. The physical volume is large enough that we can repeat the calculation in different parts of the lattice, thereby quadrupling the statistics. We use four lattice spacings ranging from 0.12 fm to 0.045 fm to control the extrapolation to zero lattice spacing.
The tensor form factor is defined via the matrix element of the tensor current :
| (1) |
where and are the particles’ momenta and is the momentum carried off by the leptons. The Lorentz invariant is related to the pion energy in the -meson rest frame via . In the finite volume that can be simulated on a computer, takes discrete values, dictated by the spatial momenta compatible with periodic boundary conditions. Because statistical and discretization errors increase with pion momentum, we restrict . The resulting simulation range of GeV is significantly smaller than the kinematically allowed range of GeV. Extending this discrete set of calculations into the full dependence is the central challenge of this work, and is met in two steps.
The two light quarks (up and down) have a mass larger than it should be, but the range simulated is wide and the smallest pion mass is 175 MeV, close to Nature’s 140 MeV. Therefore, we can apply an effective field theory of pions—chiral perturbation theory—to extrapolate the simulation data to the physical point. We use a form of chiral perturbation theory adapted to lattice QCD, with additional terms describing the lattice-spacing dependence Aubin and Bernard (2007); Bailey et al. (2015b) and with modifications needed for energetic final-state pions Bijnens and Jemos (2010). As discussed in Ref. Bailey et al. (2015a), we try several fit variations. For example, we replace the loop integrals with momentum sums appropriate to the finite volume, finding negligible changes in the results. Our final fit includes next-to-next-to-next-to-leading order analytic terms and terms to model the discretization errors of the heavy quark. The latter come from an effective field theory for heavy quarks Kronfeld (2000); Harada et al. (2002); Oktay and Kronfeld (2008).
Figure 1 shows the dependence of the errors after the chiral-continuum extrapolation just described.
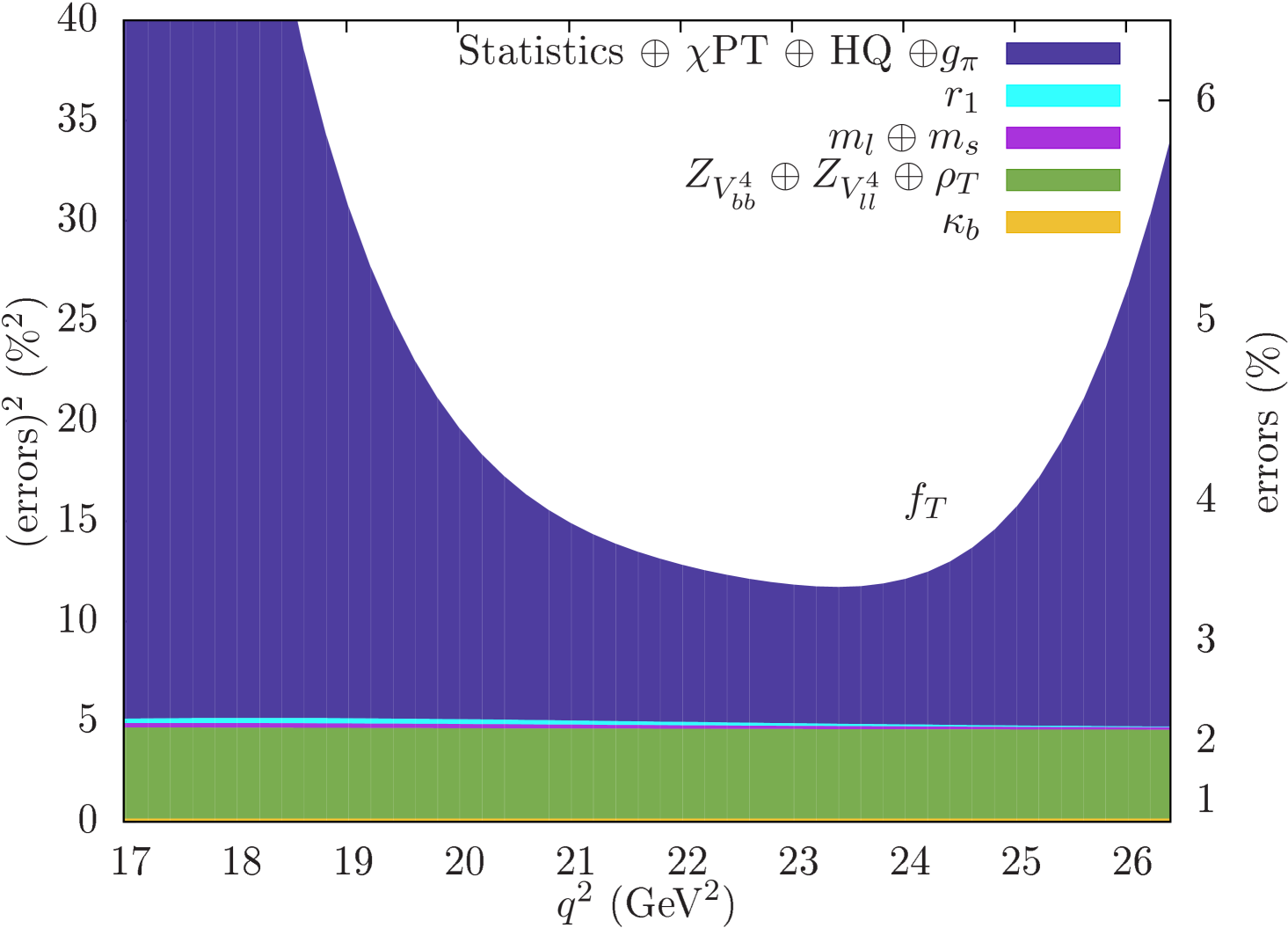
Table 1 gives a numerical error budget for .
| Source of error | dependence | |
|---|---|---|
| Statistics PT HQ | 3.8 | important |
| Scale | 0.5 | negligible |
| Nonperturbative matching | 0.7 | negligible |
| Perturbative matching | 2.0 | none |
| Heavy-quark mass tuning | 0.4 | none |
| Light-quark mass tuning | 0.5 | negligible |
| Total (Quadrature sum of above) | 4.4 | important |
The largest uncertainty comes from the statistical errors, as increased during the chiral-continuum extrapolation. This error is under good control for corresponding to the spatial momenta that we simulate, but grows large elsewhere.
The subdominant errors are as follows. To convert from lattice units to physical units, we introduce a physical distance , which is defined via the force between static quarks Bernard et al. (2000); Sommer (1994). We use it to form physical, dimensionless quantities, which are the input data for the chiral-continuum fit. At the end, we set fm Bazavov et al. (2012) based on a related lattice-QCD calculation of Bazavov et al. (2009) and the pion decay constant MeV Olive et al. (2014). To propagate the parametric uncertainty in to , we repeat the fit shifting by , leading to the second line in Table 1.
In lattice gauge theory, the tensor current does not have the normalization used in QCD phenomenology. We obtain most of the normalization nonperturbatively El-Khadra et al. (2001) from and transitions with the vector current, with statistical errors below 1%. Another matching factor remains, but, by design and in practice, it is close to unity. We calculate at the renormalization scale through first order in the QCD coupling . We estimate the resulting error of order after removing a logarithmic dependence on the matching scale , which is present in continuum QCD too. We then examine how the one-loop coefficient depends on heavy-quark mass, identifying the largest value, . Finally, we estimate the error in to be , evaluating on the second-finest lattice with fm. This yields the 2% perturbative-matching uncertainty in Table 1.
The last two uncertainties arise as follows. When generating data, we choose the simulation quark masses based on short runs and previous experience. The full analysis yields better estimates. To correct the simulation -quark mass a posteriori, we recompute on one ensemble with two additional values of the bare -quark mass. Using the slope from all three mass values, we interpolate the data for slightly from the production -quark mass to the physical value. This leaves an error due to the uncertainty in the size of the -quark mass correction. The details for are nearly identical to those for Bailey et al. (2015a), leading to the same estimate, 0.4%, for this error. The light-quark mass dependence is embedded in the chiral-continuum extrapolation, described above. The parametric uncertainty from the input light-quark mass Bazavov et al. (2010) is propagated to by repeating the fit with shifts to these parameters, and is given in the penultimate line of Table 1.
The final line in Table 1 and the upper edge of the stack in Fig. 1 represent the quadrature sum of the systematic uncertainties with the chiral-continuum fit error.
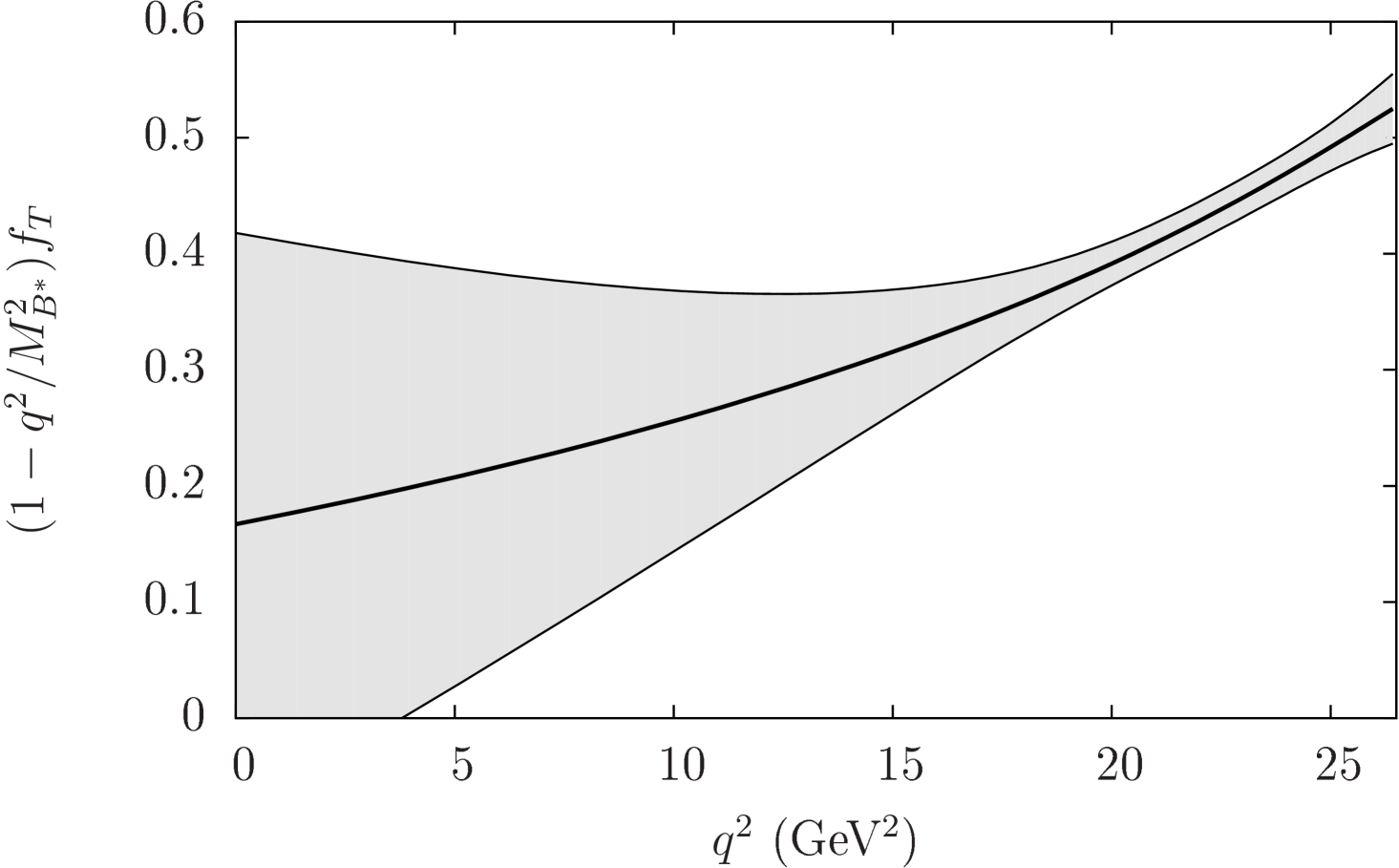
Extension to all — To extend in the chiral-continuum limit from the range of simulated lattice momenta to the full kinematic range, , with controlled errors, we use a method based on the analytic structure of the form factor.
In the complex plane, has a cut for timelike and a pole at but is analytic elsewhere. The variable
| (2) |
maps the whole plane into the unit disk, with the cut mapped to the boundary and the semileptonic region mapped to an interval on the real axis. Unitarity bounds then guarantee that an expansion of in (with the pole removed) converges for Bourrely et al. (1981); Boyd et al. (1995); Lellouch (1996); Boyd and Savage (1997). Following Bourrely, Caprini, and Lellouch (BCL) Bourrely et al. (2009), we factor out the pole and expand in :
| (3) |
choosing to minimize in the semileptonic region. Although Eq. (3) was derived for the vector form factor , we use it for the tensor form factor because the two form factors are proportional to each other at leading order in the expansion.
We determine the with a functional method connecting the independent functions of the chiral-continuum fit with the first several powers of Bailey et al. (2015a). Our preferred fit uses ; adding higher-order terms in does not significantly change the central value. Table 2 presents our final result for as coefficients of the BCL fit and the correlation matrix between them, where the errors include statistical and all systematic uncertainties.
| Fit: | 0.393(17) | 0.1(2.8) | ||
|---|---|---|---|---|
| 1.000 | 0.400 | 0.204 | 0.166 | |
| 1.000 | 0.862 | 0.806 | ||
| 1.000 | 0.989 | |||
| 1.000 | ||||
| 0.638 | 0.321 | 0.123 | 0.084 | |
| 0.321 | 0.397 | 0.162 | 0.109 | |
| 0.114 | 0.202 | 0.198 | 0.179 | |
| 0.070 | 0.152 | 0.192 | 0.180 | |
| 0.331 | 0.136 | 0.089 | 0.073 | |
| 0.203 | 0.313 | 0.198 | 0.162 | |
| 0.204 | 0.268 | 0.186 | 0.155 | |
| 0.151 | 0.203 | 0.169 | 0.149 |
This information can be used to reconstruct over the full kinematic range. Table 2 also provides the (mostly statistical) correlations between , , and . Figure 2 shows the extrapolation of to .
Implications — The largest contribution in the Standard Model to the amplitude for is proportional to the vector form factor. Assuming that new physics does not contribute significantly to the tree-level decay , one can use experimental measurements of this process to constrain the shape of , especially at low . In Ref. Bailey et al. (2015a), we obtain the CKM element from a combined fit to our lattice-QCD results for and and measurements of from BaBar del Amo Sanchez et al. (2011); Lees et al. (2012) and Belle Ha et al. (2011); Sibidanov et al. (2013). This joint fit also yields the most precise current determinations of and . To enable them to be combined with the results for from Table 2, Table 3 provides the correlations between the -expansion coefficients for all three form factors.
| 0.514 | 0.140 | 0.078 | 0.065 | |
| 0.111 | 0.221 | 0.010 | 0.049 | |
| 0.271 | 0.232 | 0.012 | 0.029 | |
| 0.204 | 0.215 | 0.013 | 0.023 | |
| 0.243 | 0.015 | 0.025 | 0.024 | |
| 0.005 | 0.134 | 0.070 | 0.057 | |
| 0.002 | 0.034 | 0.032 | 0.030 | |
| 0.044 | 0.061 | 0.005 | 0.017 |
The correlations are small, because contains independent experimental information.
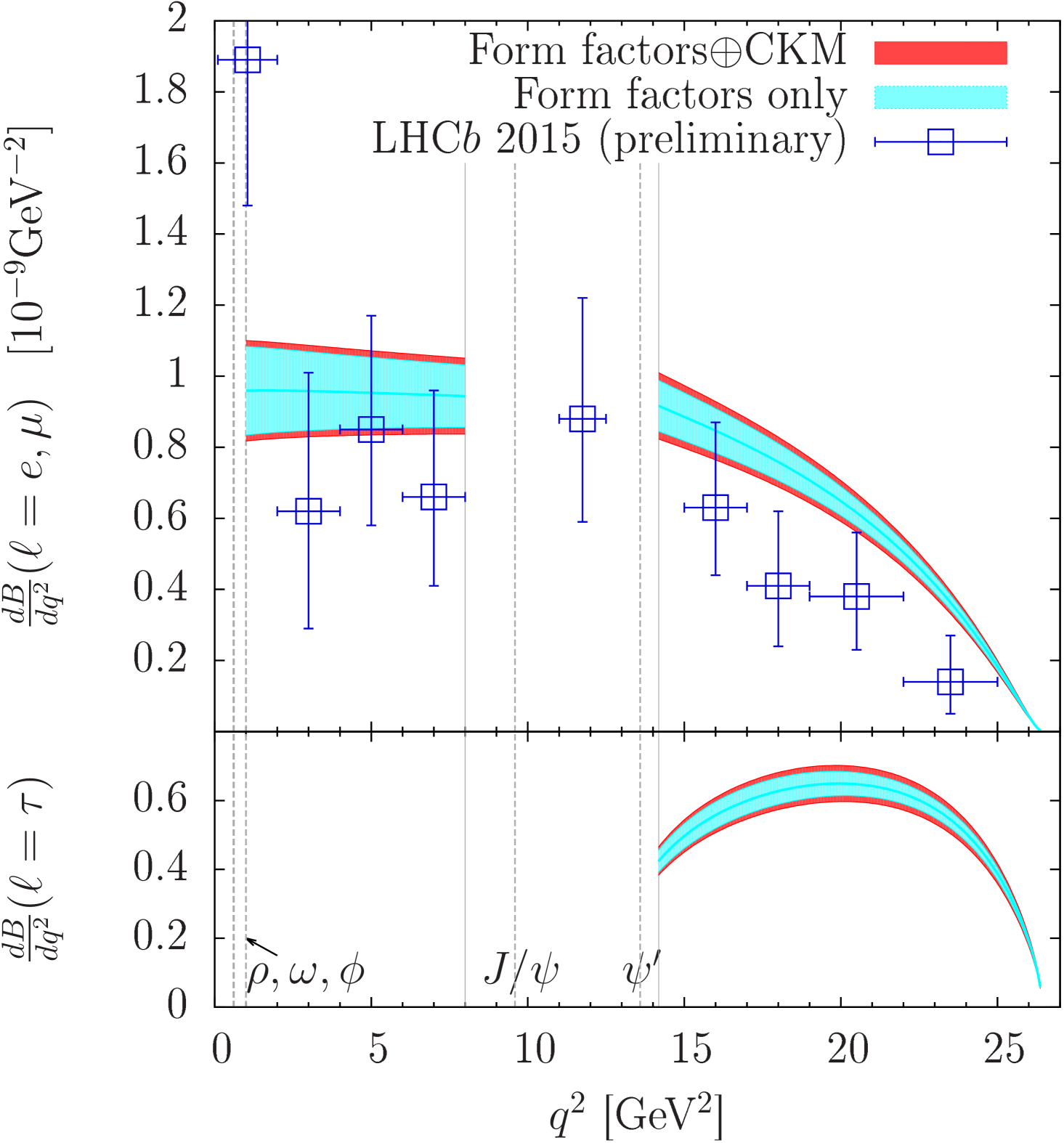
Using from this work and and just described, we show the Standard-Model partial branching fractions for in Fig. 3.
Other ingredients are needed besides the form factors. We take the Wilson coefficients from Ref. Huber et al. (2006), the CKM elements from Ref. Charles et al. (2005), the meson masses and lifetimes from Ref. Olive et al. (2014), and the - and -quark masses from Ref. Ali et al. (2014). To calculate contributions that cannot be parameterized by the form factors, we employ QCD factorization at low Beneke et al. (1999, 2000); Beneke and Feldmann (2001); Asatrian et al. (2001); Beneke et al. (2001); Asatryan et al. (2002); Asatrian et al. (2004); Beneke et al. (2005); Bobeth et al. (2007) and an operator product expansion (OPE) in powers of at large Grinstein and Pirjol (2002); Seidel (2004); Grinstein and Pirjol (2004); Greub et al. (2008); Bobeth et al. (2010); Beylich et al. (2011); Bobeth et al. (2011, 2012). Full details will be provided in Ref. Du et al. (2015).
| 1.81(11,24,6,2) | ||
| 1.92(11,22,6,3) | ||
| 1.91(11,20,6,3) | ||
| 1.89(11,18,5,3) | ||
| 1.69(10,13,3,5) | 1.11(7,8,2,4) | |
| 1.52(9,10,2,4) | 1.25(8,8,2,3) | |
| 1.84(11,11,3,5) | 1.93(12,10,4,5) | |
| 1.07(6,6,3,3) | 1.59(10,7,4,4) | |
| 4.78(29,54,15,6) | ||
| 5.05(30,34,7,15) | 4.29(26,25,7,12) | |
| 20.4(1.2,1.6,0.3,0.5) | ||
Table 4 presents numerical predictions for selected bins. The last error in parenthesis contains effects of parametric uncertainties in , , , ; of missing power corrections, taking 10% of contributions not directly proportional to the form factors; and of violations of quark-hadron duality, estimated to be 2% at high- Beylich et al. (2011). At low , the uncertainty predominantly stems from the form factors; at high , the CKM elements and form factors each contribute similar errors. Figure 3 and Table 4 represent the second main result of this Letter.
In the regions and , and resonances dominate the rate. To estimate the total BR, we simply disregard them and interpolate linearly in between the QCD-factorization result at and the OPE result at . While this treatment does not yield the full branching ratio, it does enable a comparison with LHCb’s published result, Aaij et al. (2012), which was obtained from a similar interpolation over these regions. Our result agrees with LHCb, and is more precise than the best previous theoretical estimate Ali et al. (2014) because we use directly, which avoids a large uncertainty from varying the matching scale .
Outlook – The largest uncertainty in our determination of the form factors is the combined error from statistics with chiral-extrapolation and discretization effects included. We will be able to reduce these with calculations on the MILC Collaboration’s recently generated four-flavor ensembles with physical light-quark masses Bazavov et al. (2013). LHCb’s measurement of will improve, and Belle II expects to observe the neutral decay mode . If a deviation from the Standard Model is observed, our form factors can be used to compute other observables such as asymmetries, thereby providing information about new heavy particles, such as their masses, spin, and couplings.
Note added: after this paper was submitted for publication, the LHCb experiment announced a new measurement for the differential decay rate Tekampe (2015). The new results are shown in Fig. 3. The large difference in the lowest bin is due to the presence of light () resonances, whose effects are important but cannot be estimated in a model-independent manner. Given the present experimental and theoretical uncertainties, it is too early to discern possible new-physics contributions to this process.
Acknowledgements – We thank Ulrik Egede and Tobias Tekampe from LHCb for useful correspondence. Computations for this work were carried out with resources provided by the USQCD Collaboration, the Argonne Leadership Computing Facility, the National Energy Research Scientific Computing Center, and the Los Alamos National Laboratory, which are funded by the Office of Science of the United States Department of Energy; and with resources provided by the National Institute for Computational Science, the Pittsburgh Supercomputer Center, the San Diego Supercomputer Center, and the Texas Advanced Computing Center, which are funded through the National Science Foundation’s Teragrid/XSEDE Program. This work was supported in part by the U.S. Department of Energy under Grants No. DE-FG02-91ER40628 (C.B.), No. DE-FC02-06ER41446 (C.D., L.L., S.-W.Q.), No. DE-SC0010120 (S.G.), No. DE-FG02-91ER40661 (S.G.), No. DE-FG02-13ER42001 (D.D., A.X.K.), No. DE-FG02-91ER40664 (Y.M.), and No. DE-FG02-13ER41976 (D.T.); by the National Science Foundation under Grants No. PHY-1067881, No. PHY-10034278 (C.D., L.L., S.-W.Q..), No. PHY-1417805 (J.L., D.D.), and No. PHY-1316748 (R.S.); by the URA Visiting Scholars’ program (A.X.K., Y.M.); by the MINECO (Spain) under Grant FPA2013-47836-C3-1-P, and the Ramón y Cajal program (E.G.); by the Junta de Andalucía (Spain) under Grants FQM-101 and FQM-6552 (E.G.); by the European Commission under Grant No. PCIG10-GA-2011-303781 (E.G.); by the German Excellence Initiative, the European Union Seventh Framework Programme under grant agreement No. 291763, and the European Union’s Marie Curie COFUND program (A.S.K); and by the Basic Science Research Program of the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2014027937) and the Creative Research Initiatives Program (No. 2014001852) of the NRF grant funded by the Korean government (MEST) (J.A.B). Brookhaven National Laboratory is supported by the U. S. Department of Energy under Contract No. DE-SC0012704. Fermilab is operated by Fermi Research Alliance, LLC, under Contract No. DE-AC02-07CH11359 with the U.S. Department of Energy.
References
- Bailey et al. (2015a) J. A. Bailey et al. (Fermilab Lattice, MILC), Phys. Rev. D92, 014024 (2015a), arXiv:1503.07839 [hep-lat] .
- Ball and Zwicky (2005) P. Ball and R. Zwicky, Phys. Rev. D71, 014015 (2005), arXiv:hep-ph/0406232 .
- Wang et al. (2008) J.-J. Wang, R.-M. Wang, Y.-G. Xu, and Y.-D. Yang, Phys. Rev. D77, 014017 (2008), arXiv:0711.0321 [hep-ph] .
- Duplančić et al. (2008) G. Duplančić, A. Khodjamirian, T. Mannel, B. Melić, and N. Offen, JHEP 0804, 014 (2008), arXiv:0801.1796 [hep-ph] .
- Wu and Huang (2009) X.-G. Wu and T. Huang, Phys. Rev. D79, 034013 (2009), arXiv:0901.2636 [hep-ph] .
- Faustov and Galkin (2014) R. N. Faustov and V. O. Galkin, Eur. Phys. J. C74, 2911 (2014), arXiv:1403.4466 [hep-ph] .
- Ali et al. (2014) A. Ali, A. Y. Parkhomenko, and A. V. Rusov, Phys. Rev. D89, 094021 (2014), arXiv:1312.2523 [hep-ph] .
- Li et al. (2014) Z.-H. Li, Z.-G. Si, Y. Wang, and N. Zhu, (2014), arXiv:1411.0466 [hep-ph] .
- Hambrock et al. (2015) C. Hambrock, A. Khodjamirian, and A. Rusov, (2015), arXiv:1506.07760 [hep-ph] .
- Kronfeld (2012) A. S. Kronfeld, Annu. Rev. Nucl. Part. Sci. 62, 265 (2012), arXiv:1203.1204 [hep-lat] .
- Aaij et al. (2012) R. Aaij et al. (LHCb Collaboration), JHEP 1212, 125 (2012), arXiv:1210.2645 [hep-ex] .
- Wei et al. (2008) J.-T. Wei et al. (Belle Collaboration), Phys. Rev. D78, 011101 (2008), arXiv:0804.3656 [hep-ex] .
- Lees et al. (2013) J. P. Lees et al. (BaBar Collaboration), Phys. Rev. D88, 032012 (2013), arXiv:1303.6010 [hep-ex] .
- Lutz et al. (2013) O. Lutz et al. (Belle Collaboration), Phys. Rev. D87, 111103 (2013), arXiv:1303.3719 [hep-ex] .
- Bobeth et al. (2001) C. Bobeth, T. Ewerth, F. Krüger, and J. Urban, Phys. Rev. D64, 074014 (2001), arXiv:hep-ph/0104284 .
- Demir et al. (2002) D. A. Demir, K. A. Olive, and M. B. Voloshin, Phys. Rev. D66, 034015 (2002), arXiv:hep-ph/0204119 .
- Choudhury and Gaur (2002) S. R. Choudhury and N. Gaur, Phys. Rev. D66, 094015 (2002), arXiv:hep-ph/0206128 .
- Hou et al. (2013) W.-S. Hou, M. Kohda, and F. Xu, Phys. Rev. D87, 094005 (2013), arXiv:1302.1471 [hep-ph] .
- Aliev and Savci (1999) T. M. Aliev and M. Savci, Phys. Rev. D60, 014005 (1999), arXiv:hep-ph/9812272 [hep-ph] .
- Iltan (1999) E. O. Iltan, Int. J. Mod. Phys. A14, 4365 (1999), arXiv:hep-ph/9807256 [hep-ph] .
- Erkol and Turan (2002) G. Erkol and G. Turan, JHEP 0202, 015 (2002), arXiv:hep-ph/0201055 [hep-ph] .
- Erkol et al. (2005) G. Erkol, J. W. Wagenaar, and G. Turan, Eur. Phys. J. C41, 189 (2005), arXiv:hep-ph/0408186 [hep-ph] .
- Song et al. (2008) H.-Z. Song, L.-X. Lu, and G.-R. Lu, Commun. Theor. Phys. 50, 696 (2008).
- Gripaios et al. (2015) B. Gripaios, M. Nardecchia, and S. A. Renner, JHEP 1505, 006 (2015), arXiv:1412.1791 [hep-ph] .
- Grinstein et al. (1989) B. Grinstein, M. J. Savage, and M. B. Wise, Nucl. Phys. B319, 271 (1989).
- Buras et al. (1994) A. J. Buras, M. Misiak, M. Münz, and S. Pokorski, Nucl. Phys. B424, 374 (1994), arXiv:hep-ph/9311345 .
- Huber et al. (2006) T. Huber, E. Lunghi, M. Misiak, and D. Wyler, Nucl. Phys. B740, 105 (2006), arXiv:hep-ph/0512066 .
- Altmannshofer et al. (2009) W. Altmannshofer, P. Ball, A. Bharucha, A. J. Buras, D. M. Straub, and M. Wick, JHEP 0901, 019 (2009), arXiv:0811.1214 [hep-ph] .
-
Aubin et al. (2015a)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 2064f21b676m010m050” (2015a). -
Aubin et al. (2015b)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 2064f21b676m010m050b” (2015b). -
Aubin et al. (2015c)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 2064f21b676m007m050” (2015c). -
Aubin et al. (2015d)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 2064f21b676m007m050b” (2015d). -
Aubin et al. (2015e)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 2464f21b676m005m050” (2015e). -
Aubin et al. (2015f)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 2896f21b709m0062m031” (2015f). -
Aubin et al. (2015g)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 2896f21b709m0062m031b” (2015g). -
Aubin et al. (2015h)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 3296f21b7085m00465m031” (2015h). -
Aubin et al. (2015i)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 4096f21b708m0031m031a” (2015i). -
Aubin et al. (2015j)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 4096f21b708m0031m031b” (2015j). -
Aubin et al. (2015k)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 6496f21b7075m00155m031” (2015k). -
Aubin et al. (2015l)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 48144f21b748m0072m018a” (2015l). -
Aubin et al. (2015m)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 48144f21b748m0072m018b” (2015m). -
Aubin et al. (2015n)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 48144f21b747m0036m018a” (2015n). -
Aubin et al. (2015o)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 48144f21b747m0036m018b” (2015o). -
Aubin et al. (2015p)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 56144f21b7465m0025m018” (2015p). -
Aubin et al. (2015q)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 64144f21b746m0018m018a” (2015q). -
Aubin et al. (2015r)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 64144f21b746m0018m018b” (2015r). -
Aubin et al. (2015s)
C. Aubin et al. (MILC Collaboration),
“asqtad ensemble 64192f21b781m0028m014” (2015s). - Bernard et al. (2001) C. W. Bernard et al. (MILC Collaboration), Phys. Rev. D64, 054506 (2001), arXiv:hep-lat/0104002 [hep-lat] .
- Aubin et al. (2004) C. Aubin et al. (MILC Collaboration), Phys. Rev. D70, 094505 (2004), arXiv:hep-lat/0402030 [hep-lat] .
- Bazavov et al. (2010) A. Bazavov, D. Toussaint, C. Bernard, J. Laiho, C. DeTar, L. Levkova, M. B. Oktay, S. Gottlieb, U. M. Heller, J. E. Hetrick, P. B. Mackenzie, R. Sugar, and R. S. Van de Water, Rev. Mod. Phys. 82, 1349 (2010), arXiv:0903.3598 [hep-lat] .
- Aubin and Bernard (2007) C. Aubin and C. Bernard, Phys. Rev. D76, 014002 (2007), arXiv:0704.0795 [hep-lat] .
- Bailey et al. (2015b) J. A. Bailey et al. (Fermilab Lattice and MILC Collaborations), (2015b), in preparation.
- Bijnens and Jemos (2010) J. Bijnens and I. Jemos, Nucl. Phys. B840, 54 (2010), arXiv:1006.1197 [hep-ph] .
- Kronfeld (2000) A. S. Kronfeld, Phys. Rev. D62, 014505 (2000), arXiv:hep-lat/0002008 [hep-lat] .
- Harada et al. (2002) J. Harada, S. Hashimoto, K.-I. Ishikawa, A. S. Kronfeld, T. Onogi, and N. Yamada, Phys. Rev. D65, 094513 (2002), Phys. Rev. D71 019903(E) (2005), arXiv:hep-lat/0112044 .
- Oktay and Kronfeld (2008) M. B. Oktay and A. S. Kronfeld, Phys. Rev. D78, 014504 (2008), arXiv:0803.0523 [hep-lat] .
- Bernard et al. (2000) C. W. Bernard et al. (MILC Collaboration), Phys. Rev. D62, 034503 (2000), arXiv:hep-lat/0002028 [hep-lat] .
- Sommer (1994) R. Sommer, Nucl. Phys. B411, 839 (1994), arXiv:hep-lat/9310022 .
- Bazavov et al. (2012) A. Bazavov et al. (Fermilab Lattice and MILC Collaborations), Phys. Rev. D85, 114506 (2012), arXiv:1112.3051 [hep-lat] .
- Bazavov et al. (2009) A. Bazavov et al. (MILC Collaboration), PoS CD09, 007 (2009), arXiv:0910.2966 [hep-ph] .
- Olive et al. (2014) K. A. Olive et al. (Particle Data Group), Chin. Phys. C38, 090001 (2014).
- El-Khadra et al. (2001) A. X. El-Khadra, A. S. Kronfeld, P. B. Mackenzie, S. M. Ryan, and J. N. Simone, Phys. Rev. D64, 014502 (2001), arXiv:hep-ph/0101023 .
- Bourrely et al. (1981) C. Bourrely, B. Machet, and E. de Rafael, Nucl. Phys. B189, 157 (1981).
- Boyd et al. (1995) C. G. Boyd, B. Grinstein, and R. F. Lebed, Phys. Rev. Lett. 74, 4603 (1995), arXiv:hep-ph/9412324 .
- Lellouch (1996) L. Lellouch, Nucl. Phys. B479, 353 (1996), arXiv:hep-ph/9509358 .
- Boyd and Savage (1997) C. G. Boyd and M. J. Savage, Phys. Rev. D56, 303 (1997), arXiv:hep-ph/9702300 .
- Bourrely et al. (2009) C. Bourrely, I. Caprini, and L. Lellouch, Phys. Rev. D79, 013008 (2009), arXiv:0807.2722 [hep-ph] .
- del Amo Sanchez et al. (2011) P. del Amo Sanchez et al. (BaBar Collaboration), Phys. Rev. D83, 032007 (2011), arXiv:1005.3288 [hep-ex] .
- Lees et al. (2012) J. P. Lees et al. (BaBar Collaboration), Phys. Rev. D86, 092004 (2012), arXiv:1208.1253 [hep-ex] .
- Ha et al. (2011) H. Ha et al. (Belle Collaboration), Phys. Rev. D83, 071101 (2011), arXiv:1012.0090 [hep-ex] .
- Sibidanov et al. (2013) A. Sibidanov et al. (Belle Collaboration), Phys. Rev. D88, 032005 (2013), arXiv:1306.2781 [hep-ex] .
- Tekampe (2015) T. Tekampe (LHCb), https://indico.cern.ch/event/361123/session/4/contribution/409 (2015), talk presented at DPF 2015.
- Charles et al. (2005) J. Charles et al. (CKMfitter Group), Eur. Phys. J. C41, 1 (2005), updates at http://ckmfitter.in2p3.fr, arXiv:hep-ph/0406184 [hep-ph] .
- Beneke et al. (1999) M. Beneke, G. Buchalla, M. Neubert, and C. T. Sachrajda, Phys. Rev. Lett. 83, 1914 (1999), arXiv:hep-ph/9905312 [hep-ph] .
- Beneke et al. (2000) M. Beneke, G. Buchalla, M. Neubert, and C. T. Sachrajda, Nucl. Phys. B591, 313 (2000), arXiv:hep-ph/0006124 [hep-ph] .
- Beneke and Feldmann (2001) M. Beneke and T. Feldmann, Nucl. Phys. B592, 3 (2001), arXiv:hep-ph/0008255 .
- Asatrian et al. (2001) H. H. Asatrian, H. M. Asatrian, C. Greub, and M. Walker, Phys. Lett. B507, 162 (2001), arXiv:hep-ph/0103087 [hep-ph] .
- Beneke et al. (2001) M. Beneke, T. Feldmann, and D. Seidel, Nucl. Phys. B612, 25 (2001), arXiv:hep-ph/0106067 [hep-ph] .
- Asatryan et al. (2002) H. H. Asatryan, H. M. Asatrian, C. Greub, and M. Walker, Phys. Rev. D65, 074004 (2002), arXiv:hep-ph/0109140 [hep-ph] .
- Asatrian et al. (2004) H. M. Asatrian, K. Bieri, C. Greub, and M. Walker, Phys. Rev. D69, 074007 (2004), arXiv:hep-ph/0312063 [hep-ph] .
- Beneke et al. (2005) M. Beneke, T. Feldmann, and D. Seidel, Eur. Phys. J. C41, 173 (2005), arXiv:hep-ph/0412400 [hep-ph] .
- Bobeth et al. (2007) C. Bobeth, G. Hiller, and G. Piranishvili, JHEP 0712, 040 (2007), arXiv:0709.4174 [hep-ph] .
- Grinstein and Pirjol (2002) B. Grinstein and D. Pirjol, Phys. Lett. B533, 8 (2002), arXiv:hep-ph/0201298 [hep-ph] .
- Seidel (2004) D. Seidel, Phys. Rev. D70, 094038 (2004), arXiv:hep-ph/0403185 [hep-ph] .
- Grinstein and Pirjol (2004) B. Grinstein and D. Pirjol, Phys. Rev. D70, 114005 (2004), arXiv:hep-ph/0404250 [hep-ph] .
- Greub et al. (2008) C. Greub, V. Pilipp, and C. Schupbach, JHEP 0812, 040 (2008), arXiv:0810.4077 [hep-ph] .
- Bobeth et al. (2010) C. Bobeth, G. Hiller, and D. van Dyk, JHEP 1007, 098 (2010), arXiv:1006.5013 [hep-ph] .
- Beylich et al. (2011) M. Beylich, G. Buchalla, and T. Feldmann, Eur. Phys. J. C71, 1635 (2011), arXiv:1101.5118 [hep-ph] .
- Bobeth et al. (2011) C. Bobeth, G. Hiller, and D. van Dyk, JHEP 1107, 067 (2011), arXiv:1105.0376 [hep-ph] .
- Bobeth et al. (2012) C. Bobeth, G. Hiller, D. van Dyk, and C. Wacker, JHEP 1201, 107 (2012), arXiv:1111.2558 [hep-ph] .
- Du et al. (2015) D. Du, A. X. El Khadra, E. Lunghi, R. S. Van de Water, R. Zhou, et al. (Fermilab Lattice and MILC Collaborations), (2015), in preparation.
- Bazavov et al. (2013) A. Bazavov et al. (MILC Collaboration), Phys. Rev. D87, 054505 (2013), arXiv:1212.4768 [hep-lat] .