BWT construction and search at the terabase scale

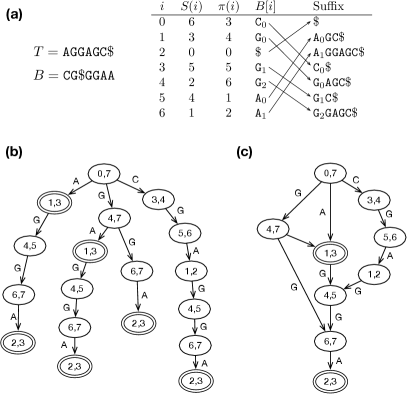
Let $\Sigma$ be an alphabet of symbols (Table 1). Given a string $P$ over $\Sigma$, $|P|$ is its length and $P[i]\in\Sigma$, $0\leq i<|P|$, is the $i$-th symbol in $P$, and $P[i,j)$ is a substring of length $j-i$ starting at $i$. Operator “$\circ$” concatenates two strings or between strings and symbols. It may be omitted if concatenation is apparent from the context.

Suppose $\mathcal{T}=(P_{0},P_{1},\ldots,P_{m-1})$ is an ordered list of $m$ strings over $\Sigma$. $T\triangleq P_{0}\$_{0}P_{1}\$_{1}\cdots P_{m-1}\$_{m-1}$ is the concatenation of the strings in $\mathcal{T}$ with sentinels ordered by $\$_{0}<\$_{1}<\cdots<\$_{m-1}$. For other ways to define string concatenation on ordered string lists or unordered string sets, see Cenzato and Lipták, (2024).

For convenience, let $n\triangleq|T|$ and $T[-1]=T[n-1]$. The suffix array of $T$ is an integer array $S$ such that $S(i)$, $0\leq i<n$, is the start position of the $i$-th smallest suffix among all suffixes of $T$ (Fig. 1a). The Burrows-Wheeler Transform (BWT) of $T$ is a string $B$ computed by $B[i]=T[S(i)-1]$. All sentinels in $B$ are represented by the same symbol “$\$$” and are not distinguished from each other. $\Sigma^{\prime}\triangleq\Sigma\cup\{\$\}$ denotes the alphabet including the sentinel.

For $a\in\Sigma^{\prime}$, let $C_{B}(a)\triangleq|\{i:B[i]<a\}|$ be the number of symbols smaller than $a$ and ${\rm rank}_{B}(a,k)\triangleq|\{i<k:B[i]=a\}|$ be the number of $a$ before offset $k$ in $B$. We may omit subscription $B$ when we are describing one string only. The last-to-first mapping (LF mapping) $\pi$ is defined by $\pi(i)\triangleq S^{-1}(S(i)-1)$, where $S^{-1}$ is the inverse function of suffix array $S$. It can be calculated as $\pi(i)=\pi_{B}(B[i],i)$, where $\pi_{B}(a,i)\triangleq C(B[i])+{\rm rank}(B[i],i)$. As $B[\pi(i)]$ immediately proceeds $B[i]$ on $T$, we can use $\pi$ to decode the $i$-th sequence in $B$.

Libsais is an efficient library for computing the suffix array of a single string. It does not directly support a list of strings. Nonetheless, we note that $T$ is a string over alphabet $\Sigma^{\prime\prime}=\{\$_{0},\$_{1},\ldots,\$_{m-1},{\tt A},{\tt C},{\tt G},{\tt T},{\tt N}\}$ with lexicographical order $\$_{0}<\cdots<\$_{m-1}<{\tt A}<{\tt C}<{\tt G}<{\tt T}<{\tt N}$. We can use $m+5$ non-negative integers to encode $T$ and apply libsais. The suffix array derived this way will be identical to the suffix array of $T$.

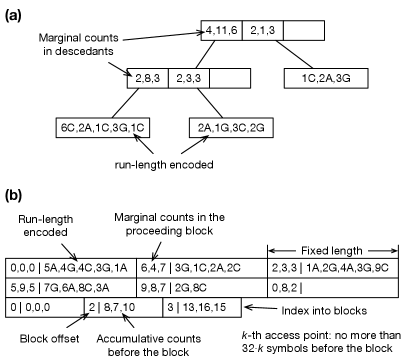
For $m$ that can be represented by a 32-bit integer and $n$ represented by a 64-bit integer, libsais will need at least $12n$ bytes to construct the suffix array. It is impractical for $n$ more than tens of billions. To construct BWT for large $n$, ropebwt3 uses libsais to build the BWT for a batch (up to 7 Gb by default) and merges it to the BWT of already processed batches (Algorithm 1). The basic idea behind the algorithm is well known (Ferragina et al., , 2010) but implementations vary (Sirén, , 2016; Oliva et al., , 2021). In ropebwt3, we encode BWT with a B+-tree (Fig. 2a). This yields $O(\log r)$ rank query (line 13) and insertion (line 17), where $r$ is the number of runs in the merged BWT. The bottleneck of the algorithm lies in rank calculation (line 8), which can be parallelized if $m_{2}>1$.

This online BWT construction algorithm does not use temporary disk space. The overall time complexity is $O(n\log r)$. The BWT takes $O(r\log r)$ in space. The memory required for partial BWT construction with libsais depends on the batch size and the longest string. B+-tree is dynamic. Ropebwt3 optionally converts B+-tree to the fermi binary format (Fig. 2b; Li, 2012) which is static but is faster to query and can be memory-mapped.

Ropebwt2 (Li, , 2014) uses the same B+-tree to encode BWT and has the same time complexity. However, it inserts sequences, not partial BWTs, into existing BWT. It cannot be efficiently parallelized for long strings. Note that independent of our earlier work, Ohno et al., (2018) also used a B+-tree to encode BWT. Its implementation (Bannai et al., , 2020) is several times slower than ropebwt2 on 152 bacterial genomes from Li et al., (2024), possibly because ropebwt2 is optimized for the small DNA alphabet.

For a string $P\in\Sigma^{*}$ (i.e. not including sentinels), let ${\rm occ}(P)$ be the number of occurrences of $P$ in $T$. Define ${\rm lo}(P)$ to be the number of suffixes that are lexicographically smaller than $P$ and ${\rm hi}(P)\triangleq{\rm lo}(P)+{\rm occ}(P)$. $[{\rm lo}(P),{\rm hi}(P))$ is called the suffix array interval of $P$, or SA interval in brief. An SA interval is important if there exists $P$ such that it is the SA interval of $P$. The SA interval of the empty string is $[0,n)$ where $n=|T|$.

If we know the SA interval of $P$, we can calculate the SA interval of $aP$ with: ${\rm lo}(aP)=\pi_{B}(a,{\rm lo}(P))$ and ${\rm hi}(aP)=\pi_{B}(a,{\rm hi}(P))$. To calculate ${\rm occ}(P)$, we start with $[0,n)$ and repeatedly apply the equation above from the last symbol in $P$ to the first. This procedure is called backward search.

By definition of BWT, if $i\in[{\rm lo}(P),{\rm hi}(P))$, $P=T[S(i),S(i)+|P|)$. We can thus locate an occurrence of $P$ in the original string $T$. However, suffix array $S$ takes $O(n\log n)$ in space and may be too large to store explicitly. With an FM-index, we only store $S(i)$ if and only if $i$ is a multiple of $s$ where $s$ is a positive integer controlling the sample rate. We calculate the rest of $S(i)$ using LF-mapping $\pi(\cdot)$.

A complication with multi-string BWT is that $\pi(i)$ does not point to the preceeding symbol when $B[i]=\$$. This is because sentinels are ordered during suffix sorting but are not distinguished from each other in BWT. We will have to store the rank of each string in $T$ (array $R$ in Algorithm 2). For convenience, we also keep the index of the string and the offset on the string instead of the offset on the concatenated string $T$.

To find the position of $i\in[{\rm lo}(P),{\rm hi}(P))$ in the original string, we repeatedly apply $\pi(\cdot)$ $k$ times until the position of $\pi^{k}(i)$ is stored. With $U$, $V$ and $R$ precalculated by IndexSSA in Algorithm 2, we can locate $i$ with

where $k$ is the smallest non-negative integer such that $B[\pi^{k}(i)]=\$$ or $\pi^{k}(i)\bmod s=0$. On average, $k\approx s$, which means each locate operation triggers $s$ rank queries.

Function Locate1 in Algorithm 2 provides a faster way to find one position in SA interval $[l,h)$. A key observation is that if the interval contains a sentinel or there exists $k$ such that $l\leq ks<h$, we can immediately locate one occurrence; if not, we can apply backward search repeatedly until an SA interval $[l^{\prime},h^{\prime})$ brackets a stored suffix array value. If $T$ consists of $m^{\prime}$ identical strings, we apply $s/\min(h-l,m^{\prime})$ rounds of backward searches on average, usually much faster than the naive algorithm. Ropebwt3 implements a generalized Locate1 function that finds multiple occurrences.

The definitions above are applicable to generic strings. With one BWT, we can only achieve backward search; forward search additionally requires the BWT of the reverse strings (Lam et al., , 2009). Nonetheless, due to the strand symmetry of DNA strings, it is possible to achieve both forward and backward search with one BWT provided that the BWT contains both strands of DNA strings (Li, , 2012).

Formally, a DNA alphabet is $\Sigma=\{{\tt A},{\tt C},{\tt G},{\tt T},{\tt N}\}$. $\overline{a}$ denotes the Watson-Crick complement of symbol $a\in\Sigma$. The complement of $\$$, ${\tt A}$, ${\tt C}$, ${\tt G}$, ${\tt T}$ and ${\tt N}$ are $\$$, ${\tt T}$, ${\tt G}$, ${\tt C}$, ${\tt A}$ and ${\tt N}$, respectively.

For string $P$, $\overline{P}$ is its reverse complement string. The double-strand concatenation of a DNA string list $\mathcal{T}=(P_{0},P_{1},\ldots,P_{m-1})$ is $\tilde{T}=P_{0}\$_{0}\overline{P}_{0}\$_{1}P_{1}\$_{2}\overline{P}_{1}\$_{3}\cdots P_{m-1}\$_{2m-2}\overline{P}_{m-1}\$_{2m-1}$. The double-strand BWT (DS-BWT) of $\mathcal{T}$ is the BWT of $\tilde{T}$. We note that if $P$ is a substring of $\tilde{T}$, $\overline{P}$ must be a substring and ${\rm occ}(P)={\rm occ}(\overline{P})$. The suffix array bidirectional interval (SA bi-interval) of $P$ is a 3-tuple defined as $({\rm lo}(P),{\rm lo}(\overline{P}),{\rm occ}(P))$.

An SA bi-interval can be extended in both backward and forward directions. To calculate the SA bi-interval of $aP$, we can use the standard backward search to compute ${\rm lo}(aP)$ and ${\rm occ}(aP)$ from ${\rm lo}(P)$ and ${\rm occ}(P)$. As to ${\rm lo}(\overline{aP})$, we note that $[{\rm lo}(\overline{aP}),{\rm hi}(\overline{aP}))\subset[{\rm lo}(\overline{P}),{\rm hi}(\overline{P}))$ because $\overline{aP}=\overline{P}\circ\overline{a}$ is prefixed with $\overline{P}$. We can thus calculate ${\rm lo}(\overline{aP})={\rm lo}(\overline{P})+\sum_{b<\overline{a}}{\rm occ}(\overline{P}b)={\rm lo}(\overline{P})+\sum_{b<\overline{a}}{\rm occ}(\overline{b}P)$.

It is easy to see that if $(k,k^{\prime},s)$ is the SA bi-interval of $P$, $(k^{\prime},k,s)$ is the SA bi-interval of $\overline{P}$, and vice versa. Therefore, we can use the backward extension of $\overline{P}$ to achieve the forward extension of $P$. Algorithm 3 gives the details. It simplifies the original formulation (Li, , 2012).

An exact match between strings $T$ and $P$ is a 3-tuple $(t,p,l)$ such that $T[t,t+l)=P[p,p+l)$. A maximal exact match (MEM) is an exact match that cannot be extended in either direction. A MEM may be contained in another MEM on the pattern string $P$. For example, suppose $T={\tt GACCTCCG}$ and $P={\tt ACCT}$. MEM $(5,1,2)$ is contained in MEM $(1,0,4)$ on the pattern string. A supermaximal exact match (SMEM) is a MEM that is not contained in other MEMs on the pattern string. In the example above, only $(1,0,4)$ is a SMEM. There are usually much fewer SMEMs than MEMs. Gagie, (2024) recently proposed a new algorithm to find long SMEMs (Algorithm 4) that is faster than our earlier algorithm (Li, , 2012) especially when there are many short SMEMs to skip. Both algorithms can also find SMEMs occurring at least $s_{\min}$ times (Tatarnikov et al., , 2023).

The prefix trie of $T$ is a tree that encodes all the prefixes of $T$ (Fig. 1b). Each edge in the tree is labeled with a symbol in $\Sigma$. A path from a node to the root spells a substring of $T$. We can label a node with the SA interval of the string from the node to the root. When we know the label of a node, we can find the label of its child using backward search. We can thus simulate the top-down traversal of the prefix trie (Lam et al., , 2008).

As is shown in Fig. 1b, different nodes in the prefix trie may have the same label. If we merge nodes with the same label (Fig. 1c), we will get a prefix DAWG (Blumer et al., , 1983). For $|T|>1$, the DAWG has at most $2|T|-1$ nodes (Blumer et al., , 1984). Each node uniquely corresponds to an important SA interval of $T$.

Let $G_{T}$ denote the prefix DAWG of $T$ and $V(G_{T})$ be the set of vertices in $G_{T}$. Given a reference string $T$ and a pattern string $P$, we can align $G_{T}$ and $G_{P}$ under affine-gap penalty with

where $u\in V(G_{P})$, $v\in V(G_{T})$, ${\rm pre}(u)$ and ${\rm pre}(v)$ are the sets of predecessors in $G_{P}$ and $G_{T}$ respectively, $q$ is the gap open penalty, $e$ is the gap extension penalty, and $s(u^{\prime},u;v^{\prime},v)$ is the match/mismatch score between the symbol labeled on edge $(u^{\prime},u)$ in $G_{P}$ and the symbol on $(v^{\prime},v)$ in $G_{T}$. This equation is similar to but not the same as our earlier result (Li and Durbin, , 2010).

On real data, $G_{T}$ may be too large to store explicitly. Ropebwt3 instead explicitly stores $G_{P}$ only and traverses it in the topological order (Algorithm 5). At a node $u\in V(G_{P})$, we use a hash table to keep $\{v\in V(G_{T}):H_{uv}>0\}$. This algorithm is exact in that it guarantees to find the best alignment. In practice, however, a large number of $v\in V(G_{T})$ may be aligned to $u$ with $H_{uv}>0$. It is slow and memory demanding to keep track of all cells $(u,v)$ with positive scores when $P$ is long. Similar to our earlier work, we only store top $W$ cells (25 by default) at each $u$. This heuristic is akin to dynamic banding for linear sequences (Suzuki and Kasahara, , 2018).

BWA-SW with the banding heuristic may miss the best matching haplotype especially given an index consisting of similar haplotypes. When the suffix on the best full-length alignment has a lot more mismatches than the suffix on suboptimal alignments, the best alignment may have moved out of the band early in the iteration and thus get missed. Nevertheless, a long read sequenced from a new sample may be the recombinant of two genomes in the index. We often do not seek the best alignment of the long read to a single haplotype. We are instead more interested in the collection of haplotypes a query sequence can be aligned to even if they do not lead to the best alignment. This now becomes possible as BWA-SW explores suboptimal alignments to multiple haplotypes.

More exactly, we perform semi-global sequence-to-DAWG alignment (i.e. requiring the query sequence to be aligned from end to end) by applying BWA-SW to the graph representing the linear query sequence $P$, from the end to the start. We can find the set of matching haplotypes $\mathcal{M}\triangleq\{v\in V(G_{T}):H_{u_{0}v}>0\}$ where $u_{0}$ represents the start of $P$. $\mathcal{M}$ may include suboptimal haplotypes caused by small variants as well as the optimal one.

Importantly, $P$ may be aligned to similar positions on $T$ with slightly different gap placements. For example, given $T={\tt CAAGCAG}$ and $P={\tt AGCG}$, the algorithm above may find the following two alignments around the same position but in different SA intervals:

   T: CAAGCAG        CAAGCAG
        ||||    or    | |||
   P:   AGCA          A-GCA

When counting hits, we want to ignore the second suboptimal alignment. In theory, we can identify this case by comparing the position of each alignment. This procedure is slow as the locate operation is costly. We instead leverage the bi-directionality to identify redundancy heuristically. Suppose $P$ can be aligned to SA bi-intervals $(k_{1},k^{\prime}_{1},s_{1})$ and $(k_{2},k^{\prime}_{2},s_{2})$ and the alignment score to the first interval is higher. We filter out the second interval if $[k_{2},k_{2}+s_{2})\subset[k_{1},k_{1}+s_{1})$ or $[k^{\prime}_{2},k^{\prime}_{2}+s_{2})\subset[k^{\prime}_{1},k^{\prime}_{1}+s_{1})$. This strategy does not avoid all overcounting but it works well on multiple real examples we have closely inspected.

In practice, we may apply this algorithm to the flanking sequence of a variant or to sliding k-mers of a long query sequence to enumerate possible local haplotypes and estimate their frequencies in the index. It is a new query type that is biologically meaningful.

We evaluated the performance of BWT construction on 100 haplotype-resolved human assemblies collected in Li et al., (2024). As we included both strands (Section 2.5), each BWT construction algorithm took about 600 billion bases as input (Table 2). grlBWT (commit 5b6d26a; Díaz-Domínguez and Navarro, 2023) is the fastest algorithm (Table 3) at the cost of $\sim$2 terabytes of working disk space including decompressed sequences. Ropebwt3 took 21 hours from input sequences in gzip’d FASTA to the final index, of which 7.7 hours was spent on libsais. It does not use working disk space and can append new sequences to an existing BWT. However, hardcoded for the DNA alphabet, ropebwt3 does not work with more general alphabets. pfp-thresholds (Rossi et al., , 2022) used more memory than the input sequences. It may be impractical with increased sample size.

Both MONI (v0.2.1; Rossi et al., 2022) and Movi (v1.1.0; Zakeri et al., 2024) use pfp-thresholds for building BWT. They generate additional data structures on top of BWT. Time spent on these additional steps were not counted. The tested version of Movi used more than one terabyte of memory to construct the final index. The Movi developer kindly provided the Movi index for the evaluation of query performance in the next section.

We also indexed the same dataset with k-mer based tools. In the lossless mode, metagraph (v0.3.6; Karasikov et al., 2024) indexed the 100 human genomes in 17 hours (Table 3). Fulgor (v3.0.0; Fan et al., 2024) is by far the fastest. However, lossy in nature, it is not directly comparable to the rest of the tools in the table.

To test scalability, we indexed a larger dataset consisting of 320 human genomes recently released by the Human Pangenome Reference Consortium (Liao et al., , 2023). Because these assemblies are more contiguous than human100 (Table 2), $m_{2}$ in Algorithm 1 is smaller, which reduces the multi-threading efficiency of ropebwt3. We can alleviate this by executing BWT merge and partial BWT construction at the same time at the cost of higher memory footprint. On human320, grlBWT is 2–4 times as fast but uses more memory (Table 3). On the largest CommonBacteria dataset (Table 2), ropebwt3 took less than a month to construct the double-strand BWT with 14.66 trillion symbols. The final index in the fermi format is 27.6 GB in size. The “dustbin” and “unknown” categories in AllTheBacteria consist of many unique sequences which are not compressed well. Indexing the entire AllTheBacteria with ropebwt3 will probably take 100–200 GB memory at the peak.

We queried 100–200 Mb human short reads (SR$+$), human long reads (LR$+$) and non-human long reads (LR$-$) against the human pangenome indices constructed above (Table 4). It is important to note that no two tools support exactly the same type of query, but the comparison can still give a hint about the relative performance.

Among the three BWT-based tools, ropebwt3 is slower than Movi but faster than MONI on finding exact matches. Movi finds pseudo-matching length (PML) which is not intended to be the longest exact match. PML corresponds to the longest MEM for only 195 out of one million short reads, and none for long reads. The longest PML of each read is on average 27% shorter than the longest exact match for LR$+$ and 22% shorter for SR$+$. Nonetheless, we believe it is possible to implement SMEM finding based on the Movi data structure with minor performance overhead.

MONI and ropebwt3 can also find inexact matches. Implementing r-index, MONI can relatively cheaply locate one SMEM. It leverages this property to extract the genomic sequence around the longest SMEM and performs Smith-Waterman extension. MONI extension is faster than BWA-SW on SR$+$ because it does not need to inspect suboptimal hits. This feature apparently focuses on short reads only. On LR$+$, MONI extension fails to extend to the ends of reads and generate incorrect output for the majority of reads.

As to k-mer indices, fulgor outputs the labels of genomes that each read have enough 31-mer matches to. In its current form, such output is not useful for pangenome analysis as we know most of reads can be mapped to all genomes. Metagraph can additionally output the contig name of each match. However, when most k-mers are present in the index, metagraph is impractically slow.

As a biological application, we used the pangenome index to identify novel sequences in reads that are absent from other human genomes. For this, we downloaded the PacBio HiFi reads for tumor sample COLO829 (https://downloads.pacbcloud.com/public/revio/2023Q2/COLO829/COLO829/), mapped them to human100 (Table 2), which includes T2T-CHM13 (Nurk et al., , 2022), and extracted $\geq$1kb regions on reads that are not covered by SMEMs of 51bp or longer. We found 95kb sequences in 43 reads. These sequences could not be assembled. NCBI BLAST suggested multiple weak hits to cow genomes. We could not identify the source of these sequences but there were few of them anyway.

When we mapped the COLO829 reads to T2T-CHM13 only and applied the same procedure, we found 55.9Mb of “novel” sequences in 25,365 reads. The much larger number is caused by regions with dense SNPs that prevented long exact matches. Counterintuitively, mapping these reads to T2T-CHM13 with minimap2 (Li, , 2018) resulted in more “novel” sequences at 78.6Mb, probably because minimap2 ignores seeds occurring thousands of times in T2T-CHM13 and may miss more alignments. Capable of finding SMEMs at the pangenome scale, ropebwt3 is more effective for identifying known sequences. It is also 16% faster and uses less memory than full minimap2 alignment against a single genome.

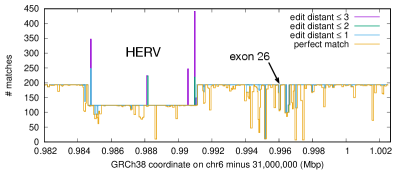
The reference human genome GRCh38 has two paralogous C4 genes, C4A and C4B, and they may have copy-number changes (Sekar et al., , 2016). In both cases, the exon 26 harbors the functional domain. We extracted the exon 26 from both genes from GRCh38. They differ at six mismatches over 157bp. We aligned both 157bp segments, one from each gene, to the human pangenome. 105 haplotypes have the same C4A exon 26 sequence, one haplotype has a mismatch at offset 128 and four haplotypes have a mismatch at 54. In case of C4B, 60 haplotypes have the same reference C4B sequence and 23 also have a mismatch at offset 54. This means among the 100 human haplotypes, there are 110 C4A gene copies and 83 C4B copies. If we increase the bandwidth from the default 25 to 200, BWA-SW will be able to align C4A exon 26 to C4B genes and output all five hits for each sequence.

Fig. 3 shows the local haplotype diversity across the entire C4A gene spanning $\sim$20.6kb on GRCh38. We can see most regions have 193 copies, except a $\sim$6.4kb HERV insertion that separates long and short forms (Sekar et al., , 2016). The dip around exon 26 is caused by the C4A–C4B difference. We could only see these alternative haplotypes with BWA-SW which reports suboptimal hits.