$B\to X_{c}\ell\bar{\nu}$ Decay as a Probe of Complex Conjugate Poles

Introduction—Inclusive decays of B-mesons play a crucial role for the determination of the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements [1, 2]. The measurement of decay spectra enables us to extract $|V_{cb}|$ with $1.1\%$-$1.5\%$ precision in Refs. [3, 4, 5]. An alternative determination of $|V_{cb}|$ can be made via the exclusive decays such as $B\to D^{(*)}\ell\bar{\nu}$, where ab initio simulation of quantum chromodynamics (QCD) is performed by lattice gauge theory [6]. Provided that nonperturbative aspects of QCD are properly controlled, the different methods to determine CKM matrix elements supposedly agree with one another.

In this context, it should be noted that there is a longstanding tension for more than a decade: the discrepancy between inclusive and exclusive $|V_{cb}|$ is observed, where Particle Data Group (PDG) 2024 [7] reports significance of 3.0$\sigma$. The interpretation via new physics is disfavored [8] since this scenario is incompatible with the $Zb\bar{b}$ coupling constraint, while the BaBar experiment recently gives the consistent result between both determinations albeit a large uncertainty [9]. Precise determinations of $V_{cb}$ improve the accuracy of $\epsilon_{K}$, representing indirect CP violation for $K^{0}-\bar{K}^{0}$ mixing.

As to the theoretical framework, a conventional method for inclusive B-meson decays is the operator product expansion (OPE) [10], rendering the observables recast into the form of the $1/m_{b}$ series [11, 12, 13, 14]. Given that nonanalytic behavior of the charm quark propagator exists solely along the timelike real axis, the perturbative expansion leads to convergent prediction for a contour that is away from the resonance region [11]. Equipped with this methodology, $|V_{cb}|$, bottom quark mass and power-correction parameters are determined so as to fit the decay spectra [3, 4].

There is a tacit assumption made in the OPE analysis, called quark-hadron duality [15, 16, 17]. The underlying difficulty arises from truncated power series, i.e., power and radiative corrections, which would lead to particularly nontrivial behavior when analytic continuation to Minkowski spacetime is implemented [18]. Violation of quark-hadron duality is hard to quantify and instead modeled by the instanton-based approach [19, 20, 21, 22, 23] as well as the resonance-based approach [24, 25, 26, 27, 28, 29, 30, 31, 32, 33] in previous works for heavy quarks. It is indicated that while duality violation is exponentially suppressed in Euclid space, it exhibits oscillatory behavior in Minkowski spacetime [18]. For semileptonic $B$-meson decays, global duality violation involving the smearing over phase space might give rise to a potential difficulty in the phenomenological discussion.

Meanwhile, there exists a nontrivial issue on strong interaction: colored particles cannot be observed individually, referred to as color confinement, where its underlying mechanism is still not clarified. In relation to this phenomenon, there are some notable aspects in analytical structures of propagators for confined particles. In particular, the existence of complex conjugate poles (CCPs) is possibly an indication of confinement, invalidating the standard Källén-Lehman spectral representation [34, 35, 36]. In previous works, CCPs of gluon [37] and quark propagators [38] are extracted by (a variant of) the Schlessinger point method [39] supplemented by Euclidean-input methods. From field-theoretic perspective, it has been known [40] that CCPs for the gluon propagator are suggested in view of the Gribov problem [41]. See also recent intensive investigations of CCPs mostly oriented for the Yang-Mills theories [42, 43, 44, 45].

In this Letter, contributions of CCPs to inclusive widths for $B$-meson decays are discussed. It should be noted that CCPs lead to novel nonanalytical behavior of the forward scattering tensor in $B\to X_{c}\ell\bar{\nu}$ decays. In the presence of CCPs, deformation of the integration contour yields corrections that cannot be evaluated perturbatively. These additional contributions can be extracted by the residue theorem, in general invalidating quark-hadron duality. Formulating in this way, we discuss the possibility that the aforementioned $|V_{cb}|$ puzzle is resolved. Furthermore, the contributions of CCPs to nonleptonic $B_{d}^{0}$-meson decays are also studied. We shall show that $|V_{cb}|$ and the $B_{d}^{0}$ lifetime can be simultaneously explained within $1\sigma$, with certain values of the pole position and the residue.

$B$-meson semileptonic decays—In the previous works [11, 12, 13, 14], inclusive decays of beauty hadrons are evaluated in the heavy quark effective theory (HQET) [46, 47, 48, 49], for which the lowest order contribution corresponds to the free bottom quark decay. Here we consider semileptonic decays with massless leptons denoted with $\ell=e,\mu$ at the rest frame of $B$ meson. The triple differential rate is given by [13]

$\displaystyle\frac{d^{3}\Gamma}{dE_{\bar{\nu}}dE_{\ell}dq^{2}}=\frac{G_{F}^{2}|V_{cb}|^{2}}{4\pi^{3}}L_{\mu\nu}W^{\mu\nu},$

(1)

where $L_{\mu\nu}$ and $W^{\mu\nu}$ represent leptonic and hadronic tensors, respectively, with $q=p_{\ell}+p_{\bar{\nu}}$. The latter quantity is related to the imaginary part of the forward scattering tensor, $W^{\mu\nu}=-\frac{1}{\pi}\mathrm{Im}T^{\mu\nu}$, with $T^{\mu\nu}$ defined by

$\displaystyle T^{\mu\nu}$

$\displaystyle=$

$\displaystyle-i\int d^{4}xe^{-iq\cdot x}\left\langle H_{v}|T[J^{\mu}(x)J^{\nu}(0)]|H_{v}\right\rangle.$

(2)

In Eq. (2), the hadronic state is normalized via $\left\langle H_{v^{\prime}}(\bm{p})|H_{v}(\bm{q})\right\rangle=v^{0}(2\pi)^{3}\delta^{(3)}(\bm{p}-\bm{q})$. By introducing a variable of $\alpha=q^{2}/[2m_{b}(q^{0}-E_{\ell})]$ and integrating Eq. (1) over $q^{0}$, one can obtain the double differential width

	$\displaystyle\frac{d^{2}\Gamma}{dE_{\ell}d\alpha}$	$\displaystyle=$	$\displaystyle-\frac{G_{F}^{2}|V_{cb}|^{2}}{4\pi^{3}}\frac{2m_{b}}{\pi}$		(3)
		$\displaystyle\times$	$\displaystyle\textrm{Im}\int_{E_{\ell}}^{q^{0}_{\textrm{max}}}(q^{0}-E_{\ell})L_{\mu\nu}T^{\mu\nu}dq^{0}.$

The expression of $T^{\mu\nu}$ relevant for $B\to X_{c}\ell\bar{\nu}$ is

	$\displaystyle\left.T^{\mu\nu}\right|_{B\to X_{c}\ell\bar{\nu}}$	$\displaystyle=$	$\displaystyle-i\int d^{4}xe^{-iq\cdot x}$		(4)
		$\displaystyle\times$	$\displaystyle\left\langle H_{v}|\bar{b}(x)\gamma^{\mu}P_{L}S(x,0)\gamma^{\nu}P_{L}b(0)|H_{v}\right\rangle.\qquad$

In Eq. (4), $S(x,y)$ represents the charm quark propagator. In the presence of CCPs, the Green function for the nonperturbative region includes

	$\displaystyle\left.S(x,y)\right|_{\rm CCPs}$	$\displaystyle=$	$\displaystyle\int\frac{d^{4}p_{c}}{(2\pi)^{4}}i\not{p}_{c}\bigg{(}\frac{R}{p_{c}^{2}+Q}+\frac{R^{*}}{p_{c}^{2}+Q^{*}}\bigg{)}$		(5)
		$\displaystyle\times$	$\displaystyle e^{-ip_{c}\cdot(x-y)},$

where the complex numbers denoted as R and Q represent the residue and the pole position, respectively. Although there are additional CCP terms that have trivial Dirac structure, we omitted those in Eq. (5) since they vanish in Eq. (4) due to chirality-projection operators.

The forward scattering tensor in Eq. (4) can be divided into separate nonanalytical structures

$\displaystyle T^{\mu\nu}=\tilde{T}^{\mu\nu}+T^{\mu\nu}_{\rm CCP}+T^{\mu\nu}_{\mathrm{CCP}^{\prime}}.$

(6)

In Eq. (6), $\tilde{T}$ represents a contribution that possesses physical cut along the timelike real axis, which is conventionally analyzed by the perturbation theory, while the other two terms are associated with the CCPs in Eq. (5).

It should be noted that the CCPs do not contribute to the result as long as the integration range is defined by the one in Eq. (3) since the two terms in Eq. (5) give a real-valued combination to the integrand. However, this is not the case when nontrivial deformation of integration contour is implemented, as explicitly discussed later.

The integration defined on r.h.s. of Eq. (3) can be carried out as follows: the phase space integral range defined by $E_{\ell}\leq q^{0}\leq q^{0}_{\rm max}$ is deformed in such a way that the contour wraps around the branch cut for $B\to X_{c}\ell\bar{\nu}$ decays. After this is implemented, the contour is given by $C_{a}$ in Fig. 1. The presence of the CCPs does not affect this procedure since each of the upper and lower domains of $C_{a}$ gives a real-valued integrand in Eq. (3), which vanishes individually.

As is conventionally discussed [11, 12, 13, 14], the perturbative evaluation of the forward scattering tensor in the local OPE encounters an uncontrollable obstacle at the vicinity of the resonance region so that further deformation should be performed. Provided that the CCPs are absent, the contour integral along $C_{a}$ in Fig. 1 is related to the one for $C_{b}$ up to sign due to Cauchy’s theorem. However, in the presence of the CCPs, the mentioned deformation leads to

$\displaystyle\frac{d^{2}\Gamma}{dE_{\ell}d\alpha}$

$\displaystyle=$

$\displaystyle\left.\frac{d^{2}\Gamma}{dE_{\ell}d\alpha}\right|_{\rm pert}+\left.\frac{d^{2}\Gamma}{dE_{\ell}d\alpha}\right|_{\rm CCPs}.$

(7)

In Eq. (7), the two terms read

	$\displaystyle\left.\frac{d^{2}\Gamma}{dE_{\ell}d\alpha}\right|_{\rm pert}$	$\displaystyle=$	$\displaystyle-\mathcal{F}(C_{b},\tilde{T}),$		(8)
	$\displaystyle\left.\frac{d^{2}\Gamma}{dE_{\ell}d\alpha}\right|_{\rm CCPs}$	$\displaystyle=$	$\displaystyle\mathcal{F}(C_{p},T_{\rm CCP})+\mathcal{F}(C_{p^{\prime}},T_{{\rm CCP}^{\prime}}),$		(9)

where we defined

$\displaystyle\mathcal{F}(\mathcal{C},\mathcal{T})=\frac{G_{F}^{2}|V_{cb}|^{2}}{4\pi^{3}}\frac{m_{b}}{\pi}\textrm{Im}\int_{\cal C}(q^{0}-E_{\ell})L_{\mu\nu}\mathcal{T}^{\mu\nu}dq^{0}.$

Since $C_{b}$ is taken sufficiently away from the resonance region as shown in Fig. 1, the perturbation theory gives a reliable prediction in Eq. (8) so that we can replace $\tilde{T}^{\mu\nu}\to T^{\mu\nu}_{\rm pert}$. In what follows, the contribution of CCPs in Eq. (9) is mainly considered since the perturbative contribution is discussed in the previous works [11, 12, 13, 14].

The integrals on r.h.s. of Eq. (9) are evaluated straightforwardly by the residue theorem. Subsequently, the integral over $\alpha$ can be also performed, resulting in the lepton energy distribution from the CCPs

	$\displaystyle\left.\frac{1}{\Gamma_{b}}\frac{d\Gamma}{dy_{\ell}}\right|_{\rm CCPs}$	$\displaystyle=$	$\displaystyle 24\mathrm{Re}\left(R\left\{-\frac{1}{3}[1-(1-y_{\ell})^{-3}]\right.\right.$		(10)
		$\displaystyle\times$	$\displaystyle(1-y_{\ell}+\hat{Q})+\left.\left.\frac{1}{2}[1-(1-y_{\ell})^{-2}]\right.\right.$
		$\displaystyle\times$	$\displaystyle\left.\left.(1+\hat{Q})\right\}\times(1-y_{\ell}+\hat{Q})^{2}\right).$

In Eq. (10), we introduced $\Gamma_{b}=G_{F}^{2}m_{b}^{5}|V_{cb}|^{2}/192\pi^{3}$, the dimensionless pole position denoted as $\hat{Q}=Q/m_{b}^{2}$, and the rescaled charged lepton energy, $y_{\ell}=2E_{\ell}/m_{b}$. Equation (10) can be generalized to the case with multiple pairs of CCPs by simply adding extra terms.

It is worth noting that Eq. (10) can be also derived from the partonic rate defined with $x_{\ell}=1-\rho_{c}/(1-y_{\ell})$

$\displaystyle\frac{1}{\Gamma_{b}}\frac{d\Gamma}{dy_{\ell}}=2y_{\ell}[3x_{\ell}^{2}y_{\ell}(2-y_{\ell})+x_{\ell}^{3}(y_{\ell}^{2}-3y_{\ell})],\quad$

(11)

by the replacement of $\rho_{c}=m_{c}^{2}/m_{b}^{2}\to-\hat{Q}$, multiplying $-2R$ as an overall factor, and taking the real part. This is interpreted as the relation between the pointlike on-shell condition for charm quark, dictated by $\delta(p_{c}^{2}-m_{c}^{2})$, and the CCPs; the integrals for these two quantities fix $q^{0}$ to $(m_{b}^{2}-X+q^{2})/2m_{b}$ with $X=m_{c}^{2}$ and $-Q^{(*)}$, leading to the mentioned correspondence.

In the heavy quark limit, meson masses are approximated by the ones of quarks, $M_{B}\simeq m_{b}$ and $M_{D}\simeq m_{c}$. Integrating Eq. (10) with respect to $y_{\ell}$ for $0\leq y_{\ell}\leq 1-\rho_{c}$, one can obtain the total width from the CCPs

$\displaystyle\frac{1}{\Gamma_{b}}\Gamma^{\mathrm{CCPs}}=\sum_{m=-3}^{3}c_{m}F_{m},$

(12)

where $F_{m}=(1-\rho^{m+1}_{c})/(m+1)$ for $m\neq-1$, $F_{-1}=-\mathrm{log}(\rho_{c})$, and

	$\displaystyle c_{3}$	$\displaystyle=$	$\displaystyle-8\mathrm{Re}(R),$
	$\displaystyle c_{2}$	$\displaystyle=$	$\displaystyle 12\mathrm{Re}[R(1-\hat{Q})],$
	$\displaystyle c_{1}$	$\displaystyle=$	$\displaystyle 24\mathrm{Re}(R\hat{Q}),$
	$\displaystyle c_{0}$	$\displaystyle=$	$\displaystyle-4\mathrm{Re}[R(1+3\hat{Q}-3\hat{Q}^{2}-\hat{Q}^{3})],$
	$\displaystyle c_{-1}$	$\displaystyle=$	$\displaystyle-24\mathrm{Re}(R\hat{Q}^{2}),$
	$\displaystyle c_{-2}$	$\displaystyle=$	$\displaystyle 12\mathrm{Re}[R(1-\hat{Q})\hat{Q}^{2}],$
	$\displaystyle c_{-3}$	$\displaystyle=$	$\displaystyle 8\mathrm{Re}(R\hat{Q}^{3}).$

For $|V_{cb}|$, we consider the CCP corrections to the integrated semileptonic width in a way analogous to the discussion in Ref. [8],

$\displaystyle|V_{cb}|=\frac{|V_{cb}^{\mathrm{OPE}}|}{\sqrt{1+\frac{\tilde{\Gamma}^{\mathrm{CCPs}}}{\tilde{\Gamma}^{\mathrm{OPE}}}}}.$

(13)

In Eq. (13), we defined $\tilde{\Gamma}^{\rm CCPs}=\Gamma^{\rm CCPs}/|V_{cb}|^{2}$ and $\tilde{\Gamma}^{\mathrm{OPE}}\simeq G_{F}^{2}(m_{b}^{\mathrm{kin}})^{5}/192\pi^{3}$, where the latter with $m_{b}^{\mathrm{kin}}$ defined in the kinetic scheme [50] arises from the perturbative contour, while $|V_{cb}^{\rm OPE}|$ represents the CKM matrix element determined by the conventional method.

$B$-meson lifetime—Contributions of the CCPs from charm quark can be also extracted for nonleptonic decays. We consider the total width of $B_{d}^{0}$ meson, which consists of $b\to c\ell\bar{\nu}~{}(\ell=e,\mu)$, $b\to c\tau\bar{\nu}$, and $b\to c\bar{q}q^{\prime}~{}(q=u,c,q^{\prime}=d,s)$. It should be noted that transitions which proceed via $b\to u$ are negligible up to high accuracy due to the CKM suppression.

The effective Hamiltonian relevant for $\Delta B=1$ nonleptonic decays reads [51]

$\displaystyle\mathcal{H}_{W}=\frac{4G_{F}}{\sqrt{2}}V_{cb}V_{qq^{\prime}}^{*}(C_{1}O_{1}+C_{2}O_{2}),$

(14)

where the Wilson coefficients are denoted by $C_{i}~{}(i=1,2)$ while the four-quark operators are

	$\displaystyle O_{1}=(\bar{c}^{\alpha}\gamma_{\mu}P_{L}b^{\alpha})(\bar{q}^{\prime\beta}\gamma^{\mu}P_{L}q^{\beta}),$
	$\displaystyle O_{2}=(\bar{c}^{\alpha}\gamma_{\mu}P_{L}b^{\beta})(\bar{q}^{\prime\beta}\gamma^{\mu}P_{L}q^{\alpha}).$

In the above relations, $\alpha$ and $\beta$ represent color indices.

In the Born approximation, widths of nonleptonic B decays differ from leptonic cases up to overall factors of $\tilde{C}=N_{c}C_{1}^{2}+N_{c}C_{2}^{2}+2C_{1}C_{2}$ and a CKM matrix element: Relations between the widths in the massless limits for $u,d,s,e,\mu$ and neutrinos are

	$\displaystyle\frac{d\Gamma^{b\to c\bar{u}q^{\prime}}}{dy_{q\prime}}$	$\displaystyle=$	$\displaystyle|V_{uq^{\prime}}|^{2}\tilde{C}\left.\frac{d\Gamma^{b\to c\ell\bar{\nu}}}{dy_{\ell}}\right|_{y_{\ell}\to y_{q^{\prime}}},\qquad\quad$		(15)
	$\displaystyle\frac{d\Gamma^{b\to c\bar{c}q^{\prime}}}{dy_{\bar{c}}}$	$\displaystyle=$	$\displaystyle|V_{cq^{\prime}}|^{2}\tilde{C}\left.\frac{d\Gamma^{b\to c\tau\bar{\nu}}}{dy_{\tau}}\right|_{y_{\tau}\to y_{\bar{c}},~{}\rho_{\tau}\to\rho_{\bar{c}}},\qquad\quad$		(16)

where we defined $y_{i}=2E_{i}/m_{b}$ with $i$ being an appropriate flavor, $\rho_{\tau(\bar{c})}=[m_{\tau(c)}/m_{b}]^{2}$, and $x_{\tau}=1-\rho_{\bar{c}}/(1+\rho_{\tau}-y_{\tau})$. In Eq. (15), the massless semileptonic decay rate is defined in Eq. (11) while the case with $\tau$ in Eq. (16) is [52]

	$\displaystyle\frac{1}{\Gamma_{b}}\frac{d\Gamma^{b\to c\tau\bar{\nu}}}{dy_{\tau}}$	$\displaystyle=$	$\displaystyle 2\sqrt{y_{\tau}^{2}-4\rho_{\tau}}\{3x_{\tau}^{2}(y_{\tau}-2\rho_{\tau})(2-y_{\tau})$		(17)
			$\displaystyle+x_{\tau}^{3}[y_{\tau}^{2}-3y_{\tau}(1+\rho_{\tau})+8\rho_{\tau}]\}.$

The relations between nonleptonic and semileptonic modes in Eqs. (15, 16) are valid also for the CCP contributions. By utilizing these relations and the correspondence between the partonic rate and the one from CCPs, discussed around Eq. (11), we can obtain CCP contributions to the nonleptonic widths; the results are ones on l.h.s. in Eqs. (15, 16) with the replacement of $\rho_{c}\to-\hat{Q}$, multiplying $-2R$ as an overall factor, and taking the real part. These can be also extracted from the direct calculation by the residue theorem. Integrating l.h.s. in Eqs. (15, 16) for $0\leq y_{q^{\prime}}\leq 1-\rho_{c}$ and $2\sqrt{\rho_{\bar{c}}}\leq y_{\bar{c}}\leq 1$, respectively, the nonleptonic widths are evaluated.

For the processes including $b\to c\bar{c}q^{\prime}$, CCPs from $\bar{c}$ quark contribute in addition to ones from $c$ quark. This can be obtained by proper procedure with Eq. (16) described as follows: after interchanging $c\leftrightarrow\bar{c}$, one carries out the replacement of $\rho_{\bar{c}}\to-\hat{Q}$, multiplies $-2R$, and takes the real part as is done before. Implemented in this way, one can find that the CCP contributions from $\bar{c}$ to the integrated width are identical to the ones from $c$. In what follows, these two types of contributions are both included for evaluating the widths of $b\to c\bar{c}q^{\prime}$ decays.

By summing over the final states, including nonleptonic and semileptonic modes, one can obtain the CCP contributions from charm quark to B-meson lifetime

$\displaystyle\tau(B_{d}^{0})=\frac{1}{\Gamma_{\mathrm{all}}^{\mathrm{CCPs}}+\Gamma^{\mathrm{OPE}}},$

(18)

where $\Gamma^{\mathrm{OPE}}$ is the OPE contribution while $\Gamma_{\mathrm{all}}^{\mathrm{CCPs}}$ is that from the CCPs.

Numerical Result—For the input parameters, the kinetic mass and the pole masses are respectively set to $m_{b}^{\rm kin}=4.573~{}\mathrm{GeV}$ [3], $m_{b}=4.78~{}\mathrm{GeV}$ [7], and $m_{c}=1.67~{}\mathrm{GeV}$ [7]. The pole position for the CCP is fixed by $\textit{Q}=(-2.325+1.145i)~{}\mathrm{GeV}^{2}$ [38]. It should be noted that the size of the CCP contributions is characterized by the residue denoted as $R=|R|e^{i\theta}$ with $-\pi<\theta\leq\pi$, since this serves as an overall factor of the nonanalytical term. In what follows, the absolute value of the residue is set to $|R|=0.115$, a value smaller than that in Ref. [38].

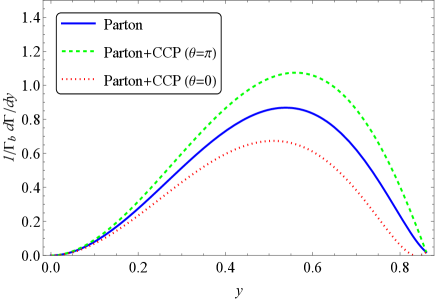
In Fig. 2, the lepton energy distributions for $B\to X_{c}\ell\bar{\nu}$ decays based on Eqs. (10, 11) are displayed for illustrating the typical magnitude of the CCP contributions with $\theta=\pi$ and $0$. One can find from Fig. 2 that the case with $\theta=\pi~{}(0)$ gives a positive (negative) contribution to the partonic rate.

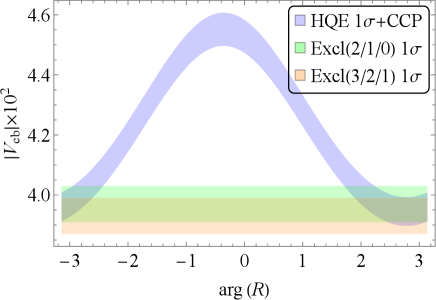
For the analysis of $|V_{cb}|$, a recent inclusive determination for $|V_{cb}^{\mathrm{OPE}}|$ is adopted in Eq. (13). As to exclusive determinations that are compared with this work, there are results based on parameterizations of form factors from Boyd-Grinstein-Lebed (BGL) [56], Caprini-Lellouch-Neubert (CLN) [57], one relying on the HQET [58, 53], etc. We adopt the third formalism, since analyticity is not intrinsically assumed for this parametrization. Those input parameters are summarized below

	$\displaystyle|V_{cb}^{\rm OPE}|$	$\displaystyle=$	$\displaystyle(42.16\pm 0.50)\times 10^{-3}~{}[3],$
	$\displaystyle|V_{cb}^{\rm exc}|$	$\displaystyle=$	$\displaystyle(39.7\pm 0.6)\times 10^{-3}~{}\quad\text{(2/1/0)}~{}[53],$
	$\displaystyle|V_{cb}^{\rm exc}|$	$\displaystyle=$	$\displaystyle(39.3\pm 0.6)\times 10^{-3}~{}\quad\text{(3/2/1)}~{}[53],$

where the last two results correspond to exclusive fitting scenarios that include different powers in the recoil-variable expansion.

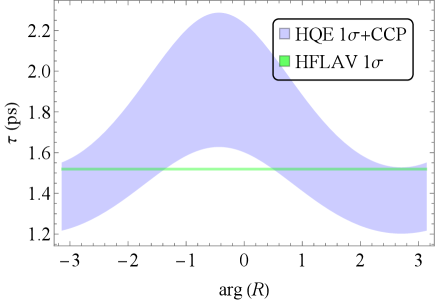
For the inputs to evaluate $\tau(B_{d}^{0})$ in Eq. (18), the conventional OPE result is given by $\Gamma^{\mathrm{OPE}}=(0.615^{+0.108}_{-0.069})$ $\mathrm{ps^{-1}}$ [54], predicted by the parameter set in Ref. [3]. The Wilson coefficients are given at next-to-leading order in QCD corrections, $C_{1}(m_{b})=1.07$ and $C_{2}(m_{b})=-0.17$ based on Ref. [51]. The CKM matrix elements for $|V_{ij}|~{}(i=u,c,j=d,s)$ and exclusive $|V_{cb}|=39.8\times 10^{-3}$ are extracted from PDG [7].

In Fig. 3, inclusive $|V_{cb}|$ including the contributions of CCPs based on Eq. (13) is exhibited as a function of $\textrm{arg}(R)$, and compared with the exclusive results. One can find that the inclusive result around $\textrm{arg}(R)=\pm\pi$ is consistent with the exclusive ones within $1\sigma$. Moreover, $B_{d}^{0}$-meson lifetime including the CCP contributions is displayed, and compared with the experimental data [55] in Fig. 4. It should be noted that the theoretical uncertainty of lifetimes are much larger than that for the experimental data. One can find from Fig. 4 that the theoretical $\tau(B_{d}^{0})$ is consistent with the experimental data within 1$\sigma$ in a neighborhood of $\theta=\pm\pi$, similar to Fig. 3. Hence, there exists a parameter region where $|V_{cb}|$ and $\tau(B_{d}^{0})$ are simultaneously explained within the $1\sigma$ range.

Conclusion—In this Letter, we have discussed the phenomenological consequence of nontrivial analytical structure from the quark propagator. In the presence of the CCPs, deformation of the integration contour, implemented for avoiding the resonance region, leads to the additional nonperturbative corrections. This gives rise to the limitation of the accuracy in the OPE analysis even if smearing over phase space is performed sufficiently. We have extracted this contribution by utilizing the residue theorem, and found that the result is also obtainable from a straightforward manner where charm quark mass square in the partonic rate is replaced by the complex-valued one, with a proper modification of the overall coefficient.

As for phenomenological observables, the integrated rate for $B\to X_{c}\ell\bar{\nu}$ and $B_{d}^{0}$-meson lifetime are analyzed. In particular, the possibility that the $|V_{cb}|$ puzzle is attributed to the CCPs is considered. In order for the inclusive $|V_{cb}|$ to be consistent with ones from the exclusive determinations, an absolute value for the residue parameter somewhat smaller than that in Ref. [38] is indicated, unless one tunes the parameters for the pole position and the argument of the residue. We have found that there exists a parameter region explaining $|V_{cb}|$ and $\tau(B_{d}^{0})$ simultaneously within $1\sigma$, which is exhibited with the particular values of the parameters with the small residue. Viewed from another way, the absolute value of the residue must be sufficiently suppressed in such a way that the CCPs do not give too large corrections to observables. Obviously, further phenomenological implication of the CCPs, not limited to heavy quark physics, is required as certain investigation for nonperturbative aspects of gauge theories.

Acknowledgment—We gratefully thank Gael Finauri for the comment. This work is supported by the Seeds Funding of Jilin University.