C11Tester: A Race Detector for C/C++ Atomics
Technical Report

Weiyu Luo University of California, IrvineIrvine, CaliforniaUSA weiyul7@uci.edu and Brian Demsky University of California, IrvineIrvine, CaliforniaUSA bdemsky@uci.edu

Abstract.

Writing correct concurrent code that uses atomics under the C/C++ memory model is extremely difficult. We present C11Tester, a race detector for the C/C++ memory model that can explore executions in a larger fragment of the C/C++ memory model than previous race detector tools. Relative to previous work, C11Tester’s larger fragment includes behaviors that are exhibited by ARM processors. C11Tester uses a new constraint-based algorithm to implement modification order that is optimized to allow C11Tester to make decisions in terms of application-visible behaviors. We evaluate C11Tester on several benchmark applications, and compare C11Tester’s performance to both tsan11rec, the state of the art tool that controls scheduling for C/C++; and tsan11, the state of the art tool that does not control scheduling.

1. Introduction

The C/C++11 standards added a weak memory model with support for low-level atomics operations (cpp11spec; c11spec) that allows experts to craft efficient concurrent data structures that scale better or provide stronger liveness guarantees than lock-based data structures. The potential benefits of atomics can lure both experts and novice developers to use them. However, writing correct concurrent code using these atomics operations is extremely difficult.

Simply executing concurrent code is not an effective approach to testing. Exposing concurrency bugs often requires executing a specific path that might only occur when the program is heavily loaded during deployment, executed on a specific processor, or compiled with a specific compiler. Some prior work helps record and replay buggy executions (deloren). Debuggers like Symbiosis (symbiosis) and Cortex (cortex) focus on sequential consistency and test programs by modifying thread scheduling of given initial executions. However, both the thread scheduling and relaxed behavior of C/C++ atomics are sources of nondeterminism in a C/C++ programs that use atomics. Thus, it is necessary to develop tools to help test for concurrency bugs. We present the C11Tester tool for testing C/C++ programs that use atomics.

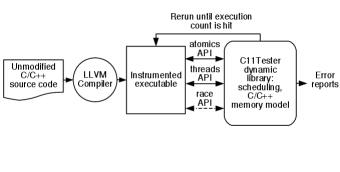
Figure 1 presents an overview of the C11Tester system. C11Tester is implemented as a dynamically linked library together with an LLVM compiler pass, which instruments atomic operations, non-atomic accesses to shared memory locations, and fence operations with function calls into the C11Tester dynamic library. The C++ and pthread library functions are overridden by the C11Tester library—C11Tester implements its own threading library using fibers to precisely control the scheduling of each thread. The C11Tester library implements a race detector and C11Tester reports any races or assertion violations that it discovers.

Refer to caption — Figure 1. C11Tester system overview

The C/C++ memory model defines the modification order relation to totally order all atomic stores to a memory location. This relation captures the notion of cache coherence. The modification order is not directly observable by the program execution — it is only observed indirectly through its effects on program visible behaviors such as the values returned by loads. Under the C/C++ memory model, modification order cannot be extended to be a total order over all stores that is consistent with the happens-before relation.

This paper presents a new technique for scaling a constraint-based treatment of the modification order relation to long executions. This technique allows C11Tester to support a larger fragment of the C/C++ memory model than previous race detectors. In particular, this technique can handle the full range of modification orders that are permitted by the C/C++ memory model.

Constraint-based modification order delays decisions about the modification order until the decisions have observable effects on the program’s behavior. For example, when an algorithm decides which store a load will read from, C11Tester adds the corresponding constraints to the modification order. This approach allows testing algorithms to focus on program visible behaviors such as the value a load reads and does not require them to eagerly decide the modification order.

Fibers provide a more efficient means to control thread schedules than kernel threads. However, C/C++ programs commonly make use of thread local storage (TLS) and fibers do not directly support TLS. This paper presents a new technique, thread context borrowing, that allows fiber-based scheduling to support thread local storage without incurring dependencies on TLS implementation details that can vary across different library versions.

1.1. Comparison to Prior Work on Testing C/C++11

Prior work on data race detectors for C/C++11 such as tsan11 (tsan11) and tsan11rec (tsan11rec) require $\textit{hb}\cup\textit{rf}\cup\textit{mo}\cup\textit{sc}$ be acyclic and thus miss potentially bug-revealing executions that both are allowed by the C/C++ memory model and can be produced by mainstream hardware including ARM processors. We have found examples of bugs that C11Tester can detect but tsan11 and tsan11rec miss due to the set of $\textit{hb}\cup\textit{rf}$ edges orders writes in the modification order.

C11Tester’s constraint-based approach to modification order supports a larger fragment of the C/C++ memory model than tsan11 and tsan11rec. C11Tester adds minor constraints to the C/C++ memory model to forbid out-of-thin-air (OOTA) executions for relaxed atomics. Furthermore, these constraints appear to incur minimal overheads on existing ARM processors (oota) while x86 and PowerPC processors already implement these constraints.

1.2. Contributions

This paper makes the following contributions:

•

Scalable Concurrency Testing Tool: It presents a tool for the C/C++ memory model that can test full programs.
•

Supports a Larger Fragment of the C/C++ Memory Model: It presents a tool that supports a larger fragment of the C/C++ memory model than previous tools.
•

Constraint-Based Modification Order: The modification order relation is not directly visible to the application, instead it constrains the behaviors of visible relations such as the reads-from relation. Eagerly selecting the modification order limits the choices of stores that a load can read from and thus limits the information available to algorithms. We develop a scalable constraint-based approach to modeling the modification order relation that allows algorithms to ignore the modification order relation and focus on program visible behaviors.
•

Support for Limiting Memory Usage: The size of the C/C++ execution graph and execution trace grows as the program executes and thus limits the length of executions that a testing tool can support. Naively freeing portions of the graph can cause a tool to produce executions that are forbidden by the memory model. We present techniques that can limit the memory usage of C11Tester while ensuring that C11Tester only produces executions that are allowed by the C/C++ memory model.
•

Fiber-based Support for Thread Local Storage: Fibers are the most efficient way to control the scheduling of the application under test, but supporting thread local storage with fibers is problematic. We develop a novel approach for borrowing the context of a kernel thread to support thread local storage.
•

Evaluation: We evaluate C11Tester on several applications and compare against both tsan11 and tsan11rec. We show that C11Tester can find bugs that tsan11 and tsan11rec miss. We present a performance comparison with both tsan11 and tsan11rec.

2. C/C++ Atomics

In this section, we present general background on the C/C++ memory model and then discuss the fragment of the C/C++ memory model that C11Tester supports. The C and C++ standards were extended in 2011 to include a weak memory model that provides precise guarantees about the behavior of both the compiler and the underlying processor. The standards divide memory locations into two types: normal types, which are accessed using normal memory primitives; and atomic types, which are accessed using atomic memory primitives. The standards forbid data races on normal memory types and allow arbitrary accesses to atomic memory types. Accesses to atomic memory types have an optional memory_order argument that explicitly specifies the ordering constraints. Any operation on an atomic object will have one of six memory orders, each of which falls into one or more of the following categories. Like all other tools for the C/C++ memory model, compilers, and work on formalization to our knowledge, C11Tester does not support the consume memory order and thus we omit consume in our presentation.

seq-cst::: memory_order_seq_cst – strongest memory ordering, there exists a total order of all operations with this memory ordering. Loads that are seq_cst either read from the last store in the seq_cst order or from some store that is not part of seq_cst total order.
release::: memory_order_release, memory_order_acq_rel, and memory_order_seq_cst – when a load-acquire reads from a store-release, it establishes a happens-before relation between the store and the load. Release sequences generalize this notion to allow intervening RMW operations to not break synchronization.
acquire::: memory_order_acquire, memory_order_acq_rel, and memory_order_seq_cst – may form release/acquire synchronization.
relaxed::: memory_order_relaxed – weakest memory ordering. The only constraints for relaxed memory operations are a per-location total order, the modification order, that is equivalent to cache coherence.

The C/C++ memory model expresses program behavior in the form of binary relations or orderings. We briefly summarize the relations:

•

Sequenced-Before: The evaluation order within a program establishes an intra-thread sequenced-before (sb) relation—a strict preorder of the atomic operations over the execution of a single thread.
•

Reads-From: The reads-from (rf) relation consists of store-load pairs $(X,Y)$ such that $Y$ takes its value from $X$ . In the C/C++ memory model, this relation is non-trivial, as a given load operation may read from one of many potential stores in the execution.
•

Synchronizes-With: The synchronizes-with (sw) relation captures the synchronization that occurs when certain atomic operations interact across threads.
•

Happens-Before: In the absence of memory operations with the consume memory ordering, the happens-before (hb) relation is the transitive closure of the union of the sequenced-before and the synchronizes-with relations.
•

Sequentially Consistent: All operations that declare the memory_order_seq_cst memory order have a total ordering (sc) in the program execution.
•

Modification Order: Each atomic object in a program has an associated modification order (mo)—a total order of all stores to that object—which informally represents an ordering in which those stores may be observed by the rest of the program.

2.1. Example

To explore some of the key concepts of the memory-ordering operations provided by the C/C++ memory model, consider the example in Figure 2, assuming that two independent threads execute the methods threadA() and threadB(). This example uses the C++ syntax for atomics; shared, concurrently-accessed variables are given an atomic type, whose loads and stores are marked with an explicit memory_order governing their inter-thread ordering and visibility properties. In the example, the memory operations are specified to have the relaxed memory ordering, which is the weakest ordering in the C/C++ memory model and allows memory operations to different locations to be reordered.

In this example, a few simple interleavings of threadA() and threadB() show that we may see executions in which $\{{\tt r1=r2=0}\}$ , $\{{\tt r1=r2=1}\}$ , or $\{{\tt r1=0}\wedge{\tt r2=1}\}$ , but it is somewhat counter-intuitive that we may also see $\{{\tt r1=1}\wedge{\tt r2=0}\}$ , in which the first load statement sees the second store but the second load statement does not see the first store. While this latter behavior cannot occur under a sequentially-consistent execution of this program, it is, in fact, allowed by the relaxed memory ordering used in the example (and achieved by compiler or processor reorderings).

Now, consider a modification of the same example, where the store and load on variable y (Line LABEL:line:store-relaxed-example and Line LABEL:line:load-relaxed-example) now use memory_order_release and memory_order_acquire, respectively, so that when the load-acquire reads from the store-release, they form a release/acquire synchronization pair. Then in any execution where r1 = 1 and thus the load-acquire statement (Line LABEL:line:load-relaxed-example) reads from the store-release statement (Line LABEL:line:store-relaxed-example), the synchronization between the store-release and the load-acquire forms an ordering between threadB() and threadA()—particularly, that the actions in threadB() after the acquire must observe the effects of the actions in threadA() before the release. In the terminology of the C/C++ memory model, we say that all actions in threadA() sequenced before the release happen before all actions in threadB() sequenced after the acquire.

So when r1 = 1, threadB() must see r2 = 1. In summary, this modified example allows only three of the four previously-described behaviors: $\{{\tt r1=r2=0}\}$ , $\{{\tt r1=r2=1}\}$ , and $\{{\tt r1=0}\wedge{\tt r2=1}\}$ .

⬇

1atomic<int> x(0), y(0);

3void threadA() {

4 x.store(1, memory_order_relaxed);

5 y.store(1, memory_order_relaxed);/*@ \label{line:store-relaxed-example} @*/

7void threadB() {

8 int r1 = y.load(memory_order_relaxed);/*@ \label{line:load-relaxed-example} @*/

9 int r2 = x.load(memory_order_relaxed);

10 printf("r1 = %d\n", r1);

11 printf("r2 = %d\n", r2);

12}

Figure 2. A Variant of Message Passing in C++

2.2. C11Tester’s C/C++ Memory Model Fragment

We next describe the fragment of the C/C++ memory model that C11Tester supports. Our memory model has the following changes based on the formalization of Batty et al. (c11popl):

1) Use the C/C++20 release sequence definition: Since the original C/C++11 memory model, the definition of release sequences has been weakened (releasesequences). This change is part of the C/C++20 standard (cpp-draft-n4849). C11Tester uses the newly weakened definition. The new definition of release sequences does not allow memory_order_relaxed stores by the thread that originally performed the memory_order_release store that heads the release sequence to appear in the release sequence.

2) Add $\textit{hb}\cup\textit{sc}\cup\textit{rf}$ is acyclic: Supporting load buffering or out-of-thin-air executions is extremely difficult and the existing approaches introduce high overheads in dynamic tools (prescientmemory; oopsla2013; toplascdschecker). Thus, we prohibit out-of-thin-air executions with a similar assumption made by much work on the C/C++ memory model — we add the constraint that the union of happens-before, sequential consistency, and reads-from relations, i.e., $\textit{hb}\cup\textit{sc}\cup\textit{rf}$ , is acyclic (vafeiadis2013relaxed).¹¹1The C/C++11 memory model already requires that $\textit{hb}\cup\textit{sc}$ is acyclic. This feature of the C/C++ memory model is known to be generally problematic and similar solutions have been proposed to fix the C/C++ memory model (mspc14; N3786; N3710; oota).

3) Strengthen consume atomics to acquire: No compilers support the consume access mode. Instead, all compilers strengthen consume atomics to acquire.

We formalize the above changes in Section LABEL:sec:restricted-model of the Appendix. Our fragment of the C/C++ memory model is larger than that of tsan11 and tsan11rec (tsan11; tsan11rec). The tsan11 and tsan11rec tools add a very strong restriction to the C/C++ memory model that requires that $\textit{hb}\cup\textit{sc}\cup\textit{rf}\cup\textit{mo}$ be acyclic.

3. C11Tester Overview

We present our algorithm in this section. In our presentation, we adapt some terminology and symbols from stateless model checking (dpor). We denote the initial state with $s_{0}$ . We associate every state transition $t$ taken by thread $p$ with the dynamic operation that affected the transition. We use $\textit{enabled}(s)$ to denote the set of all threads that are enabled in state $s$ (threads can be disabled when waiting on a mutex, condition variable, or when completed). We say that $\textit{next}(s,p)$ is the next transition in thread $p$ at state $s$ .

1:procedure Explore

s:=s_{0}

3: while

\textit{enabled}(s)

is not empty do

4: Select

p

from

\textit{enabled}(s)

t:=\textit{next}(s,p)

\textit{behaviors}(t):=\{\text{Initial behaviors}\}

7: Select a behavior

b

from

\textit{behaviors}(t)

s:=\textit{Execute}(s,t,b)

9: end while

10:end procedure

Figure 3. Pseudocode for C11Tester’s Algorithm

Figure 3 presents pseudocode for C11Tester’s exploration algorithm. C11Tester calls Explore multiple times—each time generates one program execution. Recall from Section 2 that the thread schedule does not uniquely define the behavior of C/C++ atomics. Therefore, we split the exploration into two components: (1) selecting the next thread to execute and (2) selecting the behavior of that thread’s next operation. C11Tester has a pluggable framework for testing algorithms—C11Tester generates a set of legal choices for the next thread and behavior, and then the plugin selects the next thread and behavior. The default plugin implements a random strategy.

Scheduling

Thread scheduling decisions are made at each atomic operation, threading operation, or synchronization operation (such as locking a mutex). Every time a thread finishes a visible operation, the next thread to execute is randomly selected from the set of enabled threads. However, when a thread performs several consecutive stores with memory order release or relaxed, the scheduler executes these stores consecutively without interruption from other threads. Executing these stores consecutively does not limit the set of possible executions and provides C11Tester with more stores to select from when deciding which store a load should read from. This decision also reduces bias in comparison to a purely randomized algorithm.

For example, in Figure 4, under a purely randomized algorithm, the probability that r1 = 1 is much greater than that of r1 = 2, because in order for r1 = 2, the scheduler must schedule threadA() twice before threadB() is scheduled. However, under C11Tester’s strategy, once threadA is scheduled to run, both stores at line LABEL:line:bias-first-store and line LABEL:line:bias-second-store will be performed consecutively. So when the load is encountered, the may-read-from set (defined in the paragraphs below) either only contains the initial store at line LABEL:line:bias-initial-store or contains all three stores. Thus, r1 is equally likely to read 1 or 2.

⬇

1atomic<int> x(0); /*@ \label{line:bias-initial-store} @*/

3void threadA() {

4 x.store(1, memory_order_relaxed);/*@ \label{line:bias-first-store} @*/

5 x.store(2, memory_order_relaxed);/*@ \label{line:bias-second-store} @*/

7void threadB() {

8 r1 = x.load(memory_order_relaxed);

Figure 4. Bias of a Purely Randomized Algorithm

Transition Behaviors

The source of multiple behaviors for a given schedule arises from the reads-from relation—in C/C++, loads can read from stores besides just the “last” store to an atomic object.

We use the concept of a may-read-from set, which is an overapproximation of the stores that a given atomic load may read from that just considers constraints from the happens-before relation. The may-read-from set for a load $Y$ is constructed as:

	$\displaystyle\textit{may-read-from}(Y)$	$\displaystyle=\{X\in\textit{stores}(Y)\mid\neg(Y\stackrel{{\scriptstyle\textit{hb}}}{{\rightarrow}}X)\wedge$
		$\displaystyle(\nexists Z\in\textit{stores}(Y)\text{ . }X\stackrel{{\scriptstyle\textit{hb}}}{{\rightarrow}}Z\stackrel{{\scriptstyle\textit{hb}}}{{\rightarrow}}Y)\}\text{,}$

where $\textit{stores}(Y)$ denotes the set of all stores to the same object from which $Y$ reads. C11Tester selects a store from the may-read-from set. C11Tester then checks that establishing this rf relation does not violate constraints imposed by the modification order, as described in Section 4. If the given selection is not allowed, C11Tester repeats the selection process. C11Tester delays the modification order check until after a selection is made to optimize for performance.

4. Memory Model Support

In this section, we present how C11Tester efficiently supports key aspects of the C/C++ memory model.

CDSChecker (oopsla2013) initially introduced the technique of using a constraint-based treatment of modification order to remove redundancy from the search space it explores. There are essentially two types of constraints on the modification order: (1) that a store $s_{A}$ is modification ordered before a store $s_{B}$ and (2) that a store $s_{A}$ immediately precedes an RMW $r_{B}$ in the modification order.

CDSChecker models these constraints using a modification order graph. Two types of edges correspond to these two types of constraints. Edges only exist between two nodes if they both represent memory accesses to the same location. There is a cycle in the modification order graph if and only if the graph corresponds to an unsatisfiable set of constraints. Otherwise, a topological sort of the graph (with the additional constraint that an RMW node immediately follows the store that it reads from) yields a modification order that is consistent with the observed program behavior. CDSChecker used depth first search to check for cycles in the graph. CDSChecker would add edges to the modification order graph to determine whether a given reads-from edge was plausible — if the edge made the set of constraints unsatisfiable, CDSChecker would rollback the changes that the edge made to the graph.

This approach works well for model checking where the graphs are small—the fundamental scalability limits of model checking ensure that the executions always contain a very small number of stores. This approach is infeasible when executions (and thus the modification order graphs) can contain millions of atomic stores, because the graph traversals become extremely expensive.

4.1. Modification Order Graph

We next describe the modification order graph in more detail. We represent modification order (mo) as a set of constraints, built as a constraint graph, namely the modification order graph (mo-graph). A node in the mo-graph represents a single store or RMW in the execution. There are two types of edges in the graph. An mo edge from node $A$ to node $B$ represents the constraint $A\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}B$ . A rmw edge from node $A$ to node $B$ represents the constraint that $A$ must immediately precede $B$ or formally that: $A\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}B$ and $\forall C.C\neq A\wedge C\neq B\Rightarrow(A\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C\Rightarrow B\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C)\wedge(C\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}B\Rightarrow C\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}A)$ .

C11Tester must only ensure that there exists some mo that satisfies the set of constraints, or equivalently an acyclic mo-graph. C11Tester dynamically adds edges to mo-graph when new rf and hb relations are formed. We briefly summarize the properties of mo as implications (oopsla2013) in Figure 5. C11Tester maintains a per-thread list of atomic memory accesses to each memory location. Whenever a new atomic load or store is executed, C11Tester uses this list to evaluate the implications in Figure 5 as well as additional implications for fences.

Read-Read Coherence
	$\Longrightarrow$
Write-Read Coherence
	$\Longrightarrow$
Read-Write Coherence
	$\Longrightarrow$
Write-Write Coherence
	$\Longrightarrow$
Seq-cst / MO Consistency
	$\Longrightarrow$
Seq-cst Write-Read Coherence
	$\Longrightarrow$
RMW / MO Consistency
	$\Longrightarrow$
RMW Atomicity
	$\Longrightarrow$

Figure 5. Modification order implications. On the left side of each implication,

A

B

C

X

, and

Y

must be distinct.

4.2. Clock Vectors

Due to the high cost of graph traversals for large graphs, graph traversals are not a feasible implementation approach for C11Tester. We next describe how we adapt clock vectors (l-clocks) to efficiently compute reachability in the mo-graph and scale the constraint-based modification order approach to large executions. We associate a clock vector with each node in the mo-graph. It is important to note that our use of clock vectors in the mo-graph is not to track the happens-before relation. Instead we use clock vectors to efficiently compute reachability between nodes in the mo-graph. Thus, our mo-graph clock vectors model a partial order that contains the current set of ordering constraints on the modification order.

Each event $E$ ²²2Events in each thread consist of atomic operations, thread creation and join, mutex lock and unlock, and other synchronization operations. in C11Tester has a unique sequence number $s_{E}$ . Sequence numbers are a global counter of events across all threads, which is incremented by one at each event. We denote the thread that executed $E$ as $t_{E}$ . Each node in the mo-graph represents an atomic store. The initial mo-graph clock vector $\perp_{CV_{A}}$ associated with the node representing an atomic store $A$ , the union operator $\cup$ , and the comparison operator $\leq$ for mo-graph clock vectors are defined as follows:

	$\displaystyle\perp_{CV_{A}}$	$\displaystyle=\lambda t.\text{ if }t==t_{A}\text{ then }s_{A}\text{ else }0,$
	$\displaystyle CV_{1}\cup CV_{2}$	$\displaystyle\triangleq\lambda t.max(CV_{1}(t),CV_{2}(t)),$
	$\displaystyle CV_{1}\leq CV_{2}$	$\displaystyle\triangleq\forall t.CV_{1}(t)\leq CV_{2}(t).$

Note that two mo-graph clock vectors can only be compared if their associated nodes represent atomic stores to the same memory location.

The mo-graph clock vectors are updated when new mo relations are formed. For example, if $A\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}B$ is a newly formed mo relation, then the node $B$ ’s mo-graph clock vector is merged with that of node $A$ , i.e., $CV_{B}:=CV_{A}\cup CV_{B}$ . If $CV_{B}$ is updated by this merge, the change in $CV_{B}$ must be propagated to all nodes reachable from $B$ using the union operator.

Figure 7 presents pseudocode for updating the modification order graph. The Merge procedure merges the mo-graph clock vector of the src node into the dst node and returns true if the dst mo-graph clock vector changed. The AddEdge procedure adds a new modification order edge to the graph. It first compares mo-graph clock vectors to check if the edge is redundant and if so drops the edge update. Recall that RMW operations are ordered immediately after the stores that they read from. To implement this, AddEdge checks to see if the from node has a rmw edge, and if so, follows the rmw edge. AddEdge finally adds the relevant edge, and then propagates any changes in the mo-graph clock vectors. The AddRMWEdge procedure has two parameters, where the rmw node reads from the from node. It first adds an rmw edge and then migrates any outgoing edges from the source of the edge to the rmw node. Finally, it calls the AddEdge procedure to add a normal modification order edge and to propagate mo-graph clock vector changes.

Figure 7 presents pseudocode for the helper method AddEdges that adds a set of edges to the mo-graph. The parameter set is a set of atomic stores or RMWs, and $S$ is an atomic store or RMW. The GetNode method converts an atomic action to the corresponding node in the mo-graph. If such node does not exist yet, then the method will create a new node in the mo-graph.

1:procedure Merge(Node dst, Node src)

2: if src.cv

\leq

dst.cv then

3: return false

4: end if

5: dst.cv := dst.cv

\cup

src.cv

6: return true

7:end procedure

1:procedure AddEdge(Node from, Node to)

2: mustAddEdge := (from.rmw == to

\vee

from.tid == to.tid)

3: if from.cv

\leq

to.cv

\wedge\neg

mustAddEdge then

4: return

5: end if

6: while from.rmw

\neq

null do

7: next := from.rmw

8: if next == to then

9: break

10: end if

11: from := next

12: end while

13: from.edges := from.edges

\cup

14: if Merge(to, from) then

15: Q := { to }

16: while Q is not empty do

17: node := remove item from Q

18: for each dst in node.edges do

19: if Merge(dst, node) then

20: Q := Q

\cup

dst

21: end if

22: end for

23: end while

24: end if

25:end procedure

1:procedure AddRMWEdge(Node from, Node rmw)

2: from.rmw := rmw

3: for each dst in from.edges do

4: if dst

\neq

rmw then

5: rmw.edges := rmw.edges

\cup

dst

6: end if

7: end for

8: from.edges :=

\emptyset

9: AddEdge(from, rmw)

10:end procedure

Figure 6. Pseudocode for Updating mo-graph

1:procedure AddEdges(set,

S

)

n_{S}:={\tt GetNode}(S)

3: for each

e

in set do

n_{e}:={\tt GetNode}(e)

5: AddEdge(

n_{e}

n_{S}

)

6: end for

7:end procedure

Figure 7. Helper method for adding a set of edges to the mo-graph

Theorem 4 guarantees the soundness of our use of mo-graph clock vectors. We present the theorem and its proof in Section 5. This theorem states that we can solely rely on mo-graph clock vectors to compute reachability between nodes in mo-graph.

4.3. Eliminating Rollback in Mo-graph

Prior work on constraint-based modification order utilized rollback when it was determined that a given reads-from relation was not feasible (oopsla2013; toplascdschecker). C11Tester may also hit such infeasible executions because the may-read-from set defined in Section 3 is an overapproximation of the set of stores that a load can read from. To determine precisely whether a load can read from a store, a naive approach is to add edges to the mo-graph and then utilize rollback if adding these edges introduces cycles in the mo-graph. However, the addition of clock vectors and clock vector propagation makes rollback much more expensive. It is thus critical that C11Tester avoids the need for rollback. We now discuss how C11Tester avoids rollback.

The mo-graph is updated whenever a new atomic store, atomic load, or atomic RMW is encountered. Processing a new atomic store, atomic load, or atomic RMW can potentially add multiple edges to the mo-graph. We next analyze each case to understand how to avoid rollback:

•

Atomic Store: Since an atomic load can only read from past stores, a newly created store node in mo-graph has no outgoing edges. By the properties of mo, only incoming edges from other nodes to this new node will be created. Hence, a new store node cannot introduce any cycles.
•

Atomic Load: Consider a new atomic load $Y$ that reads from a store $X_{0}$ . Forming a new rf relation may only cause edges to be created from other nodes to the node representing the store $X_{0}$ . We denote this set of ”other nodes” as $\textit{ReadPriorSet}(X_{0})$ and compute it using the ReadPriorSet procedure in Figure LABEL:alg:priorset. Lines LABEL:line:rpriorset-s1, LABEL:line:rpriorset-s2, and LABEL:line:rpriorset-s3 in the ReadPriorSet procedure consider statements 5, 4, and 6 in Section 29.3 of the C++11 standard. Line LABEL:line:rpriorset-s4 in the procedure considers write-read and read-read coherences. Therefore, the set returned by the ReadPriorSet procedure captures the set of stores from where new mo relations are to be formed if the rf relation is established.

Before forming the rf relation, C11Tester checks whether any node in $\textit{ReadPriorSet}(X_{0})$ is reachable from $X_{0}$ . If so, then having load $Y$ read from store $X_{0}$ will introduce a cycle in the mo-graph, so we discard $X_{0}$ and try another store. While it is possible for a cycle to contain two or more edges in the set of newly created edges, this also implies that there is a cycle with one edge (since all edges have the same destination).
•

Atomic RMWs: An atomic RMW is similar to both a load and store, but with the constraint that it must be immediately modification ordered after the store it reads from. We implement this by moving modification order edges from the store it reads from to the RMW. Thus, the same checks used by the load suffice to check for cycles for atomic RMWs.

Thus, C11Tester first computes a set of edges that reading from a given store would add to the mo-graph. Then for each edge, it checks the mo-graph clock vectors to see if the destination of the edge can reach the source of the edge. If none of the edges would create a cycle, it adds all of the edges to the mo-graph using the AddEdge and AddRMWEdge procedures.

5. Correctness of Mo-graph

To prove the correctness of mo-graphs, we first prove three Lemmas and then prove Theorem 4. Lemma 1 and Lemma 2 characterize some important properties of mo-graph clock vectors. Lemma 3 proves one direction in Theorem 4. Mo-graph clock vectors are simply referred to as clock vectors in the following context.

Lemma 0.

Let $C_{0}\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C_{1}\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}...\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C_{n}$ be a path in a modification order graph $G$ , such that $CV_{C_{0}}\leq...\leq CV_{C_{n}}$ . Then if any new edge $E$ is added to $G$ using procedures in Figure 7, it holds that

(5.1)

\displaystyle CV_{C_{0}}^{\prime}\leq...\leq CV_{C_{n}}^{\prime}

for the updated clock vectors. We define $CV_{C_{i}}^{\prime}:=CV_{C_{i}}$ if the values of $CV_{C_{i}}$ are not actually updated.

Proof.

To simplify notation, we define $CV_{i}:=CV_{C_{i}}$ for all $i\in\{0...,n\}$ . Let’s first consider the case where no rmw edge is added, i.e., the AddRMWEdge procedure is not called.

By the definition of the union operator, each slot in clock vectors is monotonically increasing when the Merge procedure is called. By the structure of procedure AddEdge’s algorithm, a node $X$ is added to $Q$ if and only if this node’s clock vector is updated by the Merge procedure.

Let’s assume that adding the new edge $E$ updates any of $CV_{0},...,CV_{n}$ . Otherwise, it is trivial. Let $i$ be the smallest integer in $\{0,...,n\}$ such that $CV_{i}$ is updated. Then $CV_{k}^{\prime}=CV_{k}$ for all $k\in I:=\{0,...,i-1\}$ , and we have

(5.2)

\displaystyle CV_{0}^{\prime}\leq...\leq CV_{i}^{\prime}.

If $i=0$ , then we take $I=\varnothing$ . There are two cases.

Case 1: Suppose $CV_{i}^{\prime}\leq CV_{j}$ for some $j\in\{i+1,...,n\}$ , let $j_{0}$ be the smallest such integer. Then $CV_{k}^{\prime}=CV_{k}$ for all $k\in\{j_{0},...,n\}$ , as nodes $\{C_{j_{0}},...,C_{n}\}$ will not be added to $Q$ in the AddEdge procedure, and it holds trivially that

(5.3)

\displaystyle CV_{j_{0}}^{\prime}\leq...\leq CV_{n}^{\prime}.

By line 14 to line 24 in the AddEdge procedure, we have

(5.4)

\displaystyle CV_{k}^{\prime}=CV_{k}\cup CV_{k-1}^{\prime},

for all $k\in S:=\{i+1,...,j_{0}-1\}$ . If $j_{0}$ happens to be $i+1$ , then take $S=\varnothing$ . And we have for all $k\in S$ , $CV_{k-1}^{\prime}\leq CV_{k}^{\prime}$ . Then combining with inequality (5.2), we have

CV_{0}^{\prime}\leq...\leq CV_{i}\leq...\leq CV_{j_{0}-1}^{\prime}.

Together with inequality (5.3), we only need to show that $CV_{j_{0}-1}^{\prime}\leq CV_{j_{0}}^{\prime}$ to complete the proof.

If $j_{0}=i+1$ , then we are done, because by assumption $CV_{i}^{\prime}\leq CV_{j_{0}}=CV_{j_{0}}^{\prime}$ . If $j_{0}>i+1$ , then $CV_{i}^{\prime}\leq CV_{j_{0}}$ and $CV_{i+1}\leq CV_{j_{0}}$ imply that $CV_{i+1}^{\prime}=CV_{i+1}\cup CV_{i}^{\prime}\leq CV_{j_{0}}=CV_{j_{0}}^{\prime}$ . Based on equation (5.4), we can deduce in a similar way that $CV_{i+2}^{\prime}\leq...\leq CV_{j_{0}-1}^{\prime}\leq CV_{j_{0}}^{\prime}$ .

Case 2: Suppose $CV_{i}\nleq CV_{j}$ for all $j\in\{i+1,...,n\}$ . Then by line 14 to line 24 in the AddEdge procedure, all nodes $\{C_{i},...,C_{n}\}$ are added to $Q$ in the AddEdge procedure, and $CV_{k}^{\prime}=CV_{k}\cup CV_{k-1}^{\prime}$ for all $k\in S:=\{i+1,...,n\}$ . This recursive formula guarantees that for all $k\in S$ , $CV_{k-1}^{\prime}\leq CV_{k}^{\prime}$ . Therefore, combining with inequality (5.2), we have $CV_{0}^{\prime}\leq...\leq CV_{n}^{\prime}$ .

Now suppose the newly added edge $E$ is a rmw edge. If $E:X\xrightarrow{\textit{rmw}}C_{i}$ where $i\in\{0,...,n\}$ and $X$ is some node not in path $P$ , then the path $P$ remains unchanged and AddEdge( $X$ , $C_{i}$ ) is called. Then the above proof shows that inequality (5.1) holds. If $E:C_{i}\xrightarrow{\textit{rmw}}X$ , then $C_{i}\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C_{i+1}$ is migrated to $X\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C_{i+1}$ by line 3 to line 7 in the AddRMWEdge procedure, and $C_{i}\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}X$ is added.

If $X$ is not in path $P$ , then path $P$ becomes

C_{0}\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}...\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C_{i}\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}X\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C_{i+1}\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}...\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C_{n}.

Since AddEdge( $C_{i}$ , $X$ ) is called, the same proof in the case without rmw edges applies. If $X$ is in path $P$ , then $X$ can only be $C_{i+1}$ and the path $P$ remains unchanged. Otherwise, a cycle is created and this execution is invalid. In any case, the same proof applies. ∎

Let $\vec{x}=(x_{1},x_{2},...,x_{n})$ . We define the projection function $U_{i}$ that extracts the $i^{\textit{th}}$ position of $\vec{x}$ as $U_{i}(\vec{x})=x_{i},$ where we assume $i\leq n$ .

Lemma 0.

Let $A$ be a store with sequence number $s_{A}$ performed by thread $i$ in an acyclic modification order graph $G$ . Then $U_{i}(CV_{A})=U_{i}(\perp_{CV_{A}})=s_{A}$ throughout each execution that terminates.

Proof.

We will prove by contradiction. Let $S=\{A_{1},A_{2},...\}$ be the sequence of stores performed by thread $i$ with sequence numbers $\{s_{1},s_{2},...\}$ , respectively. Suppose that there is a point of time in a terminating execution such that the first store $A_{n}$ in the sequence with $U_{i}(CV_{A_{n}})>s_{n}$ appears. Sequence numbers are strictly increasing and by the Merge procedure, $U_{i}(CV_{A_{n}})\in\{s_{n+1},s_{n+2},...,\}$ . Let $U_{i}(CV_{A_{n}})=s_{N}$ for some $N>n$ .

For $U_{i}(CV_{A_{n}})$ to increase to $s_{N}$ from $s_{n}$ , $CV_{A_{n}}$ must be merged with the clock vector of some node $X$ (i.e., some store $X$ ) in $G$ such that $U_{i}(CV_{X})=s_{N}$ . Such $X$ is modification ordered before $A_{n}$ .

If $X$ is performed by thread $i$ , then $X$ has to be the store $A_{N}$ , because $U_{i}(CV_{A_{j}})$ is unique for all stores $A_{j}$ in the sequence $S$ other than $A_{n}$ . Then $\perp_{CV_{X}}\geq\perp_{CV_{A_{n}}}$ . By the definition of initial values of clock vectors and sequence numbers, $X$ happens after and is modification ordered after $A_{n}$ . However, $X$ is also modification ordered before $A_{n}$ , and we have a cycle in $G$ . This is a contradiction.

If $X$ is not performed by thread $i$ , then $U_{i}(\perp_{CV_{X}})=0$ . For $U_{i}(CV_{X})$ to be $s_{N}$ , $X$ must be modification ordered after by some store $Y$ in $G$ such that $U_{i}(CV_{Y})=s_{N}$ . If $Y$ is done by thread $i$ , then the same argument in the last paragraph leads to a contradiction; otherwise, by repeating the same argument as in this paragraph finitely many times (there are only a finite number of stores in such a terminating execution), we would eventually deduce that $X$ is modification ordered after some store by thread $i$ . Hence, we would have a cycle in $G$ , a contradiction.

∎

Lemma 0.

Let $A$ and $B$ be two nodes that write to the same location in an acyclic modification order graph $G$ . If $B$ is reachable from $A$ in $G$ , then $CV_{A}\leq CV_{B}$ .

Proof.

Suppose that $B$ is reachable from $A$ in $G$ . Let $A\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C_{1}\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}...\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}C_{n-1}\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}B$ be the shortest path $P$ from $A$ to $B$ in graph $G$ . To simplify notation, $X\stackrel{{\scriptstyle\textit{mo}}}{{\rightarrow}}Y$ is abbreviated as $X\rightarrow Y$ in the following. As the AddRMWEdge procedure calls the AddEdge procedure to create an mo edge, we can assume that all the mo edges in $P$ are created by directly calling AddEdge.

Base Case 1: Suppose the path $P$ has length 1, i.e., $A$ immediately precedes $B$ . Then when the edge $A\rightarrow B$ was formed by calling AddEdge( $A$ , $B$ ), $CV_{B}$ was merged with $CV_{A}$ in line 14 of the AddEdge procedure. In other words, $CV_{B}=CV_{B}\cup CV_{A}\geq CV_{A}.$

Base Case 2: Suppose the path $P$ has length 2, i.e., $A\rightarrow C_{1}\rightarrow B$ . There are two cases:

(a) If $A\rightarrow C_{1}$ was formed first, then $CV_{A}\leq CV_{C_{1}}$ . When $C_{1}\rightarrow B$ was formed, $CV_{B}$ was merged with $CV_{C_{1}}$ and $CV_{C_{1}}\leq CV_{B}$ . According to Lemma 1, adding the edge $C_{1}\rightarrow B$ or any edge not in path $P$ (if any such edges were formed before $C_{1}\rightarrow B$ was formed) to $G$ would not break the inequality $CV_{A}\leq CV_{C_{1}}$ . It follows that $CV_{A}\leq CV_{C_{1}}\leq CV_{B}$ .

(b) If $C_{1}\rightarrow B$ was formed first, then $CV_{C_{1}}\leq CV_{B}$ . Based on Lemma 1, this inequality remains true when $A\rightarrow C_{1}$ was formed. Therefore $CV_{A}\leq CV_{C_{1}}\leq CV_{B}$ .

Inductive Step: Suppose that $B$ being reachable from $A$ implies that $CV_{A}\leq CV_{B}$ for all paths with length $k$ or less, for some $k>2$ . We want to prove that the same holds for paths with length $k+1$ . Let $P$ be a path from $A$ to $B$ with length $k+1$ ,

P:A=C_{0}\rightarrow C_{1}\rightarrow...\rightarrow C_{k}\rightarrow C_{k+1}=B.

We denote $A$ as $C_{0}$ and $B$ as $C_{k+1}$ in the following.

Let $E:C_{i}\rightarrow C_{i+1}$ be the last edge formed in path $P$ , where $i\in\{0,...,k\}$ . Then before edge $E$ was formed, the inductive hypothesis implies that $CV_{C_{0}}\leq...\leq CV_{C_{i}}$ and $CV_{C_{i+1}}\leq...\leq CV_{C_{k+1}}$ , because both $C_{0}\rightarrow...\rightarrow C_{i}$ and $C_{i+1}\rightarrow...\rightarrow C_{k+1}$ have length $k$ or less. Lemma 1 guarantees that

	$\displaystyle CV_{C_{0}}$	$\displaystyle\leq...\leq CV_{C_{i}},$
	$\displaystyle CV_{C_{i+1}}$	$\displaystyle\leq...\leq CV_{C_{k+1}}$

remain true if any edge not in path $P$ was added to $G$ as well as the moment when $E$ was formed. Therefore when the edge $E$ was formed, we have $CV_{C_{i}}\leq CV_{C_{i+1}}$ , and

CV_{A}=CV_{C_{0}}\leq...\leq CV_{C_{k+1}}=CV_{B}.

∎

Theorem 4.

Let $A$ and $B$ be two nodes that write to the same location in an acyclic modification order graph $G$ for a terminating execution. Then $CV_{A}\leq CV_{B}$ iff $B$ is reachable from $A$ in $G$ .

Proof.

Lemma 3 proves the backward direction, so we only need to prove the forward direction. Suppose that $CV_{A}\leq CV_{B}$ . Let’s first consider the situation where the graph $G$ contain no rmw edges.

Case 1: $A$ and $B$ are two stores performed by the same thread with thread id $i$ . Then it is either $A$ happens before $B$ or $B$ happens before $A$ . If $A$ happens before $B$ , then $A$ precedes $B$ in the modification order because $A$ and $B$ are performed by the same thread. Hence $B$ is reachable from $A$ in $G$ . We want to show that the other case is impossible.

If $B$ happens before $A$ and hence precedes $A$ in the modification order, then $A$ is reachable from $B$ . By Lemma 3, $A$ being reachable from $B$ implies that $CV_{B}\leq CV_{A}$ . Since $CV_{A}\leq CV_{B}$ by assumption, we deduce that $CV_{A}=CV_{B}$ . This is impossible according to Lemma 2, because each store has a unique sequence number and $U_{i}(CV_{A})=s_{A}\neq s_{B}=U_{i}(CV_{B})$ , implying that $CV_{A}\neq CV_{B}$ .

Case 2: $A$ and $B$ are two stores done by different threads. Suppose that $A$ is performed by thread $i$ . Let $CV_{A}=(...,s_{A},...)$ and $CV_{B}=(...,t_{b},...)$ where both $s_{A}$ and $t_{b}$ are in the $i^{\textit{th}}$ position. By assumption, we have $0<s_{A}\leq t_{b}$ .

Since $B$ is not performed by thread $i$ , we have $U_{i}(\perp_{CV_{B}})=0$ . We can apply the same argument similar to the second, third and fourth paragraphs in the proof of Lemma 2 and deduce that $B$ is modification ordered after $A$ or some store sequenced after $A$ . Since modification order is consistent with sequenced-before relation, if follows that $B$ is reachable from $A$ in graph $G$ .

Now, consider the case where rmw edges are present. Adding a rmw edge from a node $S$ to a node $R$ first transfers to $R$ all outgoing mo edges coming from $S$ and then adds a normal mo edge from $S$ to $R$ . So, any updates in $CV_{S}$ are propagated to all nodes that are reachable from $S$ . Therefore, the above argument still applies. ∎

6. Operational Model

We present our operational model with respect to the tsan11 (tsan11) core language described by the grammar in Figure 8. A program is a sequence of statements. LocNA and LocA denote disjoint sets of non-atomic and atomic memory locations. A statement can be one of these forms: an if statement, assigning the result of an expression to a non-atomic location, forking a new thread, joining a thread via its thread handle, and atomic statements. The symbol $\epsilon$ denotes an empty statement. Atomic statements denoted by StmtA include atomic loads, store, RMWs, and fences. An RMW takes a functor, F, to implement RMW operations, such as atomic_fetch_add. We omit loops for simplicity and leave the details of an expression unspecified. We omit lock and unlock operations because they can be implemented with atomic statements.

⬇

Prog ::= Stmt ;

\epsilon

Stmt ::= Stmt ; Stmt

| if (LocNA) {Stmt} else {Stmt}

| LocNA := Expr

| LocNA = Fork(Prog)

| Join(LocNA)

| StmtA

\epsilon

StmtA ::= LocNA = Load(LocA, MO)

| Store(LocNA, LocA, MO)

| RMW(LocA, MO, F)

| Fence(MO)

MO ::= relaxed | release | acquire | rel_acq

| seq_cst

Expr ::= <literal> | LocNA | Expr op Expr

Figure 8. Syntax for our core language

States:

	Tid	$\displaystyle\triangleq\mathbb{Z}$	Seq	$\displaystyle\triangleq\mathbb{Z}$	$\displaystyle\mathbb{C}$	$\displaystyle:\hbox{{Tid}}\rightarrow\hbox{{CV}}$
	$\displaystyle\mathbb{F}^{\textit{rel}}$	$\displaystyle:\hbox{{Tid}}\rightarrow\hbox{{CV}}$	$\displaystyle\mathbb{RF}$	$\displaystyle:\hbox{{Seq}}\rightarrow\hbox{{CV}}$	$\displaystyle\mathbb{F}^{\textit{acq}}$	$\displaystyle:\hbox{{Tid}}\rightarrow\hbox{{CV}}$

[RELEASE STORE] {mathpar} \inferrule* RF’ = RF [ s := C _t] ( C, RF, F^rel , F^acq ) ⇒^store_rel(s, t) ( C, RF’, F^rel , F^acq )

[RELAXED STORE] {mathpar} \inferrule* RF’ = RF [ s := F^rel _t] ( C, RF, F^rel , F^acq ) ⇒^store_rlx(s, t) ( C, RF’, F^rel , F^acq )

[RELEASE RMW] {mathpar} \inferrule* RF’ = RF [ s := C _t ∪RF _s’] ( C, RF, F^rel , F^acq ) ⇒^rmw_rel(s, t), rf(s’, t’) ( C, RF’, F^rel , F^acq )

[RELAXED RMW] {mathpar} \inferrule* RF’ = RF [ s := F^rel _t ∪RF _s’] ( C, RF, F^rel , F^acq ) ⇒^rmw_rlx(s, t), rf(s’, t’) ( C, RF’, F^rel , F^acq )

[ACQUIRE LOAD] {mathpar} \inferrule* C’ = C [ t := C _t ∪RF _s’ ] ( C, RF, F^rel , F^acq ) ⇒^load_acq(s, t), rf(s’, t’) ( C’, RF, F^rel , F^acq )

[RELAXED LOAD] {mathpar} \inferrule* F^acq ’ = C [ t := F^acq _t ∪RF _s’ ] ( C, RF, F^rel , F^acq ) ⇒^load_rlx(s, t), rf(s’, t’) ( C, RF, F^rel , F^acq ’ )

[RELEASE FENCE] {mathpar} \inferrule* F^rel ’ = F^rel [ t := C _t ] ( C, RF, F^rel , F^acq ) ⇒^fence_rel(t)

C11Tester: A Race Detector for C/C++ Atomics Technical Report

Abstract.

1. Introduction

1.1. Comparison to Prior Work on Testing C/C++11

1.2. Contributions

2. C/C++ Atomics

2.1. Example

2.2. C11Tester’s C/C++ Memory Model Fragment

3. C11Tester Overview

Scheduling

Transition Behaviors

4. Memory Model Support

4.1. Modification Order Graph

4.2. Clock Vectors

4.3. Eliminating Rollback in Mo-graph

5. Correctness of Mo-graph

Lemma 0.

Proof.

Lemma 0.

Proof.

Lemma 0.

Proof.

Theorem 4.

Proof.

6. Operational Model

C11Tester: A Race Detector for C/C++ Atomics
Technical Report