Calculated Unconventional Superconductivity via Charge Fluctuations in Kagome Metal CsV₃Sb₅

Unconventional mechanisms of superconductivity have always been a subject of intense interest in the research of quantum materials with such much celebrated examples as high–temperature superconducting cupratesCuprates , ironatesIronates and recently, nickelatesNickelates , where antiferromagnetic spin fluctuations are thought to be the primary source of the Cooper pairingHTC-1 ; HTC-2 . There is however another class of systems, for which the proximity not to the spin but to the charge density wave (CDW) instability can be linked to the formation of the Cooper pairs. The most notable example is the 30K superconductivity in potassium doped BaBiO₃BKBO where the Bi ions in the parent insulating compound exist in a charge disproportionated state.

The discoveryCsV3Sb5 of a family of non–magnetic metals CsV₃Sb₅, KV₃Sb₅, RbV₃Sb₅ with vanadium ions forming a Kagome lattice framework is currently generating a great interest due to the appearance of multiple charge–ordered states at high temperaturesChargeOrders , as well as of bulk superconductivity with T_c=2.5K in CsV₃Sb₅CsV3Sb5Supra and with T_c=0.8K in KV₃Sb₅KV3Sb5Supra whose normal state electronic structure categorizes these systems as Z₂ topological metalsCsV3Sb5Supra . Remarkably, pressure dependent studies of CsV₃Sb₅ have shown that the CDW order can be suppressed by applying a 2GPa pressure which leads to the enhanced T_c value of 8KCsV3Sb5Pressure .

Although the observed small values of $T_{c}$ are well within the reach of the conventional mechanism, theoretically calculated electron–phonon coupling constants are generally found to be smallEPI-PRL . There exists a factor–of–two discrepancy between predictions of the theory and the kinks in the band dispersions of the Fermi electrons measured by Angle Resolved Photoemission Spectroscopy (ARPES)EPI-ARPES . More importantly, several experiments performed on CsV₃Sb₅ point to a strong momentum dependence of the superconducting energy gap. Scanning tunneling microscopy (STM)STM-PRX ; STM-PRL ; STM-Nature has detected a V–shaped density of superconducting states, indicating the presence of nodes in the order parameter. On the other hard, the magnetic penetration depth experimentsSW-NPJQM ; SW-PRR ; SW-NatureComm ; SW-Nano suggest nodeless but anisotropic superconductivity. Despite been presently controversial, both observations are incompatible with the constant energy gaps which are observed in the vast majority of electron–phonon superconductors and indicate the unconventional nature of the pairing state.

Electronic instabilities on the Kagome lattice have been a subject of recent theoretical works. Its minimal three–band model of itinerant electrons with short–range hoppings is known for a wealth of features including the existence of a Dirac point at the Brillouin Zone (BZ) point $K$=(1/3,1/$\sqrt{3}$,0)2$\pi/a$ of hexagonal lattice, a van Hove singularity (VHS) at the point $M$=(0,1/$\sqrt{3}$,0)2$\pi/a$, and a dispersionless (flat) band for all wavevectors. When the Fermi level is pinned at the VHS, the Fermi surface is represented by a perfect hexagon and becomes nested along the whole line $\Gamma M$ of the BZ. In this regime, the extended Hubbard model with the on–site and intersite Coulomb interactions $U$ and $V$ has been studied using a variational cluster approachJXLi and a functional renormalization group theoryQHWang ; Thomale ; it reveals a rich variety of quantum phases including the appearance of magnetic order, charge density waves and superconductivity. The symmetries of the superconducting order parameter recovered from these studies include anisotropic s–wave state and $d_{x^{2}-y^{2}},d_{xy}$ two–fold degenerate state, for which a fully gapped chiral combination $d_{x^{2}-y^{2}}+id_{xy}$ was found to be energetically most favorable. Later studies of the Kagome based tight–binding models included renormalization group supplemented with Landau theory analysis of various charge density wave modulations seen in CsV₃Sb₅ Balents , and the low–energy effective model for various CDW induced flux phases JHu to explain the observed time–reversal symmetry breaking in KV₃Sb₅TRSHasan .

To address the issue of unconventional pairing state in CsV₃Sb₅, here we use our recently developed approachLDA+FLEX ; Hg-FLEX that evaluates superconducting pairing functions directly from first–principle electronic structure calculations of the studied material using realistic energy bands and wave functions available from density functional theory (DFT)DFT . The electronic self–energies are calculated for a manifold of correlated electrons similar to as it is done in popular DFT+DMFT approachDFT+DMFT , but they acquire full momentum and frequency resolution within this method, which diagrammatically corresponds to the so–called fluctuational–exchange (FLEX) type FLEX random phase approximation (RPA) incorporating all type of nesting–driven instabilities in the charge and spin susceptibilities. The description of unconventional superconductors in a realistic material framework without reliance on the tight–binding approximations of the electronic structures became possible using this DFT+FLEX(RPA) method. Our most recent applicationsHg-FLEX to HgBa₂CuO₄, a prototype single–layer cuprate superconductor, easily recovered a much celebrated $d_{x^{2}-y^{2}}$ symmetry of the order parameter, and the prediction of competing $s_{\pm},d_{xy}$ pairing states was givenLa-FLEX for a recently discovered high–temperature superconducting nickelate compound La₃Ni₂O₇.

The main physical picture emergent from the experimental data for CsV₃Sb${}_{5},$ is that a nearly singular behavior in the charge susceptibility plays an important role in the $2.5K$ superconductivity at ambient pressureCsV3Sb5Supra , where a variety of charge ordered phases is seen at higher temperatuesSTM-Nature , and that the rise of $T_{c}$ to 8K by applying a pressure of 2GPa CsV3Sb5Pressure is related to the suppression of the CDW. This prompts us to consider the on–site and the neighboring–site Coulomb interaction parameters $U$ and $V$ for vanadium $d$–electrons to be of the same order of magnitude with the parameter $V$ tuning the system to the instability point to allow strong charge fluctuations.

To uncover whether such charge fluctuational mechanism can explain or contribute to superconductivity in CsV₃Sb₅, we numerically evaluate the pairing interaction describing the scattering of the Cooper pairs as a function of the intersite $V$ while fixing the on–site $U\$to its representative value of 0.1 Ry (=1.36 eV). This pairing function is then used to exactly diagonalize the linearized Bardeen–Cooper–Schrieffer (BCS) gap equation on a three–dimensional k–grid of the Fermi points in the BZ. The highest eigenvalue $\lambda_{\max}$ deduced from this procedure represents a coupling constant similar to the electron–phonon $\lambda$ in conventional theory of superconductivity. We generally find $\lambda_{\max}$ to be negligible unless $V$ is tuned to the close proximity to the CDW occurring in our procedure at around 1.8 eV. We recover two nearly degenerate solutions of the superconducting order parameter from these calculations: first, of $B_{2g}$ ($d_{x^{2}-y^{2}},d_{xy}$–like) and, second, of $A_{1g}$ (anisotropic s-wave–like) symmetry. Using spectral representation for the pairing interaction, we evaluate charge fluctuation induced Eliashberg spectral functions $\alpha^{2}F(\omega)$ which were found to be strongly peaked at the frequency 7 meV. To allow estimates for the $T_{c}$, charge fluctuational contribution to the electronic mass enhancement $m^{\ast}/m_{band}=1+\lambda_{cf}$  is evaluated to produce the effective coupling constants $\lambda_{eff}=\lambda_{\max}/(1+\lambda_{cf})$ for the leading paring channels. These were found in the range of 0.2–0.4 depending on $V$ and leads to the $T_{c}\$estimates close to the values that are observed experimentally.

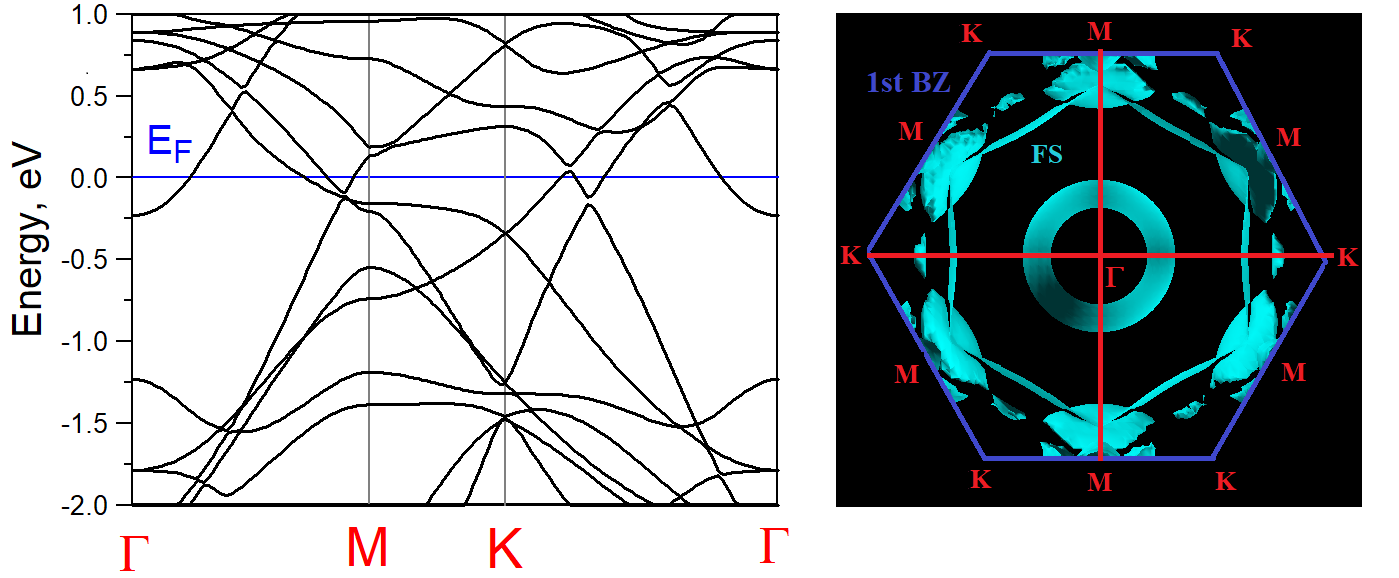
We perform our density–functional electronic–structure calculations using the full potential linear muffin–tin orbital methodFPLMTO . The result for the electronic energy bands is shown in Fig. 1(a) along major high–symmetry directions of the hexagonal BZ. In accord with the previous study CsV3Sb5Supra , it shows the band dispersions in the vicinity of the Fermi level $E_{F}$ originating from the vanadium d–orbitals. Despite their complexity, the VHS saddle point just below the Fermi level at point $M,$ the Dirac point at $K,$ and the nearly dispersionless bands at 1 eV above the $E_{F}$ are clearly distinguished. The Fermi surface shown in Fig. 1(b) is quasi–two dimensional with the visible hexagonal pattern. All these features are characteristic of the minimal tight–binding model on Kagome lattice known for its nesting along $\Gamma M.$

We further utilize our DFT+ FLEX(RPA) method to evaluate the charge fluctuation mediated pairing interaction. The Fermi surface is triangularized onto small areas described by about 6,000 Fermi surface momenta for which the matrix elements of scattering between the Cooper pairs are calculated using the approach described in Ref. Hg-FLEX . The linearized BCS gap equation is then exactly diagonalized and the set of eigenstates is obtained for both singlet ($S=0$) and triplet ($S=1$) Cooper pairs. The highest eigenvalue $\lambda_{\max}$ represents the physical solution and the eigenvector corresponds to superconducting energy gap $\Delta(\mathbf{k}j)$ where $\mathbf{k}$ is the Fermi surface momentum and $j$ numerates the Fermi surface sheets.

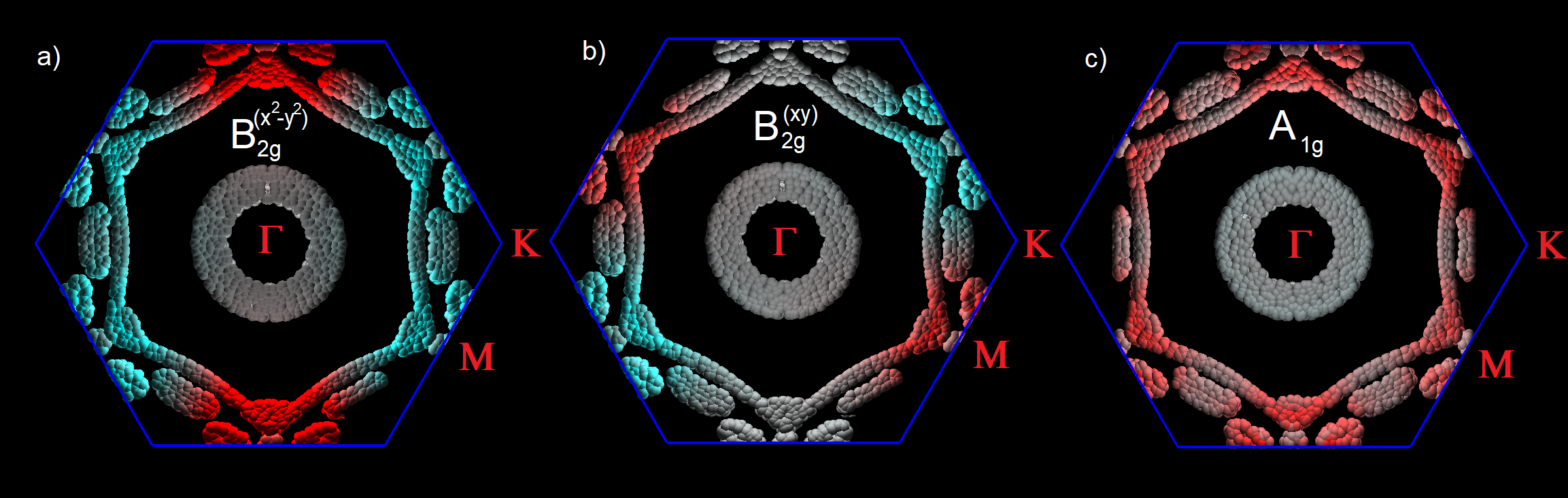
We find that there are three highest eigenvalues that appear very close to each other. The leading pairing channel is two–fold degenerate and the subleading one is non–degenerate with its eigenvalue appearing only within 6% of the maximum eigenvalue. We analyze the behavior of $\Delta(\mathbf{k}j)$ as a function of the Fermi momentum using the values of $U$=1.36 eV and $V$ = 1.75 eV. The solutions are related to the spin singlet states, and Fig. 2(a),(b) shows the behavior of the two–fold degenerate $\Delta(\mathbf{k}j)$, while Fig. 2(c) corresponds to the non–degenerate one. One can see that the two–fold degenerate eigenstate shows the behavior corresponding to the $B_{2g}$ symmetry ($d_{x^{2}-y^{2}}$–like in a) and $d_{xy}$–like in b), The plot distinguishes negative and positive values of $\Delta(\mathbf{k}j)$ by blue and red colors while zeros of the gap function are colored in grey. The non–degenerate solution of $A_{1g}$ symmetry is plotted in Fig. 2(c) where the gap function is strongly anisotropic exhibiting its maxima close to the M points of the BZ and nearly zeroes in between.

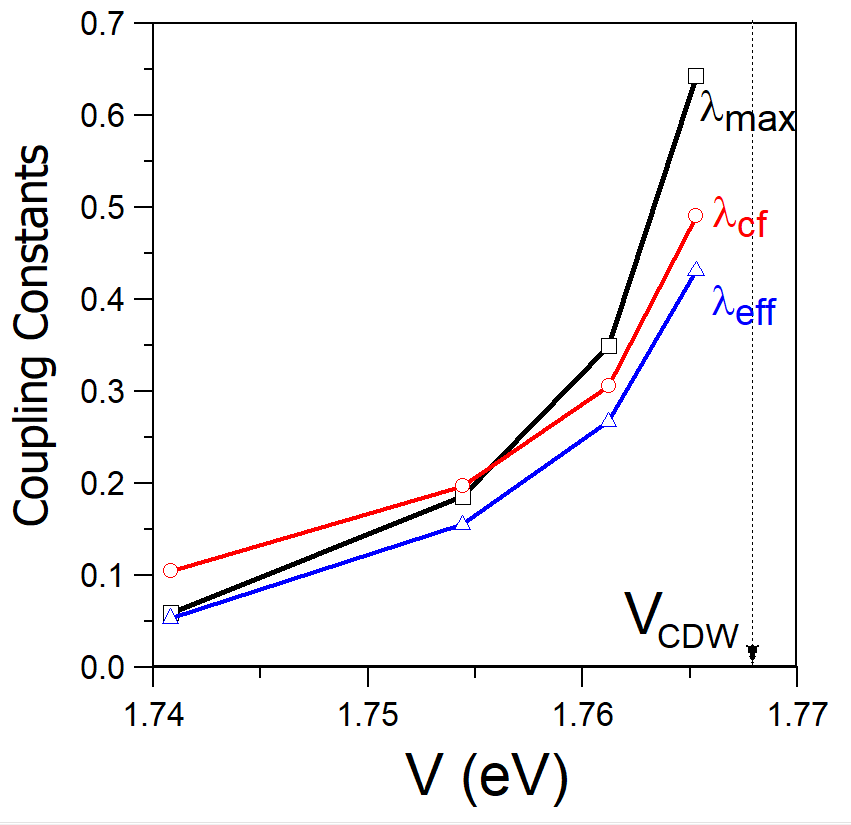
We can gain additional insight on the behavior of the eigenvalues by varying the intersite Coulomb interaction $V.$ We first evaluate the divergency of the charge susceptibility that occurs at $V_{CDW}$ slightly less than 1.77 eV. We use the range of values $V<V_{CDW}$ to extract from the BCS gap equation the behavior of the highest eigenstates $\lambda_{\max}$ and their symmetries as a function of $V$.  We find that both $B_{2g}$ and $A_{1g}$ symmetries robustly dominate over all other solutions with the two–fold degenerate $B_{2g}$ state to be only 6% larger than the non–degenerate one. Obviously, however, if the electron–phonon coupling constant $\lambda_{e-p}\ \approx 0.25$EPI-PRL is taken into account, the $A_{1g}$ pairing will become the leading one.

It is interesting to discuss the dependence of $\lambda_{\max}$ as a function of $V$ that is shown in Fig. 3 (squares connected by black lines). We see that the values of $\lambda_{\max}$ are very small unless $V$ approaches closely to $V_{CDW}$ where it reaches the values 0.2–0.6. This indicates that the charge fluctuations produce essential contribution to the pairing only in the immediate vicinity of the CDW instability.

To get insight on possible range of critical temperatures that can be obtained using the charge fluctuation mechanism, we recall that it is not the eigenvalue $\lambda_{\max}$ but the effective coupling constant $\lambda_{eff}$ enters the BCS $T_{c}$ expression: $T_{c}\approx\omega_{cut}\exp(-1/\lambda_{eff}).$ If we neglect phonons, the cutoff frequency $\omega_{cut}$ is thought here due to charge fluctuations, and $\lambda_{eff}$ incorporates the effects associated with the mass renormalization describing by the parameter $\lambda_{cf}.$ It should also be weakened somewhat by the Coulomb pseudopotential $\mu_{m}^{\ast}$ which should refer to the same pairing symmetry $m$ as $\lambda_{\max}$:

$$\lambda_{eff}=\frac{\lambda_{\max}-\mu_{m}^{\ast}}{1+\lambda_{cf}}$$

(1)

The mass enhancement can be evaluated as the Fermi surface (FS) average of the electronic self–energy derivative taken at the Fermi level

$$\lambda_{cf}=-\langle\frac{\partial\Sigma(\mathbf{k},\omega)}{\partial\omega}|_{\omega=0}\rangle_{FS}$$

(2)

Our calculated dependence of $\lambda_{cf}\$on $V$ is shown in Fig. 3 (circles connected by red lines). It is seen to exhibit the behavior very similar to $\lambda_{\max}:$ the values of $\lambda_{cf}$ are found to be modest unless $V$ lies in the vicinity of $V_{CDW}$ where $\lambda_{cf}$ is found between 0.2 and 0.5.

To give estimates for the effective coupling constant, $\lambda_{eff},$ we notice that $\mu_{m}^{\ast}$ is expected to be very small for the pairing symmetries different from the standard s–wave Alexandrov . We therefore expect this parameter to be zero for the $B_{2g}$ pairing state. The plot of $\lambda_{eff}=\lambda_{\max}/(1+\lambda_{cf})$ vs. $V$ is shown in Fig 3. One can see that the range of these values is between 0.2 and 0.4 in the proximity to the CDW.

One can easily incorporate the electron–phonon $\lambda_{e-p}\approx 0.25$EPI-PRL into this discussion. The kink in the band dispersion of the Fermi electrons will become a sum $\lambda_{cf}+\lambda_{e-p}.$ It essentially doubles as compared to the individual contributions due to phonons or charge fluctuations and will match the recent ARPES study of the electronic mass enhancement in CsV₃Sb₅EPI-ARPES . Our estimate for the $\lambda_{eff}$ in the $B_{2g}$ pairing state will be lower by 15% or so due to a slightly larger denominator in Eq.(1). For the $A_{1g}$ pairing state, our estimated $\lambda_{\max}$ due to charge fluctuations should be supplemented with $\lambda_{e-p}\approx 0.25\$but the value of $\mu^{\ast}\approx 0.12$ should be taken into account in Eq.(1). This will increase our estimate for $\lambda_{eff}$ by 10%t or so.

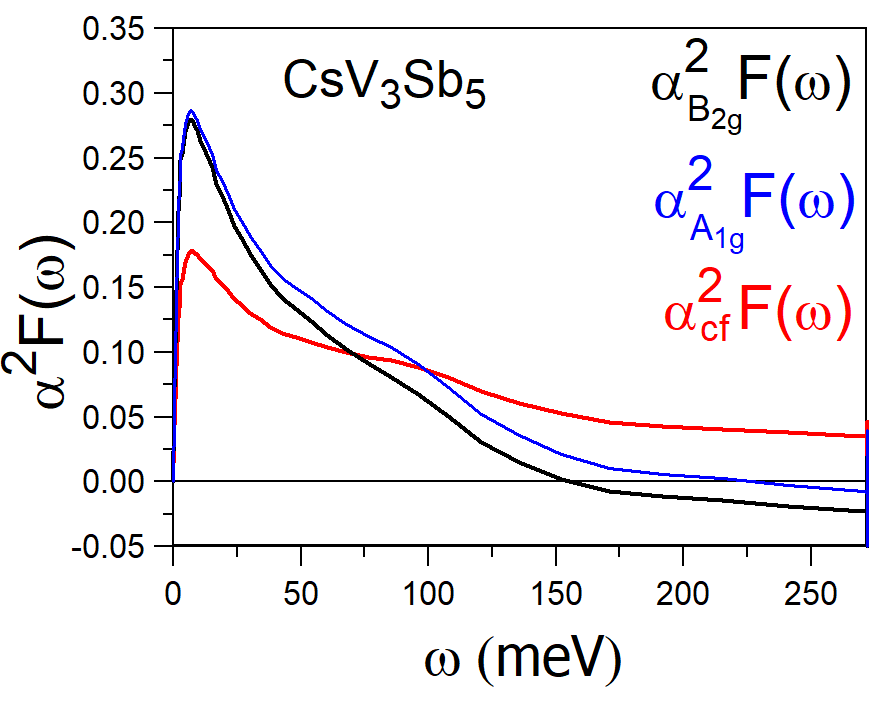
To obtain the estimates for the range of charge fluctuational energies that set the scale $\omega_{cut}\$in the BCS T_c expression, we calculate Eliashberg spectral functions $\alpha^{2}F(\omega)$ that are responsible for the pairing. Since in our method the Cooper pairs scatter on the statically screened Coulomb interaction, Re$K_{\mathbf{k}j\mathbf{,k}^{\prime}j^{\prime}}(0),$ the Kramers–Kroenig transformation provides its frequency resolution, proportional to Im$K_{\mathbf{k}j\mathbf{,k}^{\prime}j^{\prime}}(\omega)/\omega.$ The frequency resolved function Im$K_{\mathbf{k}j\mathbf{,k}^{\prime}j^{\prime}}(\omega)$ is averaged over the eigenvectors of the BCS gap equation $\Delta(\mathbf{k}j),\Delta(\mathbf{k}^{\prime}j^{\prime})$ to give rise to the superconducting $\alpha^{2}F(\omega),$ whose double inverse frequency moment evaluates the eigenvalue $\lambda_{\max}$. We perform this procedure for the leading eigenstates of $B_{2g}$ and $A_{1g}$ symmetries, and also calculate the spectral function $\alpha_{cf}^{2}F(\omega)$ whose inverse moment produces the mass enhancement parameter $\lambda_{cf}.$

We present this data in Fig.4, where the black/blue lines show the superconducting $\alpha^{2}F(\omega)$ of the $B_{2g}$ and $A_{1g}$ symmetries, respectively, while the red line describes the charge fluctuational $\alpha_{cf}^{2}F(\omega).$ A strong peak at the frequencies around 7 meV is seen in all three plots and indicates a characteristic frequency of the charge fluctuations. This can be compared to the Debye frequency of 142K=12 meV deduced from the calculated phonon spectrum of CsV₃Sb₅EPI-PRL .

We can judge about the values of $T_{c}$ obtained within the charge fluctuational mechanism using our estimated $\omega_{cut}\approx$ 7 meV and the values of $\lambda_{eff}$ that we calculate in Fig. 3. For $\lambda_{eff}=0.2,$ the BCS$\ T_{c}\approx\omega_{cut}\exp(-1/\lambda_{eff})\approx$ 0.5K. Once we get closer to the CDW instability, the effective coupling increases to the values 0.4 and the corresponding BCS $T_{c}\approx$ 7K. Should the contribution from the phonons be included in the $A_{1g}$ pairing channel, a refined estimate for $\lambda_{eff}$ is inflated by about 10% and the BCS $T_{c}^{\prime}s$ are about 20% larger than the values quoted above. Given the exponential sensitivity, these estimates are clearly within the range of the $T_{c}$’s observed experimentally.

In conclusion, we numerically estimated the charge fluctuation mediated pairing tendencies in the recently discovered Kagome metal CsV₃Sb${}_{5}.$ These cacluations are done directly using first–principle electronic structures without resorting to tight–binding approximations of any kind. Two competing pairing channels have been recovered in our study: the two–fold degenerate $B_{2g}$ nodal states ($d_{x^{2}-y^{2}},d_{xy}$ –like) and the non–degenerate $A_{1g}$ nodeless state (anisotropic s–wave–like) with the effective coupling constants in the range 0.2–0.4 depending on the strength of the nearest neighbor Coulomb repulsion between the vanadium $d$–electrons. Similar values are predicted to contribute to the electronic mass enhancement due to charge fluctuations. These estimates provide substantial contributions both to the electronic kinks of the Fermi electrons in the normal state, and to the strength of the Cooper pairing in the superconducting state.