Calculation of Coulomb breakup cross sections using a new Coulomb dynamical polarization potential
Abstract
A new method for calculating the Coulomb breakup of unstable neutron-rich isotopes at high energies is presented. The calculations employ the eikonal approximation and use a new Coulomb dynamical polarization potential (CDPP), calculated by solving the Schrödinger equation for the entire motion of the exotic projectile as a two-body cluster structure using the adiabatic approximation and incorporating excitations to the continuum. Calculations for some exotic isotopes are compared with Coulomb dissociation cross section data and found to be in good agreement.
I Introduction
Recently Mar21 , we presented a new expression for the Coulomb dynamical polarization potential (CDPP) which was obtained by solving the Schrödinger equation for the internal motion of an exotic neutron-rich projectile (considered as a two-body deuteronlike cluster structure) incident on a heavy target nucleus using the adiabatic approximation. In this work we generalize this CDPP to include both excited states of the core and excitations to the continuum. This generalized CDPP is then used to calculate the differential Coulomb dissociation (CD) cross section as a function of relative excitation energy. These calculations start from the continuity equation using the imaginary part of the CDPP. The eikonal approximation is then used to calculate the CD cross section for a number of weakly-bound neutron-rich exotic nuclei at high incident energies.
II Theory
II.1 Continuum based CDPP
In Ref. Mar21 we gave the formalism for the scattering of a weakly-bound two-body projectile (p) consisting of a core in its ground state plus a cluster of valence neutrons from a heavy-ion target and the CDPP was obtained. If the core is in an excited state, this expression for the CDPP can be easily generalized by replacing the binding energy of the valence neutron or neutron cluster with respect to the charged core of the projectile, , with an effective separation energy , where is the excitation energy of the core state of spin-parity . To solve the Schrödinger equations of the system and obtain the CDPP one may use the adiabatic approximation , where refers to the wave function of the center of mass and to that of the relative motion of the projectile; and are the coordinates of the projectile-target and the projectile valence-core systems, respectively. By making the same approximations as in Ref. Mar21 the real and imaginary parts of the CDPP can be given as:
| (1) |
where and are the regular and irregular Coulomb functions in and with where is the core-valence reduced mass, the mass of the charged core, and
| (2) |
is the wave number of the charged core in the field of the target that is associated with the wave function of the internal motion of the projectile, . It depends parametrically on the Coulomb potential between the projectile and target, and is different from the wave number of the center-of-mass motion of the system that describes the motion of the projectile along the Rutherford trajectory, where is the incident energy of the projectile and is the reduced mass of projectile-target system. This CDPP (II.1) depends on the structure of the system but does not depend on the incident energy of the projectile.
Excitations of the projectile to the continuum can be included by adding the continuum energy , a continuous variable, to so that now becomes a function of :
| (3) |
making the same approximations as before, and we accordingly obtain the Continuum based CDPP, :
| (4) |
where is now also a function of as well as .
We now consider an -transition () from a bound state with angular momentum to the -wave continuum, with where is the transition multipolarity. The initial bound state is described by the wave function of the valence neutron in the orbital relative to the core , , whereas the final state (continuum) is represented by the wave function , where in the subscript denotes the dependence on the continuum energy. Here we include the notation to indicate that the core is in state . Then, we define a new CDPP that describes this transition as
| (5) |
where can be represented by expansion in Legendre polynomials as
| (6) |
Let us define the excitation energy distribution of the -transition as
| (7) |
so that we may write
| (8) |
The radial wave function of the bound state is given by , where the single-particle wave function is usually calculated using a single-particle potential model, see for example Ref. Xu94 , by adjusting the Woods-Saxon potential parameters to reproduce the experimental neutron separation energy, taking the excitation energy of the core into account where appropriate. Typical values of the potential radius parameter range from 1.15 to 1.25 fm and the diffuseness from 0.5 to 0.7 fm. It is, however, important to note that the extracted spectroscopic factor can differ by 20 or more depending on the choice of parameters Pra03 . We choose here the potential parameters ( fm, fm) suggested by Sauvan et al. Sau00 for light neutron-rich nuclei. Note that the potential includes a Thomas form spin-orbit term with a strength fixed at 7.0 MeV for all the cases studied here.
The final state (continuum) wave function is usually calculated assuming the plane wave approximation (expanded in spherical Bessel functions and Legendre polynomials) with the radial wave function normalized as , where with relative (continuum) energy , and is the orbital angular momentum of the final state.
Now, by considering the expansions of the bound-state and the continuum plane wave functions, Eq. (7) becomes
| (9) | |||||
Instead of the single-particle wave functions, the asymptotic form for overlap integrals is often used
| (10) |
where is the Whittaker function and is the asymptotic normalization coefficient (ANC). The quantity where is the effective separation energy of the valence nucleon(s) with respect to the different core states of excitation energies . When the valence cluster is formed exclusively of neutron(s) and where is a modified spherical Bessel function and is a spherical Hankel function of the first kind. Then . Now by using the Whittaker function for the bound-state wave function, Eq. (9) becomes
| (11) | |||||
In the particular case when the initial bound state has , the radial wave function can be given analytically as the Yukawa form , so that for the transition to the -wave continuum, we obtain the following analytical function:
| (12) |
which will be especially useful since the valence neutron(s) are in a relative -state in the ground state of many light exotic projectiles of interest.
II.2 Coulomb dissociation using the CDPP
This new CDPP (8) has many potential applications to the scattering and reactions of weakly-bound neutron-rich nuclei. Here we use it to calculate Coulomb dissociation, keeping other applications for future publications. Coulomb breakup or dissociation can take place when a high energy (several hundred MeV/nucleon) projectile impinges on a heavy target and is excited by absorbing virtual photons from the time-dependent Coulomb field. Under these circumstances the electromagnetic excitation is dominated by dipole excitation Pra03 . The corresponding differential cross section for dipole excitation decomposes into an incoherent sum of components corresponding to the different core states populated by neutron removal. For each core state the cross section further decomposes into an incoherent sum over contributions from the different allowed angular momenta of the valence neutron in its initial state. In these calculations the projectile is assumed to have a core plus valence neutron structure. Choosing the lowest core states there are various ways to couple the spins of the core and the valence neutron to the total angular momentum and parity of the projectile Hei17 . Note that for heavy targets the core is assumed to act as a spectator so that the projectile core remains in its initial state after removal of a neutron Han03 .
We start from the usual formula for the absorption cross section derived from the continuity equation
| (13) |
where is the imaginary potential, the usual distorted wave function, the relative velocity, and the wavenumber in the center of mass system. By considering the imaginary CDPP (5) that describes the -transitions we can write the total absorption due to Coulomb dissociation and excitation by taking a summation over the -transitions, the different core states , and contributions from different angular momenta of the valence neutron in its initial state for each core state:
| (14) | |||||
Then, the differential cross section for the -transition with the core in state is
| (15) |
which is similar to the well-known Hussein–McVoy formula and the similar formulae for the inclusive breakup Hus85 ; Ram21 . Introducing
| (16) |
as the total absorption cross section for the core state, the breakup cross section for the core in state and the -transition from is
| (17) |
Equations (15) and (17) can be generalized to account for excitations of the target. An imaginary nuclear potential can be added to account for any other reaction channels. From Equation (17) and using the virtual photon method Ber88 one may obtain the photo-absorption cross section , the radiative neutron capture cross section , the dipole response function , and the double differential cross section . These calculations can also be generalized to consider transitions between two bound states by replacing the continuum wave function with a bound state wave function similar to .
Equation (16) can be solved by the method of partial wave expansion and the complete scattering amplitude is obtained by summing over all the partial wave scattering amplitudes. At high energies, i.e. hundreds of MeV/nucleon, the wave function will oscillate rapidly and the calculation of scattering wave functions for each partial wave becomes more complicated. In the eikonal approximation and the optical limit of the Glauber theory Gla59 , the wave function of the projectile-target system can be written in terms of the total potential, , as
| (18) |
where and is the impact parameter. Equation (16) may then easily be written as
| (19) |
where . At this point we should include the correction of the impact parameter due to Coulomb deflection of the particle trajectory: , where is half the distance of closest approach in a head-on collision of point charged particles. The relativistic correction to the kinematics can be appropriately made if one replaces the quantity with , where is the Lorentz factor Ber03 . Since the phase in Eq. (19) is integrated over it is invariant under Lorentz transformations, so no further relativistic corrections to the dynamical equations are required Mos19 .
III Application to some reactions
We now apply our model to calculate the Coulomb dissociation cross sections for some exotic projectiles (11Be, 15C, 17C) incident on a lead target at a few hundreds of MeV/nucleon. Our results using both the single particle (s.p.) wave function and the analytical formula (11) which assumes a Whittaker wave function for the bound states are summarized in Table 1. All of these calculations consider only the transition to the continuum. In addition, we define which is the ratio of the experimental to the theoretical differential cross section using the best fit in the energy range of the data. This ratio can be compared with the theoretical and empirical spectroscopic factors listed in the last two columns of Table 1. The experimental data are known to be affected by the experimental resolution, so, using the method of Ref. Mor20 , the calculated cross sections were convoluted with the detector response function obtained from simulated spectra. Since the Coulomb dissociation data of 11Be, 15C, and 17C were all measured at GSI and their experiments employed a similar setup Pal03 ; Pra03 we use the energy resolution obtained in Ref. Pal03 for all calculations. The cross section is calculated by integration up to a continuum energy of 10 MeV for most cases.
| Proj. | E/n | Core | (mb) | (mb) | Spectroscopic factors | |||||||
| s.p. | Whitt. | s.p. | Whitt. | Shell model | experiment | |||||||
| 11Be | 520 | 10Be | 60530 Pal03 | 1563 | 1649 | 0.40 | 0.40 | 0.74 Aum00 | 0.36, 0.60 Tim99 ; 0.61(5) Pal03 ; 0.72(4) Fuk04 ; 1.0(2) Nak94 | |||
| 34.4 | 58.2 | |||||||||||
| 15C | 605 | 14C | 32415 Pra03 | 570 | 643 | 0.52 | 0.48 | 0.98 Ter04 , 0.83 Sau00 | 0.91(6), 0.72(5) Nak09 ; 0.73(5), 0.97(8) Pra03 | |||
| 363 Pra03 | 8.2 | 17.1 | 1.03 Sau00 | 1.3(1) Pra03 | ||||||||
| 8.3 | 17.9 | 0.16 Sau00 | ||||||||||
| 4.8 | 10.5 | 0.46 Sau00 ; Ter04 | ||||||||||
| 3.9 | 8.8 | 0.016 Ter04 | ||||||||||
| 17C | 496 | 16C | Pra03 | 607 | 854 | 0.015 | 0.011 | 0.035 Sau00 | ||||
| 627 Pra03 | 118.9 | 145.5 | 0.28 | 0.23 | 0.16Sau00 ; Mad01 | 0.23(8),26(14) Pra03 | ||||||
| 96.8 | 162.1 | 0.23 | 0.14 | 1.41 Sau00 , 1.44 Mad01 | 0.6(4),1.6(6) Pra03 | |||||||
| 257 Pra03 | 33.9 | 60.5 | ||||||||||
| 15.5 | 30.1 | 0.76 Sau04 ; Mad01 | ||||||||||
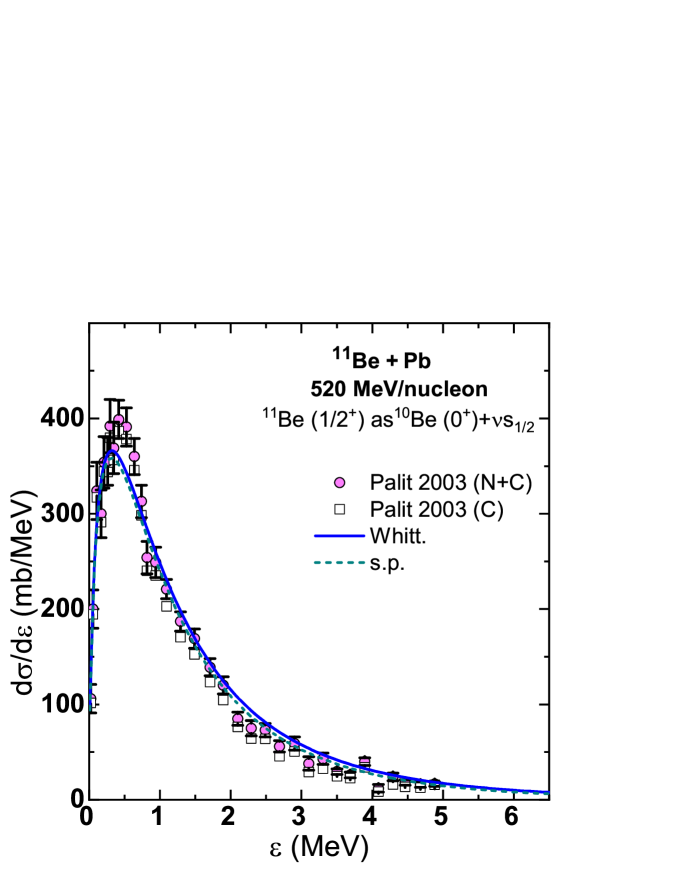
We take as our first example the Coulomb dissociation of 11Be. The ground state of 11Be is , so the ground state of the 10Be core is coupled to an -wave valence neutron and the first excited state of the core (3.368 MeV) is coupled to a -wave valence neutron. The spectroscopic factors for the single-particle configuration obtained from shell model calculations and deuteron stripping and pick-up reactions range from about –, see for example Aum00 and references therein. An analysis of the Coulomb dissociation of a 11Be projectile with an energy of 520 MeV/nucleon impinging on lead and carbon targets gives a spectroscopic factor for the single-particle configuration of 0.61(5) Pal03 . These data Pal03 include both Coulomb and nuclear contributions and the Coulomb breakup spectrum can be extracted by subtracting the nuclear contribution estimated using the data taken with the carbon target in the following way
| (20) |
where is a scaling factor. Assuming the peripheral nature of the nuclear excitation, can be taken as the ratio of the sum of the radii of the target and the projectile which is 1.8 Fuk04 ; Nak94 . Other estimates of for this reaction may be found in Refs. Fuk04 ; Nak94 ; Pal03 . The effect of the nuclear contribution on this reaction has also recently been studied in Ref. Mor20 by comparing the Equivalent Photon Method (EPM) and continuum discretized coupled channels (CDCC) calculations.
The analysis of the data using the present formalism, with the Yukawa and s.p. wave functions, gives us calculated differential cross sections in good agreement with the data, as shown in Fig. 1, and a cross section ratio of about 0.4 is obtained, which is similar to the spectroscopic factor of Ref. Tim99 . It is clear that the contribution from the configuration is small. We expect that the contribution from the higher and core states with -wave neutrons will also be small.
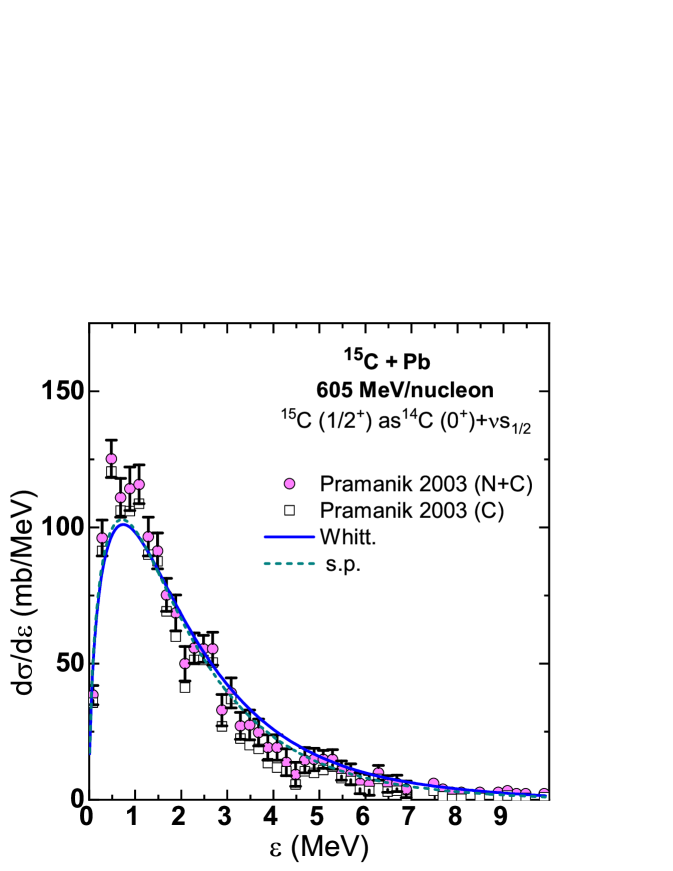
The one-neutron separation energy of 15C is 1.218 MeV and its ground-state spin-parity is , so we suppose a neutron coupled to a 14C() core. Figure 2 presents calculations of the Coulomb breakup of 15C incident on a Pb target at 605 MeV/nucleon Pra03 . The peak of the relative energy spectrum occurs at a value of 0.7 MeV. The original data Pra03 that include both Coulomb and nuclear contributions as well as the data obtained by subtracting the nuclear contribution are plotted by the filled dots and open squares, respectively. The calculated total Coulomb dissociation cross section for 15C14C++ is about 570 mb using the s.p. wave function and 643 mb using the Yukawa wave function for the configuration, and the corresponding ratios of the experimental to calculated cross sections are about 0.52 and 0.48, respectively. These ratios are compared with the spectroscopic factors calculated by the shell model Ter04 or extracted from Coulomb dissociation experiments Nak09 ; Pra03 in Table 1. There are many excited states in 14C at energies between 6–7 MeV and previous calculations with the core in these states, see Ref. Pra03 , gave small cross sections compared to the observed value of 36(3) mb. For the 6.09 MeV (), 6.90 MeV (), and 7.34 MeV () core excited states the possible neutron orbitals are or . Our calculation using the s.p. wave functions gives 4.2, 1.1, and 1 mb for dipole transitions to the -continuum and 12.4, 3.7, and 3 mb for transitions to the -continuum for the , , and core states, respectively. The calculation using the Whittaker wave functions gives 4.7, 1.3, and 1.1 mb for dipole transitions to the -continuum and 30.2, 9.2, and 7.8 mb for transitions to the -continuum for the , , and core states, respectively. If we multiply these cross sections by the corresponding spectroscopic factors from shell model calculations Sau00 ; Ter04 this gives us values of 12.1 mb and 25.4 mb from the calculations using s.p. and Whittaker functions, respectively, whereas the experimental value is 36(3) mb Pra03 . The remaining cross section may correspond to the 14C core in the other three states at 6–7 MeV.
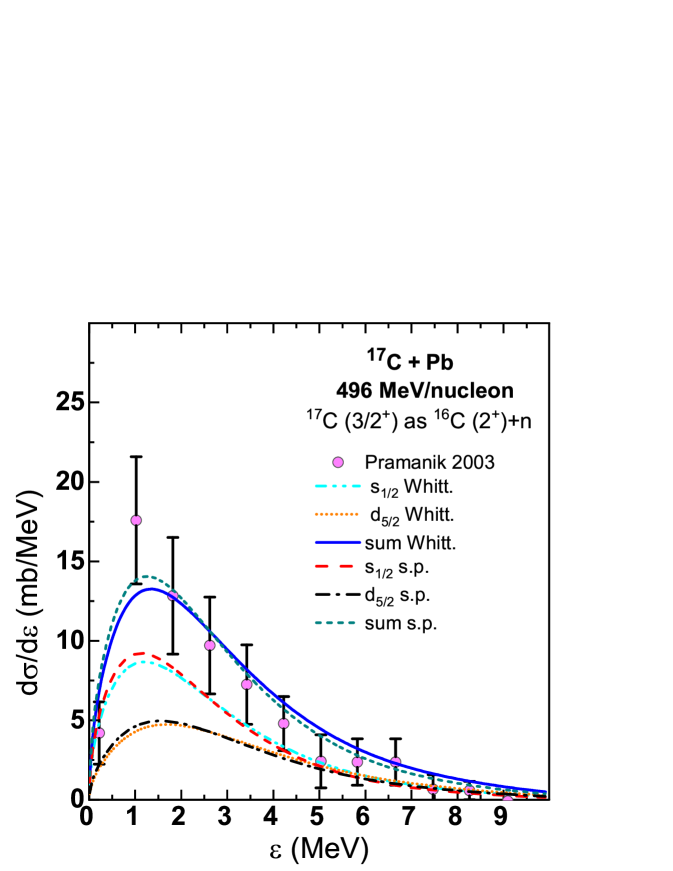
Calculations for different core excitations were performed for the 17C Coulomb breakup since this yields the 16C core mainly in excited states. The differential Coulomb dissociation cross section for is reported in Ref. Pra03 . As shown in Fig. 3, the data are well reproduced by our calculation using a Yukawa wave function for the configuration with an integrated cross section of 60 mb, similar to the reported one of 62(7) mb. The peak position is also well reproduced. The calculations using the s.p. wave functions and Whittaker wave function can fit the data with cross section ratios of about 0.28 and 0.23 for the and 0.23 and 0.14 for -orbits, respectively. The contribution of both orbits to the cross section of the 16C() excited state is not known experimentally, only the total cross section of 62(7) mb. There are thus many combinations which can fit the data, and the cross section ratio for or can be varied from zero to 0.5–0.6. As reported in Ref. Pra03 , the measured cross sections show that 64(9) % of the cross section corresponds to the (, 1.766 MeV) core state, 27(9) % to higher core excited states at 3–4 MeV and a small part of the cross section leaves the core in its ground state Pra03 . As shown in Table 1, our calculation using the s.p. wave functions for the core in its ground state with a valence neutron gives a cross section of 153 mb for the transition to the -wave and 454 mb for the transition to the -wave continuum to give a total of 607 mb, and the resulting ratio is very small (about 0.015), close to the value expected from a shell model calculation Mad01 . Calculations using the Whittaker wave functions give a cross section of 854 mb with ratio of 0.011. For the higher states, the spectroscopic factor is unknown for the valence neutron plus the (, 3.027 MeV) core state and is 0.76 for the valence neutron in the (, 4.142 MeV) core state; our calculations using s.p. and Whittaker functions give about 15 mb and 30 mb for the cross section of state, respectively, whereas the measured value is 25(7) mb Pra03 .
IV Summary and conclusions
In summary, we have presented a new method to calculate the Coulomb dissociation of exotic nuclei using an extended version of a recent model of the CDPP taking into account excited states of the core and excitation to the continuum. Breakup cross sections for two-body exotic projectiles may be calculated using this new version of the CDPP which depends on the relative excitation energy of the continuum. The method was used to calculate the differential and integrated Coulomb breakup cross sections for several exotic neutron-rich nuclei incident on lead targets at a few hundreds of MeV/nucleon. The calculations at these high energies were performed using the eikonal approximation and the results are in good agreement with the data. The calculations could easily be generalized and applied to calculate neutron removal and gamma capture cross sections. The new, extended CDPP may also be applied to low energy scattering and reaction data via the optical model or distorted wave Born approximation or coupled channel formalisms and has many potential applications.
Acknowledgments
We thank Professor Antonio Moro for his help in calculating the energy convolution of the calculated cross sections. This work was funded by the Polish National Agency for Academic Exchange (NAWA) within the Ulam Programme under grant agreement No. PPN/ULM/2019/1/00189/U/00001.
References
- (1) H. M. Maridi, K. Rusek, and N. Keeley, Phys. Rev.C 104, 024614 (2021).
- (2) H. M. Xu, C. A. Gagliardi, R. E. Tribble, A. M. Mukhamedzhanov, and N. K. Timofeyuk, Phys. Rev. Lett. 73, 2027 (1994).
- (3) U. Datta Pramanik et al., Physics Letters B 551, 63 (2003).
- (4) E. Sauvan et al., Phys. Lett. B 491 1 (2000).
- (5) M. Heine et al., Phys. Rev. C 95, 014613 (2017).
- (6) P. G. Hansen and J. A. Tostevin, Annu. Rev. Nucl. Part. Sci. 53, 219 (2003).
- (7) M. S. Hussein and K. W. McVoy, Nucl. Phys. A 445, 124 (1985).
- (8) M. Gómez-Ramos, J. Gómez-Camacho, Jin Lei, and A. M. Moro, Eur. Phys. J. A 57, 57 (2021).
- (9) C. A. Bertulani and G. Baur, Phys. Rep. 163, 299 (1988).
- (10) R. J. Glauber, in Lectures in Theoretical Physics edited by W.E. Brittin and G.L. Dunham (Interscience, New York, 1959), Vol. 1, p. 315.
- (11) C. A. Bertulani, C. M. Campbell, and T. Glasmacher, Comp. Phys. Comm. 152, 317 (2003).
- (12) L. Moschini and P.Capel, Phys. Lett. B 790, 367 (2019).
- (13) R. Palit, P. Adrich, T. Aumann, K. Boretzky, B. V. Carlson, D. Cortina et al., Phys. Rev. C 68, 034318 (2003).
- (14) T. Aumann, A. Navin, D. P. Balamuth, D. Bazin, B. Blank, B. A. Brown et al., Phys. Rev. Lett. 84, 35 (2000).
- (15) N. K. Timofeyuk and R. C. Johnson, Phys. Rev. C 59, 1545 (1999).
- (16) N. Fukuda, T. Nakamura, N. Aoi, N. Imai, M. Ishihara, T. Kobayashi et al., Phys. Rev. C 70, 054606 (2004).
- (17) T. Nakamura et al., Phys. Lett. B 331, 296 (1994).
- (18) J. R. Terry, D. Bazin, B. A. Brown, J. Enders, T. Glasmacher, P. G. Hansen, B. M. Sherrill, and J. A. Tostevin, Phys. Rev. C 69, 054306 (2004).
- (19) T. Nakamura, N. Fukuda, N. Aoi, N. Imai, M. Ishihara, H. Iwasaki et al., Phys. Rev. C 79, 035805 (2009).
- (20) V. Maddalena, T. Aumann, D. Bazin, B. A. Brown, J. A. Caggiano, B. Davids et al., Phys. Rev. C 63, 024613 (2001).
- (21) E. Sauvan, F. Carstoiu, N. A. Orr, J. S. Winfield, M. Freer, J. C. Angélique et al., Phys. Rev. C 69, 044603 (2004).
- (22) A. M. Moro, J. A. Lay, and J. Gómez-Camacho, Phys. Lett. B 811, 135959 (2020).