CAME: Competitively Learning a Mixture-of-Experts Model for First-stage Retrieval
Abstract.
The first-stage retrieval aims to retrieve a subset of candidate documents from a huge collection both effectively and efficiently. Since various matching patterns can exist between queries and relevant documents, previous work tries to combine multiple retrieval models to find as many relevant results as possible. The constructed ensembles, whether learned independently or jointly, do not care which component model is more suitable to an instance during training. Thus, they cannot fully exploit the capabilities of different types of retrieval models in identifying diverse relevance patterns. Motivated by this observation, in this paper, we propose a Mixture-of-Experts (MoE) model consisting of representative matching experts and a novel competitive learning mechanism to let the experts develop and enhance their expertise during training. Specifically, our MoE model shares the bottom layers to learn common semantic representations and uses differently structured upper layers to represent various types of retrieval experts. Our competitive learning mechanism has two stages: (1) a standardized learning stage to train the experts equally to develop their capabilities to conduct relevance matching; (2) a specialized learning stage where the experts compete with each other on every training instance and get rewards and updates according to their performance to enhance their expertise on certain types of samples. Experimental results on three retrieval benchmark datasets show that our method significantly outperforms the state-of-the-art baselines.
1. Introduction
The first-stage retrieval aims to retrieve potentially relevant documents from a large-scale collection efficiently, which is the foundation of various downstream tasks (Guo et al., 2022; Lin et al., 2021). However, relevant documents have diversified matching patterns and identifying all of them is very challenging. For example, as shown in Figure 1, from the perspective of matching scope, there are verbosity hypothesis (i.e., the entire document is about the query topic, only with more words) and scope hypothesis (i.e., a document consists of several parts concatenated together and only one of them is relevant) (Jones et al., 2000). From the perspective of matching signals, a document can be relevant to a query by either exact matching or semantic matching (Guo et al., 2016).
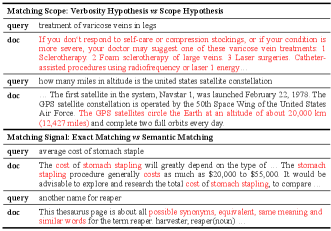
Aware of these different relevance patterns, various retrieval models have been proposed (Karpukhin et al., 2020; Formal et al., 2021; Khattab and Zaharia, 2020). In general, they can be categorized into three main paradigms: (i) Lexical Retrievers, e.g., DeepCT (Dai and Callan, 2020) and SPLADE (Formal et al., 2021), represent the document/query as a sparse vector of the vocabulary size, where the value of each dimension is the corresponding term weight. These approaches are inherently good at capturing exact matching. (ii) Local Retrievers, e.g., ColBERT (Khattab and Zaharia, 2020; Santhanam et al., 2022) and COIL (Gao et al., 2021a), conduct semantic matching between queries and documents at the term level, and measure the relevance according to the maximum similarity a query term can have to document terms. This type of method can identify the best local matching, which hereby is aligned with the scope hypothesis. (iii) Global Retrievers, e.g., DPR (Karpukhin et al., 2020) and ANCE (Xiong et al., 2020), represent the document and query as global-level low-dimension dense vectors and measure their relevance according to the similarity between the two vectors. They capture the global matching and fit in the verbosity hypothesis. Since most retrievers have their focused relevance matching patterns, it is difficult for a single model to handle various matching needs and serve all queries well. This finding is also confirmed by the observations from earlier studies (Gao et al., 2021b; Zhan et al., 2020): the retrieved results from different types of models have few overlaps, even when their overall quality is similar.
To address the issue that a single model is unable to fit all matching patterns, some work has proposed ensemble retrievers to leverage the capabilities of multiple retrieval models (Gao et al., 2021b; Kuzi et al., 2020; Shen et al., 2022). A straightforward method is to train several retrievers independently with the entire training data and aggregate their scores to produce improved results (Luan et al., 2021; Kuzi et al., 2020). However, the individual retrievers cannot interact sufficiently in such a way. A more advanced method is to learn component retrievers jointly with collaborative training mechanisms and aggregate their results. For example, following the boosting technique, CLEAR (Gao et al., 2021b) and DrBoost (Lewis et al., 2022) train each component retriever with the residuals of the other retriever(s) of the different (Gao et al., 2021b) or same type (Lewis et al., 2022); UnifieR (Shen et al., 2022) learns two retrievers and aligns one with the other based on their listwise agreements on the predictions. Such ensemble retrievers have been shown to be very effective in improving retrieval quality and are widely employed in modern search engines (Ling et al., 2017). However, no matter learning the retriever with the samples that the other component retrievers perform well (i.e, UnifieR) or poorly (e.g., CLEAR and DrBoost) on, all of them could force the retriever to compromise to unsuitable samples (i.e., matching patterns) and result in sub-optimal overall performance. Intuitively, it would be ideal to fully exploit the capabilities of different model architectures and make every component retriever especially focus on a certain type of sample. Such a “divide-and-conquer” idea has been shown to be pivotal in the Mixture-of-Experts (MoE) framework (Jacobs et al., 1991; Shazeer et al., 2017).
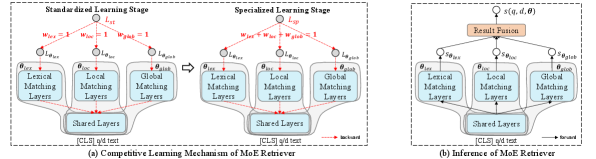
Motivated by the above, we build an MoE retrieval model consisting of multiple representative matching experts, and propose a novel mechanism to Competitively leArn the MoE model, named as CAME. Specifically, we include lexical, local, and global retrievers in a multi-path network architecture with shared bottom layers and top MoE layers. The shared bottom layers aim to extract common syntactic and semantic representations for all the experts. The MoE layers consist of three experts with different model architectures to capture pattern-specific features. To guide the component experts in CAME to specialize on certain types of samples, we competitively learn the MoE retriever in two phases. First, in the standardized learning stage, each expert is trained equally to develop the relevance matching capability and prepare for specialization. Second, in the specialized learning stage, the component experts compete with each other on every training instance, and they are trained proportionally to their relative performance among all the experts. In this way, each sample is only used to update the experts that perform decently but has no or little impact on other experts. During inference, each expert estimates the relevance score from its perspective to contribute to the final results. Noted that, in contrast to the classical MoE models that pick experts spontaneously for each input sample, our method establishes more explicit connections between the experts and samples via their relative ranking performance. From the above, we can readily urge each expert to fit the case it is skilled at and fully unleash the advantages of different model architectures.
We evaluate the effectiveness of the proposed model on three representative retrieval benchmark datasets, i.e., MS MARCO (Nguyen et al., 2016), TREC Deep Learning Track (Craswell et al., 2020), and Natural Questions (Kwiatkowski et al., 2019). The empirical results show that CAME can outperform all the baselines including various state-of-the-art single-model retrievers and ensemble retrievers significantly. In addition, we conduct comprehensive analyses on how the model components and learning mechanism impact retrieval performance. It shows that employing multi-types of retrieval experts can capture diverse relevance patterns, and the competitive learning strategy is essential to facilitate the experts to learn their designated patterns, which together boost the retrieval performance. To sum up, our contributions include:
-
•
We propose a Mixture-of-Experts retrieval model that can orchestrate various types of models to capture diverse relevance patterns.
-
•
We propose a novel competitive learning mechanism for the MoE retriever that encourages the component experts to develop and enhance their expertise on dedicated relevance patterns.
-
•
We conduct extensive experiments on three representative retrieval benchmarks and show that CAME can outperform various types of state-of-the-art baselines significantly.
-
•
We provide a comprehensive analysis on the model components, learning mechanism, and hyper-parameter sensitivity to better understand how they impact the retrieval performance.
2. Related Work
In this section, we review the most related topics to our work, including ensemble models for first-stage retrieval, and the Mixture-of-Experts framework.
2.1. Ensemble Models for First-stage Retrieval
The ensemble of several models has become a standard technique for improving the effectiveness of information retrieval (IR) tasks. It has been studied extensively in the TREC evaluations (Harman, 1995) and is the basis of Web search engines (Ling et al., 2017). Overall, there are two approaches to developing ensemble IR models (Croft, 2002), both with the motivation to improve retrieval performance by combining multiple evidences. One approach is to create models that explicitly utilize and combine multiple sources of evidence from raw data (Fisher and Elchesen, 1972). For example, existing studies have shown that combining information from multiple fields of the document can facilitate relevance estimation (Fisher and Elchesen, 1972). The other approach is to combine the outputs of several retrieval models by voting or weighted summation, where each prediction provides an evidence about relevance (Fox and France, 1987).
Recently, with the development of pre-trained language models (PLMs), a variety of neural retrievers based on different relevance hypotheses have been proposed (Guo et al., 2022; Zhao et al., 2022). Although these retrievers have achieved impressive performance on retrieval benchmarks (Formal et al., 2021; Hofstätter et al., 2021; Zhou et al., 2022; Liu and Shao, 2022), their focuses (i.e., identifying relevance patterns) are distinct due to the differences in the model architecture. To combine the benefits from different retrieval models, the idea of building ensemble retrieval models has been explored by researchers (Kuzi et al., 2020; Gao et al., 2021b; Lewis et al., 2022; Shen et al., 2022). A straightforward way is to train multiple retrievers independently and combine their predicted scores linearly to obtain the final retrieval results (Luan et al., 2021; Kuzi et al., 2020; Chen et al., 2021; Lin and Lin, 2021). Some work has been inspired by the boosting technique (Gao et al., 2021b; Lewis et al., 2022). For example, Gao et al. (2021b) proposed CLEAR to learn a BERT-based retriever from the residual of BM25, and then combined them to build an ensemble retrieval model. Also, the knowledge distillation technique is introduced into building ensemble retrievers, which tries to leverage the capability of companion retrievers to enhance the ensemble results (Shen et al., 2022). For example, Shen et al. (2022) proposed UnifieR that optimizes a KL divergence loss between the predicted scores of two retrieval models besides the ranking task loss.
The aforementioned ensemble retrievers always show better performance than a single-model retriever in practice (Nguyen et al., 2016; Craswell et al., 2020). However, their component retrievers, no matter trained independently or jointly, are not handled specially according to their strengths and weaknesses in certain relevance patterns with respect to model architectures. In contrast, built on the Mixture-of-Experts framework, our approach encourages the experts to compete with each other and specialize on suitable samples.
2.2. Mixture-of-Experts Framework
The Mixture-of-Experts (MoE) framework (Jacobs et al., 1991) is one of the techniques for building ensemble models. It builds upon the “divide-and-conquer” principle, in which the problem space is divided for several expert models, guided by one or a few gating networks. According to how and when the gating network is involved in the dividing and combining procedures, MoE implementations could be classified into two groups (Masoudnia and Ebrahimpour, 2014), i.e., the mixture of implicitly localized experts (MILE) and the mixture of explicitly localized experts (MELE). MILE divides the problem space implicitly using a tacit competitive process, such as using a special error function. MELE conducts explicit divisions by a pre-specified clustering method before the expert training starts, and each expert is then assigned to one of these sub-spaces.
The MoE framework has been widely used in various machine learning tasks (Yuksel et al., 2012; Zhao et al., 2019), such as natural language processing and computer vision, showing great potential. A major milestone in language modeling applications appears in (Shazeer et al., 2017), which encourages experts to disagree among themselves so that the experts can specialize on different problem sub-spaces. Recently, MoE has also been applied in search tasks. For example, Nogueira et al. (2018) built an MoE system for query reformulation, where the input query is given to multiple agents and each returns a corresponding reformulation. Then, the aggregator collects the ranking lists of all reformulated queries and gets the fusion results. Dai et al. (2022) proposed MoEBQA to alleviate the parameter competition between different types of questions. In addition, given the practical needs in product search, where the data comes from different domains, search scenarios, or product categories, the MoE framework is employed in various e-commerce platforms (Zou et al., 2022; Sheng et al., 2021). For example, Sheng et al. (2021) claimed that different domains may share common user groups and items, and each domain has its unique data. Thus, it is difficult for a single model to capture the characteristics of various domains. To address this problem, they built a star topology adaptive recommender for multi-domain CTR prediction.
Similarly, due to various relevance matching patterns between queries and documents, we propose an MoE-based retrieval model that aims to exploit the expertise of different retrieval models to identify diverse relevance patterns. As far as we know, this is the first work to utilize the MoE framework to first-stage retrieval.
3. Competitively Learn MoE Retriever
In this section, we first describe the first-stage retrieval task. Then, we introduce the proposed MoE-based retrieval model, competitive learning mechanism, and inference procedure of CAME.
3.1. Task Description
Given a query and a collection with numerous documents, the first-stage retrieval aims to find as many potentially relevant documents as possible. Formally, given a labeled training dataset , where denotes a textual query, is the set of relevant documents for , and is the total number of queries. Let be one of the relevant documents. The essential task is to learn a model from that gives high scores to relevant query-document pairs (, ) and low scores to irrelevant ones. Then, all documents in the collection can be ranked according to the predicted scores. In the rest of this paper, we omit the subscript for a specific query if no confusion is caused.
3.2. MoE Retriever
To capture diverse relevance matching patterns, we include three representative retrievers in our MoE model, which are lexical, local, and global matching experts. Due to the efficiency constraint in first-stage retrieval, we adopt the typical bi-encoder architecture (Bromley et al., 1993) that encodes the query and the document separately, and then employs a simple interaction function to compute their relevance score based on the obtained representations:
| (1) |
where and denote the encoder modules for the query and document respectively, is the interaction module, and the whole model is parameterized with . Following (Xiong et al., 2020; Zhan et al., 2021), the two encoders in CAME have the same architecture and shared parameters. For each encoder, the bottom layers are shared for all the experts and the upper layers are private for them, as shown in Figure 2 (a). The relevance score of each query-document pair is calculated based on all the component expert predictions with a result fusion module, as shown in Figure 2 (b). We will elaborate on each part next.
3.2.1. Shared Layers
Existing studies (Liu et al., 2019) have shown that the bottom layers of deep models tend to extract task-agnostic linguistic knowledge, so we use shared layers between the experts to capture basic textual features among all training samples. The learned common semantic and syntactic knowledge can act as the foundation to facilitate the upper layers to focus on different relevance patterns. Here, we leverage a stack of Transformer (Vaswani et al., 2017) layers to produce contextualized token embeddings:
| (2) | ||||
where ‘[CLS]’ is the special token prepended to the input text, and and denote the query and document length respectively.
3.2.2. Mixture-of-Experts (MoE) Layers
As shown in Figure 2 (a), we employ three representative expert pathways at the upper layers, introduced as follows:
Lexical Matching Expert. To identify lexical matching, we incorporate a representative lexical retriever SPLADE (Formal et al., 2021) as one of the expert pathways. It maps each token vector output by the Transformer layer into a term-weighting distribution. The distribution is predicted based on the logits output by the Masked Language Model (MLM) layer (Devlin et al., 2018):
| (3) | ||||
Then, the lexical representation for the query/document is obtained by aggregating the importance distributions over the whole input token sequence, and the relevance score is measured by dot-product:
| (4) | ||||
where and correspond to and respectively.
Local Matching Expert. To capture the local matching, we leverage the token-level query/document representations as ColBERT (Khattab and Zaharia, 2020) does in the second expert pathway. Specifically, it applies a linear layer on top of each token vector output by the final Transformer layer to compress the output dimension of local representations. Then, for every local query representation, it computes the maximum similarity (MaxSim) score across all the local document representations and sums these scores to obtain the final relevance:
| (5) | ||||
where and correspond to and respectively, and is the parameter of the shared linear layer.
Global Matching Expert. To produce the sequence-level representations and measure global matching, we design an expert pathway following DPR (Karpukhin et al., 2020). We extract the output vector of the ‘[CLS]’ token as the global query/document representation, and define the relevance by the dot-product between the two vectors:
| (6) | ||||
where means to take the output of the ‘[CLS]’ token by the last Transformer layer of .
3.3. Competitive Learning Mechanism
In the real world, human experts are often trained through different stages of education, i.e., standardized training to gain general knowledge and specialized training to obtain expertise in a specific domain. Inspired by this process, our competitive learning mechanism has two similar stages, as shown in Figure 2 (a). Remarkably, our specialized training is through competition.
We first introduce the basic training objective of general retrievers as a preliminary. They usually sample a set of negatives from for a given relevant query-document pair in the training data. For and any , the retriever parameterized by computes the relevance score with Eq. (1). Then, the probability distribution over the documents is defined as:
| (7) |
Finally, a contrastive learning loss is used to optimize the retriever:
| (8) |
As in (Karpukhin et al., 2020), in-batch negatives are generally used to facilitate the retriever learning. This objective is the basis for our two-stage competitive learning, which we will introduce next.
Standardized Learning Stage. At the beginning, to encourage the experts to develop decent relevance matching capabilities and show potentials in certain types of samples, in the first few steps, we update the component experts by considering their loss equally important for every training sample in the standardized learning loss :
| (9) |
At this stage, we sample the negative instances in Eq. (8) from the top retrieved results of BM25 (Robertson et al., 2009) excluding the relevant documents, denoted as .
Specialized Learning Stage. After the first stage, the experts show superiority on certain types of samples than the others. To enhance their expertise, in the second stage, we let them compete with each other on every training sample . The specialized learning loss is the weighted combination of the individual loss from each expert:
| (10) |
where , and is the weight of the expert ℮ in the overall loss, computed according to its relative performance across all the experts on this sample:
| (11) |
In Eq. (11), denotes the rank of in expert ℮’s predictions, which represents how effectively this expert can perform on the training instance ; is the temperature to control the degree of soft competition, where a smaller means a more intense competition; and the softmax function is applied on all the experts so that for each training sample and the experts compete for the update weights.
Similar to (Xiong et al., 2020; Zhan et al., 2021), we train CAME according to Eq. (10) first on BM25 negatives until convergence and then on hard negatives to enhance its performance. We collect hard negatives from CAME learned on BM25 negatives. Specifically, for each query, we first obtain the top retrieval results of every expert ℮ excluding the relevant ones, denoted as . Then, we sample negatives from and further train CAME with Eq. (10).
3.4. MoE Inference
During inference time (as shown in Figure 2 (b)), each expert that specializes on a specific relevance pattern can judge from its perspective to determine the relevance scores of documents. Since which expert is more trustworthy for an unseen query-document pair is unknown, we simply consider them equally authoritative. Specifically, for a test query , to obtain its top- retrieval results of CAME, we first get the top- results of every component expert ℮ from the whole collection according to the predicted score , then we sum up the document scores from each expert to determine the final top- results:
| (12) |
The score of a document that is beyond top- results of an expert is set to the score of the th document this expert has on . This simple method performs similarly or better compared to other fusion methods, e.g., combining expert results based on the summation of reciprocal ranks and learning a linear combination of the expert scores (see Table 4). We leave the study of more complex fusion methods in the future, e.g., learning to predict the probability of each relevance pattern given the query and document, and assign the authority weights to each expert for the fusion.
3.5. Discussions
Competitive Learning versus Collaborative Learning. Previous ensemble methods, such as DrBoost (Lewis et al., 2022) and UnifieR (Shen et al., 2022), usually adopt collaborative learning mechanisms which directly optimize the overall score linearly combined from the component retrievers (Lewis et al., 2022) or optimize one component towards the other based on a KL divergence loss (Shen et al., 2022). In contrast, the competitive learning we propose has the advantage of better fitting each expert to its suitable samples since: (1) the learning of each expert is based on its own error; (2) the update weight for each expert is proportional to how it performs compared to other experts. Given a training sample, when one of the experts produces less error than others, it indicates that this sample is likely to match the expert’s expertise, thus its responsibility for the sample will be increased, and vice versa. Accordingly, each expert is strengthened with suitable samples and avoids forcing itself to learn from the unsuitable ones, which further enhances its expertise in identifying corresponding relevance patterns.
Implicitly versus Explicitly MoE. With the competitive learning objective, i.e., Eq. (10&11), CAME implicitly divides the problem space into a number of sub-spaces, and the experts are trained to specialize in different sub-spaces. According to the taxonomy of MoE models (see details in Section 2.2), CAME obviously falls into the category of the mixture of implicitly localized experts (MILE) (Masoudnia and Ebrahimpour, 2014). Since the problem sub-spaces could have overlaps (multiple relevance patterns could exist for a sample), it is more reasonable to implicitly guide the experts towards suitable samples according to their own predictions compared to training a mixture of explicitly localized experts (MELE) with pre-specified explicit divisions of samples.
Runtime Overhead. During runtime, for ensemble models like CAME, since the component retrievers can perform retrieval in parallel, the query response time would not be a major concern. Also, the common practice of using approximate nearest neighbor search algorithms, such as product quantization (Jegou et al., 2010), can significantly decrease the time and memory costs of combining multiple models. Moreover, for the local matching expert that has the highest runtime overhead, i.e., ColBERT, existing methods of improving it, e.g., token pruning (Tonellotto and Macdonald, 2021; Lassance et al., 2022), can be easily applied to CAME to further reduce the overhead.
4. Experimental Settings
This section presents the experimental settings, including datasets, baselines, evaluation metrics, and implementation details.
4.1. Datasets
We conduct experiments on three retrieval benchmarks:
-
•
MS MARCO (Nguyen et al., 2016): MS MARCO passage ranking task is introduced by Microsoft. It focuses on ranking passages from a collection with over 8.8M passages. It has about 503k training queries and about 7k queries in the dev/test set for evaluation. Since the test set is not available, we report the results on the dev set.
-
•
TREC DL (Craswell et al., 2020): TREC 2019 Deep Learning Track has the same training and dev set as MS MARCO, but replaces the test set with a novel set produced by TREC. It contains 43 test queries for the passage ranking task.
-
•
NQ (Kwiatkowski et al., 2019): Natural Questions collects real questions from Google’s search logs. Each query is paired with an answer span and golden passages in Wikipedia pages. There are more than 21 million passages in the corpus. It also has over 58.8k, 8.7k, and 3.6k queries in training, dev, and test sets respectively. In our experiments, we use the version of NQ created by Karpukhin et al. (2020).
4.2. Baselines
We consider two types of baselines for performance comparison, including representative single-model and ensemble retrievers.
Representative single-model retrievers:
-
•
SPLADE (Formal et al., 2021) is the exemplar of lexical retrievers. It projects the input text to a dimensional sparse representation. We set for the FLOPS regularizer on NQ.
-
•
ColBERT (Khattab and Zaharia, 2020) is the exemplar of local retrieval models, which measures relevance by soft matching all query and document tokens’ contextualized vectors. To run ColBERT on TREC DL and NQ, we set the output dimension as 128.
-
•
COIL (Gao et al., 2021a) is a variant of ColBERT, which only calculates similarities between exact matched terms for queries and documents in the MaxSim operator. We use the output dimension of local representations with 32.
-
•
DPR (Karpukhin et al., 2020) is the basic global retrieval model with a BERT-base bi-encoder architecture.
-
•
RocketQA (Qu et al., 2020) is one of the state-of-the-art single-model retrievers, which utilizes three training strategies to enhance the basic global retriever, namely cross-batch negatives, denoised hard negatives, and data augmentation.
-
•
AR2 (Zhang et al., 2022) is the state-of-the-art single-model retriever, which consists of a global retriever and a cross-encoder ranker jointly optimized with a minimax adversarial objective.
Ensemble retrievers:
-
•
ME-HYBRID (Luan et al., 2021) first trains a local retriever and a lexical retriever independently, and then linearly combines them by fusing their predicted scores.
-
•
SPAR (Chen et al., 2021) trains a global retriever (namely ) to imitate a lexical one, and combines with another global retriever to enhance the lexical matching capacity. Here we use the weighted concatenation variant for implementation, where the two component retrievers are trained independently.
-
•
CLEAR (Gao et al., 2021b) trains a global retriever with the mistakes made by a lexical retriever to combine the capacities of both models collaboratively.
-
•
DrBoost (Lewis et al., 2022) is an ensemble retriever inspired by boosting technique. Each component retriever is learned sequentially and specialized by focusing only on the retrieval mistakes made by the current ensemble. The final representation is the concatenation of the output vectors from five component models.
-
•
DSR (Lin and Lin, 2021) densifies the representations from a lexical retrieval model and combines them with a global retriever for joint training. We use the variant of “DSR-SPLADE + Dense-[CLS]”.
-
•
UnifieR (Shen et al., 2022) is a latest and state-of-the-art method that unifies a global and a lexical retriever in one model and aligns each component retriever with the other based on their listwise agreements on the predictions.
| Method | MS MARCO Dev | TREC DL Test | NQ Test | |||
|---|---|---|---|---|---|---|
| R@1000 | MRR@10 | R@1000 | NDCG@10 | Top-20 | Top-100 | |
| Single-model Retriever | ||||||
| BM25 | 85.3 | 18.4 | 74.5 | 50.6 | 59.1 | 73.7 |
| SPLADE (Formal et al., 2021) | 96.5 | 34.0 | 85.1 | 68.4 | 77.4 | 84.8 |
| ColBERT (Khattab and Zaharia, 2020) | 96.8 | 36.0 | 72.7 | 68.7 | 78.8 | 84.6 |
| COIL (Gao et al., 2021a) | 96.3 | 35.5 | 84.8 | 71.4 | 77.9 | 84.5 |
| DPR (Karpukhin et al., 2020) | 94.1 | 31.6 | 70.4 | 61.6 | 78.4 | 85.4 |
| RocketQA (Qu et al., 2020) | 97.9 | 37.0 | 79.3 | 71.3 | 82.7 | 88.5 |
| AR2 (Zhang et al., 2022) | 98.6 | 39.5 | 82.0 | 70.0 | 86.0 | 90.1 |
| Ensemble Retriever | ||||||
| ME-HYBRID (Luan et al., 2021) | 97.1 | 34.3 | 81.7 | 70.6 | 82.6 | 88.6 |
| SPAR (Chen et al., 2021) | 98.5 | 38.6 | 82.8 | 71.7 | 83.0 | 88.8 |
| CLEAR (Gao et al., 2021b) | 96.9 | 33.8 | 81.2 | 69.9 | 82.3 | 88.5 |
| DrBoost (Lewis et al., 2022) | - | 34.4 | - | - | 80.9 | 87.6 |
| DSR (Lin and Lin, 2021) | 96.7 | 35.8 | 84.1 | 69.4 | 83.2 | 88.9 |
| UnifieR (Shen et al., 2022) | 98.4 | 40.7 | - | 73.8 | - | - |
| CAME | ||||||
4.3. Evaluation Metrics
We use the official metrics of the three benchmarks. For retrieval tasks (i.e., MS MARCO and TREC DL), the retrieval performance of top 1000 passages is compared. We report the Recall at 1000 (R@1000) and Mean Reciprocal Rank at 10 (MRR@10) for MS MARCO, and R@1000 and Normalized Discounted Cumulative Gain at 10 (NDCG@10) for TREC DL. For open-domain question answering tasks (i.e., NQ), the proportion of top- retrieved passages that contain the answers (Top-) is compared (Karpukhin et al., 2020), and we report Top-20 and Top-100. Statistically significant differences are measured by two-tailed t-test.
4.4. Implementation Details
As in UnifieR (Shen et al., 2022), for the Transformer and MLM layers in CAME, we initialize the parameters with the coCondenser (Gao and Callan, 2021) checkpoint released by Gao et al.111https://github.com/luyug/Condenser. Unless otherwise specified, the number of Transformer layers in the shared layers and MoE layers are set to 10 and 2 respectively. We adopt the popular Transformers library222https://github.com/huggingface/transformers for implementations. For MS MARCO and TREC DL, we truncate the input query and passage to a maximum of 32 tokens and 128 tokens respectively. We train CAME with the official BM25 top 1000 negatives for 5 epochs (including 1 epoch for standardized learning and 4 epochs for specialized learning), and then mine hard negatives from the top 200 retrieval results to train 3 more epochs. We use a learning rate of 5e-6 and a batch size of 64. The temperature is tuned on a held-out training subset and is set to 0.5. For NQ, we set the query and passage length to 32 and 156 respectively. We first train CAME with the official BM25 top 100 negatives for 15 epochs (including 3 epochs for standardized learning and 12 epochs for specialized learning), and then mine hard negatives from the top 100 retrieval results for 10-epoch further training. We use a learning rate of 1e-5 and a batch size of 256. The temperature is tuned on the dev set and is set to 2.0. For all these three datasets, each positive example is paired with 7 negatives for training. We control the sparsity of the lexical representations in the lexical matching expert with for the FLOPS regularizer (Formal et al., 2021), and the output dimension of local representations in the local matching expert is set to 128. We use the AdamW optimizer with , , , and set the coefficient to control linear learning rate decay to 0.1. We run all experiments on Nvidia Tesla V100-32GB GPUs.
For all the baseline models, we use the official code or checkpoint to reproduce the results, except for CLEAR, DrBoost, and UnifieR whose code is not available, so we report the evaluation results from their paper directly333We report the performance of CLEAR, DrBoost, and UnifieR from their original papers and we could not conduct significance test against them since their code is not released and their result lists are not available..
5. Results and Discussion
In this section, we present the experimental results and conduct thorough analysis of CAME to answer the following research questions:
-
•
RQ1: How does CAME perform compared to the baseline methods, including state-of-the-art single-model retrievers and ensemble retrievers?
-
•
RQ2: How does each of the two stages in the training pipeline affect the retrieval performance?
-
•
RQ3: How does each component in CAME contribute to the retrieval performance?
-
•
RQ4: How do the key hyper-parameters in CAME affect the retrieval effectiveness?
5.1. Main Evaluation
To answer RQ1, we compare the retrieval performance of CAME with all the baselines described in Section 4.2 and record their evaluation results in Table 1.
Comparisons with Single-model Retrievers. The top block of Table 1 shows the performance of the representative baseline retrieval models. From the results on three datasets, we find that: (1) Neural retrieval models built upon pre-trained language models perform significantly better than term-based retrieval models, i.e., BM25, except for R@1000 on TREC DL. (2) Among all the neural retrievers, RocketQA and AR2 have the best performance on MS MARCO and NQ probably due to their more sophisticated training strategies, such as the data augmentation (in RocketQA) and knowledge distillation (in AR2). (3) For the other methods without complex training strategies, we find that the models that achieve the best performance on each dataset are of different types. Local retriever ColBERT has the best performance on MS MARCO while SPLADE and COIL perform the best on TREC DL. SPLADE is a lexical retriever and COIL is the variant of ColBERT that only keeps the similarities between the exact matched query and document terms. Global retriever DPR has the overall best performance on NQ. This observation also supports our claim that various relevance matching patterns exist. (4) By leveraging multi-types of retrievers, CAME outperforms all the single-model baselines by a large margin in terms of almost all the metrics, showing the superiority of capturing various relevance patterns. Note that CAME should achieve even better performance if using the knowledge distillation and data augmentation techniques proposed in RocketQA and AR2.
Comparisons with Ensemble Retrievers. The performance of the ensemble retrievers are presented in the bottom block of Table 1. We have the following observations: (1) An ensemble retriever that consists of only a single type of model underperforms ensemble retrievers that have multi-types of component models. This can be seen from that DrBoost (only using global retrievers) performs worse than the others. (2) Among the methods that combine various types of retrievers (i.e., ensemble models except DrBoost), DSR and UnifieR perform the best. The superiority of DSR and UnifieR should mostly come from the elaborate joint learning strategies, which shows the importance of the learning mechanism. (3) Compared to the existing ensemble retrievers, CAME achieves significantly better performance on the three datasets in terms of almost all the metrics. For example, its performance improvements over UnifieR are 1.5% and 0.9% on MRR@10 and NDCG@10 for MS MARCO and TREC DL respectively, and the improvements over DSR are 5.1% and 2.8% regarding Top-20 and Top-100 for NQ. These performance gains further confirm CAME’s advantages from employing multi-types of retrievers to capture various relevance patterns and the competitive learning mechanism that facilitates the component expert training.
5.2. Ablation Study of Learning Mechanism
To answer RQ2, we conduct ablation studies on each stage of the learning pipeline. We only report the results on MS MARCO and NQ in Table 2 due to the space limit, and TREC DL has similar trends. Since R@1000 on MS MARCO is already near 100% and slightly differs between the variants, we also report R@100 to show the differences.
| Method | MS MARCO | NQ | |||
|---|---|---|---|---|---|
| R@1000 | R@100 | MRR@10 | Top-20 | Top-100 | |
| CAME | 98.8 | 92.5 | 41.3 | 87.5 | 91.4 |
| - hard negatives | 98.4 | ||||
| - specialized | 98.2 | ||||
| - standardized | 98.3 | ||||
We first remove the training based on hard negatives (i.e., w/o hard negatives) and see that the performance decreases by a large margin, especially on the top results (e.g., MRR@10 on MS MARCO and Top-20 on NQ). This observation is consistent with previous studies, showing that hard negatives could greatly enhance neural retrieval models (Qu et al., 2020). It should be noted that, even without using hard negatives for further learning, CAME still outperforms most baselines (see Table 1), and UnifieR (Shen et al., 2022), the best baseline which is reported to have 98.0 and 38.3 for R@1000 and MRR@10 under the same setting of using BM25 negatives only (Shen et al., 2022). It demonstrates the superiority of competitive learning in CAME.
Based on the above variant of CAME without hard negatives, we run another two ablation studies by: (1) removing the specialized learning stage and training CAME until convergence with Eq. (9) only (i.e., w/o specialized); (2) removing the standardized learning stage and training CAME with Eq. (10) from the beginning (i.e., w/o standardized). The first ablation shows that training without specialized learning leads to a substantial drop in retrieval performance, indicating that it is important to encourage component experts to compete with each other and focus on the samples they are skilled at. The second one shows that training only with the specialized learning stage would also lower the performance. Without the standardized learning process, the component experts are not readily prepared to specialize on certain relevance patterns. Then, the update weights calculated with Eq. (11) cannot reflect accurately how each training sample corresponds to the relevance matching patterns, which further makes it difficult to facilitate the experts to develop their own advantages based on suitable samples.
5.3. Study of Model Component Choices
To answer RQ3, we conduct ablation studies and compare with other alternatives for each component in CAME. Since NQ and TREC DL lead to similar conclusions, we only report the performance on MS MARCO. Note that we only show the model performance based on BM25 negatives training due to the cost of collecting hard negatives.
| Method | Fusion | Lexical | Local | Global | ||||
|---|---|---|---|---|---|---|---|---|
| R | MRR | R | MRR | R | MRR | R | MRR | |
| CAME | 98.4 | 39.0 | 97.6 | 36.1 | 96.7 | 38.8 | 97.7 | 36.8 |
| - shared layers | 98.3 | 38.1 | 97.4 | 35.1 | 96.0 | 38.0 | 97.7 | 36.0 |
| - lexical | 98.1 | 38.1 | - | - | 96.5 | 38.5 | 97.8 | 36.2 |
| - local | 98.2 | 37.8 | 97.4 | 36.1 | - | - | 97.7 | 36.7 |
| - global | 98.1 | 38.0 | 97.5 | 35.9 | 96.5 | 38.7 | - | - |
| - local&global | 97.3 | 35.1 | 97.3 | 35.1 | - | - | - | - |
| - lexical&global | 96.0 | 37.9 | - | - | 96.0 | 37.9 | - | - |
| - lexical&local | 97.7 | 35.9 | - | - | - | - | 97.7 | 35.9 |
Ablation Study of Encoder Module. For the ablation study of the encoder module, we: (1) remove the shared layers, that is, each expert has private 12 Transformer encoding layers; (2) remove one expert in the MoE layers separately; (3) remove two experts in the MoE layers simultaneously, that is, the remaining one expert is trained independently. We report the performance of overall and each component expert under every ablation setting in Table 3. By removing the shared layers, we find that MRR@10 of the fusion result decreases significantly, and the performance of every component expert is close to that of their own independent training. This shows that the shared bottom layers in CAME act as multi-task learning that can facilitate the semantic and syntactic knowledge to be better learned for relevance estimation. When removing any expert in CAME, the fusion performance degrades dramatically. Meanwhile, using two experts in MoE layers could achieve better performance than using either of them independently, e.g., the lexical expert and global expert achieve 35.1 and 35.9 on MRR@10 independently (in the bottom block), while using both of them (i.e., the variant of w/o local expert) could achieve 37.8. Furthermore, the rank-biased overlap (RBO) (Webber et al., 2010) between top 1000 results retrieved by any two independently trained experts is 42%-48%. It shows that documents may have multiple relevance patterns and the retrieval results of different experts could complement each other.
Study of Various Fusion Methods. To study the result fusion module, we compare several variants with CAME to verify our choice (see the top block of Table 4): (1) using summation/maximum of min–max normalized scores (NormSum/NormMax) instead of the summation of raw scores (Sum) in Eq. (12); (2) using reciprocal ranks (SumRR/MaxRR) instead of scores for fusion; (3) conducting learnable linear combination of model scores (LinearLayer). We can see that NormSum and LinearLayer do not outperform the simple score summation, i.e., Sum, in CAME. We also find that the fusion of reciprocal ranks has worse MRR@10 than others, probably due to their faster decay than scores. Also, maximum always yields worse results than summation, probably because multiple relevance patterns co-exist in some documents and the judgment from each expert is important to evaluate the overall relevance.
Study of Alternative Expert Learning Methods. To show the advantages of competitive learning, we compare it with alternative options of training an ensemble model with SPLADE, ColBERT, and DPR. We: (1) learn the three models independently on the entire training data that contains both suitable and unsuitable samples for each model (All-Independent) and fuse their results with score summation, reciprocal rank summation, and a learned linear combination layer; (2) learn the three independent models on their suitable samples (Suit-Independent), determined by whether the model has the best MRR@10 for the sample among all experts in CAME. As shown in the bottom block of Table 4, the fusion of reciprocal ranks performs better than scores, which is different from our observations on fusing expert results in CAME. The possible reason is that the scores obtained from the independently learned models are less comparable than those achieved by jointly learned experts in CAME. Both of them are significantly worse than CAME and the fusion variants based on competitive learning. In addition, when fusing the model results with linear combination, models trained only on suitable samples (Suit-Independent) have better ensemble performance than models trained on the whole data (All-Independent), which is consistent with the performance gains produced by the specialized learning mechanism in CAME.
| Learning Method | Fusion Method | R@1000 | R@100 | MRR@10 |
|---|---|---|---|---|
| 98.4 | 91.7 | 39.0 | ||
| Competitive | NormSum | 98.4 | 91.7 | 38.9 |
| Competitive | NormMax | 98.2 | ||
| Competitive | SumRR | 98.5 | 91.7 | 38.4 |
| Competitive | MaxRR | 98.4 | 91.3 | |
| Competitive | LinearLayer | 98.4 | 91.8 | 39.2 |
| All-Independent | Sum | |||
| All-Independent | SumRR | 98.1 | ||
| All-Independent | LinearLayer | 98.2 | ||
| Suit-Independent | LinearLayer | 98.1 |
5.4. Hyper-parameter Impact
To answer RQ4, we evaluate CAME with different hyper-parameter settings to investigate their impact on retrieval results. Again, we conduct analysis on the models trained on BM25 negatives due to the cost of collecting hard negatives.
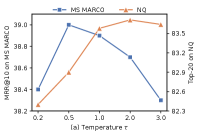
Impact of the Temperature. As shown in Figure 3 (a), we examine the effect of temperature in Eq. (11) by varying it from 0.2 to 3.0. The results indicate that has a great impact on retrieval performance, with different optimal values for the two datasets (0.5 for MS MARCO and 2.0 for NQ). MS MARCO has shorter documents than NQ on average, which could lead to that the performance of the local and global matching experts may not differ much on MS MARCO, thus it may require a smaller to make the competition between the experts more intensely to enhance their expertise.
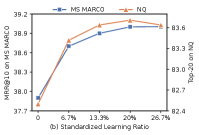
Impact of the Standardized Learning Ratio. Figure 3 (b) shows how MRR@10 changes with respect to the standardized learning ratio, where the ratio means the proportion of the standardized learning steps in the training based on BM25 negatives. For both datasets, the performance reaches the top with 20% standardized learning steps. The performance is relatively stable when the ratio is between 13.3% and 26.7%, while decreasing dramatically at smaller values. We speculate that the component experts cannot develop their expertise if they have not seen enough training samples, and once the standardized learning is enough, the ratio has a small effect on the retrieval effectiveness.
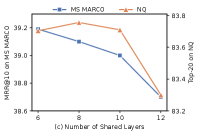
Impact of the Number of Shared Layers. As shown in Figure 3 (c), we investigate the model performance by varying the number of shared layers from 6 to 12. On both MS MARCO and NQ, the performance decreases dramatically when the number of shared layers is set to 12. This indicates that the component experts cannot develop their expertise when their private parameters are too few. In addition, we observe that with fewer shared layers, the performance becomes slightly better on MS MARCO, while 8 shared layers are better than 6 on NQ. The reason may be that fewer private layers are sufficient to learn effective experts for NQ due to its smaller size. Overall, the performance varies slightly from 6 to 10 shared layers (i.e., within 0.2%). Therefore, considering the balance between the effectiveness and efficiency of encoding, we set the number of shared layers as 10 in CAME.
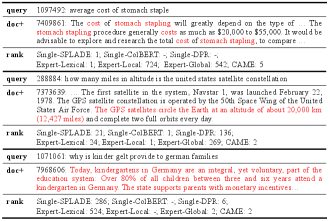
5.5. Case Study
In Figure 4, we show three representative cases in MS MARCO that have different relevance patterns to compare CAME, its component experts, and their counterparts trained independently. We find that, for each case, only one or two models could rank the relevant passage at the top positions. This supports our claim that different types of retrieval models are skilled at identifying different relevance patterns, and a single model could not handle all the cases. By contrast, CAME works well on all the three types of cases by leveraging the power of various types of retrieval experts.
We also compare the results of the component experts in CAME (denoted as “Expert-”) and their counterparts as single-model retrievers, and have some interesting observations: (1) When there are clear disagreements between different types of retrievers, the retriever that ranks the ideal passage to top positions when trained individually performs similarly or even better when it is trained as a component in CAME. The other single-model retrievers that are not good at the cases, by contrast, could have fluctuating performance when trained as experts in CAME. This indicates that the joint training of the experts in CAME with competitive learning mechanism can maintain or enhance their ability to identify their dedicated relevance patterns. (2) In the first two cases, although one component expert in CAME ranks the relevant passage at top-1, the fusion results (i.e., CAME) are not optimal. We impute it to the imperfect result fusion method. In the future, we need to explore better methods to fuse the retrieval results.
6. Conclusion and Future Work
To fully exploit the capabilities of different types of retrieval models for effective retrieval, we propose a retrieval model based on the MoE framework and a novel competitive learning mechanism for the experts training. Specifically, the MoE retriever consists of three representative matching experts, and the competitive learning mechanism develops and enhances their expertise on dedicated relevance patterns sufficiently with standardized and specialized learning. Empirical results on three retrieval benchmarks show that CAME can achieve significant gains in retrieval effectiveness against the baselines. In the future, we plan to further refine CAME in terms of both effectiveness and efficiency: (1) Using more advanced pre-trained models (Zhou et al., 2022; Liu and Shao, 2022) or exploring other result fusion methods to improve the performance; (2) Investigating methods to improve the retrieval efficiency of CAME without compromising its performance.
References
- (1)
- Bromley et al. (1993) Jane Bromley, Isabelle Guyon, Yann LeCun, Eduard Säckinger, and Roopak Shah. 1993. Signature verification using a” siamese” time delay neural network. Advances in neural information processing systems 6 (1993).
- Chen et al. (2021) Xilun Chen, Kushal Lakhotia, Barlas Oğuz, Anchit Gupta, Patrick Lewis, Stan Peshterliev, Yashar Mehdad, Sonal Gupta, and Wen-tau Yih. 2021. Salient Phrase Aware Dense Retrieval: Can a Dense Retriever Imitate a Sparse One? arXiv preprint arXiv:2110.06918 (2021).
- Craswell et al. (2020) Nick Craswell, Bhaskar Mitra, Emine Yilmaz, Daniel Campos, and Ellen M Voorhees. 2020. Overview of the TREC 2019 deep learning track. arXiv preprint arXiv:2003.07820 (2020).
- Croft (2002) W Bruce Croft. 2002. Combining approaches to information retrieval. In Advances in information retrieval. Springer, 1–36.
- Dai et al. (2022) Damai Dai, Wenbin Jiang, Jiyuan Zhang, Weihua Peng, Yajuan Lyu, Zhifang Sui, Baobao Chang, and Yong Zhu. 2022. Mixture of Experts for Biomedical Question Answering. arXiv preprint arXiv:2204.07469 (2022).
- Dai and Callan (2020) Zhuyun Dai and Jamie Callan. 2020. Context-aware term weighting for first stage passage retrieval. In Proceedings of the 43rd International ACM SIGIR. 1533–1536.
- Devlin et al. (2018) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2018. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 (2018).
- Fisher and Elchesen (1972) H Leonard Fisher and Dennis R Elchesen. 1972. General: Effectiveness of Combining Title Words and Index Terms in Machine Retrieval Searches. Nature 238, 5359 (1972), 109–110.
- Formal et al. (2021) Thibault Formal, Carlos Lassance, Benjamin Piwowarski, and Stéphane Clinchant. 2021. SPLADE v2: Sparse lexical and expansion model for information retrieval. arXiv preprint arXiv:2109.10086 (2021).
- Fox and France (1987) Edward A Fox and Robert K France. 1987. Architecture of an expert system for composite document analysis, representation, and retrieval. International Journal of Approximate Reasoning 1, 2 (1987), 151–175.
- Gao and Callan (2021) Luyu Gao and Jamie Callan. 2021. Unsupervised corpus aware language model pre-training for dense passage retrieval. arXiv preprint arXiv:2108.05540 (2021).
- Gao et al. (2021a) Luyu Gao, Zhuyun Dai, and Jamie Callan. 2021a. COIL: Revisit exact lexical match in information retrieval with contextualized inverted list. arXiv preprint arXiv:2104.07186 (2021).
- Gao et al. (2021b) Luyu Gao, Zhuyun Dai, Tongfei Chen, Zhen Fan, Benjamin Van Durme, and Jamie Callan. 2021b. Complement lexical retrieval model with semantic residual embeddings. In European Conference on Information Retrieval. Springer, 146–160.
- Guo et al. (2022) Jiafeng Guo, Yinqiong Cai, Yixing Fan, Fei Sun, Ruqing Zhang, and Xueqi Cheng. 2022. Semantic models for the first-stage retrieval: A comprehensive review. ACM Transactions on Information Systems (TOIS) 40, 4 (2022), 1–42.
- Guo et al. (2016) Jiafeng Guo, Yixing Fan, Qingyao Ai, and W Bruce Croft. 2016. A deep relevance matching model for ad-hoc retrieval. In Proceedings of the 25th ACM international on conference on information and knowledge management. 55–64.
- Harman (1995) Donna Harman. 1995. Overview of the second text retrieval conference (TREC-2). Information Processing & Management 31, 3 (1995), 271–289.
- Hofstätter et al. (2021) Sebastian Hofstätter, Sheng-Chieh Lin, Jheng-Hong Yang, Jimmy Lin, and Allan Hanbury. 2021. Efficiently teaching an effective dense retriever with balanced topic aware sampling. In Proceedings of the 44th International ACM SIGIR. 113–122.
- Jacobs et al. (1991) Robert A Jacobs, Michael I Jordan, Steven J Nowlan, and Geoffrey E Hinton. 1991. Adaptive mixtures of local experts. Neural computation 3, 1 (1991), 79–87.
- Jegou et al. (2010) Herve Jegou, Matthijs Douze, and Cordelia Schmid. 2010. Product quantization for nearest neighbor search. IEEE transactions on pattern analysis and machine intelligence 33, 1 (2010), 117–128.
- Jones et al. (2000) K Sparck Jones, Steve Walker, and Stephen E. Robertson. 2000. A probabilistic model of information retrieval: development and comparative experiments: Part 2. Information processing & management 36, 6 (2000), 809–840.
- Karpukhin et al. (2020) Vladimir Karpukhin, Barlas Oğuz, Sewon Min, Patrick Lewis, Ledell Wu, Sergey Edunov, Danqi Chen, and Wen-tau Yih. 2020. Dense passage retrieval for open-domain question answering. arXiv preprint arXiv:2004.04906 (2020).
- Khattab and Zaharia (2020) Omar Khattab and Matei Zaharia. 2020. Colbert: Efficient and effective passage search via contextualized late interaction over bert. In Proceedings of the 43rd International ACM SIGIR. 39–48.
- Kuzi et al. (2020) Saar Kuzi, Mingyang Zhang, Cheng Li, Michael Bendersky, and Marc Najork. 2020. Leveraging semantic and lexical matching to improve the recall of document retrieval systems: A hybrid approach. arXiv preprint arXiv:2010.01195 (2020).
- Kwiatkowski et al. (2019) Tom Kwiatkowski, Jennimaria Palomaki, Olivia Redfield, Michael Collins, Ankur Parikh, Chris Alberti, Danielle Epstein, Illia Polosukhin, Jacob Devlin, Kenton Lee, et al. 2019. Natural questions: a benchmark for question answering research. Transactions of the Association for Computational Linguistics 7 (2019), 453–466.
- Lassance et al. (2022) Carlos Lassance, Maroua Maachou, Joohee Park, and Stéphane Clinchant. 2022. Learned Token Pruning in Contextualized Late Interaction over BERT (ColBERT). In Proceedings of the 45th International ACM SIGIR. 2232–2236.
- Lewis et al. (2022) Patrick Lewis, Barlas Oguz, Wenhan Xiong, Fabio Petroni, Scott Yih, and Sebastian Riedel. 2022. Boosted Dense Retriever. In Proceedings of the 2022 Conference of NAACL. Association for Computational Linguistics, Seattle, United States, 3102–3117. https://aclanthology.org/2022.naacl-main.226
- Lin et al. (2021) Jimmy Lin, Rodrigo Nogueira, and Andrew Yates. 2021. Pretrained transformers for text ranking: Bert and beyond. Synthesis Lectures on Human Language Technologies 14, 4 (2021), 1–325.
- Lin and Lin (2021) Sheng-Chieh Lin and Jimmy Lin. 2021. Densifying Sparse Representations for Passage Retrieval by Representational Slicing. arXiv preprint arXiv:2112.04666 (2021).
- Ling et al. (2017) Xiaoliang Ling, Weiwei Deng, Chen Gu, Hucheng Zhou, Cui Li, and Feng Sun. 2017. Model ensemble for click prediction in bing search ads. In Proceedings of the 26th international conference on world wide web companion. 689–698.
- Liu et al. (2019) Nelson F Liu, Matt Gardner, Yonatan Belinkov, Matthew E Peters, and Noah A Smith. 2019. Linguistic knowledge and transferability of contextual representations. arXiv preprint arXiv:1903.08855 (2019).
- Liu and Shao (2022) Zheng Liu and Yingxia Shao. 2022. Retromae: Pre-training retrieval-oriented transformers via masked auto-encoder. arXiv preprint arXiv:2205.12035 (2022).
- Luan et al. (2021) Yi Luan, Jacob Eisenstein, Kristina Toutanova, and Michael Collins. 2021. Sparse, dense, and attentional representations for text retrieval. Transactions of the Association for Computational Linguistics 9 (2021), 329–345.
- Masoudnia and Ebrahimpour (2014) Saeed Masoudnia and Reza Ebrahimpour. 2014. Mixture of experts: a literature survey. Artificial Intelligence Review 42, 2 (2014), 275–293.
- Nguyen et al. (2016) Tri Nguyen, Mir Rosenberg, Xia Song, Jianfeng Gao, Saurabh Tiwary, Rangan Majumder, and Li Deng. 2016. MS MARCO: A human generated machine reading comprehension dataset. In CoCo@ NIPS.
- Nogueira et al. (2018) Rodrigo Frassetto Nogueira, Kyunghyun Cho, and CIFAR Global Scholar. 2018. New York University at TREC 2018 Complex Answer Retrieval Track.. In TREC.
- Qu et al. (2020) Yingqi Qu, Yuchen Ding, Jing Liu, Kai Liu, Ruiyang Ren, Wayne Xin Zhao, Daxiang Dong, Hua Wu, and Haifeng Wang. 2020. RocketQA: An optimized training approach to dense passage retrieval for open-domain question answering. arXiv preprint arXiv:2010.08191 (2020).
- Robertson et al. (2009) Stephen Robertson, Hugo Zaragoza, et al. 2009. The probabilistic relevance framework: BM25 and beyond. Foundations and Trends® in Information Retrieval 3, 4 (2009), 333–389.
- Santhanam et al. (2022) Keshav Santhanam, Omar Khattab, Jon Saad-Falcon, Christopher Potts, and Matei Zaharia. 2022. ColBERTv2: Effective and Efficient Retrieval via Lightweight Late Interaction. In Proceedings of the 2022 Conference of NAACL. Association for Computational Linguistics, Seattle, United States, 3715–3734. https://doi.org/10.18653/v1/2022.naacl-main.272
- Shazeer et al. (2017) Noam Shazeer, Azalia Mirhoseini, Krzysztof Maziarz, Andy Davis, Quoc Le, Geoffrey Hinton, and Jeff Dean. 2017. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. arXiv preprint arXiv:1701.06538 (2017).
- Shen et al. (2022) Tao Shen, Xiubo Geng, Chongyang Tao, Can Xu, Kai Zhang, and Daxin Jiang. 2022. UnifieR: A Unified Retriever for Large-Scale Retrieval. arXiv preprint arXiv:2205.11194 (2022).
- Sheng et al. (2021) Xiang-Rong Sheng, Liqin Zhao, Guorui Zhou, Xinyao Ding, Binding Dai, Qiang Luo, Siran Yang, Jingshan Lv, Chi Zhang, Hongbo Deng, et al. 2021. One model to serve all: Star topology adaptive recommender for multi-domain ctr prediction. In Proceedings of the 30th ACM International CIKM. 4104–4113.
- Tonellotto and Macdonald (2021) Nicola Tonellotto and Craig Macdonald. 2021. Query embedding pruning for dense retrieval. In Proceedings of the 30th ACM International CIKM. 3453–3457.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. Advances in neural information processing systems 30 (2017).
- Webber et al. (2010) William Webber, Alistair Moffat, and Justin Zobel. 2010. A similarity measure for indefinite rankings. ACM TOIS 28, 4 (2010), 1–38.
- Xiong et al. (2020) Lee Xiong, Chenyan Xiong, Ye Li, Kwok-Fung Tang, Jialin Liu, Paul Bennett, Junaid Ahmed, and Arnold Overwijk. 2020. Approximate nearest neighbor negative contrastive learning for dense text retrieval. arXiv preprint arXiv:2007.00808 (2020).
- Yuksel et al. (2012) Seniha Esen Yuksel, Joseph N Wilson, and Paul D Gader. 2012. Twenty years of mixture of experts. IEEE transactions on neural networks and learning systems 23, 8 (2012), 1177–1193.
- Zhan et al. (2021) Jingtao Zhan, Jiaxin Mao, Yiqun Liu, Jiafeng Guo, Min Zhang, and Shaoping Ma. 2021. Optimizing dense retrieval model training with hard negatives. In Proceedings of the 44th International ACM SIGIR. 1503–1512.
- Zhan et al. (2020) Jingtao Zhan, Jiaxin Mao, Yiqun Liu, Min Zhang, and Shaoping Ma. 2020. RepBERT: Contextualized text embeddings for first-stage retrieval. arXiv preprint arXiv:2006.15498 (2020).
- Zhang et al. (2022) Hang Zhang, Yeyun Gong, Yelong Shen, Jiancheng Lv, Nan Duan, and Weizhu Chen. 2022. Adversarial retriever-ranker for dense text retrieval. In ICLR.
- Zhao et al. (2022) Wayne Xin Zhao, Jing Liu, Ruiyang Ren, and Ji-Rong Wen. 2022. Dense text retrieval based on pretrained language models: A survey. arXiv preprint arXiv:2211.14876 (2022).
- Zhao et al. (2019) Zhe Zhao, Lichan Hong, Li Wei, Jilin Chen, Aniruddh Nath, Shawn Andrews, Aditee Kumthekar, Maheswaran Sathiamoorthy, Xinyang Yi, and Ed Chi. 2019. Recommending what video to watch next: a multitask ranking system. In Proceedings of the 13th ACM Conference on Recommender Systems. 43–51.
- Zhou et al. (2022) Kun Zhou, Xiao Liu, Yeyun Gong, Wayne Xin Zhao, Daxin Jiang, Nan Duan, and Ji-Rong Wen. 2022. MASTER: Multi-task Pre-trained Bottlenecked Masked Autoencoders are Better Dense Retrievers. arXiv preprint arXiv:2212.07841 (2022).
- Zou et al. (2022) Xinyu Zou, Zhi Hu, Yiming Zhao, Xuchu Ding, Zhongyi Liu, Chenliang Li, and Aixin Sun. 2022. Automatic Expert Selection for Multi-Scenario and Multi-Task Search. arXiv preprint arXiv:2205.14321 (2022).