CameraPose: Weakly-Supervised Monocular 3D Human Pose Estimation
by Leveraging In-the-wild 2D Annotations
Abstract
To improve the generalization of 3D human pose estimators, many existing deep learning based models focus on adding different augmentations to training poses. However, data augmentation techniques are limited to the ”seen” pose combinations and hard to infer poses with rare ”unseen” joint positions. To address this problem, we present CameraPose, a weakly-supervised framework for 3D human pose estimation from a single image, which can not only be applied on 2D-3D pose pairs but also on 2D alone annotations. By adding a camera parameter branch, any in-the-wild 2D annotations can be fed into our pipeline to boost the training diversity and the 3D poses can be implicitly learned by reprojecting back to 2D. Moreover, CameraPose introduces a refinement network module with confidence-guided loss to further improve the quality of noisy 2D keypoints extracted by 2D pose estimators. Experimental results demonstrate that the CameraPose brings in clear improvements on cross-scenario datasets. Notably, it outperforms the baseline method by 3mm on the most challenging dataset 3DPW. In addition, by combining our proposed refinement network module with existing 3D pose estimators, their performance can be improved in cross-scenario evaluation.
1 Introduction
Human pose estimation (HPE) is a task to predict the configuration of a particular set of human body parts from some visual input such as images or videos. Depending on the output format, it can be further divided into 2D and 3D HPE, respectively. Different from the 2D HPE that predicts the human keypoints with coordinates, the 3D HPE regresses which can be more helpful to solve difficult tasks, such as action and motion prediction[3, 7], posture and gesture recognition [14, 22], augmented reality and virtual reality [10, 12], healthcare [6, 19]. Although deep learning based methods have boosted the performance of 3D HPE [23, 24, 27, 28, 39], the error will typically increase to around two times from Human3.6M [15] to 3DHP [24] for cross-dataset scenario due to the poor model generalization [11].
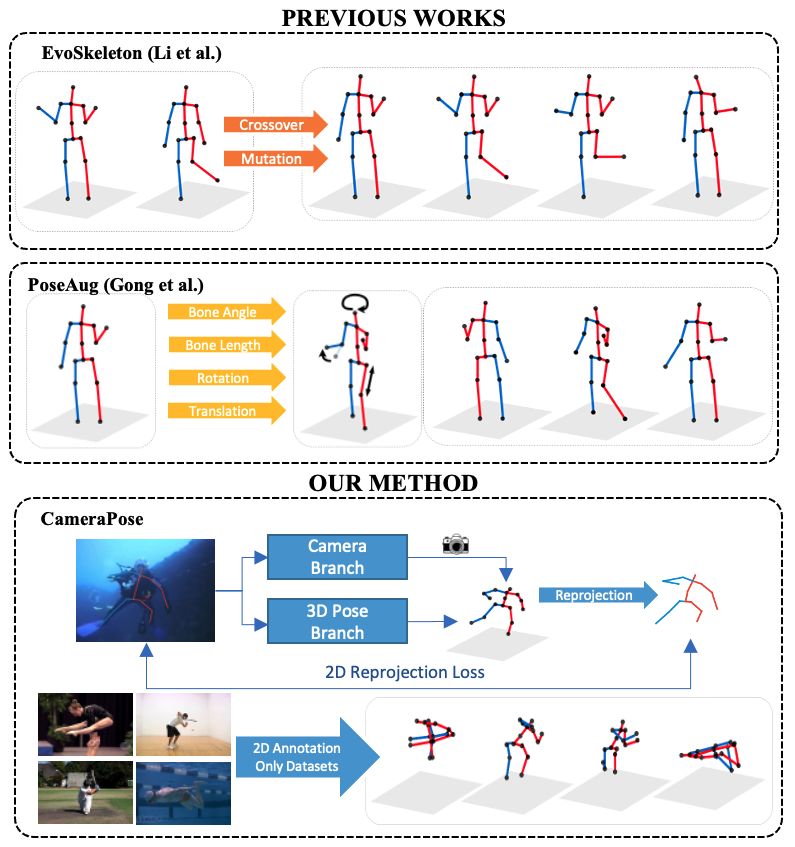
Recent works argue that poor model generalization can be mitigated by increasing the variance in training data. Therefore, many augmentation-related algorithms have been proposed to improve the 3D HPE accuracy. However, no matter it is image-based augmentation [25, 31], synthetic-based augmentation [5, 35], predefined transformation [20] or GAN-based augmentation [11], the variances added to the training data is still limited to the original 2D-3D pair. Figure 1 shows examples of augmented 2D-3D pairs with different algorithms. We can observe that the generated new pair 2D-3D cannot provide pose changes (lying to sitting etc.). Due to the limitation in the training data, the scenes or scenario are still relatively simple to the in-the-wild environment, which hinder the real-world application of these algorithms.
Different from the existing methods that rely on data augmentation for training data expansion, we proposed a novel weakly-supervised framework, CameraPose, to improve model generalization on 3D HPE by taking advantage of plentiful 2D annotations. Compared to the expensive 3D annotations, 2D annotations are less expensive, and many challenging 2D datasets [1, 17, 21] containing rich actions, poses, and scenes are available in the literature. The proposed CameraPose network can combine any existing 2D or 3D datasets in a single framework by adding a camera parameter estimation branch. Our approach also integrated the GAN-base pose augmentation framework to improve the training data diversity and ensure the camera branch’s generalization.
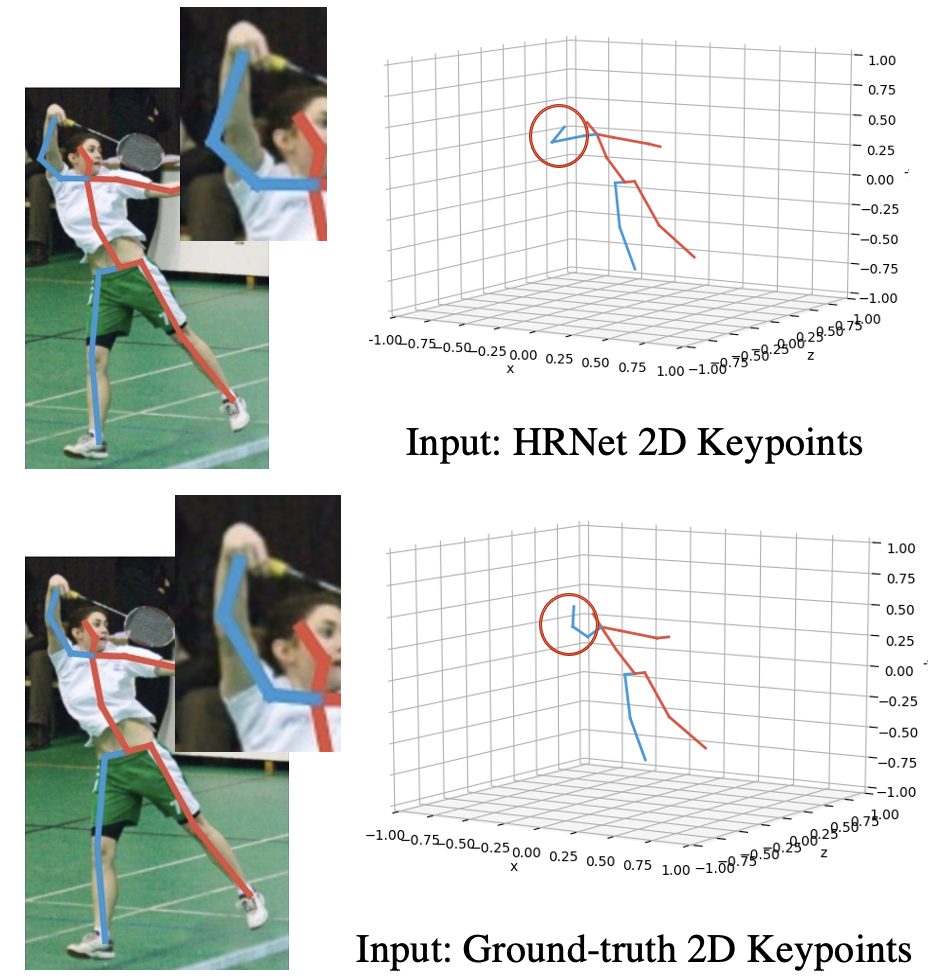
Existing 3D HPE networks usually directly use 2D keypoints from some pre-trained detectors as input to train 3D joints. However, inferred 2D keypoints will lead to the situation illustrated in Fig.2. The errors from the 2D joints estimation step will generate 3D prediction errors on some keypoints. In addition, augmentation on inaccurate 2D keypoints will further enlarge the errors in 3D joints. As shown in Table 1, the ground-truth inputs significantly boosted the accuracy in all testing cases with different pose estimators. Therefore, it is necessary to improve the 2D keypoints before feeding them into our 3D estimator network. To mitigate the error in 2D input, we propose to incorporate a refinement network that aims to infer better 2D joints based on the positions and confidence scores of detected 2D joints.
| 3D Pose Estimator |
|
|||
|---|---|---|---|---|
| 2D Keypoints Source | HRNet | Ground-truth | ||
| Zhao et al. [38] | 57.5 | 44.4 | ||
| Martinez et al. [23] | 53.0 | 43.3 | ||
| Pavllo et al. [28] | 52.2 | 41.8 | ||
Our contributions are three-fold: 1) We propose a camera parameter branch that will generate per-instance camera parameter inference so that any existing 2D keypoints datasets (without 3D labeling) can be utilized in model training. 2) We propose a Refinement Network to improve the accuracy of 2D joints, which can be helpful in the GAN-based augmentation stage, as well as the final 3D joints predictions. 3) We introduce the reprojection loss, confidence-guided refinement loss, together with the camera loss in the loss design to make the network differentiable.
2 Related Works
Fully-Supervised 3D HPE. There are a lot of papers and research that use the 2D-3D annotation pairs for a fully-supervised training manner. Tekin et al. [33] directly regress the 3D human pose from a spatio-temporal volume of bounding boxes, and Martinez et al. [23] regress the 3D human pose from a naive MLP using 2D keypoints as input and 3D keypoints as output.
On similar datasets, these end-to-end methods often perform very well. Their capacity to generalize to different settings, on the other hand, is restricted. Many studies use cross dataset training or data augmentation to address this issue [31, 25, 5, 35]. Most recently, Li et al. [20] directly augment 2D-3D pose pairs by randomly applying partial skeleton recombination and joint angle perturbation on source datasets. Then Gong et al. [11] used a generative-based model to manipulate the transformation of 3D ground-truth and then do the reprojection back to image space to get the corresponding 2D keypoints. This can be trained along with the 3D lifting network and some discriminators to ensure the augmented poses are realistic and increase the diversity of the training dataset. While effective, the major downside of all supervised approaches is that they do not generalize well to unseen poses. Therefore, their application to in-the-wild scenes is limited.
Some even use a portion amount of dataset to do the training for human pose estimation through methods like transfer learning [24, 8, 34]. As they all try to mixed 2D pose from in-the-wild images and 3D poses from laboratory settings to learn the deep features through shared representation. These methods generalize better to unseen poses because they learn distributions of realistic 3D postures and their characteristics. They can recreate out-of-distribution positions to a degree, but they have trouble with entirely undetected poses.
Weakly-Supervised 3D HPE. Some approaches use unpaired 2D-3D annotations to get some 3D priors or basis to do the 3D human pose estimation from a monocular camera. Drover et al. [9] proposed a projection layer that randomly projects the predicted 3D poses back into 2D poses and then feeds into a discriminator. Chen et al. [4] introduced cycle consistency loss into [9] extending the training with a step of lifting the projected 2D pose once again into the 3D pose. Habibie et al. [13] designed an architecture that comprises an encoding of explicit 2D and 3D features, and uses supervision by a separately learned projection model from the predicted 3D pose. Wandt et al. [36] proposed RepNet to tackle the problem with reprojection constraints by using an adversarial-based method with a sub-network that can estimate the camera. However, we argue the gap between supervised algorithms and unsupervised algorithms can be large on some challenging datasets.
As for multi-view settings, Rochette et al. [30] using multi-view consistency by moving the stereo reconstruction problem into the loss. Kocabas et al. [18] proposed another multi-view approach by applying epipolar geometry to predicted 2D pose under different views to construct the pseudo-ground-truth. Iqbal et al. [16] proposed a end-to-end learning framework adopting a 2.5D pose representation without any 3D annotations. Wandt et al. [37] then proposed a self-supervised method that requires no prior knowledge about the scene, 3D skeleton, or camera calibration and also introduced the 2D joint confidences into the 3D lifting pipeline. However, these algorithms are hard to be applied to single-view or in-the-wild predictions due to their multi-view pipeline design.
HPE with Data Augmentation. Data augmentation can help the model generalization ability by enlarging the training data [31, 25, 5, 35]. Most recently, Li et al. [20] directly augment 2D-3D pose pairs by randomly applying partial skeleton recombination and joint angle perturbation on source datasets. Then Gong et al. [11] used a generative-based model to manipulate the transformation of 3D ground-truth then do the reprojection back to image space to get the corresponding 2D keypoints. This can be trained along with the 3D lifting network and some discriminators to ensure the augmented poses are realistic and increase the diversity of the training dataset.
3 Proposed Method
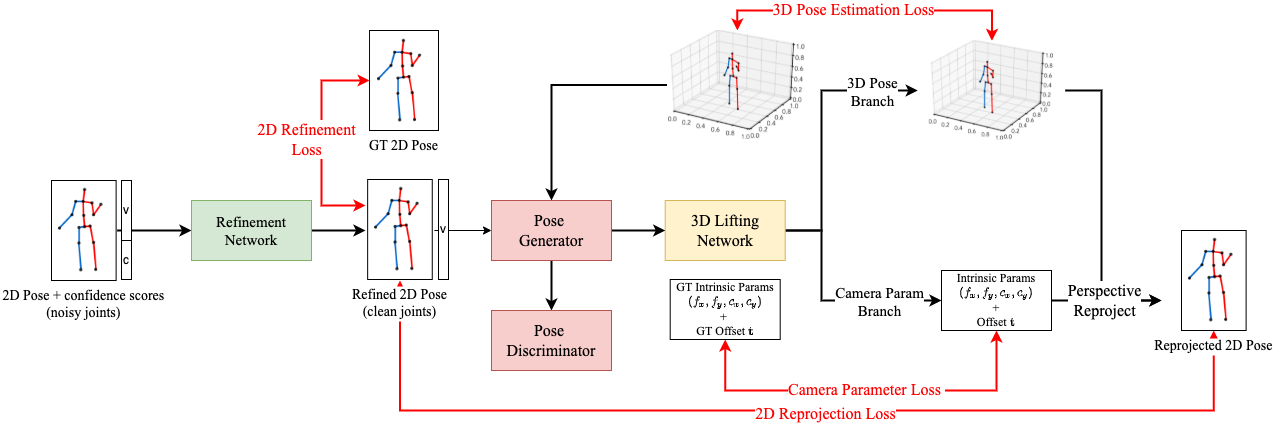
The CameraPose network consisted of three main parts: (1) Refinement Network, (2) Pose Generator/Discriminator, and (3) Weakly-Supervised Camera Parameter Branch. Figure 3 summarizes our CameraPose architecture design.
Let denotes the 2D keypoints and denotes the corresponding 3D joint position in the camera coordinate system with represents the number of joints in the framework. Our proposed network will train on two different cases of datasets: (1) 2D-3D annotated dataset ,and (2) 2D annotations only dataset by optimizing the following equation:
| (1) |
where and represent the weights of our 3D lifting model and refinement network. Furthermore we extend the design of pose augmentor to enlarge the 2D-3D annotated dataset with the augmented dataset . Therefore our end-to-end optimization procedure will become:
| (2) |
| Notation | Description |
|---|---|
| number of joints used | |
| number of samples in the batch | |
| datasets with 2D-3D annotations | |
| datasets with 2D annotations only | |
| datasets generated by the pose generator | |
| ground-truth 2D-3D annotations from | |
| ground-truth 2D annotations from | |
| augmented 2D-3D annotations from | |
| predicted 3D poses from 3D lifting network |
3.1 Refinement Network
Instead of refining on the original noisy 2D keypoints, we utilize the confidence score combined with the 2D coordinates as input to the refinement network. We first normalize the coordinates of keypoints to with respect to the input image height and width. We also normalized the confidence scores to a comparable scale by Eq. 3:
| (3) |
where denotes for L1 norm and stands for the all the heatmaps in the -th training sample while stands for the maximum value (confidence score) on the -th heatmap. The normalized confidence score will be used as the weight to compute the joint-wise mean-square error in Eq. 4.
The neural network architecture of our Refinement Network is a standard residual block consisting of fully connected layers with a hidden dimension of . The refinement loss is formulated as:
| (4) |
where we compute the mean-square-error over the number of training samples of the predicted poses and normalized ground-truth poses with joint-wise normalized confidence-weight .

3.2 Camera Parameter Branch
In this paper, the 2D-3D pose pairs are calculated in the camera coordinate system, so the camera parameters can be simplified to be the intrinsic matrix in Eq. 5 and a 3D offset . For intrinsic matrix we are essentially predicting a -dimensional vector, namely , the focal lengths , , and principal center offsets , along the and direction respectively.
| (5) |
and for the 3D offset we are predicting a -dimensional vector:
| (6) |
The camera parameter branch consists of 2 residual blocks with a hidden dimension of , which can be plugged in to any standard 3D pose estimators. There are three losses that can be involved depending on the annotations. The 2D reprojection loss as shown in Eq. 7 calculates the Euclidean distance between the reprojected 2D poses and ground truth. The mean-square error (MSE) is used in loss calculation for both the camera parameter loss and 3D inference loss as shown in Eqs. 8 and 9 respectively.
| (7) |
| (8) |
| (9) |
where stands for the predicted 3D pose from our 3D lifting network.
Since CameraPose can work on 2D-3D pose pairs as well as 2D alone pose estimations, the loss design can be different according to the availability of labels. In the case of all annotations are available during the training stage, the camera loss can be calculated as:
| (10) |
In the case of 2D annotation alone training step, the loss calculation will be from 2D reprojection error:
| (11) |
| Dataset | # of Sample | 2D Annotations | 3D Annotations | Camera Parameters |
|---|---|---|---|---|
| Human3.6M [15] | 3.6M | v | v | v |
| MPI-INF-3DHP [24] | 1.3M | v | v | v |
| 3DPW [34] | 51k | v | v | |
| Ski-Pose PTZ [29] | 20k | v | v | v |
| MPII [1] | 25k | v | ||
| MS-COCO [21] | 250k | v |
3.3 Pose Generator and Discriminator
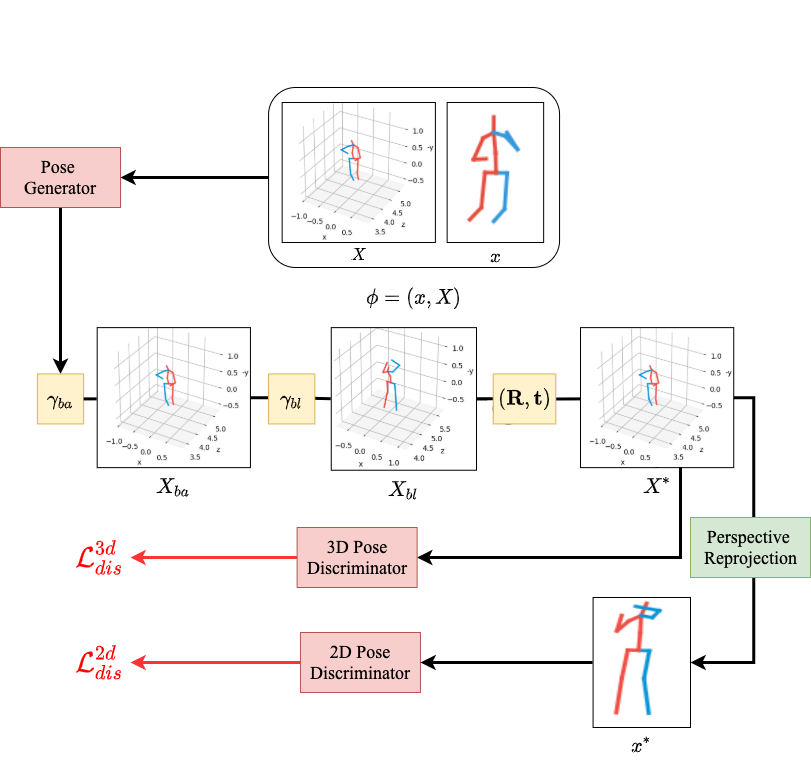
Similar to the framework in [11], we utilized both generator and discriminator to further improve the diversity in training poses. As shown in Figure 5, the generator is plugged in to the 2D pose generation stage, and the discriminator is applied on both the 2D and 3D pose inference.
The generator is actually formed by 3 simple multi-layer perceptions that generated different parameters for 3 different augmentation operations respectively: (1) changing the bone angle , (2) changing the bone length and (3) changing the camera view and position of the input 3D pose .
The discriminator part of the framework can be divided into 2 portions, the and as we want to make sure that both the augmented and formed plausible human poses in both image coordinate and camera coordinate. But in our work we not only want to ensure the goodness of the augmented poses from the generator, we also want to utilized the discriminator to regulated our reprojected 2D poses for those 2D annotations only dataset cases. The discriminators also adapt the part-aware Kinematic Chain Space (KCS) proposed in [11], they are fully connected networks with a structure similar to the pose regression network using the KCS representation [36] of 2D or 3D poses as input. Here we use the LS-GAN loss:
| (12) | ||||
| (13) | ||||
| (14) | ||||
| (15) |
as the pose discrimination loss to train the generator and discriminator.
3.4 Overall Loss
The overall framework is made differentiable and can be trained in the end-to-end fashion. We update different modules alternatively by minimizing loss in Eq. 4, Eq. 10, Eq. 11 as well as generators and discriminators with some preassigned hyper-parameters .
Then we interactively train the entire model and update the weights of 3D lifting network using the losses:
| (16) |
and
| (17) |
depending on the different datasets or we are using for the batch. We will introduce more training details and hyper-parameter settings in the Sec. 4.3.
4 Experiments
4.1 Datasets
| Method | Human3.6M (MPJPE) | 3DHP (MPJPE) | 3DPW (PA-MPJPE) |
|---|---|---|---|
| Wnadt et al. [37] | 74.3 | 104.0 | - |
| Rhodin et al. [29] | 80.1 | 121.8 | - |
| Zhao et al. [38] | 44.4 | 97.4 | - |
| Martinez et al. [23] | 43.3 | 85.3 | - |
| Cai et al. [2] | 41.7 | 87.8 | - |
| Pavllo et al. [28] | 41.80 | 92.64 | 76.38 |
| Gong et al. [11] | 39.02 | 76.13 | 66.27 |
| Ours (CameraPose) | 38.87 | 78.85 | 63.26 |
For the 2D-3D paired annotations, we utilize the most popular datasets 3D HPE dataset Human3.6M [15], 3DHP [24] and 3DPW [34]. Both Human3.6M and 3DHP were collected indoor in some laboratory environment through the MoCap (motion capture) system [26] with multiple calibrated cameras. The 3DPW is a more challenging dataset collected in outdoor environment using IMU (inertial measurement unit) sensors with mobile phone lens.
For 2D annotations only datasets, we used MPII [1] which contains a variety of in-the-wild everyday human activities. Another popular 2D dataset MS-COCO [21] is also used for qualitative analysis purposes. Although the 2D annotation dataset such as MPII is much less than Human3.6M or 3DHP in terms of sample size, these 2D annotation datasets contain more challenging human poses with different activities. Note that both Human3.6M and 3DHP are video based datasets, so that the total number of images is much larger than MPII and MSCOCO. We summarized the datasets utilized in our experiments in Table 3.
4.2 Preprocessing
Different datasets have distinctive annotations on joints, which make the model training difficult. In this paper, we used the Human3.6M format as standard one, and interpreted missing joints by labeling nearby joints for other datasets. All the joints that are not included in Human3.6M format will be discarded.
Many existing 3D HPE algorithms use the groundtruth as model input for evaluation. However, groundtruth is not available in real use cases. To evaluate the model performance on the real-world applications, we also used existing 2D detector HRNet to extract the 2D keypoints as model input and rerun results on different datasets.
Due to the various labeling schemes or joint formats difference, we preprocess other schemes into the Human3.6M format by simple interpolation of some related joints and removal of the unused joints. For example, there is no pelvis; we simply create such joint by computing the mid-point of the left and right hip of any given label. Even though such interpolations are not always perfect due to the nature of each dataset, this preprocessing procedure allows us to have a better idea and comparison on cross-dataset scenarios.
4.3 Training
CameraPose network is trained on 2 datasets: Human3.6M (2D + 3D) and MPII (2D). For the former, we followed most 3D human pose estimation training protocols using the subjects S1, S5, S6, S7, S8 from Human3.6M as our 2D-3D training data, and subjects S9, S11 for evaluation purposes. For the latter, we filtered and selected around 10k training samples by checking the joints annotations. For evaluation, MPI-INF-3DHP and 3DPW were used to get quantitative results in terms of MPJPE (mean-per-joint-position-error) and PA-MPJPE (aligned with ground-truths by rigid transformation).
The model training can be divided into 3 steps. The refinement network was trained as the first step for 100 epochs with learning rate being 0.0001 and weight decay at epochs 30, 60 and 90, respectively. Next step, the 3D lifting network along with the pose generator and discriminator was trained using Human3.6M dataset for 10 epochs with a learning rate of 0.0001. This step is for warm-up and GAN tuning which can make the following model training more stable. Finally, the model was trained in an end-to-end fashion using both 2D-3D pairs annotations as well as 2D alone annotations. In each iteration, we first updated the weights of generator and discriminator to make the generators more stable. Then the 3D lifting network was updated based on the augmented poses plus the 2D-3D annotated dataset. After that, 2D only annotations were utilized to tune the camera parameter branch. The model was trained for 75 epochs with a learning rate of 0.0005 and weight decay at 30, 60, respectively. And the weighting for loss we choose , , , and .
| Method |
|
|
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| Pavllo et al. [28] | Human3.6M (HRNet) | 57.90 | 103.86 | ||||||
| Gong et al. [11] | Human3.6M (HRNet) | 55.18 | 99.50 | ||||||
| Gong et al. [11] w/ Refinement Network | Human3.6M (HRNet) | 54.32 | 97.45 | ||||||
| CameraPose w/ Refinement Network | Human3.6M (HRNet) | 54.20 | 97.35 | ||||||
| CameraPose w/o Refinement Network | Human3.6M (HRNet) | 54.38 | 98.12 |
4.4 Quantitative Results
CameraPose Network Accuracy. We compared CameraPose with other state-of-the-art methods [2, 28, 38, 11, 23] trained on Human3.6M. For the temporal-based methods [2, 28], we implemented the single frame version for a fair comparison. Table 4 summarized the experimental results of different methods. For each column, the MPJPE or PA-MPJPE are calculated for evaluation, obtained from the same model trained and selected based on the evaluation dataset of Human3.6M. Some existing algorithms selected distinctive best models on different testing datasets, which may not reflect the generalization of models well. Instead, we selected a single model based on the accuracy of the validation of Human3.6M to make it more realistic for real-world application.

As shown in Table 4, our method outperforms the SOTA on the most challenging dataset 3DPW by a noticeable margin (mm and mm). It also has significantly higher accuracy than other weakly-supervised methods like [29] and [37]. Our model also achieves the highest accuracy on the Human3.6M dataset. Experimental results clearly show the strong generalization capability of our proposed method. Adding the camera parameter branch can help the model to learn from in-the-wild datasets with 2D annotations, which is very effective for hard examples.
The results on the 3DHP are slightly lower than SOTA methods, and we claim it is due to the fact that the 2D annotations we added from MPII are more helpful for challenging cases such as the 3DPW dataset. The best accuracy on the 3DHP dataset can be 75.54 MPJPE using our model, which outperforms the current SOTA if we select a specific model for the 3DHP dataset.
Refinement Network Accuracy. To show the effectiveness of the refinement network, we trained different models with different settings as shown in the Table 5.
We used HRNet as 2D detectors to extract the 2D keypoints on all the training and evaluation datasets. We added the refinement network to both the SOTA method [11] and our proposed model. By adding the refinement network, both PoseAug and our model have improved accuracy on both Human3.6M and 3DHP. In addition, our model outperforms the SOTA on both testing datasets. Therefore, both our proposed camera parameter network and the refinement network are useful for 3D HPE.
4.5 Qualitative Visualization
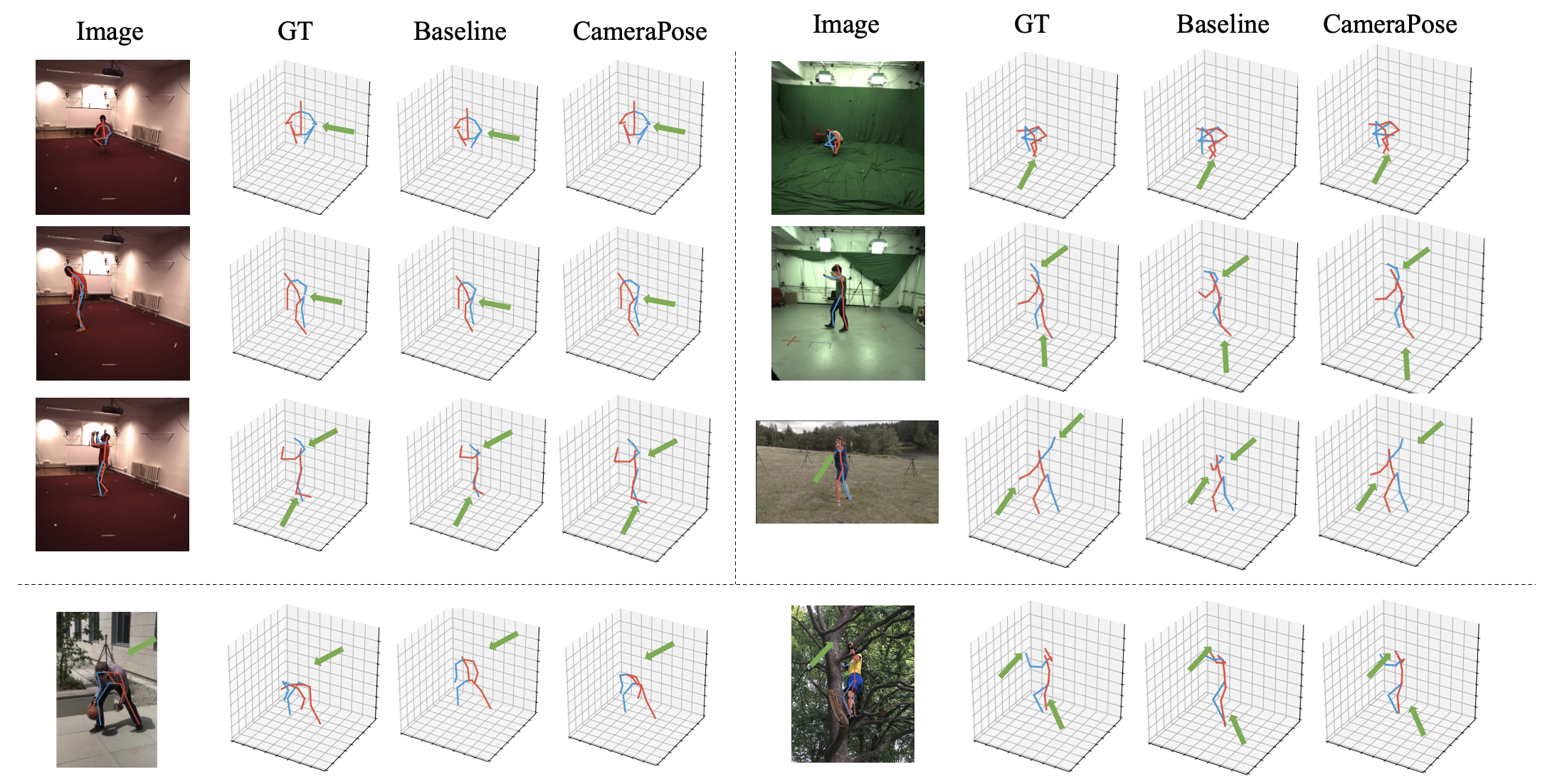
3D Pose Estimation. We choose 3 datasets (Human3.6M, 3DHP and 3DPW) to qualitative compare our proposed method and baseline [11]. As shown in Figure 6, our model has more accurate predictions on challenging datasets such as 3DPW. Note that we utilize cross-scenario training to make sure there is no overlap between training and testing datasets. We also visualize our results on datasets without 3D annotations such as MPII, MSCOCO, and SkiPose-PTZ [29] in Figure 7. The visualization results are very plausible, which indicates the capability of our model for in-the-wild prediction.
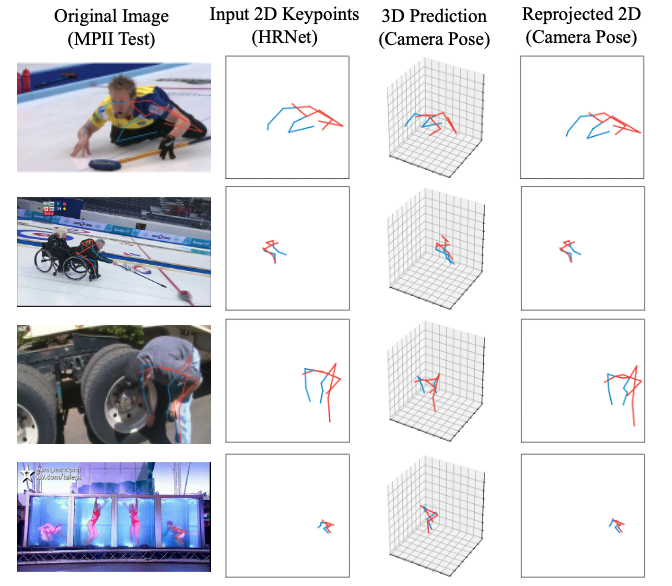
2D Reprojection. To validate the camera parameter branch, we visualize the results of our model at a different stage. Figure 8 shows the original image, input 2D keypoints from HRNet, inferred 3D poses, and reprojected 2D poses from left to right columns. It clearly shows that our CameraPose can predict well on unseen poses and the reprojected 2D poses are meaningful too.
5 Conclusions
We propose CameraPose, a weakly-supervised framework for 3D human pose estimation from a single image that can aggregate 2D annotations by designing a camera parameter branch. Given any noisy 2D keypoints from pretrained 2D pose estimator, CameraPose is able to refine the keypoints with a confidence-guided loss and feed them into the 3D lifting network. Since our approach uses the camera parameters learned from the camera branch to do the reprojection back to 2D, it can solve the problem of the lacking of the 2D-3D datasets with rare poses or outdoor scenes. We evaluate our proposed method on some benchmark datasets; the results show that our model can achieve higher accuracy on challenging datasets and be able to predict meaningful 3D poses given in-the-wild images or 2D keypoints.
References
- [1] Mykhaylo Andriluka, Leonid Pishchulin, Peter Gehler, and Bernt Schiele. 2d human pose estimation: New benchmark and state of the art analysis. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2014.
- [2] Yujun Cai, Liuhao Ge, Jun Liu, Jianfei Cai, Tat-Jen Cham, Junsong Yuan, and Nadia Magnenat Thalmann. Exploiting spatial-temporal relationships for 3d pose estimation via graph convolutional networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), October 2019.
- [3] Zhe Cao, Hang Gao, Karttikeya Mangalam, Qi-Zhi Cai, Minh Vo, and Jitendra Malik. Long-term human motion prediction with scene context. CoRR, abs/2007.03672, 2020.
- [4] Ching-Hang Chen, Ambrish Tyagi, Amit Agrawal, Dylan Drover, M. V. Rohith, Stefan Stojanov, and James M. Rehg. Unsupervised 3d pose estimation with geometric self-supervision. CoRR, abs/1904.04812, 2019.
- [5] Wenzheng Chen, Huan Wang, Yangyan Li, Hao Su, Changhe Tu, Dani Lischinski, Daniel Cohen-Or, and Baoquan Chen. Synthesizing training images for boosting human 3d pose estimation. CoRR, abs/1604.02703, 2016.
- [6] Henry M. Clever, Zackory Erickson, Ariel Kapusta, Greg Turk, Karen Liu, and Charles C. Kemp. Bodies at rest: 3d human pose and shape estimation from a pressure image using synthetic data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2020.
- [7] Enric Corona, Albert Pumarola, Guillem Alenya, and Francesc Moreno-Noguer. Context-aware human motion prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2020.
- [8] Carl Doersch and Andrew Zisserman. Sim2real transfer learning for 3d pose estimation: motion to the rescue. CoRR, abs/1907.02499, 2019.
- [9] Dylan Drover, M. V. Rohith, Ching-Hang Chen, Amit Agrawal, Ambrish Tyagi, and Cong Phuoc Huynh. Can 3d pose be learned from 2d projections alone? CoRR, abs/1808.07182, 2018.
- [10] Ahmed Elhayek, Onorina Kovalenko, Pramod Murthy, Jameel Malik, and Didier Stricker. Fully automatic multi-person human motion capture for vr applications. In EuroVR, 2018.
- [11] Kehong Gong, Jianfeng Zhang, and Jiashi Feng. Poseaug: A differentiable pose augmentation framework for 3d human pose estimation. CoRR, abs/2105.02465, 2021.
- [12] Onur G. Guleryuz and Christine Kaeser-Chen. Fast lifting for 3d hand pose estimation in ar/vr applications. 2018 25th IEEE International Conference on Image Processing (ICIP), pages 106–110, 2018.
- [13] Ikhsanul Habibie, Weipeng Xu, Dushyant Mehta, Gerard Pons-Moll, and Christian Theobalt. In the wild human pose estimation using explicit 2d features and intermediate 3d representations. CoRR, abs/1904.03289, 2019.
- [14] Zhiwu Huang, Chengde Wan, Thomas Probst, and Luc Van Gool. Deep learning on lie groups for skeleton-based action recognition. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017.
- [15] Catalin Ionescu, Dragos Papava, Vlad Olaru, and Cristian Sminchisescu. Human3.6m: Large scale datasets and predictive methods for 3d human sensing in natural environments. IEEE Transactions on Pattern Analysis and Machine Intelligence, 36(7):1325–1339, jul 2014.
- [16] Umar Iqbal, Pavlo Molchanov, and Jan Kautz. Weakly-supervised 3d human pose learning via multi-view images in the wild. CoRR, abs/2003.07581, 2020.
- [17] Sam Johnson and Mark Everingham. Clustered pose and nonlinear appearance models for human pose estimation. In Proceedings of the British Machine Vision Conference, pages 12.1–12.11. BMVA Press, 2010. doi:10.5244/C.24.12.
- [18] Muhammed Kocabas, Salih Karagoz, and Emre Akbas. Self-supervised learning of 3d human pose using multi-view geometry. CoRR, abs/1903.02330, 2019.
- [19] Jyothsna Kondragunta and Gangolf Hirtz. Gait parameter estimation of elderly people using 3d human pose estimation in early detection of dementia. In 2020 42nd Annual International Conference of the IEEE Engineering in Medicine Biology Society (EMBC), pages 5798–5801, 2020.
- [20] Shichao Li, Lei Ke, Kevin Pratama, Yu-Wing Tai, Chi-Keung Tang, and Kwang-Ting Cheng. Cascaded deep monocular 3d human pose estimation with evolutionary training data. CoRR, abs/2006.07778, 2020.
- [21] Tsung-Yi Lin, Michael Maire, Serge J. Belongie, Lubomir D. Bourdev, Ross B. Girshick, James Hays, Pietro Perona, Deva Ramanan, Piotr Dollár, and C. Lawrence Zitnick. Microsoft COCO: common objects in context. CoRR, abs/1405.0312, 2014.
- [22] Diogo C. Luvizon, David Picard, and Hedi Tabia. 2d/3d pose estimation and action recognition using multitask deep learning. CoRR, abs/1802.09232, 2018.
- [23] Julieta Martinez, Rayat Hossain, Javier Romero, and James J. Little. A simple yet effective baseline for 3d human pose estimation. In ICCV, 2017.
- [24] Dushyant Mehta, Helge Rhodin, Dan Casas, Pascal Fua, Oleksandr Sotnychenko, Weipeng Xu, and Christian Theobalt. Monocular 3d human pose estimation in the wild using improved cnn supervision. In 3D Vision (3DV), 2017 Fifth International Conference on. IEEE, 2017.
- [25] Dushyant Mehta, Oleksandr Sotnychenko, Franziska Mueller, Weipeng Xu, Srinath Sridhar, Gerard Pons-Moll, and Christian Theobalt. Single-shot multi-person 3d body pose estimation from monocular RGB input. CoRR, abs/1712.03453, 2017.
- [26] Pedro Alves Nogueira. Motion capture fundamentals a critical and comparative analysis on real-world applications. 2012.
- [27] Georgios Pavlakos, Luyang Zhu, Xiaowei Zhou, and Kostas Daniilidis. Learning to estimate 3d human pose and shape from a single color image. CoRR, abs/1805.04092, 2018.
- [28] Dario Pavllo, Christoph Feichtenhofer, David Grangier, and Michael Auli. 3d human pose estimation in video with temporal convolutions and semi-supervised training. CoRR, abs/1811.11742, 2018.
- [29] Helge Rhodin, Jörg Spörri, Isinsu Katircioglu, Victor Constantin, Frédéric Meyer, Erich Müller, Mathieu Salzmann, and Pascal Fua. Learning monocular 3d human pose estimation from multi-view images. CoRR, abs/1803.04775, 2018.
- [30] Guillaume Rochette, Chris Russell, and Richard Bowden. Weakly-supervised 3d pose estimation from a single image using multi-view consistency. CoRR, abs/1909.06119, 2019.
- [31] Grégory Rogez and Cordelia Schmid. Mocap-guided data augmentation for 3d pose estimation in the wild. CoRR, abs/1607.02046, 2016.
- [32] Ke Sun, Bin Xiao, Dong Liu, and Jingdong Wang. Deep high-resolution representation learning for human pose estimation. CoRR, abs/1902.09212, 2019.
- [33] Bugra Tekin, Isinsu Katircioglu, Mathieu Salzmann, Vincent Lepetit, and Pascal Fua. Structured prediction of 3d human pose with deep neural networks. CoRR, abs/1605.05180, 2016.
- [34] Timo von Marcard, Roberto Henschel, Michael Black, Bodo Rosenhahn, and Gerard Pons-Moll. Recovering accurate 3d human pose in the wild using imus and a moving camera. In European Conference on Computer Vision (ECCV), sep 2018.
- [35] Kathan Vyas, Le Jiang, Shuangjun Liu, and Sarah Ostadabbas. An efficient 3d synthetic model generation pipeline for human pose data augmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, pages 1542–1552, June 2021.
- [36] Bastian Wandt and Bodo Rosenhahn. Repnet: Weakly supervised training of an adversarial reprojection network for 3d human pose estimation. CoRR, abs/1902.09868, 2019.
- [37] Bastian Wandt, Marco Rudolph, Petrissa Zell, Helge Rhodin, and Bodo Rosenhahn. Canonpose: Self-supervised monocular 3d human pose estimation in the wild. CoRR, abs/2011.14679, 2020.
- [38] Long Zhao, Xi Peng, Yu Tian, Mubbasir Kapadia, and Dimitris N. Metaxas. Semantic graph convolutional networks for 3d human pose regression. CoRR, abs/1904.03345, 2019.
- [39] Xingyi Zhou, Qixing Huang, Xiao Sun, Xiangyang Xue, and Yichen Wei. Towards 3d human pose estimation in the wild: A weakly-supervised approach. In The IEEE International Conference on Computer Vision (ICCV), Oct 2017.