Capital Asset Pricing Model with Size Factor and Normalizing by Volatility Index
Abstract.
The Capital Asset Pricing Model (CAPM) relates a well-diversified stock portfolio to a benchmark portfolio. We insert size effect in CAPM, capturing the observation that small stocks have higher risk and return than large stocks, on average. Dividing stock index returns by the Volatility Index makes them independent and normal. In this article, we combine these ideas to create a new discrete-time model, which includes volatility, relative size, and CAPM. We fit this model using real-world data, prove the long-term stability, and connect this research to Stochastic Portfolio Theory. We fill important gaps in our previous article on CAPM with the size factor.
1. Introduction
Here, we briefly describe the parts of the model analyzed in this article. We remind the readers that price returns for a stock or a portfolio measure only price changes, ignoring dividends, while total returns include both price changes and dividends paid. Also, equity premium is computed as total returns minus risk-free returns (usually measured by short-term Treasury bills). We combine three main ideas in this article.
Idea 1: Capital Asset Pricing Model. We model a target stock portfolio (well-diversified) using a simple linear regression versus the benchmark stock portfolio. A typical example is the Standard & Poor 500 (S&P 500), a well-known index of large USA stocks. The classic measuring tool there is equity premia (for target and benchmark), but we can also apply this for price returns. The slope and intercept of this regression are called beta and alpha.
Idea 2: Size Effect. Small stocks, on average, have higher volatility but also higher returns than large stocks. This feature implies long-term stability: Well-diversified stock portfolios stay together and not split into several clouds. We combined these two ideas in the previous article by the second author [13]. This article is a sequel of that work. Such long-term stability is of interest in Stochastic Portfolio Theory, which constructs portfolios as functions of market weights, utilizing the observation that small stocks have higher risk and return.
Idea 3: The Volatility Index. In another article [22] by the second author, we observe that total monthly returns of the benchmark are not IID (independent identically distributed) Gaussian. However, dividing them by volatility makes them IID Gaussian. Here, volatility is measured by the Volatility Index (VIX) monthly average. The volatility itself is modeled as an autoregression of order 1 on the logarithmic scale. Similar observation holds for price monthly returns of large stocks, and for the small stocks.
In this article, we continue research of [13] by inserting Idea 3 in this setting, thus combining all three ideas. We create a new discrete-time model, and fit it using real market data from Kenneth French’s data library and Federal Reserve Economic Data web site. We then state and prove long-term stability of this market model, and interpret this for Stochastic Portfolio Theory. Unlike [13], we consider only discrete time models in this article. We fill a couple of important gaps left in the previous research [13].
In Section 2, we provide a comprehensive motivation of proposed models and historical review. Section 3 is devoted to data description and statistical fit of these models. In Section 4, we state and prove long-term stability (ergodicity) result for this model: Theorem 1, and analyze sufficient conditions for Theorem 1 to hold. We reduce the capital distribution curve to the order statistics (sorted values) of a standard normal sample. The last part of this section contains a short discussion of stability conditions for the case where volatility is constant. We have already discussed this in our previous article [13] but only for continuous time. Thus we fill a gap in our research.
In Section 5, we interpret our results in terms of Stochastic Portfolio Theory. We simulate capital distribution curve (ranked market weights vs ranks). We prove stability of this curve in Theorem 2. Next, Theorem 3 contains results about its shape: We reduce it to normal order statistics. This includes the case of constant volatility, which was studied in [13]. There, we did not have rigorous results; here, we fill this gap. Finally, the Appendix contains a discussion of the capital distribution curve based on ranked standard normal sample, continuing research of Section 5.
2. Background and Motivation
2.1. Capital Asset Pricing Model
This celebrated model, abbreviated as CAPM, compares returns of a stock portfolio with returns of the benchmark. This model was proposed by [16, 19, 25] The benchmark is usually taken to be the Standard & Poor 500 for the American stock market. The model states that the only factor which matters for a well-diversified portfolio is market exposure, otherwise known by a standard term beta and denoted by . The case corresponds to the risk-free portfolio, with guaranteed deterministic return. This is usually measured using a benchmark of a short-term rate , for example 1-month Treasury rate. The case corresponds to the market portfolio (the benchmark). When , the stock portfolio can be replciated by investing in a portfolio of risk-free bonds and the stock market benchmark, in proportions and , respectively. In other words, total returns (including price changes and dividends) of this portfolio are related to total returns of the benchmark:
| (1) |
Equivalently, we can rewrite (1) in terms of equity premia of the portfolio and of the benchmark:
| (2) |
If , this (2) still holds, and can be interpreted as shorting bonds and investing everything in the benchmark. We can treat as a risk measure: means that the portfolio is riskier than the benchmark, and means the opposite. The case does not usually happen in practice, see [1, Chapter 7].
It is not considered a big achievement if a money manager improved returns by increasing . In fact, often these managers are expected to maximize excess return: Total returns of a portfolio adjusted for market exposure. This quantity is denoted by and, accordingly, is called alpha. These two Greek letters and are standard notation in Finance. This methodology of market exposure and excess return is well-accepted by both finance academics and practitioners. One can include into (2) as
| (3) |
We also include an error term , since the model might not hold almost surely. This makes (3) a simple linear regression of upon .
Subsequent research disproved the strong claims of CAPM that market exposure is the only risk measure and quantity of interest for a diversified stock portfolio, see [8, 9], and [1, Chapter 7]. For one, there are systematic ways to generate excess return by using several factors. Also, might be unstable in the long run. Still, is an established risk measure, accepted by financial theorists, analysts, and managers. The CAPM is useful as a benchmark model, a starting point for more complicated and real-life models. Calculating for mutual funds and exchange-traded funds is common practice.
2.2. Size and value
The most well-known and accepted factors are size (average market capitalization of portfolio stocks) and value (fundamentals such as earnings, dividends, or book value, compared to price). These are well-accepted by financial academic community and are considered useful by industry practitioners, to the extent that there are multiple size- and value-based funds traded alongside the S&P 500 funds. See [3, 8, 10].
Including a few factors (for example size and value) would enrich (3). In particular, size factor is related to as follows: Well-diversified portfolios of small stocks have equity premia closely correlated with that of large stock benchmark S&P 500. This simple linear regression of vs has very large but which is slightly larger as . This can be done, for example, with exchange-traded funds tracking small, mid, and large (=benchmark) stock indices, see [13, Appendix]. The for mid-cap index is 1.15, and for small-cap index is 1.27. A natural idea then is to model as a function of a portfolio size relative to benchmark. We can try the same for , although in [13, Appendix] we have is not significantly different from zero for both small-cap and mid-cap indices. See more on the size effect in [24], and the discussion in [1, Chapter 8].
2.3. CAPM-based model with size as factor
Therefore, we developed the following model in [13]: Let = market capitalization of target portfolio, and = market capitalization of benchmark portfolio. Then the relative size (on the log scale) is defined as
| (4) |
For , the relative size is 0 (on the log scale) or 1 (on the absolute scale). This corresponds to the target portfolio having the same properties as the benchmark portfolio, with and . The simplest model is linear: For some coefficients ,
| (5) |
In fact, in [13] we have more general conditions: and are general functions of . Here, we focus only on linear functions, see [13, Example 1]. Analysis for small-cap and mid-cap funds above shows that but . Rewrite (3) as follows by plugging there (5):
| (6) |
where are IID regression residuals with mean zero. A good way to generalize (6) is to make it dynamic: a time series. To this end, we make the model complete by writing an equation for . With regard to the benchmark equity premia and market cap , we shall write this equation in the next subsection. Unlike total returns, which include dividends, price returns are computed only using price movements. The main idea is to take CAPM linear regression, and replace equity premia with price returns. We get
| (7) |
where are some coefficients (not necessarily the same as the from (6)), and are IID regression residuals with mean zero (not necessarily the same as , but possibly correlated with these). We can interpret change in logarithm as price returns:
| (8) | ||||
In real-life finance, a stock market is stable in the long run: Small stocks grow, on average, faster than large stocks. Thus formerly small stocks might become large, and formerly large stocks might become small. The relative size of a stock portfolio exhibits mean-reversion. In our article [13], we proved this for continuous time and more general systems than (6), (7), under the assumptions that the benchmark follows a lognormal Samuelson (Black-Scholes) model of geometric random walk with growth rate and total returns , and
| (9) |
This is consistent with the observation made above that and , since . Analysis of real-world finance data in [13] showed that and .
2.4. Stochastic volatility
However, there is a drawback in our modeling from [13]. We fit regressions (6) and (7) using real-world monthly data from 1926 taken from Kenneth French’s Dartmouth College Financial Data Library. Residuals are not IID. Absolute values are autocorrelated. This feature is also true for S&P 500 monthly returns themselves, see our recent article [22]. Also, these returns are not Gaussian. We wish to improve the fit of regressions (6) and (7) to make residuals closer to IID Gaussian. For S&P 500 returns, we did this in [22] as follows: We divided these returns by monthly average VIX: The S&P 500 Volatility Index computed daily by the Chicago Board of Options Exchange. Our main idea of this article [22] is (in our notation, see [22, Subsection 2.2]):
| (10) |
Similarly, it is reasonable to model normalized equity premia as IID Gaussian:
| (11) |
We did not do this in [22], but we complete this work in this article. For the original equity premia of benchmark , we plot in Figure 1 the quantile-quantile plot and the autocorrelation function for and . For the normalized equity premia , we plot these in Figure 2. We see that division by VIX is needed to model equity premia as in (11). Data for is taken from Kenneth French’s data library: Top 10% decile, January 1986–October 2024. For short-term rate , we use the 3-month Treasury rate from Federal Reserve Economic Data: start of month data. Data and Python code is available on Github repository: asarantsev/size-capm-vix
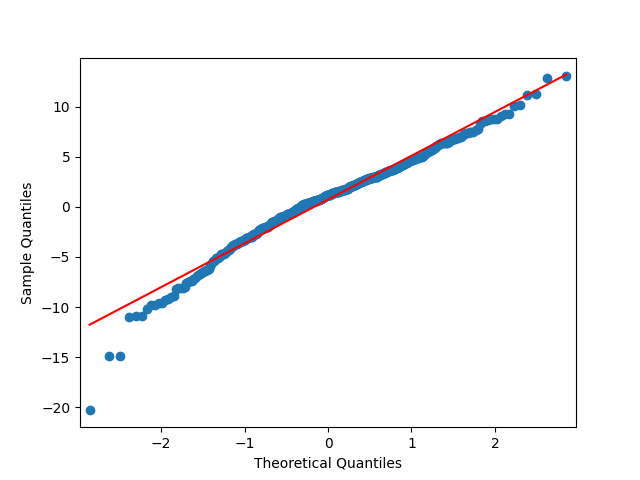
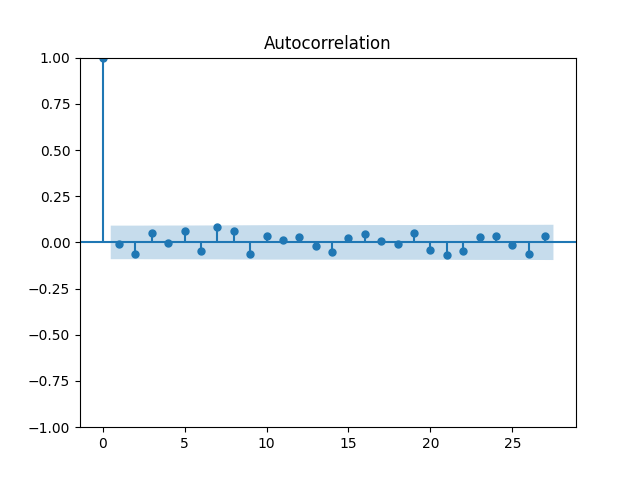
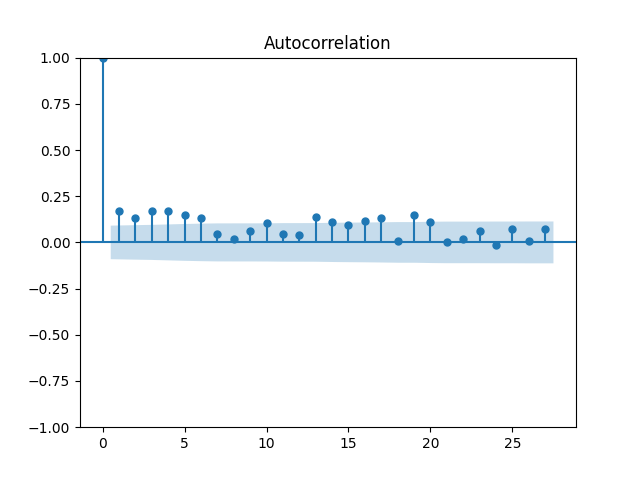
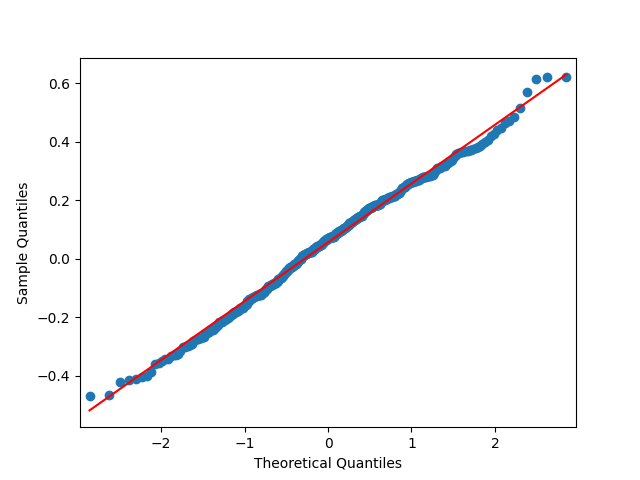
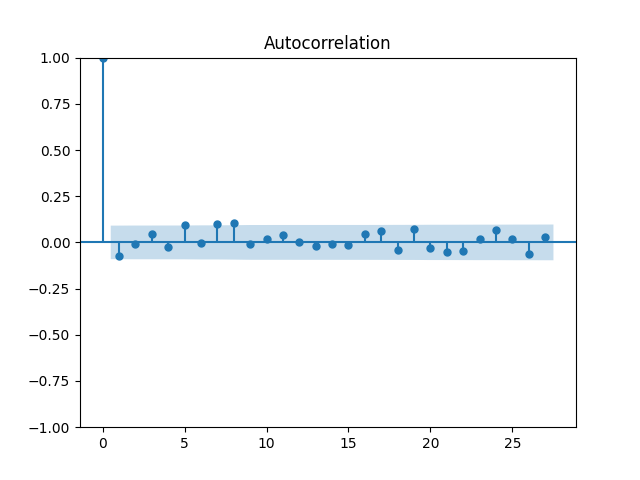
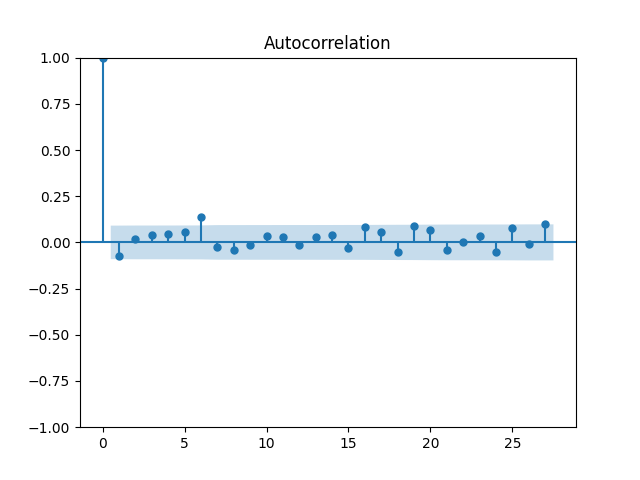
The VIX itself is modeled by an autoregression of order 1 on the log scale, see [22]:
| (12) |
Slightly abusing the notation, but following [22], in the rest of the article we use and as the intercept and the slope of this autoregression (12), instead of excess return and market exposure from the CAPM. This model (12) has good fit, as shown in [22, Section 3]. Innovations are IID but not Gaussian, with some finite exponential moments. The point estimate , and we reject the unit root hypothesis .
2.5. Capital distribution curve
A newly developed framework for portfolio management in Stochastic Portfolio Theory, see [11]. One question which concerns it is model stability: In a model of stocks, do they move together in the long run, or do they split into several subsets, moving away from each other in the long run? A related question is analysis of market weights: A market weight of a stock is its market capitalization (size) divided by the sum of all market capitalizations. Rank market weights at each time from top to bottom:
The plot of points
is called the capital distribution curve. For real-world markets, this curve is concave and straight at left upper end, see [11, 12]. See also our own plots in Figure 3. Python code and data are available in GitHub repository asarantsev/size-capm-vix The data is from Kenneth French’s Data Library.
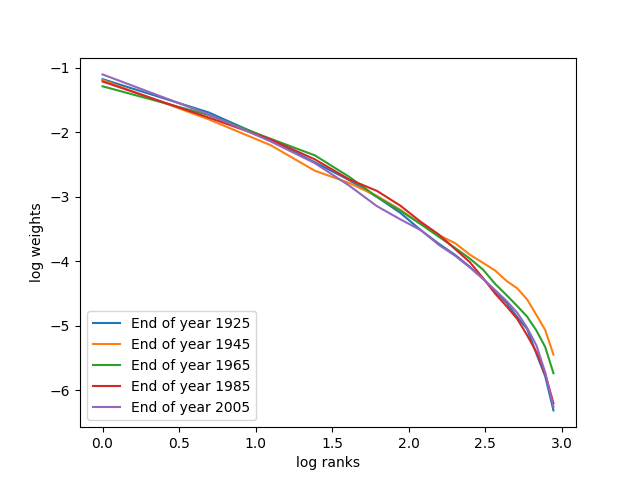
If the model is stable, the capital distribution curve is also stable in the long run: see Theorem 2. Previous research analyzed long-term stability and capital distribution curve for various continuous-time models: [7, 20]. These models were designed to capture the observations that, on average, small stocks have higher volatility and growth rates than large stocks. In [7], competing Brownian particle models were analyzed, where drift and diffusion coefficients depend on the rank of the stock, and linearity of the capital distribution curve was reproduced. In [20], the drift and diffusion depend on the market weight of a stock, but the capital distribution curve is not linear. These models do not use CAPM or VIX.
In the previous article by the second coauthor [13], devoted to the CAPM with size but without VIX (in other words, with constant volatility), we also reproduced model stability for its continuous-time version [13, Theorem 2]. Using simulation, we reproduced the linearity of the capital distribution curve. But we did not state and prove rigorous results on this. A natural question is to reproduce these results for our model here. We accomplish both tasks in this article: (a) we simulate the capital distribution curve in Subsection 5.2, which reproduces its linearity; (b) we prove results on convergence to a Poisson point process. This fills a gap in [13].
2.6. Our contributions
In this article, we combine the ideas of our articles [13] on CAPM and [22] on VIX to state a reasonable generalization of [13]. This model can be truncated: Include only price changes for the benchmark and the target (or, equivalently, market size and ), and volatility . Alternatively, it can be completed: Include also equity premia for the benchmark and the target. A truncated model contains 3 time series, and a completed model contains 5 time series.
In [13], we model (7) and (6) but with or i.i.d. Gaussian, in continuous time. The article [13] does not include VIX . However, this article is concerned with the idea from [22] that division by VIX normalized returns and premia. We replace and with and in (6). Also, we replace with and with in (7). We model as IID (but maybe not Gaussian), following (10) and (11). As mentioned in the Introduction, in Section 3 we perform statistical data analysis.
We fill two lacunas left in our research [13]. The first lacuna is stability results for discrete time. In Section 4 of this article, we state and prove this for the case of stochastic VIX. Our results work for constant volatility as well, which is the setting of [13], see (9). Next, we check the stability condition numerically. The second lacuna is rigorous results for the capital distribution curve, which are lacking in [13]. There, we present only the simulation for the constant volatility. In Section 5 of this article, we state and prove a convergence result for the capital distribution curve: Theorem 2. Next, in Theorem 3, we show a remarkable result: the curve is
where are order statistics of a conditional normal sample:
for random and . We perform the simulation in Section 5 for stochastic VIX. In Appendix, we further analyze this curve for and , and show its upper left and lower right ends replicate real-world behavior.
3. Financial Data and Statistical Analysis
3.1. Data description
We take monthly data January 1990 – September 2022. Total data points. As discussed in the Introduction and Background sections, we measure volatility as Chicago Board of Options Exchange VIX: The Volatility Index for S&P 500, monthly average data. This data is taken from Federal Reserve Economic Data (FRED) web site. For equity premia computation, we need short-term Treasury rates, which are also taken from the FRED web site.
The rest of the data is taken from Kenneth French’s Dartmouth College Financial Data Library. It contains equally-weighted portfolios of stocks split into 10 deciles by size: Decile 1 has smallest 10% stocks by size (market capitalization), Decile 2 has the next 10% smallest stocks, etc up to Decile 10, which contains top 10% largest stocks. In practice, during this time span this Decile 10 portfolio closely corresponds to the S&P 500, the classic benchmark for American stocks. (Although the S&P 500 index is size-weighted, not equally-weighted.) We also use Decile 10 as the benchmark. These portfolios are reconstituted at the end of June of each year. For each decile and each month, the data contains average market size, price returns (excluding dividends), and total returns (including dividends).
3.2. Price returns results
Our goal is to fit (7). We rewrite it as
This linear regression does not have an intercept, however. To make the model complete, we add an intercept and get:
| (13) |
For the benchmark with price returns , we take Decile 10. For the target with price returns , we use Deciles 1, …, 9. We fit these 9 linear regressions (13) separately.
| Decile | Ljung-Box | Jarque-Bera | ||||
|---|---|---|---|---|---|---|
| 1 | -.0567 | -.0116 | -.1179 | .9860 | 0 | 0 |
| 2 | -.3286 | -.0371 | -.0686 | .9941 | .75 | 0 |
| 3 | -.5481 | -.0506 | -.1110 | .9855 | .6 | .17 |
| 4 | -.5446 | -.0447 | -.1092 | .9866 | .18 | .08 |
| 5 | -.5646 | -.0433 | -.1708 | .9695 | .35 | .05 |
| 6 | -.0486 | .0074 | -.1446 | .9790 | .56 | .99 |
| 7 | -.9318 | -.0836 | -.1661 | .9673 | .55 | .06 |
| 8 | .7978 | -.0761 | -.1745 | .9651 | .11 | .09 |
| 9 | -.6832 | -.0688 | -.0437 | .9937 | .69 | .07 |
For Deciles 3–9, it is reasonable to model residuals using IID Normal. The Student -test gives -values greater than 5% for and for each decile. However, the Student -test gives -values greater than 5% for , for all deciles, except Deciles 2 and 9. Thus we see that for most deciles, we can assume but . Finally, the 95% confidence intervals for for each decile contain . Thus, for Deciles 3–9, we could model
and is between and (except Decile 9, where we fail to reject ). This model is an improvement over [13] where residuals were not IID or Gaussian.
3.3. Equity premia results
Our goal is to fit (6). Similarly to (7), we rewrite it as
This linear regression does not have an intercept, however. To make the model complete, we add an intercept and get:
| (14) |
For the benchmark with equity premia , we use Decile 10. And for the target with equity premia , we use Deciles 1, …, 9. We fit these 9 linear regressions (13) separately.
| Decile | Ljung-Box | Jarque-Bera | ||||
|---|---|---|---|---|---|---|
| 1 | -.1215 | -.0178 | .1151 | .9887 | 0 | 0 |
| 2 | -.2832 | -.0330 | -.0714 | .9937 | .73 | 0 |
| 3 | -.4680 | -.0446 | -.1113 | .9854 | .59 | .15 |
| 4 | -.4739 | -.0402 | -.1128 | .9858 | .17 | .06 |
| 5 | -.4215 | -.0339 | -.1703 | .9696 | .35 | .03 |
| 6 | .1443 | .0137 | -.1464 | .9784 | .54 | 1 |
| 7 | -.8078 | -.0746 | -.1559 | .9605 | .51 | .04 |
| 8 | -.6793 | -.0671 | -.1784 | .9643 | .12 | .05 |
| 9 | -.6596 | -.0672 | -.0432 | .9937 | .69 | .06 |
Similarly to regression (13), for Deciles 3–9, it is reasonable to model residuals using IID, but the evidence for normality is much weaker than in (13). The Student -test gives -values greater than 5% for and for each decile. However, the Student -test gives -values greater than 5% for , for all deciles, except Deciles 2 and 9. Thus we see that for most deciles, we can assume but . Finally, the 95% confidence intervals for for each decile contain . Thus, for Deciles 3–9, we could model
and is between and (except Decile 9, where we fail to reject ). Similarly to (13), this model is an improvement over [13] where residuals were not IID.
4. Long-Term Stability
4.1. Formal construction of the model
Take a sequence of five-dimensional vectors:
| (15) |
Assumption 1.
Vectors are IID with mean zero and finite second moment, with Lebesgue joint density on which is everywhere strictly positive.
These five components might be correlated between themselves. First, we model using (12) with innovations . Next, we model following (10) for some constant :
| (16) |
but we do not necessarily assume is Gaussian. We subtract because Assumption 1 states that , but the left-hand side of (16) has nonzero mean. Similarly, we model following (11) for another constant :
| (17) |
and might not be Gaussian. These two equations (16) and (17) model the benchmark. Next, we combine (6) and (7) with these new ideas, following the outline in Section 2. We can replace and with and in (6):
| (18) |
Similarly, we can replace and with and in (7):
| (19) |
Recall the definition of the relative size process
| (20) |
4.2. Stability results
Consider a discrete-time process in .
Definition 1.
This process is called time-homogeneous Markov if there exists a transition function (where is the Borel -algebra on ) such that for all , , and , we have:
Lemma 1.
Under Assumption 1, the process is Markov. Also, the truncated model is Markov. Finally, the completed model is Markov.
Proof.
It is clear from (12) that the process (and therefore ) is Markov. Together with (16), this shows that is Markov. From definition (20), we write
| (21) | ||||
Using (21), we rearrange (19) as follows:
| (22) |
But from Assumption 1, this process from (22) is Markov, too. From (21) and (16), this equation (22) shows that , or, equivalently, , is Markov. Finally, from (18) and (17), we get that the completed model is Markov. ∎
Definition 2.
A time-homogeneous Markov process has a stationary distribution if is a probability measure on , and from it follows that (and therefore for all ). Equivalently, in terms of transition function : For every ,
Definition 3.
A time-homogeneous Markov process is ergodic if it has a unique stationary distribution , and for every , we have:
Assumption 2.
We have: , and for stationary versions of ,
| (23) |
Below, we show that, if , these stationary versions exist, and Assumption 23 is well-defined. The following is the main result of this article.
Theorem 1.
Proof.
Step 1. Under Assumption 1 and , it is a well-known result that the process has a unique stationary distribution. Under (16) and (17), has a unique stationary distribution. The second condition in Assumption 23 is taken for this stationary distribution.
Step 2. Let us show that from (22) is stationary. Apply the main result of [5]. In the notation of [5], we have and . Therefore, Assumption 23 ensures that . We need only to show that
| (24) |
For any real number , we have:
| (25) |
Applying (25) to the left-hand side of (24).
| (26) |
Next, for any real numbers ,
| (27) |
From (27) and (26), the left-hand side of (24) is dominated by
| (28) |
The innovations have finite second moment (and therefore first moment) by Assumption 1. Therefore,
| (29) |
Next, is governed by an autoregression of order 1 with innovations having finite second moment. Thus the stationary distribution of also has finite second moment and therefore finite first moment. Together with (29), this proves that (28) is finite. This proves (24) and with this the stationarity of .
Step 3. Further, is stationary, and therefore is stationary. All this proves stationarity of the truncated and the completed models:
| (30) |
Step 4. Finally, let us show ergodicity for the completed model. The transition function of this five-dimensional Markov chain is strictly positive: For any set of positive Lebesgue measure, the transition probability for every . Indeed, this transition probability is a push-forward of the distribution of the innovations in under a certain smooth bijection . And for every , this probability measure and the Lebesgue measure on are mutually absolutely continuous. For the rest of this proof, we refer the reader to the classic book [17] for terminology. It is straightforward to show that this Markov chain is irreducible and aperiodic. We have already shown it has a stationary distribution. Therefore, this Markov chain is positive Harris recurrent, and by [17, Theorem 13.0.1], this Markov chain is ergodic.
4.3. First-order approximation
To check Assumption 23 is hard. But for real-world values of coefficients found in Section 3,
| (31) |
Indeed, from the data analysis we can assume , because the point estimates are not significantly different from zero. Next, , and is the growth rate of the benchmark. A well-known fact for the growth rate (for example, found in [1]) is that per annum, it is of order 10%. Per month, it is on average even less. Thus is small. This completes the explanation of (31).
For , we use the first-order approximation: . We simplify Assumption 23:
| (32) |
This is analogous to the result (9) from [13]. Let us quickly show that condition (32) holds for real-world market data. As mentioned above, we can assume . Next, we have for each of the Deciles 3–9. Finally, , because is the growth rate of the benchmark; together with the US economy, stock market indices in the USA grow in the long run. To show when the left-hand side of (32) is well-defined, we state the following result. The assumptions are reasonable in the light of discussion from Subsection 2.4.
Lemma 2.
4.4. The case of constant volatility
We stated and proved in [13] results on stationarity and ergodicity of a continuous-time analogue of our model, but with constant volatility. We did not state and prove stability result for discrete time. Here, we fill this gap. In the notation of this article, we can assume is constant. This corresponds to .
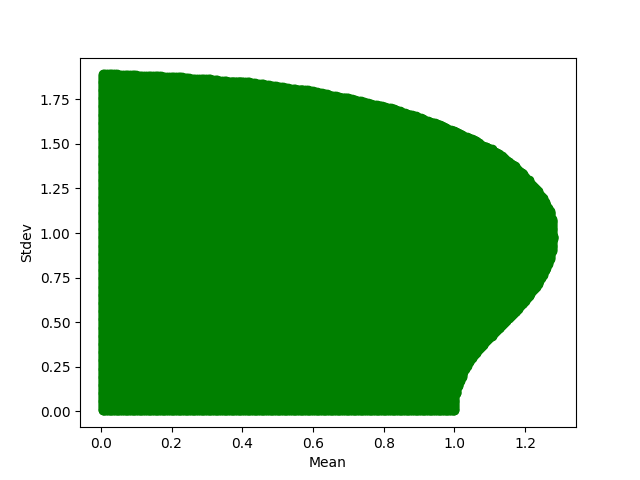
Assume IID, and . This violates Assumption 1 (positive density). But this does not affect the stationarity proof. Let us check Assumption (9). We have: . Then we can rewrite the left-hand side of Assumption 23:
| (33) | ||||
It is impossible to compute this logarithmic moment directly. But one can do this numerically using Monte Carlo. The set
is shown in Figure 4. Python code is on GitHub repository asarantsev/size-capm-vix in file gaussian-simulation.py
5. Stochastic Portfolio Theory
5.1. Capital distribution curve
Consider the benchmark and portfolios . We model each pair (benchmark, portfolio ) with this model. The model must be the same for all . We let be the market capitalization (size) for the th portfolio, and the market size of the benchmark. We define market weights as
| (34) |
We can also rank them from top to bottom:
| (35) |
Market weights and portfolios based on them are the main topic of Stochastic Portfolio Theory in both discrete time, see [6, 21, 28] and continuous time, see [11, 12].
Define by and the sequences of innovations for equity premium, as in (18), and price returns, as in (19), for the th portfolio, :
| (36) | ||||
Together with (12), (16), (17), this is a time series Markov model for series.
Assumption 3.
The -dimensional vectors
are independent identically distributed with mean zero, finite second moment, with strictly positive Lebesgue density on .
This is the main stability result. It has the meaning that if we have several portfolios, they stay in the long run as one cloud, and do not split into several clouds.
Proof.
The relative size processes are time-homogeneous Markov and ergodic:
| (37) |
Their vector is also time-homogeneous Markov and ergodic: Follows from Assumption 3 in the same way as in Theorem 1. And there exists a one-to-one continuous mapping , between and the -dimensional simplex
Thus the process of market weights from (34) is ergodic. ∎
Thus the ranked market weights process also has a stationary distribution and converges to this distribution in the long run, regardless of the initial conditions. In this stationary distribution, we can plot these ranked market weights versus their ranks on the log scale:
This plot is called the capital distribution curve. With real-world markets, this curve is linear on most span, and concave overall. Moreover, it shows remarkable long-term stability. See the famous picture in [11, Chapter 4] for eight capital dsitribution curves at end of years 1929, 1939, …, 1999; see the same picture as [12, Figure 13.4].
In our previous article [13], we captured the observation that well-diversified portfolios of small stocks have higher risk but higher return than that of large stocks. We reproduced this shape of capital distribution curve in [13] using simulation.
From (37) and (34), we get a simple expression of from :
Therefore, ranking market weights from top to bottom at any fixed time is equivalent to ranking relative size terms from top to bottom: . Thus instead of plotting the (slightly modified) capital distribution curve , we can plot .
The linearity of the capital distribution curve was rigorously proved in [7] for competing Brownian particles and disproved in [20] for volatility-stabilized models. These two types of continuous-time models both capture the property that small stocks have higher risk but higher return than large stocks. But these models do not use CAPM.
5.2. Simulation study
Instead of ranking all market weights, we can rank only weights of all portfolios but the benchmark. This technique will miss one portfolio from the capital distribution curve, but will not influence the overall behavior of the said curve. Consider the combined model:
- •
- •
- •
For simplicity, we write all equations with number coefficients, replacing by :
We pick and simulate these equations for time steps, starting from
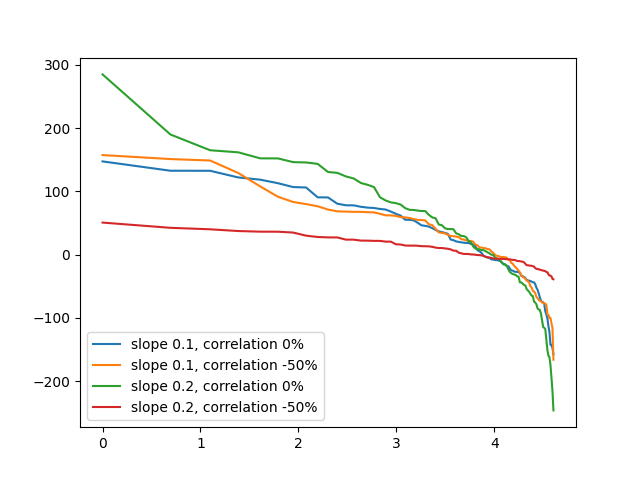
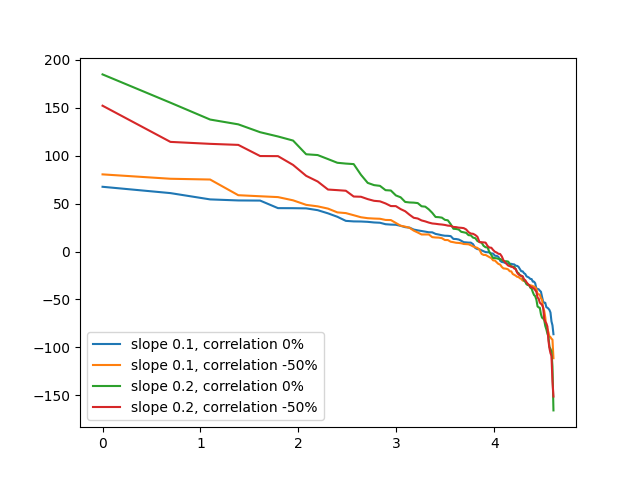
We do this for , to give enough time to converge to the stationary distribution. We see various slopes for different cases: or (this latter correlation is found in [22, Table 2, Large Price]); and or (lower and upper bound for found in Subsection 3.2). We perform two simulations for each case. Each simulation has the same values of and . We show all four curves for each simulation in Figure 5. See the Python code in the file capital-distribution-simulation.png from the GitHub repository asarantsev/size-capm-vix
5.3. Rigorous results: reduction to normal order statistics
Fix a constant . Assume the market weights , or, equivalently, relative size are in the stationary distribution, which (by Theorem 2) is limiting distribution. To stress this, we write for time argument. Thus we have the ranked (sorted, ordered from top to bottom) values of the relative size process in the stationary distribution:
Here, is the overall number of portfolios (excluding the benchmark). We are interested in the joint distribution of these sorted relative size values.
Assume IID is the standard normal sample.
Theorem 3.
There exists random variables and independent of the point process which are functions of two time series: and , such that in law,
Proof.
Fix a . Apply [5, (0.6)] to express the stationary distribution of the relative size process from (22): letting
| (38) | ||||
pick any and get:
| (39) |
We assume and are defined for all , not just . Assume is the standard deviation of innovations . From (38) and (39), given time series and , the stationary distribution of is Gaussian with mean and variance
Given time series and , the random variables are independent. Thus their standardized versions are (conditionally on and ) IID standard Gaussian:
| (40) |
∎
This motivates the following definition.
Definition 4.
We define the standard normal market curve
| (41) |
for standard normal sample and its ranked version .
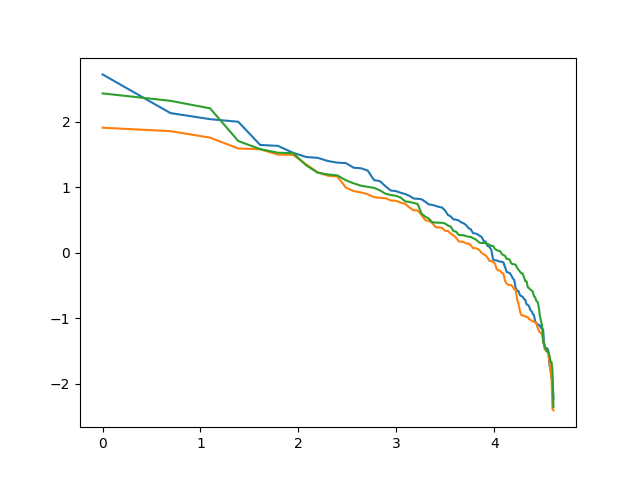
We study this curve in Appendix. The significance of Theorem 3 is as follows. Assume we rank . An immiediate consequence of Theorem 3 is that the (slightly modified) capital distribution curve for has almost the same shape as the standard normal market curve. The only difference is a shift and change in slope, both random but independent of the standard normal market slope itself. Multiplication by preserves ordering, since . We plotted three simulations of such curve in Figure 6. The Python code for this simulation in Figure 6 is available on GitHub repository asarantsev/size-capm-vix, file standard-normal-curve.py
It reproduces the real-world shape of the curve, but up to constant but random change in shift and slope, governed by and . This is why the difference in simulations in Figure 5 is greater than in Figure 6. Indeed, much of the difference between two windows in Figure 5 (for example, between the two curves with and zero correlation) is accounted for by the difference in and from simulation to simulation.
Changing the parameters of this model also affects the shape of the capital distribution curve, through the slope . This accounts for the differences within each window from Figure 5.
6. Conclusion and Further Research
We combined main results of our previous articles [13, 22]. In [13], the main model (CAPM plus linear dependence of and upon relative size) was used to capture the property that small stocks have, on average, higher risks and returns. In this article, we add to this model the normalization (division by the Volatility Index). The resulting multivariate Markov time series model fits better using real-world market data: Its residuals are better descrbied as IID Gaussian. We state and prove a simple sufficient condition (Theorem 1) for ergodicity. And we make some connections with Stochastic Portfolio Theory, adding our model to the collection of proposed models capturing this size effect. We state and prove rigorous results on the capital distribution curve.
We fill two lacunas in our previous research from [13].
First lacuna: Long-term stability results apply to the case of constant volatility from [13], see subsection 4.4 of the current article.
Second lacuna: The curve is order statistics of the normal sample (but with random mean and standard deviation), see subsection 5.3 of the current article, continued below in the Appendix. Such curve reproduces the real-world shape of the captial distribution curve: linear at the upper left end, and concave at the lower right end.
For future research, we could fit non-normal distributions for innovation series , and check conditions of Theorem 1 for the resulting distributions. Also, we could include the value effect: Stocks priced cheaply to fundamentals (earnings, dividends, book value) tend to outperform other stocks, on average. We would include, for example, dividend yield as a factor in and from CAPM. To make the model complete, we need to model dividend yield separately (for example, as an autoregression). Our goal is to statistically fit this model and prove long-term stability.
Appendix: Standard Normal Market Curve
To continue subsection 5.3, it remains to study the behavior of the curve (41) using the classic Extreme Value Theory. Most of the definitions and results of this subsection are well-known. We do not even attempt to provide an exhaustive list of references. Instead, we mention classic monograph [23] and a classic textbook [2]. For Poisson point processes on the real line, see another classic monograph [15].
Pick a function which is locally integrable: for any bounded interval .
Definition 5.
A Poisson point process on with intensity or rate is defined as a random countable subset such that . That is, the random number of points on any bounded interval is Poisson with mean .
In particular, if , then we can rank points from the rightmost to the left. In other words, the th rightmost point is well-defined. This point exists, since is integrable on for any . Denote by the th jump time of the standard Poisson process on : are IID exponential with mean 1, where by convention . For fixed , we can also express
| (42) |
Similarly, if , then we can rank points from the leftmost to the right. And the formula (42) becomes the formula for the th leftmost point:
| (43) |
See also [2, Chapter 8, Exercises 6, 7].
Definition 6.
The (standard) Gumbel distribution is defined by its cumulative distribution function .
It is known, see classic references [2, Theorem 8.3.1, Example 8.3.4] or [23, Chapter 1], that the normal distribution belongs to the Gumbel domain of attraction: Consider the maximum of IID normal variables:
After scaling, this maximum converges weakly to Gumbel distribution as :
| (44) |
where and are suitable constants. A common suggestion is
But the convergence rate for this choice of constants is not the best, as shown in [2, Example 8.3.4]. There are ways to improve this, for example [14]:
For any such sequences and , we have convergence of top ranked standardized variables to the rightmost points of , as :
| (45) |
Similarly and symmetrically, as ,
| (46) |
This convergence (45) or (46) follows from [2, Theorem 8.4.2], or [18], or [23, Chapter 4]; see also [2, Chapter 8, Exercises 6–8] and compare with (42) or (43). Recall (42) and plot this Poisson point process with -axis log scale. This represents (up to shift by and rescaling by ) the left upper end of the capital distribution curve:
| (47) |
Similarly, recall (43) and plot this Poisson point process with -axis log scale. This represents (up to shift by and rescaling by ) the right lower end of the capital distribution curve:
| (48) |
Lemma 3.
For each , the distribution of is exponential with mean .
Proof.
From definitions of , we have: and are independent; has Gamma distribution (sum of IID exponential random variables with mean ); is another exponential random variable with mean . Therefore, almost surely. What is more, the tail of the exponential distribution with mean 1 is given by:
| (49) |
Using (49), we get: for every ,
| (50) | ||||
Next, the Laplace transform of the Gamma random variable with shape is
| (51) |
Use independence of and for (50) and (51):
| (52) |
Next, apply the Laplace transform of to . The right-hand side of (52) is . This is the tail of the exponential distribution with mean . ∎
The next lemma is the key to our analysis of both ends of the standard normal curve (41). It is proved very similarly to our results in [27, Proposition A1], but we provide the full proof for completeness.
Lemma 4.
With probability , the sequence is bounded.
Proof.
From [2, Chapter 8, Problem 8.7], we know that the random variables are independent. By Lemma 3, the mean of is and the variance is . These differences all are independent. Therefore,
| (53) |
It is well-known that as , and the sequence is bounded. Also, as . By [26, Theorem 1.4.2], from (53) we complete the proof. ∎
Thus we can replace in (48) and (47) with . This result allows us to approximate curves (47) and (48) with continuous functions. The upper-left end of the curve (47) then becomes . This is a linear curve with 45 degrees of incline. Next, the lower-right end of the curve (48) becomes . Let and : Then
This function is concave but obviously not linear:
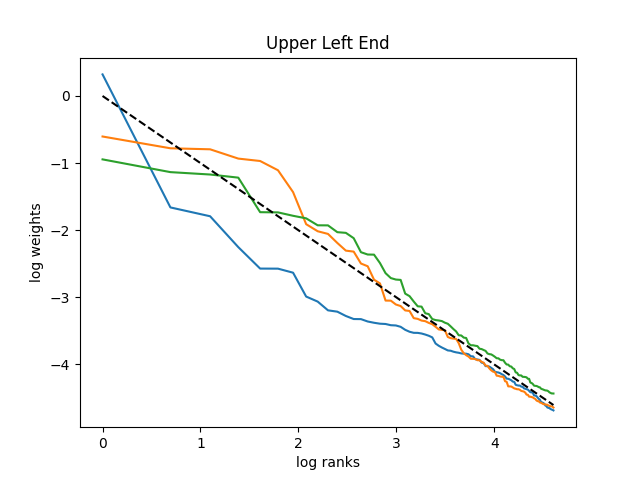
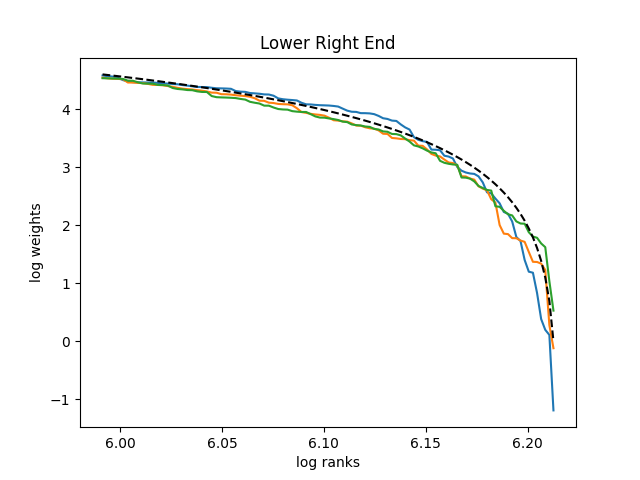
This reproduces the shape of this capital distribution curve. See Figure 7 for the upper left and lower right ends of the capital distribution curve. The simulation of for and the plot of the comparative deterministic function (with ) was done in Python. The code standard-curve-simulation.py is in GitHub repository asarantsev/size-capm-vix The shape of both ends of the curve in Figure 6 are reproduced here in Figure 7.
References
- [1] Andrew Ang (2014). Asset Management. A Systematic Approach to Factor Investing. Oxford University Press.
- [2] Barry C. Arnold, N. Balakrishnan, H. N. Nagaraja (2008). A First Course in Order Statistics. Society for Industrial and Applied Mathematics. Classics in Applied Mathematics 54.
- [3] Rolf Banz (1981). The Relationship Between Return and Market Value of Common Stocks. Journal of Financial Economics 9 (1), 3–18.
- [4] Lorenzo Bergomi (2015). Stochastic Volatility Modeling. Chapman & Hall/CRC.
- [5] Andreas Brandt (1986). The Stochastic Equation with Stationary Coefficients. Advances in Applied Probability 18 (1), 211–220.
- [6] Steven Campbell, Ting-Kam Leonard Wong (2022). Functional Portfolio Optimization in Stochastic Portfolio Theory. SIAM Journal of Financial Mathematics 13 (2), 576–618.
- [7] Sourav Chatterjee, Soumik Pal (2010). A Phase Transition Behavior for Brownian Motions Interacting Through Their Ranks. Probability Theory and Related Fields 147 (1), 123–159.
- [8] Eugene F. Fama, Kenneth R. French (1993). Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics 33 (1), 3–56.
- [9] Eugene F. Fama, Kenneth R. French (2004). The Capital Asset Pricing Model: Theory and Evidence. Journal of Economic Perspectives 18 (3), 25–46.
- [10] Eugene F. Fama, Kenneth R. French (2015). A Five-Factor Asset Pricing Model. Journal of Financial Economics 116 (1), 1–22.
- [11] E. Robert Fernholz (2002). Stochastic Portfolio Theory. Springer.
- [12] E. Robert Fernholz, Ioannis Karatzas (2009). Stochastic Portfolio Theory: an Overview. Handbook of Numerical Analysis 15.
- [13] Brandon Flores, Blessing Ofori-Atta, Andrey Sarantsev (2021). A Stock Market Model Based on CAPM and Market Size. Annals of Finance 17 (3), 405–424.
- [14] Peter Hall (1979). On the Rate of Convergence of Normal Extremes. Journal of Applied Probability 16 (2), 433–439.
- [15] John Frank Charles Kingman (1993). Poisson Processes. Oxford University Press.
- [16] John Lintner (1965). The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets. Review of Economics and Statistics 47 (1), 13–37.
- [17] Sean P. Meyn, Richard L. Tweedie (2009). Markov Chains and Stochastic Stability.
- [18] Douglas R. Miller (1976). Order Statistics, Poisson Processes, and Repairable Systems. Journal of Applied Probability 13 (3), 519–529.
- [19] Jan Mossin (1966). Equilibrium in a Capital Asset Market. Econometrica 34 (4), 768–783.
- [20] Soumik Pal (2011). Analysis of Market Weights Under Volatility-Stabilized Market Models. Annals of Applied Probability 21 (3), 1180–1213.
- [21] Soumik Pal, Ting-Kam Leonard Wong (2016). The Geometry of Relative Arbitrage. Mathematics and Financial Economics 10 (3), 263–293.
- [22] Jihyun Park, Andrey Sarantsev (2024). Log Heston Model for Monthly Average VIX. arXiv:2410.22471.
- [23] Sidney I. Resnick (1987). Extreme Values, Regular Variation and Point Processes. Springer.
- [24] Andrei Semenov (2015). The Small-Cap Effect in the Predictability of Individual Stock Returns. International Journal of Economics and Finance 38, 178–197.
- [25] William F. Sharpe (1964). Capital Asset Prices: a Theory of Market Equilibrium Under Conditions of Risk. Journal of Finance 19 (3), 425–442.
- [26] Daniel Stroock (2010). Probability Theory, An Analytic View. Cambridge University Press.
- [27] Andrey Sarantsev, Li-Cheng Tsai (2017). Stationary Gap Distributions for Infinite Systems of Competing Brownian Particles. Electronic Journal of Probability 22 (56), 1–20.
- [28] Ting-Kam Leonard Wong (2015). Optimization of Relative Arbitrage. Annals of Finance 11 (3–4), 345–382.