This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Carle’s Game: An Open-Ended Challenge in Exploratory Machine Creativity

1st Q. Tyrell Davis
Wyoming, USA qtyrelldavis@protonmail.com
Abstract

This paper is both an introduction and an invitation. It is an introduction to CARLE, a Life-like cellular automata simulator and reinforcement learning environment. It is also an invitation to Carle’s Game, a challenge in open-ended machine exploration and creativity. Inducing machine agents to excel at creating interesting patterns across multiple cellular automata universes is a substantial challenge, and approaching this challenge is likely to require contributions from the fields of artificial life, AI, machine learning, and complexity, at multiple levels of interest. Carle’s Game is based on machine agent interaction with CARLE, a Cellular Automata Reinforcement Learning Environment. CARLE is flexible, capable of simulating any of the 262,144 different rules defining Life-like cellular automaton universes. CARLE is also fast and can simulate automata universes at a rate of tens of thousands of steps per second through a combination of vectorization and GPU acceleration. Finally, CARLE is simple. Compared to high-fidelity physics simulators and video games designed for human players, CARLE’s two-dimensional grid world offers a discrete, deterministic, and atomic universal playground, despite its complexity. In combination with CARLE, Carle’s Game offers an initial set of agent policies, learning and meta-learning algorithms, and reward wrappers that can be tailored to encourage exploration or specific tasks.

Index Terms:
open-endedness, machine creativity, cellular automata, evolutionary computation, reinforcement learning

I Introduction

Intelligence is an emergent phenomenon that requires nothing more than the presence of matter and energy, the physical constraints of our present universe, and time. At the very least we know that the preceding statement is true by an existence proof, one that continues to demonstrate itself in the very act of the reader parsing it. There may be simpler ways to generate intelligence, and there are certainly paths to intelligence that are significantly more complex, but the only path that we have positive proof for so far is the evolution of life by natural selection. Put simply, an algorithm that can be described as “the most likely things to persist will become more likely to persist” is at least capable of creating intelligence — though the likelihood of this happening is unknown and shrouded in uncertainty [22] 111While I’ve often read that human existence is the result of a “a single run” of an open-ended process [47], we have no way to no for certain how many similar “runs” may have preceded (or will succeed) the experience of our own perspective. This is the anthropic principle in a nutshell [5]. Consequently the study of intelligence, both natural and artificial, from a viewpoint informed by open-ended complexity is not only an alternative approach to building artificially intelligent systems, but a way to better understand the context of Earth-based intelligence as it fits into the larger universe.

One hallmark of modern approaches to artificial intelligence (AI), particularly in a reinforcement learning framework, is the ability of learning agents to exploit unintended loopholes in the way a task is specified [1]. Known as specification gaming or reward hacking, this tendency constitutes the crux of the control problem and places an additional engineering burden of designing an “un-hackable” reward function, the substantial effort of which may defeat the benefits of end-to-end learning [43]. An attractive alternative to manually specifying robust and un-exploitable rewards is to instead develop methods for intrinsic or learned rewards [4]. For tasks requiring complex exploration such as the “RL-hard” Atari games Montezuma’s Revenge and Pitfall, intrinsic exploration-driven reward systems are often necessary [11].

Games have a long history as a testing and demonstration ground for artificial intelligence. From MENACE, a statistical learning tic-tac-toe engine from the early 1960s [13], to the world champion level chess play of Deep Blue [50] and the lesser known Chinook’s prowess at checkers [35] in the 1990s, to the more recent demonstrations of the AlphaGo lineage [38, 39, 40, 37] and video game players like AlphaStar for StarCraft II [52] and OpenAI Five for Dota 2 [2] to name just a few. Games in general provide an opportunity to develop and demonstrate expert intellectual prowess, and consequently have long been an attractive challenge for AI. While impressive, even mastering several difficult games is but a small sliver of commonplace human and animal intelligence. The following statement may be debatable to some, but mastering the game of Go is not even the most interesting demonstration of intelligence one can accomplish with a Go board.

While taking breaks from more serious mathematical work, John H. Conway developed his Game of Life by playing with stones on a game board [14]. The resulting Game demonstrated a system of simple rules that would later be proven to be computationally universal. Conway’s Life did not found the field of cellular automata (CA), but it did motivate subsequent generations of research and play and is likely the most well known example of CA.

II Life-like cellular automata crash-course

The Game of Life was invented by John H. Conway through mathematical play in the late 1960s, and it was introduced to the public in a column in Martin Gardner’s “Mathematical Games” in Scientific American in 1970 [14]. The Game was immensely influential and inspired subsequent works in similar systems and cellular automata in general. Conway’s Life demonstrated the emergence of complex behavior from simple rules and would later be proven a Turing complete system capable of universal computation [34].

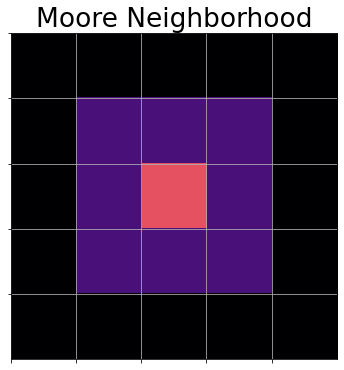
Refer to caption

Figure 1: A Moore neighborhood in purple surrounding a cell in pink.

Conway’s Life is based on the changing binary states of a 2-dimensional grid. Cell units in the grid change their state based on local information, determined solely by the sum of states of their immediate neighbors. The 3 by 3 grid surrounding each cell (excluding itself) is called a Moore neighborhood (Figure 1). Each cell’s next state is fully determined by its current state and the sum of cell states in its Moore neighborhood. Cellular Automata (CA) based on this update configuration are known as “Life-like”. Different Life-like CA can be described by the rules they follow for transitioning from a state of 0 to a state of 1 (“birth”) and maintaining a state of 1 (“survival”). Life-like rules can be written in a standard string format, with birth conditions specified by numbers preceded by the letter “B” and survival conditions by numbers preceded by “S”, and birth and survival conditions separated by a slash. For example, the rules for Conway’s Life are B3/S23, specifying the dead cells with 3 live neighbors become alive (state 1) and live cells with 2 or 3 live neighbors remain alive, all other cells will remain or transition to a dead state (state 0).

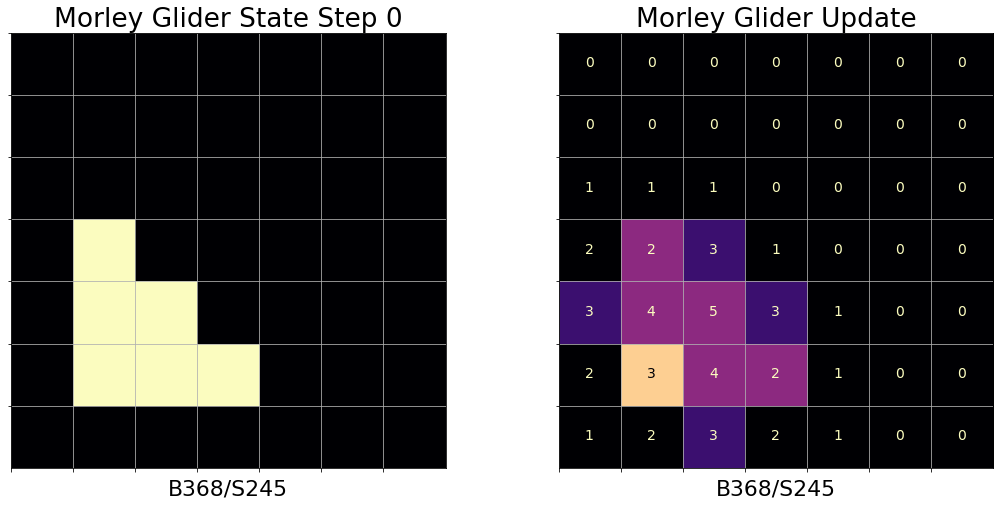
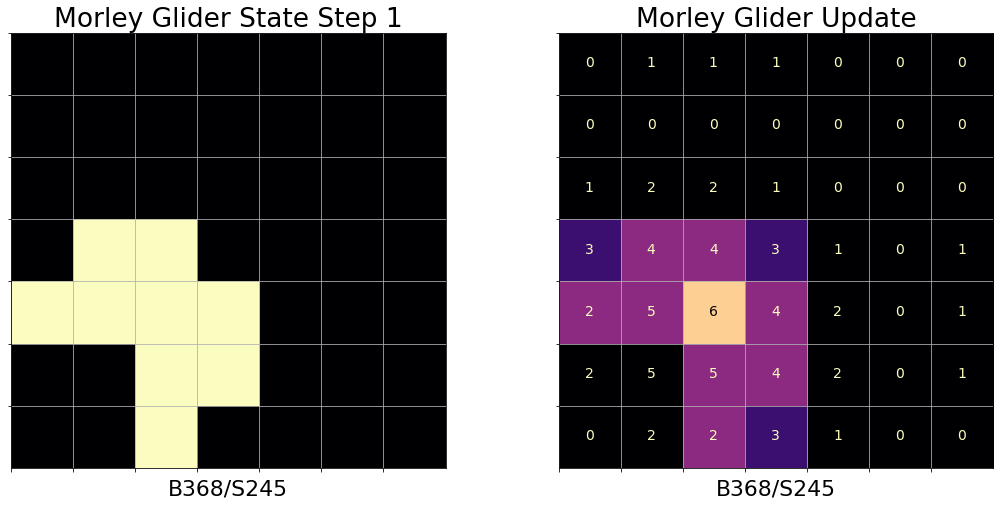
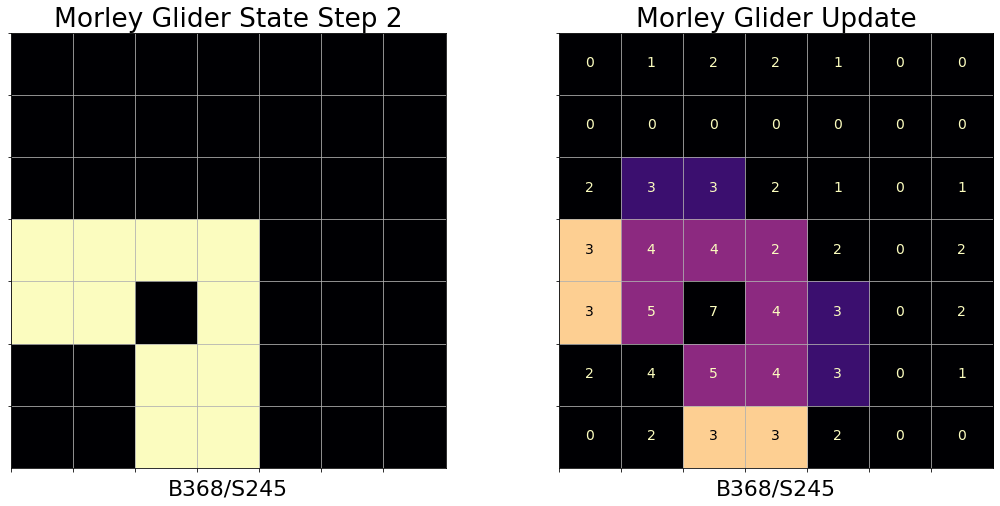
Including Conway’s Life (B3/S23), there are 29∗29=262,1442^{9}*2^{9}=262,144 possible rule variations in Life-like CA. Many of these rules support objects reminiscent of machine or biological entities in their behavior. Types of CA objects of particular interest include spaceships, objects that translocate across the CA grid as they repeat several states; puffers, spaceships that leave a path of persistent debris behind them, computational components like logic gates and memory, and many more. The update progression of a glider pattern under B368/S245 rules, also known as Morley or Move, is shown in Figure 2. An active community continues to build new patterns and demonstrations of universal computation in Life-like CA [8].

Refer to caption

Refer to caption

Refer to caption

Figure 2: The first 2 updates of a glider pattern in the B368/S245 set of rules. The Moore neighborhood values are inset in each cell, with birth and survival denoted in purple and “death” transitions denoted in pinkish yellow. Cells with a starting state of 0 and 3, 6, or 8 neighbors transition to a state of 1, while cells with a state of 1 with 2, 4, or 5 neighbors remain in a state of 1. All other cells transition to a state of 0.

III Related Work

Carle’s Game combines the fields of cellular automata, open-ended machine learning, and evolutionary computation. The growth and dynamics of cellular automata have been extensively studied [53, 36, 12, 54], and thanks to the characteristics of complexity and universal computation of many CA [54, 9, 8], CA make a good substrate for modeling physical phenomena [51]. Recent work in differentiable neural CA offer interesting possibilities for modern machine learning [26, 31, 27, 32].

Open-endedness is often a desirable trait in artificial life and evolution simulations. Evolutionary computation applied to generic reinforcement learning (RL) tasks exhibits the same phenomena of specification gaming and reward hacking as seen in conventional RL algorithms. For example, with no costs associated with individual height, evolutionary selection for body plans and policies on the basis of forward travel often discovers the unintended solution of being very tall and falling over [17, 41, 42, 23]. A more open-ended approach can limit the reward function surface that can be exploited, at least in principle, but the challenge of producing interesting results remains substantial. A system can apparently meet all the generally accepted traits of open-ended evolution and still produce uninteresting results [20].

Previous efforts to build artificial worlds include individual machine code programs competing for computational resources [33, 28], simulated creatures in physics simulators [41] [42] [56] [46], games [16, 7, 48, 45], or abstract worlds [44]. I find the open-ended universes based on cellular automata such as SmoothLife, Lenia, and genelife [30, 6, 25] particulary interesting. CA simulations are an attractive substrate for open-ended environments because they are not based on a facsimile of the physics of our own universe, nor are they an ad-hoc or abstract landscape. Instead they have their own internally consistent rules, analagous to physical laws in myriad alternative universes.

Unlike experiments in Lenia, SmoothLife, or genelife, in Carle’s Game agents interact with a CA universe, but they are not of it. Instead the role of agents is more similar to that of the decades-long exploration of Life-like cellular automata by human experimenters. CARLE also has the ability to simulate any of the 262,144 possible Life-like rules, of which many exhibit interest patterns of growth and decay and/or Turing completeness [12, 8].

Another possible advantage of CARLE comes from the simplicity of CA universes combined with execution on a graphics processing unit (GPU). CARLE is written with PyTorch [29], and the implementation of CA rules in the matrix multiplication and convolutional operations, operations that have been well-optimized in modern deep learning frameworks, makes hardware acceleration straightforward. Although CARLE does not take advantage of CA-specific speedup strategies like the HashLife algorithm [15], it uses vectorization and GPU acceleration to achieve in excess of 20,000 updates of a 64 by 64 cell grid per second. Combined with the expressiveness and versatility of Life-like cellular automata, it is my hope that these characteristics will make CARLE an enabling addition to available programs for investigating machine creativity and exploration.

IV Carle’s Game and the Cellular Automata Reinforcement Learning Environment

IV-A What’s Included

Carle’s Game is built on top of CARLE, a flexible simulator for Life-like cellular automata written in Python [55] with Numpy [19] and PyTorch. As CARLE is formulated as a reinforcement learning environment, it returns an observation consisting of the on/off state of the entire CA grid at each time step, and accepts actions that specify which cells to toggle before applying the next Life-like rule updates. The action space is a subset of the observation space and the (square) dimensions of both can be user-specified, with default values of an observation space of 128 by 128 cells and an action space of 64 by 64 cells. Although both are naturally 2D, they are represented as 4-dimensional matrices (PyTorch Tensors), i.e. with dimensions N​x​1​x​H​x​WNx1xHxW, or number of CA grids by 1 by height by width. If CARLE receives an action specifying every cell in the action space to be toggled, the environment is reset and all live cells are cleared. In addition to the CA simulation environment, CARLE with Carle’s Game includes:

  • •

    Reward Wrappers: Growth, Mobiliy, and Exploration Bonuses. CARLE always returns a reward of 0.0, but several reward wrappers are provided as part of CARLE and Carle’s Game to provide motivation for agents to explore and create interesting patterns. Implemented reward wrappers include autoencoder loss and random network distillation exploration bonuses [4], a glider/spaceship detector, and a reward for occupying specific regions of the CA universe.

  • •

    Starter Agents: HARLI, CARLA, and Toggle. I have included several agent policies as a starting point for developing innovative new policies. These shouldn’t be expected to be ideal architectures and experimenters are encouraged to explore. Starter agents include Cellular Automata Reinforcement Learning Agent (CARLA), a policy based on continuous-valued cellular automata rules, and HARLI (Hebbian Automata Reinforcement Learning Improviser), a policy again implemented in continuous-valued neural CA that learns to learn by optimizing a set of Hebbian plasticity rules. Finally, Toggle is an agent policy that optimizes a set of actions directly, which are only applied at the first step of simulation.

  • •

    Starter Algorithm: Covariance Matrix Adapataion Evolution Strategy (CMA-ES). Carle’s Game includes an implementation of CMA-ES [18] for optimizing agent policies.

  • •

    Human-Directed Evolution. In addition to reward wrappers that can be applied to CARLE, Carle’s Game includes interactive evolution (implemented in a Jupyter notebook) to optimize agent policies with respect to human preferences.

IV-B Performance

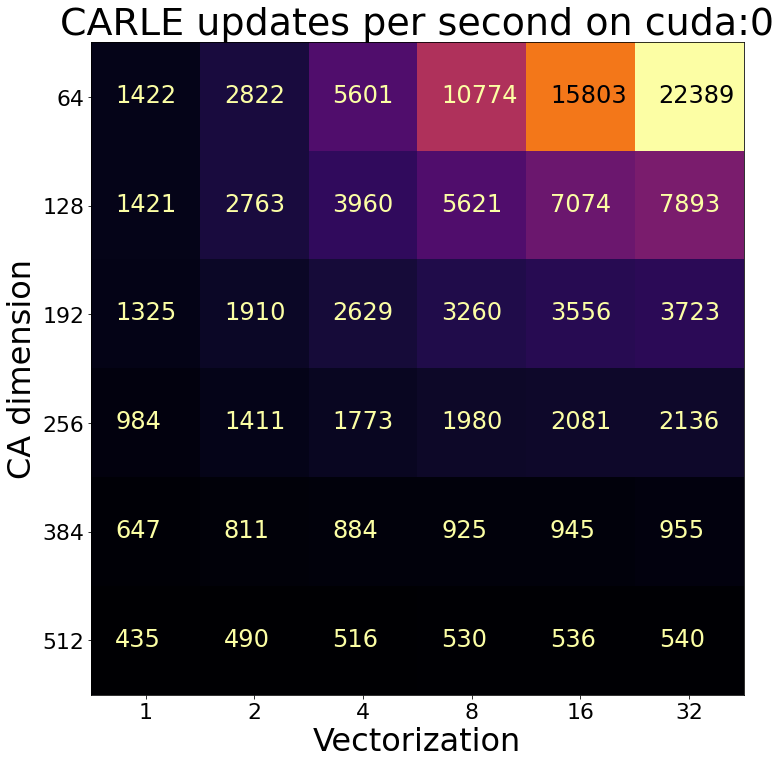
CARLE utilizes a combination of environment vectorization and GPU acceleration to achieve fast run times. On a consumer desktop with a 24-core processor (AMD 3960x Threadripper) and an Nvidia GTX 1060 GPU, CARLE runs at a speed of more than 22,000 updates per second of a 64 by 64 grid running Game of Life (B3/S23), amounting to about 90 million cell updates per second. Additional performance gains are likely available with lower precision operations with modern (RTX) GPU acceleration. To assess CARLE performance on other systems, I’ve provided the Jupyter notebook I used to create Figures 3 and 4, available at https://github.com/rivesunder/carles_game

Refer to caption

Figure 3: CARLE performance running on a 24-core CPU, measured in CA grid updates per second.

Refer to caption

Figure 4: CARLE performance running with device set to an Nvidida GTX 1060 GPU, measured in CA grid updates per second.

IV-C Reward Wrappers

The reward hypothesis, also sometimes known as the reinforcement learning hypothesis, has a somewhat ambiguous attribution [49, 24], but no matter who described the idea first it can be summarized as follows: intelligent behavior arises from an agent seeking to maximize the rewards it receives from its environment, or at least an agent’s goals can be fully described as an effort to maximize cumulative rewards. Whether this is reflective of real-world intelligence is a discussion for another time, but it does mean that open-ended environments returning no nominal reward are a challenge for most RL algorithms.

While CARLE is formulated as a reinforcement learning environment and uses the observation, reward, done, info = env.step(action) Gym API [3], the environment always returns a reward value of 0.0. Ultimately Carle’s Game uses crowd-sourced voting to evaluate user submissions, and judging machine creativity and exploration is likely to be just as subjective as judging the creative outputs of human artists and explorers. Designing a system of derived rewards, ideally in such a way as to instill an internal sense of reward for exploration, is a principal aspect of the Carle’s Game challenge. I have included several examples of potential reward wrappers that intervene between the universe of CARLE and agents interacting with it to add rewards for agents to learn from. These may be used directly and in combination to generate reward proxies or serve as a template and inspiration for custom reward wrappers.

Carle’s Game includes two implementation of exploration bonus rewards, one based on autoencoder loss and the other on random network distillation [4]. It also includes wrappers designed to reward moving machines such as spaceships and gliders and another that grants a reward for occupying specific cells in the top left corner. The corner bonus wrapper (Figure 7 yields negative reward for live cells in the right hand corners and a positive reward for live cells in top left corner, and along the diagonal of the grid universe between the action space and the top left corner. The speed reward wrapper calculates the change between the center of mass of all live cells between time steps, and while machine exploration and crowd evaluation of submissions are open-ended and subjective, developing agents that can re-discover known patterns-of-interest like spaceships and gliders provides an attractive first step that parallels early human exploration of Conway’s Life.

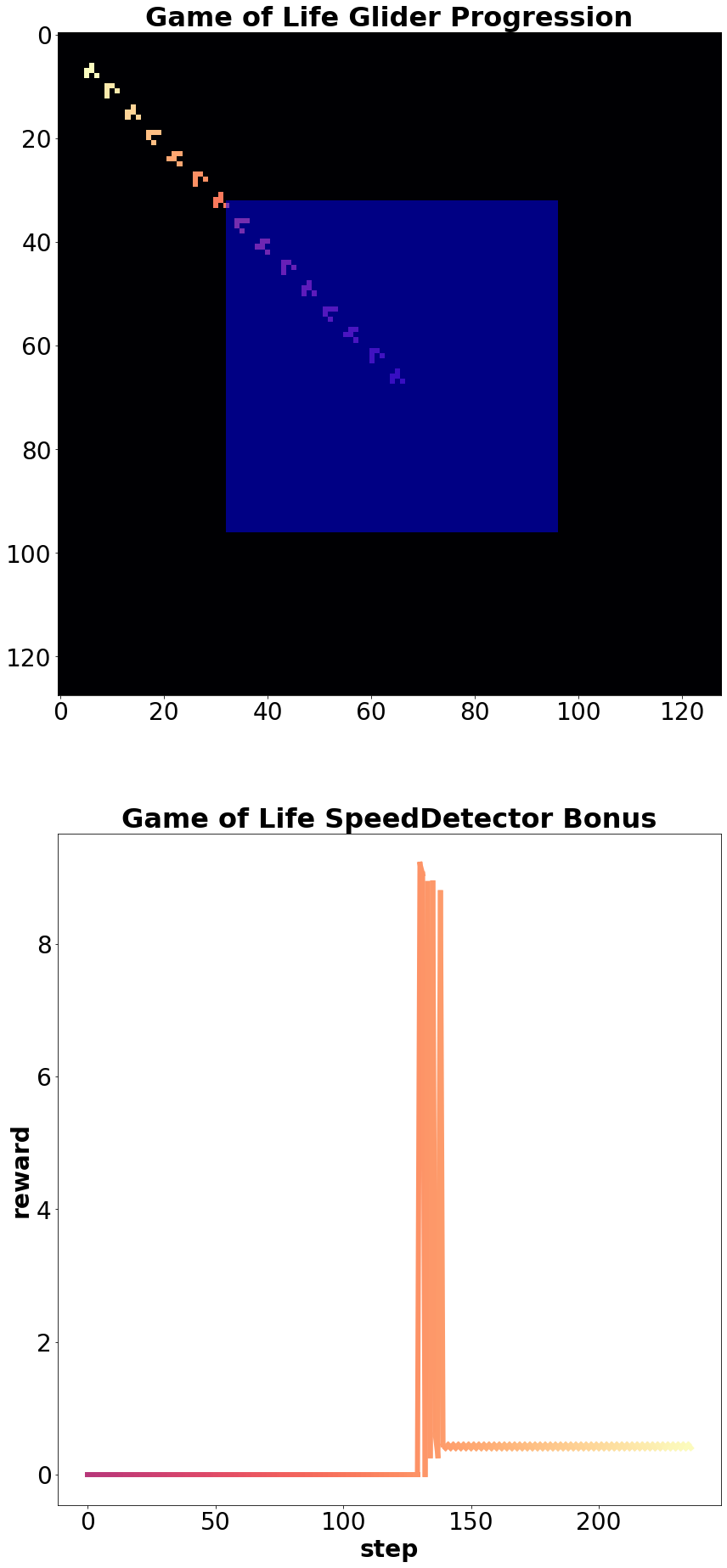
Refer to caption

Figure 5: Center of mass speed reward applied to a Game of Life glider. This reward wrapper ignores the cells in the action area (tinged in blue) when calculating the center of mass, resulting in a large reward spike when live cells first escape the action space, readily apparent in the reward curve. In this example, a Game of Life glider travels across the CA grid. After the glider exits the action space, the reward oscillates around the average speed of the object, reflecting the periodic diagonal motion of the glider.

An example of the speed-based reward wrapper applied to a Life glider is shown in Figure 5. This reward system considers cells inside of the action space to all have a central location of (0,0), leading to a large reward spike when an object first leaves the area available to agent manipulation. As CARLE simulates a toroidal CA universe, another reward spike occurs (not shown in Figure 5) when an object leaves by one edge and returns by another. This boundary crossing advantage was exploited by agents in experiments described in section V-A2.

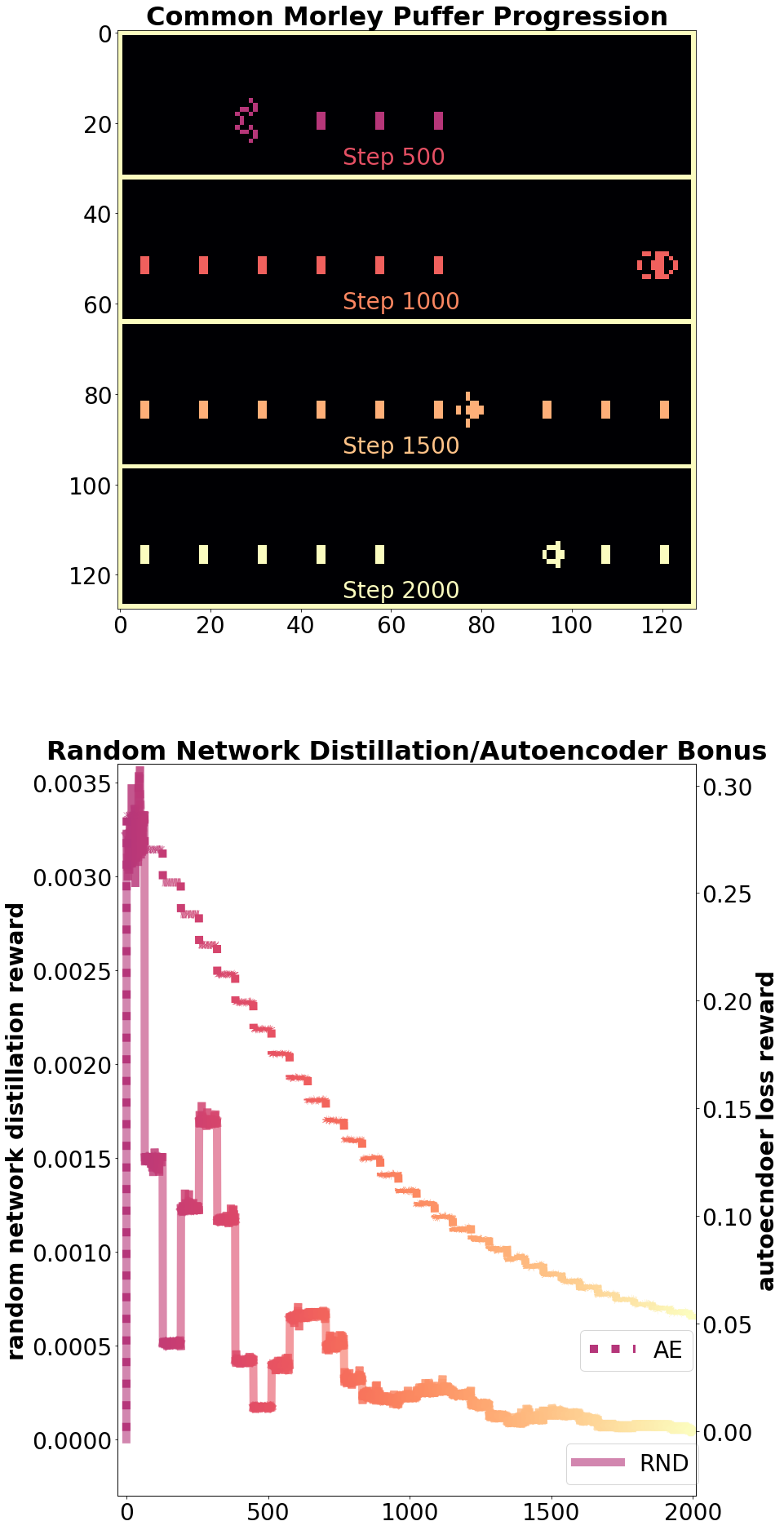
Refer to caption

Figure 6: Exploration rewards based on random network distillation and autoencoder loss. In random network distillation, a prediction model attemps to learn the input-output mapping of a random network, while autoencoder reward is based on the autoencoder loss of reconstructing environment observations directly. Snapshots of the progression of a puffer object are displayed with a color map corresponding to the color of the corresponding step in the reward curves, lighter coloration indicates later time steps. Note the different scales for random network distillation and autoencoder based rewards. Unlike the autoencoder loss reward, the implementation of random network distillation in Carle’s Game includes a fully-connected neural network layer at the output, allowing the reward system to be “surprised” and generate higher reward when the puffer disappears of the edge of the of the CA grid and re-appears on the opposite side.

Autoencoder loss and random network distillation approximate the novelty of a set of observations, as states that are visited less frequently lead to relatively poor performance compared to observations often encountered [4]. These offer slightly different behavior in practice. The autoencoder loss reward wrapper is implemented with a fully convolutional neural network model, and therefore exhibits translation equivariance in its response. Therefore the exploration bonus for a given pattern can be expected to be the same regardless of where on the CA grid the pattern appears. The implementation of random network distillation included with CARLE, on the other hand, includes fully connected neural networks in the final layers of both the random and the prediction network. The fully connected layers do not exhibit the translation equivariance of convolutional layers, so a jump in reward occurs when the Morley puffer leaves via one edge and appears on the opposite side of the grid, visible in Figure 6. Both examples are demonstrated for the same progression of a common puffer in the Morley/move rule set (B368/S245).

Refer to caption

Figure 7: A manually designed growth pattern that yields a positive cumulative reward from the CornerBonus wrapper (B3/S012345678 rules). The areas tinged in red generate a -1.0 reward for each live cell, the area tinged in purple returns a +1.0 reward for every live cell, and the area tinged in blue represents the action space.

V Carle’s Game Baselines

Refer to caption

Figure 8:

V-A Carle’s Game Baselines: Discovering the Morley Glider, Corner-Seeking, and Hacking the Mobility Reward

This section briefly presents CMA-ES training of agents using the corner bonus or a combination of the speed and random network distillation reward wrappers.

V-A1 Reaching for the Corner

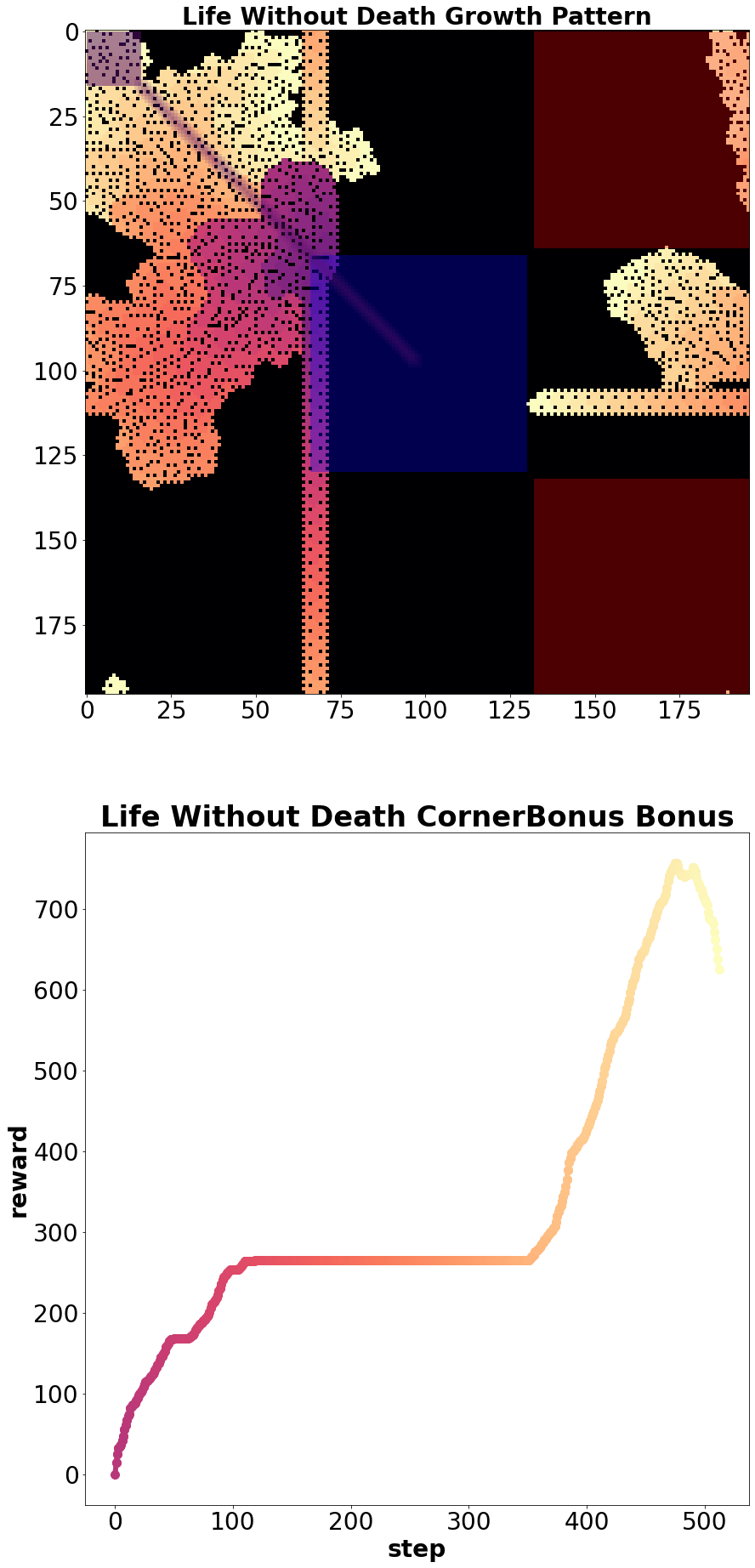
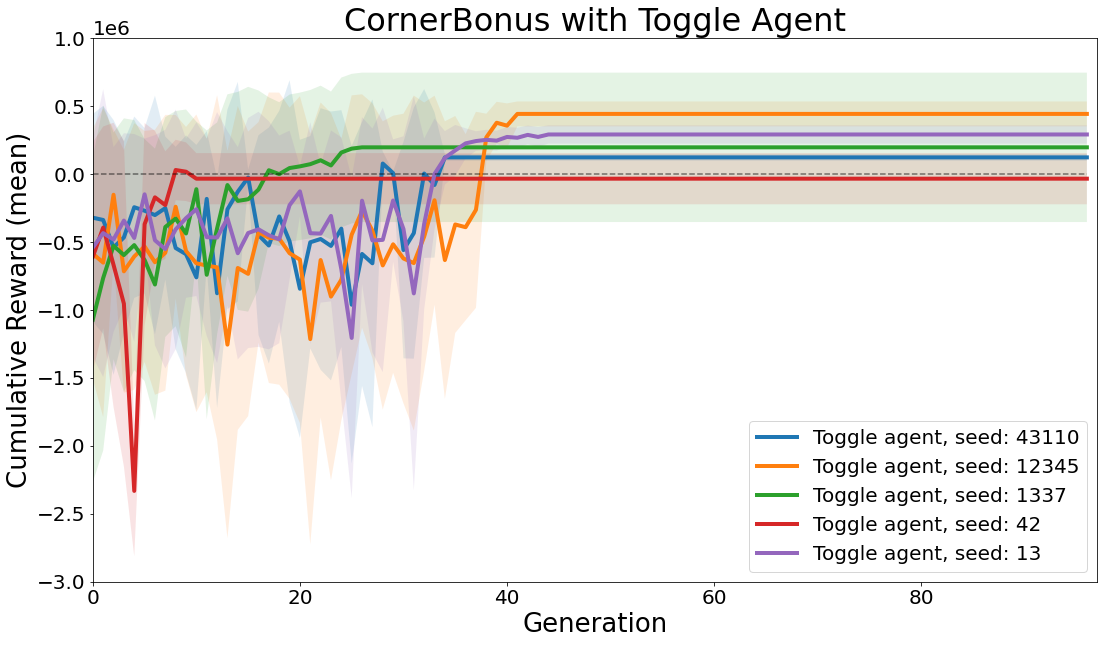
The first experiment used CMA-ES [18] to optimize patterns directly using the “Toggle” agent. The training curves are shown for 5 random seeds in Figure 8. Of the 5 random seeds, 4 experimental runs found a pattern that achieves a positive cumulative reward, i.e. a pattern that for the most part avoids the negative reward corners and occupies at least some of the positive reward cells. This experiment used the B3/S245678 growth set of rules, and an example of a manually designed pattern achieving positive cumulative reward on this task is shown in Figure 7.

V-A2 Rediscovering Gliders

A second experiment used the combination of random network distillation and a reward based on changing center of mass. This experiment was intended to investigate the ability of agents to learn to create gliders and small spaceships. Patterns were evolved directly using the Toggle agent, as well as dynamic agents CARLA and HARLI. This experiment was conducted using B368/S245 rules.

Experiments involving the Toggle agent managed to discover several patterns that produce gliders. It’s worth noting that in preliminary experiments optimizing the Toggle agent with the speed bonus directly, evolution runs with small population sizes and no exploration bonuses often got stuck in local optima and failed to find mobile patterns. Figure 9 demonstrates the discovery of a pattern that produces a glider, and another that produces a puffer.

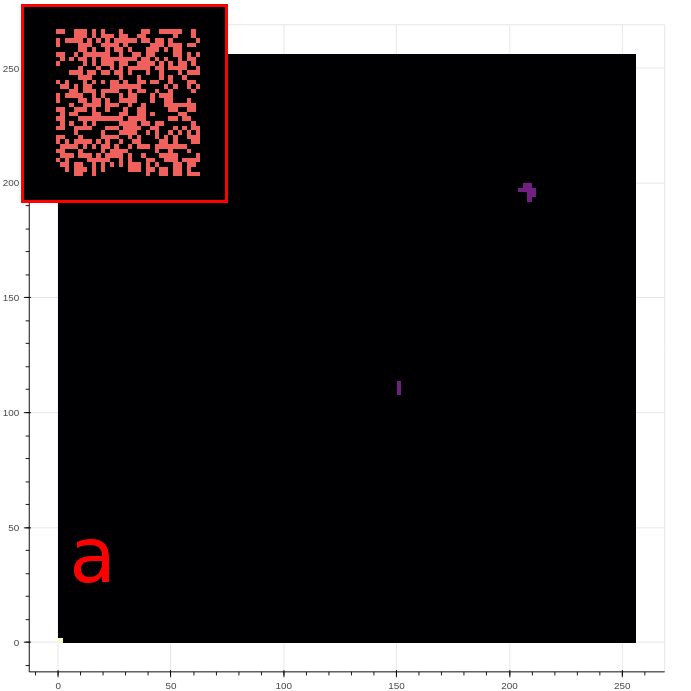
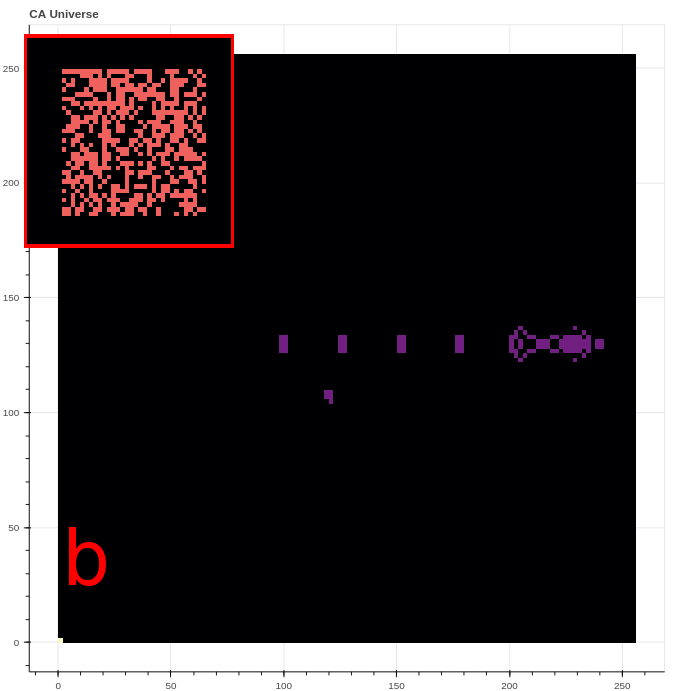
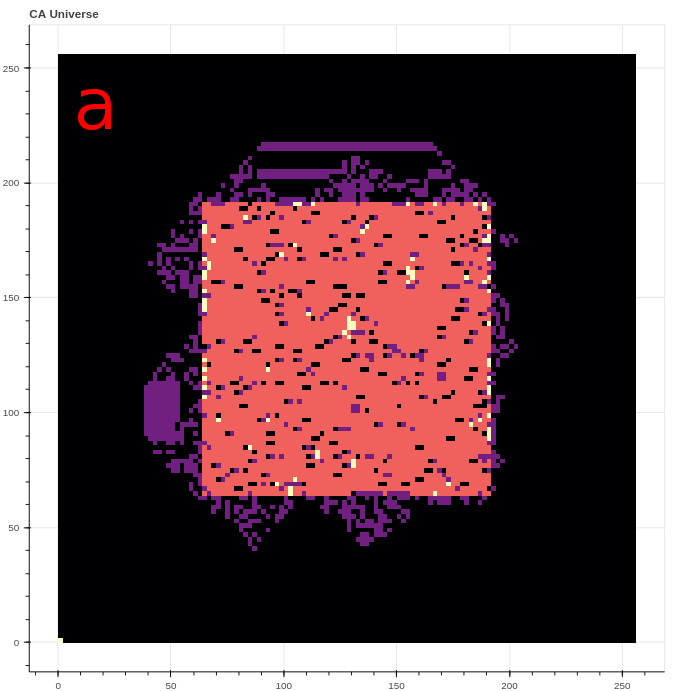
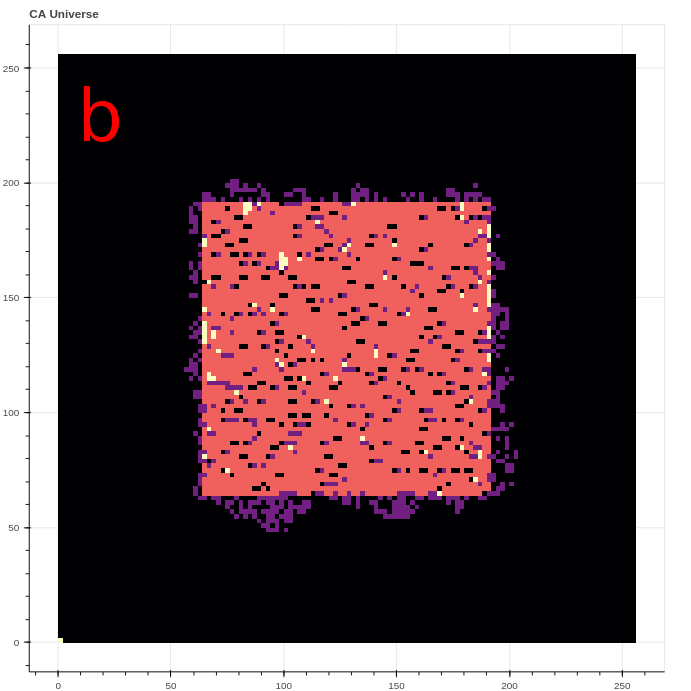
Refer to caption

Refer to caption

Figure 9: Patterns discovered by CMA-ES optimization of the Toggle agent. a) Pattern that produces a glider. b) Pattern that produces a puffer. The evolved patterns are shown inset in red.

Refer to caption

Refer to caption

Figure 10: Speed + RND reward strategies employed by CA-based agents CARLA and HARLI (CARLA examples shown here). a) Wave strategy: activating a line of cells at the action space boundaries creates a wave moving away from the action area, exploiting the center of mass calculations that consider all cells within the action space to be at (0,0)(0,0) b Chaotic boundary strategy: by continuously activating cells near the boundary, live cells continuously appear and disappear just outside of the action. So long as the live cells don’t perfectly balance each other out, this results in a changing center of mass and a continuous stream of small rewards. Unlike the Toggle agent, CARLA and HARLI are dynamic and can continuously perturb the action space, and are not constrained to learn to produce a persistent mobile pattern.

Perhaps unsurprisingly, the active agents trained in the speed reward experiment found surprising and unintended strategies to generate high rewards. The three strategies include resetting the environment, generating a “wave”, or maintaining a “chaotic boundary”. The reset strategy generates a high reward by clearing all live cells from the CA grid, effectively moving their center of mass from some finite value to the center of the grid. The wave strategy is often seen in the first few steps, and takes advantage of the “B3” rule contribution to produce a moving line of live cells visible in Figure 10a. The chaotic boundary strategy takes advantage of the jump in reward produced when live cells transiently appear just outside of the action space.

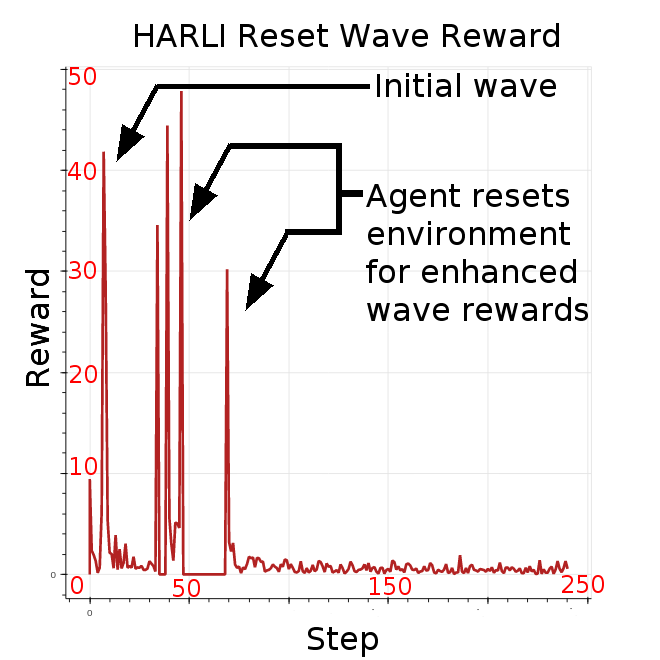
Refer to caption

Figure 11: The HARLI agent continuously modifies its parameters according to Hebbian rules with evolved weights. Crucial time points related to the environment reset strategy are called out with black arrows. Subsequent steps use the chaotic boundary strategy for a continuous stream of small rewards.

While HARLI and CARLA agents both exploit similar wave and chaotic boundary strategies, HARLI also is capable of resetting the environnment by setting all toggles to 1. The reset and wave strategy used together generate extremely high average rewards that may be 10 times greater than a common Life glider. An interactive demonstration of the reset-wave strategy at several evolutionary snapshots (trained with 4 different B3/Sxxx rules) can be found at https://github.com/riveSunder/harli_learning, and an example of this strategy under B368/S245 rules is presented in the reward plot in Figure 11.

VI Concluding Remarks

As introduced in this paper, CARLE along with Carle’s Game provides a fast and flexible framework for investigating machine creativity in open-ended environments. Optimizing initial patterns directly using the Toggle policy managed to re-discover both the glider and the common puffer in the B368/S245 Morley/Move rules. We also discussed two agents based on continuous-valued CA policies, which both managed to find effective (and frustratingly unintended) strategies for garnering rewards from a center of mass speed reward wrapper. These unintended strategies, which can be described as reward hacking exploits, underscore the challenge of providing motivation to machine learning agents in the face of complexity.

The environment CARLE is available at https://github.com/rivesunder/carle and the Carle’s Game challenge, including the code used to produce the experiments and figures described in this article, is maintained at https://github.com/rivesunder/carles_game. I intend to actively maintain these projects at least until the IEEE Conference on Games in August 2021, where Carle’s Game is among the competition tracks [21], and the code is permissively licensed under the MIT License.

References

  • [1] D. Amodei, C. Olah, J. Steinhardt, P. Christiano, J. Schulman, and D. Mané, “Concrete Problems in AI Safety,” arXiv:1606.06565 [cs], Jul. 2016, Accessed: May 25, 2021. [Online]. Available: http://arxiv.org/abs/1606.06565.
  • [2] C. Berner et al., “Dota 2 with Large Scale Deep Reinforcement Learning,” arXiv:1912.06680 [cs, stat], Dec. 2019, Accessed: May 29, 2021. [Online]. Available: http://arxiv.org/abs/1912.06680.
  • [3] G. Brockman et al., “OpenAI Gym,” arXiv:1606.01540 [cs], Jun. 2016, Accessed: May 30, 2021. [Online]. Available: http://arxiv.org/abs/1606.01540.
  • [4] Y. Burda, H. Edwards, A. Storkey, and O. Klimov, “Exploration by Random Network Distillation,” arXiv:1810.12894 [cs, stat], Oct. 2018, Accessed: May 25, 2021. [Online]. Available: http://arxiv.org/abs/1810.12894.
  • [5] B. Carter, “Large Number Coincidences and the Anthropic Principle in Cosmology,” in Confrontation of Cosmological Theories with Observational Data, M. S. Longair, Ed. Dordrecht: Springer Netherlands, 1974, pp. 291–298.
  • [6] B. W.-C. Chan, “Lenia - Biology of Artificial Life,” arXiv:1812.05433 [nlin], May 2019, Accessed: May 30, 2021. [Online]. Available: http://arxiv.org/abs/1812.05433.
  • [7] A. Channon. “The Artificial Evolution of Real Intelligence by Natural Selection.” 1998. http://www.channon.net/alastair/geb/ecal1997/channon\_ad\_ecal97.pdf [accessed 2021 May 30]
  • [8] “Re: List of the Turing-complete totalistic life-like CA” (discussion thread) at the ConwayLife.com forums https://www.conwaylife.com/forums/viewtopic.php?f=11&t=2597&sid=959494ddcb684d94aba719564af777cf [accessed 2021 May 30]
  • [9] M. Cook, “Universality in Elementary Cellular Automata,” Complex Systems, p. 40, 2004.
  • [10] T. F. Cooper and C. Ofria, “Evolution of Stable Ecosystems in Populations of Digital Organisms,” Artificial Life VIII, Standish, Abbass, Bedau (eds)(MIT Press) 2002. pp 227–232
  • [11] A. Ecoffet, J. Huizinga, J. Lehman, K. O. Stanley, and J. Clune, “Go-Explore: a New Approach for Hard-Exploration Problems,” arXiv:1901.10995 [cs, stat], 2019, Accessed: May 25, 2021. [Online]. Available: http://arxiv.org/abs/1901.10995.
  • [12] D. Eppstein, “Growth and Decay in Life-Like Cellular Automata,” arXiv:0911.2890 [nlin], pp. 71–97, 2010, doi: 10.1007/978-1-84996-217-9_6.
  • [13] Gardner, Martin. “MATHEMATICAL GAMES.” Scientific American, vol. 206, no. 3, 1962, pp. 138–154., https://www.jstor.org/stable/24937263. Accessed 30 May 2021.
  • [14] Gardner, Martin (October 1970). “Mathematical Games - The Fantastic Combinations of John Conway’s New Solitaire Game ’Life’”. Scientific American (223): 120–123. Availabe at https://web.stanford.edu/class/sts145/Library/life.pdf [accessed 2021 May 31]
  • [15] R. Wm. Gosper, “Exploiting regularities in large cellular spaces,” Physica D: Nonlinear Phenomena, vol. 10, no. 1–2, pp. 75–80, Jan. 1984, doi: 10.1016/0167-2789(84)90251-3.
  • [16] D. Grbic, R. B. Palm, E. Najarro, C. Glanois, and S. Risi, “EvoCraft: A New Challenge for Open-Endedness,” p. 17.
  • [17] D. Ha, “Reinforcement Learning for Improving Agent Design,” Artificial Life, vol. 25, no. 4, pp. 352–365, Nov. 2019, doi: 10.1162/artl_a_00301.
  • [18] N. Hansen, “The CMA Evolution Strategy: A Tutorial,” arXiv:1604.00772 [cs, stat], Apr. 2016, Accessed: May 30, 2021. [Online]. Available: http://arxiv.org/abs/1604.00772.
  • [19] C.R. Harris, K.J. Millman, S.J. van der Walt. et al. “Array programming with NumPy,” Nature 585, 357–362 (2020). DOI: 0.1038/s41586-020-2649-2. Available: https://www.nature.com/articles/s41586-020-2649-2
  • [20] A. Hintze, “Open-Endedness for the Sake of Open-Endedness,” Artificial Life, vol. 25, no. 2, pp. 198–206, May 2019, doi: 10.1162/artl_a_00289.
  • [21] https://ieee-cog.org/2021/index.html#competitions_section
  • [22] D. Kipping, “An objective Bayesian analysis of life’s early start and our late arrival,” Proc Natl Acad Sci USA, vol. 117, no. 22, pp. 11995–12003, Jun. 2020, doi: 10.1073/pnas.1921655117.
  • [23] J. Lehman et al., “The Surprising Creativity of Digital Evolution: A Collection of Anecdotes from the Evolutionary Computation and Artificial Life Research Communities,” Artificial Life, vol. 26, no. 2, pp. 274–306, May 2020, doi: 10.1162/artl_a_00319.
  • [24] M. Littman. “Michael Littman: The Reward Hypothesis”, https://www.coursera.org/lecture/fundamentals-of-reinforcement-learning/michael-littman-the-reward-hypothesis-q6x0e [accessed 2021 May 30]
  • [25] J. S. McCaskill and N. H. Packard, “Analysing Emergent Dynamics of Evolving Computation in 2D Cellular Automata,” in Theory and Practice of Natural Computing, vol. 11934, C. Martín-Vide, G. Pond, and M. A. Vega-Rodríguez, Eds. Cham: Springer International Publishing, 2019, pp. 3–40.
  • [26] Mordvintsev, et al., “Growing Neural Cellular Automata”, Distill, 2020. https://distill.pub/2020/growing-ca/ [accessed 2021 May 30]
  • [27] Niklasson, et al., “Self-Organising Textures”, Distill, 2021. https://distill.pub/selforg/2021/textures/ [accessed 2021 May 30]
  • [28] C. Ofria and C. O. Wilke, “Avida: Evolution Experiments with Self-Replicating Computer Programs,” in Artificial Life Models in Software, A. Adamatzky and M. Komosinski, Eds. London: Springer London, 2005, pp. 3–35.
  • [29] A. Paszke et al., “PyTorch: An Imperative Style, High-Performance Deep Learning Library,” arXiv:1912.01703 [cs, stat], Dec. 2019, Accessed: May 31, 2021. [Online]. Available: http://arxiv.org/abs/1912.01703.
  • [30] S. Rafler, “Generalization of Conway’s ‘Game of Life’ to a continuous domain - SmoothLife,” arXiv:1111.1567 [nlin], Dec. 2011, Accessed: May 31, 2021. [Online]. Available: https://arxiv.org/abs/1111.1567.
  • [31] Randazzo, et al., “Self-classifying MNIST Digits”, Distill, 2020. https://distill.pub/2020/selforg/mnist/ [accessed 2021 May 30]
  • [32] Randazzo, et al., “Adversarial Reprogramming of Neural Cellular Automata”, Distill, 2021. https://distill.pub/selforg/2021/adversarial/ [accessed 2021 May 30]
  • [33] T. Ray. “An Approach to the Synthesis of Life.” Artificial Life ll, SFI Studies in the Sciences of Complexity, vol. X, edited by C. G. Langton, C. Taylor, J. D. Farmer, & S. Rasmussen, Addison-Wesley, 1991. http://life.ou.edu/pubs/alife2/Ray1991AnApproachToTheSynthesisOfLife.pdf [accessed 2021 May 30]
  • [34] P. Rendell, Turing Machine Universality of the Game of Life, vol. 18. Cham: Springer International Publishing, 2016.
  • [35] J. Schaeffer et al., “Checkers Is Solved,” Science, vol. 317, no. 5844, pp. 1518–1522, Sep. 2007, doi: 10.1126/science.1144079.
  • [36] J.L. Schiff, “Introduction to cellular automata”, 2005. http://psoup.math.wise.edu/491 [accessed 2021 May]
  • [37] J. Schrittwieser et al., “Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model,” Nature, vol. 588, no. 7839, pp. 604–609, Dec. 2020, doi: 10.1038/s41586-020-03051-4.
  • [38] D. Silver et al., “Mastering the game of Go with deep neural networks and tree search,” Nature, vol. 529, no. 7587, pp. 484–489, Jan. 2016, doi: 10.1038/nature16961.
  • [39] D. Silver et al., “Mastering the game of Go without human knowledge,” Nature, vol. 550, no. 7676, pp. 354–359, Oct. 2017, doi: 10.1038/nature24270.
  • [40] D. Silver et al., “A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play,” Science, vol. 362, no. 6419, pp. 1140–1144, Dec. 2018, doi: 10.1126/science.aar6404.
  • [41] K. Sims, “Evolving 3D Morphology and Behavior by Competition,” 1994. p. 12.
  • [42] K. Sims. Evolved Virtual Creatures. 1994. http://www.karlsims.com/evolved-virtual-creatures.html [Accessed 2021 May 30]
  • [43] A. Singh, L. Yang, K. Hartikainen, C. Finn, and S. Levine, “End-to-End Robotic Reinforcement Learning without Reward Engineering,” arXiv:1904.07854 [cs, stat], May 2019, Accessed: May 25, 2021. [Online]. Available: https://arxiv.org/abs/1904.07854.
  • [44] Department of EECS (Computer Science Division) University of Central Florida, Orlando, FL 32816, L. Soros, and K. Stanley, “Identifying Necessary Conditions for Open-Ended Evolution through the Artificial Life World of Chromaria,” in Artificial Life 14: Proceedings of the Fourteenth International Conference on the Synthesis and Simulation of Living Systems, Jul. 2014, pp. 793–800, doi: 10.7551/978-0-262-32621-6-ch128.
  • [45] L. B. Soros, J. K. Pugh, and K. O. Stanley, “Voxelbuild: a minecraft-inspired domain for experiments in evolutionary creativity,” in Proceedings of the Genetic and Evolutionary Computation Conference Companion, Berlin Germany, Jul. 2017, pp. 95–96, doi: 10.1145/3067695.3075605.
  • [46] L. Spector, J. Klein, and M. Feinstein, “Division blocks and the open-ended evolution of development, form, and behavior,” in Proceedings of the 9th annual conference on Genetic and evolutionary computation - GECCO ’07, London, England, 2007, p. 316, doi: 10.1145/1276958.1277019.
  • [47] K. O. Stanley, “Why Open-Endedness Matters,” Artificial Life, vol. 25, no. 3, pp. 232–235, Aug. 2019, doi: 10.1162/artl_a_00294. http://cognet.mit.edu/sites/default/files/artl_a_00294.pdf
  • [48] J. Suarez, Y. Du, P. Isola, and I. Mordatch, “Neural MMO: A Massively Multiagent Game Environment for Training and Evaluating Intelligent Agents,” arXiv:1903.00784 [cs, stat], Mar. 2019, Accessed: May 30, 2021. [Online]. Available: https://arxiv.org/abs/1903.00784.
  • [49] R. Sutton. “The reward hyptohesis”, http://incompleteideas.net/rlai.cs.ualberta.ca/RLAI/rewardhypothesis.html [accessed 2021 May 30]
  • [50] C. J. Tan, “Deep Blue: computer chess and massively parallel systems (extended abstract),” in Proceedings of the 9th international conference on Supercomputing - ICS ’95, Barcelona, Spain, 1995, pp. 237–239, doi: 10.1145/224538.224566.
  • [51] T. Toffoli and N. Margolus, Cellular Automata Machines: A New Environment for Modeling. The MIT Press, 1987.
  • [52] O. Vinyals et al., “Grandmaster level in StarCraft II using multi-agent reinforcement learning,” Nature, vol. 575, no. 7782, pp. 350–354, Nov. 2019, doi: 10.1038/s41586-019-1724-z.
  • [53] S. Wolfram. “Statistical mechanics of cellular automata.” Reviews of Modern Physics 55, 1983. 601-644.
  • [54] S. Wolfram. “Universality and complexity in cellular automata.” Physica D: Nonlinear Phenomena 10, 1983. 1-35.
  • [55] G. Van Rossum., F.L. Drake. “Python 3 Reference Manual,” Python Software Foundation. 2009. Available: https://docs.python.org/3/reference/index.html
  • [56] L. Yaeger. “Computational Genetics, Physiology, Metabolism, Neural Systems, Learning, Vision, and Behavior or PolyWorld: Life in a New Context.” 1997.